Contractile Units in Disordered Actomyosin Bundles Arise from F-Actin Buckling

Abstract

Bundles of filaments and motors are central to contractility in cells. The classic example is striated muscle, where actomyosin contractility is mediated by highly organized sarcomeres which act as fundamental contractile units. However, many contractile bundles in vivo and in vitro lack sarcomeric organization. Here we propose a model for how contractility can arise in bundles without sarcomeric organization and validate its predictions with experiments on a reconstituted system. In the model, internal stresses in frustrated arrangements of motors with diverse velocities cause filaments to buckle, leading to overall shortening. We describe the onset of buckling in the presence of stochastic motor head detachment and predict that buckling-induced contraction occurs in an intermediate range of motor densities. We then calculate the size of the “contractile units” associated with this process. Consistent with these results, our reconstituted actomyosin bundles show contraction at relatively high motor density, and we observe buckling at the predicted length scale.

Contractility arising from interactions between myosin molecular motors and polar actin filaments (F-actin) is used ubiquitously by cells to build tension and drive morphological changes [1]. Such force transmission from molecular to cellular length scales is well understood in striated muscle, where it critically relies on highly organized structures known as sarcomeres [2]. In sarcomeres, myosin motors are restricted to the pointed end of F-actin, while passive actin cross-linkers are present at the barbed end. This arrangement is crucial to their contraction mechanism, as shown in Fig. 1(a). However, many contractile actomyosin bundles found in vivo, such as smooth muscle fibers [3], graded polarity bundles [4], and the contractile ring [5], lack a sarcomeric organization. Most recently, we have shown that in vitro bundles lacking apparent sarcomeric organization can also contract [6] [e.g., Fig. 1(b)]. In these disparate systems, contraction occurs with a well-defined contraction velocity per unit length, suggesting that contractile bundles can be meaningfully divided into elementary units that are arranged in series [5–7]. The mechanisms giving rise to such units in the absence of sarcomeric organization are not understood.

Fig. 1.

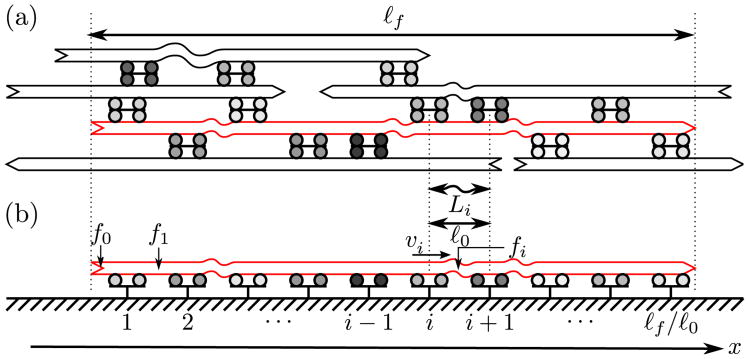
Contraction in actomyosin bundles. (a) Sarcomeric structure as in striated muscle. As motors tend to move toward the filament barbed ends, the sarcomeric structure imposes that each contractile unit (sarcomere) contracts. (b) Bundle devoid of sarcomeric organization or passive cross-linkers, as in our experiments. (c) Motors and polar filaments induce local contraction or extension depending on the geometry of their assembly (filament polarity always dictates the direction of motion [8]). (d) Time-lapse images of a bundle comprised of F-actin and fluorescent myosin thick filaments (inverted contrast) with ℓ₀ = 540 nm. The initially wavy bundle becomes taut following the addition of 1 mM ATP at t = 0 s, indicating contraction. Scale bar, 5 μm. (e) Similar experiment with ℓ₀ = 1.5 μm, showing no contraction. Scale bar as in (d). See also movie S1 [18]. (f) Bundle contraction as a function of ℓ₀. Bars indicate standard deviation (n ≥ 25).

Much theoretical work on nonsarcomeric actomyosin assemblies posits contractility as a fundamental assumption, and predicts larger-scale effects such as polarity organization [9], the appearance of topological defects [10], active stiffening [11], and oscillatory behavior in cells [12]. Models that address the microscopic origin of contractility assume that myosin motors dwell at the barbed ends of F-actin, thus acting as transient static cross-linkers [13]. This generates sufficient sarcomerelike organization to elicit contraction [14]. Experimental evidence for this behavior is unfortunately lacking, and it is thus important to investigate alternative routes to contractility.

In considering such mechanisms, it is important to recognize that actomyosin interactions can a priori elicit extension just as well as contraction. Figure 1(c) illustrates this using two elementary bundles, each made of two polar filaments—representing F-actin—and one motor—representing a whole myosin thick filament, itself comprising numerous individual myosin heads; we use this definition of a “motor” throughout. These elementary bundles contract when the motor is located in the vicinity of the filament pointed ends, but extend when it is close to the barbed ends. Overall contractility in nonsarcomeric bundles requires that the symmetry between these two competing tendencies be broken. We show in Ref. [15] that this necessitates (1) a dispersion of unloaded velocities to be present among the motors (as observed experimentally [16]) and (2) an asymmetric response of the filaments to longitudinally applied stresses, e.g., a tendency to yield under compression while resisting extension.

In this Letter, we use theory and experiments to demonstrate a mechanism for nonsarcomeric contractility compatible with these constraints. We first show experimentally that contraction in reconstituted actomyosin bundles is accompanied by F-actin buckling, an instance of the asymmetric filament response discussed above. We then investigate the general consequences of asymmetric filament response theoretically by considering the buildup of forces in a bundle with randomly arranged motors. We predict that buckling yields contraction, and occurs in an intermediate range of motor density. We also calculate a characteristic length scale between two buckles, which provides a natural size for a contractile unit. These predictions are consistent with experimental observations, suggesting that buckling underlies contractility in nonsarcomeric actomyosin bundles.

To form reconstituted actomyosin bundles, we follow the protocol described in Ref. [6]. We incubate F-actin with length ℓ_f ≃ 5 μm with smooth muscle myosin thick filaments of length ≃ 300 nm in a buffer lacking adenosine triphosphate (ATP) such that thick filaments cross-link F-actin with high affinity. In this system, the dispersion of motor velocities necessary for contraction likely arises from the variation in number of myosin heads in the thick filaments. While flexible motors have been considered as a basis for contraction [17], this is unlikely to apply here as thick filaments are significantly more rigid than F-actin. The bundle lengths range from 10 to 100 μm with 4–6 F-actin per bundle cross-section, and no sarcomeric organization is observed. By varying the concentration of myosin filaments, the average spacing ℓ₀ between two consecutive myosin filaments can be varied from 390 nm to 5.3 μm.

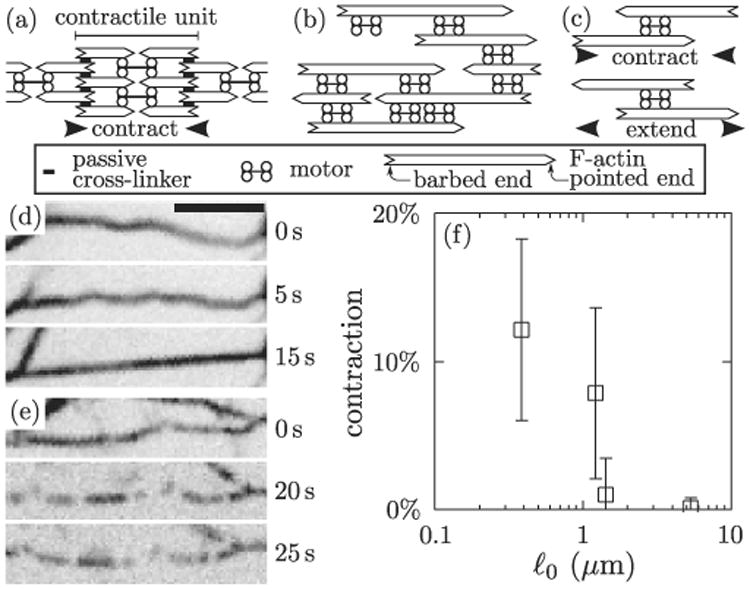
Once the bundles are formed, we perfuse a buffer containing 1 mM ATP, which causes bundles formed with high myosin density (ℓ₀ = 540 nm) to shorten by ≃ 10% rapidly (100–600 nm · s⁻¹) [Fig. 1(d) and movie S1 [18]]. In contrast, contraction does not occur at low myosin density (ℓ₀ = 1.5 μm) [Fig. 1(e) and movie S1 [18]]. A sharp transition between those two behaviors is observed at ℓ₀ = 1.3 μm [Fig. 1(f)].

To better understand the underpinnings of contractility in this system, we next examine individual bundles and observe F-actin buckling coincident with contraction [Fig. 2(a); movie S2 [18]]. Prior to ATP addition, compact bundles with aligned F-actin are observed. Upon ATP addition, the frequency of buckles increases rapidly during contraction, and then diminishes once contraction stops [Fig. 2(b)]. These F-actin buckles are dynamic, with their amplitude, curvature, and location changing over time.

Fig. 2.

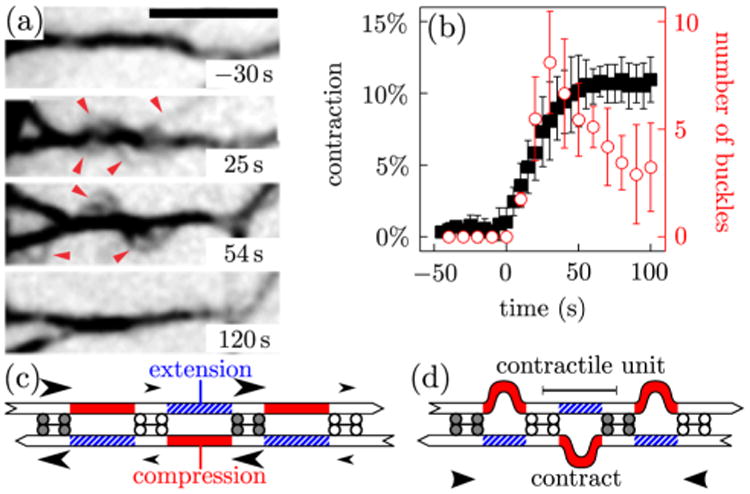
Buckling in nonsarcomeric contractile actomyosin bundles. (a) Time-lapse images of fluorescent actin (inverted contrast) showing F-actin buckling (arrowheads) following the addition of 1 mM ATP at t = 0 s. Scale bar, 5 μm. See also movie S2 [18]. (b) Relative contraction (filled squares) and number of F-actin buckles (open circles) as a function of time. Data show mean ±sd averaged over n = 3 bundles with ℓ₀ ≃ 1 μm. (c) The presence of fast (gray) and slow (white) motors generically induce compressive (solid red) and extensile (hatched blue) stresses in filaments. (d) Buckling of the compressed filaments leads to an overall shortening of the bundle.

Qualitatively, the relationship between buckling and contraction can be understood as follows. Consider two antiparallel filaments interacting through several different motors with distinct speeds [Fig. 2(c)]. As motors start to move relative to the filaments, stresses build in sections of the filament flanked by motors with different speeds. When the flanking motor proximal to the barbed end is faster than that proximal to the pointed end, compression arises. When it is slower, tension arises. Filament buckling breaks the symmetry between these respective tendencies to contraction and extension. Indeed, following buckling of the compressed filament sections, fast motors are free to move quickly while the others move slowly. This results in the growth of the compressed sections and shrinkage of the extended ones, and thus in overall bundle contraction [Fig. 2(d)]. The region centered around each buckle thus plays the role of a contractile unit, whose typical size is equal to the distance ℓ_B between two buckles.

In this picture, the contractile behavior of the bundle hinges on the ability of the motors to induce filament buckling. At high motor density, we expect the bundle to be so strongly cross-linked that buckling becomes impossible despite the sizable stresses induced by a large number of motors. At low motor density, we expect that stochastic detachment of the motors undermines stress buildup and thus prevents buckling. Here we present a mathematical model to predict the range of myosin densities enabling buckling and the contractile unit length ℓ_B. These results are then compared with the observations in Figs. 1 and 2 to validate the proposed contraction mechanism.

The key assumptions of our model are that (1) motors have a dispersion in their unloaded velocities, (2) a section of filament between two motors buckles above a certain threshold force F_B, and (3) motors intermittently detach from the filaments, thus allowing local stress relaxation. We consider a bundle of weakly deformed filaments and ask whether the forces developing within it are sufficient to induce buckling [Fig. 3(a)].

Fig. 3.

Stress buildup in bundles with nonidentical motors. (a) In a bundle with motors having nonidentical velocities (shades of gray), filaments of lengths ≈ ℓ_f are subjected to random motor forces at points ≈ ℓ₀ apart distributed throughout their length. (b) Prior to contraction, the environment of a filament of interest (red, delimited by dotted lines) can be approximated by a collection of evenly spaced motors (shades of gray).

To this end, we focus on a single filament of length ℓ_f and approximate its surroundings by an effective medium composed of evenly spaced pointlike motors separated by a distance ℓ₀ ≪ ℓ_f [Fig. 3(b)]. This divides the filament into discrete sections, which we label by i = 0,…, ℓ_f/ℓ₀. We take into account the possibility that the filaments are not straight, but bend away from the x axis, implying that the contour length L_i of filament section i can be larger than ℓ₀. Defining f_i as the tension of filament section i (f_i < 0 for a compressed filament section), we expand its force-extension relationship for small deformations,

$$L_i=L_i(f_i=0)-c{f}_i,$$ (1)

where c > 0 is the filament compliance. We refer to the motor flanked by filament sections i − 1 and i as “motor i,” and describe its operation by the simplified force-velocity relationship

$$f_{i-1}-f_i=F_i-\chi {\upsilon }_i.$$ (2)

Here υ_i denotes the local velocity of the filament at the location of motor i and χ > 0 is the motor susceptibility. Equations (1) and (2) yield a local relaxation time scale τ_r = χc/2. The time-independent stall force of motor i is denoted by F_i in Eq. (2), and is drawn from a random distribution satisfying

$${\overline{F}}_i=F_S\text{and}\overline{F_i{F}_j}-{\overline{F}}_i{\overline{F}}_j=\delta F_S^2{\delta }_{ij},$$ (3)

where bars denote averages over the motor distribution.

As a result, different motors have different unloaded velocities F_i/χ as required for contraction. Owing to the conservation of filament mass,

$$\frac{d{L}_i}{\mathit{\text{dt}}}={\upsilon }_i-{\upsilon }_{i+1}.$$ (4)

Finally, a motor bound to several filaments as in Fig. 3(a) can transiently detach from one while still holding onto the others. We thus let each motor i randomly detach from the filament with a constant rate 1/τ_d. Following detachment, local filament stresses relax instantaneously, yielding f_i = f_i−1 = (f_i + f_i−1)/2. The motor then reattaches after a time much shorter than τ_r and τ_d. Since a motor in a dense bundle is typically close to several filaments, the probability that it detaches from all filaments at the same time and leaves the bundle is negligible. We denote by 〈…〉 the average over the Poisson process of motor detachment.

We obtain the space and time evolution of the filament tension f(x, t) in the continuum limit i → x/ℓ₀ by combining Eqs. (1)–(4) and averaging over motor detachment,

$${\partial }_t\langle f\rangle -D{\partial }_x^2\langle f\rangle =({\ell }_0/2{\tau }_r){\partial }_{x}F,$$ (5)

where $D={\ell }_0^2({\tau }_r^{-1}+{\tau }_d^{-1})/2$. The right-hand side of Eq. (5) involves the spatial gradient of the stall force F(x), reflecting the fact that nonidentical motors lead to force buildup. This effect competes with the relaxation of filament forces through motor detachment, which enters through the diffusion term $D{\partial }_x^2\langle f\rangle$.

An initially relaxed filament [f(x, t = 0) = 0] experiences a vanishing average force 〈f̄〉(x, t) = 0 throughout its dynamics. To quantify the magnitude of the motor-induced stress, we use Eqs. (1)–(4) and average over motor detachment to calculate the rms filament force in the continuum limit,

$${(\overline{\langle f^2\rangle })}^{1/2}=f_{\infty }{\left\{\sum _{n\in Z\ast }\right[\frac{3}{n^2{\pi }^2}{(1-e^{-n^{2}Dt/{(2\pi {\ell }_f)}^2})}^2\left]\right\}}^{1/2}.$$ (6)

This force increases monotonically from zero at t = 0 to f_∞ = (ℓ_f/12ℓ₀)^1/2 × δF_S/(1 + τ_r/τ_d) at t = ∞ [Figs. 4(a) and 4(b)]. We next estimate the dependence of the ratio τ_r/τ_d on the experimentally accessible parameter ℓ₀. A wormlike chain model for filament elasticity yields $c\approx {\ell }_0^4/k_{B}T{\ell }_p^2$ where ℓ_p is the filament persistence length [19], and we approximate χ ≈ F_S/υ, where υ is a characteristic motor velocity. This implies ${\tau }_r/{\tau }_d\approx {({\ell }_0/{\ell }_0^{\ast })}^4$, with ${\ell }_0^{\ast }={(k_{B}T{\ell }_p^2\upsilon {\tau }_d/F_S)}^{1/4}$. We can thus distinguish two regimes for the steady-state force f_∞ [Fig. 4(a)]. For ${\ell }_0\ll {\ell }_0^{\ast }$, detachment events are rare compared to the time τ_r needed for the force to recover from such an event, and f_∞ is not affected by them. For ${\ell }_0\gg {\ell }_0^{\ast }$, f_∞ quickly decreases with increasing ℓ₀ as detachment becomes much faster than recovery.

Fig. 4.

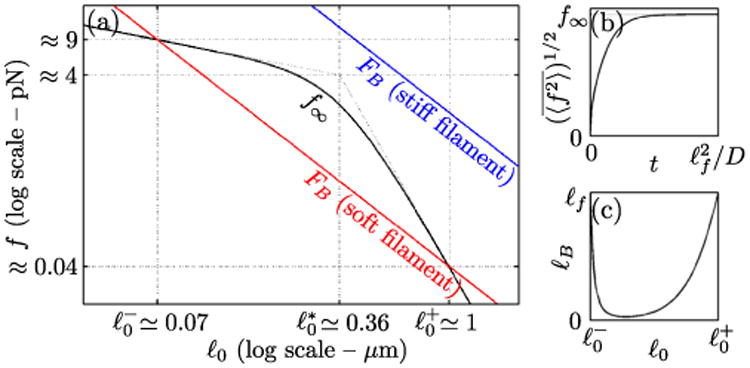
Model predictions for filament force buildup. (a) Black line: steady-state filament force f_∞, as a function of motor spacing ℓ₀ [Eq. (6)]. For ${\ell }_0\ll {\ell }_0^{\ast }$ and ${\ell }_0\gg {\ell }_0^{\ast }$, $f_{\infty }\propto {\ell }_0^{-1/2}$ and ${\ell }_0^{-9/2}$, respectively. Colored straight lines: buckling force $F_B\propto {\ell }_0^{-2}$. (b) Typical filament force ${(\overline{\langle f^2\rangle })}^{1/2}$ as a function of time [Eq. (6)]. (c) Contractile unit size ℓ_B as a function of ℓ₀ as in Eq. (8) (ℓ_f ≃ 5 μm).

Up to a prefactor of order one, contraction proceeds as in Figs. 2(c) and 2(d) if $f_{\infty }>F_B\approx k_{B}T{\ell }_p/{\ell }_0^2$ [19]. Comparing f_∞ to F_B as in Fig. 4(a), we find a threshold stiffness above which buckling cannot occur (as exampled by the upper blue line). Reasonable values for our actomyosin system are ℓ_p ≃ 10 μm, υ ≃ 200 nm · s⁻¹, δF_S ≈ F_S ≃ 1 pN, and τ_d ≃ 200 ms based on the typical time scales involved in the myosin mechanochemical cycle. Since τ_r ≳ τ_d in our experiments and detached motors reattach in ≈ 1 ms [20], our previous assumption of fast motor reattachment is justified. These values put us in the soft filament regime defined by ${\ell }_p\ll \partial F_S^4{L}_f^2{(\upsilon {\tau }_d)}^{3/2}/k_B{T}^{5/2}{F}_S^{3/2}\simeq 20\text{cm}$ (lower red line). In this regime, the lines representing F_B and f_∞ intersect at

$${\ell }_0^{-}={(k_{B}T{\ell }_p/\delta F_S{\ell }_f^{1/2})}^{2/3}\simeq 70\text{nm},$$ (7a)

$${\ell }_0^{+}={({\ell }_f^{1/2}\upsilon {\tau }_d{\ell }_p\delta F_S/F_S)}^{2/5}\simeq 1\mu \mathrm{m},$$ (7b)

meaning that buckling and contraction occur for ${\ell }_0^{-}<{\ell }_0<{\ell }_0^{+}$. This range reflects the fact that strong cross-linking ( ${\ell }_0<{\ell }_0^{-}$) suppresses buckling while sparse motors ( ${\ell }_0>{\ell }_0^{+}$) are undermined by stochastic detachment. While the regime ${\ell }_0\simeq {\ell }_0^{-}$ is not accessible experimentally, the predicted value for ${\ell }_0^{+}$ is strikingly similar to the motor spacing at which the breakdown of contraction is observed in Fig. 1(f) (1.3 μm), suggesting that the proposed mechanism is a good description of our experiments.

To characterize the contractile units resulting from this mechanism when ${\ell }_0^{-}<{\ell }_0<{\ell }_0^{+}$, we turn to the transient regime leading up to filament buckling. The filament force profile as a function of x is initially flat, and subsequently coarsens into a random walk for t = +∞. According to Eq. (5), this coarsening occurs diffusively with diffusion coefficient D. The typical filament forces at time $t\ll {\ell }_f^2/D$ are thus of order $f_{\infty }{(\sqrt{Dt}/{\ell }_f)}^{1/2}$. We denote the time that this force reaches the buckling threshold F_B by t_B, following which contraction proceeds as in Figs. 2(c) and 2(d) and the coarsening dynamics is interrupted. The distance between buckles at t_B thus yields the contractile unit size

$${\ell }_B\approx \sqrt{D{t}_B}\approx \frac{{\ell }_p^2}{{\ell }_0^3}{\left(\frac{k_{B}T}{\delta F_S}\right)}^2{(1+\frac{{\tau }_r}{{\tau }_d})}^2.$$ (8)

As illustrated in Fig. 4(c), ℓ_B is typically in the micrometer range, in agreement with the observations of Fig. 2(a) and the findings of Ref. [6].

Because of compensating effects between contractile and extensile motor-filament configurations, the familiar framework involving rigid filaments and identical motors commonly used to describe striated muscle contraction is not suited to study actomyosin bundles lacking sarcomeric organization. Here, we put forward an alternative mechanism based on our observation of buckling. The buckling arises from the nonlinear elastic response of F-actin [21] and dispersion in the speeds of myosin motors [22]. F-actin buckling has previously been invoked to explain contraction qualitatively [23]. Addition of passive cross-linkers, which are formally equivalent to immobile motors, would reinforce a dispersion of motor velocities and promote contraction.

The order-of-magnitude agreement between theory and experiments with respect to the size of contractile units and the critical myosin concentration required for contraction suggests that our current analysis offers a good description of the onset of bundle contractility. Our conclusions are robust to inclusion of features such as inhomogeneous motor spacings ℓ₀ and force dependence of the motor detachment rate (see Supplemental Material [18]). Our mechanism is a general one and applies to any one-dimensional system of polar filaments and motors. It is also generalizable to any situation where filaments respond asymmetrically to compression and extension, even if buckling is not present. Further experiments and theory are needed to better understand the molecular basis for motor inhomogeneities and filament asymmetric response in the myriad of nonsarcomeric organizations found in vivo.