Molecular dynamics studies of the energetics of translocation in model T7 RNA polymerase elongation complexes

Abstract

Translocation in the single subunit T7 RNA polymerase elongation complex was studied by molecular dynamics simulations using the posttrans-located crystal structure with the fingers domain open, an intermediate stable in the absence of pyrophosphate, magnesium ions, and nucleotide substrate. Unconstrained and umbrella sampling simulations were performed to examine the energetics of translocations. The extent of translocation was quantified using reaction coordinates representing the average and individual displacements of the RNA-DNA hybrid base pairs with respect to a reference structure. In addition, an unconstrained simulation was also performed for the product complex with the fingers domain closed, but with the pyrophosphate and magnesium removed, in order to examine the local stability of the pretranslocated closed state after the pyrophosphate release. The average spatial movement of the entire hybrid was found to be energetically costly in the post- to pretranslocated direction in the open state, while the pretranslocated state was stable in the closed complex, supporting the notion that the conformational state dictates the global stability of translocation states. However, spatial fluctuations of the RNA 3′-end in the open conformation were extensive, with the typical range reaching 3–4 Å. Our results suggest that thermal fluctuations play more important roles in the translocation of individual nucleotides than in the movement of large sections of nucleotide strands: RNA 3′-end can move into and out of the active site within a single conformational state, while a global movement of the hybrid may be thermodynamically unfavorable without the conformational change.

INTRODUCTION

Transcription driven by RNA polymerases (RNAPs) occurs via three distinct phases: initiation, elongation, and termination, characterized, respectively, by the recognition of the promoter on DNA, the processive elongation of RNA transcripts and the dissociation of RNAP and transcript from the template.^1–3 A simple and extensively studied model system for these processes is bacteriophage T7 RNAP,^4–13 a single subunit (98 kDa) polymerase containing four major subdomains (N-terminal, palm, fingers, and thumb domains; Fig. 1 and Table I), which carries out all three phases of the transcription process without extra protein components. In the initiation complex (IC), the promoter binding site in the N-terminal domain and the specificity loop recognize the promoter DNA sequence and initiate transcript synthesis. Comparisons of high-resolution structures of the elongation complex (EC)^8,9 with those of the IC have shown that the transition from the initiation to elongation phases entails a major conformational change in the N-terminal domain. The conformational change allows for the dissociation of the promoter sequence and the formation of the RNA exit and substrate entry pores essential for elongation. Subsequent structural studies of the EC^10,11 suggested that conformational changes of the fingers domain adjacent to the nucleoside triphosphate (NTP) binding site play active roles in translocation.

Figure 1.

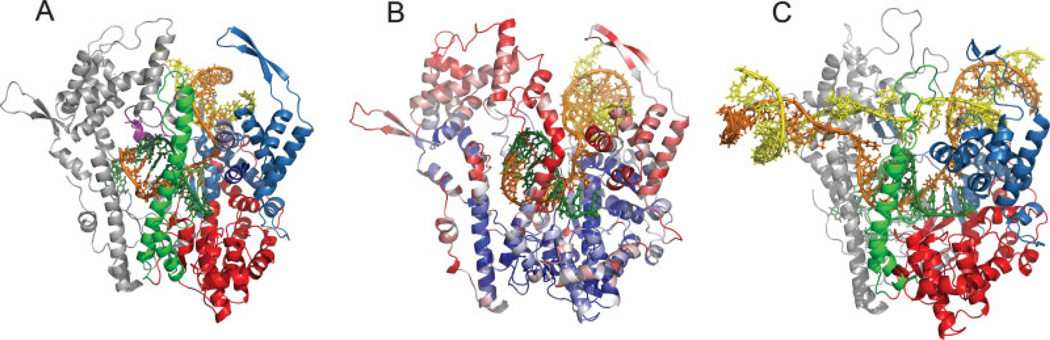
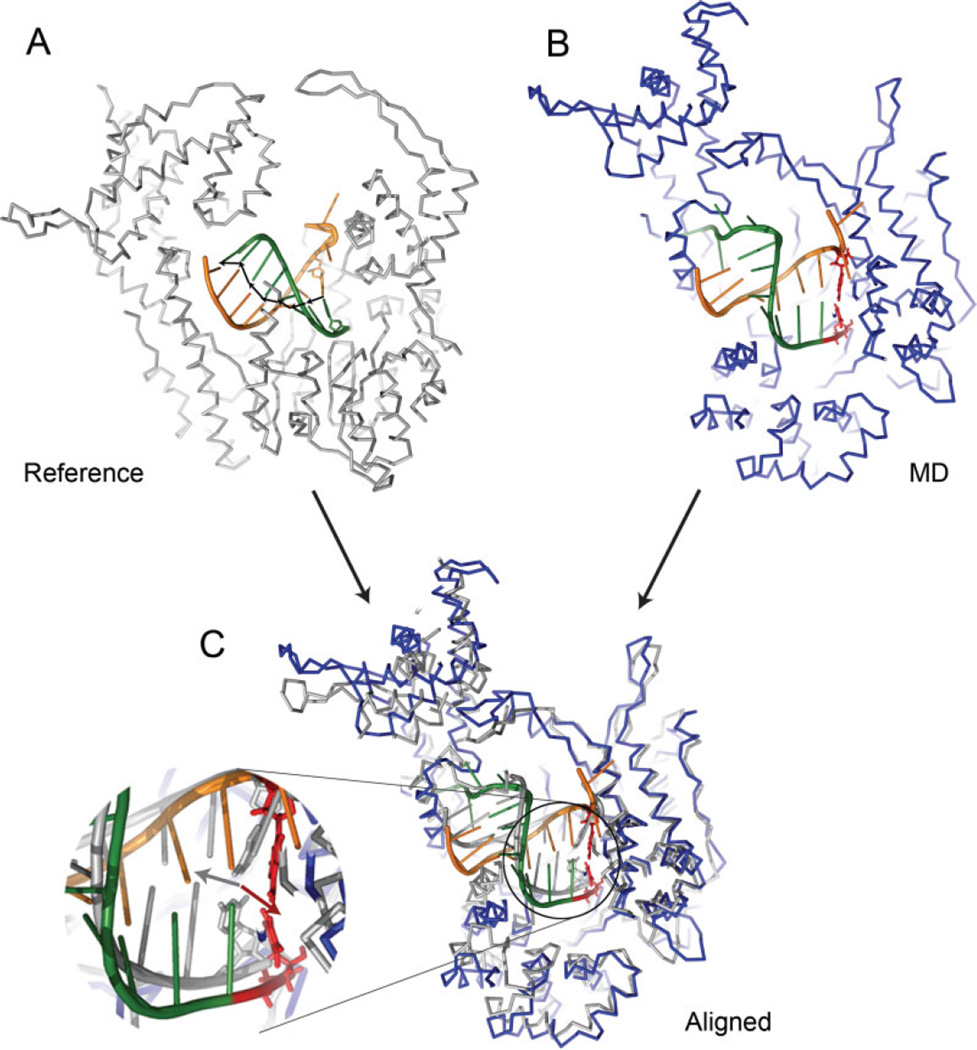
Overall EC structure. (A) A snapshot from an umbrella sampling trajectory of the posttranslocated open complex. N-terminal, fingers, thumb, and palm domains are shown in silver, blue, green, and red, respectively. The template, nontemplate, and RNA strands are shown in orange, yellow, and dark green. (B) A snapshot [from Sampling 2 (Table II)] near the pretranslocated state of the open complex. The protein backbone is shown colored according to RMSD (blue: low, red: high) of each residue with respect to (A). The thumb helix break can be seen in comparison with (A) (Table I). (C) A snapshot from the unconstrained simulation of the pretranslocated closed complex. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table I.

Statistics of Subdomain Movements and Flexibility Within the Unconstrained MD Trajectories of the Post-and Pretranslocated Models

		Total	N-terminal	Fingers	Palm	Thumb
	Residue numbers	1–883	1–325	554–784	412–553 785–883	326–411
RMSD (Å )	Posttrans	3.45	4.01	2.95	2.22	4.41
	Pretrans	3.19	3.82	3.02	2.42	2.91
RMSF (Å)	Posttrans	1.82	1.97	1.85	1.20	2.41
	Pretrans	1.32	1.55	1.39	0.91	1.28
B-factor	1H38	60.8	90.7	51.2	33.3	48.3a
	1S77	65.0	78.7	69.5	43.7	67.5a

RMSD is with respect to the crystal structure reference (1H38 and 1S77 for post- and pretranslocated models, respectively) coordinate calculated after alignment of the overall EC, and the root mean square fluctuation (RMSF) is with respect to the average coordinate of the trajectory calculated after alignment of each frame. The crystallographic B-factor of 1H38 and 1S77 structures averaged over each subdomain are shown for comparison.

^aThe B-factor for the Ala380-Val384 part of the helix is 77.2 and 113.4 for 1H38 and 1S77, respectively.

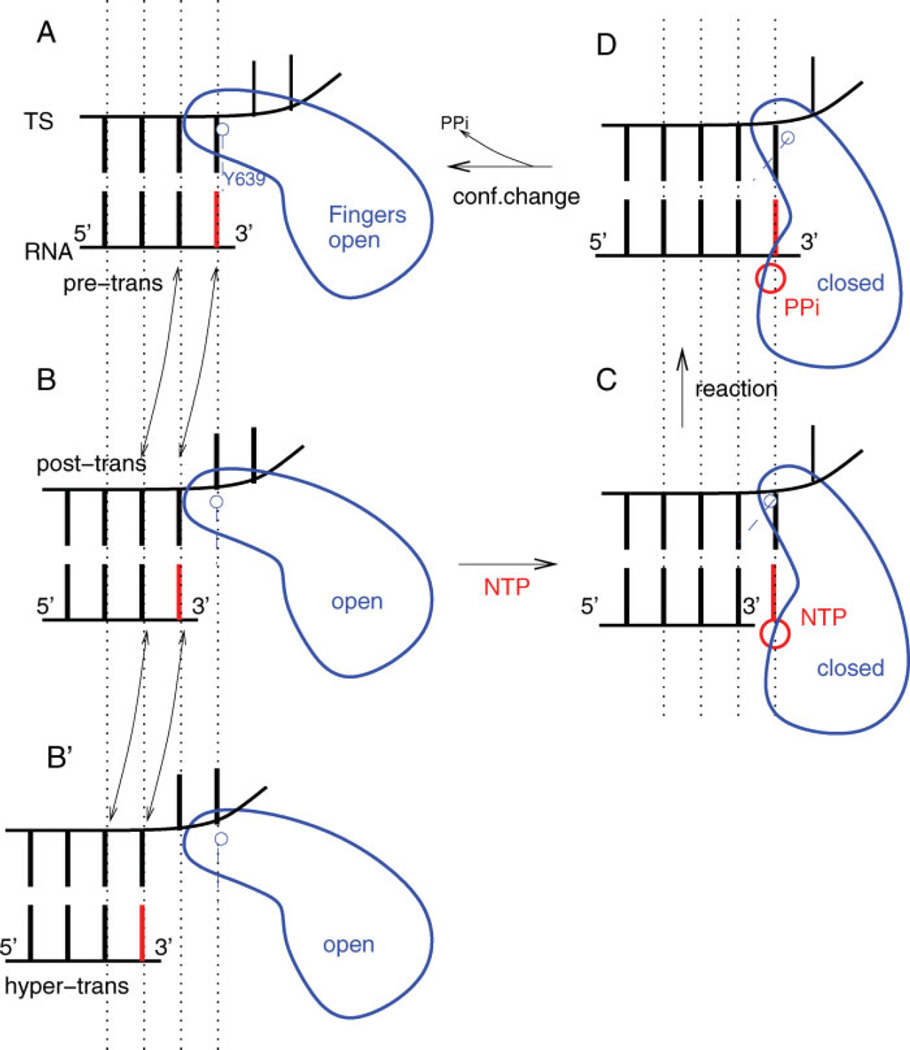
The proposed mechanism of T7 RNAP elongation based on structural data can be described as follows:¹⁰ a new NTP substrate binds to the polymerase in the posttranslocated state with the fingers domain in the open conformation [Fig. 2(B)]. The fingers domain changes its conformation to a closed state with the insertion of the bound NTP to the active site [Fig. 2(C)]. The NTP substrate is then catalytically incorporated into the 3′-end of the RNA transcript [Fig. 2(D)]. The resulting pyrophosphate (PPi) dissociation triggers the reverse conformational change from the closed to the open state [Fig. 2(A)]. Translocation then restores the posttranslocated state [Fig. 2(B)] with the RNA transcript elongated by one base.

Figure 2.

Schematic illustration of the overall elongation mechanism. (A) Pretranslocated state with fingers domain open, and the 3′-end of RNA occupying NTP binding site. (B) Posttranslocated state with fingers domain open, and the 3′-end of RNA cleared of binding site. (B′ ) Hypertranslocated state with fingers domain open, and the 3′-end of RNA two steps upstream of binding site. (C) Substrate complex with bound NTP and fingers domain closed. (D) Product complex with NMP incorporated into 3′-end of RNA and PPi bound nearby. The current work focuses on the transitions between the states (A) and (B). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

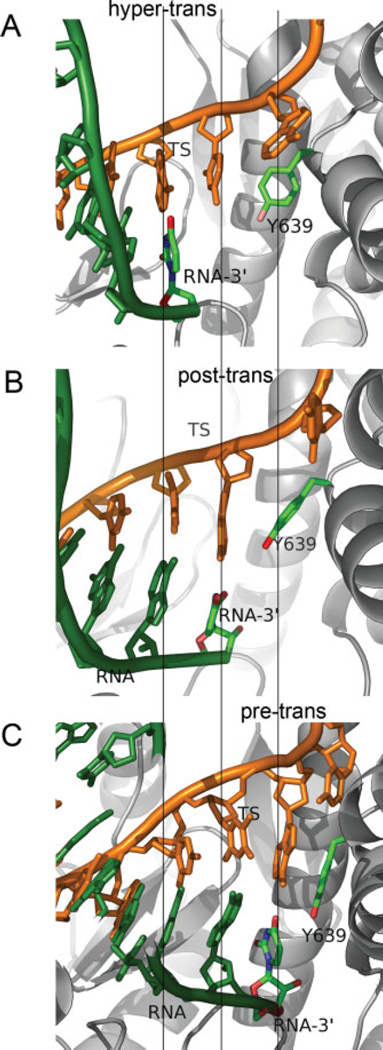
The translocation between the pre- and posttranslocated states is not the only possible spatial displacement for the hybrid. The hypertranslocated state, in particular, where the active site is placed one step further downstream from the RNA 3′-end [Fig. 2(B′)] is expected to be energetically accessible from the posttranslocated state without difficulty, since it is not directly hindered steri-cally by the fingers domain as in the backtracking step. With both the RNA-DNA base pair and nucleotide-protein interactions reduced compared to the posttrans-located state, the hypertranslocated state has been considered as a possible route of EC destabilization and termination.^14,15 Zhou et al.,¹⁵ in particular, have recently shown that for a halted T7 RNAP, hypertranslocations can lead to EC dissociation and termination. Figure 3 shows the active site configurations of the pre-, post-, and hypertranslocated states, where the RNA 3′-end is either occupying the active site, or displaced in the upstream direction by one or two base pair rise distances, respectively.

Figure 3.

Representative snapshots of the EC in three different translocation states. (A) Hypertranslocated state (x₂ ≃ 4 Å), the model state built from the posttranslocated state by rigid displacements of nucleotides upstream. (B) Posttranslocated state (x₂ ≃ 0 Å), the stable reference state of the open complex. (C) Pretranslocated state (x₂ ≃ −4 Å), extracted from an umbrella sampling trajectory generated from the posttranslocated state via constrained simulations. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Both biochemical^15,6,16–18 and single molecule^19–22 experiments suggest that thermal fluctuations play active roles in translocation. In the mechanism in which trans-location events are driven thermally, the substrate binding event is considered to act as the “pawl,” biasing the rapid forward–backward translocation equilibrium between the pre- and posttranslocated states. For T7 RNAP in particular, both ensemble⁵ and single molecule¹⁹ experiments indicate that the pre- and posttranslocated states are nearly isoenergetic, with less than 1 kcal/ mol difference in free-energy between them. Such a stochastic nature of translocation statistics is also consistent with the accessibility of the hypertranslocated state.

The exact atomic level translocation mechanism and its energetics remain to be clarified. Within the structural mechanism summarized in Figure 2, the translocation step after the PPi-release [Fig. 2(D) → (B)] could be either one-sided (posttranslocated state predominantly stable) or reversible (both pre- and posttranslocated states roughly isoenergetic). A closely related question is the degree of coupling between this translocational motion and the closed → open conformational change of the fingers domain. Structural studies¹⁰ have suggested that steric collisions created by the O-helix (and Tyr639) of the fingers domain would make the open conformation incompatible with a stable pretranslocated state. With strong structural coupling between the fingers opening and translocation, the state Figure 2(A) would be unstable and most likely bypassed in real pathways, where domain opening and translocation would instead be concerted [Fig. 2(D) → (B) without (A)].

In this work, we have used molecular dynamics (MD) simulations based on high-resolution structures of the EC, primarily focusing on the energetics of translocations in the open conformation. The state of the polymerase we examined here corresponds to the EC in the absence of ligands (NTP, PPi, and Mg²⁺). Two structures (1H38⁹ and 1MSW⁸), crystallized without these ligands, represent the stable state with the hybrid in the posttranslocated position after the PPi-release and trans-location, and we have chosen the former structure as the basis for the posttranslocated EC model [Fig. 1(A,B), 2(B), and 3(B)].

To examine local stabilities of the post- and pretranslocated states with the fingers domain open, the model pretranslocated state [Figs. 2(A) and 3(C)] was built from the posttranslocated reference state by displacing the nucleotides in the downstream direction (see Methods). In addition, a model hypertranslocated state [Figs. 2(B′) and 3(A)] was also built by similar displacements in the upstream direction. Unconstrained MD simulations were then performed using the three-model translocation states (Fig. 3) as initial structures. Considerations of the local stabilities of pre- and posttranslocated positions within the open conformer serve as tests of the structural hypothesis of the close coupling between the fingers domain opening and translocation. The stability of the hypertranslocated state, on the other hand, tests previous experimental data suggesting functional roles played by hypertranslocation. To further examine the stability of the pretranslocated state of the polymerase after PPi-release, an unconstrained MD simulation was also run from a different model EC based on the product complex (1S77,¹⁰ the crystal structure representing the pretranslocated state with bound PPi and Mg²⁺ ions and the fingers domain closed), with the PPi and metal ions removed.

The standard MD simulations provide instances of trajectories reflecting the stabilities of the initial states within the time scale sampled with relatively small computational demands. Local stabilities alone, however, do not directly yield information on the energetics of trans-locations. The question of the energetic accessibility of transitions between the pre-, post-, and hypertranslocated states can be addressed by employing a suitable reaction coordinate quantifying the degree of translocation, and considering free-energy profiles as functions of the reaction coordinate. Unconstrained MD simulations are often inadequate to sample the relevant conformational spaces required to obtain such profiles. The main computational tool used in our study to examine the energetics of trans-location is the umbrella sampling technique²³ combined with weighted histogram analysis,^24,25 which has now been applied widely to study other large biomolecular complexes including ion channels,²⁶ Src kinase,²⁷ DNA conformational landscapes,²⁸ and DNA base flipping in cytosine-5-methyltransferase.²⁹ In an umbrella sampling, a set of independent MD simulations (or “windows”) are run with appropriate constraining potentials favoring a particular range of values of the reaction coordinate, with the underlying free-energy landscape biased to allow efficient sampling. When run sufficiently long, the trajectories obtained eventually lose the memory of initial states and reach different equilibria. The resulting equilibrium statistics of the reaction coordinate within the set of simulations then reflect the underlying free-energy landscape in addition to the effects of the imposed constraining potentials. The weighted histogram analysis^24,25 then provides a means of recombining the statistics from different windows while removing the biases introduced by constraining potentials. The free-energy profile thus obtained is ideally independent of the biasing potentials used.

We performed umbrella sampling MD simulations of a model EC without bound ligands with constraining potentials acting on the translocation reaction coordinate, in addition to the unconstrained MD simulations described earlier. The unconstrained MD and free-energy trends suggest first that the overall (backward) translocation of the RNA-DNA hybrid from the post- to pretrans-located states is unfavorable when the fingers domain is open. The energetics of single nucleotide pair movements, however, were found to be much more mobile. The RNA 3′-end, in particular, readily moves into and out of the active site where the bound substrate would be inserted. By differentiating the local (active site) versus global movements of the nucleotide strands, our results support structural hypotheses regarding the conformational change, as well as demonstrating the feasibility of thermally activated evacuations of the active site on the molecular level.

METHODS

Overview of simulations

The overall computational work reported in this article consists of two major parts: unconstrained MD simulations and umbrella samplings. The pre-, post-, and hyper-translocated model states were constructed based on the posttranslocated reference crystal structure (see later), from which three unconstrained MD trajectories were obtained. In addition, the closed complex with the hybrid in the pretranslocated position, in which the bound PPi and Mg²⁺ ions were removed from the crystal structure, was also used as the starting coordinate for an unconstrained simulation. The four trajectories were analyzed to examine the time evolution of their translocation reaction coordinates. Two different versions of the reaction coordinate were examined, each representing the collective displacements of the overall RNA-DNA hybrid and the local movements of its terminus at the RNA 3′-end.

Up to four distinct umbrella sampling sets under varying conditions and sampling ranges were collected in order to ensure sufficient equilibrations of the free-energy profiles. The use of different sampling conditions for the sampling sets, including distinct initial states and magnitudes of force constant, allows one to enhance the quality of statistics when the collected histogram data from different sets are unbiased and recombined each with their respective biasing conditions in the weighted histogram analysis.²⁴ Free-energy profiles were obtained as functions of the reaction coordinates for the overall hybrid translocation and the RNA 3′-end movements.

Model building

Two different crystal structures were used to build up to four model complexes representing different translocation states. The post-, pre-, and hypertranslocated states with the fingers domain open were all based on the crystal structure 1H38.⁹ The pretranslocated model state with the fingers domain closed was based on the crystal structure 1S77.¹⁰

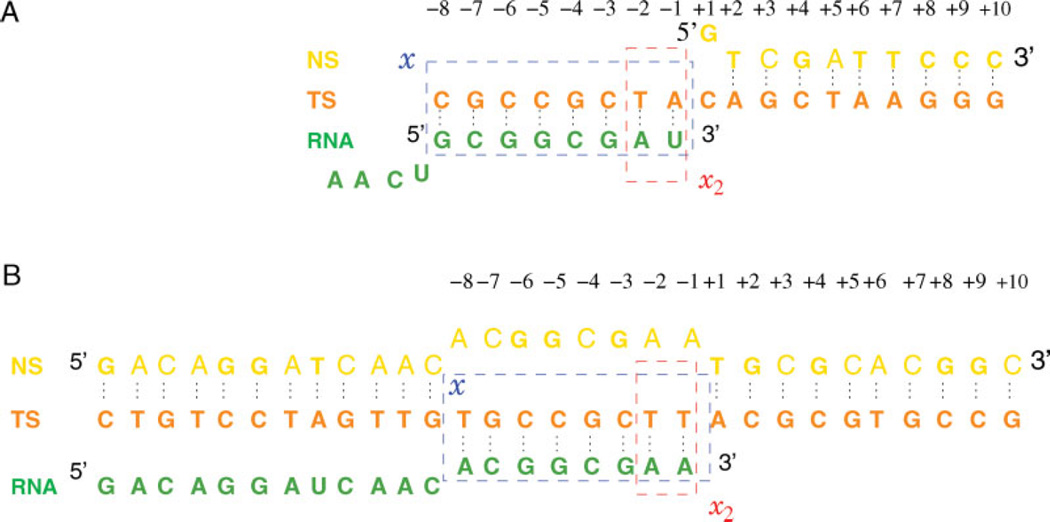
In building the posttranslocated model complex in the open state, missing fragments of the protein in the crystal structure (1H38⁹) were constructed via interpolations of known adjacent backbone atom positions, and using Swiss-PDB Viewer³⁰ to build unknown side-chain heavy atoms. The template strand (TS), nontemplate strand, and RNA transcripts were taken as in the original structure, except the first four nucleotides of RNA 5′-end missing in the structure, which were built into the model as a coil through the RNA exit pore. Figure 4(A) shows the nucleotide strand sequences of the open complex used in this article. Coordinates of all hydrogen atoms were built using the HBUILD module of CHARMM. Short energy minimizations were performed to relax the unphysical coordinates of the rebuilt atoms with the known crystal structure coordinates fixed. The overall complex was put in a pre-equilibrated water box (TIP3P model³¹ ) in orthorhombic symmetry and the overlapping solvent molecules were deleted. The total number of water molecules was ~40,000 for each of the simulated systems. Potassium ions were added randomly in solvent regions to neutralize the overall system, which was energy minimized further with all atoms allowed to move. Figure 3(B) shows the active site configuration of the posttranslocated state.

Figure 4.

Nucleotide sequence of the EC models. (A) The open complex, based on the crystal structure 1H38.⁹ (B) The closed complex, modified from the crystal structure 1S77.¹⁰ The rectangles show the sets of nucleotides used in the definition of reaction coordinates x, x₂. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

As described in Introduction, the hypertranslocated model state is of interest regarding its accessibility and stability relative to the posttranslocated state, although corresponding crystal structures do not exist. The hyper-translocated model state was thus built by taking a snapshot from the posttranslocated unconstrained MD trajectory (see later) and performing rigid translations of the nucleic acid strands by one base pair distance in the local upstream direction. The nucleotide atoms were moved into the corresponding positions one base pair upstream, after which the new base pair hydrogen bonds were forged by setting up harmonic potentials between donor and acceptor pairs and performing short energy minimizations. Figure 3(A) shows the active site configuration of the hypertranslocated model state.

The pretranslocated position for the hybrid is expected to be stable when the fingers domain is closed and PPi, Mg²⁺ are bound in the active site. To test whether the pretranslocated position is unstable when the fingers domain is in the open state with no ligands present, the pretranslocated model state with the open conformation was built from the posttranslocated reference in a way similar to the hypertranslocated model with translocations in the downstream direction. Figure 3(C) illustrates a configuration close to this pretranslocated model state (from an umbrella sampling window; see later).

The pretranslocated state with the fingers domain closed was built from the product complex 1S77.¹⁰ Missing residues were filled in by aligning the open complex model previously built and importing the protein atoms into the closed complex. The crystal structure has NT sequence in the bubble region noncomplementary with the TS. The sequence of the NT was mutated in our model such that NT and TS are complementary [Fig. 4(B)]. The RNA 3′-end deoxy-ATP in the crystal structure was changed into an rATP. The PPi and Mg²⁺ ions were deleted. The missing upstream DNA duplex was built by taking model B-DNA duplex backbone atom positions,³² mutating its sequence to match the upstream duplex sequence of Figure 4(B), and aligning it such that its downstream end is located in close proximity of the upstream end of the bubble. The missing upstream end of the RNA transcript was built as a coil as for the open complex. The complex was then solvated, neutralized, and energy minimized as for the open complex. A snapshot of the closed pretranslocated model complex is shown in Figure 1(C).

General simulation conditions

All simulations and analysis were done using a customized version of CHARMM.³³ The CHARMM force field version-22 for protein³⁴ and 27 for nucleic acid^35,36 were used in simulations. The following protocols were used for all unconstrained and umbrella sampling simulations. MD simulations were performed at constant temperature (300 K), initially with constant pressure (1 atm) for roughly 100 ps to equilibrate the box size, with the production simulations performed with constant volume. Constant pressure simulations were occasionally mixed in typically with 100 ps durations to re-equilibrate the box sizes as necessary during the sampling. All simulations were done in periodic boundary conditions using particle mesh Ewald (PME)³⁷ for electrostatics, and a van der Waals interaction cutoff of 10 Å. The approximate dimension of the simulation unit cell was 123 × 115 × 100 ų. The SHAKE algorithm was used with a time step of 2 fs. The complex center of mass was harmonically held at the center, and another residue of the protein was constrained to lie within a given cylinder defined with respect to the box axes, both with a force constant of 10 kcal/mol Ų, to prevent the overall drift and rotation of the complex.

Reaction coordinates

The translocation reaction coordinates quantifying the degree of translocation of the nucleic acid strands with respect to the protein were chosen as the average displacements of the center of mass of the base pairs for a given length of duplex relative to a reference structure, each projected along the local direction of the base pair rise of the reference. The reference structures were taken as the corresponding crystal structures, 1H38 and 1S77, respectively, for the open and closed states.

In calculating reaction coordinates for a given structure, the reference structure is first rotated to align with the dynamical structure with minimum root mean square deviation (RMSD), and displacements of base pairs relative to the reference are projected onto the local base pair rise direction of the reference, which are then averaged (Fig. 5). Two different choices were made for the base pair set used in the definition of reaction coordinates: the primary coordinate x was defined as the average translocation of the RNA-DNA hybrid that includes nucleotides −1 to −8 (Fig. 4), using the entire protein as the reference for alignment. As a specific measure of the movement of the RNA 3′-end, a second coordinate x₂ was defined as the displacement of the base pair − 1 in the direction given by those from −1 to −2. In the calculation of x₂, only the palm domain of the protein, which contains the catalytic residues,¹⁰ was used for the alignment of structures. In the current work, the reaction coordinate x was used to bias the sampling in each window, which is expected to steer the protein more efficiently by acting globally on the RNA-DNA hybrid.

Figure 5.

An illustration of the definition of translocation reaction coordinates. (A) The reference structure of RNAP (posttranslocated crystal structure for the open complex), where the black arrows show the local directions of base pair rise [v_i (i = 1,… ,7) in Eq. (1)]. (B) A structure pulled out from a dynamical trajectory. (C) The MD structure shown together with the reference, aligned to minimize the RMSD of the protein. The inset shows the close-up view of the active site, where the displacement vector (red arrow) of the 3′-end base pair in the MD structure (shown in red sticks) with respect to the reference position (silver sticks), and the corresponding reference base pair rise vector (silver arrow) are shown. The projection of the red arrow onto the silver arrow (≃−3 Å in this example) constitutes the contribution of the 3′-end base pair to the reaction coordinate. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

The translocation reaction coordinates are defined specifically by

$$x=\frac{1}{N-1}\sum _{i=1}^{N-1}({\mathbf{R}}_i-\mathbf{U}·{\mathbf{R}}_i^{(0)})·\mathbf{U}·{\mathbf{v}}_i^{(0)}$$ (1)

and analogously for x₂, which averages the displacements of the base pairs R_i within a dynamical structure relative to the reference ${\mathbf{R}}_i^{(0)}$, projected on the direction of base pair rise in the reference represented by the unit vector ${\mathbf{v}}_i^{(0)}$ after alignment via matrix U. The summation is over the set of nucleotides chosen for the reaction coordinate (Fig. 4), with the total number N = 8 and N = 2 for x and x₂, respectively. The MD simulation with constraining potential u_n = k(x – x₀)², where k is the force constant and x₀ is the potential minimum for a given window, was implemented by modifying the CONS RMSD module of CHARMM (see Supplementary Material).

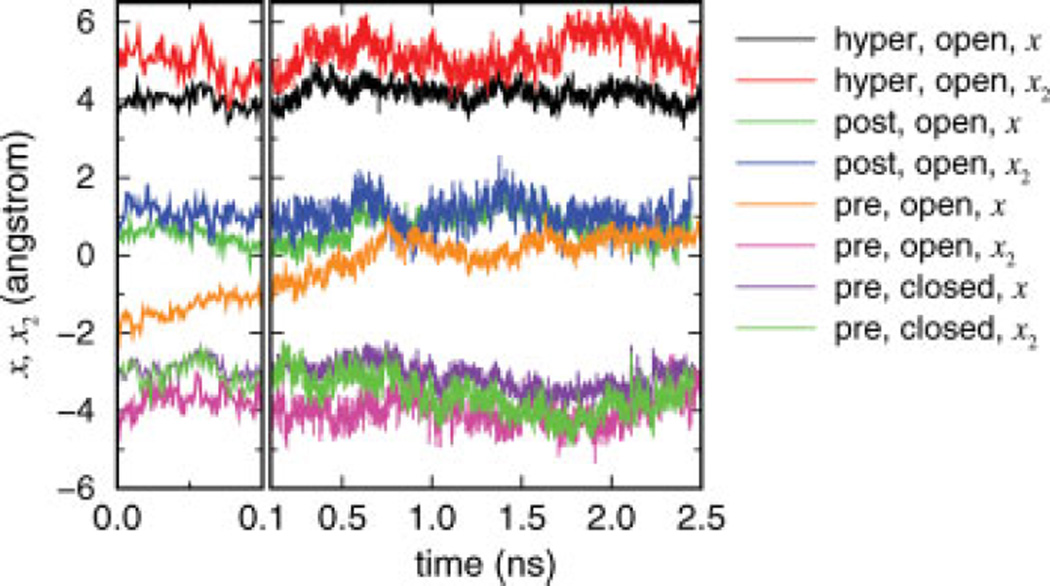
The four unconstrained MD simulation trajectories, each started from the hyper-, post-, and pretranslocated model states of the open complex, and the pretranslocated state of the closed complex, were analyzed to yield the time series of two translocation reaction coordinates x and x₂ (Fig. 6). In calculating the time series of the pretranslocated closed complex, the corresponding crystal structure (1S77; pretranslocated) was used as the reference, and 3.4 Å was subtracted from the reaction coordinate values such that the resulting values can be compared with those with the posttranslocated reference. The molecular configurations of the pretranslocated states resulting from MD simulations shown in Figure 7 were made from late-stage snapshots (at ~2.5 ns) of the unconstrained MD simulations of the open and closed pretranslocated models.

Figure 6.

Unconstrained MD simulations of the pre-, post-, and hypertranslocated models. Average (x) and 3′-end (x₂) reaction coordinate time series are shown for the four trajectories started from the hyper-and posttranslocated states (both in the open complex), and the pretranslocated states (in the open and closed complexes).

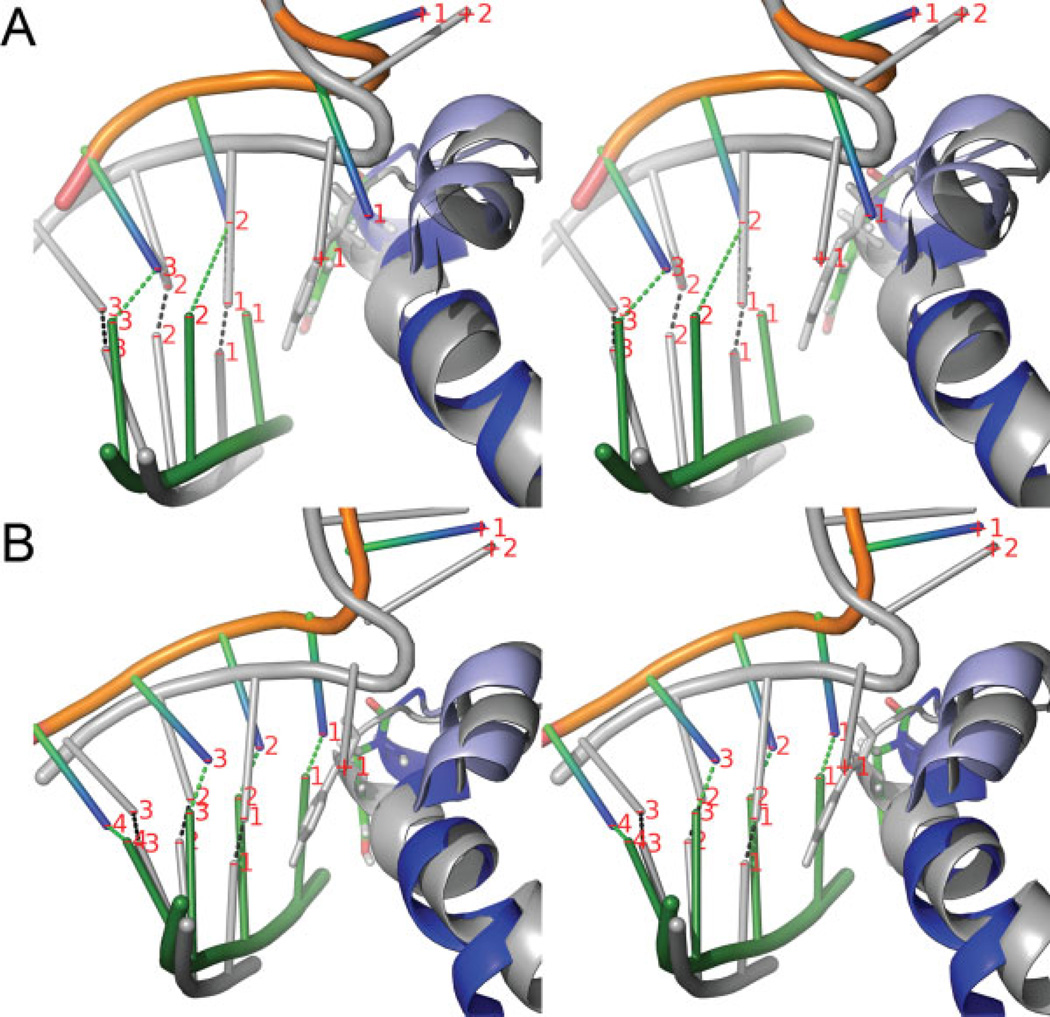
Figure 7.

Late-stage snapshots in stereoview (at ~2.5 ns) from the unconstrained trajectories started from the pretranslocated states in the (A) open and (B) closed complex, aligned with respect to the posttranslocated reference state (shown in silver). The labels show the nucleotide numbering of Figure 4 and the dotted lines indicate the base paring between the RNA and DNA. In (A), nucleotides have mostly restored the original positions of the posttranslocated state, except the −1 nucleotide pairs (RNA3′-end), which remain close to the pretranslocated positions because of the steric hindrance of the O′-helix (light blue) blocking the forward translocation of the +1 nucleotide. In (B), most of nucleotides remain stable near the pretranslocated positions. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Umbrella samplings

Umbrella sampling simulations of the EC in the open state using the full MD with PME (Samplings 1, 2, and 3 in Table II) were performed in the presence of the constraints u_n with otherwise the same conditions as for the unconstrained MD. The RMSD for alignment in each dynamical step was calculated using 7441 protein heavy atoms of known crystal coordinates. The sampling speed of constrained MD on an Intel Xeon 3.0GHz chip was approximately 100 days/ns, and 25 days/ns on a four-core AMD Opteron 2214 chip run parallel. The spacings between the potential minima x₀ of neighboring windows were 0.34 Å. In each umbrella sampling set, therefore, the windows collectively sample conformational spaces belonging to translocation intermediates between the pre-, post-, and hypertranslocated states separated by 0.34 Å (Table II).

Table II.

Sampling Sets for Free-Energy Calculations

	Force constant (kcal/mol Å2)	No. of windows	Time (ns)	Initial coordinate	Range of χ0 covered (Å)	Dynamics
Sampling 1	10	20	1.2	Posttranslocated	0 to 3.4	PME
Sampling 2	50	23	3.1	Sampling 1	−3.4 to 3.4	PME
Sampling 3	50	13	3.2	Hypertranslocated	0 to 3.4	PME
Sampling 4	50	22	10	Sampling 2	−3.4 to 3.4	GSBP

The sampling times shown are the averages over the windows. PME indicates full periodic boundary simulations using the particle mesh Ewald. The range of biasing potential minima x₀ indicates the coverage of the translocation intermediates sampled within each sampling set.

To maximize the overall efficiency of sampling conditions and ensure adequate equilibrations of the free-energy profiles obtained, different strengths of force constants and initial states were used in the sampling sets collected (Table II). In general, stronger force constants tend to give faster equilibration of individual windows, but yield smaller fluctuations of reaction coordinates within each window, thus requiring either more windows to be run or each window to be sampled longer in order to produce sufficient overlaps between histograms of neighboring windows for the weighted histogram analysis. In practice, therefore, a certain degree of trial and error is helpful in determining the optimal condition for efficiency. Sampling data collected with different strengths of biasing potential can each be unbiased separately using their respective potentials imposed, and combined together to yield the free-energy in the weighted historgram analysis.

A common initial coordinate (posttranslocated state) was used for all windows in Sampling 1, and sampling performed under fixed constraints. Sampling 2 used the final coordinates of Sampling 1 for each window to cover the same range of reaction coordinate, but was run with a stronger constraint. Convergence of profiles was further tested by Sampling 3, initiated from the hypertranslocated model state and run with the same strength of constraints as in Sampling 2 to cover the region from post-to hypertranslocated states. The time series of the three sampling sets are shown in the Supplementary Material. To rule out the possibility that sampling periods substantially longer than those with full PME MD (Samplings 1, 2, and 3) could have yielded a qualitatively different free-energy profile, Sampling 4 was performed using the generalized solvent boundary potential (GSBP)³⁸ under the same condition as Sampling 2 for 10 ns per window. In GSBP, the system is divided into the central spherical inner region (containing the hybrid and the active site in our case) and the outer region, with the latter replaced by a dielectric continuum and fixed protein atoms. In comparison to the rest of sampling sets, therefore, Sampling 4 has a large part of the protein away from the RNA-DNA hybrid and the active site fixed, possibly restricting the degree of conformational relaxation associated with translocations but allowing for much faster sampling speeds. The system for Sampling 4 with GSBP was set up using a 15 Å radius sphere centered around the active site, so that the RNA-DNA hybrid would be contained in the inner region. The Born atomic radii from Ref. 39 were used. The reaction field contributions were calculated using 10 spherical harmonics as basis functions, and the dynamics run with extended electrostatics. An example of the central inner region configuration adopted for Sampling 4 is shown in the Supplementary Material.

Free-energy analysis

Free-energy profiles shown in Figures 8 and 9 were calculated by processing the sampling data using weighted histogram analysis method.^24,25, In the weighted histogram analysis, the probability density of the reaction coordinates ρ = ρ(x, x₂) is given as

$$\rho (x,x_2)=c\frac{{\sum }_{i=1}^N{n}_i{\rho }_i^{\prime }(x,x_2)}{{\sum }_{j=1}^N{n}_j{e}^{-\beta [u_j^{\prime }(x,x_2)-f_j]}},$$ (2)

where c is an arbitrary constant fixed by a definition of zero free-energy, 1/β = k_BT is the Boltzmann constant times temperature, ${\rho }_i^{\prime }$ is the biased distribution (histogram) obtained from ith simulation run under the biasing potential $u_i^{\prime }(x,x_2)$, n_i is the total number of data points in the simulation i, and the summations are over all simulations. The free-energy constants f_i are determined self-consistently by

$$e^{-\beta f_i}=c\int dx\int d{x}_2\rho (x,x_2)e^{-\beta u_i^{\prime }(x,x_2)}.$$ (3)

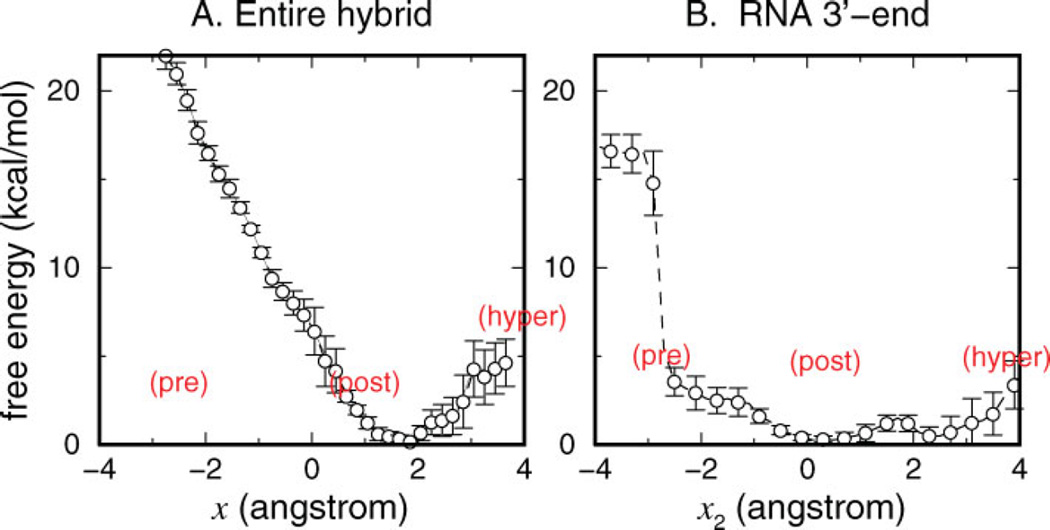
Figure 8.

Free-energy profiles of translocation. (A) G(x) as a function of the average translocation of the hybrid x. (B) G(x₂) as a function of the translocation of the RNA 3′-end x₂. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 9.

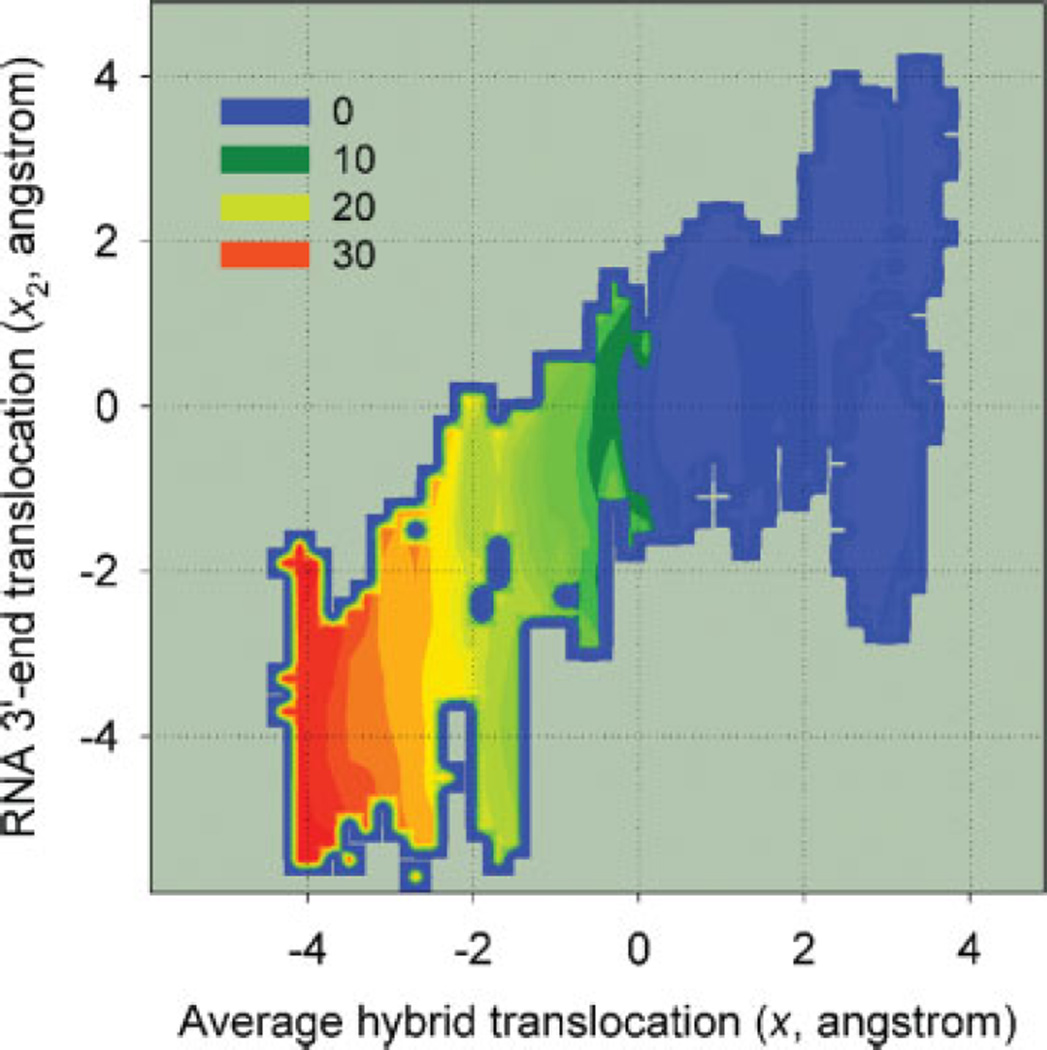
Two-dimensional landscape illustrating the coupling between x and x₂. The contour levels are in units of kcal/mol. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Equations (2) and (3) are solved iteratively. The two-dimensional landscape G(x, x₂) = − k_BTlnρ (x, x₂) was obtained by generating double time series of trajectories for x and x₂ from Sampling 2, and performing the weighted histogram analysis with a modified potential $u_n^{\prime }=u_n+k_2(x_2-x\prime )2$ but with k₂ = 0.²⁷ The one-dimensional free-energy profile G(x₂) shown in Figure 8 was obtained from the two-dimensional landscape (Fig. 9) by applying the formula e^−βG(x₂) ∝ ∫ dxe^{−βG(x,x₂)}. The free- energy profile G(x) on the other hand is directly obtained from the collection of simulation histograms by applying the one-dimensional version of Eqs. (2) and (3) for ρ(x) ∝ e^−βG(x), where x₂ has been integrated out with $u_n^{\prime }=u_n$.

To obtain best estimates of the free-energy profiles and assess convergence, trajectories in each sampling set (Table II) were divided into partially overlapping 1-ns segments and weighted histogram analyses were performed using each segment, with the resulting temporal free-energy profiles compared (Supplementary Material). Sampling 1 mainly consisted of transient equilibrations from the initial posttranslocated state toward the respective potential minima, and was not used in the free-energy analysis, while it provided good initial coordinates for Sampling 2. The one-dimensional profiles in Figure 8 were obtained by analysis of Sampling 2 data, together with additional data from Sampling 3 for the post- to hypertranslocated region (1 < x < 4 Å). The error bars in Figure 8 were estimated from the standard deviations of the partial time series free-energy data.

The Supplementary Material contains additional figures, more details of the reaction coordinate definition, the implementation of the constrained dynamics, the time series and free-energy analysis of the sampling, and movies showing aspects of the constrained dynamics.

RESULTS

Translocation reaction coordinates

The reaction coordinates quantify the degree of translocations of the RNA-DNA hybrid with respect to a reference after protein alignment along the local directions of base pair rise (Fig. 5). The definition of the reaction coordinate, when applied to a model B-DNA duplex, gave x = 3.47 Å for the elementary base pair rise distance (see Supplementary Material). The position of the nucleotide strands with respect to the protein in the reference structure of the open complex used in our study corresponds to the posttranslocated state,^8,9 for which the base pair rise distance averaged over the hybrid was x = 3.82 Å and that of the 3′-end, x₂ = 3.92 Å. The relatively larger values of the base pair rise in T7 RNAP reflects the deformation of the nucleotide strands. The posttranslocated reference state [Figs. 2(B) and 3(B)] has the value x = x₂ = 0 by definition, an ideal pretranslocated state [close to Figs. 2(A) and 3(C)] would have x₂ ≃ −4 Å, and the hypertranslocated state [Figs. 2(B′) and 3(A)], x₂ ≃ 4 Å, respectively, with x values similarly correlated.

Unconstrained MD

Figure 6 shows the reaction coordinate time series from the four unconstrained MD trajectories. The trajectory started from the posttranslocated reference has initial values of x = x₂ ≃ 0 (with the small deviation from zero due to energy minimizations), both of which remain in the neighborhood of the initial value throughout the trajectory. The time series of the trajectory started from the hypertranslocated model state likewise remain in the neighborhood of ~5 Å. The data for the post- and hypertranslocated trajectories reveal the physical gap between the two model states corresponding to one base pair step on average, and indicate that the two states are locally stable within nanosecond time scales for both the average and 3′-end translocations. The statistics also suggest that angstrom level spatial fluctuations are fairly common within nanosecond time scales in unconstrained dynamics.

The trajectory with the pretranslocated initial state of the open complex, however, shows contrasting behavior for the two reaction coordinates: the average hybrid translocation x shows rapid convergence from x ≃ −4 Å to x ≃ 0 (the initial change from −4 Å to −2 Å occurs in picoseconds), whereas the translocation of the 3′-end remains near x₂ ≃ −4 Å. The set of data show that the 3′-end largely remains in the neighborhood of the pretranslocated position, while the bulk of the rest of nucleotide pairs within the hybrid return to their respective posttranslocated positions within nanosecond time scales.

The late-stage snapshot of this trajectory shown in Figure 7(A) illustrates the molecular details of the observed behavior. In the posttranslocated open reference state (silver in Fig. 7), there is a sharp kink in the TS between the nucleotides +1 and +2 separated by the O′-helix, with the +1 nucleotide of the TS in the flipped out position, displaced by Tyr639.⁸ The pretranslocated model state built in the open complex by downstream displacements of the nucleotides (see Methods) forces the RNA 3′-end (−1) into the active site, while placing the − 1 and +1 nucleotides of the TS on the two positions occupied by the +1 and +2 in the reference. This forced backtracking of the entire hybrid is seen to have been largely reversed (as quantified by the evolution toward x ≃ 0 in Fig. 6) in Figure 7(A), where the −3, −2 nucleotides of RNA are close to those in the reference. The − 1 nucleotide of the TS, however, remains close to the +1 nucleotide position in the reference, unable to pull the +1 nucleotide forward through the O′-helix, which contribute to the maintenance of x₂ at ~ −4 Å in Figure 6.

The reaction coordinate time series of the unconstrained MD trajectory started from the pretranslocated closed complex are also shown in Figure 6. In contrast to the open complex, both the translocation states of the entire hybrid and the RNA 3′-end remain close to the pretranslocated initial position, implying that the stability of the pretranslocated position depends on the conformational state of the fingers domain. The corresponding late-stage snapshot of this trajectory shown in Figure 7(B) demonstrates that indeed all of the nucleotide pairs remain in the pretranslocated positions one step downstream with respect to the reference. It is also notable that the steric blocking by the O′-helix hindering translocational movements between the +1 and −1 nucleotides appears much less severe in the closed complex than in the open complex. It suggests that the steric hindrance contributes to the mechanism of translocation by confor-mational changes.

The unconstrained MD data thus suggest that for the open complex, the pretranslocated state is globally unfavorable, while the 3′-end of the hybrid remains in the active site when separated by the O′ -helix from its neighboring downstream nucleotide. The pretranslocated position in the closed complex, in contrast, is stable even without bound PPi.

Flexibility of subdomains

The statistics of subdomain movements and flexibility were examined using the unconstrained MD trajectories (Fig. 6) of the posttranslocated open complex, and the pretranslocated closed complex (Table I). The overall degree of conformational fluctuations around the average for the protein is slightly larger for the open complex compared to the closed, which suggests that the open state allows more flexibility in the protein conformational states. Among the major subdomains, the N-terminal domain shows relatively large deviations both from the crystallographic conformation and from its average position during the simulation, whereas the palm domain is seen as the most rigid. The flexibility of the N-terminal domain seen in the simulations is consistent with evidence from existing structural studies: the functional requirement for a massive structural rearrangement in the N-terminal domain in the transition from the IC to EC^8,9 is expected to correlate with its flexibility within the EC, as suggested by its large crystallographic B-factor (Table I).

The thumb helix within the open, posttranslocated state is fairly flexible with relatively large deviations from the crystal structure. In particular, in constrained simulations from the posttranslocate state (see later) producing states close to the pretranslocated state, it was observed that the helix breaks at a location roughly 2/3 in length from its N-terminus [Ala380-Val384; Fig. 1(B) and Supplementary movies]. The flexibility of the thumb domain has been noted previously in structural studies.⁴⁰ The observed location of the break in the thumb helix is also consistent with the relatively high B-factor of this part of the helix in crystal structures, and with the observation that the thumb helix in the crystal structures of nucleic acid-free RNAP becomes disordered at this location.⁴¹

Compared to the observed large deviation and fluctuation of the thumb helix conformation in the open state, the flexibility of the helix in the closed state is smaller, which suggests that the closed conformation suppresses its flexibility. However, the top portion of the helix remains unwound as a loop [Fig. 1(C)], distinct from the open conformation.

Umbrella sampling and free-energy profiles

Umbrella sampling MD simulations performed cover the range from x ≃ −4 Å (pretranslocated) to x ≃ 4 Å (hypertranslocated). Three major sampling sets (Samplings 1, 2, and 3; full MD with PME) in addition to one (Sampling 4; GSBP) in different conditions were collected (see Table II, Methods, and Supplementary Material). The overall trajectories of the sampling sets were used in the weighted histogram analysis^24,25 to obtain the free- energy profiles with their convergence statistics analyzed.

The comparative analysis of the free-energy profiles obtained from Samplings 2 and 4 indicated no significant differences, except the relatively smaller magnitude of fluctuations observed for each window in the Sampling 4 (Supplementary Material). Figure 8(A) shows that the free-energy profile as a function of average translocation x[G(x)] for the fingers domain in the open state exhibits two distinct regions, the post- to hypertranslocated (x > 1.5 Å), and the pre- to posttranslocated (x < 1.5 Å) regimes. The former region is characterized by a moderate (< 5 kcal/mol) barrier between the post- and hyper-translocated states. Samplings 2 and 3, in particular, bracket this equilibrium profile and converged from two opposite sides, the post- and hypertranslocated model states (Supplementary Material). The convergence of Samplings 2 and 3 therefore demonstrates that the sampling schemes employed reach equilibration within the nanosecond time scale when started from initial states that are within a single base pair rise distance. The pretranslocated regime (x < 1.5 Å), however, is sloped steeply downhill toward the minimum near x ≃ 1.5 Å. The location of the minimum is consistent with the evolution of x to a similar location within the unconstrained dynamics in Figure 6. The deviation of this minimum from the x = 0 reference likely reflects the global confor-mational deviation of the protein upon dynamics runs from the crystal structure (Table I), since the protein as a whole was used as the reference in alignment in calculating x. This part of the pretranslocated profile is further supported by the convergence of Sampling 3 (Supplementary Material).

The free-energy profile in terms of the average translocation x in Figure 8(A) indicates that the translocation of the RNA-DNA hybrid with respect to the polymerase to reach the pretranslocated state is unfavorable if the fingers domain is open. The forward translocation from the post- to hypertranslocated states, which is sterically unhindered, however, is within the range of thermal excitations. This feature of the free-energy profile G(x) is consistent with the trends observed in unconstrained dynamics (Fig. 6), where both the post- and hypertranslocated model states are seen as locally stable, whereas the pretranslocated model state quickly evolves toward the posttranslocated state.

The results extracted from the same set of trajectories for RNA 3′-end translocation [Fig. 8(B)] differ considerably, suggesting that the exact nature of the energetics depends on how one defines the translocation. Figure 9 shows that, overall, the two reaction coordinates x and x₂ are closely correlated throughout the sampled regions. It also shows that compared to x, x₂ exhibits a much larger degree of fluctuations: the isoenergetic levels in Figure 9 are mostly aligned vertically, and it is much easier to observe different degrees of 3′ -end translocation for a given position of the entire hybrid than vice versa. The free-energy as a function of 3′-end translocation [G(x₂)] in Figure 8(B) is characterized by a flat profile over a relatively wide range ( −3 < x₂ < 4 Å). The contrast of this landscape with that of G(x) in Figure 8(A) illustrates one of the major findings of our work: the single pair of nucleotides at the 3′-end moves around much more readily than the entire hybrid. The flat landscape also demonstrates the feasibility of Brownian ratchet-type mechanisms in T7 RNAP EC, by showing that thermally driven forward-backward translocations of the RNA 3′-end can occur within a given conformational state of the protein.

DISCUSSION

The trends observed in our unconstrained simulations suggest that while both the hyper- and posttranslocated states can be locally stable in the open complex, the pre-translocated state is highly unfavorable. The sharp contrast of the instability of the pretranslocated state in the open complex with the stable nature of the same state in the closed complex (Fig. 6) supports the structural hypothesis for the roles played by the conformational change in regulating the global stabilities of translocation states. In addition, the fact that the RNA 3′-end remains in the active site in the unconstrained simulation of the pretranslocated open complex adds important molecular details to the picture: the global forward translocation from the pre- to posttranslocated states seen within the trajectory is hindered sterically for the −1 nucleotide of the TS by the O′-helix [Fig. 7(A)], causing the RNA 3′-end to remain in the pretranslocated position. Based on this observation, in particular, it is reasonable to expect that the opening of the fingers domain after the PPi-release [Fig. 2(D) → (A)], which would impose the hindrance, is likely to be concerted with the forward translocation of the 3′-end.

The pretranslocated model built by displacement of the nucleic acids in a complex where the fingers subdomain is in the open conformation reveals the role played by the steric hindrance of O′-helix, which strongly disfavors the pretranslocated state in the open conformation of the complex. The energetics of translocational movements in the open conformation of fingers domain is more appropriately sampled by biased simulations based on the known stable state of the open complex, the post-translocated state. Our umbrella sampling simulations, with each window equilibrating translocation intermediates generated from the posttranslocated initial state, properly sample the conformational spaces explored by the RNA and DNA in the open conformation of the complex.

The resulting free-energy profiles reveal more general features of translocation energetics, which confirm the global instability of the pretranslocated state within the open complex. Most importantly, however, the free-energy profile of translocation of the RNA 3′-end in Figure 8(B) implies that the instability of the pretranslocated position of individual 3′-end nucleotides is much less pronounced than for the entire hybrid. The contrast between the free-energy profiles shown in Figure 8(A,B) allows us to draw the following conclusions: as suggested by structural studies comparing ECs without bound substrates versus with PPi, conformational changes in the fingers subdomain provide key mechanisms that stabilize different translocation states where a large section of nucleotide strands had been moved in its entirety. However, nucleotide strands are fairly long and flexible, and individual pairs within the RNA-DNA hybrid undergo large spatial fluctuations around the average. The range of these fluctuations for the RNA 3′-end extends to distances exceeding one step length.

Although our simulations demonstrate that the RNA-3′-end can enter the active site and displace Tyr639 [Fig. 3(C) and Supplementary movie 2], we note that the free-energy minima of both Figures 8(A) and 8(B) are close to the crystallographic reference state [Fig. 3(B)], with Tyr639 expected to be contributing to its stability in both profiles. The observed relative ease with which the RNA 3′-end enters the active site, displacing Tyr639, compared to the rigid backward translocation of the hybrid, is a quantitative difference. Specific nucleotide– protein interactions, including the effects of the thumb helix, catalytic residues, the O-helix with Tyr639 in the active site, in addition to the O′-helix, are expected to be responsible for the variable degree of fluctuations nucleotide strands experience within the EC complex. The free-energy profiles in Figure 8 can in fact be used to understand this quantitative difference between the free-energy costs of backtracking for the entire hybrid and RNA 3′-end: if one assumes that each base pair in the hybrid contributes equally to this free-energy cost, the value of G(x₂ = 22 Å) ≃ 2.5 kcal/mol in Figure 8(B) then compares favorably with G(x = −2 Å)/8 ≃ 2.1 kcal/mol from Figure 8(A).

The results indicating that the energetics of hypertrans-location involve a relatively small energetic barrier is consistent with prior studies pointing to important functional roles (e.g., in intrinsic termination) played by transcriptional pausing that can be caused by hypertrans-location or backtracking.^14,15,42,43 More generally, the stochastic aspects of translocation are expected to be largely responsible for the frequent occurrence of such pausing.^21,44 Our results suggesting that individual nucleotides and especially the RNA 3′-end are more prone to thermal fluctuations add atomic level details to this picture.

Our work on the closed complex was confined to an unconstrained simulation without bound ligands and in the pretranslocated position. Further insights into the close interplay of conformational changes with translocation could be gained by analogous samplings of translocation states within the closed complex, both with and without bound PPi, which we leave for future work. A plausible scenario based on the current results, however, is that the free-energy profile G(x) for the average translocation would shift its stable minimum to the pretranslocated state (as supported partially by the unconstrained simulation of the closed pretranslocated state in Fig. 6), while the corresponding landscape G(x₂) for the RNA 3′-end would again largely remain flat. With PPi-release, the free-energy landscapes would shift to those shown in Figure 8, stabilizing the posttranslocated state. The RNA 3′-end, however, would likely be undergoing forward-backward translocational fluctuations between the pre-and posttranslocated states irrespective of the conformational states of the fingers domain (with the forward translocation of the +1 nucleotide of the TS completed before the opening of the fingers domain). These fluctuations would only be quenched and biased into the next translocation step upon binding of NTP as in Figure 2(C). Thomen et al.¹⁹ have recently performed a single molecule study of T7 RNAP EC translocation and concluded that the force–velocity behavior is consistent with a kinetic model of largely Brownian ratchet character, with the posttranslocated state slightly more stable than the pretranslocated state by ~k_BT. Higher (subnanometer) resolution experiments of T7 RNAP, as achieved recently for the multi-subunit E. coli RNAP,²⁰ can yield direct estimates of the free-energy profile as a function of the translocation reaction coordinate,²² and could provide critical tests of computational results reported here.

A number of effects not accounted for within our study of model ECs include any reannealing or breaking of base pairs between nucleotide strands that might occur in translocation events, which had not been directly controlled, and the effects of sequence heterogeneity on the free-energy.¹⁸ An ideal translocation event for the hybrid as a whole, in particular, would melt one base pair. We hope these effects could be examined in future computational studies based on the current work. Our results nevertheless demonstrate that the potential of mean force calculations using umbrella sampling can be applied to address the energetics of polymerase trans-locations.