Quasi-Supervised Scoring of Human Sleep in Polysomnograms Using Augmented Input Variables

Abstract

The limitations of manual sleep scoring make computerized methods highly desirable. Scoring errors can arise from human rater uncertainty or inter-rater variability. Sleep scoring algorithms either come as supervised classifiers that need scored samples of each state to be trained, or as unsupervised classifiers that use heuristics or structural clues in unscored data to define states. We propose a quasi-supervised classifier that models observations in an unsupervised manner but mimics a human rater wherever training scores are available. EEG, EMG, and EOG features were extracted in 30s epochs from human-scored polysomnograms recorded from 42 healthy human subjects (18 to 79 years) and archived in an anonymized, publicly accessible database. Hypnograms were modified so that: 1. Some states are scored but not others; 2. Samples of all states are scored but not for transitional epochs; and 3. Two raters with 67% agreement are simulated. A framework for quasi-supervised classification was devised in which unsupervised statistical models—specifically Gaussian mixtures and hidden Markov models—are estimated from unlabeled training data, but the training samples are augmented with variables whose values depend on available scores. Classifiers were fitted to signal features incorporating partial scores, and used to predict scores for complete recordings. Performance was assessed using Cohen's K statistic. The quasi-supervised classifier performed significantly better than an unsupervised model and sometimes as well as a completely supervised model despite receiving only partial scores. The quasi-supervised algorithm addresses the need for classifiers that mimic scoring patterns of human raters while compensating for their limitations.

Introduction

Sleep is increasingly the subject of debate in the context of public health [1, 2]. Disorders of sleep [3] are not only unique in the spectrum of illnesses but also accompany and complicate the management of other serious neurological conditions such as epilepsy [4], Parkinson's [5] and Alzheimer's disease [6]. Human sleep has been dissected broadly into five distinct states of vigilance: Wakefulness (W), rapid eye movement or REM sleep (R), and non-REM sleep (N) with stages N1, N2, and N3 that reflect increasing sleep depth. Sleep analysis typically involves overnight monitoring in a sleep lab resulting in a polysomnogram: i.e., a suite of continuous measurements that may include an electroencephalogram (EEG), electromyogram (EMG), electrooculogram (EOG), and electrocardiogram (EKG), among other physiologically derived signals. The polysomnogram is inspected by a human expert, who labels the predominant vigilance state in sequential epochs, each typically 30s in duration, for the entire recording. Despite the adoption of detailed guidelines [7] for labeling each vigilance state by practitioners of sleep medicine, and continuing efforts to automate the process, scoring sleep in polysomnographic recordings remains a tedious and subjective exercise. Even expert raters can be uncertain about the presentation of certain vigilance states and may vary widely in their assessment of specific recordings [8].

Computational tools that segment sleep either look for intrinsic patterns in the data [9-11] to define the predominant vigilance states or model a human rater's scoring of sample data and try to mimic her performance when applied to future recordings [12, 13]. These contrasting approaches, referred to as unsupervised and supervised classification respectively, are mutually exclusive; moreover, they do not explicitly address issues of rater uncertainty and disagreement. Here we propose a simple modification to the way classifiers are applied to sleep data to address three specific scenarios:

1. A human rater is more certain about the symptoms of some vigilance states than others;

2. A rater labels all the states, but only in samples where the evidence is unambiguous; and

3. One classifier needs to mimic a panel of raters with some variance in their scoring patterns.

In our algorithmic solution to these distinct but related problems, a set of features computed from each epoch of the polysomnogram is augmented, or tagged, with a vector variable whose value depends on the available score(s). This sequence of score-augmented input variables is used to train an unsupervised classifier—Gaussian mixture models (GMMs [14]) and hidden Markov models (HMMs [15]) are used here as illustrative examples—to map the continuous-valued features onto discrete vigilance states. Minor variations on this theme are used to address each of the scoring scenarios identified above and the performance of the classifier compared with appropriate reference methods.

Methods

Overview

Descriptive features were extracted from sequential signal epochs of overnight polysomnograms derived from an online database. For each recording, the hypnogram—i.e., the sequence of vigilance state labels assigned by a human rater—was systematically modified to simulate situations in which the rater was uncertain about the identity of certain states or epochs. The vector time series of features was fitted to two different statistical classifiers, a GMM and an HMM, using a novel quasi-supervised algorithm and used to predict the sequence of true vigilance states. The predictions were compared against the hypnogram to assess the ability of the proposed algorithm to compensate for missing or imprecise scores, and tested on a second night's recording from each subject when available. The performance of fully supervised and unsupervised classifiers on the same data was also assessed as reference cases.

Description of human subject data

This analysis is based on the Sleep EDF database [16] (available from www.physionet.org [17]). The database has a total of 61 overnight expert-scored PSG recordings from healthy individuals acquired with institutional oversight and informed consent. The data were collected from two different studies: 1. Sleep cassette (SC), which includes two successive overnight in-home recordings (except in one case) from 20 subjects (10 male and 10 female, 25-34 years old) without any medications; and 2. Sleep telemetry (ST), in which PSGs were recorded in-hospital, from 22 healthy subjects (15 female and 7 male, 18-79 years old) with mild difficulty falling asleep, for two nights, one after temazepam intake. However only the placebo night was available and used in our analysis. Besides the cohort and data acquisition methods, there are no other differences between the SC and ST data sets. The entire duration of each PSG (mean duration 8.3±1.1 h, n = 61) was used in our analysis and contains EEG (Fpz-Cz and Pz-Oz channels), EOG (horizontal) and submental EMG signals (100 Hz sampling rate) as well as a hypnogram of manual scores by a trained technician. The hypnograms, which mapped 30s epochs of data onto six states (non-REM 1-4, REM, and Wake), were relabeled per the current guidelines of the American Academy of Sleep Medicine [7] by combining non-REM stages 3 and 4. Hence, each hypnogram contained up to five labels: N1, N2, N3 for non-REM, R for REM, and W for Wake.

Signal feature selection and extraction

All analysis was performed using custom-written code on the Matlab™ environment (Mathworks Ltd., Natick, MA). Frontal EEG (Fpz-Cz) from each subject was bandpass-filtered into seven distinct frequency bands, specifically delta-low (0.5-2 Hz), delta-high (2-4 Hz), theta (4-9 Hz), alpha (9-12 Hz), sigma (12-16 Hz), beta (16-30 Hz), and gamma (30-45 Hz) using Butterworth IIR filters. The mean power fraction in each band was estimated in 30s epochs and combined into a vector of seven EEG features. The root-mean-squared (r.m.s.) values of broadband EMG and EOG were also included to give a vector X of nine features for analysis. All feature values were converted to a decibel scale, i.e., 10 log₁₀(·), to make the distribution more symmetric over their dynamic range and less sensitive to outliers. The choice of spectral bands reflects commonly recognized EEG rhythms; other selections of features may be used within the same modeling and analysis framework.

Sleep scoring algorithms

Supervised and unsupervised classification

A statistical classifier assigns sample measurements X to one of N discrete categories or classes S∈{1,⋯, N} by assuming a (usually parametric) statistical model of X → S. Examples of statistical classifiers are linear discriminant analysis (LDA), artificial neural networks (ANN), and support vector machines (SVM). In order to construct the statistical model, class-labeled training samples are usually required to estimate the parameters, and the model is referred to as a supervised classifier; all the above examples belong to this category.

Other models known as unsupervised classifiers can be used to fit models to unlabeled training data and predict the class membership of future observations. Such classifiers typically look for natural clusters in the data that may coincide with the classes of interest, in this case the sequence of vigilance states underlying the polysomnogram. Of course, the states modeled by an unsupervised classifier may not conform completely to an individual human rater's perceptions of class differences and are determined by the measurements and features used to estimate the model parameters. But such classifiers can still be very useful, especially when no prior class definitions are available; common examples are k-means, linkage trees, GMMs, and HMMs—though some of these may be supervised as well.

Here we describe a method for constructing quasi-supervised classifiers: models that tend to mimic a human rater's behavior when scoring information is available but look for structural clues in the training data when the available scores are selectively applied or uncertain. To demonstrate the feasibility of this approach, we use models that rely on Bayesian inference, specifically GMMs and HMMs.

Bayesian models, GMMs, and HMMs

We provide a brief overview of Bayesian models in the context of sleep scoring and the issues relevant to GMMs and HMMs. We emphasize intuition over mathematical rigor, and refer the interested reader to other sources for a formal theoretical treatment [14, 15, 18, 19].

First, we assume that the subject is always in one of N discrete, mutually exclusive vigilance states S∈{1,⋯, N}, and that a vector of M features $\mathit{X}={[x_1,\cdots ,x_M]}^T$, X ∈ ℝ^M (T = transpose), is extracted from samples of the signals in a polysomnogram in successive windows of time (e.g., 30 s duration), so that we have a set of observations X_1:T = {X₁,⋯, X_T} that are made in states S_1:T = {S₁,⋯, S_T}. Each value in set S represents a modeled state that may—but does not necessarily—correspond directly to a human rater-scored vigilance state (N3, N2, etc.). At an arbitrary time t, the subject may be in a vigilance state S_t but the state is quantified by the observation X_t. The classifier's task is to infer S_t from X_t with acceptable accuracy. It is expected that there will be some variability and noise in the estimation of X, and this is described by a probability density function f(X) which, when integrated over a region of X, gives a probability measure P(X).

Since the N states are mutually exclusive, the probability associated with an observation X integrates the probability that X is observed in any of the states: i.e.,

$$P(\mathit{X})=\sum _{S}P(\mathit{X}\cap S)$$ (1)

The probability that X is observed, when the state is known to be S, is the conditional:

$$P(\mathit{X}|S)=P(\mathit{X}\cap S)/P(S)$$ (2)

where P(S) represents the prior probability of state S in the absence of information about X. Eq. 2 is known as Bayes rule. From the above, we get an expression for the probability distribution of X in terms of the conditional and prior probabilities:

$$P(\mathit{X})=\sum _{S}P(\mathit{X}|S)P(S)$$ (3)

Starting from an observation X, we can now compute the posterior probability of state S as:

$$P(S|\mathit{X})=P(S\cap \mathit{X})/P(\mathit{X})=P(\mathit{X}|S)P(S)/P(\mathit{X})$$ (4)

A reasonable prediction of state is the one that maximizes the posterior:

$$\widehat{S}=\underset{S}{\text{argmax}}P(S|\mathit{X})$$ (5)

A Bayesian model must assume knowledge of the conditional P(X | S), usually in a standard parametric form, in order to make predictions. The GMM is one such model [14], in which P(X | S) is expressed as a Gaussian distribution parameterized by a state-dependent mean vector μ_S ∈ ℝ^N×M and covariance matrix Σ_S ∈ ℝ^M×M. Each Gaussian component contributes to the mixture to a degree expressed by a linear coefficient α_S, which replaces the state prior P(S) in Eq. 3. A GMM constructed from sleep data would assume that the observation X can be modeled as a mixture of Gaussian components, and that each component corresponds to one of the known vigilance states (or perhaps their sub-states).

HMMs [15] can be used to capture the evolution of a process over time and have been used for modeling the dynamics of sleep [10, 20-22] An HMM adds a layer of complexity to Eq. 3 by linking the model states to one another. The purpose is to model not just independent observations but the distribution P(X_1:T) of the ordered sequence (i.e., time series) of observations generated by a latent state sequence S_1:T. In this model, the current state exclusively determines the distribution of future states (viz. the Markov property):

$$P(S_t|S_{1:t-1},{\mathit{X}}_{1:t})=P(S_t|S_{t-1})$$ (6)

This quantity is known as a state transition probability; its values for all possible combinations of S_t−1 and S_t constitute an N × N state transition matrix γ, an essential property of the HMM. In addition to Markov transitions, the current observation is assumed conditionally independent of previous observations and states given the current state:

$$P({\mathit{X}}_t|S_{1:t},{\mathit{X}}_{1:t-1})=P({\mathit{X}}_t|S_t)$$ (7)

Along with a set of state priors π = P(S), fixing γ and the conditional P(X | S) completely specifies the structure of an HMM; an assumption of stationarity makes these properties independent of time t. In our treatment, the observation X is multivariate Gaussian, and the model is therefore a Gaussian observation HMM (GO-HMM) [23]. The simplifying assumptions made above permit the recursive application of elementary rules of probability (the product rule and Bayes' theorem) to make inferences regarding the dynamics of the process underlying observations X_1:T. A common problem solved using HMMs is to decode the sequence of states S_1:T most likely to have generated X_1:T. This is commonly accomplished using the Viterbi algorithm [15]. The algorithm is initialized by computing the distribution of the first observation X₁ as δ₁(S) = P(X₁ | S), for S ∈ {1,⋯, N}, and keeping track of the preceding state that maximizes the probability of each successive observation ${\delta }_t(S^{\prime })=\underset{S}{max}[{\delta }_{t-1}(S)\gamma (S,S^{\prime })]P({\mathit{X}}_t|S^{\prime })$. At termination, the optimal path probability is $P^{\ast }(S)=\underset{S}{max}{\delta }_T(S)$ and the terminal state is the one that maximizes P*(S). We can now backtrack along the sequence δ_t to identify the most likely predecessor at each step and recover the best state sequence S_1:T.

GMM and HMM parameters are estimated from training data using maximum likelihood (ML) techniques. In ML estimation [18], a likelihood function L is defined as the joint probability density of a set X_1:T of independent and identically distributed observations for the chosen model with parameter set Θ (e.g., Θ = {α_S, μ_S, Σ_S} for a GMM):

$$L(\mathrm{\Theta }|{\mathit{X}}_{1:T})=P({\mathit{X}}_{1:T}|\mathrm{\Theta })=\prod _{\mathrm{t}=1}^{\mathrm{T}}P({\mathit{X}}_t|\mathrm{\Theta })$$ (8)

Taking the logarithm on both sides converts the product into a sum over the sample data:

$$logL=\sum _{\mathrm{t}=1}^{\mathrm{T}}P({\mathit{X}}_t|\mathrm{\Theta })$$ (9)

The likelihood function L expresses the parameters as a function of the fixed observations. ML estimation proceeds by taking the partial derivative of log L with respect to each parameter, equating it to zero, and solving the resulting system of equations for the unknown parameters Θ that maximize log L (hence the name ML). When labeled training data exist, ML estimates of GMM and HMM parameters are relatively easy to derive and compute: for instance, the ML estimate of the true mean of state S is merely the arithmetic average of independent training samples labeled as S by a human rater; similarly for the covariance matrices, state priors, and transition matrix. If no labeled training data are available, the observations become related to the parameters through hidden variables (the states S_1:T) apart from the unknowns Θ, and we have:

$$logL=\sum _{\mathrm{t}=1}^{\mathrm{T}}P({\mathit{X}}_t,S_t|\mathrm{\Theta })$$ (10)

with unknowns on either side of the conditional. This is often intractable, since log L must now be maximized over all possible state paths for S_1:T to determine the correct maximum. One solution to this problem is to use an E-M algorithm (for Expectation-Maximization) [18]. E-M is an iterative process that converges to a local maximum when given an initial guess of the model parameters. In order to avoid getting trapped in a local trough, several initial guesses within the search space are tested and the solution with greatest likelihood is selected. A popular version of E-M used for HMMs is the Baum-Welch algorithm [15].

A framework for quasi-supervised classification

We have seen how GMMs and HMMs can be estimated and used to predict state when labeled or unlabeled training data are available. Though such models are widely used, there are no methods to address situations in which sample scores are limited or uncertain. Here we propose a simple method for building quasi-supervised classifiers that use partial scores to stage sleep.

Consider a scored polysomnogram from which a sequence of labeled observations X_1:T is derived. Let each X_1:T be augmented with another vector e = [e₁,⋯, e_K]^T so that

$${\mathit{Z}}^T=[{\mathit{X}}^T{\mathit{e}}^T]\Rightarrow \mathit{Z}\in {ℝ}^{M+K}$$ (11)

where K is the number of unique states labeled by the human rater (in the hypnogram). For instance, K = 3 if the rater labels R and W but does not distinguish between N1, N2, and N3 in non-REM sleep.

Just as for X_1:T, we can model Z_1:T as an N-state GMM with parameters Θ = {α_S, μ_S, Σ_S} by initializing the parameters with randomized seeds and following the E-M algorithm until it converges to the solution with greatest likelihood. The N modeled states are not necessarily identical to the K states scored by the rater. They must be selected by the user to suit the problem at hand. This flexibility is important in different scoring scenarios, as we will see below. Finally, the values in e are chosen based on the state label S_t assigned by a human rater to each observation X_t.

Let us start with K = 5 vigilance states (for N3, N2, N1, R, and W) scored from a polysomnogram in 30 s epochs. The time series X_1:T extracted from the signals can be fitted using an E-M algorithm to a GMM or HMM with N = 5 states. If the value of e_t is uncorrelated with S_t (for instance, always a zero vector), then the E-M algorithm simply yields an unsupervised classifier that optimizes the fit of the model to the observed data. If, on the other hand, e_t bears some correlation to the scored state S_t, we can expect the model to tend toward the human rater's scoring patterns. But S is a categorical variable, and therefore incompatible with X in the augmented vector Z. So what form should e take?

Recall that S takes on values from {1,⋯, K}. Let us define e so that:

$$e_j=\{\begin{array}{c}1\text{if}S=j\\ 0\text{otherwise}\end{array},j\in \{1,\cdots ,K\}$$ (12)

Each state S is now identified by a unit vector e in K dimensions. It follows that for two observations at times t and t′:

$${\mathit{e}}_t{\mathit{e}}_{t^{\prime }}=\{\begin{array}{c}1\text{if}{S}_t=S_{t^{\prime }}\\ 0\text{otherwise}\end{array}$$ (13)

That is, the set of values assumed by e form an orthogonal basis. This lets us incorporate the state label S, a categorical variable, into the quantitative description X of a sample without otherwise altering its properties or imposing an artificial ordering on the states. Adopting this definition for e in Eq. 11, intuition tells us that if X is now set to zero, the E-M algorithm will cluster the data strictly on the basis of scores S_t —in effect, a supervised classifier. Observations augmented with similar tags e will cluster since they are closer to each other in the augmented feature space ℝ^M+K than in ℝ^M; by the same logic, samples with unlike tags are farther apart and less likely to form a cluster. Hence tagging the training samples makes an unsupervised classifier behave like a supervised one. If the tags are excluded in the training step (or all set to be identical), the E-M algorithm converges to the unsupervised model. The tags incorporate the knowledge and intuition of a human rater into the parameter estimation. While the unsupervised and supervised asymptotes are illustrative and set bounds on the resulting model, it is situations where only partial scoring information is available that determines the utility of the quasi-supervised algorithm.

To conclude, the algorithm proceeds as follows (see Fig. 1): Available categorical scores S are transformed into vector “tags” e of length equal to the number of scored vigilance states K. The tags are attached to the vector of training observations X to give augmented input variables Z. Starting with randomized initial guesses for the model parameters, a GMM or HMM is estimated from Z using the appropriate E-M algorithm with the desired number of states N specified. After stripping entries corresponding to the tag e from parameters μ_S and Σ_S, the model is then used to predict the state in epochs for which scores are unavailable or uncertain based on un-augmented observations X (i.e., not Z). This approach is quasi-supervised in that model parameters are estimated using exactly the same methods as for unsupervised classifiers—except that the samples are tagged with a score-based vector—but converges to a strictly supervised classifier when complete scoring information is incorporated into the training data. The choice of score tags e is critical and can be tailored to address different typical scoring scenarios, as illustrated below.

Figure 1.

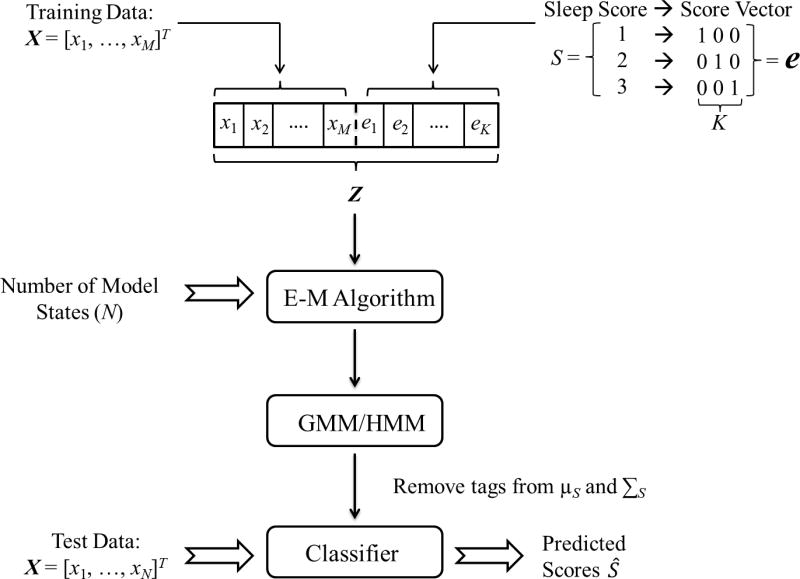
Flow diagram for quasi-supervised classification. A vector X of M features is computed from each epoch of a polysomnogram. The sleep score S is converted into a unit vector e whose length depends on the number K of states scored by the rater. X is augmented with e to give Z, the input to an E-M algorithm, which estimates the parameters of the GMM or HMM that maximizes the likelihood that a model with N≥K states explains the data. The excess dimensions are removed from the mean vector μ_S and covariance matrix Σ_S of each state in the model. The model is then used to classify new unlabeled inputs X, or the same data in which only K states were previously labeled, into N states.

Analysis procedure

The general procedure followed for analysis is the same for Problems 1 to 3 below except where noted. First, surrogates were prepared from the available hypnograms based on the requirements of each problem. Then samples of the observation vector X were augmented with a scoring vector e chosen from one of K unique values corresponding to the states scored on the surrogate hypnogram (Fig. 1). The number of states, N, to be modeled was fixed and the score-augmented variables used to estimate GMM and HMM parameters through an E-M algorithm. The models were used to predict the sequence of vigilance states in each polysomnogram and on a second night's data when available. Performance was assessed in terms of Cohen's K statistic [24], which measures the agreement in categorical scores on a sample scored by two independent raters. K was used here to assess concordance between the model predictions and true hypnogram, separately for each vigilance state and then for all states pooled together. These metrics were compared for the quasi-supervised method against reference methods in which the same algorithm was applied, but in a completely unsupervised (no tags) and completely supervised (unit basis vector tags used for all five states: K=5) manner. This is intended to help evaluate the extent to which the quasi-supervised classifier is able to compensate for incomplete score information in the training data. Since each polysomnogram is analyzed independently by the three algorithms, differences in K for the cohorts (same night and second night) were investigated using a Wilcoxon sign rank test separately for the quasi-supervised classifier versus the unsupervised and supervised classifiers respectively. In each comparison, a false positive probability p under 0.01 was considered statistically significant.

Problem 1: Human rater is uncertain about certain vigilance states

Here we consider the situation in which the rater is confident of identifying some states but not others. For instance, she is sure of the distinction between W, R, and N, but not stages of N, i.e., N1, N2, and N3. Hence labels are not available for three of the five states and completely supervised classification is not possible. On the other hand, unsupervised classification does not take advantage of the available scores for W, R, and N. In our quasi-supervised approach, we collapse stages of N into one label on the hypnogram (K = 3), and tag W, R, and N with unit vectors e (specifically [1 0 0]^T for N, [0 1 0]^T for R, and [0 0 1]^T for W) but fit the data to a GMM or HMM with N = 5 since we wish to recover all the vigilance states. The expectation is that W, R, and N will be separated by the E-M algorithm based on their disparate tags, but that three natural partitions or sub-states corresponding to N1, N2, and N3 will be required to adequately fit the model to samples of N based on the distribution of X.

We test the utility of this approach in situations where the rater does not distinguish between the following states: I. N1, N2, and N3; II. N1 and W; III. W and R; IV. N1 and N2; and V. N1 and R. These choices reflect typical sources of confusion faced by human raters in scoring sleep [8, 33, 41].

Problem 2: Human rater scores all vigilance states, but only labels epochs with clear manifestations

Suppose that the rater labels samples of all five vigilance states, but only those epochs for which he is sure of the predominant state. This can happen at the transitions between different states or in the presence of artifacts. We simulate this situation by deleting the scores from three successive epochs at each state transition in the hypnogram. In the solution, the score tags e are set to orthogonal unit vectors of length K = 5 but to a zero vector for unscored epochs. In the modeling step, as in Problem 1, we specify N = 5 states. Since e for unscored epochs is equidistant from all the unit vector tags in ℝ^K, the E-M algorithm allocates scored epochs to the five states according to the tag e, but distributes the unlabeled epochs among these states based on X.

Problem 3: Two or more raters score a polysomnogram and one model is to be trained, but there is some level of disagreement between them

Here, each rater produces a hypnogram but there is only one sequence of observations to be modeled. Since only one rater's scores were available for each recording, we simulated a scenario in which two or more human raters disagree about one-third of the time by generating surrogate hypnograms in which 33% of randomly selected epochs had their scores deleted. The quasi-supervised classifier was then used to complete the scores and its performance evaluated against the original hypnogram. While this is not strictly identical to the case of inter-rater disagreement, it is expected that it is a reasonable simulation of that scenario.

Results

Table I summarizes the incidence of states N1, N2, N3, R, and W in each hypnogram in terms of the number of 30 s epochs and the percent time spent in that state. Results of analysis for Problems 1, 2, and 3 using HMMs are presented in Tables II-IV. The corresponding results obtained using GMMs are presented in the Supplement and are referred to as Tables S1, S2, and S3. The performance of HMMs was consistently better than GMMs, with the same trends being observed in different scenarios.

Table I.

Distribution of sleep states per PSG.

State	First night (n = 42)		Second night (n = 19)
State	Epochs	% Time	Epochs	% Time
N3	146±12	15±1	149±17	16±2
N2	445±20	45±2	460±33	45±2
N1	79±7	8±1	61±8	6±1
R	188±9	19±1	188±13	18±1
W	127±10	13±1	153±9	15±1

All values reported as mean±standard error.

Table II.

HMM classifier accuracy K¹ for Problem 1 (first night PSG; n = 42).

	Scenario:	I (N1, N2, N3 pooled)	II (N1 and W pooled)	III (W and R pooled)	IV (N1 and N2 pooled)	V (N1 and R pooled)
	Unsupervised	63±4*	64±3	64±3	64±3	64±3
N3	Quasi-supervised	60±4	73±4	75±4	76±4	73±4
	Supervised	83±2	83±2	83±2†	83±2†	83±2
	Unsupervised	51±2*	51±2	50±2	51±2	49±2
N2	Quasi-supervised	57±3	70±2	73±2	69±2	69±2
	Supervised	82±1	82±1	82±1	82±1	82±1
	Unsupervised	14±3	16±3*	14±3	16±3	13±3
N1	Quasi-supervised	35±4	22±4	52±4	34±4	6±3
	Supervised	66±2	66±2	66±2	66±2	66±2
	Unsupervised	59±3	58±4	57±3	60±3	57±3
R	Quasi-supervised	90±1	89±1	68±4	91±1	74±2
	Supervised	90±1†	90±1†	90±1	90±1†	90±1
	Unsupervised	51±4	50±5	51±5*	49±5	51±4
W	Quasi-supervised	81±2	62±5	46±6	80±3	79±3
	Supervised	87±1	87±1	87±1	87±1	87±1
	Unsupervised	50±2	50±2	49±2	50±1	49±1
All	Quasi-supervised	65±2	68±2	68±2	73±2	65±2
	Supervised	83±1	83±1	83±1	83±1	83±1

¹Cohen's kappa (mean±standard error).

^*Quasi-supervised model is not significantly different (p > 0.01) from unsupervised model according to a Wilcoxon sign rank test (matched samples).

^†Quasi-supervised model is not significantly different (p > 0.01) from supervised model according to a Wilcoxon sign rank test (matched samples).

Table III.

HMM classifier accuracy K¹ for Problem 1 (second night PSG; n = 19).

	Scenario:	I (N1, N2, N3 pooled)	II (N1 and W pooled)	III (W and R pooled)	IV (N1 and N2 pooled)	V (N1 and R pooled)
	Unsupervised	58±7*	59±6	59±6	57±7*	56±7*
N3	Quasi-supervised	59±6	74±5	72±5	69±6	67±5
	Supervised	76±4	76±4†	76±4†	76±4†	76±4†
	Unsupervised	44±5*	46±5	47±5	44±5	46±6
N2	Quasi-supervised	55±4	66±4	66±3	62±4	65±4
	Supervised	72±3	72±3†	72±3†	72±3	72±3†
	Unsupervised	8±3*	7±3*	6±3	6±3*	7±3*
N1	Quasi-supervised	18±5	15±5	26±5	14±4	4±3
	Supervised	23±5†	23±5†	23±5	23±5†	23±5
	Unsupervised	41±7	40±7	39±7	40±7	40±7
R	Quasi-supervised	62±7	67±5	58±6	67±6	59±6
	Supervised	69±6†	69±6†	69±6	69±6†	69±6
	Unsupervised	54±6	51±7*	54±6*	56±5	57±5
W	Quasi-supervised	65±5	63±5	55±7	71±5	71±5
	Supervised	74±5†	74±5	74±5	74±5†	74±5†
	Unsupervised	44±4	44±4	45±4	44±3	45±4
All	Quasi-supervised	56±3	63±3	61±3	62±3	60±3
	Supervised	69±3	69±3†	69±3†	69±3	69±3

¹Cohen's kappa (mean±standard error).

^*Quasi-supervised model is not significantly different (p > 0.01) from unsupervised model according to a Wilcoxon sign rank test (matched samples).

^†Quasi-supervised model is not significantly different (p > 0.01) from supervised model according to a Wilcoxon sign rank test (matched samples).

Table IV.

HMM classifier accuracy K¹ for Problem 2 and Problem 3.

		Problem 2		Problem3
		First night PSG (in-sample test; n = 42)	Second night PSG (out-of-sample test; n = 19)	First night PSG (in-sample test; n = 42)	Second night PSG (out-of-sample test; n = 19)
	Unsupervised	63±3	57±6*	64±4	62±4
N3	Quasi-supervised	73±4	66±7	73±4	74±3
	Supervised	83±2	76±4†	83±2	80±2
	Unsupervised	50±2	46±5	50±2	51±3
N2	Quasi-supervised	75±2	71±3	77±1	72±3
	Supervised	82±1	72±3†	82±1	77±2
	Unsupervised	12±3	9±4	13±3	8±2
N1	Quasi-supervised	36±4	18±4	35±4	24±4
	Supervised	66±2	23±5†	66±2	45±4
	Unsupervised	58±3	39±7	59±3	52±4
R	Quasi-supervised	88±1	66±6	81±3	70±4
	Supervised	90±1	69±6†	90±2	80±3
	Unsupervised	51±4	56±6*	53±4	61±4
W	Quasi-supervised	73±3	64±5	66±5	73±4
	Supervised	87±1	74±5	87±1	83±3
	Unsupervised	49±2	45±4	50±1	50±3
All	Quasi-supervised	74±1	64±3	74±1	69±3
	Supervised	83±2	69±3	83±1	77±3

¹Cohen's kappa (mean±standard error).

^*Quasi-supervised model is not significantly different (p > 0.01) from unsupervised model according to a Wilcoxon sign rank test (matched samples).

^†Quasi-supervised model is not significantly different (p > 0.01) from supervised model according to a Wilcoxon sign rank test (matched samples).

Problem 1. Only some vigilance states are scored by the human rater

Tables II and S1 give the performance of the quasi-supervised algorithm in terms of Cohen's K, compared to completely unsupervised and supervised implementations, for a GMM and HMM. Results are presented separately for each state and finally for all states together. Five different scenarios are explored in which some of the vigilance states were assigned identical scores to simulate scoring uncertainty: Case I. N1, N2, and N3; Case II. N1 and W; Case III. W and R; Case IV. N1 and N2; and Case V. N1 and R. Each entry in the table represents Cohen's K averaged over 42 overnight PSGs along with the standard error of the mean.

In general—with a few exceptions for individual states—the proposed quasi-supervised classifier performs significantly better in terms of K than the unsupervised model but not as well as the completely supervised model, which represents the maximum attainable performance when complete scoring information is available. When all states are considered, K for the quasi-supervised classifiers is within the 60-80% range, which is thought to indicate excellent agreement [25]; in fact, K of 80% for five states in equal proportion would mean almost perfect agreement, which is highly unlikely in practice. In contrast, K for the unsupervised classifiers is close to 50% in all cases, i.e., moderate agreement. The HMM almost always outperformed the GMM but only by a small margin. When examining the predictions for each hypnogram, the difference was attributed to noise fluctuations in the GMM predictions that are smoothed by the HMM, which optimizes the entire sequence rather than the state in each epoch without context (see Fig. 2).

Figure 2.

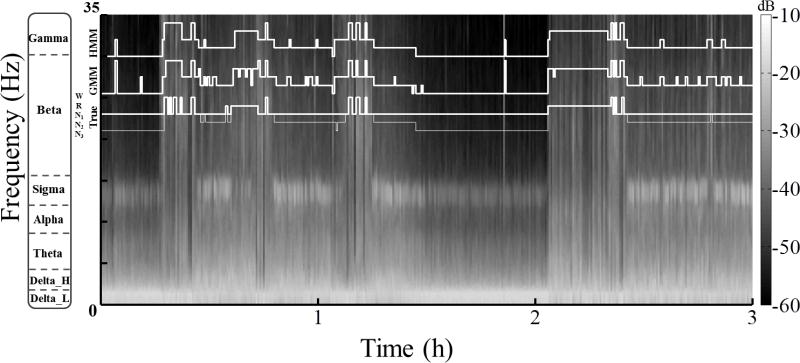
Automatic sleep scoring when only some states are labeled by the human rater in the training data (Problem 1). The figure shows a 3 h sample (starting at 2 a.m.) from a spectrogram, i.e., the distribution of signal power in decibels (dB) by frequency over time, computed for an 8 h recording in 30 s epochs of EEG from Fpz-Cz. Overlaying the image are staircase plots of the True five-state hypnogram (thin line); the surrogate three-state hypnogram (thick line), which does not differentiate between N1, N2, and N3; and the hypnograms predicted by the quasi-supervised GMM and HMM, which were trained using input features augmented with a score vector derived from the surrogate hypnogram. A comparison of model predictions with the true hypnogram shows that the GMM and HMM are able to reconstruct the unlabeled states with reasonable accuracy even as they track the human rater's scores of the labeled states. The HMM is less susceptible to noise fluctuations than the GMM, resulting in slightly better performance.

In each of the five case studies of selective scoring examined, the quasi-supervised classifier significantly improved on the unsupervised model for states that were not scored (in the surrogate hypnogram), but not to the extent that it matches the supervised model; for the scored states however, the quasi-supervised classifier rivals the supervised classifier in performance. This indicates that the proposed algorithm is able to track the human rater when scores are available but can still uncover the unscored states by modeling variability in the observed data. Fig. 2 illustrates this using a spectrogram derived from a sample polysomnogram. Although the scores used to construct the quasi-supervised models did not differentiate between N1, N2, and N3, the GMM and HMM are both able to recover the scores for these states quite well, thus saving the human rater the inconvenience of having to make these distinctions.

K appeared to be relatively low for N1, even for the supervised classifier, in all five case studies. This is easily explained by the very low incidence of N1 in the data (see Table I), which means that there are few samples for any of the classifiers to train on or distinguish from the other vigilance states. In truth, stage N1, occurring at the transition between W and N2, is notoriously hard to distinguish. While W is more easily characterized by elevated muscle tone and active EOG, and N2 displays distinctive transients such as sleep spindles and K complexes, N1 is in a gray area that human raters find hard to demarcate. These factors taken together contribute to the poor classification performance on N1. A second night's recording was available in 19 of the 42 subjects analyzed. For these subjects, Tables III and S2 give the performance of each classifier trained on the first night of recording but applied blind to data from the second night. Unlike Tables II and S1, which represents a composite of performance with and without scoring information on the same data set, the results in Tables III and S2 are strictly derived from out-of-sample classification. As expected, K for all states together was lower for all three approaches, unsupervised, quasi- and supervised while following similar trends to those noted in Tables II and S1 when comparing scored versus unscored states and GMMs versus HMMs. K for the quasi-supervised classifier was close to 60%, which is lower than in Tables II and S1 but still acceptable, especially when considering that K for the unsupervised classifier now dwells close to 45%; nor is the supervised classifier that much better at 65-70%.

Problem 2. Only some epochs are scored, but for all vigilance states

Results for Problem 2 are presented in Tables IV and S3. The overall performance of the quasi-supervised classifier is somewhat improved by a few points relative to Problem 1 for the first night analysis as well as for the second night, which is completely out-of-sample data. This is to be expected since sample scores are available here for all five vigilance states (except at the transitions between states) and the algorithm is not forced to come up with its own definitions. Of course, the unsupervised and supervised classifiers perform about the same as before since the scoring information provided to them is unchanged. From the spectrogram in Fig. 3, it can be seen that the model appears to fill in the missing scores at the transitions between states in a reasonably satisfactory manner.

Figure 3.

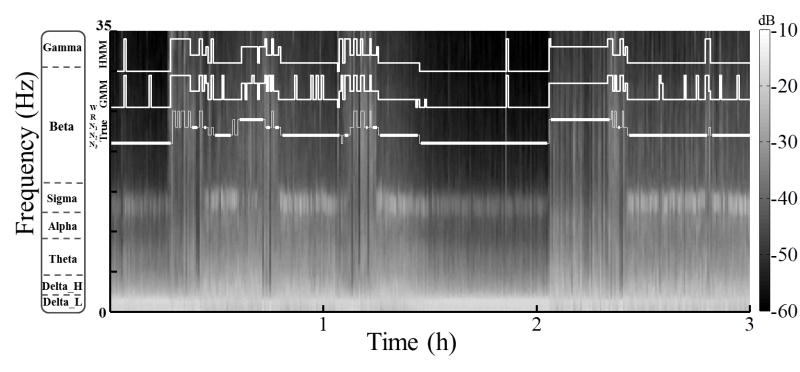
Automatic sleep scoring when all states are labeled by the human rater, but not for all epochs in the training data (Problem 2). The figure shows a 3 h sample (starting at 2 a.m.) from a spectrogram, i.e., the distribution of signal power in decibels (dB) by frequency over time, computed for an 8 h recording in 30 s epochs of EEG from Fpz-Cz. Overlaying the image are staircase plots of the True five-state hypnogram (thin line); the surrogate five-state hypnogram (thick line), in which scores are deleted for three successive epochs at each state transition; and the hypnograms predicted by the quasi-supervised GMM and HMM, which were trained using input features augmented with a score vector derived from the surrogate hypnogram. A comparison of model predictions with the true hypnogram shows that the GMM and HMM are able to track changes in vigilance state across state transitions.

Problem 3. One classifier must be constructed based on the sample scores of multiple raters

Tables IV and S3 also summarizes results for Problem 3. The performance of the GMM and HMM classifiers for in-sample and out-of-sample data is very similar to that obtained for Problem 2. It shows that even when a full third of the data is left unscored, the model is still capable of filling the blanks with reasonable accuracy.

Discussion

Computerized sleep scoring is desirable because with it comes the prospect of objective, data-driven segmentation of vigilance states that can consistently be applied to get reproducible output. Unsupervised sleep scoring has been pursued almost since the advent of digital EEG. The earliest efforts encoded heuristics used by experts in their visual analysis to process spectral measures or other quantitative features of polysomnographic signals and divide them into different states of vigilance [26, 27]. The goal was to produce a reasonable first pass segmentation that could quickly be refined by an expert into a final sequence of scores. Not surprisingly, advances in machine learning techniques have prompted various approaches—particularly probabilistic models—to the task of finding natural partitions in sleep data that could correspond to different vigilance states. The HMM is one such modeling technique that maps continuous observations onto discrete hidden states [15]. Early statistical models of sleep dynamics used Markov chain models to represent probabilistic transitions between stages of sleep extracted from expert-scored hypnograms [28]. These models have become more refined and are being used to characterize disordered sleep and the effect of medication [29, 30]. The HMM is a natural extension of the Markov chain that assumes the polysomnogram to comprise a sequence of observations generated by Markov states that are hidden from view [15]. This has contributed to its popularity in automatic sleep scoring [10, 20-22]. HMM parameters are usually estimated using unsupervised ML techniques; so the modeled states are not biased by human opinion. They are, however, dependent on the features chosen to represent the data and how much they vary between vigilance states.

Unsupervised scoring can give very reasonable results without prior training, but must ultimately satisfy the gold standard of human assessment. Despite well-defined guidelines—first suggested in the 1960s [31]—that have evolved over time to reflect a growing consensus [7, 32], agreement between human raters scoring the same recording is hardly perfect and can be quite variable. One recent study comparing sleep scores between raters from two laboratories in different countries [8] found only moderate agreement for controls (mean K = 0.57) that was still lower for a cohort with narcolepsy (mean K = 0.54). The greatest disagreement was seen between scores for stages N1 and N2, N2 and N3, and N1 and W; in Problem 1, we used our algorithm to distinguish between these states without supervision. A larger study [33] with independent raters from nine centers found better overall agreement (mean K = 0.63) although agreement by sleep stage still varied over a wide range. A rater has opinions forged by his or her training that can mutate over time and with experience. For this reason it is difficult to predict to what extent an unsupervised classifier will agree with a particular human rater.

There is another perhaps more obvious motivation for automatic sleep scoring: a computer algorithm may never be perfect in the eyes of one rater or another, but it can be programmed to behave like one. Models built for this purpose are known as supervised classifiers. A statistical model can be trained to mimic the scoring habits of a particular human rater, thus alleviating (if not eliminating) the burdensome task of manual scoring. Supervised sleep scoring also has a long history. Early efforts have used discriminant analysis [34] and distance metrics [35] of from samples of human-scored vigilance states to determine the scores of incoming data. Fisher discrimination, in which the input features are transformed to optimize the separation between samples of different states, has also been employed. More recent supervised schemes continue to make their way into this domain as and when they are developed or as increases in computing power makes it feasible to do so: these include linear discriminant analysis [36], neural networks and their variants [37], support vector machines [38], and random forest classifiers [39]. Increased computing power has also made it feasible to enlarge the feature space in a bid to better fit training data and improve performance. But the true measure of a supervised classifier remains its ability to accurately score new recordings, i.e., out-of-sample data. The ability of a classifier trained on one cohort (e.g., healthy controls) to score data from another cohort (e.g., individuals with possible sleep disordered breathing) remains a concern.

We have discussed how unsupervised classifiers can model observations unconstrained by human-defined vigilance states, and how supervised classifiers can encode and mimic a specific human rater's scoring patterns. The middle ground in which a classifier seeks its own definitions but defers to human judgment when required has not been explored. In this manuscript, we have described an algorithmic framework that compensates for rater uncertainty and incomplete training data to automatically score sleep in a polysomnogram. We accomplish this quasi-supervised classification by transforming categorical sleep scores into numerical variables or tags that link the scores to continuous-valued features extracted from the data. This sleight of hand allows an essentially unsupervised classifier to compensate for scoring uncertainty and for partial or incomplete scores in the training data. Three problem scenarios were explored using this framework:

1. In which only some states are scored by the human rater

Here the quasi-supervised model recognizes that the system may have more states than identified by the scorer. By augmenting samples of the scored states with unique tags, the classifier identified scored states with accuracy comparable to a completely supervised classifier but still distinguished unscored states in the manner of an unsupervised classifier. Consequently, overall performance on in-sample and out-of-sample data is somewhere between these extremes.

2. In which all vigilance states are scored, but not all of the epochs

In this scenario, the rater is uncertain of the prevailing state during some periods of the recording. We make the reasonable assumption that this is most likely during transitions between states and do not use those scores in the modeling step. The results demonstrate that the quasi-supervised classifier was able to fill in the blanks with reasonable accuracy, sometimes as well as the supervised classifier.

One question that might arise is whether a quasi-supervised method is really needed for addressing Problem 2. Since training samples are available for all the vigilance states, it seems that a completely supervised classifier of any sort could be trained to predict sleep scores. This is true, but only for “static” classifiers such as LDA, which model individual observations and not sequential data. For an incomplete state sequence, a supervised HMM cannot be constructed without additional considerations. The quasi-supervised algorithm proposed here allows us to proceed using an E-M algorithm for unsupervised model estimation by augmenting observations from scored and unscored epochs with distinctive tags that reflect the rater's opinion when available.

3. In which multiple raters score all the epochs and states, but sometimes disagree

Since only one professional scoring was available for the analyzed data, we generated surrogate hypnograms from the available ones to simulate the scenario in which raters disagree one-third (33%) of the time. Then a GMM/HMM was constructed using the quasi-supervised algorithm from the incomplete hypnograms in which scored epochs represent the putative consensus between multiple human raters. As was seen in Problem 2, the algorithm performed reasonably well in completing the scores.

We have treated Problems 1, 2, and 3 in isolation, but they could co-occur in a given scenario: for instance, multiple raters partially score each hypnogram based on their certainty/uncertainty with respect to some states/epochs, but with some level of disagreement. Although this composite scenario certainly merits discussion, a rigorous analysis would be more useful when two or more independent raters are actually available (rather than the simulation of consensus hypnograms that we have used in Problem 3).

In conclusion, we have described a framework for quasi-supervised classification that may prove useful for clinical sleep scoring and also for investigating the properties of vigilance dynamics through polysomnographic recordings. The proposed method is flexible enough to accommodate different situations in which scoring uncertainty occurs and computer assistance is desirable. There are some limitations in the method as presented at this time: First, since the classifier is constructed around an unsupervised learning algorithm, states that are not previously labeled by the human rater must still be identified with known vigilance states (or sub-states thereof). Here we have completed that assignment by finding the best matching state within the complete hypnogram, which is not feasible in practice. For instance, in Problem 1 the rater may identify only N, R, and W, but not stages of N. We have fitted the incompletely scored data to a five-state model on the assumption that the two excess states will emerge from N as a product of the E-M algorithm. While this was always the case in the recordings analyzed here, it need not always be so. Consider a sample from a different cohort—for instance a more elderly one—in which deep sleep (N3) is absent or poorly represented [40]. A five state model of this data may have support for N1 and N2, but the remaining state may be carved out of the distribution of X under R or W rather than N3. More investigation is necessary for defining objective criteria for labeling model states that are better aligned with human-recognized vigilance states. A graphical analysis of the linkage between the states on the basis of the ordering of common spectral measures (e.g., delta/theta power ratio, EMG amplitude) may help resolve this problem.

Secondly, while the algorithm appears to match the rater's opinion for those states that were scored in the training data, the remaining states that are identified must still appeal to the end user by some yardstick. This is not a straightforward concern to address. We speculate however that the use of quasi-supervised classifiers could, over time, help resolve discrepancies between data-driven definitions and human perceptions of vigilance. The framework proposed here for sleep scoring provides a fresh perspective on human-computer interaction that calls for further investigation.

Finally, although the quasi-supervised algorithm was applied here to data from healthy subjects, the methods do not rely on the assumption of normal sleep patterns. They are likely to apply to disordered sleep as well—for instance, the algorithm performed equally well on the ST database, in which patients reported mild difficulty falling asleep. Performance on other conditions in which sleep quality is compromised, such as in epilepsy or REM sleep behavior disorder, remains to be seen and is deferred to a future investigation.

• Three common problems associated with clinical sleep scoring are identified.

• A quasi-supervised classification framework is proposed to address these problems.

• The proposed framework compensates for rater uncertainty with reasonable accuracy.