Abstract
Individuals’ risk attitudes are known to guide choices about uncertain options. However, in the presence of others’ decisions, these choices can be swayed and manifest as riskier or safer behavior than one would express alone. To test the mechanisms underlying effective social ‘nudges’ in human decision-making, we used functional neuroimaging and a task in which participants made choices about gambles alone and after observing others’ selections. Against three alternative explanations, we found that observing others’ choices of gambles increased the subjective value (utility) of those gambles for the observer. This ‘other-conferred utility’ was encoded in ventromedial prefrontal cortex, and these neural signals predicted conformity. We further identified a parametric interaction with individual risk preferences in anterior cingulate cortex and insula. These data provide a neuromechanistic account of how information from others is integrated with individual preferences that may explain preference-congruent susceptibility to social signals of safety and risk.
Incorporating information from others into one’s own decisions can either be evolutionarily advantageous1 or yield deleterious consequences2. Although many studies have shown social influences on decision-making and attitudes3-7, the mechanisms via which individuals’ decisions incorporate others’ choices with such varying outcomes remain unknown. Here, we drew from the large literature indicating that private decisions about risky options are guided by both objective signals (that is, probability and expected values) and subjective preferences8,9, and adapted this model-based framework for explaining susceptibility to social influence during decision-making under risk. Our results provide neural and behavioral evidence that others’ choices of risky options increase the subjective value (utility) of those options and does so in a manner that varies with individual preferences, thereby explaining why the same objectively risky choice by others may be perceived as a ‘gentle nudge’ for the risk-preferring individual and a ‘strong push’ for the risk-averse individual.
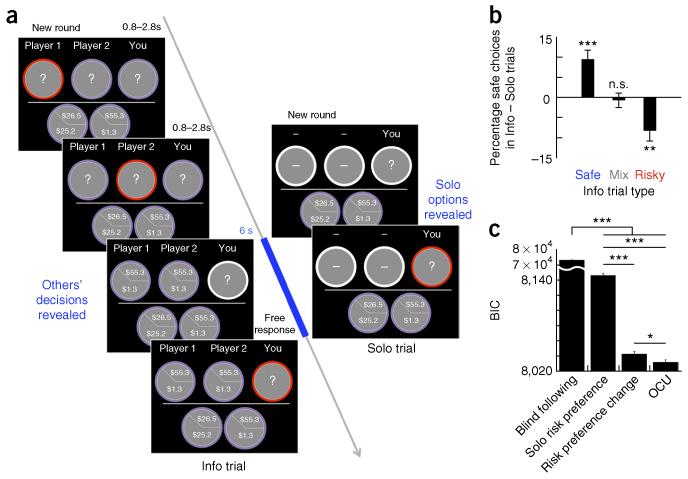
To examine how individuals incorporate information about social others’ choices during decision-making, we scanned 70 participants using functional magnetic resonance imaging (fMRI) as they made a series of choices between pairs of risky gambles alone and after viewing others’ decisions (Fig. 1a, Supplementary Fig. 1 and Online Methods). Each pair of gambles had the same high- and low-payoff probabilities, but differed in payoff spreads; thus, one gamble in each pair was objectively safer, with lower payoff variance, and the other was objectively riskier, with greater payoff variance (as described previously10; Supplementary Fig. 2 and Online Methods). Participants were instructed in groups of six and informed that, for some choices, they would be provided with information about anonymous other players’ selections (Info trials), whereas other choices would be made alone, without information about other players’ decisions (Solo trials). On Info trials, all participants played in the third position, making choices after two others’ choices were presented; this positioning was revealed only once participants were in the scanner. Participants were paid at the end of the study based on the outcome of a random single lottery drawn from all the experimental decisions the participant made, independent from any other players’ choices.
Figure 1.
OCU model best fits observers’ choices in the presence of others’ decisions about risky gambles. (a) Participants made choices between riskier and safer gambles, either alone (Solo) or with information shown about anonymous other players’ choices (Info). For each pair of gambles, the safer gamble had lower payoff variance, and the riskier gamble had greater payoff variance (Online Methods). On Info trials, two others’ decisions were displayed before the participant’s cue to enter a choice. Info and Solo trials were intermixed and drawn without replacement from a uniform distribution. (b) Relative to Solo trials, participants chose more safe gambles when the others’ choices were the safe gamble (Safe Info) and more risky gambles when the others’ choices were the risky gamble (Risky Info). Choices on Mix Info trials did not differ from Solo (repeated-measures ANOVA, F (3, 207) = 14.36, P = 1.55 × 10−6; paired t tests: Safe Info versus Solo, t(69) = 4.19, P = 0.000081; Risky Info versus Solo, t(69) = −3.14, P = 0.0025; Mix Info versus Solo, t(69) = −0.40, P = 0.69). (c) OCU for Info trials was estimated as an addition of utility in the direction (safe, risky) of others’ choices, leading to a new OCU-modified utility for each gamble in the Info trials (Uwith OCU = Usolo + OCU). Model comparison using BIC showed that the proposed OCU model best fit subjects’ choices compared against three alternatives: blind following, Solo risk preference and changes in risk preference (ANOVA, F(3, 276) = 1.79 × 106, P < 0.00001). Error bars represent s.e.m. *P < 0.05, **P < 0.01, ***P < 0.001, n.s. indicates not significant (see Online Methods for model specifications).
RESULTS
Social signals of safety and risk affect observers’ choices
Consistent with prior studies, when making Solo decisions10, participants’ choices in our paired choice lottery task revealed risk aversion (Supplementary Fig. 3a,b and Online Methods). Moreover, participants’ decisions on Info trials were strongly affected by the choices of others, such that, relative to Solo choices, participants chose the safer gamble more when both others’ choices were the safer gamble and chose the riskier gamble more when both others’ choices were the riskier gamble (Fig. 1b), regardless of payoff probability. No change in participants’ probability of choosing the safe gamble was observed when the others’ decisions were mixed (that is, one safe and one risky gamble; Fig. 1b and Supplementary Fig. 3c). In addition, a separate behavioral experiment instructing participants that Info trials were computer-generated random choices showed no influence of computer-generated options on participants’ choices (N = 30, no overlap with the N = 70 scanned participants, repeated measures ANOVA, F(3, 87) = 0.71, p = 0.55; Supplementary Fig. 4).
Other-conferred utility model explains choices under social influence
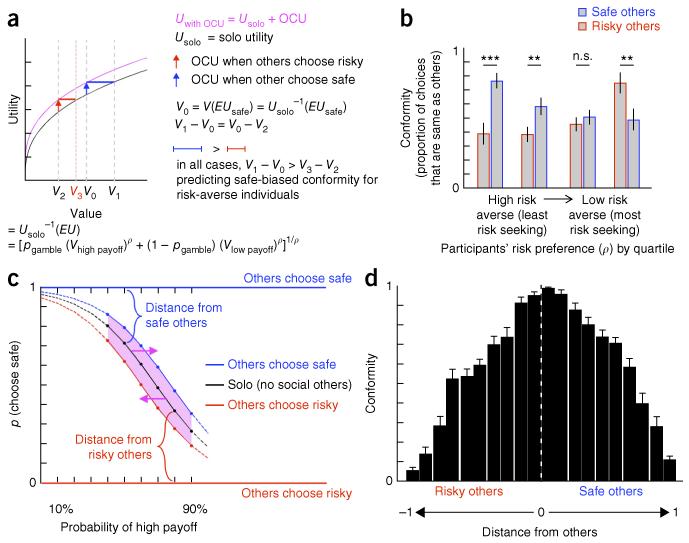
Economic utility theory has shown that private decisions about risky options are guided by both objective valuation and subjective preferences and provides a successful model for predicting participants’ choices among uncertain options8-11. We drew on this framework to evaluate potential neurobehavioral mechanisms explaining when and how individuals incorporate information from others into choices about uncertain options. The concavity (ρ) of power utility functions (of the form U(x) = xρ) has classically been used to capture individual differences in the tradeoff between value and utility12, with concave utility functions (ρ < 1) describing risk-averse individuals and convex utility functions (ρ > 1) describing risk-seeking individuals. We hypothesized that others’ choices of a gamble increase the utility of that gamble for the observer in the direction (safe, risky) of others’ choices, leading to an increased likelihood of that gamble being the preferred, and chosen, option of the observing participant. To test this possibility, we estimated other-conferred utility (OCU) for Info trials as an addition of utility to the gamble chosen by others, leading to a new OCU-modified utility for those gambles in the Info trials (Uwith OCU = Usolo + OCU; Fig. 2a and Online Methods).
Figure 2.
OCU predicts asymmetric, preference-dependent conformity and reduces distance between self and others. (a) The OCU model supposes Uwith OCU = Usolo + OCU, where OCU is an increase in utility of the (safe or risky) gamble chosen by others. The model and predictions are illustrated for ρ < 1 using U = xρ, our group estimates of ρ = 0.38 and OCU = 0.26, and, for clarity, a single menu10 of uniformly distributed gambles. Notice that, in all cases, the range of originally preferred gambles for which Uwith OCU from safe others exceeds Usolo (denoted by blue bar) is larger than the range for which Uwith OCU from risky others exceeds Usolo (red bar); thus, for risk aversion, the influence of safe others will always exceed that of risky others (simply, given concavity: V1 – V0 > V3 – V2). (b) The data support these predictions: risk-averse participants conformed more when others’ choices were safe, the bias decreased in less risk-averse participants, and, among the most risk seeking, the bias switched toward greater conformity when others’ choices were risky (paired t tests: first quartile, t(15) = −4.55, P = 3.85 × 10−4; second quartile, t(14) = −3.60, P = 0.0029; third quartile, t(15) = −1.46, P = 0.17; fourth quartile, t(14) = 3.55, P = 0.0032). (c) OCU translates (pink arrows) participants’ Solo decision probability (black line) along the x axis, resulting in reduced distance in choice probability between oneself and others and increased marginal likelihood (shaded in pink) of choosing the same option as others. (d) Participants showed greater conformity when others’ choices were closest to one’s Solo-preferred options (Pearson’s correlation, r = −0.96, P = 1.02 × 10−11, using |distance|). Error bars represent s.e.m. **P < 0.01, ***P < 0.001, n.s. indicates not significant (see Online Methods for model specifications).
This proposed OCU model explained participants’ choices on Info trials significantly better than a random-choice model (all choices at chance level; likelihood ratio test, χ2(3) = 64.06, pseudo-R2 = 0.48, P < 0.001) and three plausible alternatives. Specifically, formal model-comparison using Bayesian Information Criteria (BIC, lower values indicate better model fit) showed that the OCU model best fits participants’ choices on Info trials compared against: (i) blind following, wherein participants’ choices simply match those of others; (ii) Solo risk preference, in which participants’ risk preference estimated from Solo trials dictates choices on Info trials; and (iii) risk preference change, where the scaling parameter (ρ) of an individual’s power utility function changes in the presence of others’ choices (Online Methods). The smallest BIC was observed for the OCU model (Fig. 1c), which supports the hypothesized mechanism that others’ choices of an option increase the subjective value of that option (from Usolo to Uwith OCU), leading to an increased likelihood that participants will choose that option, and thus make the same choice as others.
A critical prediction of the OCU model is that preference-dependent asymmetries exist for the direction (safe or risky) in which others’ choices are likely to influence observers’ choices. That is, under OCU, risk-averse individuals are predicted to conform more with safe others, whereas risk-seeking individuals are predicted to conform more with risky others. This asymmetric effect of OCU is illustrated in Figure 2a for a uniformly distributed set of gambles and a risk-averse individual (plotted using our group level ρ = 0.38 from Solo trials). The x axis represents each gamble’s Usolo value (that is, V = Usolo−1 (EU), where EU = expected utility = [pgamble(Vhigh payoff)ρ + (1 − pgamble) (Vlow payoff)ρ]). We use as our reference point (V0) the value associated with the mean expected utility of safe gambles (V0 = Usolo−1 (EUsafe)), which is flanked to the left and right by values associated with risky gambles10. For decisions in which a risky gamble was the participant’s Usolo preferred gamble, but others chose the safe gamble, the resulting modified utility Uwith OCU (V0) exceeds Usolo for the originally preferred gambles between V0 and V1 (Fig. 2a). Thus, with OCU, the safe gamble chosen by others is now preferred over these originally preferred riskier gambles. Similarly, for decisions in which the safer gamble was originally preferred, but others chose a riskier gamble (for example, at V2, here mirroring V1 and symmetric around V0 for comparison), the resulting Uwith OCU (V2) exceeds Usolo for the originally preferred gambles between V2 and V3 (Fig. 2a). Given the concavity of a risk-averse individual’s power utility function, in all cases, the range of originally preferred gambles for which Uwith OCU from safe others will exceed Usolo (that is, from V0 to V1) is larger than the range for which Uwith OCU from risky others will exceed Usolo (that is, from V2 to V3); in other words, for risk aversion, the effects of safe others on an observer’s choices will always be greater than that of risky others.
A complementary example is provided in Supplementary Figure 5 showing that, for risk-seeking individuals (ρ > 1), the influence of OCU from risky others will always be greater than that of safe others. Our behavioral data support the model’s prediction of preference-dependent effects of safe and risky choices of others on observers’ decisions. Specifically, participants with the smallest ρ (most risk averse) were biased toward decisions that align with safe others, the bias decreased in participants who are less risk averse, and, among the most risk seeking, the bias switched in the direction of increased conformity with risky others (Fig. 2b and Supplementary Fig. 6a).
OCU increased the marginal likelihood on any pair of gambles that an observer would choose the same option as others, relative to that which would be predicted from their individually estimated solo risk preference. The utility boost was reflected in a lateral translation of the observer’s choice probability function (Online Methods), and the translation decreased the distance between others’ (risky or safe) choices and those predicted by an observer’s Solo risk preference (Fig. 2c). Thus, a feature of OCU is that decisions that are the same as others (that is, conforming or aligning) ought to be more likely when others’ choices are closer to that which one would make alone. This was seen in participants’ increased conformity at smaller distances between one’s own Solo preference–estimated choices and others’ decisions (Fig. 2d). The negative relationship between conformity and distance from others was observed independent of payoff probability (Supplementary Fig. 6b,c) and was present in 94% of participants.
Neural responses support OCU and preference-dependent effects on observers’ choices
To assess whether a neural instantiation of OCU exists, we performed event-related fMRI analyses of participants’ neural responses at the time at which they viewed others’ decisions (Info trials). These analyses revealed robust activation in ventromedial prefrontal cortex (vmPFC), a region known to encode subjective value or utility across domains and commodities during value-guided decision-making13,14. Specifically, ventromedial PFC responses varied parametrically with OCU-modified utility, but not with participants’ Solo utility of these gambles (Fig. 3a and Supplementary Table 1). Moreover, participants with greater sensitivity in vmPFC to OCU were more likely to conform with others’ choices; this relationship was not observed for Solo utility (Fig. 3b). The vmPFC sensitivity to OCU, coupled with this response predicting conformity above and beyond that for Usolo, supports the hypothesis that others’ choices about uncertain options confer increased value to those options, resulting in the greater likelihood that options aligning with others’ choices will be selected. We note that our focus was on neural responses for OCU-modified utility of chosen versus unchosen gambles (Uwith OCU chosen gamble – Uwith OCU unchosen gamble) as the broadest OCU-modified variables likely to be encoded, but other OCU-modified variables may contribute with varying weight to participants’ choices and ought to be topics of future investigation (see Supplementary Fig. 7 for potential other variables to which others’ choices may confer value).
Figure 3.
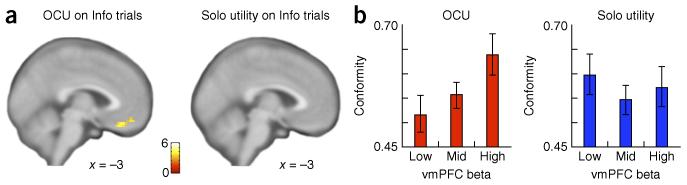
vmPFC encodes OCU and predicts conformity. (a) When viewing others’ choices, trial-by-trial OCU-modified utility was encoded in vmPFC (left; Uwith OCU chosen gamble – Uwith OCU unchosen gamble, displayed at P < 0.001 uncorrected, k > 15 contiguous voxels; cluster significant at P < 0.01 family-wise error (FWE), small volume correction (SVC)), whereas no neural responses were identified at this threshold that tracked Solo utility on Info trials (right; Usolo chosen gamble – Usolo unchosen gamble). (b) Left, vmPFC response from the cluster in the left panel of a was positively correlated with participants’ conformity (proportion of choices that are same as others’ choices; first eigenvariate of neural responses to Uwith OCU extracted from the cluster in a; Pearson’s correlation, r = 0.28, P = 0.035; confirmed with leave-one-out validation; Online Methods). Bars show mean conformity for participants with low, middle and high vmPFC responses to OCU (binned by tercile). Right, no relationship was observed between neural sensitivity to Solo utility and conformity (Pearson’s correlation, r = 0.012, P = 0.93; confirmed with leave-one-out validation, Online Methods; effect size comparisons between vmPFC betas predicting conformity: [betaUwith OCU – betaUsolo] predicting conformity versus betaUsolo predicting conformity, z = 2.02, P = 0.043). Error bars represent s.e.m.
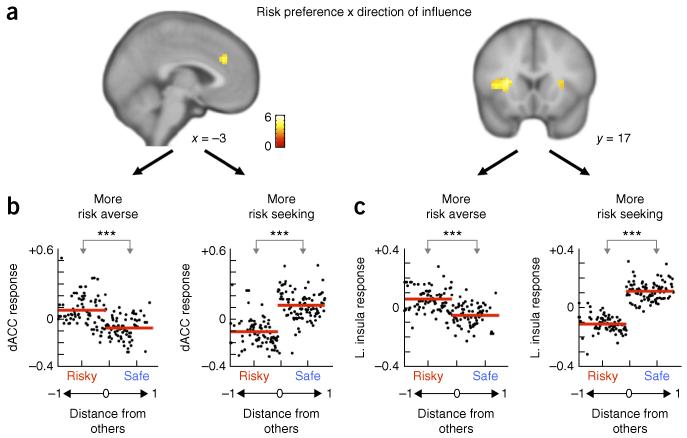
As discussed above, the OCU model revealed that individual risk preferences biased the influence of others’ choices. Consistent with this, the neuroimaging analyses revealed that trial-by-trial direction (that is, safe or risky) of others’ choices interacted with individual risk preferences in dorsal anterior cingulate cortex (dACC) and anterior insula (Fig. 4a and Supplementary Table 2), such that increased responses in these regions were identified for others’ choices that were incongruent with participants’ Solo risk preferences (Fig. 4b,c). That is, more risk-averse participants showed greater activation in both dACC and insula when others’ choices of risky gambles were displayed, whereas less risk-averse subjects showed greater activation when others chose the safer gambles (Fig. 4b,c). This pattern is consistent with the core roles of the dACC and insula in encoding conflict and variance8,9,15, including that in the social domain6. Of note, the neural sensitivity to direction of others’ choices was seen only when participants conformed; no significant neural encoding of direction was observed in non-conforming trials (P > 0.01 uncorrected). The specificity of dACC, insula and vmPFC responses to conforming trials points to a neurobehavioral integration of OCU with individual risk preferences that leads to choices that align (or not) with others’ decisions.
Figure 4.
dACC and insula track preference-dependent response to others’ choices. (a) On conforming trials, trial-by-trial direction (safe, risky) of others’ choices interacted with participants’ risk preferences in dACC and insula (displayed at P < 0.001 uncorrected, k > 15 contiguous voxels; the dACC was significant at P < 0.01 FWE, SVC; the insula was significant at P < 0.01 FWE). (b,c) For both dACC (b) and insula (c), participants showed increased responses to others’ choices that were incongruent with participants’ Solo risk preferences (participants’ first eigenvariate modulated by direction of influence; b left, t(714) = 11.85, P = 1.12 × 10−29; b right, t(847) = −19.49, P = 3.35 × 10−70; c left, t(714) = 13.55, P = 2.072 × 10−37; c right, t(847) = −31.31, P = 1.37 × 10−143). Trials pooled across subjects as a function of distance from others (Fig. 2c) are shown; each point is the average fitted response of the pooled trials at a given distance. Red lines indicate mean responses to risky and safe others. ***P < 0.001.
DISCUSSION
Our results provide a model-based explanation for variations in the influence of others’ choices on individuals’ decisions about uncertain options. Specifically, we present neural and behavioral evidence that others’ choices of gambles confer subjective value to those gambles and does so with preference-dependent consequences.
The vmPFC response to OCU is consistent with studies showing a key role of vmPFC in representing a common subjective value ‘currency’ across domains16-18. These studies found that the valuation signal is sensitive to social feedback19,20, even when controlling for the subjective value of stimuli21. However, whether and how social information is incorporated with internal preferences to affect decision-making remains unknown. Our data reveal that, in the presence of others’ decisions, vmPFC encodes an integrated signal combining the subjective value of information from others with one’s individual preferences, perhaps related to this region’s combining of self and other information that occurs during observational learning22,23 and actions made for others17. In our case, this valuation signal was seen independent of any revealed outcomes for self or others, existed over and above the Solo subjective valuation predicted by one’s risk preference, and predicted conformity beyond what participants’ Solo risk preferences would alone indicate.
The data also emphasize that choices that align with others both maximize utility and have the least distance between one’s risk preferences and others’ choices. Here, activations in dACC and insula encode the discrepancies between self preferences and others’ choices and are consistent with previous literature pointing to these regions’ roles in encoding variance, social discrepancies and other task-relevant conflicts5,6,8,9,18,24,25. In addition, the specificity of these neural responses to conforming trials suggests that alignment with others is a controlled, affective process when self-other discrepancy is high and supports the rejection of the simple blind following model for explaining conformity. More generally, these findings point to functional roles of insula, dACC and vmPFC in linking individual risk preferences with perceptions of social influence and conformity (or not).
Our observed shifts in risky choices are also consistent with studies that have shown influences of group information on risk attitudes and other behaviors3,26. The proposed OCU model provides a mechanistic explanation of how this information from others is incorporated in decision-making. The comparison of the OCU model against alternative possibilities explaining participants’ choices under social influence demonstrates that individual risk preferences neither change in the face of information about others’ choices nor fully predict choices in a group, but rather serve as a basis against which information from others is compared and combined to guide choices. Thus, OCU explains why the same objectively risky choices made by others may have strong or weak influences on different observers’ behavior and suggests mechanisms that support positive assortment on risk preferences27. The dependence of choices on both OCU and individual risk preferences also suggests why social signals do not inevitably lead to alignment: when the signal sent by others is too discrepant from one’s Solo-preferred choice, OCU on the less-preferred option is unlikely to exceed the utility of the Solo-preferred option and individuals will follow their Solo risk preferences.
The effects of information from others on individuals’ choices are vast and bidirectional1,2: adolescents are prone to risky decisions in the presence of peers28 and, on the flip side, positive social support is among the strongest predictors of remission across psychiatric illnesses29. Many other examples exist, and extend from the trading floor, where herding yields surges and declines in asset values7,30,31, to schooling fish, who send and respond to signals of safety and danger32. OCU contributes to an explanation of conformity in risky decision-making and evokes neural value signals in vmPFC that predict the likelihood of observers conforming (or not) with social others’ decisions. Equally important, our proposed OCU model provides a way in which individual preferences are integrated with perceptions of information from others and may explain why the pernicious effects of negative peer pressure are most evident in those who are most vulnerable20,33. In sum, our data support a mechanistic account of asymmetric neurobehavioral responding to social signals of safety and risk and also suggest the potential to affect changes in individual decision-making by modulating the value of social nudges.
ONLINE METHODS
Participants
70 healthy MRI-compatible humans (male/female = 52/18, age = 33.19 ± 12.01) participated in the current study. All participants provided written informed consent and were paid for their participation. The study was approved by the Institutional Review Boards of Baylor College of Medicine and Virginia Tech. Three participants were excluded from the fMRI data analysis due to scanner artifact or excessive movement (>5 mm in the x, y, or z direction). No statistical methods were used to predetermine sample sizes, but our N was similar to those reported in previous publications examining individual differences in the neural substrates of decision-making7,17,34,35.
Experimental procedures
During fMRI scanning, participants made a series of choices between two gambles, one of which was objectively riskier than the other (Supplementary Fig. 1). At the start of every trial, a new pair of gambles was presented on the lower half of the screen. Each pair of gambles had the same high- and low-payoff probabilities but different payoff spread (as described previously10). For each pair, the safer (safe) gamble had lower payoff variance, and the riskier (risky) gamble had greater payoff variance. The decisions were made under two conditions: either alone (Solo) or following information provided about two other players’ decisions (Info). Participants were instructed in groups of six and informed that on some indicated trials, decisions would be made privately where no players’ choices would be revealed to others, and that on other trials decisions would be made publicly such that a random subset of players’ choices would be revealed to others. Up to three participants were scanned per session (due to limits on scanner availability), and as necessary, lab members (unknown to participants) were randomly selected to be present during instructing to bring each instruction group to 6. Participants were instructed that the order of decision-making would be shown on the computer screen in the scanner before the game began, and that the order of play would remain the same throughout the task. Once in the scanner, all participants were assigned to the third position; thus, on Info trials, all participants made their choices after two anonymous others’ choices were presented. To ensure consistency of procedures, all instructions were provided through illustrated slides, a brief quiz was administered following the slides, and any erroneous answers were addressed before scanning.
During scanning, Solo and Info trials were intermixed, and for the Info trials, participants viewed each gamble in each of three group compositions. Specifically, Info trials consisted of (i) ‘safe, safe’ trials where the two others’ displayed decisions were the safer, lower variance gamble, (ii) ‘risky, risky’ trials where the two others’ displayed decisions were the riskier, higher variance gamble, and (iii) ‘mix’ trials in which the two others’ decisions were mixed (one safer and one riskier) was presented before the participant’s decision. Trial types were drawn without replacement from a uniform distribution; similarly, the specific gambles shown were also drawn without replacement, so that each gamble was used only once per condition, and all gambles were used in each condition. In total, each participant had 96 trials (4 lottery menus × 6 payoff probabilities × 4 trial types (Solo; Info: ‘safe, safe’; Info: ‘risky, risky’; Info: ‘mix’)). The trial order was randomized for menu × probability × trial type with a unique order per participant. The lottery menus and their development are described below. For the present study, eight unique lottery menus (M1-M8) with 10 paired gambles (from 10% to 100%) were developed as described previously10 (Supplementary Fig. 2a and see below). During scanning, we used six paired gambles from each of these eight menus (48 unique pairs). Specifically, from each of the eight lottery menus, we selected the 6 pairs symmetric around the mean indifference point (for each menu, gambles 40%, 50%, 60%, 70%, 80% and 90% probability of high payoff). To avoid potential biases for or against any particular menu, for each participant, gambles from four of the eight lottery menus were randomly selected to be presented.
Participants were paid at the end of the study, based on the outcome of a random single lottery drawn from all the experimental decisions the participant made, and no player’s choices affected the payoff of any other player. To avoid the possible effects of gamble outcomes on participants’ choices during the game, only the outcome of the final single lottery selected for payout was presented. The group instruction and anonymous presentation were implemented to avoid learning effects while maintaining the social nature of the task.
Behavioral analyses
For model-free behavioral analyses, Info trials were divided according to the two other players’ choices that were displayed before the participant’s choice: (i) ‘safe, safe’, (ii) ‘risky, risky’, and (iii) ‘mix’ Info trials, described above. To compare the proportion of safe choices between trial types, we used repeated measures analysis of variance (ANOVA). Paired t tests were used for post-hoc analyses between the conditions. Data distributions were assumed to be normal but this was not formally tested. MATLAB R2013b (MathWorks) was used for all statistical tests of behavior.
Behavioral model specifications and model comparison
For model comparison at the group level (Fig. 1c), for each model, all 96 trials per participant were used for leave-one-out group level parameter estimation (repeated 70 times per model). We used BIC to compare goodness-of-fit of the models for explaining participants’ decisions. After identifying OCU as the best fitting model, subsequent individual parameter estimations were conducted with custom MATLAB R2013b scripts using maximum log-likelihood estimation (MLE) at the individual subject level. For all individual model fitting, participants for whom no unique solution was found were excluded from analyses specific to that model; the number of participants excluded is indicated for each model. The fminsearch function in MATLAB with different initial values starting estimation was used to obtain all estimated parameters.
Estimates of individual risk preferences
Briefly, utility theory indicates that participants’ ‘utility’ or subjective valuation for an uncertain option predicts the choice of that option, above and beyond that which would be predicted by its objective expected value8,9,18,36,37. Individual risk preferences were first estimated from participants’ Solo choices (24 trials) using a basic two-parameter model including risk preference (ρ) and sensitivity to the difference between the utilities of the paired options (μ)38. The utilities of each of the paired gambles were calculated and used for measuring the probability of selecting the lower variance (safe) over the higher variance (risky) option.
| (1) |
| (2) |
| (3) |
where Usolo:safe (or Usolo:risky) is the utility of the safe (or risky) option and pgamble is the probability of earning the high payoff. V represents the payoff amounts for each gamble and for each pair has the relationship Vhigh payoff:risky > Vhigh payoff:safe > Vlow payoff:safe > Vlow payoff:risky. The estimated risk preference coefficient ρ from Solo choices indicates whether a participant is risk neutral (ρ = 1), risk seeking (ρ > 1) or risk averse (0 < ρ < 1). The probabilistic choice between the options was modeled using the softmax function. Eight participants showed no unique solution for Solo risk preference individual estimates and were excluded from analyses using the Solo risk preference model (leaving N = 59; Fig. 4).
OCU and other potential models explaining decisions with information about others’ choices (Info trials)
Our primary hypothesis was that others’ choices of a risky (or safe) option confers increased utility (that is, OCU) of that option to an observing participant and affects the observer’s choices. To test this possibility, we compared the model fit of OCU at the leave-one-out group level against three alternative models for explaining participants’ behavior: (i) blind following, wherein participants’ choices simply match those of others; (ii) Solo risk preference, in which participants’ Solo risk preference dictates choices on Info trials; and (iii) risk preference change, where the scaling parameter (ρ) of an individual’s power utility function (equations (1) and (2)) changes in the presence of others’ choices. Each is detailed below.
OCU
OCU was estimated as a constant addition of utility to the (safe or risky) gamble chosen by others. The OCU-modified utility on Info trials (Uwith OCU) of each option was computed.
| (4) |
| (5) |
| (6) |
where OCU is the OCU being individually estimated and indicator δ(.) = 1 if the others chose the indicated options on that trial (0, otherwise), and p′ is the adjusted probability of choosing the safe option on Info trials. The sign and range of OCU were not restricted in the estimation. In addition, we tested a form of the OCU model including separate OCU variables for ‘safe, safe’ (from equation (4)) and ‘risky, risky’ (from equation (5)) trials, respectively. The fit for this direction-separated OCU model was not better than the general OCU model (BICOCU = 8,033; BICdirection-separate-OCU = 8,040), so only the general form OCU model was included in subsequent analyses (Fig. 1c). 11 participants showed no unique solution for OCU individual estimates and were excluded from analyses using individual estimates from the OCU model (leaving N = 56; Fig. 3; see Supplementary Fig. 8 for the additional analyses with the smallest subset of included participants).
Blind following
One alternative hypothesis for explaining decisions made with information from others is that participants might blindly follow others’ choices and choose whichever options the others choose. In this model, on ‘safe, safe’ and ‘risky, risky’ trials, p(choosing safe option) is expected to be 1 or 0, respectively. Model free analyses showed that participants’ choices on the mixed trials did not differ from those made on Solo trials (Supplementary Fig. 3c). Thus, on ‘mix’ trials, the probability of choosing safe was modeled using the softmax function (equation (3)) as was done for Solo trials. A general version of the blind following model (g blind follow) was also tested, which hypothesized Uwith OCU:safe – Uwith OCU:risky = constant on Info trials. This estimated constant should induce a constant probability g (0 ≤ g ≤ 1) of following risky and safe others (equation (6)). The fit for this general model was worse than the direction-specific blind following model (BICblind follow = 73,161; BICg-blind follow = 73,170), so only the blind following model including direction of others’ choices was used to compare against OCU (Fig. 1c).
Solo risk preference
Another plausible alternative we tested is that participants’ Solo risk preferences may fully predict what they choose in the group. This model is identical to that used to estimate Solo risk preferences, but the estimate included all decisions in all trial types (Solo; Info: ‘safe, safe’; Info: ‘risky, risky’; Info: ‘mix’).
Changing risk preference
Finally, participants might change their risk preferences based on their observations of others’ decisions, such that the shape of an individual’s utility function changes under others’ influence. Changing risk preference was modeled as
| (7) |
where risk preference ρ is estimated as indicated in equations (1)–(3), indicator δ(.) = 1 only if the others chose the indicated options in the trial, and 0 otherwise. The sign of Δρ was not restricted in the estimation. Three different μs were also estimated; two μs each for ‘safe, safe’ and ‘risky, risky’, and the last μ for both Solo and Mix trials.
OCU predicts preference dependent alignment with signals of safety and risk
As outlined throughout, the range of gambles for which Uwith OCU will exceed Usolo for originally preferred gambles and lead to conformity with others’ choices is dependent on the direction of influence (that is, safe or risky) and the concavity of the power utility function (ρ). These relationships are schematically depicted in Figure 2a and Supplementary Figure 5. We summarize this dependency here, using the notation defined in the main text and Figure 2a where: V0 is the value associated with the mean expected utility of safe gambles (V0 = Usolo−1 (EUsafe)); V1 is a risky gamble with greater utility than V0; and V2 is the mirror gamble of V1 symmetric around and with smaller utility than V0. Uwith OCU from safe others will exceed Usolo for the range of originally preferred risky gambles between V0 and V1; and Uwith OCU from risky others will exceed Usolo for the value of originally preferred safer gambles between V2 and V3.
The range of gambles for which Uwith OCU will exceed Usolo for originally preferred gambles and lead to conformity is dependent upon the direction of influence (safe or risky) and concavity (ρ) of the power utility function.
If ρ < 1 (concave), then V1 – V0 > V3 – V2, indicating greater influence of safe others.
If ρ = 1 (linear), then V1 – V0 = V3 – V2, indicating equal influence of risky and safe others.
If ρ > 1 (convex), then V1 – V0 < V3 – V2, indicating greater influence of risky others.
Distance from others
Distance from others may explain variability in the effects of social others on observers’ decisions, including why some individuals are susceptible to negative peer pressure while others respond adaptively to positive social influence33,39,40. In the current study, conformity (or equivalently, alignment) is defined as choosing the same option as others. Under the OCU model, a lateral translation of the decision probability leads to an increased probability of choosing the same option as others at each probability of high payoff (Fig. 2c). This allows a measure of distance between choices predicted by one’s Solo risk preferences and the safe or risky choices of others. Specifically, distance was calculated as follows:
| (8) |
where p(choosing safe option) was calculated using individually estimated risk preferences from Solo trials. Thus, positive distance indicates safe influence trials (safe, safe) and negative distance indicates risky influence trials (risky, risky).
OCU translates participants’ decision probability functions
We show here that OCU leads to a lateral translation of the decision probability function. Under OCU, the addition of utility in the direction of others’ choices changes participants’ probability of choosing one gamble over the other as computed with the softmax function. The probability of choosing the safe option can first be rewritten as softmax function g (.) of pgamble (probability of high payoff) in the ‘Solo’ trials.
| (9) |
| (10) |
where a = (Vhigh payoff:safe)ρ − (Vlow payoff:safe)ρ − (Vhigh payoff:risky)ρ + (Vlow payoff:risky)ρ, b = (Vlow payoff:safe)ρ − (Vlow payoff:risky)ρ and V represents the payoff amount for each gamble with the relationship Vhigh payoff:risky > Vhigh payoff:safe > Vlow payoff:safe > Vlow payoff:risky. Introducing the choices of others (for example, others choose safe) adds OCU to the option chosen by others (safe gamble in the current example) and affects the decision probability.
| (11) |
| (12) |
Thus, the addition of other conferred utility leads to a lateral translation of the decision probability softmax function and manifests as an increased probability of choosing the option chosen by others.
fMRI acquisition and pre-processing
All scans were collected on a 3.0-T Siemens Trio scanner. High-resolution T1-weighted scans were acquired using the MP-RAGE sequence (Siemens). Echo planar images (EPI) were collected during the entire task procedure to measure blood oxygenation-level-dependent (BOLD) signal. Scans were angled 30° from the AC-PC line. Standard scanner parameters were as follows: repetition time (TR) = 2,000 ms, echo time (TE) = 30 ms, slices = 34, slice thickness = 4 mm, flip angle: 90°, voxel size: 3 × 3 × 3.4 mm3. Preprocessing analyses were performed with SPM8b (http://www.fil.ion.ucl.ac.uk/spm/)41, including slice timing correction, motion correction, co-registration, normalization to the Montreal Neurological Institute (MNI) template, and spatial smoothing using 6-mm Gaussian kernel. Images were resampled to 3 × 3 × 3 mm3 voxels during normalization. A high-pass filter of 1/128 Hz was applied to all scans and autocorrelation of the hemodynamic responses were modeled as a first-order autoregressive process.
General linear model analyses
We performed event-related fMRI analyses of participants’ neural responses at the time at which they viewed the others’ decisions. Two separate design matrices were used for general linear model analyses: one for neural responses independent from final decision (design matrix 1), and the other coding participants’ alignment with others on each trial (that is, conform or not-conform; design matrix 2). OCU-modified utilities were added as parametric modulators to the general linear model (see design matrix 1 below), and individual risk preferences were used as second level regressors (see design matrix 2 below) to examine the effects of OCU and subjective preferences on neural responses. For each design matrix, realignment parameters were included to model movement artifacts. A list of all task-related regressors and parametric modulators associated with each design matrix is provided below. FWE with small volume correction where indicated was used for multiple comparisons (based on regions of interest (ROIs) defined from independent fMRI studies).
In design matrix 1 (DM1), all trials (Solo; Info: ‘safe, safe’; Info: ‘risky, risky’; Info: ‘mix’) regardless of choice were modeled as linear regressors. The events in each regressor were convolved with the canonical hemodynamic response function, its temporal derivative and the dispersion derivative. The task-related regressors were as follows:
-
1)
Player1Cue: on Info trials, cue indicating Player 1’s choice was being made. At the same time, the new pair of gambles was revealed.
-
2)
InfoViewP1P2: on Info trials, simultaneous revelation of both other players’ decisions
-
3)
SoloViewGambles: for Solo trials, revelation of new pair of gambles
-
4)
KeypressInfo: Info trial key presses during the decision period
-
5)
KeypressSolo: Solo trial key presses during the decision period
Neural responses to InfoViewP1P2 and SoloViewGambles were modeled as 6-s duration events.
To assess the neural substrates of OCU, parametric modulators associated with the utility differences between chosen and unchosen options (ΔU) were applied to InfoViewP1P2 (ΔU = Uwith OCU chosen gamble – Uwith OCU unchosen gamble). Uwith OCU was calculated with each individual’s OCU parameter estimated from the OCU model and was used for participants’ chosen and unchosen options (equations (4) and (5)). The ΔU parametric modulator was transformed to a
where E(ΔU) and σ(ΔU) are mean and s.d. of utility differences (ΔU) over all trials, respectively. To test the hypothesis that on Info trials, participants track OCU modified utilities (Uwith OCU), but not Solo utilities (Usolo), parametric modulators associated with the Solo utility difference between chosen and unchosen options (Usolo chosen gamble – Usolo unchosen gamble) were also applied to InfoViewP1P2 (equations (1) and (2)).
In the second design matrix (DM2), to test effects of conformity with others’ choices, the same task related regressors as DM1 were used, with the InfoViewP1P2 regressor additionally separated by conformity (or not) as follows:
-
1)
InfoViewP1P2_conform: on Info trials, simultaneous revelation of both other players’ decisions when the participant chose the same option as others.
-
2)
InfoViewP1P2_notconform: on Info trials, simultaneous revelation of both other players’ decisions when the participant chose the option different from others.
As with DM1, the events of interest (SoloViewGambles, InfoViewP1P2_conform, InfoViewP1P2_notconform) were modeled as 6-s duration events. Three parametric modulators were applied to the InfoViewP1P2_conform and InfoViewP1P2_notconform events: (i) direction of others’ influence (+1 for distance > 0 (safe influence), −1 for distance < 0 (risky influence), and 0 for distance = 0), (ii) magnitude of influence (|distance|), and (iii) probability of earning high payoff (40%, 50%, 60%, 70%, 80%, 90%).
At the first level, contrast images were generated for each participant that reflected whole-brain activity correlated with utility differences, direction, magnitude of influence and probability of earning high payoff, each on a trial-by-trial basis. Second-level models were constructed as one-sample t-tests using contrast images from the first-level model. Inclusive cerebrum masking was used at the second-level. To investigate the interaction between individual risk preference and the neural response to direction of influence, participants’ estimated risk preferences (from Solo trials, log transformed) were added as a second-level regressor to DM2 (see Supplementary Fig. 9 for gender-controlled analyses). FWE with SVC where indicated was used for multiple comparisons. Functional brain regions implicated in subjective value encoding13,14,16,19-21,42 and conflict processing6,15,24 were identified as ROIs. For SVC, the small volumes were defined as spheres with 10mm radius, centered based on previously published independent studies: vmPFC42 (center at x = 0, y = 32, z = −18) and dACC15 (center at x = 4, y = 28, z = 28).
ROI analyses and robustness checks
The vmPFC ROI for beta extraction in Figure 3b was defined as the cluster correlated with trial-by-trial other-conferred utilities thresholded at whole brain P < 0.001 (peak voxel at x = −3, y = 35 and z = −20; kE = 19) from DM1. Correlations between the extracted betas and behavioral conformity (see below) were tested to investigate the link between neural responses to OCU and behavioral decisions. Standard effect size comparison techniques were used to compare the effect sizes between vmPFC betas predicting conformity for: (betaUwith OCU – betaUsolo) predicting conformity versus betaUsolo predicting conformity; Fisher r-to-z′ transformation to normalize the effect size coefficients, then assessing the significance of the difference between the two normalized coefficients (Z = (z′r1 – z′r2)/SEz′r1 – z′r2). Leave-one-out cross-validation analyses were performed consecutively. We re-estimated the same second-level analysis 56 times (N = 56 participants whose OCU model had unique estimated parameter solutions), leaving one subject out each time. A new set of voxels showing local maximum nearest to the group peak voxel (x = −3, y = 35, and z = −20) was identified from these iterations. The robustness of the results presented in Figure 3b was confirmed using leave-one-out cross-validation (Pearson’s correlation; OCU: r = 0.27, P = 0.042; solo utility: r = 0.10, P = 0.46). A sphere centered at each new voxel with radius of 10 mm defined the ROI, and was used to extract the mean beta from the left-out subject. Correlations between the extracted betas and behavioral conformity were tested as described above.
The dACC and insula ROIs for beta extraction in Figure 4b,c were defined as the significant clusters from the second-level interaction (direction of influence × risk preference, conform trials) thresholded at whole brain P < 0.001 (dACC: peak voxel at x = −3, y = 32 and z = 31; kE = 27; insula: peak voxel at x = −27, y = 17 and z = 10; kE = 96) from DM2. The first eigenvariates of the direction effect for each participant from the dACC and insula ROIs are plotted for high- and low-risk preference participants, identified with median split (based on individual risk preferences estimated from solo trials). The values plotted in Figure 4b,c are modulated by direction and pooled across subjects as a function of distance.
Task development and piloting
The lotteries used in our task were adopted from a previous study10 in which participants were presented with a menu of ten choices between two paired risky gambles. In their design, the probability of high payoff increased in 10% increments for both gambles going down the menu while the outcomes remained the same, and the probability of high payoff was the same for each gamble in the pair. For each pair of gambles, the payoff variance for one option (option A, safe) was always lower than the variability of the other option (option B, risky). Thus, in a menu of paired options, at lowest high-payoff probabilities, the expected value difference favors option A, and when the probability of the high-payoff outcome increases enough, participants should switch over to option B. This ‘switch point’ varies in relation to participants’ risk preferences, and individual subjects’ risk aversion coefficients can be estimated using a basic power utility function (Online Methods).
For the present study, we developed eight unique lottery menus (M1-M8) with 10 paired gambles (from 10% to 100%; Supplementary Fig. 2a). As per the previous study10, in any pair of gambles, a safer option had smaller payoff variance than a riskier option and for each menu, the outcome values were kept constant, and the risk-neutral ‘switch point’ between the safer and riskier gambles, was between the high probabilities of 40 and 50%. We piloted these gambles (8 menus × 10 gambles per menu) in 54 behavioral participants (N = 54, no overlap with the N = 70 scanned participants) with each pair of gambles presented in random order (rather than the columnar menu format used previously10). These pilot data verified that the chosen payoff amounts and format were appropriate for revealing individual differences in risk preferences. To calculate participants’ indifference points, we estimated participants’ probabilistic decision functions (softmax) from their choices and measured the payoff probability where the probability of choosing the safe option was at chance level. As done in previous studies10,24,26, participants were risk averse, with the average indifference (switch over) point between the high payoff probabilities of 60 and 70% (Supplementary Fig. 3a). For scanning, we used six paired gambles from each of the eight menus that we pilot tested (48 unique pairs).
A Supplementary Methods Checklist is available.
Supplementary Material
ACKNOWLEDGMENTS
We thank R. Montague, T. Lohrenz and S. LaConte, and gratefully acknowledge the technical assistance of J. Lu, J. Shin, and members of the Chiu and King-Casas laboratories. This work was supported in part by the US National Institutes of Health (MH091872 and MH087692 to P.H.C. DA036017 to B.K.-C.).
Footnotes
Note: Any Supplementary Information and Source Data files are available in the online version of the paper.
AUTHOR CONTRIBUTIONS
G.I.C., B.K.-C. and P.H.C. designed the experiments. D.C., G.I.C., B.K.-C. and P.H.C. analyzed the data. All of the authors discussed the analyses and results. D.C. and P.H.C. drafted the initial manuscript. All of the authors revised and approved the final manuscript.
COMPETING FINANCIAL INTERESTS
The authors declare no competing financial interests.
References
- 1.van de Waal E, Borgeaud C, Whiten A. Potent social learning and conformity shape a wild primate’s foraging decisions. Science. 2013;340:483–485. doi: 10.1126/science.1232769. [DOI] [PubMed] [Google Scholar]
- 2.Lee IH. Market crashes and informational avalanches. Rev. Econ. Stud. 1998;65:741–759. [Google Scholar]
- 3.Myers DG, Lamm H. The group polarization phenomenon. Psychol. Bull. 1976;83:602. [Google Scholar]
- 4.Biele G, Rieskamp J, Krugel LK, Heekeren HR. The neural basis of following advice. PLoS Biol. 2011;9:e1001089. doi: 10.1371/journal.pbio.1001089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Izuma K, Adolphs R. Social manipulation of preference in the human brain. Neuron. 2013;78:563–573. doi: 10.1016/j.neuron.2013.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Klucharev V, Hytönen K, Rijpkema M, Smidts A, Fernández G. Reinforcement learning signal predicts social conformity. Neuron. 2009;61:140–151. doi: 10.1016/j.neuron.2008.11.027. [DOI] [PubMed] [Google Scholar]
- 7.Lohrenz T, Bhatt M, Apple N, Montague PR. Keeping up with the Joneses: interpersonal prediction errors and the correlation of behavior in a tandem sequential choice task. PLoS Comput. Biol. 2013;9:e1003275. doi: 10.1371/journal.pcbi.1003275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huettel SA, Stowe CJ, Gordon EM, Warner BT, Platt ML. Neural signatures of economic preferences for risk and ambiguity. Neuron. 2006;49:765–775. doi: 10.1016/j.neuron.2006.01.024. [DOI] [PubMed] [Google Scholar]
- 9.Preuschoff K, Bossaerts P, Quartz SR. Neural differentiation of expected reward and risk in human subcortical structures. Neuron. 2006;51:381–390. doi: 10.1016/j.neuron.2006.06.024. [DOI] [PubMed] [Google Scholar]
- 10.Holt CA, Laury SK. Risk aversion and incentive effects. Am. Econ. Rev. 2002;92:1644–1655. [Google Scholar]
- 11.Rangel A, Camerer C, Montague PR. A framework for studying the neurobiology of value-based decision making. Nat. Rev. Neurosci. 2008;9:545–556. doi: 10.1038/nrn2357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bernoulli D. Exposition of a new theory on the measurement of risk. Econometrica. 1954;22:23–36. transl. [Google Scholar]
- 13.Hare TA, Camerer CF, Rangel A. Self-control in decision-making involves modulation of the vmPFC valuation system. Science. 2009;324:646–648. doi: 10.1126/science.1168450. [DOI] [PubMed] [Google Scholar]
- 14.Chib VS, Rangel A, Shimojo S, O’Doherty JP. Evidence for a common representation of decision values for dissimilar goods in human ventromedial prefrontal cortex. J. Neurosci. 2009;29:12315–12320. doi: 10.1523/JNEUROSCI.2575-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fan J, Hof PR, Guise KG, Fossella JA, Posner MI. The functional integration of the anterior cingulate cortex during conflict processing. Cereb. Cortex. 2008;18:796–805. doi: 10.1093/cercor/bhm125. [DOI] [PubMed] [Google Scholar]
- 16.Ruff CC, Fehr E. The neurobiology of rewards and values in social decision making. Nat. Rev. Neurosci. 2014;15:549–562. doi: 10.1038/nrn3776. [DOI] [PubMed] [Google Scholar]
- 17.Sip KE, Smith DV, Porcelli AJ, Kar K, Delgado MR. Social closeness and feedback modulate susceptibility to the framing effect. Soc. Neurosci. 2014;10:35–45. doi: 10.1080/17470919.2014.944316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Somerville LH, Kelley WM, Heatherton TF. Self-esteem modulates medial prefrontal cortical responses to evaluative social feedback. Cereb. Cortex. 2010;20:3005–3013. doi: 10.1093/cercor/bhq049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zaki J, Schirmer J, Mitchell JP. Social influence modulates the neural computation of value. Psychol. Sci. 2011;22:894–900. doi: 10.1177/0956797611411057. [DOI] [PubMed] [Google Scholar]
- 20.Behrens TE, Hunt LT, Woolrich MW, Rushworth MF. Associative learning of social value. Nature. 2008;456:245–249. doi: 10.1038/nature07538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burke CJ, Tobler PN, Baddeley M, Schultz W. Neural mechanisms of observational learning. Proc. Natl. Acad. Sci. USA. 2010;107:14431–14436. doi: 10.1073/pnas.1003111107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Christopoulos GI, King-Casas B. With you or against you: Social orientation dependent learning signals guide actions made for others. Neuroimage. 2015;104:326–335. doi: 10.1016/j.neuroimage.2014.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Christopoulos GI, Tobler PN, Bossaerts P, Dolan RJ, Schultz W. Neural correlates of value, risk, and risk aversion contributing to decision making under risk. J. Neurosci. 2009;29:12574–12583. doi: 10.1523/JNEUROSCI.2614-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ridderinkhof KR, Ullsperger M, Crone EA, Nieuwenhuis S. The role of the medial frontal cortex in cognitive control. Science. 2004;306:443–447. doi: 10.1126/science.1100301. [DOI] [PubMed] [Google Scholar]
- 25.Campbell-Meiklejohn DK, Bach DR, Roepstorff A, Dolan RJ, Frith CD. How the opinion of others affects our valuation of objects. Curr. Biol. 2010;20:1165–1170. doi: 10.1016/j.cub.2010.04.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Eliaz K, Ray D, Razin R. Choice shifts in groups: A decision-theoretic basis. Am. Econ. Rev. 2006;96:1321–1332. [Google Scholar]
- 27.Attanasio O, Barr A, Cardenas JC, Genicot G, Meghir C. Risk pooling, risk preferences, and social networks. Am. Econ. J. Appl. Econ. 2012;4:134–167. [Google Scholar]
- 28.Chein J, Albert D, O’Brien L, Uckert K, Steinberg L. Peers increase adolescent risk taking by enhancing activity in the brain’s reward circuitry. Dev. Sci. 2011;14:F1–F10. doi: 10.1111/j.1467-7687.2010.01035.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.King-Casas B, Chiu PH. Understanding interpersonal function in psychiatric illness through multiplayer economic games. Biol. Psychiatry. 2012;72:119–125. doi: 10.1016/j.biopsych.2012.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Raafat RM, Chater N, Frith C. Herding in humans. Trends Cogn. Sci. 2009;13:420–428. doi: 10.1016/j.tics.2009.08.002. [DOI] [PubMed] [Google Scholar]
- 31.Burke CJ, Tobler PN, Schultz W, Baddeley M. Striatal BOLD response reflects the impact of herd information on financial decisions. Front. Hum. Neurosci. 2010;4:48. doi: 10.3389/fnhum.2010.00048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Miller N, Garnier S, Hartnett AT, Couzin ID. Both information and social cohesion determine collective decisions in animal groups. Proc. Natl. Acad. Sci. USA. 2013;110:5263–5268. doi: 10.1073/pnas.1217513110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pfeifer JH, et al. Entering adolescence: resistance to peer influence, risky behavior, and neural changes in emotion reactivity. Neuron. 2011;69:1029–1036. doi: 10.1016/j.neuron.2011.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Edelson MG, Dudai Y, Dolan RJ, Sharot T. Brain substrates of recovery from misleading influence. J. Neurosci. 2014;34:7744–7753. doi: 10.1523/JNEUROSCI.4720-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Medic N, et al. Dopamine modulates the neural representation of subjective value of food in hungry subjects. J. Neurosci. 2014;34:16856–16864. doi: 10.1523/JNEUROSCI.2051-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hsu M, Bhatt M, Adolphs R, Tranel D, Camerer CF. Neural systems responding to degrees of uncertainty in human decision-making. Science. 2005;310:1680–1683. doi: 10.1126/science.1115327. [DOI] [PubMed] [Google Scholar]
- 37.Kahneman D, Tversky A. Prospect theory: An analysis of decision under risk. Econometrica. 1979;47:263–291. [Google Scholar]
- 38.Sokol-Hessner P, et al. Thinking like a trader selectively reduces individuals’ loss aversion. Proc. Natl. Acad. Sci. USA. 2009;106:5035–5040. doi: 10.1073/pnas.0806761106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Allen JP, Chango J, Szwedo D, Schad M, Marston E. Predictors of susceptibility to peer influence regarding substance use in adolescence. Child Dev. 2012;83:337–350. doi: 10.1111/j.1467-8624.2011.01682.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ouimette PC, Finney JW, Moos RH. Twelve-step and cognitive-behavioral treatment for substance abuse: A comparison of treatment effectiveness. J. Consult. Clin. Psychol. 1997;65:230. doi: 10.1037//0022-006x.65.2.230. [DOI] [PubMed] [Google Scholar]
- 41.Friston KJ, et al. Statistical parametric maps in functional imaging: a general linear approach. Hum. Brain Mapp. 1994;2:189–210. [Google Scholar]
- 42.Clithero JA, Rangel A. Informatic parcellation of the network involved in the computation of subjective value. Soc. Cogn. Affect. Neurosci. 2014;9:1289–1302. doi: 10.1093/scan/nst106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.