Scalable Brain Network Construction on White Matter Fibers

Abstract

DTI offers a unique opportunity to characterize the structural connectivity of the human brain non-invasively by tracing white matter fiber tracts. Whole brain tractography studies routinely generate up to half million tracts per brain, which serves as edges in an extremely large 3D graph with up to half million edges. Currently there is no agreed-upon method for constructing the brain structural network graphs out of large number of white matter tracts. In this paper, we present a scalable iterative framework called the ε-neighbor method for building a network graph and apply it to testing abnormal connectivity in autism.

1. Introduction

Structural brain connectivity has been usually modeled as a network graph using white matter fiber tracts in DTI. The whole gray matter has been traditionally parcellated into n disjoint regions. White matter fibers provide information of how one gray matter region is connected to another via a n × n connectivity matrix. The connectivity matrix is then thresholded to produce a binarized adjacency matrix, which is further used in constructing a graph with n nodes^6,8,9,18 However, there is no gold standard for gray matter parcellation which makes the identification of node depend on the choice of parcellation. Depending on the scale of parcellation, the parameters of graph, which characterize graph topology, vary considerably up to 95%.^6,18 Another problem of the parcellation is the arbitrariness of thresholding connectivity matrix. The topological parameters such as sparsity and clustering coefficients change substantially depending on the level of threshold.⁸

The problems of parcellation and the subsequent arbitrary thresholding can be avoided if we do not use any parcellation in building the network. So the question is whether if it is possible to themselves serve as the edges connecting nodes.construct a network graph without the usual parcellation scheme. This paper presents a novel network graph modeling technique called the ε-neighbor construction that avoids parcellation and the subsequent thresholding of the connectivity matrix. Instead of using the pre-specified parcellation, we propose to use the two end points of fibers as network nodes while the fibers themselves serve as the edges connecting nodes.

The ε-neighbor construction is motivated by the Rips complex of point cloud data,⁷ which has been used to characterize the topology of the point cloud data. The Rips complex is a graph constructed by connecting two data points if they are within specific distance ε. The problem of the Rips complex is that given n data points, it exactly produces a graph with n nodes so the resulting graph becomes very complicated when n becomes large. Unlike the Rips complex, the ε-neighbor method does not use all data points in constructing a graph so it significantly reduces the complexity of data. Further, while the point cloud data does not have any hidden topological constraint, the two end points of white matter fibers are connected so we are actually dealing with paired point cloud data. So the ε-neighbor construction is different from building the Rips complex and offers substantial computational advantage.

2. DTI Acquisition and Preprocessing

The DTI data from 31 subjects were used in this study: (i) 17 subjects with high functioning autism spectrum disorders (ii) 14 control subjects matched for age, handedness, IQ, and head size. The Autism Diagnostic Interview-Revised¹⁵ was used for diagnoses by trained researchers.³ Diffusion weighted images were acquired in 12 non-collinear diffusion encoding directions with diffusion weighting factor of b=1000 s/mm2 in addition to a single (b=0) reference image. Eddy current related distortion and head motion of each data set were corrected using AIR¹⁷ and distortions from field inhomogeneities were corrected using custom software algorithms based on.¹¹ The six tensor elements were calculated using non-linear fitting methods¹

We have used nonlinear tensor image registration algorithm given in¹⁹ for spatial normalization. This approach combines full tensor co-registration and high-dimensional diffeomorphic spatial normalization. The registration is based on an iterative strategy^12,19 where the initial template was computed as the average of original DTI. After DTI were alined to a template space, we perform streamline based tractography using the TENsor Deflection (TEND) algorithm,^2,13 Figure 1 shows the subsampled tractography result for a single subject.

Figure 1.

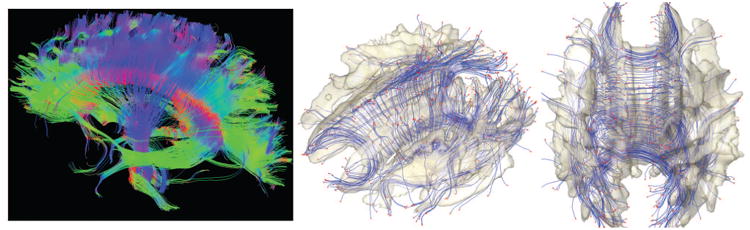
White matter fiber bundles obtained using TEND algorithm.¹³ The end points of tracts are identified and colored as red. The surface is the isosurface of the template FA map so most of tracts are expected to end outside of the surface. The ε-neighbor method uses the proximity of the end points in constructing the network graph.

3. ε-Neighbor Construction

Suppose a whole brain tractography result yields k number of tracts. The i-th tract consists of two end points e_i1 and e_i2. In constructing the network graph, we only need to worry about the two end points of of a tract since all other points along the tract are connected to these two end points. The end points of tracts are considered as nodes of a graph while the tracts are considered as edges of the graph. The TEND algorithm can generate upward of half million tracts but it is not practical to construct a massive graph with half million edges. So we have developed a scalable iterative network graph construction technique called the ε-neighbor construction.

Let _k = { _k, ℰ_k}be a 3D graph with vertex set _k and edge set ℰ_k at the k-th iteration. We define the distance d(p, 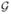_k) of a point p to the graph 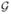_k to be the shortest Euclidean distance between p and all points in 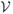_k

$$\mathrm{d}(\mathrm{p},{\mathcal{G}}_k)=\underset{\mathrm{q}\in {\mathcal{V}}_k}{min}\Vert \mathrm{p}-\mathrm{q}\Vert .$$

We say point p is the ε-neighbor of graph 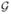_k if d(p, 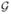_k) ≤ ε. The threshold ε will be called the resolution of graph and it determines the scale at which we construct the graph. Larger the value of ε, cruder the constructed graph becomes with less number of nodes. Consider a tract with two end points e₁₁ and e₁₂. The algorithm then starts with the graph 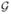₁= { 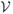₁, ℰ₁}with 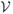₁ = {e₁₁, e₁₂}, ℰ₁ = {e₁₁ e₁₂}. For the edge set ℰ₁, we simply denote the edge connecting two nodes e₁₁ and e₁₂ as e₁₁ e₁₂. In the next iteration, we add the second tract with two end points e₂₁, e₂₂ to the existing graph 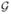₁. There are four possibilities:

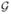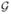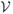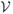• e₂₁ and e₂₂ are all ε-neighbors of ₁Since the end points e₂₁ and e₂₂ are close to the already existing graph ₁we do not change the vertex set. i.e. ₂ = ₁. Now check if the edge e₂₁ e₂₂ is in the edge set ℰ₁ and add them if it is not found in the edge set. In this case we have ℰ₂ = ℰ₁ ∪ {e₂₁ e₂₂}.

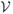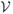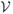• Only e₂₁ is an ε-neighbor. We only to add e₂₂ to ₁ and let ₂ = ₁ ∪ {e₂₁}, ℰ₂ = ℰ₁ ∪ {e₂₁ e₂₂}.

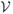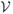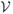• Only e₂₂ is an ε-neighbor. We add e₂₁ to ₁ and let ₂ = ₁ ∪ {e₂₂}, ℰ₂ = ℰ₁ ∪ {e₂₁ e₂₂}.

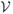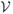• e₂₁ and e₂₂ are not ε-neighbors. We add the end points to the vertex set and add the edge to the edge set. In this case, e₂₁ e₂₂ forms a disjoint edge and we have ₂ = ₁ ∪ {e₂₁, e₂₂}, ℰ₂ = ℰ ₁ ∪ {e₂₁ e₂₂}.

The procedure is iteratively performed to every tracts until we exhaust all the tracts. The MATLAB code for performing ε-neighbor construction is given in brainimaging.waisman.wisc.edu/∼chung/graph.

4. Connected Components

The constructed 3D networks graph can be uniquely parameterized by transforming the graph into adjacent matrices. The adjacency matrix 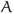= (a_ij) of a graph is constructed on the fly at each iteration by checking if we are adding a new edge to the existing edge set. If nodes i and j are connected, we let a_ij = 1 and a_ij = 0 otherwise. The adjacency matrix is symmetric. The adjacency matrix contains sufficient information to reconstruct the graph. For the subsequent analysis on connected components, 6mm-neighbor graph was used. This particular resolution is chosen since it is the largest integer resolution that produces the node numbers below 1000.

As an illustration of ε-neighbor method, we characterize the abnormal brain network in autism using the connected components of a graph. The number of connected components of a graph is a topological invariant that measures the number of structurally independent or disjoint subnetworks. It can be interpreted as the zeroth Betti number β₀ in algebraic topology.⁵ The connected components can be identified using the Dulmage-Mendelsohn decomposition,¹⁶ which has been widely used for decomposing sparse matrices into block triangular forms in speeding up matrix operations. Figure 3 shows connected components in 4 brain networks. All nodes in the same connected component are colored identically. Most of nodes belong to the largest connected component indicating the brain network is highly connected. There are only 4% of nodes that are not connected to the largest connected component while the remaining 96% are all connected in average. We have plotted those 4% of nodes that are not part of the largest connected component for all subjects (Figure 4). Figure 4 shows the clustering pattern between the groups differs. Although these nodes are scattered in most parts of brain, high concentration of clustering occurs on the right parietal lobe for the control subjects. We tested if the size of the largest connected components differ between the groups. At 6mm resolution, control subjects have 642.86±68.60 nodes in the largest component while autistic subjects have 607.12 ± 39.39 nodes. Note that we do not need to account for brain size difference since networks constructed in the normalized space. The cluster size difference is significant (p-value = 0.079). We expect a larger sample size would increase the statistical significance.

Figure 3.

All nodes in the same connected component are colored identically. DTI-based brain network is characterized by one dominant component that connects almost all regions of brain.

Figure 4.

Superimposition of all 4% of nodes that do not belong the largest cluster for all 30 subjects. Nodes from the control are colored as blue circle while nodes from the autistic subjects are colored as solid red circle. The control subjects show high clustering on the right parietal lobe.

5. ε-Filtration

The analysis in the previous section characterizes networks at the last iteration of the ε-neighbor construction. In this section, we present the idea of quantifying the network over all iterations via ε -filtration, which is motivated by the Rips filtration in persistent homology.

For each given ε, we have Rips complex _ε. By increasing the ε value, we have the Rips filtration, a sequence of larger Rips complexes:

$${\mathcal{G}}_{{\mathrm{\epsilon }}_1}\subset {\mathcal{G}}_{{\mathrm{\epsilon }}_2}\subset {\mathcal{G}}_{{\mathrm{\epsilon }}_3}\subset \dots ,$$

for ε₁ ≤ ε₂ ≤ ε₃ ≤ ….^4,7,10 During the Rips filtration, the topological features such as the Betti numbers change. The topological change over the filtration can be visualized by using the barcode. In the barcode, we plot the zeroth Betti number β₀ over the changing ε value. The resulting bar code is a decreasing function of ε and its decreasing pattern can be used to discriminate groups.¹⁴ Although the Rips filtration completely characterizes the topological change of a network, it is difficult to biologically interpret what it really means to have changing network over scale ε.

Similar to the Rips filtration, the ε-filtration is a sequence of networks obtained from the ε-neighbor method. At the k-th iteration, we have a network _k. As the number of iteration increases, we are generating a sequence of larger networks

$${\mathcal{G}}_1\subset {\mathcal{G}}_2\subset {\mathcal{G}}_3\subset \dots ,$$

which we will call the ε-filtration. On the other hand, the ε-filtration is much easier to interpret since it shows the actual process of network construction.

We computed the size of the largest component in each iteration in the ε-filtration (Figure 5). It is always an increasing function and at about 6000 iterations, we begin to see the significant group difference in the increasing pattern. For instance, at 6000, 7000 and 8000 iterations, we have the p-values of 0.058, 0.038, 0.04 respectively. The control network (blue) is integrating into the largest component much faster than the autistic network (red). The growth of the size of the largest component is higher in controls. A schematic understanding of the underlying process is given in Figure 6. The control subjects are expected to have hub nodes that speed up the integration of disjoint components into the largest component.

Figure 5.

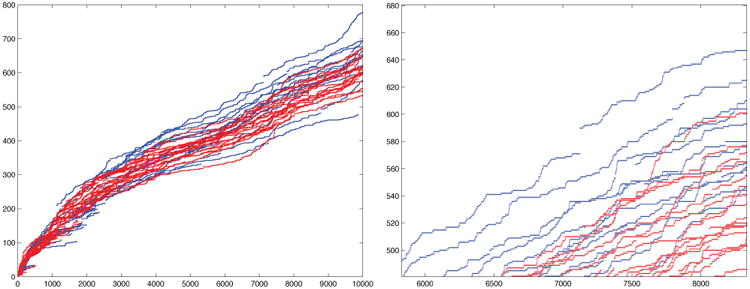
The size of largest connected component (vertical) over the number of iterations in the ε-filtration showing group difference (control = blue, autism= red). At about 10000 iterations, we have 642.86 ± 68.60 and 607.12 ± 39.39 nodes in the control and autistic subjects respectively. Sudden jumps in the plot is caused by the introduction of hub nodes that connect all the disjointed components.

Figure 6.

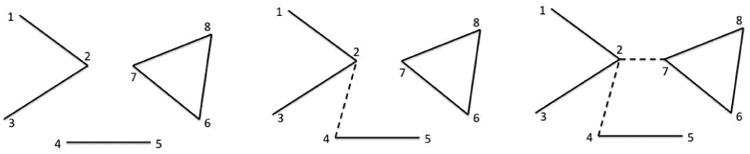
An example of how the size of connected component changes in the ε-filtration. Originally a network consists of three disjoint components {1,2,3}, {4,5}, {6, 7, 8}. The size of the largest components is 3. In the next iteration, we connect the nodes 2 and 4 and obtain two components {1,2, 3,4,5}, {6, 7, 8}. The size of the largest component is 5. In the 2nd iteration, we connect the nodes 2 and 7 and eventually obtain a giant component of size 8. The node 2 is more than a hub and connects all disjoint components together. By removing the node 2, the giant components disintegrate into three disjoint components. The sudden jumps in Figure 5 are showing the introduction of such nodes in the network.

6. Conclusion

We have presented a novel data-driven connectivity graph construction method for DTI. The proposed ε-neighbor network construction can avoid the problem of parcellation and arbitrary connectivity matrix thresholding. The method is applied in showing abnormal connectivity pattern in autistic subjects in the ε-filtration. The autistic network shows slower integration rate than the control network in the filtration demonstrating reduced network integration capability and efficiency.

Figure 2.

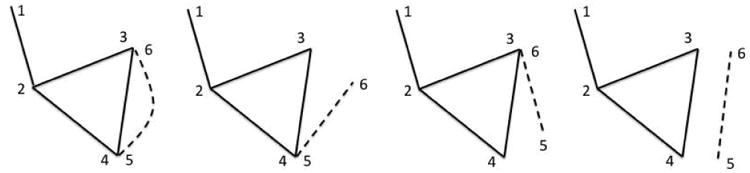
Example of constructing 3D network graph by adding one tract at a time to the existing graph. There are four possible cases of connecting the two end points (indexed 5 and 6) of the tract to the existing graph with nodes {1,2,3,4}. Depending on the proximity of {5, 6}to nodes {1, 2,3,4}, we either do nothing, or add connect one node (either 5 or 6) or add two nodes (both 5 and 6) to the graph.