Abstract
During angiogenesis, sprouting microvessels interact with the extracellular matrix (ECM) by degrading and reorganizing the matrix, applying traction forces and producing deformation. Morphometric features of the resulting microvascular network are affected by the interaction between the matrix and angiogenic microvessels. The objective of this study was to develop a continuous-discrete modeling approach to simulate mechanical interactions between growing neovessels and the deformation of the matrix in vitro. This was accomplished by coupling an existing angiogenesis growth model which uses properties of the ECM to regulate angiogenic growth with the nonlinear finite element software FEBio (www.febio.org). FEBio solves for the deformation and remodeling of the matrix caused by active stress generated by neovessel sprouts, and this deformation was used to update the ECM into the current configuration. After mesh resolution and parameter sensitivity studies, the model was used to accurately predict vascular alignment for various gel boundary conditions. Alignment primarily arises passively as microvessels convect with the deformation of the matrix, but active alignment along collagen fibrils plays a role as well. Predictions of alignment were most sensitive to the range over which active stresses were applied and the viscoelastic time constant in the material model. The computational framework provides a flexible platform for interpreting in vitro investigations of vessel-matrix interactions, predicting new experiments, and simulating conditions that are outside current experimental capabilities.
Keywords: Angiogenesis, morphogenesis, extracellular matrix, cellular mechanics, cell-matrix interactions, finite element modeling, growth modeling
1 Introduction
New vasculature arises from existing vasculature by the process of angiogenesis. A number of challenges within medical and bioengineering research are associated with angiogenesis and the expansion of the microvasculature. In normal tissue, angiogenesis is involved with exercise, reproduction, and development of the embryo (Chung and Ferrara 2011; Egginton et al. 1998; Jaffe 2000). In pathological tissue, angiogenesis is associated with cancer and atherosclerosis causing uncontrolled vessel growth, while ischemia, scar formation, and poor wound healing involve insufficient vessel growth and perfusion (Annex 2013; Carmeliet 2004; Ellis et al. 2006; Folkman 1997; Peirce and Skalak 2003). Bioengineering challenges concerning angiogenesis involve promoting neovascularization of scaffolds for engineering tissue implants (Bouhadir and Mooney 2001; Novosel et al. 2011; Phelps and Garcia 2010). Angiogenesis is highly sensitive to both the local chemical and mechanical microenvironment (Conway et al. 2001; Folkman 1997; Ingber 2002; Shiu et al. 2005), and although extensive research has been performed regarding the chemical regulation of angiogenesis, the mechanical factors that regulate angiogenesis remain poorly understood.
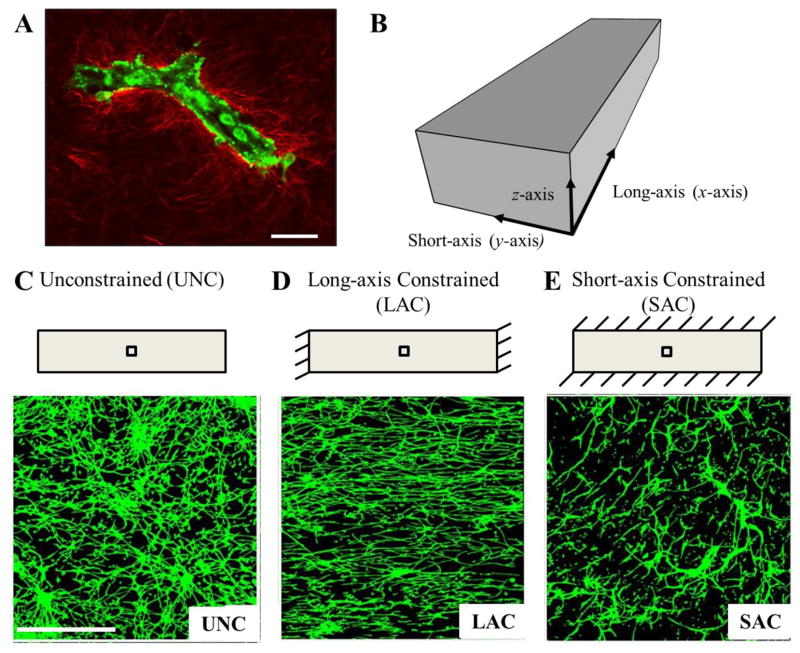
Neovessels expand the vascular bed through the extracellular space via extension and mitosis, applying traction and migrating along components of the extracellular matrix (ECM) (Vernon and Sage 1999). Successful tissue neovascularization requires that the topology of the new network meets the perfusion and metabolic requirements for that tissue (Pries and Secomb 2005). Mechanical interactions during angiogenesis, i.e. traction applied by neovessels to the ECM and the corresponding deformation, are important regulators of growth and neovascularization. Mechanical aspects of the ECM including material properties, density and boundary conditions modulate these mechanical interactions. For example, using a 3D in vitro organ culture model of microvessel fragments within a type-I collagen gel, we have demonstrated that changing the matrix boundary conditions drastically affects the topology and rate of growth of the new vascular network (Fig. 1) (Chang et al. 2012; Edgar et al. 2014; Krishnan et al. 2007; Krishnan et al. 2008; Nunes et al. 2010; Underwood et al. 2014). Microvessels within free-floating, unconstrained constructs grew into a microvascular network with no preferred orientation (Fig. 1C). When the long-axis of the hexahedral constructs was constrained, microvessels aligned along this constrained axis (Krishnan et al. 2007; Krishnan et al. 2008) (Fig. 1 D). However, this alignment did not correlate with stress within the gel, as constraining the short-axis of the gel did not lead to alignment along that direction (Underwood et al. 2014) (Fig. 1 E). Additionally, when the density of the matrix was increased, the rate of angiogenic growth and branching decreased and neovascularization was reduced (Edgar et al. 2014). In all of these experiments, we found that restricting cells from deforming and remodeling the matrix (i.e., increasing the apparent stiffness, either through increasing density or adding a boundary constraint) reduced angiogenesis. However, the dynamic relationship between cell-generated forces, the deformation of the ECM, and angiogenic growth and neovascularization requires further characterization and study.
Figure 1.
Boundary constraints induce alignment during in vitro culture of angiogenic microvessel fragments in three-dimensional collagen gels. Microvessel fragments were harvested from rat fat pads and cultured in a type-I collagen matrix. (A) A parent microvessel fragment in three-dimensional collagen gel imaged using two-photon microscopy. Endothelial cells and pericytes were imaged using autofluoresence (green), collagen fibrils were imaged using second-harmonic generation (red). Scale bar 20 μm. (B) Schematic of a hexahedral vascularized construct subjected to various boundary conditions. The long-axis of the gels was defined as the x-axis, the short-axis as the y-axis, and the thickness of the gel as the z-axis. (C) Schematic (top) and confocal image (bottom) of unconstrained vascularized construct. The interior black box in the schematic indicates the location of image acquisition using confocal microscopy. Microvessel growing in the free-floating unconstrained gels had no preferred orientation. Scale bar 500 μm. (D) When the long-axis of the gel was constrained, microvessels were highly aligned along the constrained axis. (E) In contrast, constraining the short-axis of the constructs resulted in random microvessel alignment, demonstrating that alignment does not correlate with stress in the matrix due to an imposed boundary constraint. Rather, transverse matrix deformation produces the alignment, and this deformation depends on the local effective stiffness of the ECM.
Morphogenic processes such as angiogenesis occur across different physical scales. Individual cellular behavior within neovessel sprouts at the microscale (< 1 mm) regulates the emergent properties of the new vascular network at the tissue macroscale (> 1 mm), such as vascular perfusion, branching, and orientation. In vitro cell and organ culture models typically do not permit the manipulation of experimental conditions and observation of the response across length scales (i.e., changing properties at the macroscale while observing behavior at the microscale and vice versa), providing insufficient information on how individual neovessel sprouts react in response to macroscopic changes to the ECM such as the addition of a boundary constraint. Additionally, data from these experiments are often limited to a single time point and do not provide information into dynamic regulation of angiogenic growth. Therefore, we designed and implemented a computational model of angiogenesis in order to supplement our experimental efforts. This growth model uses information about the local ECM to determine neovessel growth and branching and is capable of accurately describing angiogenesis across changes in matrix fibril orientation and density (Edgar et al. 2013; Edgar et al. 2014). However, in these past studies the properties of the matrix remained constant during simulations and did not include changes that occur as a result of matrix deformation. Neovessels change the properties that regulate their growth as they deform and remodel the matrix, creating a dynamic feedback loop in which growth is coupled to matrix deformation. To the best of our knowledge, no existing model of angiogenesis includes the capability to study the dynamic biomechanical regulation of growth with regards to macroscopic tissue morphology.
The objective of this research was to expand our existing growth model to include these dynamic mechanical interactions between neovessels and the matrix, and to demonstrate the ability of the computational framework to describe and predict experimental morphometric and geometric measurements of angiogenesis. We coupled our discrete computational model of angiogenesis with the nonlinear finite element (FE) software FEBio (Maas et al. 2012). FEBio was used to solve for the deformation caused by cell-generated forces applied to the ECM, and this solution was used to update the biophysical properties of the ECM, creating a dynamic feedback between matrix mechanics and angiogenic growth. The framework was calibrated using simulations of long-axis constrained gels with the goal of describing the results for vascular alignment seen in the experiments. The model was then used to predict vascular alignment in the other two experimental boundary conditions (unconstrained, short-axis constrained) to demonstrate how these individual mechanical interactions produce global vascular alignment in a general sense. The resulting modeling framework provides a flexible and robust platform for investigating the dynamic biomechanical regulation of complex cellular processes such as angiogenesis. Many morphogenic processes involve a similar biomechanical regulation of cellular behavior over time, and in the future these methods could be extended to study similar processes such as neurogenesis and lymphangiogenesis as well as tumor formation and metastasis.
2 Methods
2.1 Culture of Vascularized Constructs
Collagen-based vascularized constructs were used as a 3D in vitro model of sprouting angiogenesis. Microvessel fragments were isolated and cultured using methods described previously (Hoying et al. 1996; Krishnan et al. 2007; Krishnan et al. 2008; Underwood et al. 2014). All components were obtained through Invitrogen (Carlsbad, CA) unless otherwise noted. Epididymal fat pads were harvested from male Sprague-Dawley rats in accordance to the University of Utah Institutional Animal Care and Use Committee and then minced and subjected to limited digestion with collagenase (Worthington Biochemical, Lakewood, NJ). Fragments were then washed twice and re-suspended in L-15 media. The solution was sequentially filtered through 350 and 30 μm sterile nylon filters to remove both large clumps of tissue and single cells. The remaining microvessels were re-suspended in 3.0 mg/ml liquid collagen at 50,000 fragments/ml and poured into Teflon molds to cast the vascularized constructs into a hexahedral shape (20.5 × 5.5 × 3.0 mm). Unconstrained (UNC) constructs were left free-floating in media during culture (Fig. 1C). Long-axis constrained (LAC) constructs were created by inserting a stainless steel mesh into the liquid collagen solution prior to polymerization in order to prevent contraction along the long-axis (x-axis) during growth (Krishnan et al. 2008; Underwood et al. 2014) (Fig. 1D). Short-axis constrained (SAC) constructs were similarly constrained along the short-axis (y-axis) using a stainless steel mesh (Underwood et al. 2014) (Fig. 1E). Microvessel constructs were cultured for 6 days in serum-free culture media (Bottenstein and Sato 1979) supplemented with rhVEGF (Peprotech, Rocky Hill, NJ). A total of 7 constructs were cultured for each boundary condition (Nexp = 7). Gel contraction was defined as the negative of axial engineering strain along each direction (εxx, εyy, and εzz) and was calculated by collecting digital images of the vascularized constructs and measuring the final dimensions at the geometric center. Acellular controls were used to obtain measurements in the reference configuration.
2.2 Imaging and Quantification of Microvessel Alignment
After 6 days of culture, constructs were fixed in paraformaldehyde and stained with Isolectin GS-IB4 conjugated to Alexa 488 to fluorescently label endothelial cells. Three-dimensional image datasets of vascular networks within the collagen gels were obtained using laser scanning confocal microscopy. The constructs were oriented within the long-axis parallel to the horizontal imaging axis (x-axis) and imaging was performed at the geometric center of each construct. Each volumetric image dataset consisted of 4 adjacent (2 × 2) 10× stacks with a 2.5 μm step size through the thickness (z-direction) covering a depth of 300 μm. The assembled mosaic datasets had dimensions of 2548 × 2548 × 300 μm (1024 × 1024 × 120 voxels). Datasets were processed and skeletonized using the AMIRA™ software (Visage Imaging, San Diego, CA) as described previously (Krishnan et al. 2007; Krishnan et al. 2008; Underwood et al. 2014). To quantify vascular alignment in the 3D image data, a custom software application WinFiber3D (Maas 2007–2011) was used to measure the angle that each microvessel formed relative to the long-axis (x-axis) of the construct.
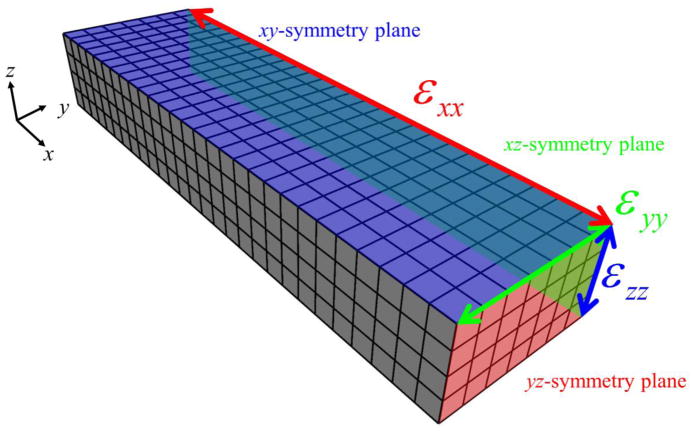
2.3 Finite Element Mesh
The vascularized constructs were discretized using a rectilinear hexahedral FE mesh. To reduce computational cost, a 1/8th symmetry model was created. Symmetry planes were defined in the xy-, xz-, and yz-planes at the geometric center of the construct (Fig. 2). Nodes along the xy-, xz-, and yz-symmetry planes were constrained in the z, y, and x directions, respectively. When simulating a LAC gel, nodes along the face of the mesh normal to the –x direction were fully constrained representing the boundary condition imposed by the stainless steel mesh. In the SAC simulations, nodes along the face of the mesh normal to the –y direction were fully constrained. Simulations of the UNC constructs included no additional nodal constraints beyond the symmetry constraints. At the conclusion of each simulation, the gel contraction (εxx, εyy, and εzz) was measured along where the symmetry planes intersect, corresponding to the geometric center of the construct, in order to compare to experimental data.
Figure 2.
FE representation of vascularized collagen gels. Symmetry was applied when constructing the mesh, creating an 1/8th symmetry model. Nodes along the xy-, xz-, and yz-symmetry planes were constrained in the z, y, and x directions, respectively. At the conclusion of each simulation, the gel contraction (εxx, εyy, and εzz) was measured along where the symmetry planes intersect, corresponding to the geometric center of the construct.
2.4 Discrete Computational Model of Microvessel Growth
Microvessel geometry was predicted by angio3d, a computational growth model of microvessel fragments during spontaneous angiogenesis (Edgar et al. 2013; Edgar et al. 2014). The model predicts the direction and rate of microvessel growth based on physical properties of the ECM, including collagen fibril orientation and matrix density, and the model has been validated against experimental measurements of angiogenic growth within vascularized constructs with both randomly orientated and aligned ECM (Edgar et al. 2013) and for various levels of matrix density (Edgar et al. 2014).
Matrix density and fibril orientation were specified at each node of the FE mesh. During initialization, a random collagen fibril unit vector, θ, was generated for each node, as collagen fibrils are randomly aligned in both acellular and vascularized constructs at Day 0 (Krishnan et al. 2008). The initial collagen density ρ0 was also prescribed at each node, based on the 3.0 mg/ml density in the experiments. Microvessels were represented as a discrete collection of end-to-end line segments. The model was initialized by seeded initial line segments throughout the mesh at random position and orientation. Both ends of each segment were designated active growth tips, and any segment with an active growth tip was referred to as a sprout. At each discrete time step, neovessel elongation (i.e., growth) was simulated by the addition of a new line segment v at each active tip location (Fig. 3A). Local ECM information was used to determine the orientation of the new segment, described by the unit vector v̂, and the length of the new segment, described by the magnitude ||v||. The FE trilinear shape functions were used to interpolate nodal values of fibril orientation and matrix density to the location of the sprout:
| (1) |
| (2) |
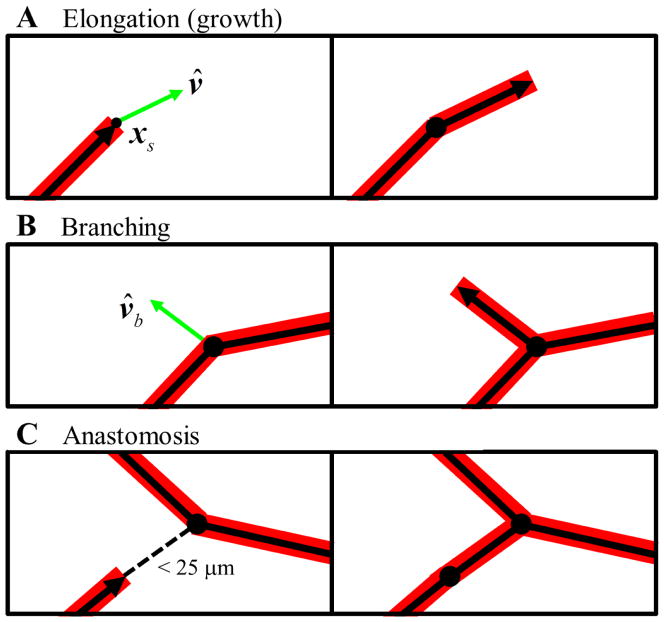
Figure 3.
Angiogenesis was simulated using a discrete growth model. Microvessels were represented as a collection end-to-end line segments. Segments with an active growth tips were defined as sprouts, indicated by the segments with an arrowhead. (A) Neovessel elongation (i.e., growth) was simulated by creating new line segments at all active sprout tips. The direction of the new segment, v̂, was determined by local collagen fibril orientation and the direction of the parent segment. After the growth step, the active tip was transferred to the new segment from the parent segment. (B) Branching was modeled as a random process. During each time step, all segments in the simulation generated a random number. If this number was less than the branching probability b0, than that segment was allowed to branch and a new active sprout was created along the direction of v̂b. (C) Anastomosis, the fusing of two microvessels, was permitted for any active sprout within 25 μm of another vessel. This was simulated by creating a new line segment connecting the two vessels and disabling all growth tips.
In these equations, xs is the position of the active sprout tip, θj and ρj are the fibril orientation vector and matrix density at node j, and Nj is the value of the shape function for node j evaluated at the sprout position. The direction of a new neovessel segment (v̂, the net direction of growth over the time step) was determined by a weighted average of the parent sprout’s direction and the local collagen fibril orientation (Edgar et al. 2014). The length of a new segment, ||v||, representing the net amount of growth that occurred over the time step, was calculated from experimental data and scaled relative to local matrix density as described previously (Edgar et al. 2014). After each elongation step, the active sprout tip was transferred from the parent segment to the new segment accordingly.
Branching, the spontaneous formation of a new sprout along an existing vessel, was modeled as a random process. At each time step, a random number between 0 and 1 was generated for all segments. If the number exceeded a branching probability, b0, then a branch was formed and a new segment was created (Fig. 3B). The direction of the new branch, v̂b, was determined by local collagen orientation and the projector formed by the outer product of the direction of parent segment, v̂, with itself such that
| (3) |
where θ is the collagen fibril orientation at the position of the new branch point as determined by Eqn. (1) and I is the second-order identity tensor. The branching probability for each segment was scaled according to local matrix density such that the probability of forming a branch decreased as density increased as described previously (Edgar et al. 2014). The formation of new vascular connection within the emerging network via anastomosis was permitted for all active sprouts within close proximity of another vessel. If a sprout was within 25 μm of another segment, the vessels anastomose by creating a line segment connecting the active sprout and intersection point (Fig. 3C). After anastomosis, any active growth tips involved in the event were inactivated. This method of simulating anastomosis provides accurate predictions of morphometric data describing the vascular network such as number of branch points, number of free ends, and network interconnectivity (Edgar et al. 2014).
2.5 Vessel Boundary Conditions
If a new segment crossed the boundaries of the simulation domain, the segment was divided into a portion inside the mesh, vi, and a portion outside the mesh, vo (Supplementary Fig. 1 A, B):
| (4) |
Two types of boundaries were considered. The faces of the mesh that did not correspond to the edge of the gel space (i.e., where the gel contacts the stainless steel mesh or at symmetry planes) were considered mesh boundaries. When a new segment penetrated one of these faces while simulating growth, vo was simply discarded (i.e., vo set to 0) and v was replaced by vi and the growth tip was deactivated (Supplementary Fig. 1 C). The other faces of the mesh represent the edges of the construct. When a new segment was found to grow beyond one of these faces (construct boundaries), the portion of the new segment outside of the mesh, vo, was decomposed into a component that laid within the boundary face, v||, and a component normal to the boundary face, v⊥,
| (5) |
| (6) |
where n is the unit normal of the boundary face. A new line segment was set to v|| and this became the new growth tip of the neovessel (Supplementary Fig. 1 D). This caused vessels that encountered a construct boundary to change direction and grow along the boundary face, as it was observed that vessels exhibit this behavior upon encountering the edge of the matrix during culture (Underwood et al. 2014).
2.6 Representation of Active Stress Produced by Microvessels
Each active sprout was assigned an active stress field σs to represent the stress generated by the sprout tip on the ECM as cells in the neovessel sprout apply traction. To calculate the active stress at a position x inside the mesh due to a particular sprout located at xs, a distance vector r was drawn such that
| (7) |
The active stress produced on the ECM by the sprout tip was then calculated based on the length (||r||) and orientation (r̂) of this vector:
| (8) |
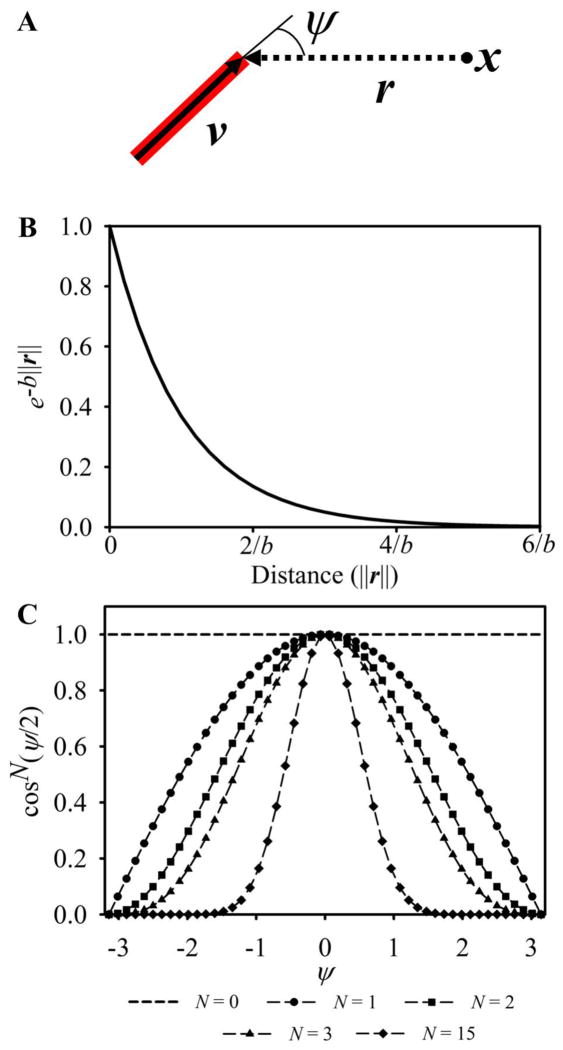
This mathematical representation of the sprout stress was chosen to mimic the ‘fan’ deformation pattern of collagen fibrils that has been observed around sprout tips during angiogenic growth (Kirkpatrick et al. 2007). The exponential term in Eqn. (8) caused sprout stresses to be localized around the sprout tip. The cosine power term, which is a function of the angle ψ, gives the stress field directionality. The angle ψ was measured between the sprout orientation vector, v, and the vector r (Fig 4A). The parameters a, b, and N were adjustable parameters: a scaled the magnitude of the sprout stress, b determined the range over which the sprout acts, and N controlled the width of the stress field (Fig. 4B, C).
Figure 4.
Each active sprout tip was assigned an active sprout stress field. (A) When calculating stress at a point x, a vector r was drawn from x to the location of the sprout tip. The active stress applied to the mesh was calculated using Eqn. (8) and was a function of the distance away from the sprout, ||r||, and ψ, the angle formed between r and the direction of the sprout, v. (B) The exponential component of Eqn. (8) caused stress to exponential decrease as the distance away from the sprout increased, localizing stress around the sprout tip. By a distance of 5/b, stress essentially drops to zero. (C) The width of the sprout stress field was controlled by N, the exponent in the cosine power term. If N was set to 0, then the stress field was isotropic and had no preferred orientation (dashed line, no markers). Setting N greater than or equal to 1 caused the majority of force to be directed into the regions directly in front of the neovessel tip, and the width of the sprout force field decreased for larger values of N.
2.7 Symmetry of Sprout Stress Fields
Each sprout stress field was mirrored across symmetry planes to account for the influence of microvessels in the portions of the construct that were not represented by the FE mesh. The total active stress contribution from a single sprout, σA, was determined by a sum of the sprout stress, σs, defined by Eqn. (8) and the 7 mirrored sprout stress fields such that
| (9) |
Each mirrored sprout stress field was calculated using Eqn. (8) at a mirrored sprout position, . Each of the 7 mirrored sprout positions for a sprout at was calculated by the equation
| (10) |
where s was a vector that contained the x-, y-, and z-coordinates of the geometric center of the construct ([s] = [10.25 2.75 1.5]T mm). The contents of the matrix A were dependent on which symmetry planes were being considered when calculating ,
| (11) |
Each of the 7 mirrored stress fields was calculated by determining a mirrored sprout position based on Eqn. (10), drawing a mirrored distance vector r′ using Eqn. (7), and calculating the mirrored stress using Eqn. (8).
2.8 Constitutive Model
At any time during the simulation, the total stress at a location in the construct was determined by the sum of the active stress component σA and the passive stress response σP, governed by the constitutive model, such that
| (12) |
The material behavior of construct was represented with a composite constitutive model based on mixture theory (Bowen 1976) in order to account for the time-varying properties of the constructs as the gels were gradually vascularized during angiogenesis. The passive stress σP was defined as a weighted sum of the material behavior of the microvessels, σV, and the ECM, σECM,
| (13) |
where ϕ is the volume fraction of the element that is occupied by microvessels. At the beginning of culture, ϕ ≪ 1 and the acellular ECM component dominates the total material response. As growth progresses, ϕ increases and the total material response shifts towards the properties of the vascularized construct.
An isotropic neo-Hookean constitutive model was used to represent the material properties of the vascularized construct (modulus Evess, ν = 0.0). The stress in this material due to deformation was calculated as
| (14) |
where J is the Jacobian and B is the left Cauchy deformation tensor. A hyperelastic constitutive model based on a uniform continuous fiber distribution was used to represent the ECM (Ateshian et al. 2009). This model captures the equilibrium material behavior of collagen gels including nonlinear elasticity, strain-induced anisotropy, low modulus in compression, and a strain-dependent Poisson’s ratio (Roeder et al. 2009). This model consists of a fiber component that only acts in tension (with a nonlinear fiber modulus Efib) embedded within a ground matrix material. The ground matrix was set as an isotropic neo-Hookean material with modulus EM and Poisson’s ratio ν = 0.0 as water was free to leave the gel during deformation due to the slow rate of cellular loading. The total stress in this material due to deformation, σECM, was calculated as a sum of the stress in the ground substance and fiber components, such that
| (15) |
| (16) |
| (17) |
| (18) |
In these equations, In is the fiber invariant of the deformation and N and n are the vectors along the fiber orientation in the reference and current configuration respectively, and H(●) is the Heaviside step function used to ensure that these fibers only contribute stress under tension. The stress contribution from the fiber components σfib is calculated by the surface integration of a unit sphere spanned by all directions of n. To accurately represent the material behavior of the native collagen gels, this constitutive model needed to represent a large disparity in stiffness in tension and compression. The two constitutive models used in this framework exhibit drastically different behavior in compression vs. tension (Supplementary Fig. 2 A, B). Experimental data obtained during uniaxial extension of hexahedral acellular collagen gels was used to calibrate the material model parameters (Supplementary Fig. 2 C) (Krishnan et al. 2007). Values of the material coefficients can be found in Table 1.
Table 1.
Baseline values for all parameters within the model. These values were used in all simulations except for during the parameter sensitivity analysis, in which the parameters were varied with respect to the baseline values listed here. The percentage that each parameter was varied during the parameter sensitivity study is listed in the column on the far right.
| Parameter | Description | Value | Vary |
|---|---|---|---|
| Nfrag | Number of initial neovessel parent fragments | 2114 | -- |
| b0 | Branching probability | 0.1 | -- |
| a | Sprout stress magnitude (per single sprout) | 3.72 μPa | 50% |
| b | Sprout stress range | 250 μm | 25% |
| N | Sprout stress width (cosine exponent) | 2 | 50% |
| EM | ECM constitutive model: Stiffness of ground matrix (governs compressive response) | 34.52 Pa | 50% |
| Efib | ECM constitutive model: Nonlinear fiber stiffness (governs tensile response) | 345.2 Pa | 50% |
| Evess | Microvessel constitutive model: Modulus | 3.452 kPa | 50% |
| τ | Viscoelastic time constant | 1.08 seconds | 25% |
Previous research has demonstrated that stress within vascularized constructs is dissipated over a time scale of seconds (Underwood et al. 2014). This behavior is most likely due to the large water content within collagen gels. To include this behavior within the material model, viscoelastic behavior akin to a Maxwell Fluid model was added. The time-varying second Piola-Kirchhoff stress, S(t), was defined as
| (19) |
| (20) |
where the passive elastic stress SP was the pull-back of the passive Cauchy stress σP as determined by Eqn. (13), G(t) was the reduced relaxation function, and τ was the relaxation time constant.
2.9 Coupling the Discrete Growth Model with ECM Mechanics
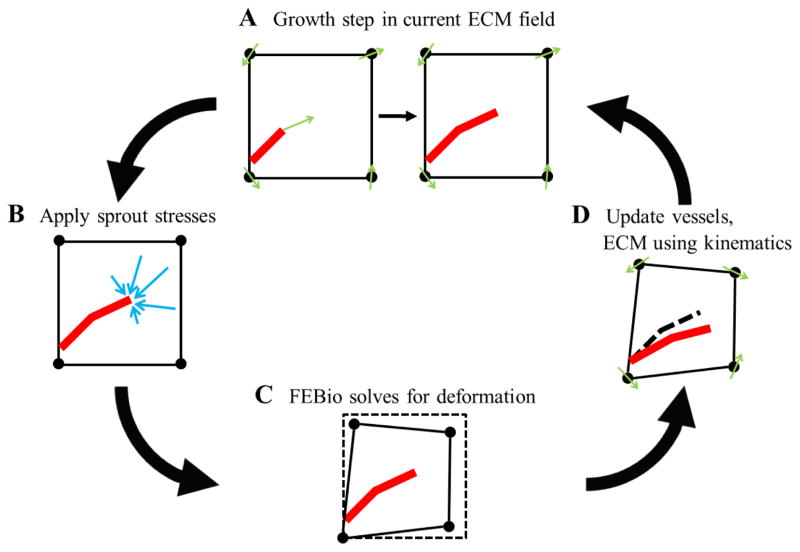
FEBio, a nonlinear FE software, was used to solve for the deformation of the ECM in response to cellular loading (Maas et al. 2012). The coupling between angio3d and FEBio was accomplished through AngioFE, a “plugin” file for FEBio. A plugin is a precompiled, dynamically linked library that can be associated with an executable at run-time. The AngioFE is available online for download at http://febio.org/plugins/angiofe/. AngioFE has access to all the base classes in the FEBio and angio3d libraries, allowing it to perform all the computations required for the simulation, including simulating microvessel growth, applying active stress to the mesh, and calling the nonlinear FE solver. FEBio loads the plugin file at startup and executes all tasks within AngioFE. This framework allows users to include new functionality into their FE analysis without the need to edit and rebuild the entire FEBio source code. First, angio3d simulated a growth step using fibril orientation and matrix density information in the ECM field at time step n (Fig. 5A). Then, sprout stresses were applied to the mesh (Fig. 5B). Next, FEBio was called to solve for the deformation field using the cell-generated loading scenario (Fig. 5C). Finally, the deformation field predicted by FEBio was used to update microvessel position and orientation as well as fibril orientation and density in the ECM field for the next time step n+1 (Fig. 5D). The next growth in angio3d step used this updated ECM field.
Figure 5.
Schematic of the coupling between the discrete growth model angio3d and the nonlinear FE software FEBio. (A) First, angio3d simulated a growth step using fibril orientation and matrix density information in the ECM field at time step n. (B) Then, a sprout stress field was applied to the mesh at each active sprout tip location. (C) FEBio was then used to solve for the deformation caused by the sprout loading scenario. (D) Lastly, the kinematic information predicted by FEBio was used to update the growth model for the next time step n+1. This process included displacing and re-orientating microvessels, re-orientating collagen fibrils, and updating matrix density. The next growth step in angio3d took place in this updated ECM field.
Microvessels were updated to the deformed configuration by interpolating nodal displacement to the location of each segment position, xs, using the shape functions within the mesh. At time step n, the current position of a segment was calculated as
| (21) |
where was the displacement vector for node j at time n, and Nj was the shape function for node j evaluated at the previous position of the segment, . Nodal displacement was defined as the change in position of node j between time points n and n−1. This method of updating microvessel positions meant that microvessel deformation was compatible with the deformation of the ECM.
The biophysical properties of the ECM that regulated growth were updated to the current configuration as well. Free vectors representing collagen fibril orientation were updated to the current configuration using the deformation gradient tensor, F,
| (22) |
where was the collagen fibril orientation vector for node j at time n, was the deformation gradient tensor for node j at time n−1, and was the initial fibril orientation vector for node j. Fibril orientation vectors were normalized after each update to ensure these vectors remained unit vectors. Matrix density was updated into the current configuration using the conservation of mass. Assuming the total mass of matrix within each element does not change through the simulation, but matrix density changes as the element undergoes volume change due to the deformation the volume change during the deformation can be measured through the Jacobian, J= det(F). The matrix density for node j at time n was calculated as
| (23) |
where was the Jacobian for node j at time n−1 and was the initial matrix density for node j. After this update, AngioFE then began the next time step n+1 and called angio3d to calculate the next growth step within the updated ECM field.
2.10 Simulation of Angiogenesis with Various Boundary Conditions
Initial microvessel fragments were seeded in a random distribution within the simulation domain based on the seeding density in the experiments. Unless otherwise noted, parameters were prescribed at the values listed in Table 1. The ECM material coefficients were fit to experimental testing of acellular collagen gels and the vessel material coefficient was scaled relative to this experimentally determined value (Krishnan et al. 2004). The value for the branching probability b0 was determined in a previous study (Edgar et al. 2014). The sprout stress magnitude a was determined by matching gel contraction in the LAC simulations to measurements from the experiments. The other sprout stress parameters b and N were prescribed in order to re-create the ‘fan-shape’ deformation patterns seen in collagen fibrils using live two-photon imaging of angiogenic neovessels (Kirkpatrick et al. 2007).
In the first study, we performed a mesh convergence study by running simulations at various levels of mesh resolution. Convergence was based on the contractile strains predicted by the simulations. Three simulations were run at each mesh resolution with different seedings of the random number generator. Contraction was considered converged once the difference between predictions of contraction for the next mesh resolution level dropped below a predetermined threshold (ε = 1e-3). After the required mesh resolution was determined, microvessel alignment was measured at the geometric center of the gel, corresponding to the region that was imaged during the experiments. Then, a parameter sensitivity study was performed on the model. The three sprout stress parameters (a, b, N) and four material coefficients (EM, Efib, Evess, τ) were all increased and decreased by 50% (25% in the case of some parameters due to high sensitivity) of their baseline values in Table 1. Three simulations were performed for each parameter variation at the same random seeds used for the mesh resolution determined in the convergence study. Sensitivity was quantified by normalizing the percent change in contraction by the percent change in the parameter.
After the mesh convergence study and parameter sensitivity studies were completed using the LAC geometry and boundary conditions, the modeling framework was used to predict growth in two additional rectangular boundary conditions: unconstrained (UNC), and short-axis constrained (SAC). The converged mesh from the LAC simulations was used and the boundary conditions were modified accordingly. Contraction and microvessel alignment were measured at the geometric center of the construct from each simulation and the data was compared to data from the constrained construct experiments. A two-tailed Student’s T-test with unequal variance (Welch’s T-test) was performed between experimental and computational gel contraction data to detect any statistical difference (α = 0.05). If a statistical difference could not be detected, a TOST-test (Two One-Sided T-test (Richter and Richter 2012)) was performed to test for statistical equivalence (α = 0.05, Θ = 0.3).
3 Results
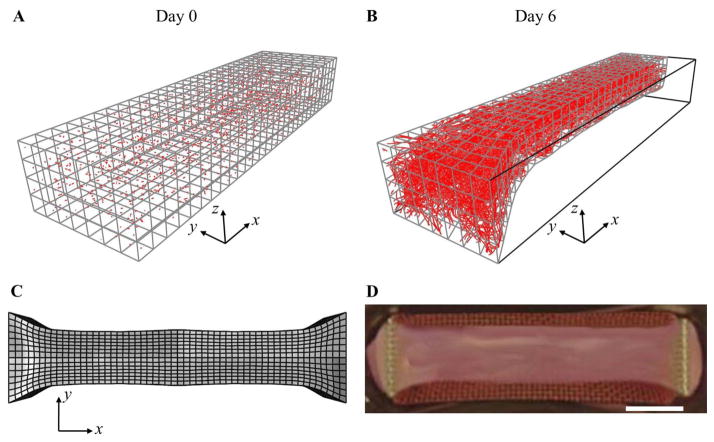
Growth in the vascularized constructs was consistent throughout all experiments. Neovessels sprouts from parent vessel fragments were evident at Days 2–3, and each experiment resulted in a well-established microvascular network within the construct by Day 6. Gel contraction and microvessel alignment data from the experiments resembled data from previous studies (Underwood et al. 2014). In the LAC simulations, the free faces of the construct contracted inward forming a “neck” shape, with the most contraction occurring at the right side of the mesh corresponding to the center of the construct (Fig. 6). Each simulation resulted in a deformed mesh that closely resembled the shape of the constrained constructs at Day 6.
Figure 6.
Simulation of a long-axis constrained (LAC) vascularized gel. These results used the converged mesh resolution determined during convergence study. (A) At Day 0, the mesh was seeded with initial microvessel fragments. (B) At Day 6, the gel has become highly perfused by microvessels and has deformed into a ‘necked’ shape as seen in the LAC experiments. (C) Full-geometry construction of the gel as predicted by the deformed FE mesh. (D) The deformed gel geometry predicted in the simulation closely resembled the shape of long-axis constrained vascularized gels at Day 6. Scale bar 2 mm.
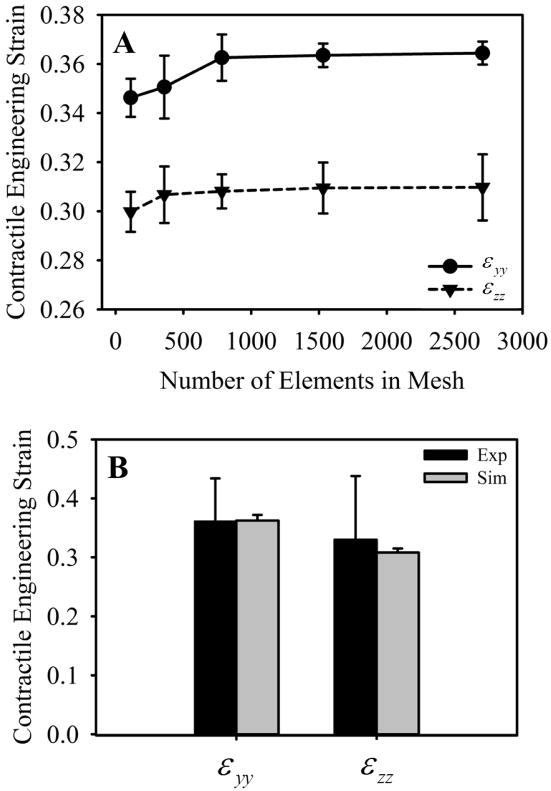
In order to determine a mesh resolution for which contraction in y and z was fully converged, we ran simulations with increasing mesh resolution. As mesh resolution was increased, contraction along the y and z axes converged toward ~0.36 and ~0.30, respectively (Fig. 7A). Contraction in y (εyy) and contraction in z (εzz) were both converged at a mesh resolution of 784 elements. Contraction results from the 784-element simulations were within one standard deviation of contraction measured in the experiments (Fig. 7B). Microvessels within the experiments were highly aligned along the long-axis of the construct (i.e., the constrained axis) at Day 6 of growth, and the computational model predicted similarly aligned microvasculature in the simulation of a LAC gel (Fig. 8).
Figure 7.
Mesh convergence and gel contraction. (A) Mesh convergence was determined by running simulations with increasing levels of mesh refinement. Convergence was determined when predictions of contraction differed less than 1e-3 from results using the next mesh refinement level. Contraction in y and z were both converged at a resolution of 784 elements. (B) Engineering strain (gel contraction) from the experiments, shown in black, and the 784-element simulations, shown in gray. The model was able to produce good predictions of gel contraction, as values of εyy and εzz where both within one standard deviation of contraction measured in the experiments.
Figure 8.
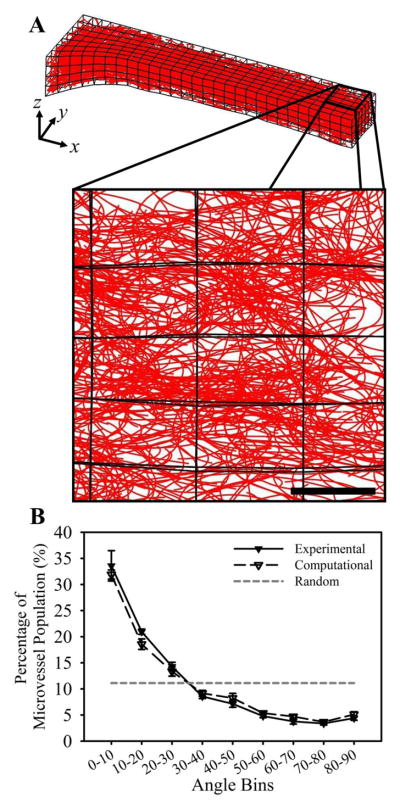
Microvessel alignment. (A) The computational model predictions of aligned microvessels within a LAC gel. The subset of microvessels shown below is a z-projection of microvessels at the geometric center of the gel (the right side of the mesh) and corresponds to the region of that was imaged using confocal microscopy. Scale bar 300 μm. (B) The computational model predicted a distribution of microvessel alignment that was in excellent agreement with experimental measurements. Measurements were obtained by measuring the angle that each vessel formed with respect to the long-axis (x-axis) of the gel. Microvessels within the experiments and simulations were both highly aligned along the long-axis as seen in the large amount of vessels within the more acute angle bins. The gray dashed line illustrates expected data for a random network.
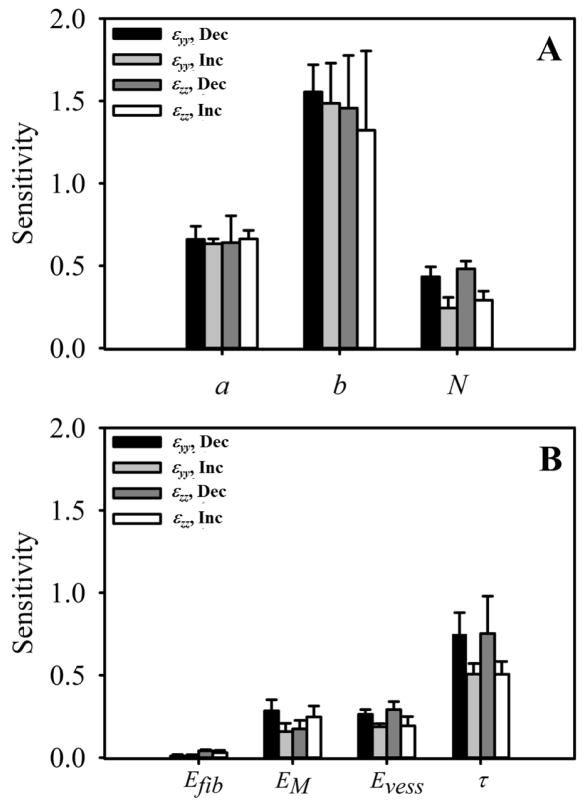
The sensitivity analysis of the sprout stress parameters demonstrated that the model was most sensitive to b, the parameter controlling the sprout stress range, while changes in the magnitude a and the width of the stress field, controlled by N, had much less of an effect (Fig. 9A). There was little to no difference in sensitivity between εyy and εzz. Increasing the sprout stress range by decreasing the parameter b caused a more pronounced change in gel contraction than increasing b. The model predictions were sensitive to changes in the viscoelasticity relaxation time constant, τ, while contraction was relatively insensitive to changes in the other parameters of the constitutive models (Fig. 9B). Decreasing the time constant sped up the rate of stress dissipation within the simulations, and the model was more sensitive to decreases in the time constant than increases. Additionally, the model was more sensitive to changes in the compressive modulus of the ECM material EM than the tensile modulus Efib and showed roughly the same preference for Evess as EM.
Figure 9.
Sensitivity analysis of the model parameters associated with the sprout stress field and material model. Numerous simulations were run as each parameter was increased or decreased. The percent change in contraction that occurred in response to the variation in the parameter was collected. We normalized this value by the percent change in the parameter to quantify sensitivity. Variation in εyy as each parameter decreases or increases can be seen in black and light gray, respectively. Variation in εzz as each parameter decreases or increases can be seen in dark gray and white, respectively. (A) Sensitivity analysis of the sprout stress parameters: a (magnitude), b (range), and N (controls the width of the stress field). The model was highly sensitive to changes in b, and was more sensitive to decreases in this parameter rather than increases. The model was relatively insensitive to the other two sprout stress parameters. (B) Sensitivity analysis for the material model parameters: Efib (tensile modulus of ECM material), EM (compressive modulus of ECM material), Evess (modulus of the microvessel material, and τ (time constant for viscoelastic relaxation). Gel contraction was most sensitive to changes in the viscoelastic relaxation time, while relatively insensitive to the other parameters. Contraction was also more sensitive to variations in the compressive modulus for the ECM material (EM) compared to changes in the tensile modulus (Efib).
Simulations of each construct boundary condition (UNC, LAC, SAC) predicted a deformed construct geometry and vascular alignment that closely resembled data from the constrained gel experiments (Fig. 10). Contraction measured for each boundary condition was statistically indistinguishable from experimental data via student’s T-test. Additionally, a statistical equivalence was detected between experimental and computational data via TOST-test for the following datasets: εxx and εyy for the UNC gels, εyy for the LAC gels, and εxx for the SAC gels. Deformation in the UNC case was essentially isotropic (Fig. 10A), while the LAC constructs deformed only along the y and z directions due to the boundary constraint (Fig. 10B). In the SAC constructs, the long-axis was unconstrained but still effectively stiff along this direction due to the long aspect ratio of the construct resulting in very little contraction along x (Fig. 10C). Vascular alignment predicted in simulations of each boundary condition closely resembled alignment data measured in the experiments (Fig. 10D, E). The simulation accurately predicted randomly aligned microvessel in the UNC and SAC constructs and vessels aligned along the long-axis in the LAC constructs (Fig. 10E).
Figure 10.
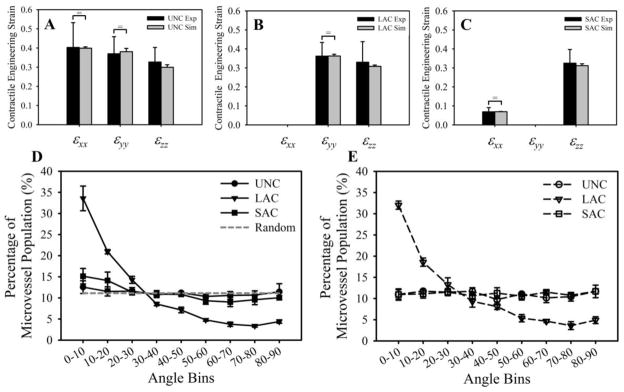
Gel contraction and microvessel alignment for each of the three boundary conditions. (A–C) Engineering strain (gel contraction) was measured at the geometric center of each construct for the unconstrained (A), long-axis constrained (B), and short-axis constrained (C) constructs. Experimental measurements are shown in black, computational predictions of gel contraction are in gray. Statistical equivalence as detected by TOST-test is indicated by the bracket and equal sign. (D, E) Distributions of microvessel alignment with respect to the long-axis (x-axis) of the gel measured from the experiments (D) and predicted by the simulations (E). Microvessels in the LAC experiments were highly aligned along the long-axis, while randomly oriented in the UNC and SAC conditions. The computational simulations accurately predicted microvessel alignment in each of the three boundary conditions.
4 Discussion
We developed, implemented and performed a global validation of a computational framework that simulated angiogenic growth coupled to matrix deformation. The coupled growth model accurately predicted gel contraction and microvessel alignment during simulations of each gel boundary conditions. The model predicted random alignment within the UNC and SAC simulations and aligned microvasculature when simulating the LAC constructs, similar to what we found in the vascularized construct experiments. There are two mechanisms in the modeling framework that regulate microvessel alignment. The first mechanism for alignment occurs as microvessels convect with the anisotropic deformation of the matrix. This mechanism results from interpolating nodal displacement predicted by FEBio to the microvessel and can be interpreted as passive alignment. If the deformation field generated by sprout forces was isotropic, microvessels grew and deformed equally in all directions with no preferred orientation, as was the case for UNC constructs. However, in the LAC case the presence of the boundary constraint caused the construct to undergo anisotropic deformation. In the LAC constructs the length of the construct was fixed along the constrained axis as the construct contracted laterally. This displacement caused vessels to move inward along the y and z directions as these dimensions of the construct contracted, leaving the microvessels oriented along the x-axis. In the SAC case, the high effective stiffness prevented the construct from deforming along the long-axis, so εxx was considerably reduced. However, εzz was unaffected in this case so microvessels were contracted along z and randomly aligned within the xy-plane, similar to the UNC case.
The second alignment mechanism occurs as microvessels grow along collagen fibrils, which themselves become aligned passively. This is often referred to as contact guidance. As the construct contracted, the orientation of collagen fibrils was updated by the deformation gradient. In the LAC case, the deformation of the construct caused fibril orientation vectors to contract along the y and z direction, leaving these vectors aligned along the x-axis. This further caused neovessels to align along the constrained axis as the vessels received directional cues from the collagen fibrils through contact guidance. This can be interpreted as an active alignment mechanism, as it results from neovessels receiving information from the ECM, integrating these signals, and then growing along a certain direction based on this signal. For example, such a signal could be available binding sites along the length of aligned collagen fibrils. A distinct advantage of this modeling framework is that the mechanisms for passive and alignment can be deactivated individually. In doing so, we observed that passive alignment is the predominate mechanism governing microvessel alignment in these cultures. The addition of active alignment improved the accuracy of predictions, but the results were much more sensitive to the passive alignment mechanism. Additionally, alignment results were sensitive to the angle formed by new sprouts during branching. Previous formulations of the model enforced perpendicular sprouts when calculating branching, but we found that this reduced vascular alignment in the simulations as vessels sprouting from aligned microvessels in the later stages of the simulation were formed perpendicular to the preferred alignment direction and could not align quickly due to the persistence growth component. Scaling the projector tensor formed by the outer product of v in Eqn. (3) by one-half ensured that new sprouts still grew divergent from the parent sprout but facilitated better alignment of new vessels along collagen fibrils, improving alignment results in the simulations.
The model presented here presents a unique approach to modeling angiogenesis and tissue morphogenesis. The deformation of the macroscale was driven by cellular biomechanical activity at the microscale. The coupling of the discrete angiogenic growth model to FEBio allowed the model to track information at the small scale while resolving deformation at the macroscale. Individual neovessel sprouts generated localized stress fields that change position as the matrix deformed and neovessels grew. New stress fields were added when a new branch point emerged, stress fields were removed due to an anastomosis. By using a continuous field to represent each sprout stress field, we did not have to homogenize stress over the mesh; rather, stress could be calculated at any required location (see Eqns. (7), (8)). The use of the FE method provided the means to homogenize the various discrete microscale aspects within the model across the continuum. Shape functions within the mesh were used to interpolate ECM fibril orientation, matrix density, and nodal displacement to the microscale. The material properties of the vascular network were homogenized using the volume fraction ϕ within the composite material model (see Eqn. (13)). The microvascular network was represented using a simple isotropic material, but the framework could be expanded to include an orthotropic material to represent the anisotropy induced by vascular alignment. The use of the dynamic discrete growth model to simulate angiogenesis allowed our framework to include the path-dependent aspects of angiogenesis as well. Growth was applied over discrete time steps using current information from the vascular network and ECM field. At the end of each time step, both the vascular components and the ECM field was updated using the kinematics information predicted by FEBio (i.e., displacing and re-orientating sprouts, re-orientating collagen fibrils, and updating density). This created the dynamic link between cellular biomechanical activity and the matrix that exists during angiogenesis. Due to these features, we believe that this modeling framework presents a unique framework to investigate the complex biomechanical regulation of morphogenic processes such as angiogenesis that have often proven difficult to study in the past.
ECM contraction was sensitive to changes in the stress field that neovessels applied to the ECM during growth. This result was expected. In our model, the sprout force field represented the force applied directly at the focal adhesions and how these forces were transmitted through the ECM, as the fibrillar structure of the matrix was not represented explicitly. Contraction was particularly sensitive to the range over which these sprout force fields acted, controlled by the parameter b. Microvessels in our constructs were cultured in growth media supplemented with VEGF, an important growth factor during angiogenesis. VEGF binding to the receptor VEGFR2 in endothelial cells leads to the production of stress fibers and focal adhesions, the motility and contractility machinery of the cell, through the Rho-ROCK (Rho Kinase) pathway (van Nieuw Amerongen et al. 2003; Yang et al. 2011). As endothelial cells apply traction at focal adhesions attached to the ECM, collagen fibrils are pulled toward the sprout tip, condensing and reorienting towards the sprout in a characteristic ‘fan’ pattern (Kirkpatrick et al. 2007). The deformation generated by neovessel sprouts extended up to 1000 μm from the sprout tip (Kirkpatrick et al. 2007). Using this information, we set the b to 1/250 μm−1, which caused the exponential function in Eqn. (8) to effectively drop to zero at a distance of 1000 μm. The parameter a controlled the magnitude of the sprout force field and was optimized to match the contraction results from the LAC construct experiments. The width of the ‘fan’ shape was controlled by N, the exponent on cosine in Eqn. (8). We used a cosine power term as the exponent on the cosine term caused force to directed in front to the vessel, and we estimated the value of N from data from Kirkpatrick et al. (Kirkpatrick et al. 2007). Additionally, we found that making the sprout force field too narrow by choosing a high value of N caused unequal contraction along y and z. In the experiments, contraction was essentially equal along y and z, and the ratio of εzz to εyy was ~0.9. The simulations predicted a ratio εzz to εyy of ~0.8 for values of N = 0 (isotropic) up to N = 3, at which point the ratio began to decrease. At N = 15, the ratio of εzz to εyy dropped below 0.6, indicating that making the sprout force fields too narrow produced unrealistic contraction.
In these initial simulations, materials were represented using relatively simple constitutive models. The constitutive model used in the simulations can be interpreted of as a simple spring and dashpot connected in series with an active contractile element connected in parallel. The sprout stress parameters controlled the load applied to the system by active contraction, the elastic material parameters Efib, EM, and Evess controlled the response of the spring, while the time constant τ controlled the response of the dashpot. When choosing the constitutive models and setting values for the parameters, we had to account for the changes that occurred in the vascularized constructs during culture. The tensile modulus of the ECM material, Efib, was determined to fitting the material to experimental data from uniaxial testing of 3.0 mg/ml collagen gels (Fig. 4C) (Krishnan et al. 2004). We prescribed the other two moduli, EM and Evess, relative to this experimentally-determined value. During the development of the model, we found that a large discrepancy between stiffness in tension and compression was required in order for the constructs to deform realistically. For example, if a standard neo-Hookean material was set at the modulus determined from the uniaxial testing data, the constructs would tend to twist and buckle rather than contract inward as seen in the experiments as the neo-Hookean material has the same modulus in tension and compression. In order to ensure sufficient tension-compression non-linearity and realistic deformation of the type I collagen gel during our simulations, we set the compressive modulus of the ECM material, EM, to by 10× less than the tensile modulus Efib.
We found that model predictions were more sensitive to the compressive modulus than the tensile modulus, as the deformation of the construct primarily involves contraction. In the LAC simulations, Efib only scales the magnitude of tension that develops along the constrained axis while EM controls how the construct deforms at the beginning of the simulation while the construct is primarily acellular. The microvessel material model exerts its control on contraction as the construct becomes increasingly vascularized and the microvessel volume fraction increases. Contraction in simulations involving variations in Evess only deviate from the baseline simulations at ~Day 4. We have found through mechanical testing that the vascularized constructs become ~1.5× more stiff during culture as angiogenic neovessels apply traction, secrete proteases, and generate new cell-matrix adhesions (Krishnan et al. 2007). In our simulations, the volume fraction of microvessels was used to weight the stress response from the microvessel material model, and this volume fraction on average reached a maximum of about ~0.015 by Day 6. Therefore, we set the microvessel material modulus Evess to be 100× the stiffness of the ECM compressive modulus, EM, in order to cause this increase in stiffness. Note that the microvessel material is meant to actually represent the properties of the vascularized construct as a whole. The composite material model is designed to slowly transition from properties of an acellular collagen construct to a mature vascularized construct as the volume fraction of microvessels slowly increases during growth.
Of the material parameters within the model, contraction and thus vascular alignment was most sensitive to changes in τ, the viscoelastic relaxation time constant. In previous research, we observed that constrained vascularized constructs treated with Cytochalasin-D to prevent cell-generated contraction did not retract after being cut away from the constraint (Underwood et al. 2014). These results led us to postulate that stress is dissipative rather than accumulative in these constructs, and that stress relaxation occurs within several seconds. Therefore, we set τ to 1.09 seconds, causing the reduced relaxation function to reach near complete relaxation in ~4–5 seconds. In the simplified version of the material model, the viscoelastic component acts as a dashpot. The force in the dashpot is proportional to the time constant τ and the rate of deformation, therefore decreasing τ while keeping the amount of cell-generated loading unchanged causes the rate of deformation to increase. Contraction vs. time in the simulations with a decreased τ had a steeper slope than baseline simulations with larger values of τ. Although we were able to prescribe a value of τ based on the experiments involving Cytochalasin-D, future experiments could track construct deformation over time, allowing us to confirm that the rate of deformation and the time constant within our model are truly valid. Additionally, the amount of viscous stress dissipation may not stay constant over the culture. The rate of dissipation could change as neovessels contract, remodel, and expunge water from the fibrillar structure of the matrix, and adding a time-varying time constant to our simulations would allow us to include this behavior.
Other theoretical and computational approaches have been utilized to study the role of mechanical interactions between cells and the ECM during tissue growth (Ateshian and Humphrey 2012; Barocas et al. 1995; Barocas and Tranquillo 1997; Rausch et al. 2011; van Oers et al. 2014). Although numerous mathematical and computational approaches have been utilized to study angiogenesis (Peirce 2008; Qutub et al. 2009), to our knowledge no computational models have ever been proposed to study the coupling between mechanical interactions with the ECM and neovessel growth during angiogenesis. The most relevant study demonstrated that cell-generated traction forces produce alignment perpendicular to gel contraction by modeling the fibroblast-mediated compaction of collagen gels (Barocas and Tranquillo 1997). Matrix compaction was driven by an active stress that depended on cell concentration and orientation. The active stress parameter in their study was 1.4×10−7 N·cm/cell. For comparison, active stress in our model based on the initial seeding concentration of fragments was 7.44×10−15 N·cm/fragment. However, differences between approaches prevent a direct comparison. Parameters reported by Barocas and Tranquillo were normalized per cell, cells were treated as a continuous component of a biphasic material, and their formulation for active stress was homogenous and applied to the entire domain. Nevertheless, the similarity of predictions related to the effects of cell-generated traction forces is encouraging, and suggests that our approach could be extended to other biological processes that involve discrete cellular structures that mechanically interact with the ECM in 3D including mechanotaxis, tumor growth, neurogenesis, wound healing, embryonic development, and tissue morphogenesis. Our approach accommodates the extension to include other physics such as solute transport, convection, reaction and diffusion, and many of these capabilities have been added to the FEBio framework recently (Ateshian et al. 2013; Ateshian et al. 2014).
Supplementary Material
Acknowledgments
Financial support from National Institutes of Health #R01HL077683, R01GM083925 and R01EB015133 is gratefully acknowledged.
References
- Annex BH. Therapeutic angiogenesis for critical limb ischaemia. Nature reviews Cardiology. 2013;10:387–396. doi: 10.1038/nrcardio.2013.70. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Humphrey JD. Continuum mixture models of biological growth and remodeling: past successes and future opportunities. Annu Rev Biomed Eng. 2012;14:97–111. doi: 10.1146/annurev-bioeng-071910-124726. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Maas S, Weiss JA. Multiphasic finite element framework for modeling hydrated mixtures with multiple neutral and charged solutes. J Biomech Eng. 2013;135:111001. doi: 10.1115/1.4024823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Nims RJ, Maas S, Weiss JA. Computational modeling of chemical reactions and interstitial growth and remodeling involving charged solutes and solid-bound molecules. Biomech Model Mechanobiol. 2014;13:1105–1120. doi: 10.1007/s10237-014-0560-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Rajan V, Chahine NO, Canal CE, Hung CT. Modeling the matrix of articular cartilage using a continuous fiber angular distribution predicts many observed phenomena. J Biomech Eng. 2009;131:061003. doi: 10.1115/1.3118773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barocas VH, Moon AG, Tranquillo RT. The fibroblast-populated collagen microsphere assay of cell traction force--Part 2: Measurement of the cell traction parameter. J Biomech Eng. 1995;117:161–170. doi: 10.1115/1.2795998. [DOI] [PubMed] [Google Scholar]
- Barocas VH, Tranquillo RT. An anisotropic biphasic theory of tissue-equivalent mechanics: the interplay among cell traction, fibrillar network deformation, fibril alignment, and cell contact guidance. J Biomech Eng. 1997;119:137–145. doi: 10.1115/1.2796072. [DOI] [PubMed] [Google Scholar]
- Bottenstein JE, Sato GH. Growth of a rat neuroblastoma cell line in serum-free supplemented medium. Proceedings of the National Academy of Sciences of the United States of America. 1979;76:514–517. doi: 10.1073/pnas.76.1.514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouhadir KH, Mooney DJ. Promoting angiogenesis in engineered tissues. Journal of drug targeting. 2001;9:397–406. doi: 10.3109/10611860108998775. [DOI] [PubMed] [Google Scholar]
- Bowen RM. Theory of mixtures. Academic Press; New York: 1976. [Google Scholar]
- Carmeliet P. Manipulating angiogenesis in medicine. Journal of internal medicine. 2004;255:538–561. doi: 10.1111/j.1365-2796.2003.01297.x. [DOI] [PubMed] [Google Scholar]
- Chang CC, et al. Determinants of microvascular network topologies in implanted neovasculatures. Arteriosclerosis, thrombosis, and vascular biology. 2012;32:5–14. doi: 10.1161/ATVBAHA.111.238725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung AS, Ferrara N. Developmental and pathological angiogenesis. Annual review of cell and developmental biology. 2011;27:563–584. doi: 10.1146/annurev-cellbio-092910-154002. [DOI] [PubMed] [Google Scholar]
- Conway EM, Collen D, Carmeliet P. Molecular mechanisms of blood vessel growth. Cardiovascular research. 2001;49:507–521. doi: 10.1016/s0008-6363(00)00281-9. [DOI] [PubMed] [Google Scholar]
- Edgar LT, Sibole SC, Underwood CJ, Guilkey JE, Weiss JA. A computational model of in vitro angiogenesis based on extracellular matrix fibre orientation. Computer methods in biomechanics and biomedical engineering. 2013;16:790–801. doi: 10.1080/10255842.2012.662678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar LT, Underwood CJ, Guilkey JE, Hoying JB, Weiss JA. Extracellular matrix density regulates the rate of neovessel growth and branching in sprouting angiogenesis. PloS one. 2014;9:e85178. doi: 10.1371/journal.pone.0085178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egginton S, Hudlicka O, Brown MD, Walter H, Weiss JB, Bate A. Capillary growth in relation to blood flow and performance in overloaded rat skeletal muscle. Journal of applied physiology. 1998;85:2025–2032. doi: 10.1152/jappl.1998.85.6.2025. [DOI] [PubMed] [Google Scholar]
- Ellis LM, Rosen L, Gordon MS. Overview of anti-VEGF therapy and angiogenesis. Part 1: Angiogenesis inhibition in solid tumor malignancies. Clinical Advances in Hematology and Oncology. 2006;4(suppl):1–10. quz 11–12. [PubMed] [Google Scholar]
- Folkman J. Angiogenesis and angiogenesis inhibition: an overview. EXS. 1997;79:1–8. doi: 10.1007/978-3-0348-9006-9_1. [DOI] [PubMed] [Google Scholar]
- Hoying JB, Boswell CA, Williams SK. Angiogenic potential of microvessel fragments established in three-dimensional collagen gels In vitro cellular & developmental biology. Animal. 1996;32:409–419. doi: 10.1007/BF02723003. [DOI] [PubMed] [Google Scholar]
- Ingber DE. Mechanical signaling and the cellular response to extracellular matrix in angiogenesis and cardiovascular physiology. Circulation research. 2002;91:877–887. doi: 10.1161/01.res.0000039537.73816.e5. [DOI] [PubMed] [Google Scholar]
- Jaffe RB. Importance of angiogenesis in reproductive physiology. Seminars in perinatology. 2000;24:79–81. doi: 10.1016/s0146-0005(00)80062-2. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick ND, Andreou S, Hoying JB, Utzinger U. Live imaging of collagen remodeling during angiogenesis American journal of physiology. Heart and circulatory physiology. 2007;292:H3198–3206. doi: 10.1152/ajpheart.01234.2006. [DOI] [PubMed] [Google Scholar]
- Krishnan L, Hoying JB, Nguyen H, Song H, Weiss JA. Interaction of angiogenic microvessels with the extracellular matrix American journal of physiology. Heart and circulatory physiology. 2007;293:H3650–3658. doi: 10.1152/ajpheart.00772.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan L, Underwood CJ, Maas S, Ellis BJ, Kode TC, Hoying JB, Weiss JA. Effect of mechanical boundary conditions on orientation of angiogenic microvessels. Cardiovascular research. 2008;78:324–332. doi: 10.1093/cvr/cvn055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan L, Weiss JA, Wessman MD, Hoying JB. Design and application of a test system for viscoelastic characterization of collagen gels. Tissue engineering. 2004;10:241–252. doi: 10.1089/107632704322791880. [DOI] [PubMed] [Google Scholar]
- Maas SA. WinFiber3D. Musculoskeletal Research Laboratories, University of Utah; Salt Lake City, UT, USA: 2007–2011. ( http://mrl.sci.utah.edu/software/winfiber3d) [Google Scholar]
- Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: finite elements for biomechanics. Journal of biomechanical engineering. 2012;134:011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novosel EC, Kleinhans C, Kluger PJ. Vascularization is the key challenge in tissue engineering. Advanced drug delivery reviews. 2011;63:300–311. doi: 10.1016/j.addr.2011.03.004. [DOI] [PubMed] [Google Scholar]
- Nunes SS, Krishnan L, Gerard CS, Dale JR, Maddie MA, Benton RL, Hoying JB. Angiogenic potential of microvessel fragments is independent of the tissue of origin and can be influenced by the cellular composition of the implants. Microcirculation. 2010;17:557–567. doi: 10.1111/j.1549-8719.2010.00052.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce SM. Computational and mathematical modeling of angiogenesis. Microcirculation. 2008;15:739–751. doi: 10.1080/10739680802220331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirce SM, Skalak TC. Microvascular remodeling: a complex continuum spanning angiogenesis to arteriogenesis. Microcirculation. 2003;10:99–111. doi: 10.1038/sj.mn.7800172. [DOI] [PubMed] [Google Scholar]
- Phelps EA, Garcia AJ. Engineering more than a cell: vascularization strategies in tissue engineering. Current opinion in biotechnology. 2010;21:704–709. doi: 10.1016/j.copbio.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pries AR, Secomb TW. Control of blood vessel structure: insights from theoretical models. American journal of physiology Heart and circulatory physiology. 2005;288:H1010–1015. doi: 10.1152/ajpheart.00752.2004. [DOI] [PubMed] [Google Scholar]
- Qutub AA, Mac Gabhann F, Karagiannis ED, Vempati P, Popel AS. Multiscale models of angiogenesis. IEEE Eng Med Biol Mag. 2009;28:14–31. doi: 10.1109/MEMB.2009.931791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rausch MK, Dam A, Goktepe S, Abilez OJ, Kuhl E. Computational modeling of growth: systemic and pulmonary hypertension in the heart. Biomech Model Mechanobiol. 2011;10:799–811. doi: 10.1007/s10237-010-0275-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richter SJ, Richter C. A method for determining equivalence in industrial applications. Quality Engng. 2012;14:375–380. [Google Scholar]
- Roeder BA, Kokini K, Voytik-Harbin SL. Fibril microstructure affects strain transmission within collagen extracellular matrices. Journal of biomechanical engineering. 2009;131:031004. doi: 10.1115/1.3005331. [DOI] [PubMed] [Google Scholar]
- Shiu YT, Weiss JA, Hoying JB, Iwamoto MN, Joung IS, Quam CT. The role of mechanical stresses in angiogenesis. Critical reviews in biomedical engineering. 2005;33:431–510. doi: 10.1615/critrevbiomedeng.v33.i5.10. [DOI] [PubMed] [Google Scholar]
- Underwood CJ, Edgar LT, Hoying JB, Weiss JA. Cell-generated Traction Forces and the Resulting Matrix Deformation Modulate Microvascular Alignment and Growth during Angiogenesis. Am J Physiol Heart Circ Physiol. 2014 doi: 10.1152/ajpheart.00995.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Nieuw Amerongen GP, Koolwijk P, Versteilen A, van Hinsbergh VW. Involvement of RhoA/Rho kinase signaling in VEGF-induced endothelial cell migration and angiogenesis in vitro. Arteriosclerosis, thrombosis, and vascular biology. 2003;23:211–217. doi: 10.1161/01.atv.0000054198.68894.88. [DOI] [PubMed] [Google Scholar]
- van Oers RF, Rens EG, LaValley DJ, Reinhart-King CA, Merks RM. Mechanical cell-matrix feedback explains pairwise and collective endothelial cell behavior in vitro. PLoS Comput Biol. 2014;10:e1003774. doi: 10.1371/journal.pcbi.1003774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vernon RB, Sage EH. A novel, quantitative model for study of endothelial cell migration and sprout formation within three-dimensional collagen matrices. Microvascular research. 1999;57:118–133. doi: 10.1006/mvre.1998.2122. [DOI] [PubMed] [Google Scholar]
- Yang MT, Reich DH, Chen CS. Measurement and analysis of traction force dynamics in response to vasoactive agonists. Integrative biology: quantitative biosciences from nano to macro. 2011;3:663–674. doi: 10.1039/c0ib00156b. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.