Neural dynamics of social tie formation in economic decision-making

Abstract

The disposition for prosocial conduct, which contributes to cooperation as arising during social interaction, requires cortical network dynamics responsive to the development of social ties, or care about the interests of specific interaction partners. Here, we formulate a dynamic computational model that accurately predicted how tie formation, driven by the interaction history, influences decisions to contribute in a public good game. We used model-driven functional MRI to test the hypothesis that brain regions key to social interactions keep track of dynamics in tie strength. Activation in the medial prefrontal cortex (mPFC) and posterior cingulate cortex tracked the individual’s public good contributions. Activation in the bilateral posterior superior temporal sulcus (pSTS), and temporo-parietal junction was modulated parametrically by the dynamically developing social tie—as estimated by our model—supporting a role of these regions in social tie formation. Activity in these two regions further reflected inter-individual differences in tie persistence and sensitivity to behavior of the interaction partner. Functional connectivity between pSTS and mPFC activations indicated that the representation of social ties is integrated in the decision process. These data reveal the brain mechanisms underlying the integration of interaction dynamics into a social tie representation which in turn influenced the individual’s prosocial decisions.

INTRODUCTION

Unlike most animal species, humans cooperate with individuals beyond kin and reproductive partners. We also have close affective relationships with genetically unrelated individuals and the strength of these relationships influences our level of cooperation with others. Neural studies of human social behavior have recently begun to explore the question of affective attachment such as friendship (Krienen et al., 2010; Fareri et al., 2012), sympathy (Decety and Chaminade, 2003) and romantic attachment (Aron et al., 2005; Fisher et al., 2005; Zeki, 2007). Notably, the posterior superior temporal sulcus (pSTS) is implicated in response to cooperative partners (Singer et al., 2006), friends and loved ones (Bartels and Zeki, 2000), while the medial prefrontal cortex (mPFC) is involved in making trait judgments of close friends (Heatherton et al., 2006; Fareri et al., 2012), in cooperative decisions (McCabe et al., 2001; Rilling et al., 2004) and in trust (Krueger et al., 2007). However, only already existing ties have been investigated while behavioral evidence suggests that interpersonal ties can form rapidly during interaction with strangers and play an important role in social decision-making processes (van Dijk et al., 2002; Sonnemans et al., 2006). The development of such interpersonal affective bonds has not been accounted for in formal mathematical models of social decision-making either, with only few exceptions (van Dijk and van Winden, 1997). The brain processes underlying the dynamics of tie formation are still unknown. More importantly, the neural mechanisms by which social ties modulate economic decision-making remain to be elucidated (Hein et al., 2010).

Economic models of interdependent utilities formalize the care for others in our choice by allowing one’s utility to depend on the utility of interacting partners (Sobel, 2005). The weight attributed to interaction partners’ well-being in one’s own utility is typically considered as stable, reflecting a personality trait, like in the well-known inequality aversion models (Fehr and Schmidt, 1999; Bolton and Ockenfels, 2000). There is a growing awareness though that our preferences may change depending on the relationship we form with the person we are interacting with (van Winden et al., 2008) and that flexible social preferences should be allowed for (Bowles, 2008; Fehr and Hoff, 2011).

Here we investigate a model of choice, based on the theoretical model of van Dijk and van Winden (1997), where the weight attributed to the welfare of a specific interacting partner—denoted as a social tie—is allowed to be dynamic and assumed to depend on two driving factors: past interaction experiences (the existing tie) and impulses generated by the current behavior of the partner. The social ties model captures behavior remarkably well in two- and four-player public good games (PGGs) (Pelloux et al., 2013, unpublished data). In addition, it appears to perform better than fixed social preferences models, including inequality aversion type of models (such as Fehr and Schmidt, 1999) in tracking the often complex dynamic contribution patterns.

We combined a direct model-based measure of tie formation with functional magnetic resonance imaging (fMRI) to characterize brain computations underlying the dynamics of social tie formation and its role in economic decision-making. The social tie model was estimated in the context of a repeated pair-wise PGG. Such a game is designed to study situations where individuals make contributions to goods that benefit the whole group (e.g. neighborhood crime watch or pollution reduction), while being tempted to benefit from the group provision without suffering the cost of contributing themselves. Our goal was to test whether brain regions dynamically track the tie formed between a participant and a counterpart. We were interested in distinguishing regions encoding the impact derived from the other player’s choices (the impulse component of the ties mechanism) and regions encoding a more integrated, long-term signal corresponding to the tie. Furthermore, we investigated how the tie is incorporated in the decision to contribute to the public good. We hypothesized that the tie formed between interactive partners might be encoded in the pSTS, temporo-parietal junction (TPJ), amygdala, AI and the ACC, with some of these regions encoding the choice of the counterpart, and other regions keeping track of the tie. If the tie with the counterpart does influence decisions, we should observe tie-related signals during subsequent decisions. Choosing to contribute to the public good might implicate regions involved in valuation and action selection such as the orbitofrontal cortex, the mPFC and the posterior cingulate cortex (PCC).

METHODS

Participants

Twenty-nine pairs of healthy volunteers participated in the experiment for financial compensation. The brain activity of one participant of each pair was measured using fMRI; for the second participant, behavior only was monitored. Participants were Dutch or international exchange students at the University of Amsterdam. One pair was excluded because of MRI data acquisition problems. For three scanned participants, we obtained a constant alpha (tie) value of 0, based on the behavioral model estimation; therefore, it was not possible to estimate any parametric modulation of the tie value in the fMRI model. Thus, 25 scanned participants (12 females) and their interaction partners were included in the fMRI analyses. Scanned participants had an average age of 22.57 (s.d. ±2.49). Their 25 interaction partners had an average age of 23.3 (s.d. ±4.5). The study was approved by the local ethics committee, and complied with relevant laws and institutional guidelines. Written informed consent was obtained from all participants prior to experimentation.

Experimental procedure

Participants were tested in pairs. Of each pair, one subject was positioned in the scanner while the other was seated in a separate room. The procedure was fully anonymous, such that subjects would never see each other or get any information about the other subject other than through computer-interfaced interaction. Each pair played 29 rounds of a PGG. Before the first and after the 25^th rounds of the PGG, subjects were administered a distributional outcome test (DOT) (Fahrenfort et al., 2012), an empirical measure of interpersonal ties. After the second DOT, they played the remaining four rounds of the PGG. In standard PGGs, contributions typically drop in the last rounds. The second DOT was thus administered before the end of the PGG in order to avoid any contamination of the end of game effect on the tie measurement. Participants then completed a post-scan questionnaire related to the task and the balanced emotional empathy scale (BEES) (Mehrabian and Epstein, 1972; Mehrabian, 1997). After the experiment, participants were paid out according to their earning during the tasks. Earnings summed up to an average of 45 euros per participant. Results concerning the DOT, the last four PGG rounds and the BEES have been published elsewhere (Fahrenfort et al., 2012).

Public good game

Participants played 29 rounds of a non-linear PGG with the same interaction partner. In each round, participants could freely divide 12 monetary units (MU) between their private account and a public account. The private account generated earnings for the participant only, whereas the public account benefitted both players. The payoff consequences of contributions to the public account were made explicit by use of an on-screen payoff matrix (Table 1).

Table 1.

Payoff matrix of the PGG

Contribution		Other
		0	1	2	3	4	5	6	7	8	9	10	11	12
	0	80	94	108	122	136	150	164	178	192	206	220	234	248
	1	85	99	113	127	141	155	169	183	197	211	225	239	253
	2	88	102	116	130	144	158	172	186	200	214	228	242	256
	3	89	103	117	131	145	159	173	187	201	215	229	243	257
Y	4	88	102	116	130	144	158	172	186	200	214	228	242	256
O	5	85	99	113	127	141	155	169	183	197	211	225	239	253
U	6	80	94	108	122	136	150	164	178	192	206	220	234	248
	7	73	87	101	115	129	143	157	171	185	199	213	227	241
	8	64	78	92	106	120	134	148	162	176	190	204	218	232
	9	53	67	81	95	109	123	137	151	165	179	193	207	221
	10	40	54	68	82	96	110	124	138	152	166	180	194	208
	11	25	39	53	67	81	95	109	123	137	151	165	179	193
	12	8	22	36	50	64	78	92	106	120	134	148	162	176

Each line corresponds to a possible contribution of the participant (YOU), columns are possible contributions of the partner (OTHER). The number in each cell denotes the payoff of the participant given both contributions. The standard Nash equilibrium is a contribution of 3 by both players, thus earning 131. The social optimum (Pareto optimal solution) is to contribute 10, with a payoff of 180.

Payoffs of subject (i) in this table were given by

$$P={14}^{\text{*}}(g_i+g_j)+{32}^{\text{*}}(12-g_i)-{(12-g_i)}^2-160\text{,}$$ (1)

where g_i stands for a subject i’s own contribution to the public account, whereas g_j denotes the other subject’s contribution to the public account. The game has an interior standard Nash equilibrium, equal to a contribution of 3 MU. The social optimum is also interior in the action space and corresponds to a contribution of 10 MU. Payoffs were expressed in MU and paid out according to the exchange rate 100 MU = 0.60 Euro. Prior to the PGG, extensive instructions were given, followed by nine multiple-choice questions to ascertain that instructions were understood.

Time course of a trial

Each trial consisted of three phases: (i) decision about contribution; (ii) decision about expectation of the other’s contribution; and (iii) feedback (Figure 1 and Supplementary Figure S2 for details).

Fig. 1.

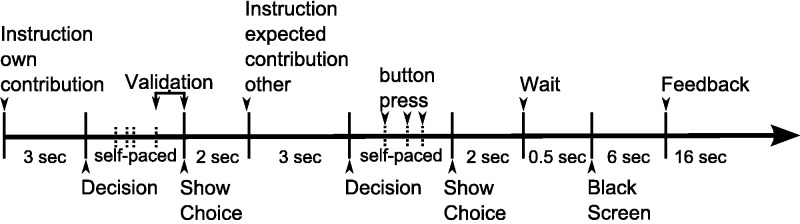
Schematic task timeline. Two participants simultaneously played in a PGG. Each participant was first asked to choose how much they wanted to contribute to the public good. Participants were first presented with an instruction screen with the sentence ‘How do you want to allocate your MU this round?’ during 3 s. Then the payoff matrix appeared with the choice options of the participant depicted as rows and the choice options of the partner depicted in columns. They could navigate between rows to make their choice using two buttons of an MR-compatible response box placed in the subject’s right hand and validated their choice at any time using a third button. This choice period was self-paced, thus introducing some natural variability in trial time course. Their choice was shown during 2 s. Then, a second instruction screen displaying ‘How do you think the other will allocate his or her MU in this round?’ was presented during 3 s. The payoff matrix appeared and they could choose the expected contribution of the other by navigating between columns of the matrix (self-paced). This choice was also shown during 2 s. A screen displayed ‘Please wait for the other to respond’ during 500 ms followed by a black screen displayed until the other participant had completed their choice, with a minimum of 6 s. The feedback screen, displayed during 16 s, then showed both participants’ contributions to the public account as well as the participant’s payoff.

Social ties model estimation

The behavioral model implemented in this study is based on the theoretical social ties model of van Dijk and van Winden (1997). In this model positive or negative bonds between interacting people are assumed to develop. This is formalized via the concept of an interdependent utility function by allowing the weight attached to another individual’s utility to express the bond developed during interaction with that individual. Importantly, and in contrast with other models, this weight is dynamic and evolves over time depending on the positive or negative interaction experiences of the individuals that are involved. In the case of our PGG, these experiences concern the observed contributions of an interacting partner compared with a reference contribution. Theoretically, the social ties model is appealing because it can in principle account for various kinds of behavior observed in the literature, such as selfish behavior, behavior related to fixed other-regarding preferences like altruism, spite and inequity aversion, as well as mimicking behavior and reciprocity (van Winden, 2012).

More specifically, our mathematical model comprises the following equations. We consider dyads, consisting of individuals i and j. Individual i’s social tie at time t with j is formalized by attaching a weight α_ijt to j’s payoff (denoted as P_jt) in i’s utility function (denoted as U_it):

$$U_{it}=P_{it}+{\alpha }_{ijt}.P_{jt}.$$ (2)

The dynamics of the social tie mechanism is represented by:

$${\alpha }_{ijt}={\delta }_{1i}.{\alpha }_{ijt-1}+{\delta }_{2i}.I_{ijt-1},$$ (3)

where δ_1i ≥ 0 and δ_2i ≥ 0. The parameter δ_1i indicates the tie persistence (which is inversely related to tie decay) and δ_2i the tie proneness of individual i. The parameter δ_2i indicates the strength with which an interaction experience, represented by the impulse I_ij, feeds the social tie. This impulse is itself assumed to be determined by the difference between the observed actual behavior of the other and some reference point. In the PGG considered here, the impulse is taken to correspond to the other’s contribution (denoted by g_jt) minus a reference contribution ($g_{it}^{\text{ref}}$).

$$I_{ijt}=g_{jt}-g_{it}^{\text{ref}},$$ (4)

Equations (1)–(4) are a discrete time implementation of the model of van Dijk and van Winden (1997). We extend this model to allow for stochasticity by applying the following probabilistic choice function:

$${\pi }_{ikt}=\frac{{\text{e}}^{{\theta }_i{U}_{ikt}}}{{{\displaystyle \sum }}_{k=0}^K{\text{e}}^{{\theta }_i{U}_{ikt}}},$$ (5)

where π_ikt stands for the probability that i chooses contribution k at period t (with K indicating the maximum contribution), and θ_i is a parameter calibrating how sensitive i’s choice is to differences in utility (choices are random if θ_i = 0, while utility is maximized if θ_i → ∞).

We estimated the social ties model for the scanned group. Parameter estimation was done using maximum likelihood estimation with the Matlab function fmincon. The estimation was first run at the group level, for model selection purposes. Then it was run separately for each individual, using participant’s contributions in the 25 rounds of the PGG before the DOT interruption. The θ, δ₁ and δ₂ parameters were estimated individually. Previous work revealed that the model performed better when the reference contribution was put equal to the standard Nash equilibrium as opposed to one’s own contribution or the expected contribution of the other (Pelloux et al., 2013, unpublished data). We thus used the standard Nash equilibrium contribution as the reference contribution in the impulse ($g_{it}^{\text{ref}}=3$). The value of α was computed according to equation (3), using zero for its starting value (for parsimony, as the use of an additional free parameter rendered similar parameter estimates). We thus obtained a series of 25 values of α for each participant. These values were then used as a parametric regressor in the fMRI models (see below).

fMRI: data acquisition and analyses

See supplementary material for images acquisition and pre-processing methods.

fMRI model

Voxel-wide differences in BOLD contrast within the smoothed normalized images were examined using FMRIB Software Library (FSL) FEAT. Standard neuroimaging methods using the general linear model (GLM) were used with the first level (individual subject effects) analyses providing contrasts for higher level (group effects) analyses.

Multiple event-related regressors of interests were included in the same GLM (instruction own contribution, decision, button press(es), decision validation, show choice, instruction expected contribution other, decision expected contribution other, button press(es) 2, decision validation 2, show choice2 and feedback; Figure 1) in order to attribute signal variance to all known sources of variance. Both instruction periods were modeled as epochs of 3-s duration, time-locked to the display of the instruction screens. The decision period was modeled as a variable epoch, time-locked to the display of the payoff matrix and ending with the button press indicating choice validation (self-paced). Similarly the decision of the expected contribution of the partner had its onset locked to the payoff matrix display and lasted until response validation. Two delta function regressors modeled button presses to navigate between rows and columns of the payoff matrix to choose the contribution level and expected contribution of the partner, respectively. The validation periods were modeled with two regressors time-locked to the last option selection and ending with the decision validation button press. Both post-decision periods (show choice) were modeled as epochs of 2-s duration, time-locked to the decision validation button press. The feedback period started with the display of the feedback screen, with 16-s duration.

Additional regressors of interest were introduced to model parametric modulations. The social tie parameter estimated with the behavioral model was introduced at the time of decision. Given the lengthy average decision time, it is difficult to determine exactly what time-window optimally reflects variables that track the decision mechanism. However, signals related to the output of the decision are more likely to occur just prior to confirmation of this decision rather than at the beginning of the decision phase. Therefore, the effect of contribution level was modeled during the validation phase. The expected contribution of the other and the expected payoff (computed from the participant’s actual contribution and the expected contribution of the other) were added to the model during the period in which participants reported the expected contribution of the other. The parametric effects of the impulse and of the payoff were added as modulators of the feedback regressors. All regressors were convolved with a canonical double-gamma hemodynamic response function, applying temporal filtering and without temporal derivative. Orthogonalization was not applied.

Inter-individual differences in tie-persistence and tie-proneness were investigated, using the individual δ₁ and δ₂ estimates—as additional regressors in the higher-level analysis.

Statistical threshold, activations localization and reported statistics

Reported coordinates conform to the Montreal Neurological Institute space. Activations are reported as significant when P < 0.05, corrected for multiple comparisons using cluster-wise control of family-wise error (FWE) rate with an initial cluster threshold of z = 2.3 (P = 0.01), unless specified. Anatomic labeling of activated regions was performed using atlases in FSLview.

RESULTS

Behavior

Scanned participants and their interaction partner’s choices are shown in Supplementary Figure S1. Scanned participants contributed an average of 6.258 MU in the public good and their non-scanned counterpart 6.235 MU. They expected their partner to contribute 6.215 and 6.687 MU, respectively. Quite a few pairs of participants manage to reach full cooperation (e.g. participants 1, 6, 13, 17, 20, 22, 23, 24 and 25, Supplementary Figure S1). The scanned group earned an average of 152.55 MU (SEM = 3.84) per trial which summed up to 26.54 euros (SEM = 0.67). The non-scanned group earned 151.94 MU (SEM = 3.96) per trial, and gained 26.44 euros (SEM = 0.69) overall in the PGG. There was no difference in contribution level and earnings (t-test P > 0.9) between the two groups. The average time for choosing how many MU to contribute was 14.14 s (SEM = 2.48) for the scanned participants and 14.49 s (SEM = 1.19) for their interaction partners.

Model estimation and comparison

Our estimates provide direct evidence of social ties being formed during the interaction in a PGG. The model significantly explained participant’s choices (Log likelihood = −1604.82, Wald χ² = 3606.2, P < 0.0001) and all parameters were significant (θ = 0.0456, SE =0.0037, P < 0.001; δ₁ = 0.4960, SE = 0.0583, P < 0.001; δ₂ = 0.0832, SE = 0.0090, P < 0.001). The model performed better than the same model excluding δ₁ (LR test: χ² = 48.94, P < 0.0001), or excluding δ₂ (χ² = 380.90, P < 0.0001). Ipso facto our findings run counter to the standard assumption of fixed selfish preferences. Moreover, the observed tie-persistence (δ₁ = 0.496) indicates that behavior is not only driven by direct reciprocity, but also modulated by previous experiences (impulses). The estimate of this parameter further indicates that the impact of an impulse is reduced to 10% of its original value after almost three rounds. Individual fits (Supplementary Figure S1) suggest that the model performed very well in capturing variability in behavior as predicted contributions closely matched actual contributions for many participants. As strategic motives might be implicated in this game, we compared the myopic-non strategic -version of the social ties model with an extended version accounting for expected reciprocity (Supplementary material). The extended model allowing for (one-period) forward-looking behavior did not perform better, at the group level, than the standard, myopic model described above (χ² = 0.0106, P = 0.92). The standard, more parsimonious model with three parameters (θ, δ₁ and δ₂) and without forward-looking was thus selected for further analyses, in particular for computing the tie parameter used in the fMRI analyses. We also compared the social tie model with a model of fixed social preferences, where α is directly estimated on the data, and an inequality aversion model adapted from Fehr and Schmidt (1999), exploiting our finding that participants are rather myopic (non-strategic) and that we have data regarding the expected contribution of the other (Supplementary material). To compare the model performance, we computed for each model the root-mean-squared error (RMSE) which reflects the difference between the choices predicted by a model and the actual choices of the participants (Supplementary material). The social tie model provided the best RMSE (1.9955) compared with the fixed preferences model (RMSE = 2.2578) and the inequality aversion model (RMSE = 2.1591).

fMRI results

In the model, the tie parameter is updated with an impulse function which is the distance between the contribution of the other player and the standard Nash equilibrium contribution. Thus, if the neural computations are in line with our model, the impulse function should be first represented in the participant’s brain during the feedback phase, providing a signal to update the tie value. If the tie has a role in the decision process, we hypothesized that its amplitude would modulate the brain activity during the subsequent choice phase.

Parametric effect of the social tie (alpha) parameter during the choice phase

During the choice period, pSTS and TPJ [peak voxels Montreal Neurological Institute (MNI) coordinates (x, y, z); left: (−54, −56, 8) and right: (52, −62, 24)], PCC (2, −34, 70) and several areas in the frontal lobe showed a negative parametric modulation by the social tie parameter estimated using our behavioral model (Figure 2 and Supplementary Table S2). Because some pairs of participants showed very little variability in their decisions, resulting in almost constant tie values (participants 20–25 in Supplementary Figure S1), we also report results excluding those participants. Prefrontal cortex activations, especially in mPFC, did not survive, suggesting that these activations might capture decision-related signals not directly related to tie-encoding. The positive contrast only revealed activation in the occipital cortex which is likely to be related to higher visual and motor activity associated with stronger tie rather than encoding the tie per se.

Fig. 2.

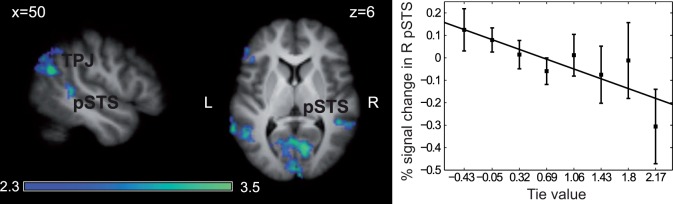
Parametric effect of social ties. Top: At the time of choice, activity in the pSTS and TPJ was parametrically modulated by the value of the tie estimated by the behavioral model. Z map projected on the participants’ averaged brain. Bottom: Percent signal change (±SE) in the right STS cluster from the parametric analysis (235 voxels, peak voxel MNI coordinate: 46, −40, 0). The tie value was binned into eight equal categories. The x axis shows the median tie value of each category.

Parametric effect of the impulse during the feedback phase

During the phase in which the other player’s contribution and the payoff were revealed, the bilateral insula and right superior temporal gyrus, TPJ and pSTS were parametrically modulated by the impulse (i.e. contribution of the other minus the standard Nash equilibrium contribution). (Figure 3 and Supplementary Table S3).

Fig. 3.

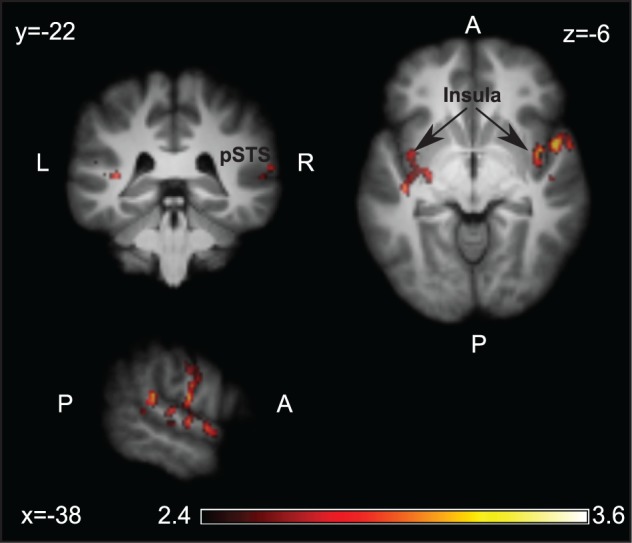
Parametric effect of the impulse. Brain areas in which activity showed a parametric modulation by the impulse during the feedback phase. Z map projected on the participants’ averaged brain.

Activity related to the model parameters δ₁ and δ₂

In our model, δ₁ represents the tie persistence and thus reveals the speed at which the tie deteriorates over time if the interaction is not maintained. δ₂ represents the tie proneness, the impact of the other’s behavior on the new tie. These two parameters are thought to reflect stable personality traits in our model. We thus tested the hypothesis that inter-individual differences in these two parameters will result in different activity in brain areas encoding the tie when a decision is made. We used the δ₁ and δ₂ parameters as parametric regressors at the higher level of brain data analysis. During the decision phase, δ₁ correlated with activity in the right TPJ (MNI coordinate at P < 0.001 unc., 46, −74, 18) and right pSTS (46, −40, 12) and δ₂ correlated with activity in the left TPJ (−54, −46, 26).

Parametric effect of contribution magnitude

We next looked at brain areas whose activity was directly involved in the process of deciding how much to contribute (see ‘fMRI model’ section in ‘Methods’ section). The post-central gyrus (46 −28, 62) and posterior cingulate (0, −16, 32), bilateral insula (left: −44, 6, −4; right: 32, −12, −6), and mPFC (6, 54, −2) were modulated parametrically by contribution magnitude (Figure 4 and Supplementary Table S4).

Fig. 4.

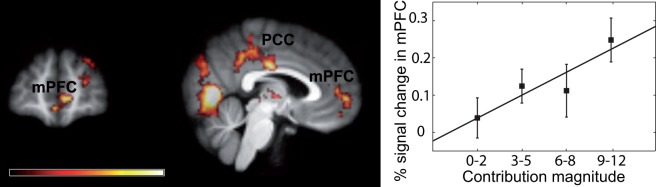
Parametric effect of the contribution to the public good. Top: At the time of choice, activity in the mPFC and PCC was parametrically modulated by the contribution to the public good by the subject in the current trial. Z map projected on the subjects’ averaged brain. Bottom: Percent signal change (±SE) in the mPFC cluster from the parametric analysis (345 voxels, MNI coordinate: 6, 54, −2; Supplementary Table S4), where the contribution magnitudes were groups into four categories.

Connectivity

Given the structure of our model, an important implication of our finding is that neural activity encoding the tie value will influence activity of regions implicated in the decision process. Using psychophysiological interactions (PPIs, Supplementary material for methods), we found a significant increase in correlations between the activity in pSTS and activity of mPFC and PCC during the decision phase (PPI analysis, masking with results from parametric effect of contribution, Figure 5). In order to confirm that the common signal between the two sets of areas contains information related to the tie values, a beta seed correlation analysis was performed, testing for correlations between the parameter estimates of the tie value regressors in the pSTS (MNI coordinate 46, −40, 0) and parameter estimates of the contribution magnitude regressors in the whole brain. Results confirmed the link between the activity related to tie encoding in the pSTS and to contribution magnitude in the mPFC. Parameter estimates of the tie parametric effect at the beginning of the decision phase significantly correlated with parameter estimates of the contribution parametric effect during the validation phase.

Fig. 5.

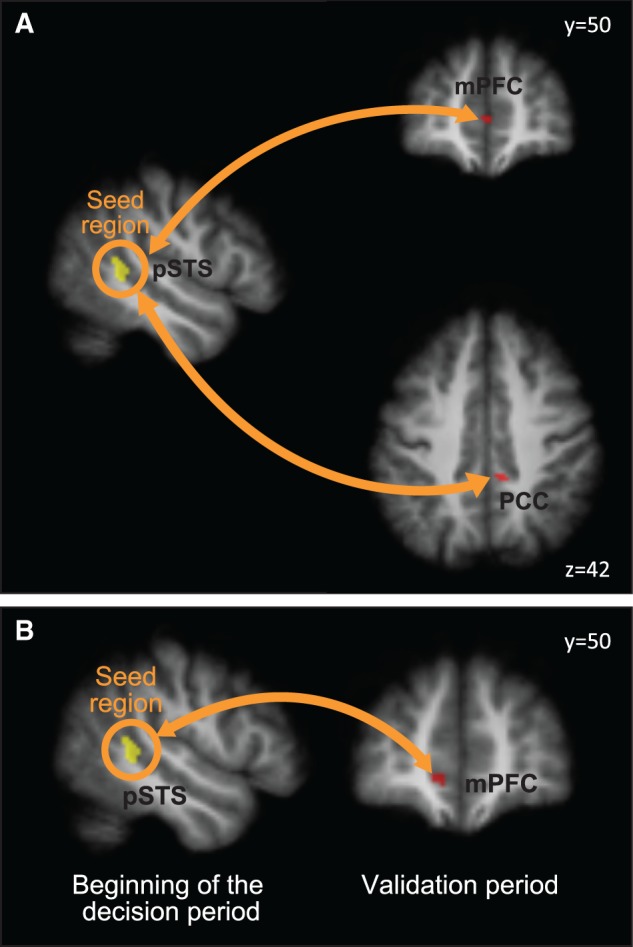
Connectivity analysis. (A) PPI from the pSTS. Psychophysiological interactions associated with decision events with pSTS activations as seed region and mPFC and PCC as target regions. The brain slice on the left shows the seed region, functionally defined from the parametric analysis of the tie parameter (also reported in Figure 2, FWE cluster corrected, initial threshold z = 2.5). The brain slice on the right shows the PPI results at P < 0.001 uncorrected, masked with activation map from Figure 4. (B) Beta seed correlation results. At the time of decision, activity related to tie encoding in the pSTS correlated with activity related to the contribution in the mPFC. The image on the right shows the voxels which activity significantly correlated with the seed region. T map projected on the subjects’ averaged brain, P < 0.001, uncorrected.

DISCUSSION

In this study we aimed at characterizing the brain mechanisms implicated in choosing how much to contribute in a repeated PGG. We tested a model of choice in which the weight attributed to another individual’s utility is allowed to evolve as a function of the reactions to the other’s behavior. In our computational framework, this weight represents the social tie that forms between the subject and the other player as the interaction unfolds. We identified specific computational signals needed to keep track of the tie and to mediate the influence of the tie in the decision process.

The model of the tie mechanism presented here has two main components, an existing tie value and an impulse function. The impulse function captures the impact of the other’s choice, relative to a reference contribution level, in the previous trial on the new tie value. Because the (selfish) Nash contribution level performed best as reference level, brain activations related to the impulse can be interpreted simply as encoding the other’s choice, as the latter two variables differ by a constant only, their effect cannot be distinguished in fMRI analyses. At the time participants saw the other player’s choice, this information was encoded in the insula, a region previously implicated in social affective reaction like empathy (Singer et al., 2004b; Fahrenfort et al., 2012), and the superior temporal gyrus and pSTS, an area implicated in inferring others’ beliefs and intentions (Saxe and Wexler, 2005; Frith and Singer, 2008) or perceiving the behavioral relevance of other agents (Carter et al., 2012). In the model, the impulse function is used to update the tie value. This tie value represents how much we care about the other. The tie builds over time and therefore constitutes an integrated signal. It represents the history of the interaction with the other, more particularly the history of the reactions to the other’s behavior, and can thus be seen as a stock variable of these impulses. We found that the tie value was specifically encoded in the pSTS and TPJ. This finding extends previous results showing a correlation between pSTS activity and liking ratings of an interacting partner (Fahrenfort et al., 2012), and a role of pSTS in signaling social significance such as keeping track of other agent’s strategies (Haruno and Kawato, 2009), one’s influence on the other agent’s choices (Hampton et al., 2008), cooperativeness in a prisoner’s dilemma game (Singer et al., 2004a), as well as the reliability of another person’s advice (Behrens et al., 2008). Inter-individual differences in the way the impulse impacts the new tie and the decay of the tie were also found in the pSTS and TPJ. pSTS and TPJ activity thus reflected a signal integrating the choice of the other in the previous round with the tie previously formed with the other. The relationship between the tie value and the pSTS and TPJ activity was negative. This is consistent with previous findings concerning the brain underpinnings of friendship (Bartels and Zeki, 2000), although another study reports the opposite relationship (Krienen et al., 2010). It is not clear whether the role of the pSTS and TPJ in inferring other’s beliefs and intentions and their involvement in encoding social ties are supported by the same neurons within these regions. If this is the case however, it makes sense that growing closer to somebody decreases activity in these regions as efforts are made to infer the intentions of others also decreases with closeness.

Finally, we found that the activity of the pSTS at the beginning of the choice phase correlated with the activity of the mPFC at the end of the choice phase. Other studies have indicated a role for this region in decision-making (Glimcher, 2009), especially in a social context (Hampton et al., 2008; Bault et al., 2011). All components of our behavioral model are reflected in the activity of specific regions, which together seem to constitute a network involved in updating and maintaining social preferences.

The pSTS and TPJ are consistently activated during social interaction. Yet the nature of the tasks used in many experiments makes it difficult to determine the type of computation they might perform. Nevertheless recent model-based fMRI studies have hypothesized learning mechanisms based on reinforcement learning and belief-based models (Behrens et al., 2008; Hampton et al., 2008; Haruno and Kawato, 2009; Zhu et al., 2012; Fouragnan et al., 2013; van den Bos et al., 2013). The learning in our social tie model is very different from reinforcement learning and belief-based models, as it concerns the nature of the valuation function itself, via U_it(.; α_ijt), instead of the value of a choice option for a given valuation function, like a standard Q-value. In a sense, the learning involves an ‘internal state’, namely one’s social preferences, and not how one can reach one’s goal optimally by acting on the environment. The social tie model thus accounts for decisions that may decrease the agent’s reward as long as it benefits an interaction partner who proved to be kind or cooperative in the past.

In addition, previous fMRI studies investigating socially interactive decisions have focused on strategic motives such as predicting intentions of others in order to select the best responding action (Behrens et al., 2008; Hampton et al., 2008) or building a positive reputation in order to benefit from the favors of others in the future (King-Casas et al., 2005). A computational role of pSTS and TPJ has been established in evaluating the intentions of others (Behrens et al., 2008) and the influence of one’s own behavior on others (Hampton et al., 2008). Note that in our study allowing for strategic motives such as expected reciprocity did not improve our model performance. We extend these previous findings by showing that pSTS and TPJ dynamically encode the weight attached to the well-being of others in cooperative decisions. Neural processing of other-regarding preferences has been previously attributed to areas of the reward system, mainly the striatum. It has been argued though that it was unclear whether such activity truly reflects social preferences or the value of the social situation to the individual (Behrens et al., 2009). To our knowledge, this is the first time trial-by-trial other-regarding preferences have been estimated and regressed against BOLD measurements. We found that activity of the pSTS and TPJ reflected dynamic other-regarding preferences rather than the striatum, consistent with a role of these regions in signaling cooperative partners (Singer et al., 2006), friends and loved ones (Bartels and Zeki, 2000).

Interestingly, our results parallel those of Hampton et al. (2008) who aimed to uncover the neural underpinnings of a model of choice that includes the influence that a player’s action has on an opponent’s strategy. They found that, while mPFC tracked the predicted reward associated with a particular choice, a signal that may be used to guide choice during a game, activity in pSTS corresponded to an update of the influence signal once feedback about the game has been provided (Hampton et al., 2008). Thus, results from the application of quantitative models to these two different social decision-making environments appear consistent with a role of the pSTS in signaling social information relevant to the current situation and goal of the agent, and in modulating decision guiding signals in the mPFC.

We found a higher correlation between the pSTS and mPFC activity during the decision phase than during other events of the trial. Previous studies reported functional connectivity between the pSTS or TPJ and the (ventro-) medial frontal cortex while resting (Mars et al., 2012), making prosocial decisions (Hare et al., 2010) or choosing among social rewards (Smith et al., 2014). Other studies found similar connectivity during the feedback period (Hampton et al., 2008; van den Bos et al., 2013) when prediction error signals are computed in the brain. In addition to showing that activity of the pSTS and mPFC synchronized during decisions using PPI, we further suggest that the signal shared between these two regions contains information about the tie value. Indeed, beta seed correlations revealed that pSTS tie-related signals during the decision process modulated mPFC signals related to the output of the decision at the time participants validated their choice. Given the temporal ordering between the two signals, we may reasonably assume that signals in the pSTS modulate mPFC activity. The tie information is thus integrated into the decision process through interacting brain networks including the pSTS, TPJ on one hand, and the mPFC and PCC on the other hand.

An alternative theory of the role of TPJ proposes that its higher activity during social decision-making may be attributed to attentional effects, as social interaction might be demanding in that respect (for a review, see Carter and Huettel, 2013). Although we modeled response times in our fMRI analyses, we cannot rule out completely such an explanation. Indeed, the payoff matrix in our task contains information that might take time to process, yielding to relatively long response times. However, if attention is influenced by the tie strength, it will be internally rather than externally reorienting as the process of tie building requires integrating information that arises from the context and personal goals. We thus concur with the proposition of Carter and Huettel (2013) that TPJ integrating information derived from attention is not incompatible with a role of this region in signaling social significance.

To conclude, although reciprocity-based social preferences models take into account immediate past actions of interaction partners, we show that the longer-term history of the interaction can influence behavior significantly. Thus, the use of a social preferences model in which the attitude toward the interaction partner is formed in an endogenous and dynamic way, reflecting the development of bonds between individuals, appears appealing. Indeed, we showed that such a social ties model of dynamic other-regarding preferences tracks rather closely individuals’ contributions in a PGG and that specific brain areas track the developing ties, providing evidence of the biological plausibility of this model.

SUPPLEMENTARY DATA

Supplementary data are available at SCAN online.

Conflict of Interest

None declared.