Progressive changes in T₁, T₂ and left-ventricular histo-architecture in the fixed and embedded rat heart

Abstract

Chemical tissue fixation, followed by embedding in either agarose or Fomblin, is common practice in time-intensive MRI studies of ex vivo biological samples, and is required to prevent tissue autolysis and sample motion. However, the combined effect of fixation and sample embedding may alter tissue structure and MRI properties. We investigated the progressive changes in T₁ and T₂ relaxation times, and the arrangement of locally prevailing cardiomyocyte orientation determined using diffusion tensor imaging, in embedded ex vivo rat hearts fixed using Karnovsky’s solution (glutaraldehyde–formaldehyde mix). Three embedding media were investigated: (i) standard agarose (n = 3 hearts); (ii) Fomblin (n = 4 hearts); and (iii) iso-osmotic agarose (n = 3 hearts); in the latter, the osmolarity of the fixative and embedding medium was adjusted to 300 mOsm to match more closely that of native tissue. The T₁ relaxation time in the myocardium showed a pronounced decrease over a 48-h period following embedding in Fomblin (−11.3 ± 6.2%; mean ± standard deviation), but was stable in standard agarose- and iso-osmotic agarose-embedded hearts. The mean myocardial T₂ relaxation time increased in all embedded hearts: by 35.1 ± 14.7% with standard agarose embedding, 13.1 ± 5.6% with Fomblin and 13.3 ± 1.4% with iso-osmotic agarose. Deviation in the orientation of the primary eigenvector of the diffusion tensor occurred in all hearts (mean angular changes of 6.6°, 3.2° and 1.9° per voxel after 48 h in agarose-, Fomblin- and iso-osmotic agarose-embedded hearts, respectively), indicative of progressive structural changes in myocardial histo-architecture, in spite of previous exposure to fast-acting tissue fixation. Our results suggest that progressive structural changes occur in chemically fixed myocardium, and that the extent of these changes is modulated by the embedding medium, and by osmotic gradients between the fixative in the tissue and the surrounding medium.

INTRODUCTION

Myocardial histo-architecture is known to have a profound impact on the physiological properties of the heart, influencing both mechanical (1) and electrical (2) behaviour. Over recent years, diffusion tensor imaging (DTI) has emerged as a powerful tool for the nondestructive determination of the histo-architectural properties of the heart (3–6). Using this method, the voxel-wise diffusion tensor can be decomposed into its eigenvectors to provide information regarding the locally prevailing orientation of myocytes, whose longitudinal direction is usually (if histo-anatomically incorrectly) referred to as ‘fibre orientation’. The eigenvalues of the diffusion tensor can be used to determine scalar properties, such as the apparent diffusion coefficient (ADC) and fractional anisotropy (FA), which describe the local magnitude and spatial distribution of water diffusibility, respectively. In addition to determining the ‘myofibre architecture’ in healthy left-ventricular myocardium (7–9), DTI has also been used to quantify the structural changes caused by pathologies such as ischaemia (10–12).

Currently, the majority of cardiac DTI studies are performed on ex vivo hearts, particularly when high-resolution three-dimensional data are required. This is primarily because of the long scan times required to collect these datasets (8,13), as well as the susceptibility of the technique to motion and flow artefacts (14). In order to prevent autolysis in ex vivo samples during this period, tissue is generally fixed using either formaldehyde-based solutions, such as formalin, or a formaldehyde–glutaraldehyde mix, such as Karnovsky’s fixative. Formaldehyde fixation facilitates rapid tissue penetration because of the small size of formaldehyde molecules, and initial binding to proteins generally occurs within 24 h (15). However, the formation of inter-protein methylene bridges required for complete tissue stabilisation proceeds much more slowly, and complete tissue fixation may require several weeks (16). Conversely, glutaraldehyde molecules react quickly to ensure rapid cross-linking of proteins, and can render tissue resistant to osmotic stress after 24 h of fixation (17). However, tissue penetration is 10 times slower than with formaldehyde (18). Karnovsky’s solution [a mixture of glutaraldehyde and formaldehyde in cacodylate buffer (19)] is superior to either aldehyde fixative alone, as formaldehyde rapidly penetrates the tissue to swiftly ‘pre-stabilise’ proteins in a given configuration (important, in particular, for mechanically active tissues such as the heart), which are then permanently fixed by glutaraldehyde. Therefore, we chose to use this fixative in the present study of left-ventricular histo-anatomy.

Following fixation, ex vivo samples can be embedded in aqueous gels, such as low-melting-temperature agarose (20–22) or gelatine (7), or in water-free substances, such as Fomblin (8,10,23). The later is a perfluoropolyether with a low dielectric effect, which is susceptibility matched to tissue and produces no MR signal, facilitating the segmentation of tissue from the surrounding embedding medium during post-processing. However, gel embedding has the advantage that motion artefacts, for instance those caused by gravitational forces or by vibrations during rapid gradient switching for high-resolution DTI scans, will be minimised, as the sample is ‘fixed in place’ more firmly within the test tube by a more viscous embedding medium. This is not the case with liquid Fomblin embedding, in which the myocardial tissue samples can float if not properly filled and restrained, and therefore more complex mounting approaches may be required to prevent sample motion during DTI.

The action of aldehyde fixation on the cross-linking of proteins throughout the intra- and extracellular spaces of tissues alters the local chemical environment, which, in turn, will alter MRI contrast mechanisms (24). This may lead to erroneous extrapolation from ex vivo MRI data to the in vivo setting. Several groups have investigated fixation-induced changes in parameters such as the T₁ and T₂ relaxation times and water diffusion in non-cardiac tissues, such as the human brain (25,26), mouse brain (27), rat nervous tissue (24,28), human and pig spinal cord (29), bovine nasal cartilage (30) and model biological tissues comprising erythrocyte ghosts suspended in buffer and agarose (31). The progressive effect of tissue fixation, once the sample is removed from the fixative and placed in a surrounding embedding medium, has not yet been investigated, however, and data on fixation effects on cardiac tissue are missing. Here, we examine the progressive effect of tissue fixation and embedding on MR parameters and cardiac histo-anatomy using excised rat hearts. As a high-resolution (~ 100 μm) DTI scan can take 48 h or more to complete [8,13], we aimed to assess the stability of the magnetisation relaxation and DTI parameters in ex vivo embedded rat myocardium over a similar time period. The dependence of these parameters on the type of embedding medium used (either low-melting-temperature agarose or Fomblin) and the osmolarity of the fixative was also investigated.

METHODS

Sample preparation

All investigations conform to the UK Home Office guidance on the Operation of Animals (Scientific Procedures) Act of 1986. Hearts were isolated from female Sprague Dawley rats [246 ± 19 g, mean ± standard deviation (SD)] after cervical dislocation, and swiftly (< 90 s) connected via the aorta to a constant-flow (5–6 mL/min) Langendorff perfusion system (32). An incision in the pulmonary artery was made to avoid the build-up of fluid reaching the right heart via the coronary circulation. The tissue was initially washed (2 min) with heparin-containing ‘normal Tyrode’ (NT) solution [containing 140 mm NaCl, 5.4 mm KCl, 1 mm MgCl₂, 1.8 mm CaCl₂, 11 mm glucose, 5 mm N-2-hydroxyethylpiperazine-N′-2-ethanesulphonic acid (HEPES) and 5 IU/mL heparin, oxygenated] before cardioplegic arrest was induced by perfusion with high-potassium solution (HiK⁺; 20 mm KCl, 125 mm NaCl, 1 mm MgCl₂, 1.8 mm CaCl₂, 11 mm glucose, 5 mm HEPES, oxygenated). Immediately after cardiac arrest, tissue was fixed by coronary perfusion with 20 mL of the fast-acting Karnovsky’s fixative [2% formaldehyde and 2.5% glutaraldehyde mix in sodium cacodylate buffer (19); see Table 1]. During the whole procedure, hearts were positioned in a fluid-filled glass container to keep their cavities free from bubbles. Fixed hearts were stored in Karnovsky’s fixative for 24 h prior to embedding [for details, see ref. (13)].

Table 1.

Fixative and buffer used in this investigation. All solutions at controlled pH (pH 7.4)

Solution	Paraformaldehyde	Sodium cacodylate	Glutaraldehyde (50%)	Osmolarity (mOsm)
Karnovsky (200 mL)	4 g in 100 mL H2O, pH 7.4	4.28 g in 100 mL H2O, pH 7.4	8 mL in 100 mL H2O	1210 ± 5
Cacodylate buffer		4.28 g in 100 mL H2O, pH 7.4		385 ± 5

For embedding, hearts were repeatedly rinsed in sodium cacodylate buffer (60 min at 4°C), and then processed depending on protocols (i)–(iii): (i) For the standard agarose preparation, hearts were stabilised in a 28-mm-diameter NMR tube using low-melting-point 2% agar (NuSieve GTG Agarose 50080, Lonza, Slough, Berkshire, UK). Cacodylate buffer was left inside the cavities to prevent the ventricle walls from collapsing. (ii) For the Fomblin preparation, hearts were stabilised using an in-house-designed cradle inside the NMR tube, which was then filled with Fomblin (Series LC08, Performance Fluids, Nelson, Lancashire, UK). Fomblin was also syringed into the ventricular cavities to replace the sodium cacodylate buffer. Intra and extra-cardiac cavities were continuous with each other, preventing the build-up of transmural pressure gradients. (iii) For the iso-osmotic agarose preparation, the osmolarity of all solutions (including Karnovsky’s, cacodylate buffer and agar) was maintained at 300 ± 5 mOsm. The agar for this preparation was prepared by dissolving 2 g of low-melting-point agar in 100 mL of 300 mOsm cacodylate buffer [instead of distilled water as used in (i)]. Cardiac cavities were filled with buffer, and the preparation was embedded in the NMR tube. The hearts prepared using the methods described above are referred to as: (i) standard agarose; (ii) Fomblin; and (iii) iso-osmotic. In total, 10 hearts were embedded [n = 3 for preparation (i), n = 4 for (ii) and n = 3 for (iii)], and scanned in a horizontal position within the magnet.

Image acquisition

Hearts were imaged using a Varian 9.4-T (400 MHz) MR system (Varian Inc., Palo Alto, CA, USA), comprising a horizontal magnet (bore size, 210 mm), a VNMRS Direct Drive console and shielded gradient system (1 T/m; rise time, 130 μs). A birdcage coil with an inner diameter of 28 mm (Rapid Biomedical, Rimpar, Germany) was used to transmit–receive the NMR signals. Data acquisition was initiated as soon as possible after sample embedding (3.7 ± 0.2 h, all samples mean ± SD), and continued over a period of 48 h. All experiments were conducted at the ambient temperature inside the magnet (19.1 ± 0.8°C, all samples mean ± SD), and the temperature throughout the testing of an individual sample was stable to within ± 0.5°C.

T₁ and T₂ data acquisition

T₁ measurements were made using a snapshot FLASH (fast low-angle shot) two-dimensional multi-slice pulse sequence (33), with segmented k-space acquisition (64 k-space lines per segment), and a final data matrix size of 128 × 128 over a 26 × 26 mm² field of view (FOV). Five axial slices (thickness, 1 mm) were equally spaced from the apex to the base of the heart, and data were acquired at 10 points during each inversion recovery (TE/TR = 1.37/2.84 ms; TR/segment = 187.0 ms). The delay between inversion pulses was greater than 5 × T₁. Ten averages were acquired for each image, resulting in a total scan duration of 10 min.

T₂ was measured with a multi-spin-echo two-dimensional pulse sequence (same slice and data matrix parameters as used for T₁ data acquisition, but sampling four averages). Sixteen echoes were collected per excitation, with TR = 4s and ΔTE = 5.2 ms. The total scan duration was 34 min.

DTI data acquisition

Three-dimensional DTI data were obtained using a fast spin-echo diffusion-weighted pulse sequence. The FOV was 26 × 26 × 26 mm, with a data matrix of 64 × 64 × 64, resulting in an isotropic resolution of 406 μm. Eight echoes were acquired per excitation, with TR = 1 s. The central line of k space was collected during the third echo, resulting in an effective TE (TE_eff) of 36.3 ms. Unipolar diffusion gradients were applied in six directions according to an optimised scheme based on the electrostatic repulsion principle (34), with a gradient strength of 30 G/cm, duration of 2.5 ms and separation of 15 ms. This resulted in a b value of 703 s/mm², accounting for all imaging gradients and cross-terms between imaging and diffusion gradients (35). The number of signal averages (NSA) acquired was three, and the scan duration was 3 h per acquisition.

In order to investigate the influence of resolution, diffusion gradient scheme and diffusion weighting (b value), two-dimensional DTI data were also acquired at each time point, using a fast spin-echo pulse sequence with eight echoes per excitation and the following acquisition parameters: TR = 2 s; TE_eff = 25 ms (central line of k space was collected during the first echo); FOV, 26 × 26 mm; matrix size, 128 × 128; in-plane resolution, 203 μm; slice thickness, 1 mm; 21 contiguous slices covering the entire length of the heart. Unipolar diffusion gradients were applied in 15 directions (again using a scheme based on electrostatic repulsion), with a gradient strength of 30 G/cm, duration of 2.7 ms, separation of 20 ms and a b value of 1040s/mm².

All imaging protocols were repeated at 4.2-h intervals over a 48-h period, without removing the sample from the magnet. In order to additionally assess the long-term stability of the three embedding techniques, the above protocol was repeated for one heart from each group, 1 week after embedding. In addition, a single heart from the most stable group [iso-osmotic agarose, (iii)] was re-scanned 1 month later for the bootstrap analysis described below.

Data analysis

T₁ and T₂ values were calculated by applying a monoexponential fit to the image data. The signal-to-noise ratio (SNR) was measured in the myocardium at each time point, using the unweighted (b = 0) images in the DTI datasets. Diffusion tensors were calculated on a voxel-by-voxel basis via a weighted linear least-squares fitting method, using in-house software developed in IDL (ITT Corporation, Boulder, CO, USA). Tensors were then diagonalised to produce the sorted eigenvectors (ν₁, ν₂, ν₃) and eigenvalues (λ₁, λ₂, λ₃). From these, FA and ADC were calculated using:

$$\mathrm{FA}=\frac{\sqrt{{({\lambda }_1-{\lambda }_2)}^2+{({\lambda }_2-{\lambda }_3)}^2+{({\lambda }_1-{\lambda }_3)}^2}}{\sqrt{\left[2\right({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2\left)\right]}}$$ (1)

$$\mathrm{ADC}=\frac{({\lambda }_1+{\lambda }_2+{\lambda }_3)}{3}$$ (2)

Changes in FA, ADC and ν₁ [the primary eigenvector, which is aligned to the locally prevailing cell orientation (5,6)] were measured on a voxel-by-voxel basis at each time point. Temporal deviations in ν₁ were determined by measuring the angle (θ) between the primary eigenvector at a given time point ν₁(t), and the primary eigenvector in the same voxel at the first time point ν₁(t₀), i.e.

$$\theta =\text{arccos}[\mid {\mathit{v}}_1(t)\cdot {\mathit{v}}_1(t_0)\mid ]$$ (3)

The orientation of voxel-wise primary eigenvectors was also expressed in terms of the helix angle α (36). The helix angle is the angle between the projection of the primary eigenvector onto the tangential plane (parallel to the epicardial surface) and the transverse (equatorial) plane of the heart. Myofibre orientation generally undergoes a smooth transition from a left-handed helical arrangement at the epicardium, to an equatorially circumferential arrangement in the mid-ventricular wall, to a right-handed helical arrangement in subendocardial tissue [e.g. refs. (4,37)]. The prevailing myofibre population in each DTI voxel in the myocardium was categorised into three types: left-handed helical fibre (LHF), − 60° < α < − 30°; circumferential fibre (CF), − 30° ≤ α ≤ 30°; and right-handed helical fibre (RHF), 30° < α < 60° (38). Using multiple regions of interest spanning the septal, anterior, lateral and interior walls of the left ventricle, regional changes in the fraction of LHF, CF and RHF over time were quantified.

Cone of uncertainty (COU) measurements

In order to quantify the precision of the ν₁ measurement, and to examine how this varies with changes in SNR, we performed tests on an iso-osmotic agarose-embedded (iii) heart, 1 month after embedding. The heart was removed from the scanner in the interim period, but remained embedded in the NMR tube, and was stored at 4°C. First, we verified that the sample was stable in terms of ν₁ orientation (SD of 0.1° over 48 h). The three-dimensional DTI protocol described above was then carried out three times with NSA = 1, and repeated with an increasing number of averages to collect replicates of the three-dimensional DTI data over an SNR range of 140–370 (SNR was measured using the unweighted b = 0 image). The repeated DTI measurements were used to carry out a bootstrap analysis of the precision of the measurements of ν₁. The method used was similar to that described in ref. (39). Briefly, the replicates of the DTI experiments (at a fixed SNR) were used to create 100 bootstrap samples of a complete DTI dataset from the collective pool of data, by randomly selecting (with replacement) one measurement for each gradient direction including a b = 0 image [i.e. no diffusion weighting, see detail in ref. (39)]. The mean primary eigenvector of the 100 bootstrap samples (Ψ₁) was calculated in each voxel using the dyadic formalism described in ref. (40). The angular deviation between each of the bootstrap samples of ν₁ and Ψ₁ was calculated in each voxel, and the 95% percentile of these 100 values was taken as the 95% confidence interval (or COU of Ψ₁ for that voxel). The COU is equivalent to the precision in the measurement of ν₁ for a given level of SNR. This process was repeated over the range of SNR values, so that the variation in COU could be measured as a function of SNR.

Statistical analysis

Unless otherwise stated, scalar DTI parameters and T₁ and T₂ values are expressed as the mean value over all voxels within the myocardium, and all data are shown as the mean ± SD. All statistical analysis was performed using SPSS (SPSS, Chicago, IL, USA). The first and last points in the time series of the relaxation time and DTI parameter measurements were compared using a two-tailed unpaired t-test. A value of p < 0.05 was considered to be statistically significant.

RESULTS

T₁ and T₂ relaxation times

Initial values of the mean T₁ and T₂ relaxation times in the myocardium, measured at the first time point (t₀), are given in Table 2. The standard agarose- (i) and Fomblin-embedded (ii) hearts started with similar T₁ values at t₀, but the iso-osmotically embedded (iii) hearts had initial T₁ values that were approximately 50% higher [p < 0.01 cf. (i) and (ii)]. The initial T₂ relaxation time was also highest in the iso-osmotically embedded hearts, but only significantly so when compared with the Fomblin group [mean T₂ in (iii) was 92% higher than the mean T₂ in (ii), p < 0.05].

Table 2.

Values for T₁, T₂, fractional anisotropy (FA) and apparent diffusion coefficient (ADC) in the myocardium at t₀ (mean ± standard deviation)

Preparation	T1 (ms)	T2 (ms)	FA	ADC (×10−4, mm2/s)
(i) Standard agarose	879 ± 63iii	41.8 ± 8.2	0.28 ± 0.03	8.81 ± 0.13
(ii) Fomblin	787 ± 62iii	27.5 ± 1.5iii	0.27 ± 0.02	7.99 ± 0.60
(iii) Iso-osmotic agarose	1247 ± 124i,ii	53 ± 16ii	0.25 ± 0.03	8.74 ± 0.77

All values are means ± standard deviation. Mean value of T₁ in (iii) is statistically significantly different from that in (i) (p < 0.01) and (ii) (p < 0.001). There is no statistically significant difference between T₁ in (i) and (ii) (p > 0.05). The only significant difference in T₂ values is between groups (ii) and (iii) (p < 0.05). There are no statistically significant differences between the mean FA and ADC values from each group. All comparisons determined by one-way analysis of variance followed by post-hoc Bonferroni multiple comparisons with other preparations. Superscripts show which preparations are significantly different within each category.

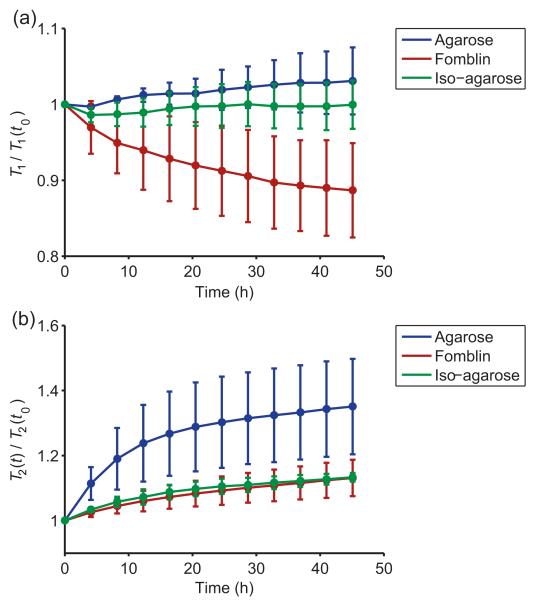
The time series of the mean myocardial T₁ and T₂ values for each preparation (normalised with respect to the first time point t₀) are shown in Fig. 1. Mean myocardial T₁ values decreased over time in the Fomblin-embedded (ii) hearts, showing a significant (− 11.3 ± 6.2%) reduction by the final time point t_f, 48 h after embedding (p = 0.04). However, in the standard (i) and iso-osmotic (iii) agarose-embedded hearts, stable myocardial T₁ values were observed (p > 0.05). T₂ values in the myocardium increased rapidly over time in standard agarose-embedded hearts (increase of + 35.1 ± 14.7% at t_f compared with t₀, p = 0.03), whereas both Fomblin- and iso-osmotically embedded hearts showed a gradual increase in myocardial T₂ (ii: + 13.1 ± 5.6%, p = 0.02; iii: + 13.3 ± 1.4%, p = 0.04).

Figure 1.

Temporal evolution of mean myocardial T₁ (a) and T₂ (b) values for all heart preparations. Within each group, data points are normalised to the value measured at the first time point (t₀). Data points represent means for each group; error bars are standard deviations.

DTI

The initial values of the mean FA and ADC in the myocardium of each heart are given in Table 2. Mean values of FA and ADC were not statistically significantly different between any of the groups. In addition, the time course of mean myocardial FA and ADC values showed no statistically significant change over 48 h (p > 0.05).

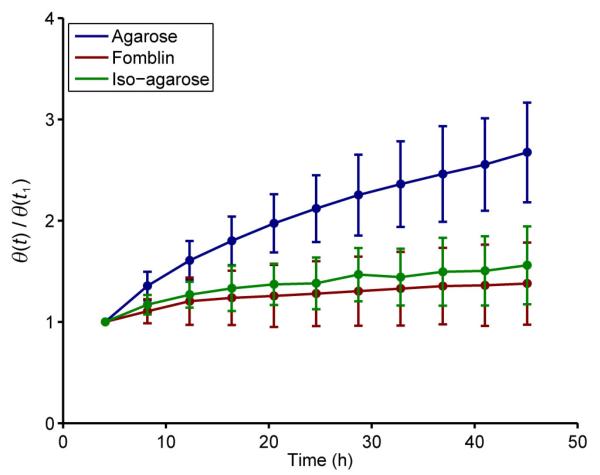
The mean value of θ [the mean voxel-wise angular deviation of ν₁ compared with ν₁(t₀)] as a function of time is shown for all preparations in Fig. 2. Each value is normalised to the value at the first time point following the start of the experiment (t₁ = 4.2 h) in order to illustrate the change in the deviation of ν₁ over time. A clear increase is seen in the mean value of θ over time in all preparations. However, in the standard agarose-embedded (i) hearts, the increase in θ is more pronounced. The mean value of θ at t₁ was 4.0 ± 0.3° in this group and, by t_f, this had increased to 10.5 ± 1.4° (a 6.5° increase in the mean angular deviation of ν₁ over 44 hours). In the Fomblin (ii) and iso-osmotic agarose (iii) groups, the increase in θ was considerably lower (3.2° and 1.9°, respectively see Table 2). A very similar pattern was observed in the two-dimensional multi-slice DTI data, where the observed mean increase in θ at t_f was 5.2° after 48 h in the standard agarose-embedded (i) hearts, whereas, in the Fomblin- (ii) and iso-osmotic agarose-embedded (iii) hearts, it was 2.7° and 1.3°, respectively (data not shown).

Figure 2.

Time series plot of θ, the mean angular deviation of the primary eigenvector from its original value at t₀, for each preparation. Within each group, values of θ are normalised to the value at t₁. Data points represent the mean ± standard deviation for each group.

Effect of SNR on COU and θ(t)

The measured COU around ν₁ decreased from 5.9° at SNR = 140 to 2.8° at SNR = 370, and followed the following relation:

$$\text{COU}\propto {\text{SNR}}^{-0.7}$$ (4)

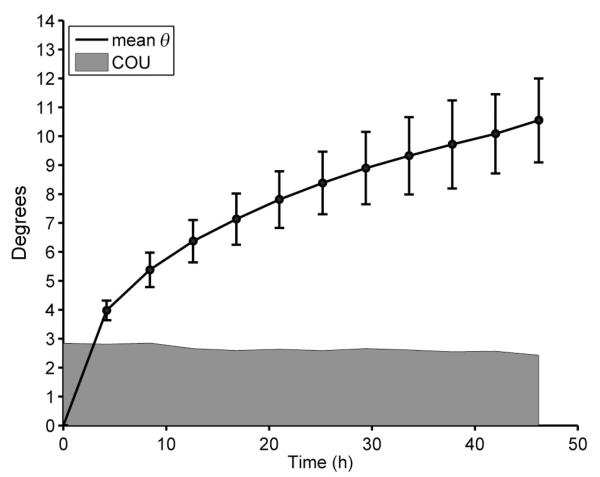
with R² = 0.97. The mean SNR at t₀ was 324 ± 26 in standard agarose- (i), 188 ± 30 in Fomblin- (ii) and 218 ± 94 in iso-osmotic agarose-embedded (iii) hearts. As SNR changed throughout the course of the experiments in all hearts (Table 3), because of the continuous changes in the T₁ and T₂ relaxation times, the resultant change in precision in the measurement of ν₁ had to be accounted for. As SNR was measured at each time point (using the b = 0 image for each DTI dataset), and the relationship between SNR and COU had also been measured, we were able to plot the expected level of precision in the measurement of ν₁ at each time point in conjunction with θ(t). An example of this for standard agarose-embedded hearts (i) is shown in Fig. 3. The mean value of θ at the first time point (mean change in orientation of ν₁ at t₁ = 4 h, compared with t₀) already exceeds the variation expected as a result of the precision in the measurement of ν₁. Between t₁ and t_f (48 h), the value of θ increased steadily, by 6.6°, whereas the change in COU was only 0.3°. In Table 3, the mean changes in θ, COU (precision) and SNR at t_f for each group are shown. In all preparations, the changes observed in the mean value of θ are at least six times greater than the change in the precision.

Table 3.

Change in value of the cone of uncertainty (δCOU), θ (δθ) and signal-to-noise ratio (δSNR) at t_f for each preparation

Preparation	δCOU (deg) at tf	δθ (deg) at tf	δSNR (%) at tf
(i) Standard agarose	0.3	6.6	11.7 ± 9.4
(ii) Fomblin	0.4	3.2	8.9 ± 5.8
(iii) Iso-osmotic agarose	0.3	1.9	12.0 ± 6.7

Figure 3.

Measured vales of θ as a function of time for the standard agarose-embedded hearts (i). The shaded area shows the cone of uncertainty (COU) around the orientation of v₁, based on the bootstrap analysis of the diffusion tensor imaging (DTI) data. Data points represent the mean of the three hearts in this group; error bars are standard deviations.

Sample stability 1 week after embedding

Only minor changes in T₁, T₂ and θ were observed in all samples 1 week after embedding: the overall mean changes in T₁ and T₂ were 2.2 ± 2.1% and 1.7 ± 1.4%, respectively, over a 48-h period (mean ± SD of the three hearts tested, one from each group; t_f = 48 h compared with t₀). Most importantly, the value of θ remained effectively constant, with variations in the mean value of just 0.3 ± 0.1° between t₀ and t_f.

Helix angles

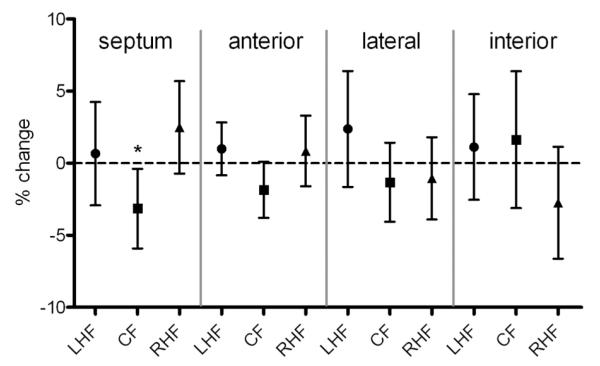
The mean change at t_f in the fractions of LHF, CF and RHF in the four aspects of the left-ventricular wall (septum, anterior, lateral, interior) are shown for all hearts in Fig. 4. The only regional change that is statistically significant for all hearts is the decrease in the fraction of CF in the septal wall (mean decrease of − 3.1% for all hearts, p = 0.03).

Figure 4.

Mean change in percentage of left-handed helical fibres (LHF), circumferential fibres (CF) and right-handed helical fibres (RHF) at t_f in the four walls of the left ventricle. Data points show the mean values for all hearts; error bars show 95% confidence intervals. *Statistically significant change (p < 0.05).

DISCUSSION

T₁ and T₂ relaxation

It has been shown previously in non-cardiac tissue that the action of aldehyde-based fixatives on ex vivo samples decreases the T₁ and T₂ relaxation times from their prefixation values (24–26). It has also been reported that washing non-cardiac tissue samples in buffer after fixation can reverse the initial decrease in T₂ values caused by fixation (31,41). This can be explained by the fact that washing removes free fixative from the interstitial spaces in the tissue (41). Our results show that T₂ values continue to increase in all embedded Karnovsky’s fixed hearts (all of which were washed with cacodylate buffer following fixation) up to 48 h post-embedding. The continuous increase in T₂ could be indicative of a reduction of free fixative in the tissue, caused by continued reactions between the free fixative and tissue and the loss of fixative from the tissue as a result of osmolarity gradients between fixed tissue and embedding medium. The increase in T₂ is much greater in standard agarose-embedded hearts (i), which is the only embedding approach used that is associated with a large osmotic gradient between interstitial fluid and an embedding medium that contains water (i.e. agarose). This may result in an influx of water from the embedding medium into the myocardium, and subsequent ‘dilution’ of free fixative in the tissue. Both the influx of water (inherently resulting in higher T₂ values) and the dilution of unreacted fixative could contribute to an increase in myocardial T₂. This influx of water into the myocardium does not occur in Fomblin-embedded hearts because of the lack of water in the embedding medium. It is also unlikely to occur in the iso-osmotically embedded hearts because of the lack of osmotic gradients. Accordingly, the change in T₂ values in these two embedding protocols follows a similar trend and reaches less pronounced peak levels, compared with standard agarose embedding. The remaining slow increase in T₂ relaxation times observed in these hearts may be a result of a gradual reaction of residual unreacted fixative with the myocardium, which would slowly decrease the remaining bulk fixative in the interstitial spaces in the tissue.

It has also been shown that changes in T₁ values, caused by aldehyde fixation, are not a result of the presence of bulk fixative in the tissue per se, but of continued chemical reactions between fixative and tissue; therefore, washing samples after fixation does not reverse the reduction in T₁ relaxation times caused by the fixative (24). All samples in this study were perfusion fixed via the coronary vasculature, ensuring optimal and swift delivery of the fixative to all cells of the heart [each myocyte is surrounded by four to five capillaries in the myocardium of healthy Sprague Dawley rats (42)], and this was followed by immersion fixation for 24 h before embedding. However, the continued decay in T₁ values observed in Fomblin-embedded hearts is indicative of progressive effects of the fixative on the myocardium, after the sample has been removed from the fixative. This could be a result of the continuous, slow action of the ‘second-stage’ formaldehyde fixation process, in which protein-bound formaldehyde molecules continue to react with free proteins, forming methylene cross-links (16). If this is the case, continuous action of the second-stage formaldehyde fixation process is much reduced in the agarose- (i) and iso-osmotic-embedded (iii) hearts, as T₁ is relatively stable in these samples. In the case of (i), the influx of water into the myocardium from the surrounding embedding medium may have interfered with progressive tissue–fixative interactions. In the case of (iii), the reduction in continued tissue–fixative interactions could be a consequence of the lower osmolarity Karnovsky’s solution used in this preparation, which was approximately five times more dilute compared with the ‘standard’ approach. This would also explain why the initial myocardial T₁ values were much higher in the iso-osmotic hearts: T₁ shortening caused by tissue fixation is less pronounced when a dilute Karnovsky’s solution is used.

DTI parameters

The fact that the angular deviation of the primary eigenvectors increases steadily over time in all hearts suggests that progressive structural changes in the myofibre orientation occur, regardless of the type of embedding used. However, one must also consider the influence that changes in SNR, as a result of changes in the T₁ and T₂ relaxation time, may have on the measurements. The results shown in Table 3 confirm that any change in COU over 48 h would be very small in all hearts. In addition, the group that experienced the greatest change in SNR over the 48-h period was that using iso-osmotic embedding (iii; mean increase of 12.0%); this group showed the lowest mean change in θ (1.9°).

The fact that the time course of θ follows a similar pattern in the two-dimensional and three-dimensional DTI data suggests that the changes observed in ν₁ are reproducible when the diffusion gradient scheme, b value and spatial resolution are altered. Overall, this confirms that the change in θ over time primarily represents actual structural change, rather than an artefact of the measurement process.

Regional structural change

The decrease in the fraction of circumferentially oriented myofibres in the septal wall over time is an area that warrants further investigation. The ventricular cavities remained filled with buffer/Fomblin throughout the experiments, and so it is possible that the shift in fibre orientation is a result of internal stresses in the myocardium, caused by changes in water content, and possibly osmotic pressure in preparation (i).

Previous studies by our group have investigated the propagation of electrical activation within MR-derived computational three-dimensional finite element models of the ventricles [method described in refs. (13,43)]. We have shown that a mean angular change in the orientation of ν₁ of just 3° can result in a 10% change in electrical activation time in some regions of the myocardium, following an initial electric stimulus (Hales PW, Bishop M). In areas in which the proportion of CF has decreased, and the proportion of LHF has increased, modelled electrical propagation will be artificially faster in the apico-basal direction, because of a higher proportion of longitudinally oriented fibres, and will reduce the accuracy in the representation of the physiological behaviour of the heart, as it would have been seen in vivo.

Thus, during time-intensive MRI or DTI studies of ex vivo hearts, it is important to ensure that the MR and tissue water diffusion characteristics remain stable. Although tissue fixation and sample embedding are necessary, we have shown that the combined effect of the two processes may not prevent, or even increase, changes in MR properties representative of cardiac histo-anatomical structure over time. Preparation (i) (standard agarose embedding) showed the greatest increase in θ and T₂ over 48 h, and it is therefore the least favourable preparation method. Preparation (iii) (iso-osmotic embedding) showed the lowest absolute change in θ, and resulted in the most stable T₁ and T₂ values, making it the most stable sample embedding method investigated. Continuous structural change can be reduced by scanning tissue 1 week after fixation. However, this only offers an apparent solution to the problem, as the tissue, although more stable, will be less representative of its native state after this period of fixation. Further research is needed to characterise the detailed effects of fixation on myocardial histo-anatomy over time.

Abbreviations used

ADC

apparent diffusion coefficient

CF

circumferential fibre

COU

cone of uncertainty

DTI

diffusion tensor imaging

FA

fractional anisotropy

FLASH

fast low-angle shot

FOV

field of view

HiK⁺

high-potassium solution (modified Tyrode solution)

LHF

left-handed helical fibre

NSA

number of signal averages

NT

normal Tyrode

RHF

right-handed helical fibre

SD

standard deviation

SNR

signal-to-noise ratio