Subcellular Size

Abstract

All of the same conceptual questions about size in organisms apply equally at the level of single cells. What determines the size, not only of the whole cell, but of all of its parts? What ensures that subcellular components are properly proportioned relative to the whole cell? How does alteration in organelle size affect biochemical function? Answering such fundamental questions requires us to understand how the size of individual organelles and other cellular structures is determined. Knowledge of organelle biogenesis and dynamics has advanced rapidly in recent years. Does this knowledge give us enough information to formulate reasonable models for organelle size control, or are we still missing something?

In general, larger cells contain larger organelles, and alterations in organelle size are characteristic of some diseases (e.g., cancer). But there is much to be learned about how the size of subcellular structures is controlled.

WHAT DOES SIZE CONTROL MEAN WITHIN A CELL?

A fundamental unanswered question in cell biology is how cells control the size of their organelles and other components. Different cell types can be distinguished in micrographs, in large part, because their organelles are of different sizes. This is true for different cell types, but also true in disease. Cytopathology is based on the ability to distinguish different types of cancer cells based, at least in part, on the size of the nucleus and nucleolus, two structures that have historically been easiest to visualize using chemical stains. The fact that organelle size changes can be predictive of disease progression strongly implies that organelle size is functionally important, a possibility we will discuss below.

SIZE AND DIMENSION

But, what do we mean when we talk about the size of an organelle? Size is a common-sense word that we use all the time, but the question is whether two people can talk about the size of something and mean two different things. First of all, there are different dimensions one can use to describe the size of an object. Perhaps the most fundamental way to describe size is by a characteristic linear dimension, such as length or diameter, but it is just as valid to describe the surface area of an object (with units of length squared), or the volume of the object (with units of length cubed). At some level, size and shape need to be discussed together. It is therefore safest, when talking about organelle size, to focus on cases in which the shape of the organelle does not change, so that if its size increases based on one measurement, the other descriptors of size will also increase. This will at least allow us to put a series of such organelles into a defined order based on their size and say, for example, that the nucleus is larger in cell type X than in cell type Y, regardless of whether we measure size by diameter, or surface area, or volume. But for organelles with complex geometries, such as the branching networks of mitochondria or endoplasmic reticulum (ER), deciding on what number to use to characterize “size” is not so easy and will ultimately depend on what aspect of size is more relevant to organelle function.

Another fundamental question in describing size is what to do when a particular organelle is present in more than one physically distinct copy within a cell. In such a case, we could ignore the number and just measure the average size of all the copies, or we could just count how many copies there are and ignore the size of each one, but either approach would be missing key information. Again, our guide must be biological relevance. If the function of an organelle is primarily to serve as a reaction vessel or storage tank, then what matters most would be the total volume of all copies of that organelle. Total volume would also be the most important measurement if we were concerned about whether or not the organelles could all fit inside a cell of a given size. On the other hand, for some organelles, their function depends on the size of each individual copy, for example, the cilia on the surface of an airway epithelial cell. It is, therefore, important to always consider whether we care more about the size of an individual organelle or the total aggregate size of all copies of that organelle.

WHAT DOES CONTROL MEAN?

The big question that this chapter seeks to address is how the cell controls the size of its organelles, but what does it mean to say that size is controlled? What if size was not controlled? How would that be different from what we actually observe? The only way to say whether or not the size of an organelle is “controlled” is to have some clear idea of what sizes would be observed in the absence of such control; otherwise, the word “control” would be inappropriate. What is our “null hypothesis” for organelle size? This question can only be answered in relation to the mechanism of organelle assembly. For example, in equilibrium polymers, size is exponentially distributed (Philips et al. 2013), so if we see a narrower size distribution, it would be appropriate to say that size is “controlled.” For tiny objects like bacteriophage tails that are small relative to the diameter of a bacterial cell, the exponential distribution is a reasonable null hypothesis. Thus, bacteriophage tails clearly pass the bar for saying that there is control of size. Their length distribution is much narrower than predicted for unregulated self-assembly (Wagenknecht and Bloomfield 1975), and cannot be trivially accounted for by the additional constraint of a finite cell size. For large objects, the finite size of the cell will, at the very least, force the size distribution to be truncated, as will a finite supply of precursor material (see below). Whether we want to consider such effects as representing a form of “control” or not is a matter of semantics.

For organelles with more complex assembly pathways, it is even less obvious what our null hypothesis ought to be. We might be tempted to apply a statistical mechanics formalism, and enumerate the possible ways to distribute a fixed quantity of total material among N distinct organelles. But such an approach would ignore the manner in which organelles are actually built. As a thought experiment, let us imagine a membrane-bound organelle that can exchange membrane vesicles with an infinite source of membrane (the ER). If the rate of vesicles trafficking into the organelle from the ER is a constant α, independent of the size of the organelle, and the rate of vesicles budding off from the organelle is proportional to its total surface area S with a proportionality constant β, then the steady-state surface area would be α/β. The distribution of sizes would depend on how constant α and β really are, and the time scales over which they fluctuate. For most organelles, trafficking is not characterized at such a quantitative level, and so even asking the simple question of whether or not organelle size is “controlled” becomes difficult. We can avoid some of these philosophical questions by restricting our discussion to what the organelle size actually is, how this size influences function, and what molecular components may alter the size, without needing to specify in advance whether or not size is “controlled.”

Absolute Size Versus Scaling of Cellular Structures

It is generally observed that any given organelle is larger in larger cells. This has long been recognized in the case of nuclei, but seems to hold true for many other organelles as well. Such proportionality between the size of subcellular structures and the size of the whole cell has been termed “scaling,” and we say that a particular organelle scales with the size of the cell. This represents a subcellular version of the types of scaling trends seen at the organismal level where, for instance, leg length scales with body length. In the study of biological size, two types of scaling relations are often distinguished: isometry and allometry. Isometry refers to cases in which a size of interest (e.g., length of the arms) is linearly proportional to a reference size (e.g., body height). Allometry refers to nonlinear scaling relations, frequently characterized by power law relations, in which the size of a structure is proportional to the reference size raised to some power. For example, if we are dealing with spheres, the surface area scales as the radius raised to the second power. Many biological examples of such allometric relations at the level of whole organisms were cataloged by Huxley in 1932, and their study has been an important thread in organismal biology ever since. Table 1 summarizes instances in which the size of subcellular structures seems to scale relative to cell size. Examples of subcellular structures whose size does not scale with cell size include centrioles and kinetochores. Chromosomes are an interesting case because, although there is a clear correlation between genome size and cell size across different species, one tends to assume that the genome content within cells of a given species will be constant, regardless of cell size. In fact, even within cells of a given organism, there is a correlation between total genomic DNA content and cell size. Increased ploidy via endoreduplication (that may or may not be accompanied by polyteny) is well known in Drosophila, for example, in the giant cells of the salivary gland. But the same trend seems to hold true even in humans. As discussed by Gillooly et al. (2015), there is a strong positive correlation between cell size and DNA content in cells of the human body. When considering the correlation between haploid genome size and average cell size between different species, clearly it cannot be the case that cell size in an individual actively changes the size of the genome. For ploidy variation, the situation is a bit less clear. It could be that when an organism wants to increase cell size in a given tissue, it increases ploidy as a way to drive increased cell growth. But it is also possible that DNA content is increased in larger cells because of some cell size measurement mechanism that feeds back onto the DNA replication machinery. These ideas are discussed in much greater detail in Gillooly et al. (2015).

Table 1.

Examples of subcellular structures scaling with cell size

Subcellular structure	References
Nucleus volume	Jorgensen et al. 2007; Neumann and Nurse 2007
Nucleolus volume	Noel et al. 1971; Wuehr et al. 2008
Mitotic spindle length	Hara and Kimura 2009
Mitotic chromosome size	Kieserman and Heald 2011
Centrosome volume	Decker et al. 2011
Nematocyst volume	Kramer and Francis 2004
Lipid droplet volume	Uchida et al. 2011
Vacuole surface area	Chan and Marshall 2012
Vacuole volume	Uchida et al. 2011; Chan and Marshall 2012
Mitochondria volume	Posakony et al. 1977
Mitochondria length	Rafelski et al. 2012
Chloroplast volume	Pellegrini 1980
Ciliate oral apparatus	Bakowska and Jerka-Dziadosz 1980

What Does Scaling Tell Us?

The importance of scaling relations is that they may suggest possible mechanisms for size differences. If two structures both grow exponentially, then their sizes will be related by a power law scaling relation whose slope is determined by the ratio of their doubling times. Thus, in cases of exponential growth, allometric scaling relations arise automatically and tell us about relative growth rates. Another source of allometric scaling is differences in dimensionality. For example, if we take a series of spheres and plotted their surface versus their radius on a log–log plot, we get a straight line with a slope of two. This has nothing to do with how fast the sphere is growing; it simply reflects the shape of spheres. In addition to mathematical relations that fix scaling relations, physical constraints can do the same thing. For example, the frequency of standing sound waves in an organ pipe scales to the length of the pipe for purely physical reasons. Scaling can, thus, arise from either relative growth or physical necessity. It is, thus, tempting, whenever we see such an allometric scaling relation, to seek the explanation in terms of either relative growth rates or in physical or mathematical mechanisms; and if such explanations were successful, it would mean that we could use the scaling relation itself as a way to probe growth rates and physical constraints.

However, very nice-looking mathematical scaling relations can arise because of genetically programmed regulatory pathways. The classic example of this is deer antlers. The weight of an adult male deer's antlers is related to the deer's body weight by an allometric scaling relation characterized by a clear power law, giving a straight line when antler weight is plotted against body weight on a log–log plot. The natural interpretation of such a plot is that the deer's body and antlers are growing at two different rates, and the ratio of these rates dictates the power law exponent. However, such an explanation is completely wrong because deer shed their antlers every year. Each year, the antlers have to grow back to a larger size than they did the year before, which requires the growth rate to actually increase each year. So really, it is not antler size, but antler growth rate that seems to depend on body weight or age, and this suggests that some growth-regulating pathway must be actively controlling the rate of antler growth to ensure that the antlers reach a size appropriate to body size. We will refer to this type of scaling as “programmed scaling.” Examples of programmed scaling within cells include the control of spindle length by katanin activity (Loughlin et al. 2011), and the control of nucleus volume by the nuclear import machinery (Levy and Heald 2010). In these cases, species with larger cells are thought to express katanin with lower microtubule severing activity (in the case of spindles) or nuclear import machineries with higher intrinsic rates of import (in the case of the nucleus), so that the resulting structures are of a size appropriate to the cell size.

The yeast vacuole provides an interesting example in which different ways of analyzing data give different perspectives on scaling. In one study, the ratio of vacuole volume to cell volume was plotted as a function of cell size and was shown to increase as cells grow during the cell cycle, which suggests the idea of a programmed scaling relation in which the scaling changes over time in the cell cycle (Uchida et al. 2011). On the other hand, when vacuole volume was plotted versus cell volume on a log–log plot, a clear power-law scaling relation was seen (Chan and Marshall 2012), suggesting a possible explanation in terms of relative growth rates or physical constraints. Interestingly, the vacuole surface area is proportional to cell volume, although the volume scales with a power law exponent of 1.4 relative to cell volume. But as we have mentioned, a power law scaling relation can also be explained by programmed scaling; so, as yet, the origin of this scaling trend remains uncertain. Because the volume of a sphere is proportional to the surface area of the sphere raised to the 3/2 power, a scaling exponent close to 1.5 suggests that perhaps cells are actively maintaining the vacuole surface area to be a fixed proportion of cell volume (programmed scaling), and then the vacuole volume automatically takes on a 3/2 power law scaling because of the spherical shape of the vacuoles.

How to Probe Size Control Mechanisms

Is there any way to distinguish the different types of scaling experimentally? One way to test programmed scaling is to experimentally manipulate cell size by nongenetic means, such as cutting a cell in half, and ask how this affects size. A strict programmed scaling model would predict that the size of a subcellular structure would not be altered by a physical change in cell size, because cell size is not a causal determinant of organelle size. Microsurgical studies have shown that when a Stentor cell is cut in half, each half readjusts the size of its cortical structures to have the same proportion that they would have had in an intact full-sized cell (Morgan 1901), indicating that size of these structures can actively readjust in response to cell size changes. Recently, a similar experiment was performed for mitotic and meiotic spindles, by encapsulating droplets of Xenopus extract using microfluidic methods. These studies (Good et al. 2013; Hazel et al. 2013) showed that altering the volume of the cytoplasm is sufficient to alter the size of the spindles, supporting the idea that, although programmed scaling may be critical in setting species-specific differences, cell size itself can also play a direct role for scaling within cells of a given species.

Another way of testing scaling models is by experimentally modifying the size of the cellular structure. For example, when flagella grow in the green alga Chlamydomonas, they start out growing rapidly and then gradually their growth rate slows down as they approach their final steady-state length. One could invoke programmed scaling to explain this trend by saying that the flagellar assembly pathway executes a program including timers that gradually reduce the speed of growth as a function of time after induction of flagellar assembly. Such a program would be consistent with the fact that the Chlamydomonas genome expresses a complex transcriptional program when it grows a new flagellum (Stolc et al. 2005; Albee et al. 2013). But experiments in which flagellar assembly is initiated starting from a nonzero length show that growth rate is a function of the length of the flagellum and not time since induction (Marshall et al. 2005), thus arguing against programmed scaling as the only mechanism at work.

Limiting Precursor Model—The Simplest Size Control System

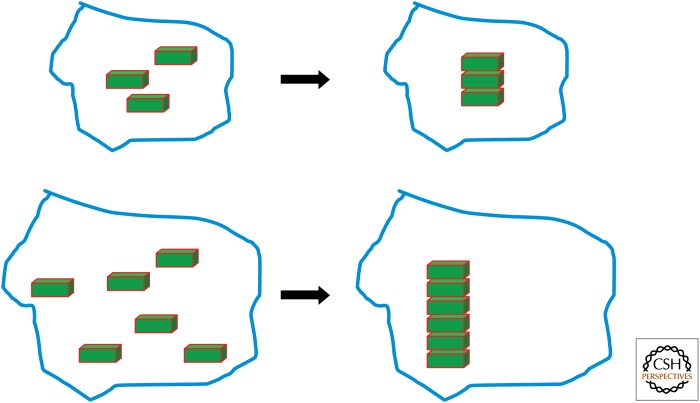
What is the simplest way to control size of a subcellular structure that would also be able to explain scaling as a direct function of cell size? Bigger cells are bigger because they have more biomass than small cells, and this means that, at least in principle, they should have more copies of every molecular species. For any given protein, we would imagine that if a cell doubles its size, it will then contain twice as much of that protein. The density, presumably, would be the same, only the total quantity would double. Quantification of individual reporter proteins as a function of cell size has confirmed the idea that larger cells contain more of each protein, although the relation may be more mathematically complex than simply maintaining a constant concentration of each protein (Cookson et al. 2010). We, therefore, can take as a starting point that, for any subcellular structure, its constituent molecules are present in larger numbers in larger cells. The crudest imaginable mechanism that a subcellular structure could form would be by aggregation, in which all of the component molecules adhere to each other in a big sticky mass. The size of this aggregated mass would depend only on the number of component molecules available, and, therefore, larger cells would be able to build larger structures. This is termed a limiting precursor model (Fig. 1). One hallmark of a limiting precursor system would be that increases in size of the structure should correlate with increases in the production of key precursors. Such a correlation has been reported for the length of microvilli, which correlates with production of cellular actin (Stidwell and Burgess 1986).

Figure 1.

In the absence of any additional regulation, large cells will contain more precursor molecules (green) and will, therefore, be able to assemble larger structures. If availability of precursor determines the size of a subcellular structure, it will, therefore, naturally scale in proportion to cell volume.

One nice feature of the limiting precursor model is that it makes relatively simple predictions of how to relate size to precursor quantity. In the case of irreversible aggregation, in which, eventually, 100% of the component molecules are incorporated into the aggregates, then the size of the aggregate would be determined only by the quantity of precursor protein and nothing else. In this case, a very clear prediction can also be made about the relation between the size and copy number of the structure—If one cell has just one aggregate, and another cell has two aggregates, then the sum of the size of the two aggregates would have to be equal to the size of the single aggregate, because in both cases the same total quantity of precursor is consumed.

For equilibrium structures, in which the components can associate and dissociate according to their affinity, the situation becomes more complicated. When the aggregates first start to form, the precursor would be present at a high concentration and so growth would occur by aggregation. But as the aggregate grows, it would deplete precursor so that the growth rate would drop, and eventually the net addition of new subunits would exactly balance the spontaneous dissociate of subunits, resulting in an equilibrium structure. The point at which this balance occurs would depend on when the concentration of precursor drops below some critical value. What kind of scaling relation would such a model predict?

Consider a simple case in which a single aggregate forms by adding new subunits, with a rate that depends on the product of an association rate constant k_on and the concentration F of free precursors in the cytoplasm. Meanwhile, monomers are able to dissociate at some rate that may be dependent on the size of the aggregate. Here, the details of the aggregate's shape become important because one can imagine cases like linear polymers, in which dissociation only occurs from the ends, or spherical aggregates, in which dissociation only occurs from the surface. We consider the linear polymer as the simplest case, because in that case, the dissociation rate is constant and independent of the size of the aggregate. Taking this case, and letting S be the size of the aggregate (in terms of the number of subunits), T be the total number of precursors present in the cell including both assembled and free subunits, and V be the volume of the cell, we obtain a simple equation that governs the growth of the aggregate:

$$\frac{dS}{dt}=k_{\text{on}}\left(\frac{T-S}{V}\right)-k_{\text{off}}.$$

The first term on the right-hand side arises from the fact that assembly depends on concentration, that is, the available free monomer pool (T – S) divided by the volume. This equation is easily solved for the steady-state solution by setting the rate of change dS/dt to zero, which yields

$$S_{\text{eq}}=T-\frac{k_{\text{off}}}{k_{\text{on}}}V.$$

If we further assume that the total quantity of precursor protein T is proportional to the total cell volume V (say with proportionality constant b), we end up with

$$S_{\text{eq}}=\left\{b-\frac{k_{\text{off}}}{k_{\text{on}}}\right\}V.$$

Thus, for the equilibrium polymer example, the simple limiting precursor predicts isometric scaling of aggregate size with cell volume.

The main reason for going through this simple mathematical exercise is to illustrate how many assumptions this type of model forces us to make. First, we have to assume (or measure) the relation of precursor quantity to cell volume. Second, we have to understand how the size of the aggregate affects the rate of association and dissociation of monomers. For aggregate shapes other than linear polymers, this can be quite complicated to do.

As is so often the case with mathematical models, we may lack enough knowledge of the system to know what assumptions are reasonable; and, in this case, further experiments are called for. Can we test the idea of a limiting precursor mechanism experimentally without having to know every detail of the growth and disassembly process? One potentially straightforward test is to experimentally alter precursor levels and ask how this affects size. For Chlamydomonas flagella, this has been performed by chopping off the flagella and forcing new ones to grow in cells treated with protein synthesis inhibitors. The result of such experiments is that flagella regrow to half their normal length (Rosenbaum et al. 1969), and, if the exercise is repeated, they grow to one quarter their normal length. Such sequential reduction in size provides strong support that depletion of precursors is sufficient to reduce size, and also gives us a way to estimate the effective size of the precursor pool. A limitation of such experiments, however, is that precursor quantity might become limiting when enough precursor has been removed, but might not be limiting under normal conditions.

A second way to probe limiting precursor models is to determine how aggregate size might vary as a function of aggregate number. If instead of a single growing aggregate, we had N aggregates, and letting S now represent the average size of all of the aggregates present, then the concentration of free precursor would change from (T – S)/V to (T – NS)/V. It will be left as an exercise for the reader to see that the new equilibrium size becomes

$$S_{\text{eq}}=\frac{1}{N}\left\{b-\frac{k_{\text{off}}}{k_{\text{on}}}\right\}V.$$

Changing the number of aggregates thus preserves a linear proportionality with cell volume, but now the average size of the aggregates is a decreasing function of the number of aggregates so that if a cell contains twice as many aggregates, each one would be half as large. This leads to a simple way of testing for whether or not a limiting precursor mechanism might be at work—vary the number of copies of the organelle and ask how the size changes. This was performed for flagella by Kuchka and Jarvik, who used mutations of Chlamydomonas that alter centriole segregation to produce cells with between one and six flagella, and then measuring the lengths of the flagella. Such experiments show that length is indeed a decreasing function of number, but the decrease is not as steep as the limiting precursor model predicts (Kuchka and Jarvik 1982; Marshall et al. 2005). In contrast, a more recent analysis of centrosome size in Caenorhabditis elegans has provided very strong support for such a limiting precursor mechanism based in part on the clear 1/N dependence of size on number (Decker et al. 2011). This type of limiting precursor model has been reviewed in more detail by Goehring and Hyman (2012), who present additional evidence for this type of mechanism.

The limiting precursor mechanism is a particularly simple and direct way that the size of a subcellular structure can be made to scale with the size of the entire cell. Is there any reason to believe that additional mechanisms would ever be required? One possible drawback of this type of mechanism is that, when multiple copies of the organelle are present, it may not always provide a way to ensure equality of size among the different copies (Fig. 2). In the formulation that we have given here, the size of the aggregates only influences the growth rate indirectly, via depletion of free precursors from the cytoplasmic pool. If there were two aggregates present, then the growth rate would only depend on the sum of their two sizes, and this would influence both aggregates; and so there is no built-in way for the size of any particular aggregate to influence its own growth rate relative to the other aggregates that might be present. Thus, if one aggregate happens to be larger than another, there is no way to correct this difference in size. But in living cells, organelles can adjust their size to maintain equality. For example, Chlamydomonas flagella can actively adjust their size to be equal to each other, so that if one of two flagella is severed, the other flagellum will shorten to achieve the same length as the shorter one (Rosenbaum et al. 1969), a phenomenon known as the “long zero” response.

Figure 2.

The limiting precursor model affects size by making growth rate a function of free precursor concentration. Therefore, the assembly rate only depends on the sum of the sizes of all copies of a structure, and not on their individual sizes. As a result, as long as the same number of precursor molecules has been consumed, the growth rate for all copies of the structure, big or small, will be the same, and the cell cannot correct any inequalities in size between different copies of the structure in the same cell.

The only way to force equal sizes for different copies of a structure is for their assembly or disassembly, or both, to be somehow directly dependent on their individual sizes. But now we are moving out of the realm of a strict limiting precursor model. If the size of a subcellular structure can determine its growth or disassembly rates by some mechanism other than depletion of precursors from the cytoplasm, then we are left with the question of what this mechanism might be.

Feedback Control of Assembly or Disassembly as a Function of Size

Most organelles are dynamic structures that undergo constant turnover (Fig. 3), and if the assembly and disassembly components of the organelle turnover process are size dependent, it is possible to have a system in which only a unique size is stable. But such regulation requires a way for the cell to measure the size of the organelle and modulate assembly and/or disassembly pathways of the organelle.

Figure 3.

Association and dissociation of precursors within a dynamic structure can produce defined sizes capable of equalization if either the assembly or disassembly rate is regulated by the size of a particular structure. This requires a mechanism to sense size and produce some size-dependent signal.

One way this can occur is via molecular rulers, in which one molecule serves as a reference that is compared with the size of the whole structure, and assembly is only allowed to proceed when the structure is smaller than the ruler molecule (Fig. 4). This has been shown in bacteriophage tails and several bacterial structures (Cornelis et al. 2006), but clear-cut cases of molecular rulers in eukaryotic cells seem harder to identify. The protein nebulin was thought to serve as a ruler to determine size of actin-thin filaments in sarcomeres, but more recent data have argued that nebulin does not regulate thin-filament length but rather helps regulate the overlap of thick and thin filaments (Castillo et al. 2009).

Figure 4.

Ruler molecules align with a growing structure and only allow growth to continue if the structure is smaller than the size of the ruler, thus producing structures with a defined size independent of precursor pool increases or copy number of the structure. This is a common mechanism for prokaryotic and viral structures.

One problem with molecular rulers is that the size range they can control is limited by the lengths that proteins can reasonably achieve. How else could the size of a subcellular structure be measured, if not using a fixed ruler? One very interesting proposal is the idea that a subcellular structure might act as an antenna to recruit factors that lead to its own disassembly, so that larger structure would recruit more disassembly factors and disassemble more rapidly. Such an antenna model has been shown for microtubules, which can recruit depolymerizing kinesins along their length, and which then move to the tip and mediate disassembly (Varga et al. 2009).

The key principle of the antenna model is that a larger structure can attract a larger number of disassembly factors. A related model is an assembly-factor dilution model, in which a protein or protein complex necessary for assembly is distributed around the structure in such a way that its density decreases as the structure gets larger. As long as a mechanism exists to keep the total quantity of the assembly factor fixed, and as long as its activity is sensitive to dilution within the structure (e.g., if its function is cooperative), then it is possible for the assembly rate to become a decreasing function of size. This type of model was proposed for regulating length of flagella (Marshall and Rosenbaum 2001). Assembly of flagella requires intraflagellar transport (IFT) (Scholey 2003), an intracellular transport process mediated by kinesin pulling protein complexes called the IFT particles that carry cargo proteins, such as tubulin (Hao et al. 2011; Bhogaraju et al. 2013) to the growing tip of the flagellum (Fig. 5). IFT is required for maintenance of flagellar length after assembly (Kozminski et al. 1995). Quantitative measurements showed that the number of IFT particles inside a flagellum was independent of flagellar length, so that the particles were more dilute in longer flagella (Marshall and Rosenbaum 2001; Marshall et al. 2005; Engel et al. 2009). The additional facts that (1) flagellar microtubules need IFT-mediated transport to grow, and (2) that flagellar microtubules undergo continuous disassembly requiring continuous assembly to maintain a steady-state length (Marshall and Rosenbaum 2001), together led to a simple model for length control. The rate at which IFT particles transport new tubulin to the distal tip would depend on the frequency of arrival of IFT particles at the tip, and this frequency would decrease in longer flagella because the fixed number of IFT particles each require a longer time to move out to the tip, deliver cargo, and return to the base to get more cargo. If the flagellum were to become long enough, the assembly rate would drop below the disassembly rate and further growth would cease, and then flagellum would maintain this steady-state length. As previously shown (Marshall et al. 2005), we can represent this model by considering the rate of change of length that it predicts:

$$\frac{dL}{dt}=A\frac{(T-NL)}{L}-D,$$

where L is the length, N is the number of flagella, T is the total flagellar protein precursor pool in the cell, D is the length-independent disassembly rate of the flagellum, and A is a constant that represents factors determining IFT efficiency, such as speed and cargo carried per IFT particle as well as the total number of IFT particles loaded in the flagellum, which was found to be independent of length (Engel et al. 2009). Note that this model as originally stated assumes that both the disassembly rate D and the cargo carried per particle are independent of length. However, neither of these assumptions is necessary for the model to give a stable steady-state length. It is also to be noted that the first term, which describes the steady-state rate of assembly, depends on the precursor pool size T, with the term (T – NL) representing the remaining pool left in the cell when all N flagella have grown to a length L. The model, thus, incorporates a key part of the limiting precursor model. However, in this model, the assembly rate also depends on 1/L. This dependence was initially postulated because a single IFT particle moving back and forth in the flagellum would deliver cargo to the tip at a rate proportional to 1/L because the longer it has to travel, the less frequently it can make a delivery. This model is easily solved for the steady-state solution by setting the rate of change to zero and solving for the length to yield:

$$L=\frac{T}{N+(D/A)}.$$

Figure 5.

Flagellar length regulation by intraflagellar transport (IFT). IFT particles (red) collect tubulin dimers (yellow) and carry them out along the flagellar outer doublet microtubules to the flagellar tip where there is constant turnover of tubulin. The number of IFT particles in the flagellum is independent of length, but this apparent constancy is likely to reflect active regulation of the injection of new IFT particles as a function of flagellar length. The signals that provide this regulation are only partially understood and we do not know how the cell knows how long the flagellum is.

Note, first of all, that this result predicts the steady-state length to be proportional to the total pool of flagellar precursor protein, and can recapitulate the regeneration of half-length flagella when protein synthesis is inhibited. Because the number of flagella, N, appears in the denominator, the average flagellar length is predicted to decrease as number increases; and, in fact, this equation has been shown capable of exactly fitting the dependence of flagellar length on number (Marshall et al. 2005).

The model can also account for the ability of the cell to equalize the lengths of its two flagella when one of them is severed. As mentioned above, when one flagellum of a Chlamydomonas cell is severed, it grows back just as it would if both flagella had been severed, but, whereas the short flagellum is growing back, the long flagellum shortens until the two flagella reach equal length, at which point they continue to grow together while keeping their lengths equal (Rosenbaum et al. 1969). This behavior is recapitulated by the steady-state model based on IFT-dependent, assembly-balancing, length-independent disassembly (Marshall and Rosenbaum 2001; Ludington et al. 2012), because when one flagellum is severed, the short flagellum undergoes net growth at a high rate. Thus, consuming cytoplasmic precursor and forcing the remaining flagellum to become shorter. It is worth noting that, during prior studies of flagellar length equalization, it was sometimes noted that the long flagellum would “overshoot,” becoming shorter than the short growing flagellum (Rosenbaum et al. 1969). This is not explained by the steady-state balance model. However, when flagellar length equalization was analyzed in carefully controlled microfluidic growth conditions, in which cells were provided with a constant supply of freshly aerated medium instead of being trapped under a coverslip, the overshoot was no longer observed, suggesting that, in at least some cases, the overshoot might represent a stress response rather than part of the normal length-control system (Ludington et al. 2012).

A key element of the steady-state balance model described above is the central role of IFT in regulating the rate of assembly, and, thus, in determining steady-state length. Such a central role for IFT in determining length is called into question by reports that flagella in temperature-sensitive mutants in one of the motor subunits of the IFT motor kinesin-2 appear to have less kinesin-2 even at permissive temperatures, without becoming proportionally shorter as one might expect (Walther et al. 1994). This report measured the quantity of kinesin-2 associated with isolated flagellar microtubules stripped away from the flagellar membrane. However, the vast majority of the kinesin-2 motor does not copurify with these microtubules, but instead is almost entirely present in the soluble fraction of flagella in biochemical preparations (Pazour et al. 2005); hence, the pool of kinesin-2 that was found to be reduced at permissive temperatures in the mutant represented only a miniscule portion of the total kinesin-2. Thus, the relevance of those results for the role of IFT in length control is by no means clear. Moreover, other reported analyses of the same conditional mutant at permissive temperature found little or no reduction of kinesin or other IFT protein levels relative to wild type (Kozminski et al. 1995; Mueller et al. 2005; Wang et al. 2009). Furthermore, live-cell microscopy by Piperno and coworkers showed that conditional kinesin-2 mutants had no effect on the frequency or speed of IFT particles at permissive temperatures (Iomini et al. 2001). Thus, the majority of available evidence suggests that these mutants do not affect the quantity of IFT at permissive temperatures; hence, the fact that flagellar length is close to wild type is not surprising. In more direct support of a role for IFT in determining length, when the same temperature-sensitive mutant in kinesin-2 was grown at temperatures that were intermediate between fully permissive and fully restrictive, the cells grew intermediate-length flagella (Marshall et al. 2005), directly confirming that maintenance of normal flagellar length requires normal IFT activity.

In considering how IFT quantity might relate to steady-state length at a more quantitative level, for example, if one wanted to test the steady-state balance model by carefully varying the IFT quantity, it is worth noting that reduction in IFT quantity would decrease the parameter A in the equations above. Because the steady-state solution is L = T/(N + D/A), reduction in the value of A will cause the denominator to increase and, thus, will cause length to decrease. However, because D/A is just one of two terms in the denominator, a given decrease in A will not produce a proportional decrease in L. L is, therefore, less sensitive to variation in A than expected by a purely linear relationship.

The constancy of IFT particle number central to this model is easy to achieve if the flagellum is a closed system and particles can neither enter nor exit. Unfortunately, such a closed system scenario is unlikely to be the case. Photobleaching studies in trypanosome flagella have shown that IFT particles in the flagellum are returned to a pool associated with the basal body (Buisson et al. 2013), and similar results are seen in Chlamydomonas (data not shown). Quantitative image analysis of IFT in living Chlamydomonas cells shows that IFT particles are injected at a total rate that is proportional to the inverse of flagellar length (Ludington et al. 2013). Because the injection rate scales as 1/L, and the round-trip transit time of each particle in the flagellum scales as L, the total quantity of IFT particles inside the flagellum at steady state should be length independent. Thus, the length-dependent injection of IFT particles can explain the apparent length independence of IFT particle content. But what signals regulate IFT injection as a function of flagellar length?

There are currently six kinases proposed to play a role in flagellar length modulation in Chlamydomonas: LF2 (Tam et al. 2007), LF4 (Berman et al. 2003), LF5 (Tam et al. 2013), CALK (Pan et al. 2004), CNK2 (Bradley and Quarmby 2005), and GSK3 (Wilson and Lefebvre 2004). Out of these five kinases, CALK is of particular interest because phosphorylation of its activation loop residues correlates with flagella length, such that CALK becomes increasingly phosphorylated as flagella become longer (Cao et al. 2013). This would be consistent for CALK playing a role in a feedback loop of some kind; however, RNAi of CALK does not affect flagellar length and it seems that the output of CALK activity is related to induction of flagellar disassembly (Pan et al. 2004). LF2 and CNK2 also appear to regulate flagellar disassembly rather than assembly (Marshall and Rosenbaum 2001; Hilton et al. 2013); hence, these are not candidates for regulating IFT. The function of LF5 is not known. Another candidate kinase is PKA, implicated by pharmacological studies in mouse cells showing PKA activation increased IFT speed (Besschetnova et al. 2010). But PKA activation also increased ciliary length, and because IFT speed is a function of length (Engel et al. 2009), the speed increase following PKA activation may be a side effect of the ciliary elongation. In contrast to these cases, live-cell imaging has shown that the lf4 mutation leads to increased injection of IFT into flagella, independently of its effect on flagellar length because the increase is seen even in flagella in a wild-type length range (Ludington et al. 2013). But even in an LF4 null mutant, IFT injection rate is still proportional to 1/L. Therefore, LF4 just adjusts the gain of the control system, but is not essential for the length dependence. Similarly, treatment of cells with lithium increases flagellar length (Wilson and Lefebvre 2004) and increases the injection of IFT proteins (Ludington et al. 2013), suggesting that the lithium target GSK3 may play a role in regulating IFT injection in response to length, but again lithium treatment does not render injection length independent, but simply alters the gain of the system much like the lf4 mutation. Therefore, both of these kinases seem more like gain-regulating inputs rather than core components of a length sensor pathway. In addition to kinases, IFT is also regulated by small G proteins (Qin 2012) and almost certainly other types of signals as well. At the moment, the molecular nature of the length sensor regulating IFT remains unknown.

A recent study of flagellar protein cargo moving by IFT has indicated that at least one cargo protein, DRC4, is loaded onto IFT particles in a length-dependent manner (Wren et al. 2013). The DRC4 protein is involved in flagellar motility and is not a length-determining structural component. But if bona fide structural components like tubulin were to have a similar length-dependent cargo loading, this would be a potential second regulated feature of flagellar assembly that would have to be taken into account for a full understanding of length regulation. Simulations performed by Wren et al. (2013) using quantitative numbers derived from studies of DRC4 incorporation argued that, without such regulated cargo loading, the regulation of IFT by length would not be sufficient to account for the kinetics of flagellar regeneration, which appears to contradict prior simulation studies showing that regulation of IFT by length is in fact sufficient to account for kinetics of flagellar regeneration (Marshall and Rosenbaum 2001). This apparent discrepancy arises because the model of Wren et al. incorporates a term x that represents the change in flagellar length per unit of cargo loaded. In the model as we have formulated it above, this term x would lead to a new expression for the rate of change:

$$\frac{dL}{dt}=x{A}^{\prime }\frac{(T-NL)}{L}-x{D}^{\prime }.$$

In this case, we have replaced the former constants A and D with new constants A′ and D′ because, in our initial model, the constant A included the influence of cargo per particle.

As is obvious from inspection of the equation, this value x is a factor in both the assembly and disassembly terms; hence, it affects kinetics rather than the steady-state value. This is because, when we solve for the steady-state length, we set dL/dt to zero and then any factors that are present in the remaining two terms can be canceled out. This is similar to the situation in chemical kinetics—If the off rate and on rate are both changed by the same constant value, this has no effect on the equilibrium constant. When the value of x derived from analysis of DRC4 loading was used, the kinetics are too slow as shown by Wren et al. (2013); but we do not know the value of x for a bona fide structural element like tubulin. If a higher value for x is used instead of that found for the dynein regulatory protein DRC4, then there is absolutely no difficulty in obtaining kinetics that match observed rates of flagellar assembly. So the discrepancy is not fundamental, but only apparent. Nevertheless, the fact that at least some and possibly all IFT cargoes can have their binding modulated as a function of flagellar length suggests a feedback pathway regulating cargo association, and this needs to be viewed as an additional control loop in what is clearly a very complex control system.

Moreover, IFT regulation is probably only part of the story of flagellar length control. Although original models for flagellar length control assumed that disassembly was length independent (Marshall and Rosenbaum 2001), recent studies have found evidence that disassembly is also regulated by length (Hilton et al. 2013). If flagellar disassembly increases when flagella become too long, this would represent a redundant pathway for regulating size in parallel to the pathway regulating IFT. As predicted by such a model, a double mutant of lf4, which affects the regulation of IFT, and cnk2, which affects the regulation of disassembly, results in flagella far longer than either individual mutant (Hilton et al. 2013). The fact that CALK activation is modulated as a function of length (Cao et al. 2013), and CALK down-regulation by RNAi affects disassembly (Pan et al. 2004), suggests that CALK may be part of the signaling pathway regulating disassembly in response to flagellar length increase.

Flagella have been used as a model system for understanding organelle size control because of their relatively simple linear geometry, which makes size control a one-dimensional problem. If even such a simple model organelle has such a complex size control system, it suggests we will have a long way to go in understanding the size control mechanisms for more complicated organelles.

Why Do We Care about Subcellular Size

Alterations in organelle size and scaling are hallmarks of cancer, and although they are routinely used as the basis for diagnosis by cytopathologists, these changes are poorly understood. We should be able to extract far more information about cell alterations from the same types of cytological images if we actually understood how these alterations arose. But we could go beyond diagnosis. If it is really true that a particular change in organelle size or scaling plays a causal role in the etiology of cancer, then it might be possible to drive the cell to a less malignant state by driving the organelle back to a more normal size.

These potential applications hinge on the assumption that organelle size is important for organelle function. We believe this to be true on theoretical grounds, because the total size of an organelle will set limits on the quantity of enzymes and intermediates it can contain, and the surface-to-volume ratio will affect the relative rates of internal reactions and exchange with the rest of the cell. Rigorously testing a functional role for organelle size requires a mechanistic knowledge of how size is regulated, and this is still lacking.

CONCLUDING REMARKS

Clearly, we are a long way from understanding how the size of subcellular structures is controlled. Simple mechanisms like limiting precursors are certainly part of the story, but by themselves cannot account for phenomena like equalization of size among different copies of a structure. Rulers play a clear role in prokaryotes but may not be extensively used in eukaryotes. Programmed scaling, by genetic tuning of factors involved in assembly and disassembly of cellular structures, can help to explain differences between species but cannot account for the ability of subcellular structures to rescale their size in response to physical changes in cell volume. Ultimately, learning how size control and scaling work will require a combination of physical principles and molecular regulatory pathways, and neglecting either aspect will prevent us from understanding how size is determined.