Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 May 29.
Published in final edited form as: Mol Biosyst. 2011 May 11;7(7):2238–2244. doi: 10.1039/c1mb05031a

Hi-Fi transmission of periodic signals amid cell-to-cell variability

Andreja Jovic a, Susan M Wade b, Atsushi Miyawaki c, Richard R Neubig b, Jennifer J Linderman d,*, Shuichi Takayama a,e,*
PMCID: PMC4449260  NIHMSID: NIHMS693398  PMID: 21559542

Abstract

Since information in intracellular calcium signaling is often frequency encoded, it is physiologically critical and experimentally useful to have reliable, convenient, and non-invasive methods to entrain it. Because of cell-to-cell variability, synchronization of intracellular signaling across a population of genetically identical cells can still be difficult to achieve. For intrinsically oscillatory signaling pathways, such as calcium, upon continuous stimulation, cell-to-cell variability is manifested as differences in intracellular response frequencies. Even with entrainment using periodic stimulation, cell-to-cell variability is manifested as differences in the fidelity with which extracellular inputs are converted into intracellular signals. Here we present a combined theoretical and experimental analysis that shows how to appropriately balance stimulation strength, duration, and rest intervals to achieve entrainment with high fidelity stimulation-to-response ratios for G-protein-coupled receptor-triggered intracellular calcium oscillations. We further demonstrate that stimulation parameters that give high fidelity entrainment are significantly altered upon changes in intracellular enzyme levels and cell surface receptor levels. Theoretical analysis suggests that, at key threshold values, even small changes in these protein concentrations or activities can results in precipitous changes in entrainment fidelity, with implications for pathophysiology.

Introduction

To coordinate function, cells in a population convert extracellular chemical cues into intracellular signals. Many intracellular signals that trigger cellular programs are frequency encoded based upon the type, magnitude (concentration), and temporal pattern of extracellular stimulation 1-3. For instance, it has been shown that the frequency of intracellular calcium signals can dictate which genes are expressed 4. Therefore, understanding how extracellular stimulation parameters enable faithful conversion of extracellular cues into appropriate frequency encoded intracellular signals would provide insight into physiological mechanisms of cell population synchronization as well as benefit in vitro studies that aim to dissect the role of periodic intracellular signaling 5.

A challenge for achieving cellular synchronization is that even for genetically identical cells, cell-to-cell variability exists; thus, for the same external stimuli, each cell in a population may respond differently. This paper analyzes the under-studied topic of how cell-to-cell variability can compromise the fidelity with which extracellular entrainment signals are converted into intracellular signals. The manuscript further provides extracellular stimulation parameter ranges that can maximize the number of cells in a population that are synchronized in their intracellular signaling responses despite cell-to-cell variability.

The experimental setup we use to provide periodic extracellular chemical cues is a microfluidic device. Even with such timed stimulations, however, synchronization can be impaired by skipped calcium responses 5, meaning that not every extracellular stimulation event elicited an intracellular calcium response. Thus, to enable high fidelity conversion of extracellular cues into intracellular signals, stimulation parameters must be optimized. We explore how the stimulant concentration (C), stimulation duration (D), and rest period (R) can improve intracellular calcium response fidelity to the extracellular cues despite cell-to-cell variability within cell populations. In this context, fidelity signifies the percentage of cells in a population that exhibit an intracellular calcium response to every periodic stimulation event (i.e. the percentage of cells that did not show skipped calcium responses). We additionally show that changes in receptor and regulatory protein levels or activities can alter fidelity, potentially providing insight into pathophysiology. Simulations of single-cell dynamics suggest that at certain critical points, small changes in protein levels (receptors and Regulators of G-protein signaling proteins) could result in abrupt changes in calcium response fidelity to periodic stimulation.

Results

Experimentally observed cell-to-cell variability and effect of stimulation parameters on fidelity in silico

Upon continuous exposure to carbachol (25 nM), HEK293 cells exhibited intracellular calcium oscillations with an average period of ∼50 s. Lowering the concentration to 10 nM resulted in a higher average oscillation period (∼110 s) (Fig. S1). A great deal of variability was observed in the periods of the calcium oscillations at the single cell level (Fig. S1 and S2A), highlighting the variability that exists within this single cell population.

A population of in silico cells with cell-to-cell variability was constructed by using an ordinary differential equation model of calcium signaling (Fig. S3) 5; individual cell parameters (receptor and G protein numbers) were drawn randomly from a distribution to mimic differences in protein levels between cells, as has been done previously 6. Continuous stimulation of this in silico cell population reproduced the experimentally-observed variability in calcium oscillation frequency (Fig. S2B, Fig. S4). To obtain insights into effects of cell-to-cell variability beyond what is possible in conventional culture dishes, we tested a periodic stimulation protocol with the mathematical model. Simulations predicted cell-to-cell variability manifested as various amounts of calcium response skipping (Fig. S2C).

To quantify the level of synchronization of calcium response in the cell population to periodic stimulation (both in simulations and experiments), we used the ‘calcium response fidelity’ metric. Response fidelity represented the fraction of cells in a population that responded to 90% of the periodic stimulation events. To observe whether the response fidelity could be enhanced within the simulations, we then manipulated three periodic stimulation parameters: stimulant concentration (C), stimulation duration (D), and rest period (R). The model predicted that increasing any one of these parameters would increase the overall response fidelity (Fig. S5).

Microfluidic setup for experimentally controlling intracellular calcium signals with seconds resolution

To experimentally test whether altering periodic stimulation parameters could enhance the calcium response fidelity as predicted by simulations, we developed a microfluidic device capable of generating periodic patterns of chemical stimulation 5 (Fig. 1A). Fig. 1B depicts the periodic chemical delivery patterns produced by the device, demonstrating not only reproducibility, but also an ability to control delivery events on a timescale appropriate for triggering G-protein-mediated calcium signals (seconds to minutes). Temporal chemical patterns were generated by alternately pumping from a ‘media-only’ reservoir and a stimulant-containing reservoir (Fig. 1C). Stimulation parameters that we varied using this device were C, D, and R (Fig. 1D).

Fig. 1.

Fig. 1

Open in a new tab

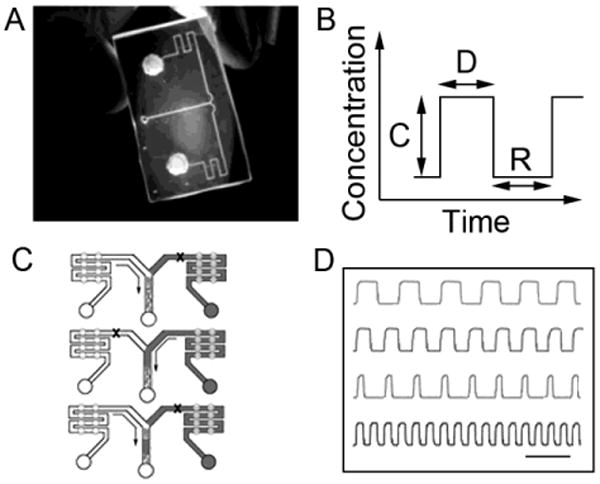
Microfluidic platform for generating periodic stimulation. A) Microfluidic chip filled with fluorescein. B) The platform is able to control three periodic stimulation parameters: stimulant concentration (C), stimulation duration (D), and the rest period (R). C) Periodic stimulation is generated by alternately pumping exclusively from the ‘media-only’ reservoir (left) and the ‘stimulant’ reservoir (right); black ‘x’s represent channels that are valved-off. D) Periodic stimulation patterns generated by the platform are reproducible and enable a high level of control over the stimulation parameters portrayed in B); (Scale Bar = 90 s).

Experimental modulation of periodic stimulation parameters and protein levels or activity can modify fidelity

In Fig. 2A, we show that cells continuously exposed to a small concentration of chemical stimulant (25 nM Carbachol) in our microfluidic device exhibit calcium oscillations, although with oscillation frequencies that differed between cells as had been seen in experiments in Petri dishes (Fig. S2A). Upon periodic stimulation, the maximum number of calcium oscillations per stimulation event could be controlled by sufficiently decreasing the parameter ‘D’, such that it was shorter than the intrinsic calcium oscillation frequency within cells such that no more than one spike would fit within a single stimulation duration. Increasing values of C (within a range close to or below Kd), D (within a range that still only elicited a single calcium spike), or R individually while keeping the other stimulation parameters fixed increased response fidelity in the cell population (Fig. 3A-C). The microfluidic system also allowed periodic stimulation with one chemical (carbachol) while maintaining a constant level of a different chemical. For example, periodic carbachol stimulation in the constant presence of a competitive M3 receptor antagonistic, atropine, was performed and observed to exhibit lower fidelity levels compared to untreated cells (Fig. 4). We also performed periodic carbachol stimulation on genetically engineered cells exposed to doxycycline, which induced expression of Regulator of G-protein Signaling 4 (RGS4) proteins (Fig. S6). RGS4 has been shown to be a critical component involved in the generation of intracellular calcium oscillations mediated by G-protein-coupled receptors 7. We found that upon increasing RGS4 levels, response fidelity levels decreased compared to cells with endogenous RGS4 expression (Fig. 4). These results corresponded with the marked decrease in average oscillation period upon application of doxycycline and atropine, respectively, to cells continuously stimulated with carbachol (Fig. S7).

Fig. 2.

Fig. 2

Open in a new tab

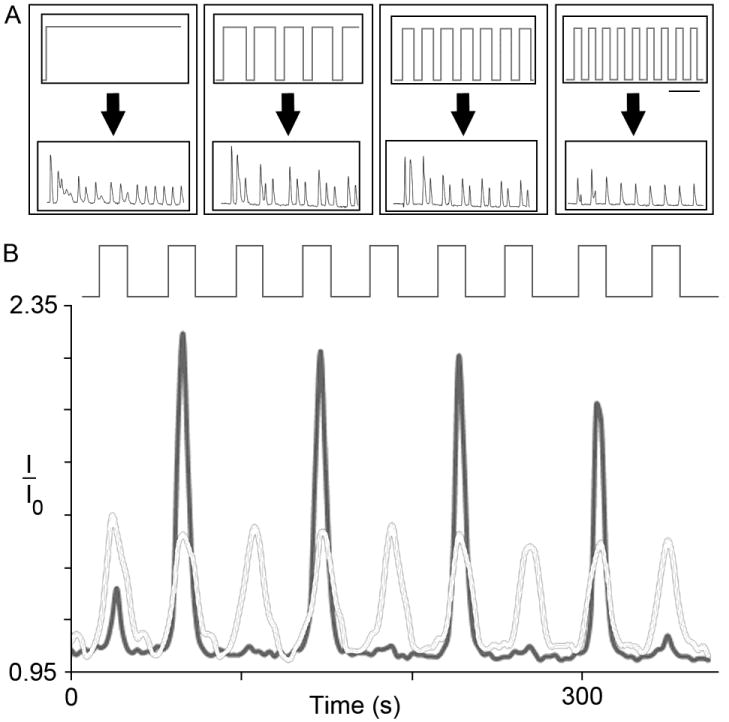
Periodic stimulation controls the timing of intracellular calcium signals and reveals loss of fidelity associated with phase-locking. A) Continuous stimulation with low concentrations of carbachol lead to an oscillatory intracellular calcium response. Periodic stimulation is able to dictate the number of calcium oscillations per stimulation event (from three to one, going from left to right), demonstrating the high level of control afforded by the microfluidic system; (Scale Bar = 80 s). B) Periodic stimulation uncovered loss of fidelity to the input signal in experiments, as assessed by the responses of adjacent cells; the dark trace represents a cell that responded to every other stimulation event, while the light trace represents an adjacent cell that responded to every stimulation event. The stimulation parameters used were: C = 10 nM carbachol, D = 24 s, and R = 24 s. Traces represent FRET measurements taken over a 6 minute period. I/I0 represents the FRET ratio normalized to the minimum intensity (I0), as has been done previously 37.

Fig. 3.

Fig. 3

Open in a new tab

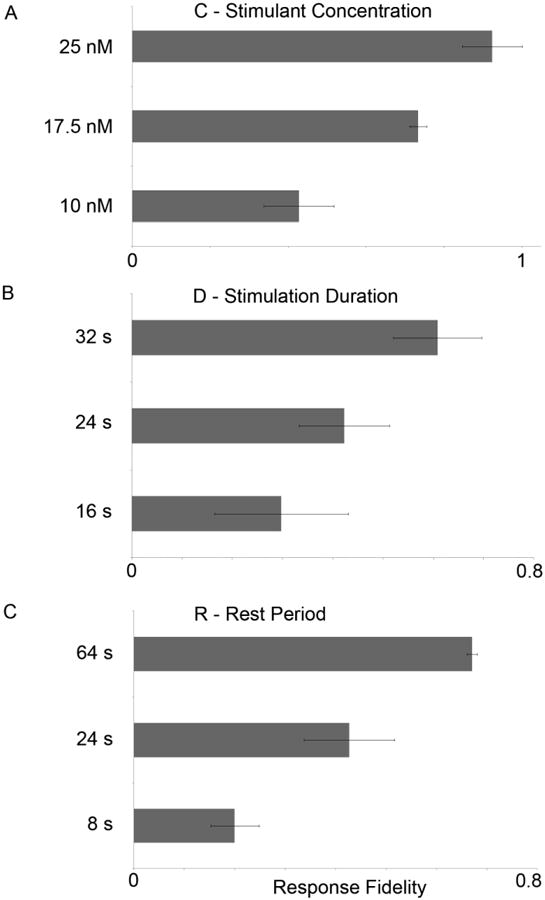
Periodic stimulation parameters modulate calcium response fidelity of a cell population with cell-to-cell variability. A) Increasing the stimulant concentration (C) increases the calcium response fidelity; parameters ‘D’ and ‘R’ were both fixed at 24 s. B) Increasing the stimulation duration (D) increases the calcium response fidelity; parameters ‘C’ and ‘R’ were fixed at 10 nM and 24 s, respectively. C) Increasing the rest period (R) increased the calcium response fidelity; ‘C’ and ‘D’ were fixed at 10 nM and 24 s, respectively. Bars represent the standard deviation. All conditions were statistically significant based upon the Student T-test, with p < 0.05.

Fig. 4.

Fig. 4

Open in a new tab

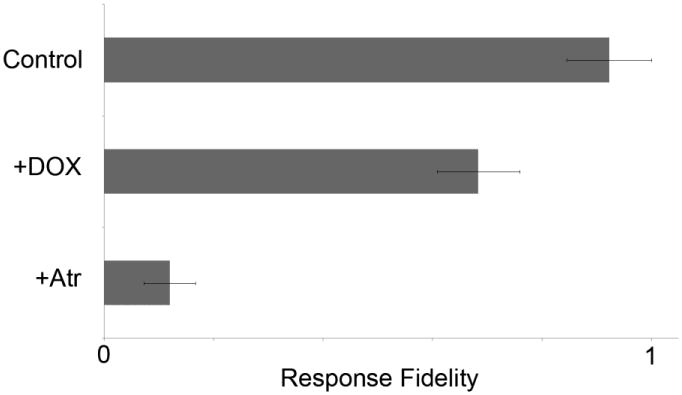
Drugs and protein expression levels also alter response fidelity in a cell population with cell-to-cell variability. Exposure to 1 μg/mL Doxycycline (DOX) increased RGS4 expression levels in our cells, leading to a reduction in calcium response fidelity (middle graph) compared to untreated cells. Cells treated with 1 nM Atropine (Atr) (bottom graph) showed significantly lower response fidelity compared to untreated cells. For each condition, cells were exposed to C = 25 nM Carbachol, D = 24 s, and R = 24 s. Bars represent the standard deviation. All conditions were statistically significant based upon the Student T-test, with p < 0.05.

Large changes in fidelity due to small changes in protein levels and potential downstream consequences

The experiments in Fig. 4 indicate that changes in levels or activity of even a single protein type can significantly modulate response fidelity within a cell population. To gain insight into single-cell dynamics, we used a mathematical model of calcium signaling to analyze how changes in protein levels affect fidelity. To quantify response fidelity at the single-cell level, we used the phase-locking ratio, which represents the number of calcium signal responses divided by the number of periodic stimulation inputs 5. Under some periodic stimulation conditions, very small changes (<1%) in the level of a single type of protein resulted in abrupt changes in the phase-locking ratio (Fig. 5, Fig. S8). This theoretical result was unexpected because it suggested that small perturbations caused by deterministic processes, such as protein production or degradation, or noise in the signaling pathways could drastically alter cell response fidelity at threshold protein levels. We observed several instances in experiments where cells exhibited abrupt changes in phase-locking ratio (example trace depicted in Fig. S9), consistent with this prediction.

Fig. 5.

Fig. 5

Open in a new tab

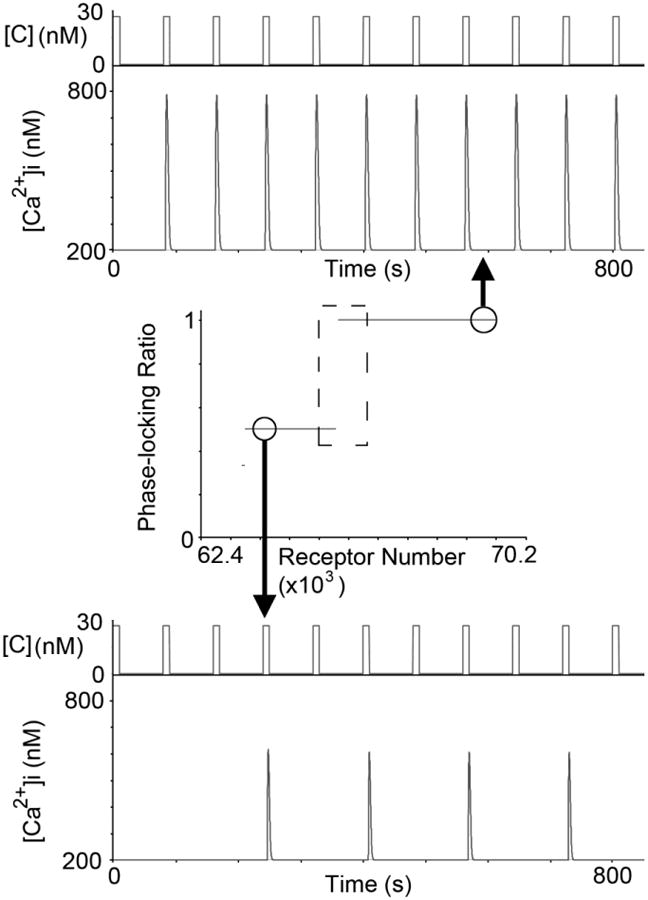
Small changes in protein levels are predicted to have drastic effects on the phase-locking ratio. Within the dashed box area, less than a 1% change in receptor number results in a precipitous change between a phase-locking ratio of 0.5 (bottom) and 1 (top). The periodic stimulation conditions for this simulation were C = 30 nM, D = 10 s, and R = 70 s.

Discussion

Frequency encoded intracellular signaling is critical for controlling cell behavior. Because of cell-to-cell variability, even a single population of cells exposed to the same stimulus may display different intracellular responses (and ultimately different behaviors) 8-11. Thus, determining the role of extracellular cell stimulation parameters and cell intrinsic protein activity on intracellular signal entrainment is vital for understanding physiological cell behavior. The information can also provide strategies for experimentally modulating intracellular signaling frequencies in vitro for mechanistic studies that systematically modulate intracellular signaling patterns. For example, while microfluidic setups are highly programmable in delivering extracellular stimulation 12, one must still know what stimulation program to use to enable efficient intracellular signal entrainment in cell populations that typically inherently manifest cell-to-cell variability.

We note that several approaches have been developed to control the timing of intracellular calcium signals, including the ‘calcium clamp’ method, developed by Dolmetsch et al. 4, or using large stimulant concentrations 13. The former method renders cells non-functional for further analysis because of irreversible depletion of calcium stores and certain mechanistic detail is lost because receptor pathways are bypassed; with the latter method, large concentrations (greater than the Kd value) can cause signaling system desensitization and are also likely far from physiological 14.

To provide a complimentary approach, we used a microfluidic setup to address cells with small concentrations of chemical stimulants but with optimized temporal patterns of stimulation (Fig. 1). The dark trace in Fig. 2B is representative of the types of skipped responses that are observed under sub-optimal conditions. To quantify the response fidelity at the population level, we measured the percentage of cells in the population that responded to 90% or more of the stimulation events; in other words, we quantified the number of cells that did not display skipped calcium responses. Implementing a combined theoretical and experimental approach, we found conditions where the stimulant concentration is still within a physiological range (i.e. near the Kd value) yet resulted in high response fidelity; increasing the stimulant concentration (C), the stimulation duration (D), and the rest period (R) increased response fidelity (Fig. 3). Specifically for C in the oscillatory signaling range, R can likely be arbitrarily large because it dictates the length of recovery 5; similar observations were made in other cell types 15, 16. There are limitations on D: D must be long enough to ensure that a response results, but short enough to avoid the occurrence of two or more responses per stimulation (Fig. 2A). For the stimulant and cell type used here, D in the range of 20-40s was most appropriate. To an extent, these findings support the theoretical study of Koseska et al. 17, which demonstrated that signaling heterogeneity could be overcome to an extent by the degree of cell-cell chemical communication; while in their study, these chemicals were released by neighboring cells, we show in this study that externally applied chemical stimulation is also effective in this context.

We also showed that changes in activity or expression (for both membrane bound and intracellular proteins) of even a single protein can significantly alter response fidelity (Fig. 4). These results provide potential insight into the pathophysiology of periodically stimulated systems. For this study, we focused on the M3 muscarinic receptor signaling pathway, which has been shown to be a critical component of lung 18, heart 19, nervous system 20, and bladder function 21. In addition, the receptor is involved in glucose regulation and periodic insulin release from pancreatic islets 22. Insulin secretion from individual islets is mediated in part by intracellular calcium signaling 23, 24. Periodic insulin release results from synchronized release from many islets 25; however the synchronization source is still unknown 26. Recent studies have shown that periodic acetylcholine exposure (eliciting intracellular calcium responses) might play a role in this synchronization 27. Pancreatic islets may be a physiological system where high fidelity entrainment in response to periodic chemical stimulation is important, and may be sensitive to changes in protein activity and expression levels (such as M3 receptors 22 and RGS4 28).

Analysis using mathematical models further showed that near threshold values, small changes in protein levels could result in precipitous changes in the phase-locking ratios which are indicative of response fidelity (Fig. 5, Fig. S8). The phase-locking ratio is obtained by dividing the number of system responses by the number of stimulation events. The simulations in Fig. 5 and Fig. S8 exhibit robustness in the phase-locking ratio for large concentration ranges, and then for critical values, abruptly drop by half. For example, our simulations predicted that a ∼10% change in stimulation strength (which could be due to small changes in protein levels) could lead to a 50% loss of fidelity and major changes in downstream signals such as cAMP (Fig. S10). Calcium is known to control or influence many important cellular operations, such as gene expression, growth, and migration 29; this theoretical result indicates that instabilities in calcium signaling can be propagated downstream and potentially alter cell behaviors. In this context, these types of critical points may reflect potential pathophysiology and tipping points that are manifested as disease or drug side-effects in just a few cells among a seemingly homogeneous population. Our mathematical model suggested that these tipping points arose as a result of non-linearity in IP3 signaling that was then propagated to calcium signaling (Fig. S11).

In conclusion, we experimentally and theoretically analyze the role of cell-to-cell variability in compromising intracellular signaling entrainment fidelity within apparently “homogenous” cell populations. We then further present concrete experimental strategies for maximizing response fidelity of periodic biological signals in such cell populations despite the cell-to-cell variability, using appropriate stimulation durations and rest periods for the externally applied chemical stimulations. These results are interesting in and of themselves, but, perhaps even more importantly, they provide the foundation for new future directions of inquiry. Are precipitous changes in fidelity triggered by small changes in protein levels or activity that are observed in our simulations physiologically relevant for diseases? Can we use high fidelity intracellular calcium entrainment to modulate downstream phenotypic consequences? For this study we focused upon oscillatory calcium signaling, whose frequency controls gene expression 4 and activation of effector proteins such as Ras 30. Although underappreciated, many oscillatory systems can exhibit skipped responses under periodic stimulation conditions 31. The combined theoretical and experimental methodology presented here may thus be broadly applicable to analysis and regulation of other oscillatory signaling systems as well, including NFkB 32, ERK 33, PKA 34, and p53 35.

Methods

Cell Culture, Microfluidics, and Imaging

HEK293 cells were cultured in Dulbecco's Modified Eagle's Medium (DMEM) (Invitrogen) supplemented with 10% Fetal Bovine Serum (FBS) (Gibco) and were maintained at 37°C with 5% CO2 in 24-well plates. 0.25% Trypsin/EDTA (Gibco) was used to detach cells from plates and transfer them to the microfluidic setup. These cells stably expressed the human muscarinic acetylcholine M3 receptor, and the doxycycline-inducible RGS4-C2S was generated using the Flp-In T-Rex system from Invitrogen. The Kpn1/Xho1 digested insert of C-terminal HA-tagged RGS4-C2S 36 was ligated into the pcDNA5/FRT/TO vector. Flp-In T-REX 293 cells in 6-well plates (400,000 cells/well) were co-transfected with the RGS4 containing pcDNA5/FRT/TO and pOG44 (3.6μg pOG44, 0.4μg pcDNA5/FRT/TO, 10μl Lipofectamine 2000). Two days after transfection, 200μg/ml hygromycin was added to the wells to select for stably transfected cells. Cell pools were tested for Zeocin sensitivity and doxycycline-induced RGS4 expression was verified by Western blot (Fig. S5). RGS4-C2S expressing cells were subsequently transfected with the M3 receptor cloned into pcDNA3.1+ (Missouri S&T cDNA Resource Center, Rolla, MO) and neomycin resistant clones were selected for with G418. Cells were maintained in DMEM, 10% FBS, 15μg/ml blasticidin, 200 μg/ml hygromycin B, and 400 μg/ml G418.

Cells were transiently transfected with the calcium FRET probe YC3.60 37 using Lipofectamine2000 (Invitrogen). Microfluidic devices (Fig. 1) were created and imaging of intracellular calcium signaling was carried out as described in Ref. 5. Cells were periodically stimulated with the M3 agonist carbachol (Calbiochem). For Fig. 4 (bottom graph), atropine (Invitrogen) was applied to periodically stimulated cells at a concentration of 1 nM in the microfluidic devices.

Computation of ‘Response Fidelity Percentage’ and ‘Phase-locking Ratios’

Cells were exposed to 9 chemical (carbachol) stimulation events, and the number of intracellular calcium responses for each run was recorded. Calcium spikes that were above levels of background noise (typically more than 10% maximum calcium spike height) but did not reach an amplitude greater than 33% of the maximum calcium spike height were not counted as true calcium spikes, as has been done previously 5. The calcium response fidelity was calculated for each experiment by counting the number of cells in the population that responded to 90% of the stimulation inputs divided by the total number of responding cells in that experiment. Averages and standard deviations were computed for each experimental condition. Statistics were based upon three experiments (each of no less than 20 cells) for each experimental condition. Between 85-106 cells were examined for each experimental condition. The unpaired Student t-test was used to statistically compare pairs of experimental conditions; p < 0.05 was used as a threshold of statistical significance. The phase-locking ratios in Fig. 5 and Fig. S6 were computed by counting the number of in silico cell intracellular calcium responses and dividing by the number of stimulation events; true calcium spikes were assessed identically to what was done experimentally.

Determining stimulation conditions for hi-fi transmission of periodic signals

We present the following protocol in order to assess how stimulation parameters (C, D, and R) can be modified to achieve high fidelity transmission of intracellular signals for a general oscillatory system. Initially, one must assess how the oscillation period changes with stimulant concentration. In a majority of cases, one expects the period to decrease with increases in stimulant concentration (C). Based upon the relationship between C and period, one can then determine an appropriate C to use. Since skipped responses are generally believed to occur when the forcing period is less than the intrinsic oscillation period 31, using C values that result in the smallest oscillation period are best; the results of Fig. S7 explain how changes in protein levels can shift the oscillation period and ultimately the response fidelity (Fig. 4). Having established an appropriate C range to use, one can then shift focus upon the parameters D and R. With C and R fixed, one can then periodically stimulate cells while varying the stimulation duration; for most oscillatory systems, it is expected that larger D would result in greater fidelity. However, caution must be applied since one does not want a D large enough to elicit two or more responses (Fig. 2). To avoid this effect, one can analyze the C vs. period data to observe what the shortest period in the population was, and use this as a maximum for D. Finally, one can assess the effect of R upon fidelity, by fixing C and D, and varying R. In most cases, it appears that larger R results in larger fidelity; R does not appear to have the same restrictions that D does in terms of its length, for the system studied here.

Mathematical models

We used our recently-developed calcium model 5 that incorporates mechanisms described by Politi et al. 38 and includes ligand/receptor/G-protein dynamics 6 (Fig. S3), to predict the effects of periodic stimulation and protein parameters on calcium response fidelity (Fig. S5) and the phase-locking ratio (Fig. 5, Fig. S8). For Fig. S8, hydrolysis rates were converted into RGS concentrations by using the linear relationship for G-protein hydrolysis rate vs. RGS4 concentration obtained by Lan et al. 39; similarly, for Fig. 5, receptor number was extrapolated by assuming a cell radius of ∼2.5 μm, yielding values that were similar to those in Ref. 40.

The calcium-cAMP signaling model by Gorbunova and Spitzer 41 was used to predict cAMP behaviors with low and high fidelity intracellular calcium signaling (Fig. S10). The parameter ‘α’ represented the stimulation input. Original parameters and initial conditions were used for this model.

All models were coded in MATLAB version 7.8.0 (MathWorks Inc, Natick, MA) and the system of ODEs was solved with the stiff solver ode15s.

Generation of In Silico Cell Populations with Cell-to-Cell Variability

We used Latin Hypercube Sampling (LHS) 42-45 to generate populations of in silico cells with intercellular variability. This in silico cell population was then used to evaluate the effect of periodic stimulation parameters on the response fidelity percentage (Fig. S5). Using LHS code from Marino et al. 43 (http://malthus.micro.med.umich.edu/lab/usadata/), the G-protein concentration and receptor density were sampled for each in silico cell from a normal distribution with a 25% standard deviation. LHS was run for 500 iterations, effectively generating 500 in silico cells with unique receptor densities and G-protein concentrations. These in silico cells were then subjected to periodic stimulation and calcium response fidelity percentages were assessed for each condition, as depicted in Fig. S5. Representative individual calcium traces are depicted in Fig. S2C.

Supplementary Material

Graphical Abstract
Supplementary Information

Acknowledgments

We would like to thank the following funding sources for support of this study: Rackham Predoctoral Fellowship, the Microfluidics in Biomedical Sciences Training Grant (NIH T32 EB005582), NIH grants HL084370, CA136829, and R33 HL092844. In addition, we would like to acknowledge the following individuals for their technical assistance and/or helpful comments: Tom Bersano, Bryan Howell, Michelle Cote, Khamir Mehta, Benita Sjogren, and Levi Blazer.

References

  • 1.Brabant G, Prank K, Schofl C. Trends Endocrinol Metab. 1992;3:183–190. doi: 10.1016/1043-2760(92)90169-2. [DOI] [PubMed] [Google Scholar]
  • 2.Paszek P, Jackson DA, White MR. Curr Opin Genet Dev. 2010;20:670–676. doi: 10.1016/j.gde.2010.08.004. [DOI] [PubMed] [Google Scholar]
  • 3.White MRH, Spiller DG. Cell Cycle. 2009;8:2677–2678. [PubMed] [Google Scholar]
  • 4.Dolmetsch RE, Xu KL, Lewis RS. Nature. 1998;392:933–936. doi: 10.1038/31960. [DOI] [PubMed] [Google Scholar]
  • 5.Jovic A, Howell B, Cote M, Wade SM, Mehta K, Miyawaki A, Neubig RR, Linderman JJ, Takayama S. PLoS Comput Biol. 2010;6:e1001040. doi: 10.1371/journal.pcbi.1001040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Mahama PA, Linderman JJ. Biotechnology Progress. 1994;10:45–54. [Google Scholar]
  • 7.Luo X, Popov S, Bera AK, Wilkie TM, Muallem S. Molecular Cell. 2001;7:651–660. doi: 10.1016/s1097-2765(01)00211-8. [DOI] [PubMed] [Google Scholar]
  • 8.Nakamura N, Yamazawa T, Okubo Y, Iino M. Mol Syst Biol. 2009;5:247. doi: 10.1038/msb.2009.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Altschuler SJ, Wu LF. Cell. 2010;141:559–563. doi: 10.1016/j.cell.2010.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Losick R, Desplan C. Science. 2008;320:65–68. doi: 10.1126/science.1147888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Huang S. Development. 2009;136:3853–3862. doi: 10.1242/dev.035139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Jovic A, Howell B, Takayama S. Microfluid Nanofluid. 2009;6:717–729. [Google Scholar]
  • 13.Prank K, Waring M, Ahlvers U, Bader A, Penner E, Moller M, Brabant G, Schofl C. Systems Biology. 2005;2:31–34. doi: 10.1049/sb:20050002. [DOI] [PubMed] [Google Scholar]
  • 14.Anslyn EV, Dougherty DA. Modern physical organic chemistry. University Science; Sausalito, CA: 2006. [Google Scholar]
  • 15.Zemkova H, Balik A, Kretschmannova K, Mazna P, Stojilkovic SS. Cell Calcium. 2004;36:89–97. doi: 10.1016/j.ceca.2003.12.003. [DOI] [PubMed] [Google Scholar]
  • 16.Schofl C, Brabant G, Hesch RD, Zurmuhlen AV, Cobbold PH, Cuthbertson KSR. Am J Physiol. 1993;265:C1030–C1036. doi: 10.1152/ajpcell.1993.265.4.C1030. [DOI] [PubMed] [Google Scholar]
  • 17.Koseska A, Zaikin A, Kurths J, Garcia-Ojalvo J. PLoS One. 2009;4:e4872. doi: 10.1371/journal.pone.0004872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Roffel AF, Elzinga CR, Zaagsma J. Pulm Pharmacol. 1990;3:47–51. doi: 10.1016/0952-0600(90)90009-8. [DOI] [PubMed] [Google Scholar]
  • 19.Wang ZG, Shi H, Wang HZ. British Journal of Pharmacology. 2004;142:395–408. doi: 10.1038/sj.bjp.0705787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Wess J. Trends Pharmacol Sci. 2003;24:414–420. doi: 10.1016/S0165-6147(03)00195-0. [DOI] [PubMed] [Google Scholar]
  • 21.Abrams P, Andersson KE, Buccafusco JJ, Chapple C, de Groat WC, Fryer AD, Kay G, Laties A, Nathanson NM, Pasricha PJ, Wein AJ. Br J Pharmacol. 2006;148:565–578. doi: 10.1038/sj.bjp.0706780. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Gautam D, Han SJ, Hamdan FF, Jeon J, Li B, Li JH, Cui YH, Mears D, Lu HY, Deng CX, Heard T, Wess J. Cell Metabolism. 2006;3:449–461. doi: 10.1016/j.cmet.2006.04.009. [DOI] [PubMed] [Google Scholar]
  • 23.Ashcroft FM, Proks P, Smith PA, Ammala C, Bokvist K, Rorsman P. J Cell Biochem. 1994;55 Suppl:54–65. doi: 10.1002/jcb.240550007. [DOI] [PubMed] [Google Scholar]
  • 24.Bergsten P, Grapengiesser E, Gylfe E, Tengholm A, Hellman B. J Biol Chem. 1994;269:8749–8753. [PubMed] [Google Scholar]
  • 25.Pedersen MG, Bertram R, Sherman A. Biophys J. 2005;89:107–119. doi: 10.1529/biophysj.104.055681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Fendler B, Zhang M, Satin L, Bertram R. Biophys J. 2009;97:722–729. doi: 10.1016/j.bpj.2009.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Zhang M, Fendler B, Peercy B, Goel P, Bertram R, Sherman A, Satin L. Biophys J. 2008;95:4676–4688. doi: 10.1529/biophysj.107.125088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.de Azua IR, Scarselli M, Rosemond E, Gautam D, Jou W, Gavrilova O, Ebert PJ, Levitt P, Wess J. Proc Natl Acad Sci U S A. 2010;107:7999–8004. doi: 10.1073/pnas.1003655107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Berridge MJ, Bootman MD, Roderick HL. Nature Reviews Molecular Cell Biology. 2003;4:517–529. doi: 10.1038/nrm1155. [DOI] [PubMed] [Google Scholar]
  • 30.Kupzig S, Walker SA, Cullen PJ. Proc Natl Acad Sci U S A. 2005;102:7577–7582. doi: 10.1073/pnas.0409611102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Machlup S, Sluckin TJ. J Theor Biol. 1980;84:119–134. doi: 10.1016/s0022-5193(80)81040-x. [DOI] [PubMed] [Google Scholar]
  • 32.Nelson DE, Ihekwaba AEC, Elliott M, Johnson JR, Gibney CA, Foreman BE, Nelson G, See V, Horton CA, Spiller DG, Edwards SW, McDowell HP, Unitt JF, Sullivan E, Grimley R, Benson N, Broomhead D, Kell DB, White MRH. Science. 2004;306:704–708. doi: 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
  • 33.Shankaran H, Ippolito DL, Chrisler WB, Resat H, Bollinger N, Opresko LK, Wiley HS. Mol Syst Biol. 2009;5:332. doi: 10.1038/msb.2009.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Ni Q, Ganesan A, Aye-Han NN, Gao X, Allen MD, Levchenko A, Zhang J. Nat Chem Biol. 2011;7:34–40. doi: 10.1038/nchembio.478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Lahav G, Rosenfeld N, Sigal A, Geva-Zatorsky N, Levine AJ, Elowitz MB, Alon U. Nature Genetics. 2004;36:147–150. doi: 10.1038/ng1293. [DOI] [PubMed] [Google Scholar]
  • 36.Bodenstein J, Sunahara RK, Neubig RR. Mol Pharmacol. 2007;71:1040–1050. doi: 10.1124/mol.106.029397. [DOI] [PubMed] [Google Scholar]
  • 37.Nagai T, Yamada S, Tominaga T, Ichikawa M, Miyawaki A. Proc Natl Acad Sci U S A. 2004;101:10554–10559. doi: 10.1073/pnas.0400417101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Politi A, Gaspers LD, Thomas AP, Hofer T. Biophys J. 2006;90:3120–3133. doi: 10.1529/biophysj.105.072249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Lan KL, Zhong HL, Nanamori M, Neubig RR. J Biol Chem. 2000;275:33497–33503. doi: 10.1074/jbc.M005785200. [DOI] [PubMed] [Google Scholar]
  • 40.Zhang L, Buxton ILO. Faseb Journal. 1991;5:A1586–A1586. [Google Scholar]
  • 41.Gorbunova YV, Spitzer NC. Nature. 2002;418:93–96. doi: 10.1038/nature00835. [DOI] [PubMed] [Google Scholar]
  • 42.Blower SM, Dowlatabadi H. Int Stat Rev. 1994;62:229–243. [Google Scholar]
  • 43.Marino S, Hogue IB, Ray CJ, Kirschner DE. J Theor Biol. 2008;254:178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.McKay MD, Beckman RJ, Conover WJ. Technometrics. 1979;21:239–245. [Google Scholar]
  • 45.Kinzer-Ursem TL, Linderman JJ. PLoS Comput Biol. 2007;3:84–94. doi: 10.1371/journal.pcbi.0030006. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Graphical Abstract
NIHMS693398-supplement-Graphical_Abstract.tif (927.9KB, tif)
Supplementary Information
NIHMS693398-supplement-Supplementary_Information.pdf (357.2KB, pdf)

RESOURCES