Diverse coupling of neurons to populations in sensory cortex

Abstract

A large population of neurons can in principle produce an astronomical number of distinct firing patterns. In cortex however, these patterns lie in a space of lower dimension^1-4, as if individual neurons were “obedient members of a huge orchestra”⁵. Here we use recordings from the visual cortex of mouse and monkey to investigate the relationship between individual neurons and the population, and to establish the underlying circuit mechanisms. We show that neighbouring neurons can differ in their coupling to the overall firing of the population, ranging from strongly coupled “choristers” to weakly coupled “soloists”. Population coupling is largely independent of sensory preferences, and it is a fixed cellular attribute, invariant to stimulus conditions. Neurons with high population coupling are more strongly affected by non-sensory behavioural variables such as motor intention. Population coupling reflects a causal relationship, predicting a neuron’s response to optogenetically-driven increases in local activity. Moreover, population coupling indicates synaptic connectivity: a neuron’s population coupling, measured in vivo, predicted subsequent in vitro estimates of the number of synapses received from its neighbours. Finally, population coupling provides a compact summary of population activity: knowledge of the population couplings of N neurons predicts a substantial portion of their N² pairwise correlations. Population coupling therefore represents a novel, simple measure that characterises each neuron’s relationship to a larger population, explaining seemingly complex network firing patterns in terms of basic circuit variables.

The cortex represents its computations through the joint activity of multiple neurons. This activity can be remarkably diverse even among neighbouring neurons, belonging to the same morphological and laminar cell class. In sensory cortex, neighbouring neurons not only respond to diverse stimulus features ^6-8, but also use diverse strategies to encode information. For example, mean firing rate differs by orders of magnitude across neurons ^9-11, and it appears to constitute an invariant property of each cell, persisting across multiple stimulus conditions and spontaneous activity¹². Do other invariant dimensions exist that characterise the diversity of firing of cortical neurons? Ideally, such dimensions would not only help explain the complex patterns of activity produced by cortical populations, but also relate directly to underlying circuit variables.

To characterise how different cortical neurons relate to large-scale firing patterns, we considered their relationship to the “population rate”: the summed activity of all neurons in the recorded population at any moment in time^13-16. We recorded first from populations of 20-80 neurons in deep layers of area V1 in awake head-fixed mice using multi-site silicon probes (Fig. 1a). Consistent with previous reports^17-19, population rate was not strictly controlled by sensory stimulation, but showed coherent fluctuations even spontaneously in the absence of sensory stimuli (Fig. 1b-c), closely tracking the simultaneously recorded local field potential (LFP, Fig. 1d).

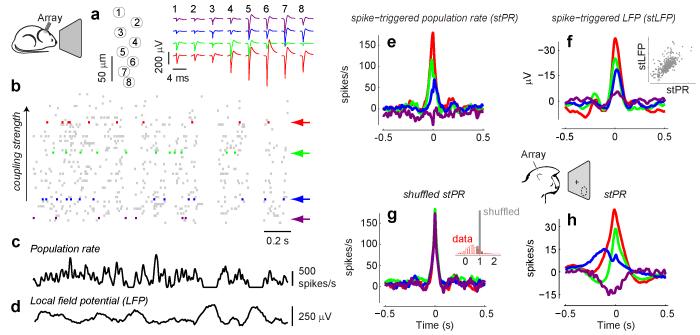
Figure 1. Neighbouring neurons differ markedly in population coupling during spontaneous activity.

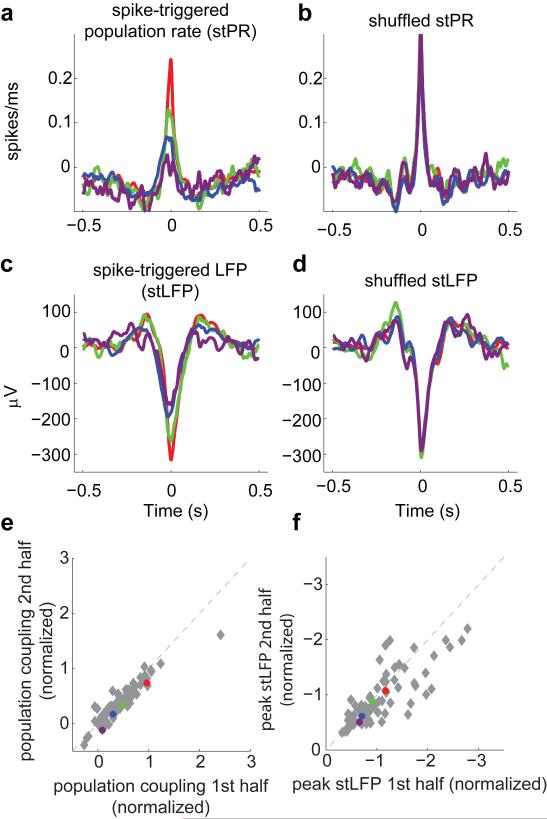
a, Schematic of a single shank of silicon electrode array, and spike waveforms of four example wide-spiking neighbour neurons measured with the array in deep layers of V1 of an awake mouse. b, Population raster of spontaneous activity in 66 neurons recorded from the whole array. Cells are arranged vertically in order of population coupling. Arrows indicate the four example neurons shown in a. c, Population rate measured by summing all the spikes detected on the entire array. d, Local field potential (LFP) measured on a shank adjacent to that on which the example neurons were recorded (LFP waveforms were similar across shanks). e, Spike-triggered population rate (stPR) for the four example neurons. The spike train of each neuron was excluded from the population rate before computing its stPR. f, The spike-triggered local field potential (stLFP) for the four example cells (inverted for ease of comparison) resembles their stPR (shown in e). Inset: normalised magnitudes of stPR and stLFP (see Methods) are highly correlated across cells (ρ=-0.71, P<10⁻¹⁰⁰, rank correlation, n=431 neurons). g, Differences in population coupling disappear after shuffling spikes in a manner that preserves each neuron’s mean firing rate and the population rate. Inset: population couplings in the actual spike trains (red) and after shuffling (grey), for neurons from all experiments. h, stPR of four example neurons simultaneously recorded in primate area V4, computed as in e.

During spontaneous activity, neighbouring neurons differed widely in their coupling to the population. The spike-triggered population rate typically had a single peak centred close to zero (Fig. 1e, Extended Data Fig. 1), whose height was large for some neurons and small or even reversed for others. The variation in population coupling across neurons was continuous, and neurons did not appear to fall into discrete classes of distinct coupling. This diversity in coupling, however, represented a robust property of individual cells: computing coupling from separate data segments yielded highly consistent results (Extended Data Fig. 2a). A similar result was seen when correlating spikes with the LFP (Fig. 1f, Extended Data Fig. 2b). These variations in population coupling were not trivially explained by differences in mean firing rate: shuffling the spike times across neurons and time, while preserving each neuron’s mean rate and the population rate distribution¹⁴, destroyed the diversity in population coupling between neurons (Fig. 1g, Extended Data Fig. 2c). Moreover, diversity in population coupling was not restricted to mouse V1: it was also observed in primate area V4 (Fig. 1h) and in rat auditory cortex (Extended Data Fig. 3).

Population coupling differed both between and within cell classes. Based on spike shape²⁰, we classified ~13% of the cells in mouse V1 as narrow-spiking putative interneurons (Extended Data Fig. 4a), with the remainder likely primarily pyramidal cells. Narrow-spiking cells tended to have higher population coupling than wide-spiking cells (medians of 0.84 and 0.50; P<10⁻⁶). Nevertheless this difference between classes was substantially smaller than the variability within each class (Extended Data Fig. 4). Strongly coupled neurons were more likely to exhibit bursting and to have a lower firing rate. However, even cells with similar firing rate and bursting dynamics could show great variation in coupling (Extended Data Fig. 4b-d).

We next asked to what degree population coupling can explain the patterns of spontaneous correlated activity in a population. To this end, we generated random population activity patterns, constrained so that each neuron’s population coupling and mean rate matched the original data, as did the distribution of population rate over time (Fig. 2a). We found that pairwise correlations in the resulting synthetic activity resembled those observed in the recorded activity (Fig. 2b). The accuracy of this prediction was higher when the population rate showed stronger variance, indicating that the single statistic of coupling was able to capture the correlations induced by globally-coordinated fluctuations (Fig. 2c). If coupling was not included, however, the performance of the model was substantially impaired (Fig. 2c-d).

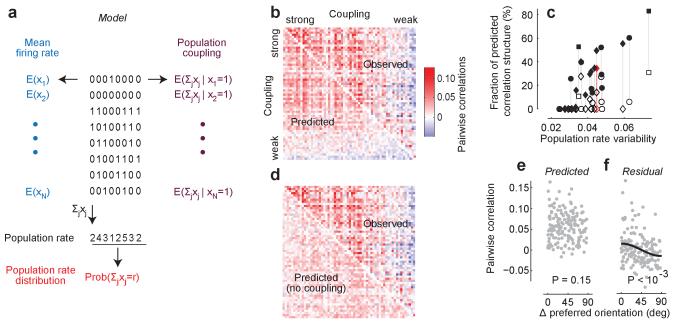
Figure 2. A simple model based on population coupling predicts the structure of pairwise correlations in a cortical population.

a, The model generates random spike patterns subject to three constraints: that the population coupling of each neuron, the mean firing rate of each neuron, and the distribution of the population rate, must match those in the original data. b, Random activity generated by the model produces pairwise correlations that are similar to those measured in the original spike trains (n=67 units in one experiment; correlations computed in 20ms bins). The upper triangle shows observed pairwise correlations, and the lower one shows pairwise correlations predicted by the model. Neurons are arranged in order of population coupling (arrows). The values on the diagonal (all 1s) have been removed. Similarity of observed and predicted correlations is indicated by the symmetry of the upper and lower triangles. c, Percentage of explainable correlation structure predicted, as a function of the variability of population rate (filled symbols, see Methods). The model captures pairwise correlations, but only in experiments in which the population rate fluctuates. It cannot predict them when population rate is mostly constant (a highly desynchronised cortical state). Recordings were obtained from mouse V1 in wakefulness (diamonds) or under anaesthesia (circles), or from A1 of awake rat (squares), all spontaneous activity; note that a variety of states is observed in all conditions. Open symbols show predictions of model that ignores population coupling. The example experiment in b is shown in red. d, Same as b, for predictions made without using population coupling. Such predictions fail to capture the structure of pairwise correlations (open markers in c). e, The model cannot predict a relationship between similarity of preferred orientation and spontaneous pairwise correlations (P=0.15, Pearson correlation). f, As a result, this correlation is retained in the residual pairwise correlations obtained by subtracting the modelled from actual correlations (ρ=0.26, P<10⁻³, Pearson correlation), indicating that the predictions of coupling and orientation sum linearly. The black line in f shows regression on cos(2Δθ).

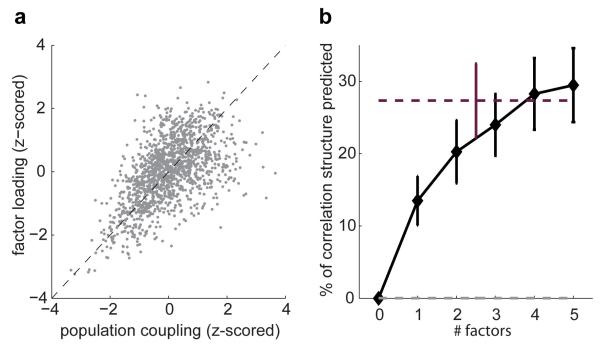
These results indicate that much of the pairwise correlation in the population is explained by the coupling of each neuron to population rate, with coupling strengths that vary between neurons. The underlying model is parsimonious, requiring only order N parameters to predict order N² pairwise correlations. Moreover, the model is intuitive, involving procedures among the simplest in neuroscience: summing the activity of multiple neurons, and correlating the spike train of each neuron with the result. To assess whether more advanced procedures would yield different results, we used a variant of latent variable analysis designed for discrete spike count data^4,21 to obtain the weights of individual neurons to the first detected factor. Reassuringly, these weights were highly correlated with population coupling (Extended Data Fig. 5a): latent variable analysis found the same basic structure as our simple coupling model.

The ability of the model to predict correlations may appear surprising given that it operates without knowledge of the neurons’ sensory tuning. In primary sensory areas, neurons with similar sensory selectivity show stronger stimulus-independent correlations^1,3,5,22, and we indeed observed a significant relationship between orientation preference similarity and spontaneous correlations (Pearson correlation ρ=0.26, P<10⁻³, for n=163 pairs of cells with orientation selectivity index>0.6). The coupling model of course could not predict this relationship; indeed, its predictions of correlations were independent of orientation preference similarity (P=0.15, Fig. 2e). Population coupling, however, represented a much better predictor of pairwise correlations than orientation preference similarity (ρ=0.63, P<10⁻⁹); moreover, the two predictors are independent, representing complementary predictions that sum to explain the fine structure of pairwise correlations within a population (Fig. 2f).

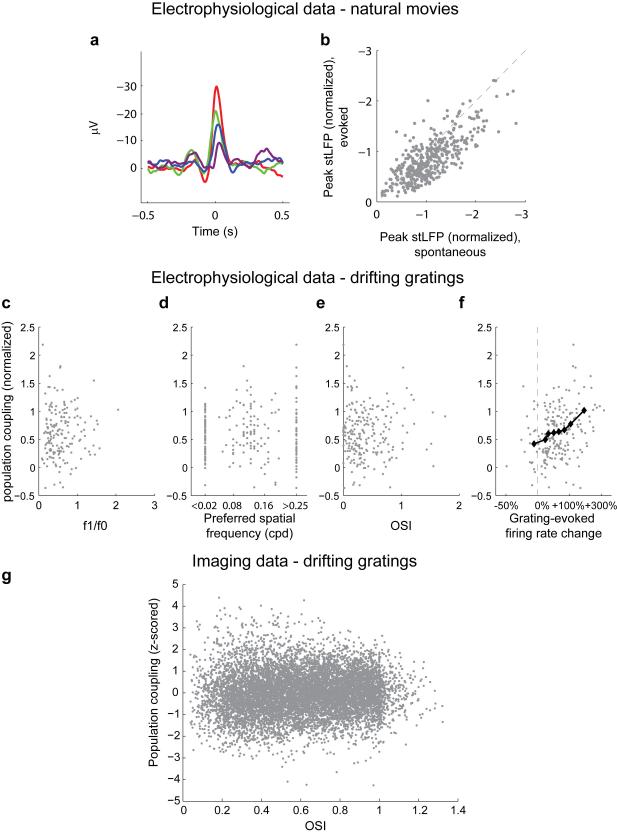
Population coupling was invariant to visual stimulation, and showed little relationship to basic visual properties. We measured population coupling across neurons during responses to natural movies, and found that it closely resembled that obtained during spontaneous activity (Fig. 3a-b, Extended Data Fig. 6a-b). Differences in coupling, therefore, reflect invariant properties of each neuron, rather than differences in the responses of each neuron to a specific set of stimuli. Both strongly and weakly coupled cells could respond to natural movies, showing reliable modulation by visual stimuli (Fig. 3c-d). In responses to gratings, moreover, population coupling showed no relationship to orientation selectivity, spatial frequency preference, or linearity of spatial summation (Extended Data Fig. 6c-e).

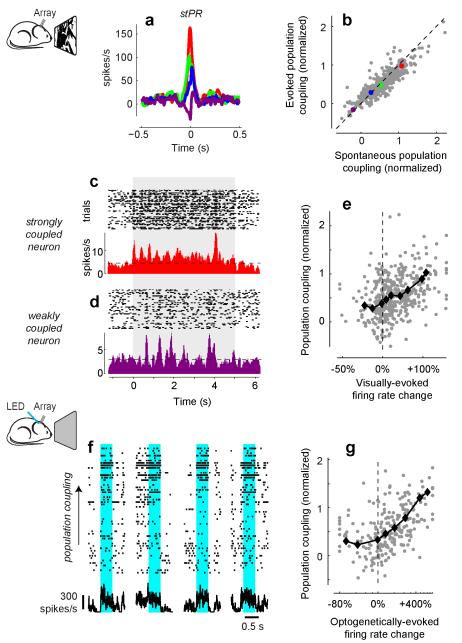
Figure 3. Population coupling under natural and optogenetic stimulation conditions.

a, Spike-triggered population rate (stPR) for the four example neurons in Fig. 1a-h during responses to a natural movie. The curves are similar to those measured during spontaneous activity (Fig. 1e). b, Comparison of population coupling during spontaneous and evoked activity, across cells and experiments (ρ=0.88, P<10⁻¹⁰⁰, rank correlation). c, Spike rasters (one row per presentation of a natural movie) and corresponding firing rate for a strongly coupled neuron (red neuron in a). Dashed line indicates baseline firing rate. d, Same, for a weakly coupled neuron (purple neuron in a). e, The increase in mean firing rate of a cell in response to natural movie presentations (relative to baseline) correlates with population coupling measured during spontaneous activity (ρ=0.38, P<10⁻¹⁵, rank correlation, n=431 neurons from 13 recordings in 8 animals). Black diamonds: running median. Points outside the x-axis range appear at the border for display purposes. f, Population rasters showing activity of deep-layer V1 neurons during four example trials (out of 75 in total), where the network was optogenetically driven by blue light in a mouse expressing Channelrhodopsin-2 sparsely in layer 5. Neurons are sorted by their population coupling during spontaneous activity. g, Change in mean firing rate evoked by optogenetic stimulation correlates with population coupling measured during spontaneous activity (ρ=0.51, P<10⁻¹⁰⁰, rank correlation, n=237 neurons). Points outside the x-axis range appear at the border for display purposes.

However, population coupling predicted the overall increase in mean firing rate caused by a visual stimulus. Strongly coupled cells exhibited a larger increase in mean firing rate during visual stimulation, both in responses to natural stimuli (Fig. 3c-e; ρ=0.38, P<10⁻¹⁵, n=431) and in responses to drifting gratings (ρ=0.32, P=2*10⁻⁶, n=217; Extended Data Fig. 6f). Thus population coupling – a quantity defined on a time scale of tens of milliseconds, and measurable during spontaneous activity – predicts the temporally extended, nonspecific elevation in firing rate seen during sensory stimulation.

These correlates of population coupling do not prove that the relationship between population rate and individual cells’ firing is causal. To test causality, we used transgenic mice that express Channelrhodopsin-2 in a subset of layer 5 pyramidal neurons²³. Light stimulation (0.5 s pulses at ~2 mW/mm² using a blue LED) strongly increased network activity (Fig. 3f). A control experiment (brief laser pulses at 100 mW/mm²) indicated that in most cells this increase was driven synaptically: only a few cells (~5%) reliably responded at short enough latencies (< 5 ms) to indicate direct optogenetic depolarization. While strongly coupled cells substantially increased their firing in response to blue LED stimulation, activity in weakly coupled cells showed little increase, or even decreased (Fig. 3g). Therefore, the diverse coupling of individual neurons to population rate reflects differences in the causal influence of the population on these cells.

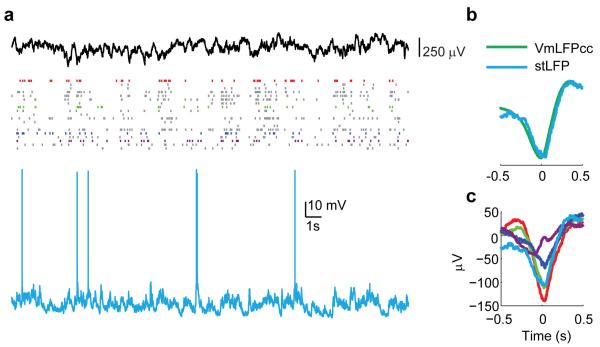
These observations suggest that more strongly coupled neurons might receive stronger synaptic input from neighbouring neurons. Consistent with this view, intracellular in vivo measurements indicated that population coupling measured from a neuron’s spike train resembles the coupling measured from the neuron’s subthreshold membrane potential, which mostly reflects synaptic inputs (Extended Data Fig. 7; see also Ref. ¹⁷).

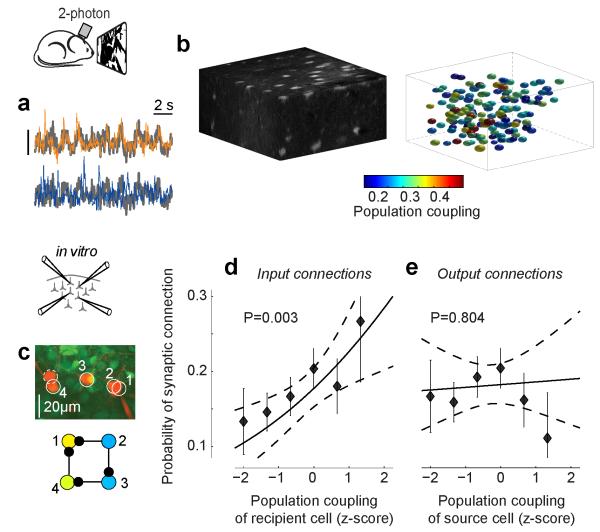
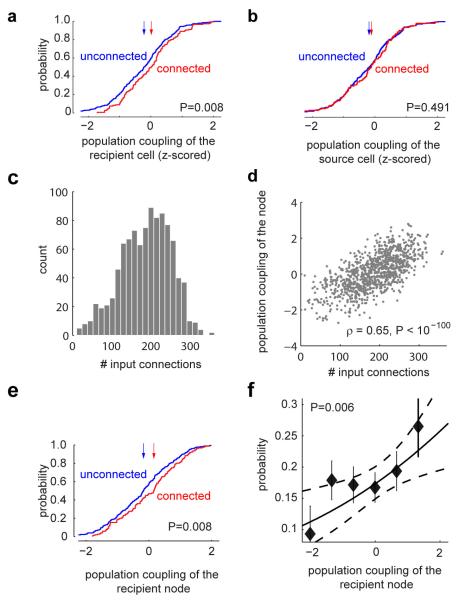
To investigate whether population coupling is related to synaptic connectivity, we studied cortical populations that were first imaged in vivo and then recorded in vitro^24,25. Population activity in superficial cortical layers was measured during presentation of natural movies and images in lightly anaesthetised mice. As in deeper layers, these cells showed a wide heterogeneity in population coupling (Fig. 4a-b). Coupling was not related to a cell’s spatial location (Fig. 4b, Extended Data Fig. 8a), and we observed no correlation between in vivo coupling and intrinsic properties such as resting potential, input resistance and spike threshold (Extended Data Fig. 8b-d). Population coupling was again consistent between the halves of each recording, even when these halves contained different sets of stimuli (ρ=0.85, P<10⁻⁹, n=4215 neurons from 15 experiments). Next, we analysed synaptic connectivity using paired in vitro whole-cell recordings of the same neurons (Fig. 4c). We focused on pyramidal cells, identified by somatodendritic morphology when filled with Alexa dye, and by a regular-spiking firing pattern.

Figure 4. Neurons with strong population coupling receive more synaptic inputs from their neighbours.

a, Neurons in superficial layers of mouse V1 were bulk-loaded with OGB-1 and their activity recorded using 2-photon imaging during presentation of natural movies and images. Population coupling was assessed as the correlation between each cell’s calcium signal with the summed signal of all other neurons. The two coloured traces show a segment of activity from a strongly and a weakly coupled neuron (orange and blue), each superimposed on the averaged population activity (gray). Scalebar: 20% ΔF/F for each single neuron, 5% for population average. b, Left, structural scan of an imaged volume measuring ~260×260×56 μm. Right, pseudocolour representation of population coupling for each of 147 neurons in the volume. c, Synaptic connectivity of a subset of the imaged neurons was later assessed using simultaneous in vitro whole-cell recordings. Top, four example pyramidal cells (solid white circles), recorded in vitro together with an additional fast-spiking interneuron (dashed circle) that was excluded from later analysis. Bottom, four synaptic connections were found between these 4 pyramidal neurons, shown here coloured by their in vivo population coupling. The two weakly coupled neurons (blue) received 0 or 1 inputs, while the strongly coupled neuron (yellow) received two inputs. d, Logistic regression estimate of probability to receive a synaptic connection as a function of the population coupling of the target (dashed black lines: 95% confidence intervals, error bars: mean and S.E. for binned data). e, As in d, for outgoing connections.

These paired recordings revealed a significant correlation between a neuron’s population coupling and its probability of receiving synaptic input from its neighbours (Fig. 4d). According to a logistic regression fit, a pyramidal cell whose population coupling was one standard deviation below the average had a probability of 0.14 to receive a connection from a neighbouring neuron, whereas for a pyramidal neuron whose coupling was a standard deviation above the mean this probability increased to 0.23 (i.e., a 65% increase). In contrast, there was no correlation between a neuron’s population coupling and the probability that it provided synaptic outputs to neighbouring cells (Fig. 4e). These results are consistent with a correlation between population coupling and input connection probability as high as ρ=0.65 (Extended Data Fig. 9).

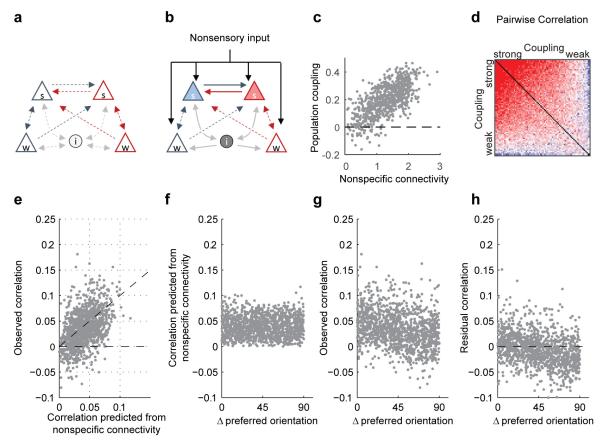
These data suggest that diversity in mean input connectivity may form the circuit mechanism for diversity in population coupling. The diversity in mean input connectivity that we have observed is separate from the tendency of cortical pyramidal cells to receive more synaptic connections from cells with similar sensory tuning^24,25. Thus, if the network is stimulated nonspecifically (for example by optogenetic activation of a random neuronal subset, Fig. 3f-g), the effects of this nonspecific stimulation – amplified by recurrent cortical connections – will be largest for neurons with strong mean input connectivity (Extended Data Fig. 10a-b). To make these intuitive ideas more precise, we extended an established modelling framework²⁶, and analysed mathematically a model cortical circuit in which different excitatory neurons have different mean input probability (see Supplementary Information). This model reproduced many of our experimental findings, including the relationship between population coupling and mean input connectivity (Extended Data Fig. 10c; Fig. 4d), the structure of spontaneous pairwise correlations (Extended Data Fig. 10d; Fig. 2b), and the additivity of correlations predicted by sensory tuning similarity and by population coupling strength (Extended Data Fig. 10e-h; Fig. 2e-f).

If neurons with stronger population coupling are more likely to be driven by nonspecific excitation, they may show greater modulation by non-sensory factors, which are believed to be conveyed to sensory cortex by diffuse, nonspecific inputs^15,19. To test this hypothesis, we analysed population recordings made from area V4 of monkeys performing a cued-saccade task²⁷. Consistent with the hypothesis, strongly coupled neurons increased their firing rate during saccade preparation into their receptive field (Fig. 5a). Weakly coupled neurons, instead, often showed the opposite effect (Fig. 5b). Overall, there was a marked correlation between a neuron’s population coupling, and its modulation by saccade preparation (ρ=0.37, P=10⁻⁹, Fig. 5c).

Figure 5. Population coupling under top-down stimulation conditions.

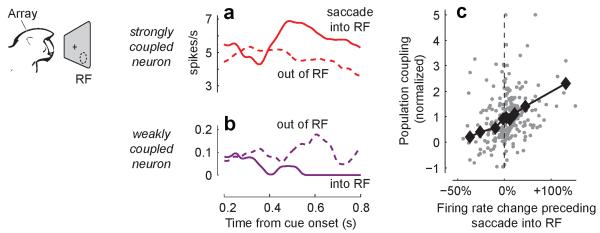
a, Mean firing rate of an example neuron in primate V4 with strong population coupling (red neuron in Fig. 1h). This neuron showed higher firing rate (solid curve) while saccades were prepared into its receptive field (RF) than outside of it (dashed curve). b, An example neuron with weak population coupling (purple neuron in Fig. 1h) showed suppressed firing during saccade preparation into its RF. c, The change in firing rate of V4 neurons during saccade preparation into their RF (relative to saccade out of their RF) correlates with population coupling (ρ=0.37, P=10⁻⁹, rank correlation, n=262 neurons). Black diamonds: running median.

In conclusion, population coupling constitutes a previously unappreciated dimension characterising the relationship of individual neurons to population activity. Strongly coupled neurons (“choristers”) are more strongly activated during multiple conditions that nonspecifically increase the activity of their local network: not only sensory stimuli, but also spontaneous fluctuations and top-down modulation. Conversely, weakly coupled neurons (“soloists”) are more immune to these population-wide events. Population coupling differs both across and within cell classes; it remains to be determined whether this within-class diversity reflects further subdivisions of these classes (such as pyramidal cells with different long-range axonal targets^28,29), or continuous within-class variation in cellular parameters such as input connection probability. Moreover, a neuron’s population coupling need not be fixed for life: indeed, neurons that rats learn to use while controlling a brain-machine interface show increased correlation with LFP³⁰, indicating increased population coupling, and thus suggesting an increase in mean synaptic input strength. This single, simple variable relating each neuron’s participation in the population code to underlying circuit connectivity may prove critical to understanding cortical computation and plasticity.

Methods

Electrophysiological recordings

Recordings in mouse primary visual cortex were performed under licenses from the UK Home Office in accordance with the Animal (Scientific Procedures) Act 1986. In the electrophysiological experiments, recordings were made from male and female mice older than 6-7 weeks, of C57BL/6J or Thy1-ChR2 line 18 strains²³. Randomization was not required as all animals were treated similarly.

For recordings from awake mice, animals were first implanted with a custom-built head plate and recording chamber under isoflurane anaesthesia. After 3 days of recovery accompanied by Rimadyl treatment, the mice underwent 2-3 head-restraint acclimatization sessions. On the recording day, the animals were briefly anaesthetised with isoflurane and a craniectomy of ~1.5 × 1.5 mm was made above the left primary visual cortex. The dura was resected with a 30G needle and the brain was covered with Ringer solution and Kwik-Cast (WPI Inc.). At least 1.5 hours of recovery between this procedure and the beginning of the recording were allowed, a period that was more than sufficient for the animals to fully resume their normal behaviour in their home cage. In some animals, an additional recording was performed the following day; in this case the brain was again protected with Ringer solution and Kwik-Cast in between the two recording sessions. Thirteen recordings were made in 8 animals, of which 5 recordings were in 3 Thy1-ChR2 line18 mice, and the rest in C57BL/6J mice. Recordings were made with Buzsaki32 or A4x8 silicon probes (NeuroNexus technologies, Ann Arbor MI), lowered to a depth of 550-1050 μm (median 700 μm) by a PatchStar manipulator (Scientifica, Uckfield UK). Signals were amplified and stored for offline analysis using the Cerebus data acquisition system (Blackrock Microsystems, Salt Lake City UT). For electrophysiological recordings in anaesthetised animals (Fig. 2 and Extended Data Fig. 7), anaesthesia was induced with a mixture of Fentanyl citrate, Fluanisone and Midazolam (0.8 mg/kg, 25 mg/kg and 12.5 mg/kg, respectively). A total of 9 recordings from anaesthetised animals were analysed. In a few of these experiments, whole-cell recordings were performed in parallel with the silicon probe population recording. The whole-cell intracellular recordings were performed following the standard techniques for blind patching^17,31,32, with the patch pipette positioned ~200-400 μm away from the plane of the silicon probe shanks.

For the electrophysiological data, the experimental setup was similar to the one described in refs. ³³ except that mice were standing in a custom built tube, instead of on a floating Styrofoam ball. Briefly, visual stimuli were presented on two of the three available LCD monitors, positioned ~25cm from the animal and covering a field of view of ~120° × 60°, extending in front and to the right of the animal. Visual stimuli analysed in the present study consist of multiple presentations of natural movie video clips (taken from The Life of Mammals, BBC, London UK) and drifting gratings (100% and 25% contrast, 2 Hz, 12 directions, spatial frequencies of 0.02, 0.04 0.08 and 0.25 cpd). For recordings of spontaneous activity, the monitors showed a uniform grey background.

Recordings in auditory cortex (Extended Data Fig. 3) were made in awake, head-fixed male rats, in accordance with protocols approved by the Rutgers University Animal Care and Use Committee. Experimental details were previously described in refs. ^3,18,34. In the recordings analysed here, silicon probes with 4 shanks, and 4 contacts in a tetrode configuration on each shank were used (NeuroNexus technologies, Ann Arbor MI).

Recordings in primate area V4 were made in two male monkeys (Macaca mulatta) using 16-channel U-Probes (Plexon Inc, Dallas TX), in accordance with NIH Guide for the Care and Use of Laboratory Animals, the Society for Neuroscience Guidelines and Policies, and Stanford University Animal Care and Use Committee; full experimental details were previously described in ref. ²⁷. Briefly, as part of the behavioural task, a cue presented near the central fixation point indicated the direction of a saccade that would be necessary at the end of the trial to obtain a reward in the event of a change in the orientation of a peripheral stimulus.

Optogenetic stimulation

For in vivo electrophysiological recordings with optogenetic stimulation, we used Thy1-ChR2 line 18 mice, a transgenic line in which ChR2 is expressed in a sparse subset of cortical L5 pyramidal cells²³. In these mice, in addition to recording spontaneous and visually evoked activity, we also recorded activity in response to optogenetic stimulation consisting of 500 ms light pulses of ~2 mW/mm² intensity, delivered by a 470 nm (blue) LED (M470F1, Thor Labs, Newton NJ), and focused on a circular area of ~1 mm² centred on the silicon probe insertion site.

To estimate the proportion of recorded neurons directly activated by ChR2, we performed a control experiment, in which 20 and 40 Hz trains of five 2 ms pulses of ~100 mW/mm² intensity were delivered to the silicon probe insertion site using a MBL-III-473nm-150mW blue light laser (CNI, Chungchun China). Reliable, short latency (< 5 ms) and low jitter (< 1 ms) responses were found in ~5% of the units, indicating that ~95% of cells were driven polysynaptically rather than directly.

Data analysis (electrophysiology)

Spikes were detected and visually verified using the programs NDmanager and Neuroscope³⁵. Spike sorting involved an automated stage, performed using KlustaKwik³⁶, and a manual verification stage for which Klusters³⁵ or KlustaViewa³⁷ were used. Detailed analysis of coupling to population rate and LFP was performed only for units with isolation distance > 20 (see refs. ^38,39). Units were selected and sorted blind to measures of population coupling and all other cellular parameters.

Population rate (e.g. in Fig. 1c) was computed by accumulating all the detected spikes (both well-isolated units and multi-unit activity) with 1 ms resolution, and smoothing the resulting vector with a Gaussian of half-width 12 ms. The population rate used to compute the stPR for any individual unit did not include the spikes of that unit. The baseline level of each stPR (which reflects the mean population rate) was subtracted.

For stLFP computations, raw extracellular signals were first digitally band-pass filtered offline between 0.1 and 200 Hz to isolate the local field potential. For units recorded on a particular shank, the LFP was taken from an adjacent shank (200 μm away), to avoid contaminating the stLFP by the spike waveform itself. The size of stLFP was taken as the ordinate value of the negative peak of the crosscorrelation in a 1 s interval around 0 lag. stLFPs were normalized similarly to stPRs (see below).

The size of the stPR was quantified as the value of the spike-triggered population rate at 0 time lag. Thus, the population coupling of unit i is given by:

$$c_i=\frac{1}{\mid \mid f_i\mid \mid }\int f_i\left(t\right)\sum _{j\ne i}\left(f_j\right(t)-{\mu }_j)dt$$

Here, f represents the smoothed firing rate of a neuron (Gaussian kernel of half width $12∕\surd 2$ ms), μ is its mean firing rate, and ||f|| represents its norm (i.e., the number of spikes fired). To compare the sizes of stPRs across recordings, they were normalized by the median size of the stPR of the shuffled data in each recording (see next paragraph).

Spike shuffling was performed according to the previously described raster marginals model¹⁴. In more detail, the recording was first divided into non-overlapping 1 ms bins. A binary matrix was then constructed with one column for each time bin and one row for each isolated unit as well as additional rows for the multiunit spiking on each shank. Each matrix element contained a 1 if the corresponding unit spiked in the corresponding time bin. To shuffle, random 2-by-2 submatrices were repeatedly chosen with each row and column of the submatrix containing a 0 and 1; the positions of 0s and 1s were then exchanged in the submatrix, which leaves the summed values of each row and column identical. As we have discussed previously¹⁴, such a shuffling procedure produces in the limit a uniform sample from a distribution subject to the constraints on the mean firing rate and population rate distribution of the original data.

To characterise the responses of individual cells to drifting grating stimuli, the response for each orientation was averaged across trials, contrasts and spatial frequencies, and the orientation with the highest value was taken as preferred. The spatial frequency which evoked the highest response along the preferred orientation was taken as the preferred spatial frequency. The orientation selectivity index (OSI) was computed as (R_pref−R_ortho)/(R_pref+R_ortho), where R_pref and R_ortho are the responses in the preferred and orthogonal orientations. f1/f0 was taken as the ratio between the power of the average response around 2 Hz (which was the temporal frequency of the drifting grating stimuli) and the mean increase in the firing rate above the spontaneous level.

In primate area V4, we measured the firing rate changes during saccade preparation for isolated single neurons. Spikes were counted during the interval between 0.5s after cue onset and the end of the post-cue period (i.e., start of the blank period), and were converted to firing rates for each trial based on the duration of that period. We compared firing rates from trials for which the cue indicated a saccade into the RF would be required and trials for which the cue indicated a saccade to an orthogonal location outside the RF would be required. Only spikes from correctly performed trials were considered for this analysis. Peak stPR size was measured identically to rodent electrophysiological recordings, and was computed from the continuous recording of the entire experimental session.

2-photon imaging

All procedures were performed under licenses from the UK Home Office in accordance with the Animals (Scientific Procedures) Act 1986. In the imaging experiments C57BL/6J mice of P22-26 age and both sexes were used. Anesthesia was induced with Fentanyl, Midazolam and Medetomidine (0.05 mg/kg, 5.0 mg/kg and 0.5 mg/kg, correspondingly) and later maintained by isoflurane (0.3–0.5%) in a 60:40% mixture of oxygen and nitrous oxide. The experimental setup for 2-photon imaging was described in refs. ^24,25. Briefly, visual stimuli were presented on an LCD monitor ~20 cm from the animal, covering a field of view of ~105° × 85°. The calcium-sensitive dye Oregon Green Bapta-1 (OGB-1) was bulk loaded into the superficial layers of the cortex together with sulphorhodamine 101 to distinguish glia from neurons.

We used two datasets in the analysis, recorded from 18 and 15 animals, respectively. In the first dataset (previously described in ref. ²⁴), visual stimuli included full-field and localised drifting gratings and natural movies. The gratings were shown at 100% contrast, 2 Hz temporal frequency, spatial frequency of 0.035 cpd, and 8 directions. Cortical areas of ~285 × 285 μm were imaged at 7.6 Hz and 256 × 256 pixel resolution, and the imaging was performed for ~8-16 different depths, 7 μm apart.

In the second dataset (not previously reported), static natural images and natural movies (either video clips from The Life of Mammals or cage scenes from a head-mounted mouse camera) were presented. A volume of ~200 × 200 × 50 μm was imaged simultaneously at 512 × 512 × 4 pixel resolution using a piezoelectric objective mover. In each experiment 2-3 such volumes were imaged.

After in vivo imaging, whole-cell in vitro recordings of the imaged neurons were performed as previously described²⁴. Briefly, at the end of the in vivo imaging session the brain was removed, 300 μm thick coronal slices were cut and the slice containing the in vivo imaged region was located by the presence of OGB-1. A simultaneous recording from several nearby neurons was performed using a standard whole-cell in vitro protocol. Synaptic connections between neurons were tested using 30 Hz trains of five suprathreshold 5 ms current pulses, and checking for postsynaptic responses in the other cells. The current injection train was repeated at least 30 times with 15 s interval. Pyramidal cells and interneurons were distinguished by spike width, resting membrane potential, responses to 1 s depolarizing currents, and somatodendritic morphology when filled with Alexa dye. For the analysis of the relationship between coupling strength and probability to receive (provide) a synaptic connection (Fig. 4), we excluded pairs where the potential target (source) cell was an interneuron or a neuron for which no in vivo calcium trace was available. Simultaneously patched neurons could have been imaged non-simultaneously, which happened when the cells resided in different imaging planes or volumes. In total, 379 neurons were recorded; of 854 potential input connections tested, 146 synaptic connections were found. Of 854 potential output connections tested, 155 synaptic connections were found. (The number of potential input and output connections were equal by coincidence: some of the input connections were not analysed as output connections because one of the cells was either an interneuron or had no in vivo data, and vice versa.)

Data analysis (imaging)

Outlines of recorded neurons were detected semi-automatically using custom software written in MATLAB (Mathworks, Natick MA). All pixels within individual outline were averaged to give for each neuron a single ΔF/F signal, which was additionally high-pass filtered above 0.02 Hz to correct for slow artefacts such as photobleaching.

The population coupling of each cell was estimated by a similar formula to that used in spike train data:

$$c_i=\frac{1}{\mid \mid f_i\mid \mid }\int f_i\left(t\right)\sum _{j\ne i}\left(f_j\right(t)-{\mu }_j)dt,$$

where now f represents the continuous fluorescence trace of a cell (ΔF/F), and ||f|| its standard deviation. Note that c_i is proportional to the Pearson correlation of cell i with the summed activity of all other neurons. To pool data across multiple experiments, the normalization factor was computed not by spike shuffling (which is not possible for calcium traces) but by z-scoring the population coupling values within each recording.

For grating responses, the orientation selectivity index (OSI; Extended Data Fig. 6g) was estimated as (R_best−R_ortho)/(R_best+R_ortho), where R_best and R_ortho are the interpolated responses to drifting gratings in the best direction and the directions orthogonal to it.

Statistics

Unless explicitly stated otherwise, comparisons between pairs of sets of values were made using Wilcoxon rank sum test and correlations were measured using Spearman’s rank correlation coefficients (an important exception being the pairwise spike train correlations, for which, as commonly accepted, we used Pearson correlation).

Pairwise correlation prediction

To predict pairwise correlations from coupling values, we used an extension of the raster marginals model¹⁴ that now also included a population coupling parameter for each neuron. The spike trains of all neurons are first converted into a binary 0-1 matrix with 20 ms bins. The parameters extracted correspond to: (i), the total number of 1s in row i, for all i between 1 and the number of rows N; (ii), the total number of columns whose sum is i, for all i between 0 and N; and (iii) the inner product of each row with the sum of all rows (representing the stPR for the unit corresponding to the row).

Pairwise correlations were predicted by constructing a random matrix that respects the constraints represented by the above parameters, and computing the correlations between all pairs of rows in this random matrix. To construct such a random matrix we first construct a random matrix that respects constraints (i) and (ii), as described in ref. ¹⁴, and then perform a sequential operation to impose satisfaction of constraint (iii). This sequential operation consists of repeatedly exchanging 2×2 submatrices between rows whose population coupling is too high and too low. Specifically, observe that if there exists a row n_i for which < n_i, Σ_j n_j > (the inner product with the sum of all rows) is too high, then there must also exist another row for which this inner product is too low; this is because Σ_i < n_i, Σ_j n_j > = < Σ_i n_i , Σ_j n_j >, which depends only on the population rate distribution and is thus invariant to submatrix exchange.

The satisfaction of constraint (iii) occurs by repeatedly finding a pair of rows that violate the constraint in opposite directions, while such pairs exist. For each such pair of rows, we find a pair of columns that forms a 2-by-2 sub-matrix such that each row and column of it contains a 0 and 1, and switch the 0s and 1s in a way that preserves constraints (i) and (ii) and reduces the violation of constraint (iii) in this pair of rows. This procedure is repeated until (iii) is satisfied (up to a small error of at most N).

To measure how well this method could predict pairwise correlations, we used crossvalidation. Time bins were divided at random into an equally-sized training and test set. Model parameters were fit from the training set, and the prediction error of the model was quantified as $S{S}_{modelErr}={\Sigma }_{i<j}{(c_{ij}-{\widehat{c}}_{ij})}^2$, where c_ij is the correlation between neurons i and j measured in the test set, and ${\widehat{c}}_{ij}$ the correlation predicted by the model with parameters estimated on the training set. This error was compared to a “ground truth” prediction, $S{S}_{dataErr}={\Sigma }_{i<j}{(c_{ij}-c_{ij}^{\prime })}^2$, where $c_{ij}^{\prime }$ is the correlation between neurons i and j as directly measured in the training set. The quality of the model fit was defined to be the fraction of explainable variance: [SS_tot − SS_modelErr]+/[SS_tot−SS_dataErr], where $S{S}_{tot}={\Sigma }_{i<j}{(c_{ij}-\stackrel{‒}{c})}^2$ and $\stackrel{‒}{c}$ is the mean pairwise correlation.

Latent variable analysis of the population recordings was performed using the publically available toolbox of Lars Buesing and Jacob Macke (bitbucket.org/mackelab/pop_spike_dyn; see also ref. ²¹). The toolbox uses a nuclear norm minimization method4 to fit a low dimensional model of the form s_t~Poission (e^y_t), where y_t = Cx_t + d. The latent variables x_t were modelled using a multivariate Gaussian distribution. The performance of this model was assessed by its ability to predict pairwise correlations, quantified with cross-validation measure described above. To generate correlations we fitted the parameters of the model and then used these parameters to sample spike count vectors.

Extended Data

Extended Data Figure 1. Pearson correlation between spike trains of individual units and the population rate.

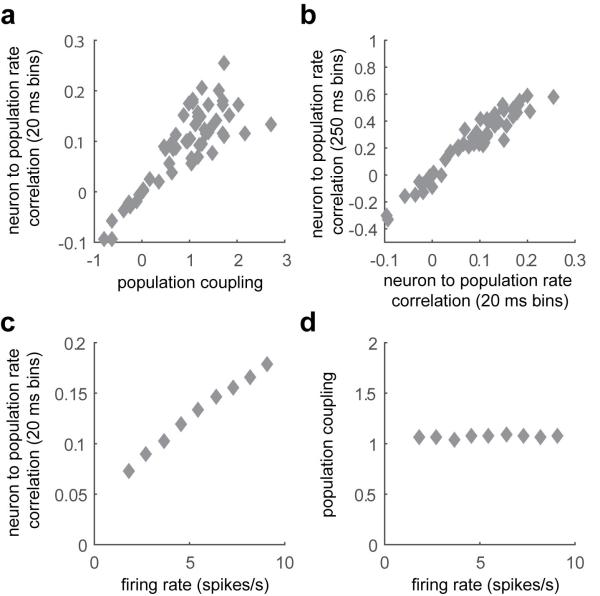
To estimate the relation of a neuron to the population, an alternative to stPR would have been to compute the Pearson correlation coefficient of the the neuron’s spike train with the summed population rate of all other recorded cells (a measure we term “Pearson coupling”). This measure, however, is biased by firing rate. a, Pearson coupling and stPR were computed for a set of individual units in an example experiment. Pearson coupling is related to the stPR, but not identical to it. b, The numerical value of the Pearson coupling depends strongly on the bin size used, but the correlations measured with different bin size are tightly related. c, Pearson correlation is biased by firing rate^40,41. The spike train of a single cell was “thinned” to different firing rates by keeping only a random subset of its spikes; Pearson correlation with the population was recalculated for different values of firing rate. A strong effect of firing rate is seen. d, Performing the same analysis for population coupling (measured by stPR) demonstrates that this measure does not suffer from rate bias. For this reason, we chose to quantify population coupling with stPR in this work.

Extended Data Figure 2. Neighbouring neurons differ markedly in population coupling during spontaneous activity.

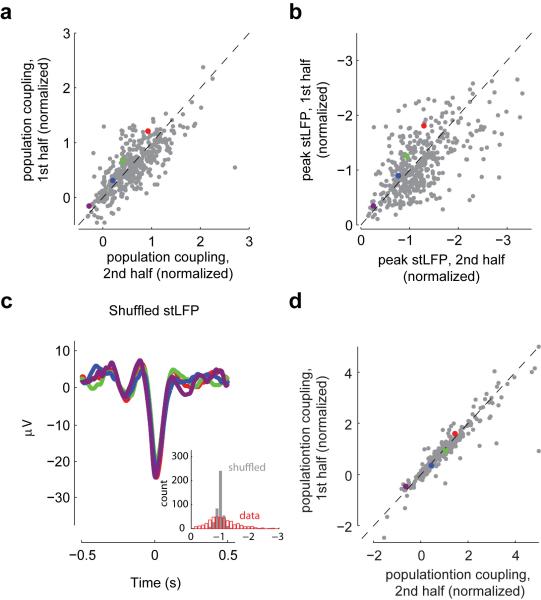
a, Dividing the data into two halves shows that population coupling, measured as the height of stPR at 0 time lag, is highly consistent over time (n=431 neurons from 13 experiments; ρ=0.76, P<10⁻¹⁰⁰, rank correlation). Coloured dots represent the four example cells. b, As in a for peak stLFP (ρ=0.58, P<10⁻⁹). c, Differences in stLFP disappear after shuffling spikes in a manner that preserves each neuron’s mean firing rate and the population rate (cf. Fig. 1g). Inset: stLFPs in the actual spike trains (red) and after shuffling (gray), for neurons from all experiments (cf. Fig. 1g). d, stPR size of V4 neurons is consistent over time (n=262 neurons from 43 experiments; ρ=0.95, P<10⁻¹⁰⁰, rank correlation).

Extended Data Figure 3. Neighbouring neurons in auditory cortex differ markedly in population coupling.

a, Spike-triggered population rate (stPR) for four example neurons recorded on the same electrode shank, during spontaneous activity in rat primary auditory cortex. b, Differences in population coupling disappear after shuffling spikes in a manner that preserves each neuron’s mean firing rate and the population rate distribution. c,d As in (a,b) for the spike-triggered local field potential (stLFP). e, Dividing the data into two halves shows that population coupling, measured as the height of stPR at 0 time lag, is highly consistent over time (n=76 neurons from 3 experiments; ρ=0.92, P<10⁻¹⁰⁰, rank correlation). Colored dots represent the four example cells. f, As in e, for stLFP (ρ=0.81, P<10⁻¹⁰⁰, rank correlation).

Extended Data Figure 4. Firing rate, burstiness and population coupling.

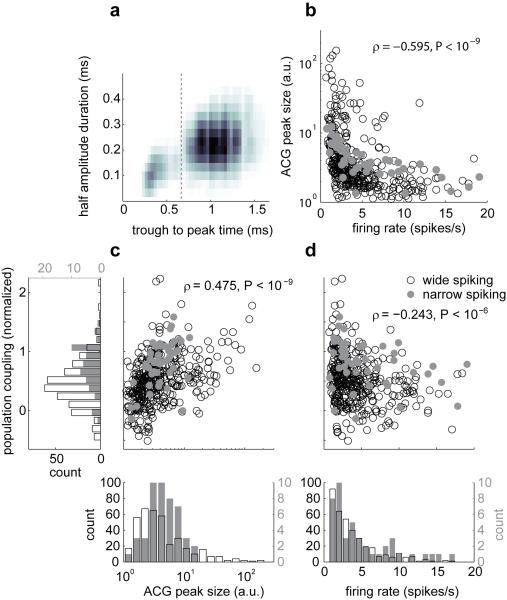
a, Similarly to other studies^20,42 our recordings allow separation of narrow spiking (putative Pvalb+ inhibitory) and wide spiking (primarily excitatory pyramidal) neurons. Here, we used a trough to peak time of 0.66 ms as the separation criterion. b, There is a negative correlation between burstiness (the ratio between the peak and baseline of a neuron’s autocorrelogram) and mean firing rate, which is also the case individually for wide spiking (n=384, ρ=−0.60, P<10⁻⁹, rank correlation) and narrow spiking (n=47, ρ=−0.82, P<10⁻⁹, rank correlation) neurons. c, There is a positive correlation between burstiness and population coupling, which is also the case individually for wide spiking (ρ=0.46, P<10⁻⁹, rank correlation) and narrow spiking (ρ=0.50, P=4·10⁻⁴, rank correlation) neurons. d, There is a negative correlation between firing rate and population coupling, which is also the case individually for wide spiking (ρ=−0.27, P=10⁻⁷, rank correlation) and narrow spiking (ρ=−0.37, P=0.01, rank correlation) neurons. The correlation between population coupling and firing rate can be predicted from the correlations between burstiness and firing rate and between population coupling and burstiness: the partial rank sum correlation between population coupling and firing rate, once burstiness is taken into account, is insignificant (ρ=0.06, P=0.25). This is also the case for wide spiking (ρ=0.01, P=0.78) and narrow spiking (ρ=0.07, P=0.65) neurons individually.

Extended Data Figure 5. Latent variable analysis.

a, Population coupling of each neuron is highly correlated with its loading in a single-factor latent variable model (see Methods). The similarity of each cell’s population coupling and loading indicates that the low-dimensional structure found by the latent variable model is homologous to that found by the coupling model. b, Percent of pairwise correlation structure explained by a latent variable model with 1-5 factors (black), and by the coupling model introduced in the present study (dashed purple line). Error bars show S. E. While the coupling model outperforms latent variable models with less than four degrees of freedom, this difference may arise primarily from the assumption of a Gaussian distribution for the latent variables. Indeed, if the population rate distribution generated by the latent variable model is substituted into the coupling model instead of the (correct) populate rate distribution, extremely poor performance results (dashed grey line; almost on top of the x-axis).

Extended Data Figure 6. Population coupling and visual stimulation in mouse V1.

a, stLFPs computed for the four example neurons of Fig. 1a-f, from intervals of natural movie presentation (inverted for ease of comparison, cf. Fig. 1f). b, Comparison of stLFP size during spontaneous and evoked activity across all experiments (ρ=0.72, P<10⁻¹⁰⁰, rank correlation). c-e, Population coupling is plotted vs. the f1/f0 ratio, preferred spatial frequency and orientation selectivity index (OSI) for neurons recorded in the infragranular layers of V1. All correlations are statistically insignificant. f, Similar to movie presentations (cf. Fig. 3e), the mean change in the activity of a cell in response to grating presentations (relative to baseline, averaged across contrasts and orientations) correlates with population coupling measured during spontaneous activity (ρ=0.32, P=2*10⁻⁶, n=217, rank correlation). Black diamonds: running median. g, In the 2-photon imaging data (of ~10,000 cells) only a very weak correlation between OSI and population coupling was found (ρ=0.066, P<10⁻⁹, rank correlation).

Extended Data Figure 7. stLFP reflects the correlation between membrane potential (Vm) and LFP.

a, Example of a silicon probe population recording performed simultaneously with a whole-cell recording (in an anaesthetised animal). Four neurons shown in colour were recorded on the same shank of the silicon probe. b, Comparison of stLFP and Vm-LFP crosscorrelation (VmLFPcc, appropriately scaled along the ordinate axis) for the intracellularly recorded cell. c, stLFP for the four neurons from a and the intracellularly recorded neuron, exhibiting diversity in the strength of coupling to LFP.

Extended Data Figure 8. Population coupling in 2-photon data is not correlated with location and intrinsic properties of the neurons.

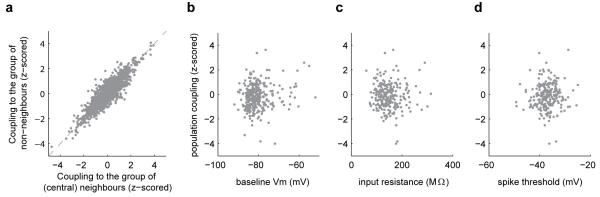
a, For each neuron in the central region of the imaging field (defined as a square 1/4 of the total imaging area), we compared its coupling to the population of all other neurons in the central region, with its coupling to population of all neurons outside of the central region. The two were highly similar; this was the case because the two population rate signals were themselves highly correlated (on average across experiments the Pearson correlation was 0.77). Thus, differences in population coupling measured between cells do not reflect differences in the fraction of nearby neurons imaged. b-d, No significant correlation was observed between population coupling (measured in vivo) and resting potential, input resistance and spike threshold (subsequently measured in vitro).

Extended Data Figure 9. Correlation between input connectivity and population coupling.

a, Cumulative distribution of population coupling of a target pyramidal neuron when an input connection was present (red) and when it was absent (blue). The medians (arrows) are significantly different. b, As in a, for population coupling of the source pyramidal cells. (The distributions shown were used for the logistic regression analysis in Fig. 4). c-f, We constructed random directed graphs of 1000 nodes (each node representing a L2/3 pyramidal cell) with the probability of connection from node j to node i given by $\sqrt{p_{in}^i{p}_{out}^j}$, where the propensities to receive and provide connections (p_in and p_out, correspondingly) were randomly and independently chosen for each node from a Gaussian distribution. The resulting distribution of the number of input connections in a typical network is shown in c; the number of output connections was (by construction) similarly distributed. In addition, each node was assigned a population coupling value, highly correlated to the number of its input connections (on average ρ=0.65); this correlation in a typical network is shown in d. We next asked how the relationship between measured connectivity and population coupling would look if we sample from 33 such randomly generated networks (equal to the number of animals used in our experimental data), the same amount of data empirically available in our in vitro recordings (i.e., the connections between 2-3 randomly selected groups of 2-6 nodes). Results very similar to those of Fig. 4 were typically obtained (e,f; cf. a and Fig. 4d; error bars in f indicate standard error for binned data). In particular, when the entire procedure was repeated 1000 times, in over 30% of the cases the P-value of the difference between the medians (presented in a,e) was higher (i.e., less statistically significant) than the value of 0.008 obtained in the actual data. Thus, the results shown in Fig. 4 and in a are consistent with a strong correlation between connection probability and population coupling.

Extended Data Figure 10. Mathematical model for the relationship between nonspecific connectivity, specific connectivity, and correlations.

a, A recurrent network where excitatory cells (triangles) send synaptic connections (arrows) to each other and to inhibitory cells (circles). Weakly coupled neurons (bottom) receive only connections from neurons with similar sensory preference (e.g. for stimulus orientation, indicated in blue vs. red). Strongly coupled neurons (top) also receive nonspecific connections from neurons of different sensory preference. b, The effect of nonspecific drive, such as caused by non-sensory top-down inputs, or occurring due to artificial optogenetic stimulation, is amplified through recurrent connections, leading to stronger activation of neurons with greater mean local input (darker shading). c,d correlations predicted by the model (analytically derived in Supplementary Information): c - population coupling vs. nonspecific connectivity c_i, for all simulated excitatory neurons. d - pseudocolor plot of predicted pairwise correlations for a random subset of excitatory neurons, ordered by population coupling. e-h, dependence of correlations on specific and nonspecific connectivity. e - predicted correlations based on nonspecific connections vs total observed correlations. f - predicted correlation based on nonspecific connectivity vs. difference in preferred orientation. As in the experimental data (Fig. 2e), no relation is observed. g - observed correlation vs difference in preferred orientation. As has been widely reported, observed correlations are largest for neurons of similar orientation preference. h - residual correlation (after removing prediction from nonspecific connectivity) vs difference in preferred orientation. Again as in our experimental data (Fig. 2f), the residual correlation is largest for neurons of similar orientation preference, indicating an additive relationship between correlations generated by specific connections and correlations generated by nonspecific connections.