SPECTRAL CLUSTERING STRATEGIES FOR HETEROGENEOUS DISEASE EXPRESSION DATA

Abstract

Clustering of gene expression data simplifies subsequent data analyses and forms the basis of numerous approaches for biomarker identification, prediction of clinical outcome, and personalized therapeutic strategies. The most popular clustering methods such as K-means and hierarchical clustering are intuitive and easy to use, but they require arbitrary choices on their various parameters (number of clusters for K-means, and a threshold to cut the tree for hierarchical clustering). Human disease gene expression data are in general more difficult to cluster efficiently due to background (genotype) heterogeneity, disease stage and progression differences and disease subtyping; all of which cause gene expression datasets to be more heterogeneous. Spectral clustering has been recently introduced in many fields as a promising alternative to standard clustering methods. The idea is that pairwise comparisons can help reveal global features through the eigen techniques. In this paper, we developed a new recursive K-means spectral clustering method (ReKS) for disease gene expression data. We benchmarked ReKS on three large-scale cancer datasets and we compared it to different clustering methods with respect to execution time, background models and external biological knowledge. We found ReKS to be superior to the hierarchical methods and equally good to K-means, but much faster than them and without the requirement for a priori knowledge of K. Overall, ReKS offers an attractive alternative for efficient clustering of human disease data.

1. Introduction

The explosion of gene expression and other data collection from thousands of patients of several diseases has created novel questions about their meaningful organization and analysis. The Cancer Genome Atlas (TCGA)¹ initiative for example provides large heterogeneous datasets from patients with different types of cancers including breast, ovarian and glioblastoma. However, unlike data from model organisms and cell lines that have uniform genetic background, and where experiments are conducted under controlled conditions, disease samples are typically much more heterogeneous. Differences in the genetic background of the subjects, disease stage, progression, and severity as well as the presence of disease subtypes contribute to the overall heterogeneity. Discovering genes or features that are most relevant to the disease in question and identifying disease subtypes from such heterogeneous data remains an open problem.

Clustering, the unsupervised grouping of data vectors into classes with similar properties is a powerful technique that can help solve this problem by reducing the number of features one has to analyze and by extracting important information directly from data when prior knowledge is not available. As such, it has formed the basis of many feature selection and classification methods^2,3. Hierarchical and data partitioning algorithms (like K-means) have been used widely in many domains⁴ including biology^5,6. They have become very popular due to their intuitiveness, ease of use, and availability of software. Their biggest drawbacks come from the usually arbitrary selection of parameters, such as the optimal number of clusters (for K-means) or an appropriate threshold for cutting the tree (for hierarchical clustering).

When applied to datasets from model organisms and cell lines, these clustering approaches have been quite successful in identifying biologically informative sets of genes^5,6. However, the heterogeneity of the disease samples hinders their efficiency in them. Figure 1 shows an example of such a dataset; a dendrogram produced from the breast cancer TCGA data, in comparison to dendrogram generated from the less heterogeneous yeast expression data. It is obvious that the structure of the data makes it difficult to find a threshold to prune the tree to produce a satisfactory number of clusters, since every newly formed cluster is joined with a singleton node each time. Thus, despite its popularity, classical hierarchical clustering frequently performs poorly in discovering a satisfactory group structure within gene expression data. Tight clustering⁷ and fuzzy clustering⁸ attempt to build more biologically informative clusters either by focusing only on closely related genes while ignoring the rest, or by allowing overlap in cluster memberships. However, both methods suffer from long execution times. Similarly, Affinity Progation⁹ has been applied on gene clustering successfully but at a significant cost in execution time.

Fig. 1.

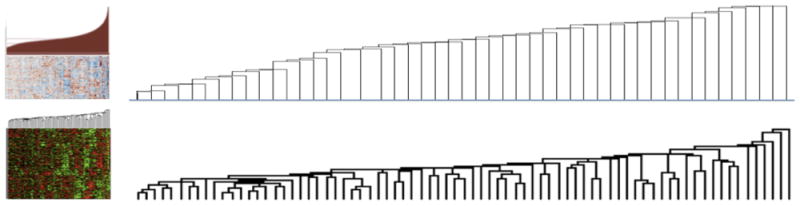
Clustering patient data is more difficult than cell-based data. Partial views of dendrograms constructed from hierarchical clustering of the TCGA Breast Cancer expression data (top) and the yeast expression data (from Spellman et al.¹¹). The dendograms suggest that it is easier to select a threshold to prune the tree and generate potentially meaningful clusters for the yeast data but not so for the breast cancer data.

More recently, spectral clustering approaches have been used for data classification, regression and dimensionality reduction in a wide variety of domains, and has also been applied to gene expression data¹⁰. The spectral clustering formulation requires building a network of genes, encoding their pairwise interactions as edge weights, and analyzing the eigenvectors and eigenvalues of a matrix derived from such a network. To our knowledge, no systematic attempt has been made to-date to test and compare the performance of existing clustering methods in large-scale disease gene expression data, perhaps due to unavailability of suitable size datasets. In this paper, we evaluate the standard K-means and hierarchical clustering methods on three large TCGA datasets. The evaluation is performed using intrinsic measures and external information. We introduce ReKS (Recursive K-means Spectral clustering), and compare it to the two aforementioned methods on the TCGA data. ReKS leverages the global similarity structure that spectral clustering provides, while saving on computing time by performing recursion. At each recursion step, we exploit the distribution of eigenvalues to select the optimal number of partitions, thus eliminating the need for pre-specifying K. We show that ReKS is very useful in deriving important biological information from patient gene expression data. Furthermore, we show how to add prior information from KEGG pathway to refine the cluster boundaries.

2. Method

2.1. Spectral Clustering

The spectral clustering formulation requires building a network of genes, encoding their pairwise interactions as edge weights, and analyzing the vectors and eigenvalues of a matrix derived from such a network. This procedure is well established in the literature¹² so here we limit our discussion to the main points of the algorithm and use a Markov chain perspective to help us reason further about the idiosyncrasies of the algorithm when applied to cancer expression data.

A convenient framework for understanding the spectral method is to consider the partitioning of an undirected graph G = (V, E) into a set of distinct clusters. Here the genes are represented as vertices υ_i for i =1 … N where N is the total number of genes and network edges have weights w_ij that are non-negative symmetric (w_ij = w_ji) to encode the strength of interaction between a given pair of genes. Affinities denote how likely it is for a pair of genes to belong to the same group. Here we used as affinities a modified form of the correlation coefficient ρ_ij, calculated on the gene expression vectors:

$$w_{\mathit{ij}}=\exp \left(-{\left(\sin \frac{\mathit{arccos}({\rho }_{\mathit{ij}})}{2}\right)}^2\right)$$ (1)

This is distance measure previously found to give empirical success in the clustering of gene expression data⁹. Note that high affinities correspond to pairs of genes that are likely to belong in the same group (e.g., participate in a pathway). In this paper, we ensured that the network is connected so that there is a path between any two nodes of the network. Our goal is to group genes into distinct clusters so that genes within each group are highly connected to each other, while genes in distinct clusters are dissimilar.

Spectral methods use local (pairwise) similarity (affinity) measurements between the nodes to reveal global properties of the dataset. The global properties that emerge are best understood in terms of a random walk formulation on the network^13-15. The random walk is initiated by constructing a Markov transition matrix over the edge weights. Representing the matrix of affinities w_ij by W and defining the degree of a node by d_j = Σ_iw_ij, a Markov transition matrix M can be defined over the edge weights by

$$M=W{D}^{-1}$$ (2)

where D is a diagonal matrix stacked with degree values d_j. The transition matrix M can be used to set up a diffusion process over the network. In particular, a starting distribution p⁰ of the Markov chain evolves to p = M^βp⁰ after β iterations. As β approaches infinity, the Markov chain can be shown to approach a stationary distribution: M^∞ = π 1^T is an outer product of 1 (a column vector of N 1s) and π (column vector of length N). It is easy to show that π is uniquely given by: π_i = d_i/Σ_j d_j and is the leading eigenvector of M: Mπ = π with eigenvalue 1.

We can analyze the diffusion process analytically by using the eigenvectors and eigenvalues of M. From an eigen perspective the diffusion process can be seen as¹⁴:

$$p^{\beta }=\pi +{\sum }_2^n{\lambda }_j^{\beta }{D}^{0.5}{u}_j{u}_j^T{D}^{-0.5}{p}^0$$ (3)

where the eigenvalue λ₁ = 1 is associated with stationary distribution π. The eigenvectors are arranged in decreasing order of their eigenvalues, so the second eigenvector u₂ perturbs the stationary distribution the most as λ₂ ≥ λ_k for k > 2. The matrix u₂ u₂^T has elements u_2,i × u_2,j, which means the genes that share the same sign in u₂ will have their transition probability increased, while transitions across points with different signs are decreased. A straightforward strategy for partitioning the network is to use the sign of the elements in u₂ to cluster the genes into two distinct groups.

Ng et al¹⁶ showed how this property translates to a condition of piecewise constancy on the form of leading eigenvectors, i.e. elements of the eigenvector have approximately the same value with-in each putative cluster. Specifically, it was shown that for K weakly coupled clusters, the leading K eigenvectors of the transition matrix M will be roughly piecewise constant. The K-means spectral clustering method is a particular manner of employing the standard K-means algorithm on the elements of the leading K eigenvectors to extract K clusters simultaneously. We follow the recipe in Ng et al where instead of using a potentially non-symmetric matrix M, a symmetric normalized graph Laplacian L = D^−0.5WD^−0.5, whose eigenvalues and eigenvectors are similarly related to M, is used for partitioning the graph.

Spectral approaches have also some drawbacks. Their basic assumption of piecewise constancy in the form of leading eigenvectors need not hold on real data. Much work has been done to make this step robust, including the introduction of optimal cut ratios¹⁷ and relaxations^18,19 and highlighting the conditions under which these methods can be expected to perform well¹⁴. Spectral methods can be slow as they involve eigen decomposition of potentially large matrices (O(n³)). Recent attempts at addressing this issue include implementing the algorithm in parallel²⁰, speeding eigen decomposition with Nystrom approximations²¹, building hierarchical transition matrices²² and embedding distortion measures for faster analysis of large-scale datasets²³.

2.2. Recursive K-means Spectral clustering algorithm (ReKS)

In this paper, we will pursue a recursive form of K-means spectral clustering (ReKS), apply it on cancer expression data from patients and understand the intrinsic structure of the data by establishing a baseline clustering result. ReKS first defines an affinity matrix of all pairwise similarities between genes. We reduce the computational burden with sparse matrices, such that each gene is connected to a small number of its neighbors (default: 15) with varying affinities, and extract only a small subspace of eigenpairs (default: 20). In each recursion step, we determine the most appropriate subspace in which to run K-means using the eigengap heuristic, which is to compute the ratio of successive eigenvalues and pick K that satisfies: max{i: λ_i / λ_i+1, for i = 1 to 20}. We apply the eigengap heuristic at each recursion level to determine the optimal number of partitions at that level. In addition, to improve the convergence of the K-means algorithm we initiate the algorithm with orthogonal seed points. For each newly formed cluster, we extract the corresponding affinity sub-matrix and repeat the procedure.

In Figure 2(a) we illustrate the top two levels of ReKS recursion on the GBM dataset. At level-1 an obvious partition exists for the original affinity matrix. The genes are split into two clusters at this node, and for each cluster, a new affinity matrix is computed.

Fig. 2.

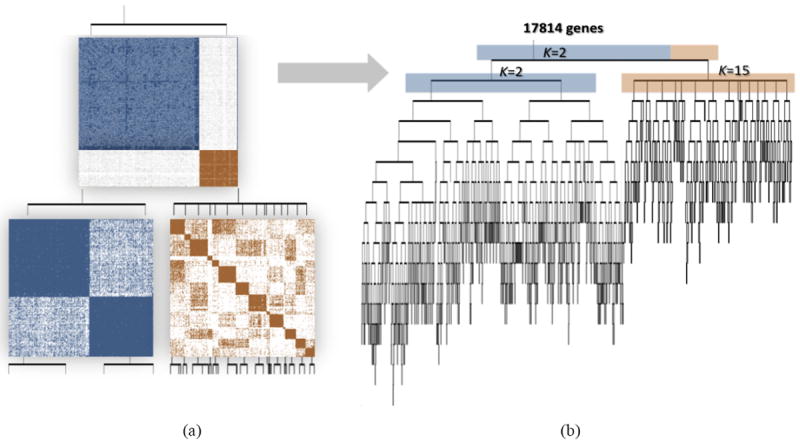
(a) Demonstration of the ReKS method on the GBM dataset at the first two iterations of K-means spectral decomposition recursions: two clusters are visible in the affinity map constructed from the entire dataset at the first level. From each, a new affinity matrix is constructed and spectral clustering repeated on the sub-affinity matrix. (b) Complete tree obtained by ReKS iterations. Each leaf node corresponds to a gene cluster in the final partition.

ReKS performs this procedure iteratively stopping when further split would cause all clusters to be 35 or smaller in size. The stopping threshold corresponds to the average number of genes that participate in a KEGG²⁴ pathway. In the end, we arrive at a tree where each leaf node represents a gene cluster. Note that with this procedure clusters of smaller than 35 genes could be obtained, for example due to an early split off the tree, as long as there is a cluster that is large in size. Figure 2(b) presents the full tree generated by ReKS on the GBM dataset.

3. ReKS evaluation on cancer patient data

3.1. Data

We applied ReKS on the three most complete TCGA gene expression datasets to date: Glioblastoma multiform (GBM) with a total of 575 tumor samples, Ovarian serous cystadenocarcinoma (OV) with a total of 590 tumor samples, and Breast invasive carcinoma (BRCA) with a total of 799 tumor samples. The level 3, normalized and gene-collapsed data obtained from the TCGA portal were downloaded and no further normalization was performed.

3.2. Comparison of ReKS and other clustering strategies on TCGA data

We compare our method against four other partition solutions: (1) average linkage hierarchical clustering, (2) average linkage hierarchical clustering on the spectral space, (3) K-means and (4) K-means on the spectral space. These algorithms are chosen to cover a range of common clustering techniques and clustering assumptions.

Agglomerative clustering methods build a hierarchy of clusters from bottom up. It is perhaps the most popular on gene expression data analysis²⁵, due to its ease of use and readily available implementations. We performed hierarchical agglomerative clustering using Euclidean distance and average linkage. A maximum number of clusters is specified to be comparable to the number of clusters K obtained when running ReKS. Since this choice might be considered favorable to ReKS, we also performed hierarchical clustering on the top three eigenvectors in the spectrum, using cosine distances to measure the distance on the resulted unit sphere. Note that hierarchical clustering is done from bottom up, using local similarities, and does not embed the global structure in its tree.

Similarly, standard K-means and K-means performed on the spectral space are included for benchmarking purposes. Given a number of clusters, K, the algorithm iteratively assigns members to centroids and re-adjusts the centroids of the clusters. K-means tends to perform well as it directly optimizes the intra-cluster distances, but tends to be slow especially as K increases. Here we used the default implementation of the K-means clustering algorithm in Matlab, with Euclidean distance, again using the K obtained from ReKS. We also ran K-means on the spectral space, effectively performing ReKS only once without choosing an optimal number of eigenvectors to use, but instead using K top eigenvectors.

Shown in Figure 3 are the distributions of the cluster sizes when applying the five methods to the three TCGA datasets. Hierarchical clustering, whether in the original or the eigenspace, produces a very skewed distribution of cluster sizes that is possibly an artifact of focusing on only local similarities. The K-means methods and ReKS produce cluster sizes that span roughly the same range. However, the K-means methods produce distributions that are artificially Gaussian, with relatively little clusters that contain small number of genes.

Fig. 3.

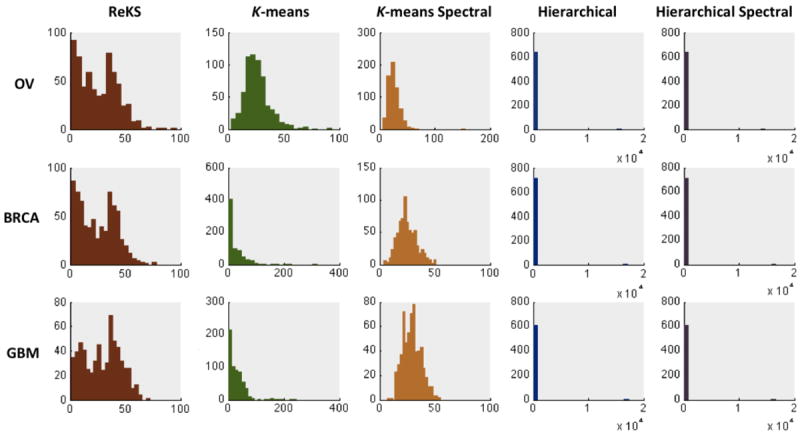
Distribution of cluster sizes of ReKS and of other methods

3.3. Cluster quality evaluation

We evaluate the quality of the clusters obtained from each of the five methods (ReKS, K-means, K-means spectral, Hierarchical, Hierarchical spectral) using both intrinsic, statistical measures as well as external biological evidence, as detailed in the sections below.

3.5.1. Calinski-Harabasz

To evaluate the quality of the clusters, we used the Calinski-Harabasz measure²⁶, defined by:

$$\mathit{CH}=\frac{\mathit{traceB}/(K-1)}{\mathit{traceW}/(N-K)}$$ (4)

where traceB denotes the error sum of squares between different clusters, traceW is the intracluster square differences, K is the number of objects, and K is number of clusters. This statistic is effectively an adjusted measure of the ratio of between- vs. within- group dispersion matrices. A larger value denotes a higher compactness of the cluster compared to the inter-cluster distances. Figure 4(a) shows the performance of ReKS compared across other methods. Not surprisingly, ReKS outperforms hierarchical clustering in both the original data space as well as the spectral space, as hierarchical clustering produces some very large clusters with no apparent internal cohesion. The K-means based methods and ReKS are comparable in terms of cluster separation across the datasets.

Fig. 4.

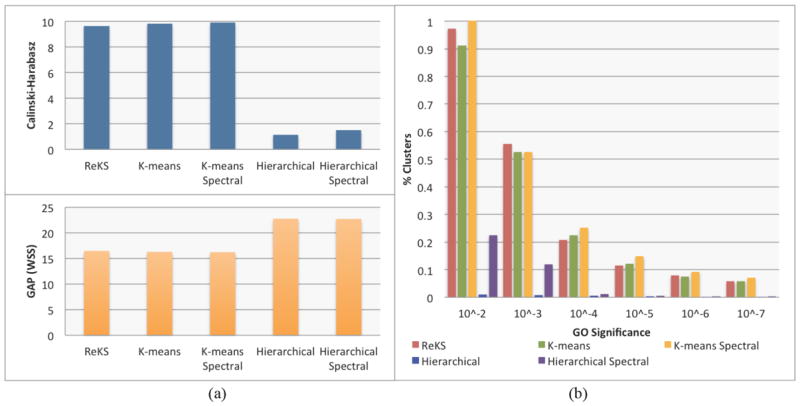
(a) Cluster validity comparison with other methods using the Calinski-Harabasz and the GAP statistics (b) Gene Ontology(GO) enrichment across different range of p-values

3.5.2. GAP Statistic

The Gap statistic was proposed as a way to determine optimal cluster size²⁷. In short, it is the log ratio of a reference within-cluster sum of square errors over the observed within-cluster sum of squares errors. The reference is usually built from a permutated set of genes that form K random clusters. Since we are comparing the (five) methods across the same dataset with the same K, it is fair to compare the performance of the observed within sum-of squares error only. With this direct proxy, ReKS performs at the same level as K-means based methods (shown in Figure 4(a)), and achieved a significantly lower sum-of-square distances than the hierarchical methods.

3.5.3. Gene Ontology Enrichment

Since no ground truth exists for gene cluster partition, we examine the overall quality of the clusters in terms of the amount of enrichment for Gene Ontology (GO) annotations. For each cluster, we test for GO enrichment using a variant of the Fisher’s exact test, as described in the weight01 algorithm of the topGO²⁸ package in R. The significance level of the test indicates the degree a particular GO annotation is over-represented in a given cluster. For a partition, we calculate the proportion of clusters annotated with a GO term at a p-value threshold. If a cluster has less than five members, the test is not performed. As shown in Figure 4(b), compared to hierarchical clustering, we observe that ReKS contains higher percentage of clusters that are significant at the specified levels, and especially so with more stringent p-value thresholds, and performs roughly the same as K-means methods. Finally, we observe that the spectral methods tend to perform better than their non-spectral counter-parts.

3.5.4. Execution Time

Table 1 shows the execution time of the five methods on a 3.4 GHz Intel Core i7 CPU. ReKS is slower than hierarchical clustering but compares favorably to K-means methods.

Table 1.

Average execution time of the five methods

Methods	ReKS	K-means	K-means Spectral	Hierarchical	Hierarchical Spectral
Execution time	373s	6000s	1774s	90s	22s

3.4. Incorporation of Prior Information

We use existing expert knowledge as prior information (from KEGG pathway²⁴) to guide our clustering method, aiming to generate partitions that are even more biologically meaningful. The KEGG database includes a collection of manually curated pathways constructed from knowledge accrued from the literature. For the purposes of ReKS, we assume that the genes in a KEGG pathway are fully connected to each other (i.e., should belong in the same cluster). We code this prior knowledge in a constraint matrix U in which each column U_c is a pathway, and u_ic = 1, u_jc = -1 if a pair of genes i,j participate in the same KEGG pathway c. Similar to what was detailed in Ji et al.²⁹, where they supplied a prior for document clustering using K-means spectral decomposition, we apply a penalty term to the normalized graph Lapacian as follows:

$$L^{\prime }=D^{-0.5}(W+\beta U^{T}U)D^{-0.5}$$ (5)

where β ≥ 0 controls the degree of enforcement of the KEGG prior knowledge. As shown in Ji et al., the eigenvectors of the K smallest eigenvalues of L’ form the eigen-space represents a transformation of the affinity space embedded with prior information. We then proceeded to apply the K-means algorithm within the eigenspace, and iterate recursively as we did with ReKS. As shown in Figure 5(a), when we use a large amount of prior, not surprisingly the GO significance becomes very large. We observe the significance of the clusters do not drop very fast as β decreases. Therefore, small amount of prior at roughly β = 0.2 may be enough to enhance the biological significance of the ReKS clustering results.

Fig. 5.

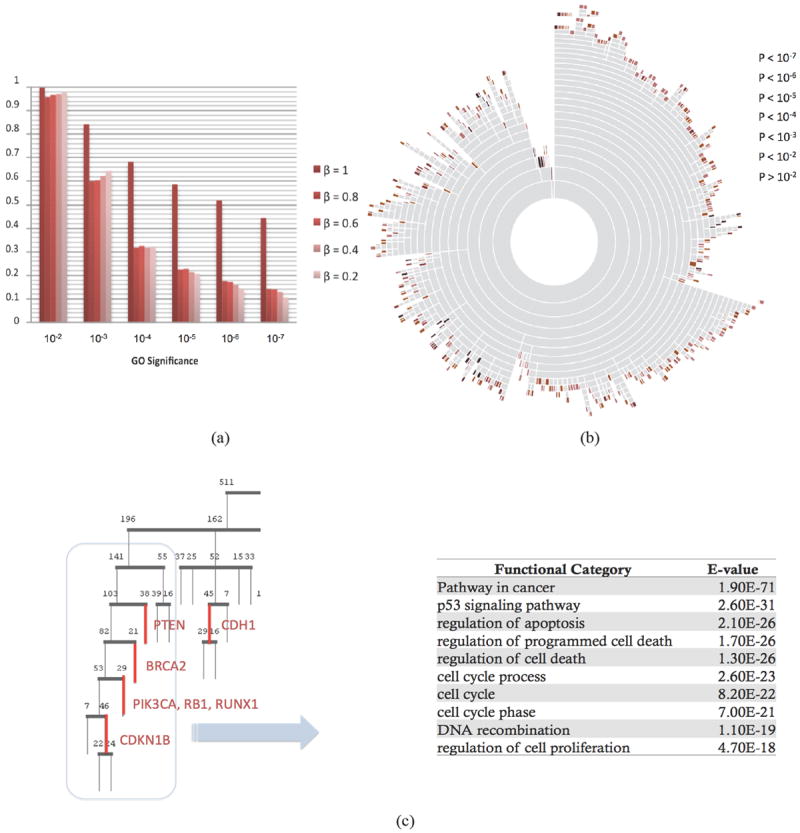
(a) Effect of incorporation of prior information on the GO significance of the obtained clusters. β controls the degree of enforcement of the KEGG prior knowledge (b) A sunburst diagram for the BRCA dataset. In this alternative representation of the ReKS clustering results, each concentric circle represents a level of the tree. Each ring is sub-divided into clusters. The color of a leaf node denotes the GO significance of the cluster. There exists a small anti-correlation (ρ = -0.2112, p < 10^-7) between the level from which a cluster splits off, and its GO significance (c) A part of the tree enriched with genes implicated for breast cancer (level 2 and down), and the GO significance and categories of the 169 gene super-cluster (grey box).

We applied ReKS on the TCGA datasets at β = 0.2. A total of 715, 639, and 610 clusters are obtained for BR, OV, and GBM respectively. As shown in Figure 5(a), we observe that there exists a slight anti-correlation between how early a cluster splits off the tree and how significant the cluster is (ρ = -0.2112, p <10^-7). As a preliminary observation, how early a cluster is formed seems to imply the “tightness” of the cluster, this result seems to suggest that there is a slightly higher chance the clusters that form early to be more biologically significant. For example, in Figure 5(b) there is a tight histone H1 cluster that splits off the BRCA tree at the third level on the top. It has been shown that EB1089 treatment of breast cancer cell lines (MCF-7, BT20, T47D, and ZR75) is correlated with a reduction in CdK2 kinase activity towards phosphorylation of histone H1 and a decrease in DNA synthesis³⁰. This cluster was not found in K-means spectral, Kmeans, and spectral hierarchical clustering results, and only exists in a mega-cluster in hierarchical clustering partition. Additionally, upon examining the resulted tree closely, we found that a few genes that have been implicated for breast cancer³¹ cluster together or close to each other on the tree, as shown in Figure 5(c). When considering a few of these sub-clusters together, the top functional categories that emerged are indeed caner and p53 pathways. We found several of these examples throughout the tree, all within 12 levels up to which the composition of the clusters remains stable when splitting the data into training and test sets. We note that PIK3CA, RB1, and RUNX1 do not cluster together in any of the other methods we compared to, nor does the rest of the genes we examined. This example suggests that the tree structure could be useful for inferring additional previously unknown biomarkers.

4. Discussion

In this study, we demonstrate the utility of a new recursive spectral clustering method we proposed as an alternative to traditional methods for clustering large-scale, human disease expression data. Consistent with previous findings²⁵, hierarchical methods are faster but perform relatively poorly. K-means methods can be accurate when the number of groups K is known. However, in the case of gene clustering of disease samples we are rather agnostic as to the number of the clusters we should expect. ReKS does not require the number of clusters to be known a priori, and is an order of magnitude faster than the original K-means algorithm. Also, compared to K-means spectral, ReKS enjoy a considerable speed gain by performing the decomposition and clustering iteratively, while maintaining a comparable performance even without directly minimizing the overall inter- and intra- cluster distances(sec 3.4).

By incorporating prior pathway information in the algorithm, ReKS additionally guides the clustering process toward a more biologically meaningful partition. We showed that the clusters obtained are biologically relevant in their enrichment in GO terms, and the size of the clusters has a more natural distribution than that of K-means or hierarchical clustering partitions. The clusters, being rather compact and constrained in size, could then be used in subsequent studies, where clusters of genes could potentially be used as predictors for disease classification. Not only does ReKS provide a partition of the gene space, the resulting tree structure provides a hint to the relative tightness of the clusters and potential targets. In the future, we wish to investigate the relationship between the relative position of the cluster in the tree and their potential strengths in classifying disease labels and other clinical variables. Also, it is possible to automatically calculate the optimal number of neighbors to be considered in each recursion level. For example, we can use an approach similar to eigengap, where the distribution of similarities for each node will be compared to the global distribution to identify the optimal number of informative neighbors. The above results indicate that, when applied to large clinical datasets, recursive spectral clustering offers an attractive alternative to conventional clustering methods.