Abstract
The Breakage Fusion Bridge (BFB) process is a key marker for genomic instability, producing highly rearranged genomes in relatively small numbers of cell cycles. While the process itself was observed during the late 1930s, little is known about the extent of BFB in tumor genome evolution. Moreover, BFB can dramatically increase copy numbers of chromosomal segments, which in turn hardens the tasks of both reference-assisted and ab initio genome assembly. Based on available data such as Next Generation Sequencing (NGS) and Array Comparative Genomic Hybridization (aCGH) data, we show here how BFB evidence may be identified, and how to enumerate all possible evolutions of the process with respect to observed data. Specifically, we describe practical algorithms that, given a chromosomal arm segmentation and noisy segment copy number estimates, produce all segment count vectors supported by the data that can be produced by BFB, and all corresponding BFB architectures. This extends the scope of analyses described in our previous work, which produced a single count vector and architecture per instance. We apply these analyses to a comprehensive human cancer dataset, demonstrate the effectiveness and efficiency of the computation, and suggest methods for further assertions of candidate BFB samples. Source code of our tool can be found online.
Key words: : algorithms, combinatorial proteomics, computational molecular biology, dynamic programming, genetic variation, RNA, sequence analysis
1. Introduction
The origin of a tumor cell is marked by genomic instability (Hanahan and Weinberg, 2011). Spontaneous, viral, or other kinds of mechanisms may cause genomic segment deletions, duplications, translocations, inversions, etc., producing rearranged genomes with a possibly malignant nature. Thus, decoding mechanisms that generate rearranged genomes is critical to understanding cancer. Numerous mechanisms were proposed, including the faulty repair of double-stranded DNA breaks by recombination or end-joining and polymerase hopping caused by replication fork collapse (Carr et al., 2011; Hastings et al., 2009). These mechanisms are generally not directly observable, so their elucidation requires the deciphering of often subtle clues after genomic instability has ceased. An important source of information in this respect is the architecture of the rearranged genome, that is, the description of its chromosomes in terms of concatenations of segments from the original genome.
Breakage Fusion Bridge (BFB) is one model of a genome rearrangement process, which was first proposed by Barbara McClintock in the 1930s (McClintock, 1938, 1941). Recently, it has seen renewed interest as a possible mechanism in tumor genome evolution (Bignell et al., 2007; Campbell et al., 2010; Greenman et al., 2012). BFB begins with a telomeric loss on a chromosome, including a loss of a sequential pattern that signals the location of chromosome termination. During cell division the telomere-lacking chromosome replicates, and its two sister chromatids fuse together (possibly due to some DNA repair mechanism falsely induced by the cell). This fusion produces a dicentric chromosome of palindromic structure, which is later torn apart at some random point as the centromeres of the dicentric chromosome migrate to opposite poles of the cell. One part of the torn chromosome includes the fusion region and some tandemly inverted chromosomal suffix duplication, and the other part lacks the corresponding suffix. The two daughter cells receive these rearranged chromosomes, both are missing the telomeric region, and the cycle can repeat (Fig. 1).
FIG. 1.
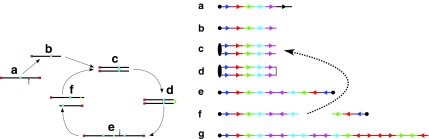
The BFB process. To the left, the different stages of a BFB cycle are presented. To the right, corresponding modifications over an exemplary chromosomal arm are shown. (a) A normal chromosome. (b) The chromosome loses its telomere. (c) The chromosome is duplicated during cell division. (d) Sister chromatids are fused together. (e) Centromeres migrate to opposite poles of the cell. (f) The fused chromosome is torn apart at some random position between the two centromeres, causing one copy to have an inverted suffix duplication, while the other copy has a trimmed suffix. Both copies lack a telomere and therefore may undergo additional BFB cycles. (g) After several BFB cycles, the chromosome architecture exhibits significant increases in segment copy numbers, as well as fold-back patterns.
In contrast to other mechanisms, BFB can actually be observed in progress using methods that have been available for decades (McClintock, 1941). Cytogenetic techniques can reveal the anaphase bridges, dicentric chromosomes, and homogeneously staining regions that have long been the canonical evidence for BFB. However, these techniques are useful only in cases where the BFB cycles are ongoing. While useful in understanding the mechanism, they do not address the question of whether BFB occurs extensively in evolving tumor genomes.
Recently, researchers (including us) have started looking at modern available data in order to demonstrate BFB occurrence after the process has ceased, including Fluorescent In Situ Hybridization (FISH), Array Comparative Genomic Hybridization (aCGH), and Next Generation Sequencing (NGS) data. These methods take advantage of distinctive BFB features exposed by such data, including the abundance of fold-back inversions (i.e., duplicated chromosomal segments arranged in a head-to-head orientation (Bignell et al., 2007; Campbell et al., 2010), patterns of interleaving segments of alternating orientations (Kitada and Yamasaki, 2008; Reshmi et al., 2007), and combinatorial properties of segment counts when copy number variations are due to BFB (Kinsella and Bafna, 2012; Zakov et al., 2013). In fact, if the architecture of the rearranged genome is known, it is possible to decide if this architecture can be produced by BFB (Kinsella and Bafna, 2012). Properties of the space of different BFB evolutions are explored in Greenman et al. (2012).
Partial knowledge regarding the architecture can be revealed by FISH analyses (Kitada and Yamasaki, 2008), which uses fluorescence markers to identify the physical locations of predetermined sequences on the rearranged genome. However, such experiments are relatively expensive and can only be performed in a small number of cases. A more common measurement is NGS data, which contain a big set of short sequenced reads extracted from a donor genome. Such data is typically used for predicting the entire donor genomic sequence by computationally assembling the reads, sometimes facilitated by consulting a similar presequenced reference genome. Unfortunately, BFB and other mechanisms can produce massively rearranged and highly repetitive genomes. This complicates the task of assembly-based sequencing due to the multiple ambiguous manners the repetitive reads may be assembled, and the lack of a relevant reference template. Nevertheless, NGS data can still be analyzed in order to infer some indirect information regarding the donor genome architecture (Alkan et al., 2009; Chiang et al., 2009; Medvedev et al., 2009; Yoon et al., 2009). After aligning the reads against a reference genome, their genomic location distribution can be used in order to identify segments on the reference genome of coherent read coverage, and to estimate the number of times each such segment repeats in the donor genome. We will refer to the output of the latter kind of analysis as copy number data. Other methods to obtain copy number data are based on analyzing aCGH data (Eckel-Passow et al., 2011; Greenman et al., 2010; Olshen et al., 2004; Venkatraman and Olshen, 2007) (Fig. 2). Due to the noisy nature of both NGS and aCGH data, count estimates may be inaccurate, and the true segment count is likely to fall within some interval of integers around the estimated value. We use the term noisy copy number data when referring to information regarding such intervals of possible count values. In addition to copy number data, NGS data can be used in order to produce contigs (chromosomal segments that may be assembled unambiguously), and aberrant segment adjacencies can be exposed by discordant reads, restricting the set of possible contig-based architectures.
FIG. 2.

(a) aCGH data for a part of the q-arm of human chromosome 14 in the NCI-H508 cell line. Each data point corresponds to a probe on the array, where its x-coordinate gives the probe's sequence chromosomal position, and y-coordinate gives its measured intensity (log-ratio). The data points are clustered into segments, and an estimated segment copy number appears above each segment. (b) A visualization of the corresponding noisy copy number data. Estimated counts appear in light blue, and the column around each count represents possible deviations from the estimation. The region under the red curly bracket reflects a BFB candidate. Its corresponding estimated counts are [5, 12, 5, 11, 7, 12, 7, 14, 4, 14, 4], which under minor modifications yield the two BFB vectors [5, 13, 5, 11, 7, 12, 8, 14, 4, 14, 4] or [5, 11, 5, 11, 7, 12, 8, 14, 4, 14, 4]. Data is taken from Bignell et al. (2010) [segmentation and copy number analysis were computed using the PICNIC software (Greenman et al., 2010)].
In previous work (Kinsella and Bafna, 2012; Zakov et al., 2013), we showed how to analyze noisy copy number data in order to decide if it is likely to observe the input data under the assumption that the underlying rearrangement process is BFB. Specifically, we designed algorithms that produce a single BFB architecture over the given segments in which segment counts are supported by the data, if such an architecture exists. We applied these algorithms in order to analyze a comprehensive aCGH dataset of cancer cell lines (Bignell et al., 2010), as well as sequence data from primary tumors (Campbell et al., 2010), and identified a small subset of candidate samples exhibiting BFB hallmarks. Here, we extend the scope of the analysis and describe algorithms that report all count settings supported by the data, which can be explained by BFB, and all corresponding BFB architectures. Although the theoretical time bounds for these new algorithms may be exponential, we show that in practice they are efficient and apply an informed search (Pearl, 1984) optimization that further improves their practical efficiency.
Therefore, our proposed algorithms satisfy an important need. While our work postulates the existence of BFB using statistical arguments, additional physical assertions can be obtained with FISH and aberrant read analyses. Starting with noisy copy number data, our tool can be used to enumerate all possible BFB architectures. These candidate architectures can then be used toward a small set of FISH experiments (with a limited number of fluorescence markers) to validate and refine the predicted genomic architecture.
2. Problem Definition
Computational BFB-related problems were previously formulated in Kinsella and Bafna (2012) and Zakov et al. (2013). For completeness, we give here the main definitions from these works and formulate new problems first addressed here.
A DNA segment σ is a string over the DNA nucleotide alphabet A, C, G, T. The reversed segment of a segment σ, denoted here by 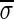 , is the string obtained by reading σ backwards and replacing each nucleotide with its complementary nucleotide (A ↔ T, C ↔ G). For example, the reverse of a segment σ = CGGAT is the segment
, is the string obtained by reading σ backwards and replacing each nucleotide with its complementary nucleotide (A ↔ T, C ↔ G). For example, the reverse of a segment σ = CGGAT is the segment 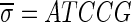 . In the rest of this article, it is assumed we operate on a given chromosomal arm with a fixed segmentation and denote its list of k segments by
. In the rest of this article, it is assumed we operate on a given chromosomal arm with a fixed segmentation and denote its list of k segments by 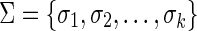 , ordered from the centromeric segment σ1 to the telomeric segment σk. The term “string” refers to a genomic architecture over these segments, that is, a concatenation of segments from Σ and their reversed forms. Greek letters α, β, γ, and ρ denote strings, and bar notation indicates reversed strings. For example, if
, ordered from the centromeric segment σ1 to the telomeric segment σk. The term “string” refers to a genomic architecture over these segments, that is, a concatenation of segments from Σ and their reversed forms. Greek letters α, β, γ, and ρ denote strings, and bar notation indicates reversed strings. For example, if 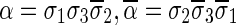 . An empty string is denoted by ɛ. The notation αl,t represents the continuous chromosomal region
. An empty string is denoted by ɛ. The notation αl,t represents the continuous chromosomal region 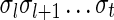 , where αl,t = ɛ when t < l. To facilitate reading,
, where αl,t = ɛ when t < l. To facilitate reading,  are replaced by
are replaced by 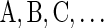 in concrete examples.
in concrete examples.
A BFB cycle applied over a chromosomal arm can be viewed as a special rearrangement procedure, in which some telomeric suffix of the arm is duplicated, inverted, and concatenated tandemly at the telomeric end of the arm. A string β can be derived from a string α via a BFB process if it is possible to apply a series of zero or more BFB cycles over α and obtain β (Fig. 3a). This notion is formally captured by the following definition.
FIG. 3.
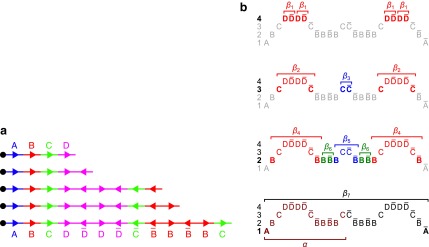
(a) A BFB process generating a string α:  . (b) The layers of the BFB palindrome
. (b) The layers of the BFB palindrome 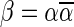 . The block collections are B4 = {4β1}, B3 = {2β2, β3}, B2 = {2β4, β5, 2β6}, and B1 = {β7}.
. The block collections are B4 = {4β1}, B3 = {2β2, β3}, B2 = {2β4, β5, 2β6}, and B1 = {β7}.
Definition 1 For two strings α, β, say that
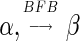 if α = β, or there are some strings ρ, γ such that γ ≠ ɛ, α = ργ, and
if α = β, or there are some strings ρ, γ such that γ ≠ ɛ, α = ργ, and
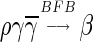 . Say that α is an l-BFB string
if
. Say that α is an l-BFB string
if
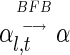 for some t, and say that α is a BFB string if it is an l-BFB string for some l.
for some t, and say that α is a BFB string if it is an l-BFB string for some l.
It is worth mentioning that in reality a BFB cycle can also delete a suffix of a chromosome in case we consider the trimmed chromosomal arm. It is simple to show that for any BFB process that contains such suffix-trimming cycles there is an equivalent process in which only elongation cycles occur (Kinsella and Bafna, 2012). For example, the BFB string 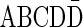 obtained by the process
obtained by the process 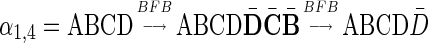 can also be obtained by the process
can also be obtained by the process 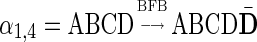 . Thus, we can assume without loss of generality that all BFB cycles are of the form of a tandem suffix duplication.
. Thus, we can assume without loss of generality that all BFB cycles are of the form of a tandem suffix duplication.
By definition ɛ = αl,l−1 is an l-BFB string for every l ≥ 1. For a nonempty string α, define top(α) = max {t : σt appears in α} and define top(ɛ) = 0. It is simple to observe that when α is an l-BFB string, it must start with the prefix αl,t for t = top(α), since BFB cycles can only duplicate previously appearing letters and never generate new ones.
The count vector
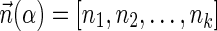 of a string α is a vector of integers, where for every 1 ≤ l ≤ k, nl is the total number of occurrences of σl and
of a string α is a vector of integers, where for every 1 ≤ l ≤ k, nl is the total number of occurrences of σl and  in α. For example, for
in α. For example, for 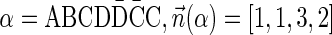 . Say that a vector
. Say that a vector 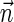 is a BFB vector if there exists some BFB string α such that
is a BFB vector if there exists some BFB string α such that 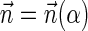 . In the previous example
. In the previous example 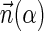 is a BFB vector due to the BFB process
is a BFB vector due to the BFB process 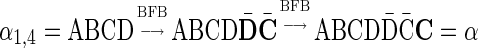 .
.
The computational analyses presented in this article aim to detect evidence for BFB, given a preanalyzed segmentation of the genome and corresponding copy number data. We assume that noisy copy number data is represented by a weight function
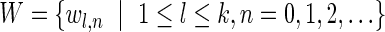 , where wl,n is a nonnegative weight associated with the copy number n for the l-th segment. It may be assumed w.l.o.g. that all weights wl,n satisfy 0 ≤ wl,n ≤ 1. The weight of a count vector
, where wl,n is a nonnegative weight associated with the copy number n for the l-th segment. It may be assumed w.l.o.g. that all weights wl,n satisfy 0 ≤ wl,n ≤ 1. The weight of a count vector 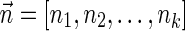 is given by
is given by 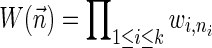 , and by assumption
, and by assumption 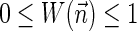 . In some cases, we refer to prefixes
. In some cases, we refer to prefixes 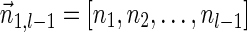 and suffixes
and suffixes 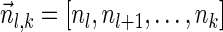 of
of  , which may be empty if l = 1 or l = k + 1, respectively. Define the weights of such subvectors accordingly, that is,
, which may be empty if l = 1 or l = k + 1, respectively. Define the weights of such subvectors accordingly, that is, 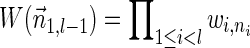 and
and 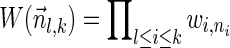 , where the weight of an empty vector is 1 by definition. Thus, for every
, where the weight of an empty vector is 1 by definition. Thus, for every 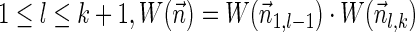 .
.
If some data analysis produces segment count probabilities Pr (nl = n) for every segment σl and every count 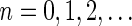 , weights can be set to these probabilities choosing wl,n = Pr (nl = n). This way, the weight of a count vector is the probability this vector reflects the true segment counts given the observed data. Another way to set weights given such probabilities would be to choose weights by setting
, weights can be set to these probabilities choosing wl,n = Pr (nl = n). This way, the weight of a count vector is the probability this vector reflects the true segment counts given the observed data. Another way to set weights given such probabilities would be to choose weights by setting 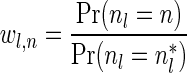 , where
, where 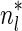 is the most likely count for the l-th segment. Here, the weight of a count vector gives the ratio between its probability and the probability of a most likely vector. Nevertheless weights are more general than probabilities and can be used as a heuristic count error modeling even when no probabilistic model is available.
is the most likely count for the l-th segment. Here, the weight of a count vector gives the ratio between its probability and the probability of a most likely vector. Nevertheless weights are more general than probabilities and can be used as a heuristic count error modeling even when no probabilistic model is available.
In Zakov et al. (2013), several variants of BFB problems were formulated. Below we restate these problems and add two new variants addressed in the current work:
BFB problem variants
Input:
A count vector
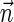 , or a weight function W and a minimum weight threshold 0 < η ≤ 1.
, or a weight function W and a minimum weight threshold 0 < η ≤ 1.
1. The decision variant (Zakov et al., 2013): given
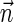 , decide if
, decide if
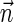 is a BFB vector.
is a BFB vector.2. The string search variant (Zakov et al., 2013): if
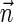 is a BFB vector, find a BFB string α such that
is a BFB vector, find a BFB string α such that
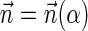 .
.3. The vector search variant (denoted the distance variant in Zakov et al., 2013): given W and η, report a maximum weight BFB vector
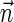 in case there exists such a vector with
in case there exists such a vector with
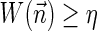 , and otherwise report “FAILED.”
, and otherwise report “FAILED.”4. The exhaustive vector search variant: given W and η, report all BFB vectors
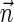 with
with
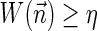 .
.5. The exhaustive string search variant: given W and η, report all BFB strings α such that
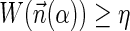 .
.
For a count vector 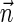 , define
, define 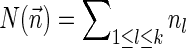 and
and 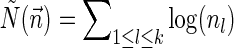 . Note that
. Note that 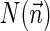 is the total length of a string admitting
is the total length of a string admitting 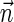 , and
, and 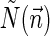 is proportional to the number of bits needed for representing
is proportional to the number of bits needed for representing 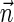 . For a weight function W and a weight η, define
. For a weight function W and a weight η, define 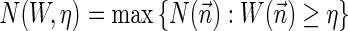 , and
, and 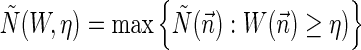 . In Zakov et al. (2013), it was shown that the BFB decision variant can be solved using
. In Zakov et al. (2013), it was shown that the BFB decision variant can be solved using 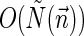 bit operations (i.e., linear time in the input length), the string search variant can be solved in
bit operations (i.e., linear time in the input length), the string search variant can be solved in 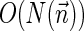 operations (i.e., linear time in the output length), and that the vector search variant can be solved using at most a subexponential number of operations 2O(log2 N(W,η)). Here, we give algorithms for the two new exhaustive search variants. While theoretically the output of these algorithms can be exponential with respect to N(W, η), we show that for realistic inputs this output is manageable. In addition, we describe an Informed Search (IS) approach that significantly reduces the running time in practice by eliminating irrelevant search paths and traversing only paths that are guaranteed to produce valid solutions.
operations (i.e., linear time in the output length), and that the vector search variant can be solved using at most a subexponential number of operations 2O(log2 N(W,η)). Here, we give algorithms for the two new exhaustive search variants. While theoretically the output of these algorithms can be exponential with respect to N(W, η), we show that for realistic inputs this output is manageable. In addition, we describe an Informed Search (IS) approach that significantly reduces the running time in practice by eliminating irrelevant search paths and traversing only paths that are guaranteed to produce valid solutions.
3. Algorithms
In this section we develop algorithms for the two exhaustive search variants of the BFB problem. Next, we describe some ideas taken from Zakov et al. (2013), upon which the algorithms presented here are built.
3.1. Notation and previous results
An l-BFB palindrome is an l-BFB string of the form 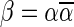 . It can be shown that
. It can be shown that 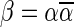 is an l-BFB palindrome if and only if α is an l-BFB string. By definition,
is an l-BFB palindrome if and only if α is an l-BFB string. By definition, 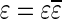 is an l-BFB palindrome for every l ≥ 1. In addition, observe that when
is an l-BFB palindrome for every l ≥ 1. In addition, observe that when 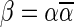 we have that
we have that 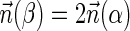 . This allows replacing the question “is there a BFB string admitting the count vector
. This allows replacing the question “is there a BFB string admitting the count vector 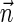 ” by the equivalent question “is there a BFB palindrome admitting the count vector
” by the equivalent question “is there a BFB palindrome admitting the count vector 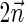 ”.
”.
An l-block is a string of the form 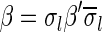 , where β′ is an (l +1)-BFB palindrome. It can be shown that an l-block is a special form of an l-BFB palindrome, and that every l-BFB palindrome is some palindromic concatenation of l-blocks. Nevertheless, not every palindromic concatenation of l-blocks yields a valid l-BFB palindrome. For example, two copies of the 2-block
, where β′ is an (l +1)-BFB palindrome. It can be shown that an l-block is a special form of an l-BFB palindrome, and that every l-BFB palindrome is some palindromic concatenation of l-blocks. Nevertheless, not every palindromic concatenation of l-blocks yields a valid l-BFB palindrome. For example, two copies of the 2-block 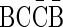 and one copy of the block
and one copy of the block 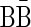 can be concatenated to form the 2-BFB palindrome
can be concatenated to form the 2-BFB palindrome 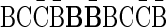 . The validity of this palindrome can be asserted from the process
. The validity of this palindrome can be asserted from the process 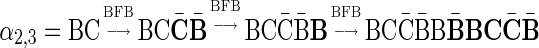 . On the other hand, the only palindromic concatenation of one copy of
. On the other hand, the only palindromic concatenation of one copy of 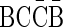 and two copies of
and two copies of 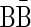 is the string
is the string 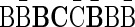 . This string is not a valid BFB string, since a BFB string over the letters {B, C} must start with the prefix α2,3 = BC. Claim 1 in Zakov et al. (2013), recited here in the Appendix, gives a required and sufficient condition for block concatenations that form valid BFB palindromes.
. This string is not a valid BFB string, since a BFB string over the letters {B, C} must start with the prefix α2,3 = BC. Claim 1 in Zakov et al. (2013), recited here in the Appendix, gives a required and sufficient condition for block concatenations that form valid BFB palindromes.
The idea of decomposing BFB palindromes into blocks allows us to adopt a layeresd view of BFB palindromes, as follows (Fig. 3). Let 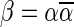 be a 1-BFB palindrome, where
be a 1-BFB palindrome, where 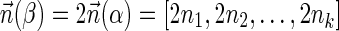 . As claimed above, β is a palindromic concatenation of 1-blocks. Denote by B1 the collection of all 1-blocks whose concatenation forms β. Every 1-block in B1 is a string of the form
. As claimed above, β is a palindromic concatenation of 1-blocks. Denote by B1 the collection of all 1-blocks whose concatenation forms β. Every 1-block in B1 is a string of the form  , where β′ is some 2-BFB palindrome. As there are 2n1 occurrences of A and
, where β′ is some 2-BFB palindrome. As there are 2n1 occurrences of A and  in β, and each block in B1 contains exactly two such occurrences, the total number of blocks in B1 is exactly n1. Masking the letters A and
in β, and each block in B1 contains exactly two such occurrences, the total number of blocks in B1 is exactly n1. Masking the letters A and  from all blocks in B1, the collection becomes a 2-BFB palindrome collection of size n1. The 2-BFB palindromes in this collection can be further decomposed into two-blocks, yielding a collection B2 of two-blocks. Similarly as above, B2 contains exactly n2 blocks. This process can continue inductively, yielding for every 1 ≤ l ≤ k a corresponding collection Bl of l-blocks, whose size is nl. One may also imagine an additional collection in this series Bk+1, containing zero (k + 1)-blocks.
from all blocks in B1, the collection becomes a 2-BFB palindrome collection of size n1. The 2-BFB palindromes in this collection can be further decomposed into two-blocks, yielding a collection B2 of two-blocks. Similarly as above, B2 contains exactly n2 blocks. This process can continue inductively, yielding for every 1 ≤ l ≤ k a corresponding collection Bl of l-blocks, whose size is nl. One may also imagine an additional collection in this series Bk+1, containing zero (k + 1)-blocks.
This layered view is exploited in a reversed order by the algorithms in Zakov et al. (2013), developing a BFB palindrome given an input count vector 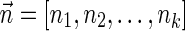 : Starting with an empty collection Bk+1 of (k + 1)-blocks, the algorithm computes iteratively a sequence of collections
: Starting with an empty collection Bk+1 of (k + 1)-blocks, the algorithm computes iteratively a sequence of collections 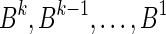 , each collection Bl is an l-block collection of size nl. In order to generate Bl, the algorithm first concatenates (l + 1)-blocks from Bl+1, forming a collection B of (l + 1)-BFB palindromes of size nl (this procedure is called folding). Then, each (l + 1)-BFB palindrome β′ ∈ B is wrapped with a pair of σl segments, rendering it into an l-block
, each collection Bl is an l-block collection of size nl. In order to generate Bl, the algorithm first concatenates (l + 1)-blocks from Bl+1, forming a collection B of (l + 1)-BFB palindromes of size nl (this procedure is called folding). Then, each (l + 1)-BFB palindrome β′ ∈ B is wrapped with a pair of σl segments, rendering it into an l-block 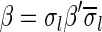 , and Bl is set to be the collection containing all these l-blocks. The final collection of 1-blocks B1 is folded one more time into a single 1-BFB palindrome
, and Bl is set to be the collection containing all these l-blocks. The final collection of 1-blocks B1 is folded one more time into a single 1-BFB palindrome 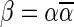 , and the algorithm returns the half-length prefix α of this palindrome as a BFB string admitting the input count vector
, and the algorithm returns the half-length prefix α of this palindrome as a BFB string admitting the input count vector 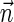 .
.
Figure 3b illustrates a possible run of the algorithm over the input count vector 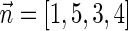 . First, the algorithm initializes an empty collection of blocks B5. In the first iteration, there is a need to perform concatenations of blocks in B5 and produce n4 = 4 BFB palindromes. Such palindromes may only be obtained by concatenating zero elements (as there are no elements in B5), and so four empty strings are generated in this folding process, yielding the BFB palindrome collection {4ɛ}. Next, each palindrome in this collection is wrapped by σ4 = D and
. First, the algorithm initializes an empty collection of blocks B5. In the first iteration, there is a need to perform concatenations of blocks in B5 and produce n4 = 4 BFB palindromes. Such palindromes may only be obtained by concatenating zero elements (as there are no elements in B5), and so four empty strings are generated in this folding process, yielding the BFB palindrome collection {4ɛ}. Next, each palindrome in this collection is wrapped by σ4 = D and 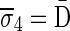 , producing the collection of blocks
, producing the collection of blocks 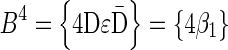 . In the next iteration, the collection B4 needs to reduce its size from n4 = 4 into n3 = 3 by concatenating its elements to produce BFB palindromes. In this example, there are two concatenations of two elements the form β1β1, and one concatenation of zero elements that produces an empty string ɛ. The BFB palindromes in the resulting folded collection {2β1β1, ɛ}, are wrapped by σ3 = C and
. In the next iteration, the collection B4 needs to reduce its size from n4 = 4 into n3 = 3 by concatenating its elements to produce BFB palindromes. In this example, there are two concatenations of two elements the form β1β1, and one concatenation of zero elements that produces an empty string ɛ. The BFB palindromes in the resulting folded collection {2β1β1, ɛ}, are wrapped by σ3 = C and 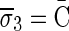 , yielding the block collection
, yielding the block collection 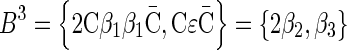 . This process continues for two more iterations, generating similarly the collections B2 = {2β4, β5, 2β6} and B1 = {β7}. All elements in the last collection B1 are then concatenated into a single BFB palindrome β (in this example B1 contains a single element β7, and so β = β7), and the returned string α is the half-length prefix of this palindrome.
. This process continues for two more iterations, generating similarly the collections B2 = {2β4, β5, 2β6} and B1 = {β7}. All elements in the last collection B1 are then concatenated into a single BFB palindrome β (in this example B1 contains a single element β7, and so β = β7), and the returned string α is the half-length prefix of this palindrome.
The ability of the schematic algorithm above to process the entire input vector 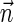 and produce a corresponding BFB string depends on its ability to fold intermediate collections Bl computed along its run. In cases where it cannot fold some intermediate block collection, it returns a fail message, implying no BFB string admits the input vector
and produce a corresponding BFB string depends on its ability to fold intermediate collections Bl computed along its run. In cases where it cannot fold some intermediate block collection, it returns a fail message, implying no BFB string admits the input vector 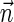 .
.
A case where folding cannot be applied is, for example, the case where n2 = 2, 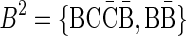 , and n1 = 1. In this case, since both possible concatenations
, and n1 = 1. In this case, since both possible concatenations 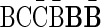 and
and 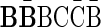 of the two elements in B2 are non-palindromic, the folding procedure must fail at this stage. Another example of a fail folding is the case where n2 = 3,
of the two elements in B2 are non-palindromic, the folding procedure must fail at this stage. Another example of a fail folding is the case where n2 = 3, 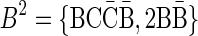 , and n1 = 1. In this case, though there exists a palindromic concatenation
, and n1 = 1. In this case, though there exists a palindromic concatenation 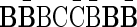 of all three elements in B2, this concatenation is not a valid BFB palindrome (see example above), and so the collection may not be folded.
of all three elements in B2, this concatenation is not a valid BFB palindrome (see example above), and so the collection may not be folded.
In Zakov et al. (2013), it was shown that the ability to fold a block collection depends on a property called the signature of the collection. A signature 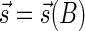 of an l-BFB palindrome collection B is an infinite sequence of integers
of an l-BFB palindrome collection B is an infinite sequence of integers 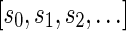 with the following properties: (1) the first nonzero element in
with the following properties: (1) the first nonzero element in  (if there is such an element) must be positive, (2) the cardinality of
(if there is such an element) must be positive, (2) the cardinality of  , defined by
, defined by 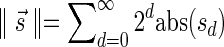 (where abs(sd) is the absolute value of sd), equals the size of B, and (3) the values sd depend only in multiplicities of distinct elements in B and their top values. The prefix of a signature
(where abs(sd) is the absolute value of sd), equals the size of B, and (3) the values sd depend only in multiplicities of distinct elements in B and their top values. The prefix of a signature 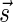 up to its d-th element is denoted by
up to its d-th element is denoted by 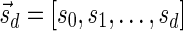 . The formal definition of a signature is given in the Appendix, and we refer intrigued readers to Zakov et al. (2013) for an elaborated discussion on its properties.
. The formal definition of a signature is given in the Appendix, and we refer intrigued readers to Zakov et al. (2013) for an elaborated discussion on its properties.
We will use the notation 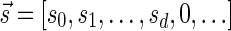 to imply that the remaining signature elements after position d are all zeros. From property (2), it follows that for a signature
to imply that the remaining signature elements after position d are all zeros. From property (2), it follows that for a signature 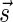 such that
such that 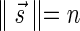 , all signature elements sd for d > log n are zeros, thus signatures can be explicitly represented by a relatively small number of nonzero elements. In particular, from properties (1) and (2) it follows that the only signature of an empty collection is
, all signature elements sd for d > log n are zeros, thus signatures can be explicitly represented by a relatively small number of nonzero elements. In particular, from properties (1) and (2) it follows that the only signature of an empty collection is 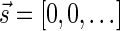 , and that the only signature of a collection containing a single element is
, and that the only signature of a collection containing a single element is 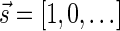 . Otherwise, two collections of the same size may have different signatures. From property (3), wrapping an l-BFB palindrome collection (i.e., replacing each l-BFB palindrome β in the collection with an (l − 1)-block
. Otherwise, two collections of the same size may have different signatures. From property (3), wrapping an l-BFB palindrome collection (i.e., replacing each l-BFB palindrome β in the collection with an (l − 1)-block 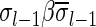 ) does not affect its signature.
) does not affect its signature.
Signatures can be ranked according to their lexicographic order. That is, say that 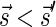 if there exists an index d such that
if there exists an index d such that  and
and 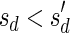 , and say that
, and say that 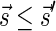 if
if 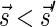 or
or  . Lemma 2 below implies that the signature series
. Lemma 2 below implies that the signature series 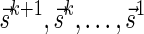 corresponding to the block collections series
corresponding to the block collections series 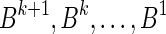 in a layered representation of a BFB palindrome is lexicographically nondecreasing.
in a layered representation of a BFB palindrome is lexicographically nondecreasing.
Lemma 2 Let B be an l-block collection with a signature
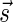 . For any folding B′ of B and its corresponding signature
. For any folding B′ of B and its corresponding signature
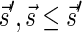 . In addition, for any signature
. In addition, for any signature
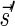 such that (1)
such that (1)
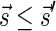 and (2)
and (2)
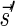 is the lexicographically minimal signature among all signatures of cardinality
is the lexicographically minimal signature among all signatures of cardinality
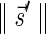 that meet (1), there exists a folding B′ of B whose signature is
that meet (1), there exists a folding B′ of B whose signature is
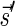 .
.
The proof of Lemma 2 follows from Claims 14 and 28 in Zakov et al. (2013) (Supporting Information). The signatures corresponding to the four block collections in Figure 3b are 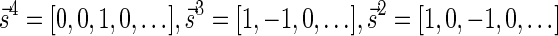 , and
, and 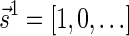 , respectively. Observe that the cardinality of each signature equals the size of the corresponding collection (i.e., the corresponding count in
, respectively. Observe that the cardinality of each signature equals the size of the corresponding collection (i.e., the corresponding count in 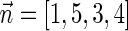 ), and that
), and that 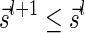 for every 1 ≤ l < 4.
for every 1 ≤ l < 4.
3.2. Valid signature series
Definition 3 A valid signature series for a vector
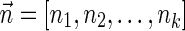 is a series of lexicographically nonincreasing signatures
is a series of lexicographically nonincreasing signatures
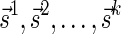 , satisfying
, satisfying
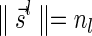 for every
for every
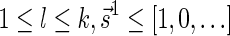 , and
, and
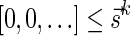 .
.
For convenience, we will sometimes consider the signatures 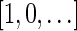 and
and 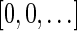 as fixed sentinel additions at the beginning and ending of a valid signature series and mark them respectively by
as fixed sentinel additions at the beginning and ending of a valid signature series and mark them respectively by 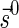 and
and 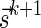 . If
. If 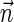 is a BFB count vector, there exists a BFB palindrome β with
is a BFB count vector, there exists a BFB palindrome β with 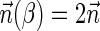 , and a corresponding collection series
, and a corresponding collection series 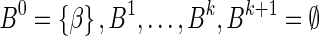 in the layers representation of β. Lemma 2 implies that the corresponding signature series for this collection series is a valid signature series for
in the layers representation of β. Lemma 2 implies that the corresponding signature series for this collection series is a valid signature series for 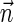 , since for every 0 ≤ l ≤ k, Bl is obtained by applying a folding operation over Bl+1 that can only increase the lexicographic signature rank, and a wrapping operation that does not change the signature. On the other hand, if there exists a valid signature series
, since for every 0 ≤ l ≤ k, Bl is obtained by applying a folding operation over Bl+1 that can only increase the lexicographic signature rank, and a wrapping operation that does not change the signature. On the other hand, if there exists a valid signature series 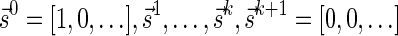 for
for 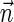 , it is possible to generate a BFB palindrome β with
, it is possible to generate a BFB palindrome β with 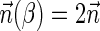 as follows. Run the schematic layered algorithm described above with respect to
as follows. Run the schematic layered algorithm described above with respect to 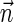 , where each time a folding operation is applied it is such that yields the minimal signature increment with respect to its input and output collections. Since
, where each time a folding operation is applied it is such that yields the minimal signature increment with respect to its input and output collections. Since 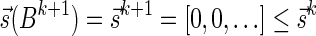 and
and 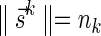 , Lemma 2 implies that it is possible to fold Bk+1 into a (k + 1)-BFB palindrome collection of size nk, and that the lexicographically minimal signature
, Lemma 2 implies that it is possible to fold Bk+1 into a (k + 1)-BFB palindrome collection of size nk, and that the lexicographically minimal signature 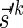 of such a collection satisfies
of such a collection satisfies 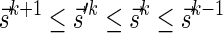 . Inductively, each generated block collection Bl in this process has a corresponding signature
. Inductively, each generated block collection Bl in this process has a corresponding signature 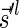 that satisfies
that satisfies 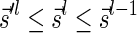 , and from Lemma 2 it can be folded into the next collection in the series Bl−1 without a folding failure. We hence get the following conclusion:
, and from Lemma 2 it can be folded into the next collection in the series Bl−1 without a folding failure. We hence get the following conclusion:
Conclusion 4 A vector
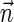 is a BFB vector if and only if it has a valid signature series. Moreover, any subsequence of a BFB vector is also a BFB vector, evident by the corresponding subseries of a valid signature series for the full vector.
is a BFB vector if and only if it has a valid signature series. Moreover, any subsequence of a BFB vector is also a BFB vector, evident by the corresponding subseries of a valid signature series for the full vector.
For example, the vector 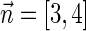 is a BFB vector, due to the valid signature series
is a BFB vector, due to the valid signature series 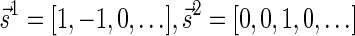 . A corresponding BFB string may be obtained by
. A corresponding BFB string may be obtained by 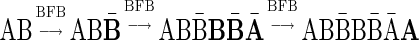 . An example for a vector that does not have a valid signature series is the vector
. An example for a vector that does not have a valid signature series is the vector 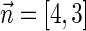 . The only signatures with cardinality 4 that rank lexicographically between
. The only signatures with cardinality 4 that rank lexicographically between 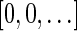 and
and 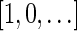 are the signatures
are the signatures 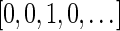 and
and 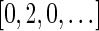 , and the only such signature with cardinality 3 is
, and the only such signature with cardinality 3 is 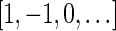 . The latter signature does not precede lexicographically any of the two possible 4-cardinality signatures, therefore no valid signature series for
. The latter signature does not precede lexicographically any of the two possible 4-cardinality signatures, therefore no valid signature series for  exists.
exists.
A valid signature series for a given count vector, if exists, can be computed iteratively by processing the counts in the vector one by one. This process can be done either by traversing the counts from n1 to nk, or traversing them in a reversed order. Next, we describe this computation.
Let 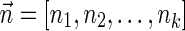 be a BFB vector, and let 1 ≤ l ≤ k + 1. Define the right-maximal signature
be a BFB vector, and let 1 ≤ l ≤ k + 1. Define the right-maximal signature
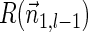 of the prefix
of the prefix 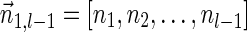 of
of 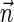 to be
to be  if l = 1, and otherwise to be the lexicographically maximal signature
if l = 1, and otherwise to be the lexicographically maximal signature 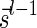 in some valid signature series
in some valid signature series 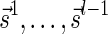 for
for  . Similarly, define the left-minimal signature
. Similarly, define the left-minimal signature
 of the suffix
of the suffix 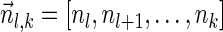 of
of  to be
to be  if l = k + 1, and otherwise to be the lexicographically minimal signature
if l = k + 1, and otherwise to be the lexicographically minimal signature 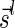 in some valid signature series
in some valid signature series 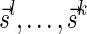 for
for 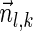 .
.
Lemma 5 Let
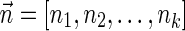 be a BFB vector. For every 1 ≤ l′ ≤ l ≤ k + 1,
be a BFB vector. For every 1 ≤ l′ ≤ l ≤ k + 1, 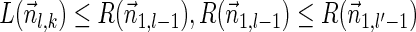 , and
, and
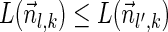 .
.
Proof: We start by showing the first inequality in the lemma. If l = 1 or 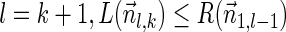 follows immediately. Otherwise, consider a valid signature series
follows immediately. Otherwise, consider a valid signature series  for
for 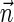 . Note that its prefix
. Note that its prefix 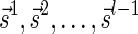 is a valid signature series for
is a valid signature series for 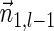 , and its suffix
, and its suffix 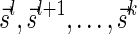 is a valid signature series for
is a valid signature series for 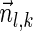 . Thus, by definition,
. Thus, by definition, 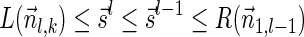 .
.
To show the second inequality in the lemma, let 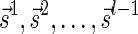 be a valid signature series for
be a valid signature series for 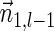 such that
such that 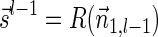 . Observe similarly as above that
. Observe similarly as above that 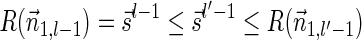 . The last inequality in the lemma is shown symmetrically. ■
. The last inequality in the lemma is shown symmetrically. ■
The MIN-DECREMENT procedure (Algorithm 1) gets as an input a signature 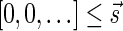 and an integer n ≥ 0, and returns the lexicographically maximal signature
and an integer n ≥ 0, and returns the lexicographically maximal signature 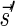 such that
such that 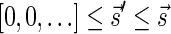 and
and 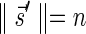 if such a signature exists, and otherwise it returns a fail message. Here, for an integer m ≠ 0, the notation dm represents the maximum integer such that m divides by
if such a signature exists, and otherwise it returns a fail message. Here, for an integer m ≠ 0, the notation dm represents the maximum integer such that m divides by 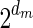 . Thus, for example,
. Thus, for example, 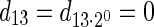 , and
, and 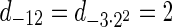 . The correctness of this computation is shown in the Appendix. Symmetrically, the MIN-INCREMENT procedure gets as an input a signature
. The correctness of this computation is shown in the Appendix. Symmetrically, the MIN-INCREMENT procedure gets as an input a signature 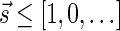 and an integer n ≥ 0, and returns the lexicographically minimal signature
and an integer n ≥ 0, and returns the lexicographically minimal signature 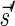 such that
such that 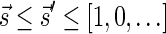 and
and 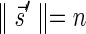 if such a signature exists, and otherwise it returns a fail message. The pseudocode for this procedure is given in the Appendix, and its proof is symmetric to that of the MIN-DECREMENT procedure.
if such a signature exists, and otherwise it returns a fail message. The pseudocode for this procedure is given in the Appendix, and its proof is symmetric to that of the MIN-DECREMENT procedure.
Lemma 6 If
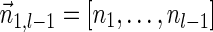 is a BFB vector,
is a BFB vector, 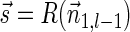 , and MIN-DECREMENT(
, and MIN-DECREMENT(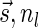 ) does not fail and returns a signature
) does not fail and returns a signature
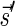 , then
, then
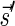 is the right-maximal signature for the BFB vector
is the right-maximal signature for the BFB vector
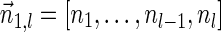 . Symmetrically, if
. Symmetrically, if
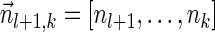 is a BFB vector,
is a BFB vector, 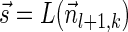 , and MIN-INCREMENT(
, and MIN-INCREMENT(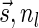 ) does not fail and returns a signature
) does not fail and returns a signature
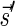 , then
, then
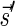 is the left-minimal signature for the BFB vector
is the left-minimal signature for the BFB vector
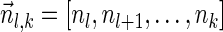 .
.
Proof: We show the first part of the lemma, where the second part is shown symmetrically. First, note that the constructed vector 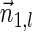 is indeed a BFB vector, due to the corresponding valid signature series obtained by adding
is indeed a BFB vector, due to the corresponding valid signature series obtained by adding  to a valid signature series for
to a valid signature series for 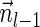 whose last signature is
whose last signature is 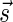 . Note that
. Note that  . From Lemma 5
. From Lemma 5 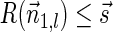 , and since
, and since 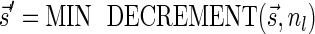 it follows that
it follows that 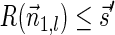 . From the maximality of
. From the maximality of 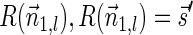 . ■
. ■
Lemma 6 implies a simple algorithm for deciding if a given vector 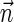 is a BFB vector. Such an algorithm tries generating a valid signature series for
is a BFB vector. Such an algorithm tries generating a valid signature series for 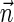 either by starting from the first signature
either by starting from the first signature 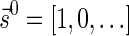 , and generating each signature
, and generating each signature 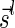 by applying the MIN-INCREMENT procedure with respect to
by applying the MIN-INCREMENT procedure with respect to 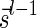 and nl, or by starting from the last signature
and nl, or by starting from the last signature 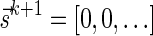 , and generating each signature
, and generating each signature 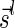 by applying the MIN-DECREMENT procedure with respect to
by applying the MIN-DECREMENT procedure with respect to 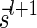 and nl. If the MIN-INCREMENT or MIN-DECREMENT procedures fail at some stage, then the algorithm reports
and nl. If the MIN-INCREMENT or MIN-DECREMENT procedures fail at some stage, then the algorithm reports 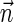 not to be a BFB vector. Otherwise, the algorithm succeeds to generate a valid signature series for
not to be a BFB vector. Otherwise, the algorithm succeeds to generate a valid signature series for 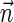 , and reports
, and reports 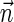 to be a BFB vector. As a matter of fact, Algorithm DECISION-BFB in Zakov et al. (2013) is equivalent to the right-to-left version of the above algorithm.
to be a BFB vector. As a matter of fact, Algorithm DECISION-BFB in Zakov et al. (2013) is equivalent to the right-to-left version of the above algorithm.
3.3. Solving the exhaustive BFB variants
In this section, let W be a weight function, and 0 < η ≤ 1 some weight threshold. Let 0 ≤ l ≤ k, and consider the set of all signature-weight pairs of the form 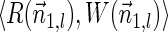 such that
such that 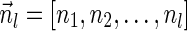 is a BFB vector and
is a BFB vector and 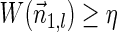 . Say that the pair
. Say that the pair 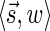 within this set dominates the pair
within this set dominates the pair 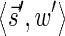 if
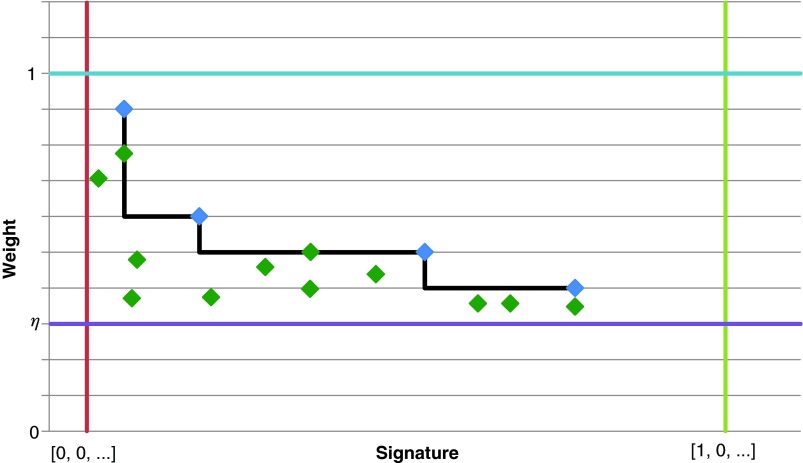
if 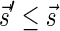 and w′≤w. Define the l-th boundary curve Cl with respect to W and η as the maximal subset of these pairs satisfying that no pair in Cl dominates another pair in Cl, and note that Cl is unique. Traversing the pairs in Cl from lowest to highest lexicographic signature rank, the series of signature values strictly increases, while the series of weight values strictly decreases, yielding a steplike curve (Fig. 4). Given W and η, Algorithm 2 generates boundary curves Cl for every 0 ≤ l ≤ k, which will later be exploited by algorithms for the BFB exhaustive vector and string search variants.
and w′≤w. Define the l-th boundary curve Cl with respect to W and η as the maximal subset of these pairs satisfying that no pair in Cl dominates another pair in Cl, and note that Cl is unique. Traversing the pairs in Cl from lowest to highest lexicographic signature rank, the series of signature values strictly increases, while the series of weight values strictly decreases, yielding a steplike curve (Fig. 4). Given W and η, Algorithm 2 generates boundary curves Cl for every 0 ≤ l ≤ k, which will later be exploited by algorithms for the BFB exhaustive vector and string search variants.
FIG. 4.
A boundary curve. Points correspond to pairs of the form 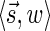 , with x-coordinate reflecting the lexicographic rank of
, with x-coordinate reflecting the lexicographic rank of 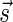 , and y-coordinate equaling w. Blue points belong to the boundary curve, and green points are dominated by points on the curve.
, and y-coordinate equaling w. Blue points belong to the boundary curve, and green points are dominated by points on the curve.
Proof: [Algorithm 2] Note that a pair in C0 corresponds to a right-maximal signature and a weight of an empty vector. By definition, the only such pair is the pair 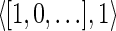 , and the algorithm correctly sets C0 to contain this single pair (line 1). Now, assuming inductively the algorithm has computed correctly the curve Cl−1, we prove it also computes correctly Cl. It is clear from lines 6 and 7 of the algorithm that no pair in the set Cl computed by the algorithm dominates another pair in this set. It therefore remains to show that after the l-th loop iteration was executed: (1) for every BFB vector
, and the algorithm correctly sets C0 to contain this single pair (line 1). Now, assuming inductively the algorithm has computed correctly the curve Cl−1, we prove it also computes correctly Cl. It is clear from lines 6 and 7 of the algorithm that no pair in the set Cl computed by the algorithm dominates another pair in this set. It therefore remains to show that after the l-th loop iteration was executed: (1) for every BFB vector 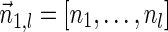 with
with 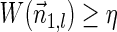 there exists a pair
there exists a pair 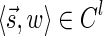 , which dominates
, which dominates 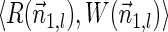 , and (2) for every pair
, and (2) for every pair 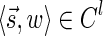 there exists some BFB vector
there exists some BFB vector 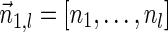 such that
such that 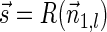 and
and 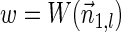 .
.
We start by showing (1). Let 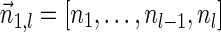 be a BFB vector with
be a BFB vector with 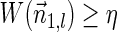 , and consider its prefix
, and consider its prefix 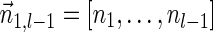 . Observe that
. Observe that 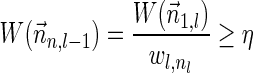 . As
. As 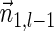 is also a BFB vector, the inductive assumption implies that Cl−1 contains a pair
is also a BFB vector, the inductive assumption implies that Cl−1 contains a pair  that dominates
that dominates  . From Lemma 5,
. From Lemma 5, 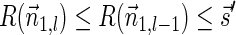 . Since
. Since 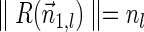 , running MIN-DECREMENT
, running MIN-DECREMENT  does not fail, and returns a signature
does not fail, and returns a signature  such that
such that 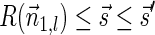 and
and 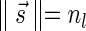 . As
. As 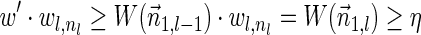 , it follows that the algorithm runs the code in lines 5–7 with respect to nl and
, it follows that the algorithm runs the code in lines 5–7 with respect to nl and  . In particular, the algorithm updates Cl with the pair
. In particular, the algorithm updates Cl with the pair 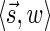 for
for 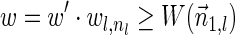 (lines 6–7). Therefore, at the end of the l-th iteration, either Cl contains
(lines 6–7). Therefore, at the end of the l-th iteration, either Cl contains 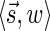 , or it contains some other signature-weight pair that dominates
, or it contains some other signature-weight pair that dominates 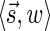 , and so it contains a pair that dominates
, and so it contains a pair that dominates 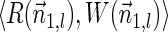 .
.
To show (2), assume that Cl contains a pair 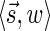 . This pair was added to Cl in line 7 of the algorithm, which means there exists some pair
. This pair was added to Cl in line 7 of the algorithm, which means there exists some pair 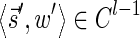 such that for
such that for 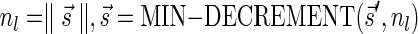 , and
, and 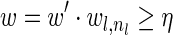 . From the inductive assumption, there is BFB vector
. From the inductive assumption, there is BFB vector 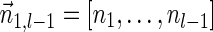 such that
such that 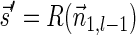 and
and 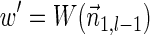 . For the vector
. For the vector 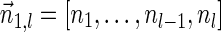 , lemma 6 implies that
, lemma 6 implies that 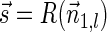 . In addition,
. In addition, 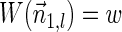 , and the lemma follows. ■
, and the lemma follows. ■
In Appendix section 6.2 we show that the number an of all signatures with cardinality n satisfies 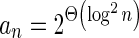 . Since no two pairs in a boundary curve share the same signature, the number of pairs in a boundary curve with cardinality n is bounded by
. Since no two pairs in a boundary curve share the same signature, the number of pairs in a boundary curve with cardinality n is bounded by 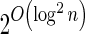 . It would be quite realistic to assume that for a segment l and its corresponding most likely count
. It would be quite realistic to assume that for a segment l and its corresponding most likely count 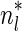 , all counts n such that wl,n ≥ η satisfy
, all counts n such that wl,n ≥ η satisfy 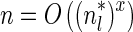 for some constant x. This implies that the total number of different elements in a boundary curve is bounded by the subexponential term
for some constant x. This implies that the total number of different elements in a boundary curve is bounded by the subexponential term 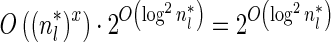 . In particular, the number of candidates
. In particular, the number of candidates 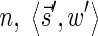 examined in line 4 of Algorithm 2 is
examined in line 4 of Algorithm 2 is 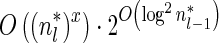 . Over each such candidate, the condition in line 6 is examined, and it may induce at most one insertion of a pair into Cl, and possibly one future deletion from Cl (if the inserted pair is dominated by a pair that is inserted into Cl later on). It is possible to maintain the pairs in Cl sorted, and implement the condition check in line 6 and insertions and deletions from Cl in line 7 in
. Over each such candidate, the condition in line 6 is examined, and it may induce at most one insertion of a pair into Cl, and possibly one future deletion from Cl (if the inserted pair is dominated by a pair that is inserted into Cl later on). It is possible to maintain the pairs in Cl sorted, and implement the condition check in line 6 and insertions and deletions from Cl in line 7 in 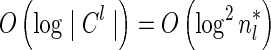 time per operation, for example, using a self-balancing binary search tree (Knuth, 1998). Thus, the l-th iteration of the algorithm runs in
time per operation, for example, using a self-balancing binary search tree (Knuth, 1998). Thus, the l-th iteration of the algorithm runs in 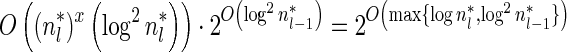 time, and the total running time of the algorithm is
time, and the total running time of the algorithm is 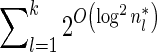 .
.
Next, we present Algorithm 3 for the BFB exhaustive vector search variant. The algorithm processes the segments of the input one by one, starting from the k-th segment down to the first segment. The notation [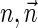 ] is used for denoting a vector whose first element is the integer n, and its remaining suffix is the vector
] is used for denoting a vector whose first element is the integer n, and its remaining suffix is the vector 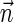 .
.
Proof: [Algorithm 3] By definition, if the boundary curve Ck is empty, it implies there is no BFB vector 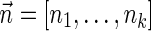 with
with 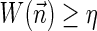 . In this case, the algorithm correctly reports there is no solution to the input (line 1).
. In this case, the algorithm correctly reports there is no solution to the input (line 1).
Otherwise, we show for every 1 ≤ l ≤ k+1 that the following invariant holds: After Ql is fully computed, Ql contains
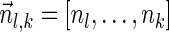 if and only if
if and only if
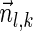 is a suffix of some BFB vector
is a suffix of some BFB vector
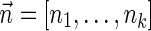 of weight
of weight
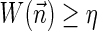 . In particular, this invariant proves that the returned value Q1 (line 9) is indeed the solution for the BFB exhaustive vector search variant, and so it only remains to establish the correctness of the invariant.
. In particular, this invariant proves that the returned value Q1 (line 9) is indeed the solution for the BFB exhaustive vector search variant, and so it only remains to establish the correctness of the invariant.
For l = k + 1, the fact that Qk+1 contains a single empty suffix (line 2) derives the invariant in a straightforward manner. Otherwise, assuming inductively the invariant holds with respect to Ql+1, we prove it also holds with respect to Ql.
Let 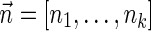 be a BFB vector of weight
be a BFB vector of weight 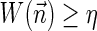 , and consider its two suffixes
, and consider its two suffixes 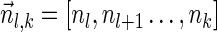 and
and 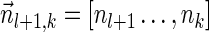 . From the inductive assumption,
. From the inductive assumption, 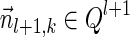 . From Lemma 6,
. From Lemma 6, 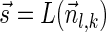 satisfies that
satisfies that 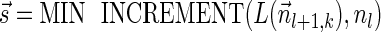 . Since
. Since 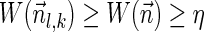 , the condition in line 5 holds, and lines 6–8 are executed with respect to
, the condition in line 5 holds, and lines 6–8 are executed with respect to  and
and  . Note that the prefix
. Note that the prefix  of
of 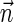 is a BFB vector with
is a BFB vector with 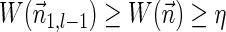 . From the definition of Cl−1, there exists a pair
. From the definition of Cl−1, there exists a pair 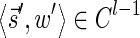 that dominates the pair
that dominates the pair 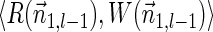 . From Lemma 5,
. From Lemma 5, 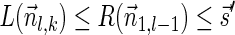 . In addition,
. In addition, 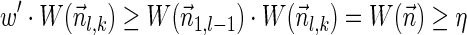 , and so the condition in line 7 holds, and the algorithm adds
, and so the condition in line 7 holds, and the algorithm adds 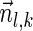 into Ql in line 8.
into Ql in line 8.
For the other direction of the invariant, let 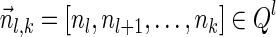 . Due to the manner it was constructed (lines 5–6), its suffix
. Due to the manner it was constructed (lines 5–6), its suffix 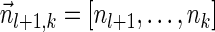 is in Ql+1, and from Lemma 6,
is in Ql+1, and from Lemma 6, 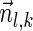 is a BFB vector with
is a BFB vector with 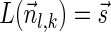 . From line 7, there exists a pair
. From line 7, there exists a pair 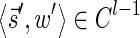 such that
such that 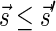 and
and 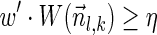 , and so from the definition of Cl−1 there exists a BFB vector
, and so from the definition of Cl−1 there exists a BFB vector 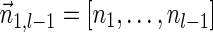 for which
for which 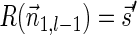 and
and 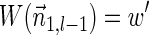 . The concatenation of
. The concatenation of  and
and  gives the vector
gives the vector 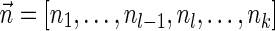 , whose weight satisfies
, whose weight satisfies 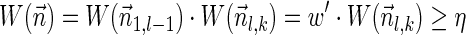 . In addition,
. In addition, 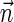 is a BFB vector, due to the corresponding valid signature series obtained by concatenating a valid signature series for
is a BFB vector, due to the corresponding valid signature series obtained by concatenating a valid signature series for 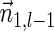 that ends with
that ends with  and a valid signature series for
and a valid signature series for 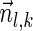 that starts with
that starts with 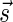 , concluding this direction of the proof. ■
, concluding this direction of the proof. ■
Finally, we describe an algorithm for the exhaustive BFB string search variant. This algorithm applies a similar approach to the exhaustive vector search algorithm in order to produce all BFB strings whose count vector weights are at least η. The pseudocode for this computation is given in Algorithm 4. It starts by generating signature curves exactly as done by Algorithm 3. Then, in each iteration l, instead of computing a set Ql of count vectors, the algorithm computes a set Pl of l-block collections. The initial collection Pk+1 contains a single empty (k + 1)-block collection. In the l-th iteration, for each (l + 1)-block collection Bl+1 ∈ Pl+1, all possible foldings of Bl+1 are enumerated, and each such folding is rendered into an l-block collection Bl as described in section 3.1 (the term “wrapped folding” in line 5 of the algorithm refers to these l-block collections). The notation W (Bl) is used for denoting the weight of the vector 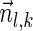 such that
such that 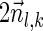 is the summation of count vectors of all strings in Bl. The signature and weight of Bl are examined against Cl−1 similarly as done in line 7 of Algorithm 3, and if meeting the condition Bl is added into Pl. After P1 is computed, all foldings of collections B1 in P1 into 1-BFB palindromes are enumerated, and all half-length prefixes of such palindromes are reported. Algorithm 4 can be proven similarly to Algorithm 3, using the following invariant: At the end of the l-th iteration, Pl contains all l-block collections Bl such that there exists some 1-BFB palindrome β in which the l-th layer's block collection is Bl, and the weight of the vector
is the summation of count vectors of all strings in Bl. The signature and weight of Bl are examined against Cl−1 similarly as done in line 7 of Algorithm 3, and if meeting the condition Bl is added into Pl. After P1 is computed, all foldings of collections B1 in P1 into 1-BFB palindromes are enumerated, and all half-length prefixes of such palindromes are reported. Algorithm 4 can be proven similarly to Algorithm 3, using the following invariant: At the end of the l-th iteration, Pl contains all l-block collections Bl such that there exists some 1-BFB palindrome β in which the l-th layer's block collection is Bl, and the weight of the vector  such that
such that  satisfies
satisfies  .
.
4. Results
In order to test our algorithms we have used cancer data taken from the Cancer Genome Project dataset (Bignell et al., 2010). This data covers aCGH samples (Affymetrix Genome-Wide Human SNP Array 6.0) from 746 human cancer cell lines. Segmentation and segment copy numbers are as reported by Bignell et al. (2010), who used the PICNIC software (Greenman et al., 2010) for this analysis. In total, the dataset contains about 35,000 chromosomal arms (746 samples, 23 or 24 chromosomes per sample, 2 arms per chromosome), each arm is segmented, and each segment is assigned an estimated copy number based on the observed aCGH data. As shown in Zakov et al. (2013), short BFB-like count vectors have a high probability to emerge even when the genome was rearranged with mechanisms different from BFB. Thus, in order to detect significant BFB evidence we have filtered the set of chromosomal arms to include only arms with at least eight consecutive segments such that no adjacent segments share the same copy number estimation. After this filtration, the remaining subset included 6589 chromosomal arms. As the estimated counts reflect the expected segment copy numbers in all copies of the chromosome in the sample, we have corrected the counts by reducing p − 1 from each count, where p is the ploidy (i.e., the number of copies) of the chromosome in the sample. Typically p = 2, but since these are heavily rearranged cancer genomes, chromosomal losses and whole chromosomal duplications are not rare. We therefore allowed the value of p to vary between 1 and 5, and run the BFB analyses for each value.
As currently no analysis tool available produces count weights, we have derived such weights from the expected counts reported by PICNIC (after correcting for ploidy). Specifically, for a segment whose observed count is n, the weight of a count n′ was defined by 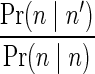 , where
, where 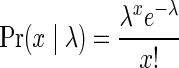 is the probability to observe the value x for a random variable distributing according to the Poisson distribution with parameter λ. For each of the obtained weight functions, we used the DISTANCE-BFB algorithm from Zakov et al. (2013) to report all longest BFB subvectors with weight at least η = 0.7. Out of the 6589 samples, 54 samples had for at least one ploidy value 1 ≤ p ≤ 5 a BFB subvector of length at least 8. Some samples had long BFB subvectors with respect to more than one ploidy value, and the total number of obtained BFB vectors was 86.
is the probability to observe the value x for a random variable distributing according to the Poisson distribution with parameter λ. For each of the obtained weight functions, we used the DISTANCE-BFB algorithm from Zakov et al. (2013) to report all longest BFB subvectors with weight at least η = 0.7. Out of the 6589 samples, 54 samples had for at least one ploidy value 1 ≤ p ≤ 5 a BFB subvector of length at least 8. Some samples had long BFB subvectors with respect to more than one ploidy value, and the total number of obtained BFB vectors was 86.
Then, we considered the segment coordinates and weight functions corresponding to the obtained subvectors and ran Algorithm 3 in order to find all BFB vectors of weights at least η = 0.7 with respect to these weight functions. For these 86 instances, a total number of 19154 heavy BFB vectors were found, with an average of 222 solutions per instance. This reveals an interesting property of the problem when applied over this data: the vast majority of samples, 6535 out of 6589, cannot be explained by any BFB count vector (and thus are unlikely to be obtained from BFB), yet each one of those 54 samples that can be explained by BFB has about several tens or hundreds of corresponding count vectors.
The above analysis was run by two variants of our algorithm—the IS variant described by Algorithm 3, and a variant that runs a similar procedure without applying the IS optimization (essentially, it runs the same code as Algorithm 3, with the exceptions that it does not generate the boundary curves in line 1 and does not apply the condition in line 7 before adding new elements to collections Ql). The disadvantage of the non-IS variant is in that sets of the form Ql maintains BFB vectors 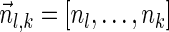 , which may not be suffixes of some BFB vectors
, which may not be suffixes of some BFB vectors 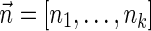 of weight at least η. To measure the gain of the IS algorithm, we count the number of signature increment attempts the algorithms perform (line 5). On average, the IS variant performed 57-fold less increments, with a total number of 5672346 increment attempts over all 86 vectors, versus 325343441 for the non-IS algorithm. While the IS variant has a clear efficiency advantage over the non-IS variant, this advantage might be considered more modest than expected. A possible reason for that is that maximum copy number values reported in Bignell et al. (2010) were limited to 14, even when the data suggests higher copy numbers. In general, higher copy numbers usually imply a higher number of alternative heavy counts, which in turn induce a higher number of possible heavy count vectors. For example, when comparing the two algorithms over the synthetic count vector
of weight at least η. To measure the gain of the IS algorithm, we count the number of signature increment attempts the algorithms perform (line 5). On average, the IS variant performed 57-fold less increments, with a total number of 5672346 increment attempts over all 86 vectors, versus 325343441 for the non-IS algorithm. While the IS variant has a clear efficiency advantage over the non-IS variant, this advantage might be considered more modest than expected. A possible reason for that is that maximum copy number values reported in Bignell et al. (2010) were limited to 14, even when the data suggests higher copy numbers. In general, higher copy numbers usually imply a higher number of alternative heavy counts, which in turn induce a higher number of possible heavy count vectors. For example, when comparing the two algorithms over the synthetic count vector 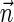 = [3, 8, 111, 8, 5, 150, 11, 170, 4, 53, 100, 75, 49, 10, 42, 18], using the same Poisson-based weights as described above and requiring that output vectors weigh at least η = 0.85, the non-IS algorithm runs 218 seconds1 and performs over 20 million signature increments, whereas the IS algorithm runs 120 milliseconds and performs 635 signature increments. Both algorithms return exactly the same output—a set of 18 BFB vectors. Other simulated inputs can cause memory explosion for the non-IS variant, while being handled efficiently by the IS variant.
= [3, 8, 111, 8, 5, 150, 11, 170, 4, 53, 100, 75, 49, 10, 42, 18], using the same Poisson-based weights as described above and requiring that output vectors weigh at least η = 0.85, the non-IS algorithm runs 218 seconds1 and performs over 20 million signature increments, whereas the IS algorithm runs 120 milliseconds and performs 635 signature increments. Both algorithms return exactly the same output—a set of 18 BFB vectors. Other simulated inputs can cause memory explosion for the non-IS variant, while being handled efficiently by the IS variant.
5. Discussion and Conclusions
The problem of detecting breakage fusion bridge is challenging, but significant progress has been made in the last few years. Our work suggests that while rare, BFB does occur in tumor-derived cell lines and also in primary tumors. In this work, we describe algorithms that can be used to enumerate all possible BFB architectures given uncertain copy number data.
The results of our analyses heavily depend on the input weights, which in turn depend on separated analyses applied to biological data. While we used here a simple Poisson-based model in order to render fixed available count estimations into weight functions, it is clear that more realistic weighing can be applied. Examining Figure 2, for example, one can observe that different segments demonstrate different variance in signal intensities, implying that some count estimates are more reliable than others. Incorporating segment lengths and signal variance information when choosing count weights is likely to produce more meaningful weights and improve the quality of the analyses output.
Different measurements can yield other types of BFB evidence. For example, deep sequencing experiments can sequence reads spanning genomic breakpoints. In a BFB modified genome, it is expected that many of these breakpoints reflect fold-back inversions (i.e., concatenations between reference segments and their inverted form), while such fold-back patterns are less common in other rearrangement mechanisms (Campbell et al., 2010). Thus, identification of high or low fold-back pattern frequencies can support or weaken the conjecture BFB has occurred, respectively. Such evidence is less frequent in currently available data, as reliable breakpoint information requires sequencing to a relatively high depth of coverage (while copy number data can be obtained also from sequencing with a lower depth of coverage or from aCGH experiments). When given though, such information can be integrated and improve the quality of BFB calling (Zakov et al., 2013).
As a last note, we would like to point out the fact that the concept of Informed Search (IS) was used here in a slightly unorthodox manner. Generally, IS methods attempt to reduce computation time in practice by exploiting additional information about the search space (given as an input to the algorithm or such that can be efficiently computed). Typically, such methods apply heuristic information for prioritizing the order in which different regions of the search space are examined to accelerate the search for a single solution to the input instance (e.g., the A* and AO* algorithms in Pearl, 1984). In contrast, the two search algorithms described in this article exploit exact information encapsulated in the computed boundary curves, utilize it for pruning the search space from regions that are guaranteed to contain no solution to the given instance, and thus accelerate the search for all solutions.
6. Appendix
In this Appendix we complete some of the technical details omitted above. We show how BFB palindromes are composed recursively from shorter palindromes, describe how to derive signatures of BFB palindrome collections, show there are 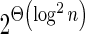 different signatures of cardinality n, prove the MIN-DECREMENT algorithm correctness, and give the pseudocode for the MIN-INCREMENT algorithm. Most of the material in this section appears in Zakov et al. (2013) and is given here for completeness, except for the lower bound over the number of signatures with a given cardinality, which is first established here.
different signatures of cardinality n, prove the MIN-DECREMENT algorithm correctness, and give the pseudocode for the MIN-INCREMENT algorithm. Most of the material in this section appears in Zakov et al. (2013) and is given here for completeness, except for the lower bound over the number of signatures with a given cardinality, which is first established here.
6.1. Recursive decomposition of BFB palindromes
Definition 7 A string α is a convexed l-palindrome if α = ɛ, or α = γβγ, γ is a convexed l-palindrome, β is an l-BFB palindrome, and top(γ) < top(β).
Thus, for example, the following strings are all convexed 1-palindromes: γ = ɛAĀɛ [a 1-block with top(γ) = 1], γ′ = 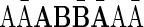 = γβγ [for the 1-bock β =
= γβγ [for the 1-bock β = 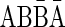 , with top(γ′) = top(β) = 2], and
, with top(γ′) = top(β) = 2], and 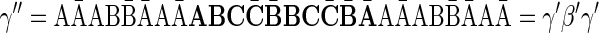 [for the 1-BFB palindrome β′ =
[for the 1-BFB palindrome β′ = 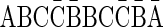 , with top(γ′′) = top(β′) = 3]. Note that every l-BFB palindrome α is also a convexed l-palindrome, since either α = ɛ or α = ɛαɛ.
, with top(γ′′) = top(β′) = 3]. Note that every l-BFB palindrome α is also a convexed l-palindrome, since either α = ɛ or α = ɛαɛ.
Claim 1 in Zakov et al. (2013) A string α is an l-BFB palindrome if and only if α = ɛ, α is an l-block, or α = βγβ, such that β is an l-BFB palindrome, γ is a convexed l-palindrome, and top(γ) ≤ top(β).
Therefore, for the 1-BFB palindrome β = 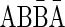 and the convexed 1-palindrome
and the convexed 1-palindrome 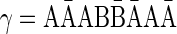 , the string
, the string 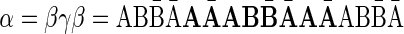 is a 1-BFB palindrome. A BFB process that yields this string can be, for example,
is a 1-BFB palindrome. A BFB process that yields this string can be, for example, 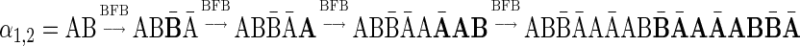 . More generally, the above claim lays the rules for constructing BFB palindromes by concatenating shorter BFB palindromes and convexed palindromes, rather than applying a sequence of BFB cycles. Its proof is given in Zakov et al. (2013). These composition rules are used in order to enumerate all foldings of a given l-BFB palindrome collection by the exhaustive BFB string search algorithm.
. More generally, the above claim lays the rules for constructing BFB palindromes by concatenating shorter BFB palindromes and convexed palindromes, rather than applying a sequence of BFB cycles. Its proof is given in Zakov et al. (2013). These composition rules are used in order to enumerate all foldings of a given l-BFB palindrome collection by the exhaustive BFB string search algorithm.
6.2. Signature computation and counting
Let 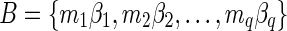 be an l-BFB palindrome collection. Define mod2 (B) to be the subcollection of B containing a single copy of each distinct element with an odd count in B. For example, for B = {2ß1, ß2, 5ß3, 6ß4}, mod2 (B) = {ß2, ß3}. Define
be an l-BFB palindrome collection. Define mod2 (B) to be the subcollection of B containing a single copy of each distinct element with an odd count in B. For example, for B = {2ß1, ß2, 5ß3, 6ß4}, mod2 (B) = {ß2, ß3}. Define 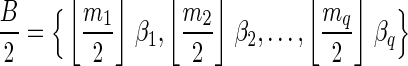 . In the above example,
. In the above example,  . Observe that
. Observe that 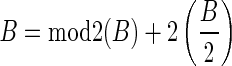 .
.
In order to compute the signature of B, we first recursively decompose it into subcollections. Define B0 = B. For every d ≥ 0, define Ld = mod2 (Bd), 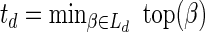 or td = ∞ when Ld = ∅,
or td = ∞ when Ld = ∅, 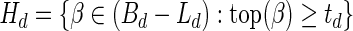 , and
, and 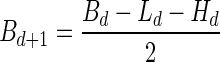 . Now, the signature
. Now, the signature  is computed as follows: s0 = |L0|, and
is computed as follows: s0 = |L0|, and 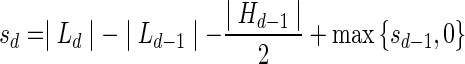 for every d > 0. Table 1 gives a signature computation example for a collection B = {2β1,5β2,6β3,2β4,4β5}. We assume that elements are ordered with decreasing top values, that is top(βi) ≥ top(βi+1) for i = 1,2,3,4. It can be asserted that the signature cardinality equals to the collection size:
for every d > 0. Table 1 gives a signature computation example for a collection B = {2β1,5β2,6β3,2β4,4β5}. We assume that elements are ordered with decreasing top values, that is top(βi) ≥ top(βi+1) for i = 1,2,3,4. It can be asserted that the signature cardinality equals to the collection size: 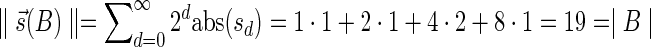 .
.
Table 1.
Signature Computation
| d | Bd | Ld | Hd | sd |
|---|---|---|---|---|
| 0 | {2β1, 5β2, 6β3, 2β4, 4β5} | {β2} | {2β1, 4β2} | 1 |
| 1 | {3β3, β4, 2β5} | {β3, β4} | {2β3} | −1 |
| 2 | {β5} | {β5} | ∅ | −2 |
| 3 | ∅ | ∅ | ∅ | −1 |
| 4 | ∅ | ∅ | ∅ | 0 |
 |
 |
 |
 |
 |
Next, we show how to count the number of different signatures with a given cardinality. The only signature with cardinality 0 is the signature 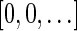 . In a signature
. In a signature 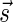 with cardinality
with cardinality 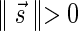 there must be at least one nonzero element. It can be asserted from the above signature definition that the first nonzero element in a signature must be positive. Nevertheless, we will relax this requirement and assume a signature can be any series of integers. Let bn denote the number of such relaxed signatures of cardinality n, and let an denote the number of signatures of cardinality n in which the first nonzero element is positive. The only signatures with cardinality 1 are the signatures
there must be at least one nonzero element. It can be asserted from the above signature definition that the first nonzero element in a signature must be positive. Nevertheless, we will relax this requirement and assume a signature can be any series of integers. Let bn denote the number of such relaxed signatures of cardinality n, and let an denote the number of signatures of cardinality n in which the first nonzero element is positive. The only signatures with cardinality 1 are the signatures 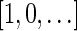 and
and 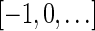 . Therefore, a0 = a1 = 1 and b0 = 1,b1 = 2. With the exception of n = 0, it is simple to observe that
. Therefore, a0 = a1 = 1 and b0 = 1,b1 = 2. With the exception of n = 0, it is simple to observe that 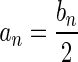 , for example, by observing that any signature
, for example, by observing that any signature 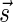 of the latter kind can be uniquely matched to a pair of signatures of the former kind—
of the latter kind can be uniquely matched to a pair of signatures of the former kind—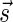 itself, and the signature
itself, and the signature 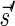 in which all elements have the same absolute values as in
in which all elements have the same absolute values as in 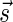 and opposite signs.
and opposite signs.
For n > 1, partition the set of all signatures 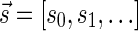 with
with 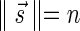 into two subsets: signatures with abs(s0) > 1, and signatures with abs(s0) ≤ 1. Every signature
into two subsets: signatures with abs(s0) > 1, and signatures with abs(s0) ≤ 1. Every signature  in the first group corresponds to a unique signature
in the first group corresponds to a unique signature 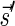 of cardinality n − 1, where
of cardinality n − 1, where 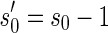 if s0 > 1 and
if s0 > 1 and 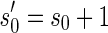 if s0 < −1, and all other elements in
if s0 < −1, and all other elements in  equal to the corresponding elements in
equal to the corresponding elements in  . Every signature
. Every signature  in the second group corresponds to a unique signature
in the second group corresponds to a unique signature  of cardinality
of cardinality  , which is obtained by removing from
, which is obtained by removing from  its first element (i.e., setting
its first element (i.e., setting 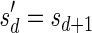 for every d ≥ 0). Therefore, the sizes of these groups are bn−1 and
for every d ≥ 0). Therefore, the sizes of these groups are bn−1 and 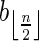 , respectively, and so
, respectively, and so 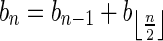 . As
. As 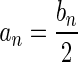 , we get that
, we get that
 |
with the initial terms a0 = a1 = 1. The series {an} is cataloged in the On-Line Encyclopedia of Integer Sequences (OEIS), entry A033485 (Sloane, 2007). Next, we show subexponential lower and upper bounds over an.
Claim 8 The series {an} satisfies
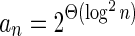 for every integer n ≥ 0.
for every integer n ≥ 0.
Proof: To show an upper bound, observe that for 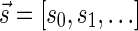 with
with 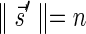 it immediately follows that abs(sd) ≤
it immediately follows that abs(sd) ≤ 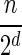 for every d ≥ 0, and in particular sd = 0 for d > log n. For d ≤ log n,
for every d ≥ 0, and in particular sd = 0 for d > log n. For d ≤ log n, 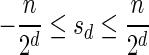 , and so it is possible to represent sd using log n − d + 2 bits. Thus, the number of bits needed for representing
, and so it is possible to represent sd using log n − d + 2 bits. Thus, the number of bits needed for representing 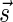 can be bounded by
can be bounded by 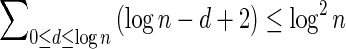 , and the total number of different signatures with cardinality n is at most
, and the total number of different signatures with cardinality n is at most  .
.
A lower bound over an is next given by showing that 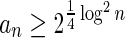 . For n < 4 the inequality can be asserted in a simple manner. For n ≥ 4, assuming inductively that
. For n < 4 the inequality can be asserted in a simple manner. For n ≥ 4, assuming inductively that 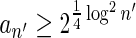 for every n′ < n, we show that
for every n′ < n, we show that 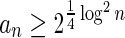 . First, observe that
. First, observe that 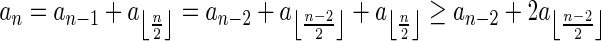 . When n divides by 4,
. When n divides by 4,
 |
From the inductive assumption, we get that  . When n divides by 4 with a reminder of 1, 2, or 3, the inequality is proven similarly. ■
. When n divides by 4 with a reminder of 1, 2, or 3, the inequality is proven similarly. ■
6.3. The Min-Increment and Min-Decrement Procedures
We next turn to prove the correctness of the MIN-DECREMENT procedure, and give the pseudocode of the symmetric MIN-INCREMENT procedure. We start by showing in Lemma 9 an elementary property of signatures, and then use this property to derive the procedures' implementation.
Lemma 9 Let
 and
and
 be two signatures, such that
be two signatures, such that
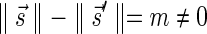 . Then, there exists an index 0 ≤ d ≤ dm such that
. Then, there exists an index 0 ≤ d ≤ dm such that
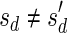 . In addition, for the minimum such index d,
. In addition, for the minimum such index d, 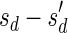 is even when d < dm, and
is even when d < dm, and
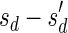 is odd when d = dm.
is odd when d = dm.
Proof: By definition, m does not divide by 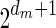 , and so
, and so
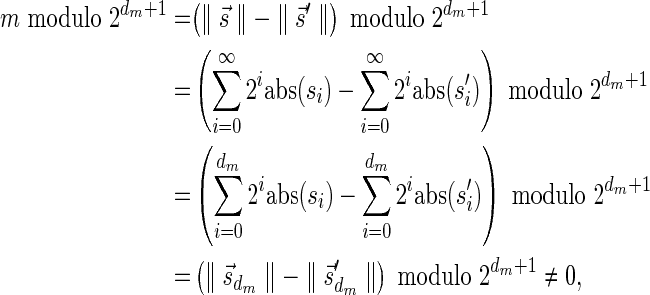 |
therefore, there must be an index 0 ≤ d ≤ dm such that  . Let d be the minimum such index (where
. Let d be the minimum such index (where  ). Similarly as above,
). Similarly as above,
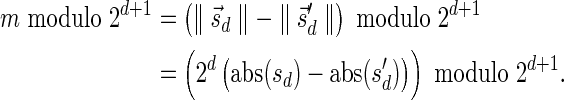 |
Now, if d < dm then m modulo 2d+1 = 0, therefore abs(sd) − abs(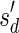 ) must be even, and in particular
) must be even, and in particular 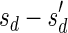 is even. If d = dm, m modulo 2d+1 ≠ 0, abs(sd) − abs(
is even. If d = dm, m modulo 2d+1 ≠ 0, abs(sd) − abs(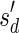 ) must be odd, and in particular
) must be odd, and in particular 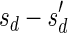 is odd. Next, we show the correctness of the MIN-DECREMENT procedure (Algorithm 1). ■
is odd. Next, we show the correctness of the MIN-DECREMENT procedure (Algorithm 1). ■
Proof: [MIN-DECREMENT] First, note that if 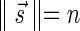 , then
, then 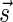 satisfies the requirements on the output of the procedure, and due to line 1 in the procedure
satisfies the requirements on the output of the procedure, and due to line 1 in the procedure 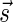 is indeed the returned signature.
is indeed the returned signature.
Otherwise, assume there exists a signature 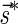 such that
such that 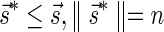 , and
, and 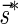 is the lexicographically maximal signature among all signatures satisfying these requirements. For this purpose, we do not make the assumption that
is the lexicographically maximal signature among all signatures satisfying these requirements. For this purpose, we do not make the assumption that 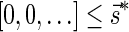 . We will show that if
. We will show that if  exists then the signature
exists then the signature 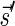 computed in lines 3–5 of the procedure equals to
computed in lines 3–5 of the procedure equals to 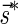 , and that otherwise a fail message is returned in line 7. Note that when
, and that otherwise a fail message is returned in line 7. Note that when 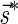 exists yet
exists yet 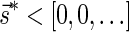 , the procedure returns a fail message in line 6.
, the procedure returns a fail message in line 6.
Under the assumption 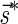 exists, the value of m computed line 1 is
exists, the value of m computed line 1 is 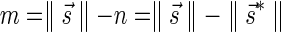 . From Lemma 9, there exists an index 0 ≤ d* ≤ dm such that
. From Lemma 9, there exists an index 0 ≤ d* ≤ dm such that  , and
, and 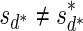 . Since
. Since 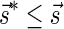 , it must hold that
, it must hold that 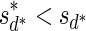 , and so
, and so 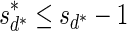 . Therefore,
. Therefore, 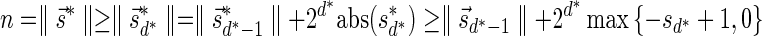 . In particular, d* satisfies the condition in line 2. Consequentially, if the condition in line 2 does not hold, it contradicts the existence of
. In particular, d* satisfies the condition in line 2. Consequentially, if the condition in line 2 does not hold, it contradicts the existence of  , and the procedure indeed returns a fail message in this case (line 7).
, and the procedure indeed returns a fail message in this case (line 7).
Next, assume the condition in line 2 is met, and let 0 ≤ d ≤ dm be the maximum index satisfying 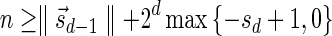 , as selected in line 3. Thus, d ≥ d*. Denote δ = 1 if d = dm, and δ = 2 if d < dm. We will consider separately the two cases of computing the signature
, as selected in line 3. Thus, d ≥ d*. Denote δ = 1 if d = dm, and δ = 2 if d < dm. We will consider separately the two cases of computing the signature 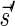 in lines 3–5. In both cases, the prefix
in lines 3–5. In both cases, the prefix 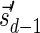 of
of 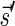 is set to be identical to the prefix
is set to be identical to the prefix 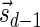 of
of 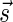 .
.
Case 1: 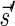 is computed according to lines 3 and 4. In this case,
is computed according to lines 3 and 4. In this case, 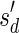 is set to sd − δ in line 3, and
is set to sd − δ in line 3, and 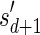 is set to
is set to 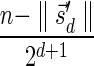 in line 4. All values
in line 4. All values 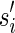 for i > d + 1 are implicitly set to zeros. Also, the condition
for i > d + 1 are implicitly set to zeros. Also, the condition 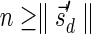 holds in line 4, in particular
holds in line 4, in particular 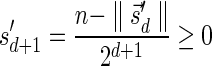 , and so abs
, and so abs 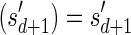 . Observe that
. Observe that 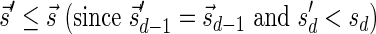 , and that
, and that 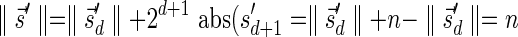 .
.
By definition, 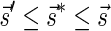 . Since
. Since  , it follows that
, it follows that  . In addition, since d* ≤ d and since
. In addition, since d* ≤ d and since 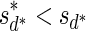 , it must be that d = d*. From Lemma 9,
, it must be that d = d*. From Lemma 9, 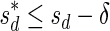 , and since
, and since 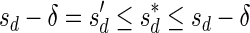 it follows that
it follows that 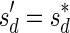 , thus
, thus 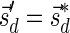 . Finally, since
. Finally, since 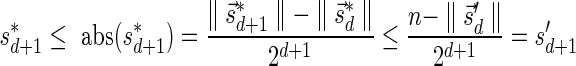 , it follows that
, it follows that  . Now, as
. Now, as 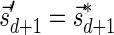 , and since
, and since  , it follows that for every i > d + 1, we have that
, it follows that for every i > d + 1, we have that  , and so
, and so  .
.
Case 2:  is computed according to lines 3 and 5. Here, the condition in line 4 does not hold, that is. (and due to the initialization of
is computed according to lines 3 and 5. Here, the condition in line 4 does not hold, that is. (and due to the initialization of  in lines 3–4),
in lines 3–4), 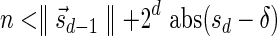 . Now,
. Now,  is set to be
is set to be 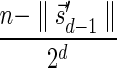 in line 5, and all values
in line 5, and all values  for i > d are implicitly set to zeros. We start by showing it that sd > 0 in this case.
for i > d are implicitly set to zeros. We start by showing it that sd > 0 in this case.
Assume by contradiction that sd ≤ 0. As d ≤ dm, the number 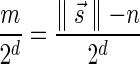 is an integer. We get that
is an integer. We get that 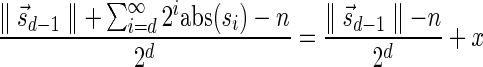 is an integer for the integer
is an integer for the integer 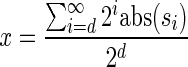 , and so
, and so 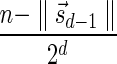 is an integer. From the conditions in lines 2 and 4 and since sd ≤ 0 by assumption,
is an integer. From the conditions in lines 2 and 4 and since sd ≤ 0 by assumption, 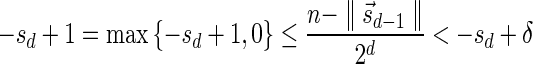 . Therefore, it must be that δ = 2, and that
. Therefore, it must be that δ = 2, and that 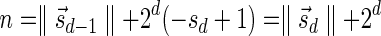 . Moreover, since δ = 2, it follows that d < dm. Nevertheless, we get that
. Moreover, since δ = 2, it follows that d < dm. Nevertheless, we get that 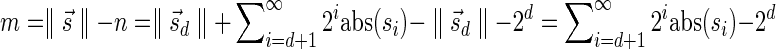 . This implies that m does not divide by 2d+1 ≤ 2dm, in contradiction to the definition of dm.
. This implies that m does not divide by 2d+1 ≤ 2dm, in contradiction to the definition of dm.
As we have established that sd > 0, we can observe that 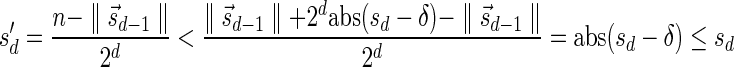 . Therefore,
. Therefore, 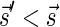 . It can be shown similarly as in Case 1 that
. It can be shown similarly as in Case 1 that 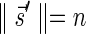 and that
and that 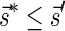 , completing the proof. ■
, completing the proof. ■
The MIN-INCREMENT procedure is proven symmetrically, and its pseudocode is given in Algorithm 5. It is in fact a simplified version of the SIGNATURE-FOLD procedure in Zakov et al. (2013) (Supporting Information).
Acknowledgments
The authors are thankful to the anonymous JCB and RECOMB reviewers for their helpful comments. The research was supported by grants from the NIH (RO1-HG004962) and the NSF (CCF-1115206, IIS-1318386).
Author Disclosure Statement
No competing financial interests exist.
Running time was measured for an intel Core i7 processor with Microsoft Windows 7 operating system; code is implemented in Java.
References
- Alkan C., Kidd J.M., Marques-Bonet T., et al. 2009. Personalized copy number and segmental duplication maps using next-generation sequencing. Nat. Genet. 41, 1061–1067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bignell G.R., Greenman C.D., Davies H., et al. 2010. Signatures of mutation and selection in the cancer genome. Nature 463, 893–898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bignell G.R., Santarius T., Pole J.C., et al. 2007. Architectures of somatic genomic rearrangement in human cancer amplicons at sequence-level resolution. Genome Res. 17, 1296–1303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campbell P.J., Yachida S., Mudie L.J., et al. 2010. The patterns and dynamics of genomic instability in metastatic pancreatic cancer. Nature 467, 1109–1113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr A.M., Paek A.L., and Weinert T. 2011. DNA replication: failures and inverted fusions. Semin. Cell Dev. Biol. 22, 866–874 [DOI] [PubMed] [Google Scholar]
- Chiang D.Y., Getz G., Jaffe D.B., et al. 2009. High-resolution mapping of copy-number alterations with massively parallel sequencing. Nat. Methods 6, 99–103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckel-Passow J.E., Atkinson E.J., Maharjan S., et al. 2011. Software comparison for evaluating genomic copy number variation for Affymetrix 6.0 SNP array platform. BMC Bioinform. 12, 220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenman C., Bignell G., Butler A., et al. 2010. PICNIC: an algorithm to predict absolute allelic copy number variation with microarray cancer data. Biostatistics 11, 164–175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenman C., Cooke S., Marshall J., et al. 2012. Modelling breakage-fusion-bridge cycles as a stochastic paper folding process. arXiv. Available at: http://arxiv.org/abs/1211.2356 [DOI] [PMC free article] [PubMed]
- Hanahan D., and Weinberg R.A. 2011. Hallmarks of cancer: the next generation. Cell 144, 646–674 [DOI] [PubMed] [Google Scholar]
- Hastings P.J., Lupski J.R., Rosenberg S.M., et al. 2009. Mechanisms of change in gene copy number. Nat. Rev. Genet. 10, 551–564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinsella M., and Bafna V. 2012. Combinatorics of the breakage-fusionbridge mechanism. J. Comput. Biol. 19, 662–678 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitada K., and Yamasaki T. 2008. The complicated copy number alterations in chromosome 7 of a lung cancer cell line is explained by a model based on repeated breakage-fusion-bridge cycles. Cancer Genet. Cytogenet. 185, 11–19 [DOI] [PubMed] [Google Scholar]
- Knuth D.E. 1998. The Art of Computer Programming, Volume 3: Sorting and Searching. International Monetary Fund, Washington, DC [Google Scholar]
- McClintock B. 1938. The production of homozygous deficient tissues with mutant characteristics by means of the aberrant mitotic behavior of ring-shaped chromosomes. Genetics 23, 315–376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClintock B. 1941. The stability of broken ends of chromosomes in zea mays. Genetics 26, 234–282 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedev P., Stanciu M., and Brudno M. 2009. Computational methods for discovering structural variation with next-generation sequencing. Nat. Methods 6, 13–20 [DOI] [PubMed] [Google Scholar]
- Olshen A.B., Venkatraman E., Lucito R., et al. 2004. Circular binary segmentation for the analysis of array-based dna copy number data. Biostatistics 5, 557–572 [DOI] [PubMed] [Google Scholar]
- Pearl J. 1984. Heuristics. Addison-Wesley Publishing Company, Reading, MA [Google Scholar]
- Reshmi S., Roychoudhury S., Yu Z., et al. 2007. Inverted duplication pattern in anaphase bridges confirms the breakage-fusion-bridge (bfb) cycle model for 11q13 amplification. Cytogenet. Genome Res. 116, 46–52 [DOI] [PubMed] [Google Scholar]
- Sloane N.J. 2007. The on-line encyclopedia of integer sequences, 130. In Towards Mechanized Mathematical Assistants. Springer, New York: Available at: http://oeis.org/A033485 [Google Scholar]
- Venkatraman E.S., and Olshen A.B. 2007. A faster circular binary seg-71 mentation algorithm for the analysis of array cgh data. Bioinformatics 23, 657–663 [DOI] [PubMed] [Google Scholar]
- Yoon S., Xuan Z., Makarov V., et al. 2009. Sensitive and accurate detection of copy number variants using read depth of coverage. Genome Res. 19, 1586–1592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zakov S., Kinsella M., and Bafna V. 2013. An algorithmic approach for breakage-fusion-bridge detection in tumor genomes. Proc. Natl. Acad. Sci. USA 110, 5546–5551 [DOI] [PMC free article] [PubMed] [Google Scholar]