Significant association between body composition phenotypes and the osteocalcin genomic region in normative human population

Abstract

Osteocalcin, a major inorganic component of bone matrix and marker of bone formation, is also involved in regulation of glucose and fat mass metabolism. However, much uncertainty remains about whether the above effect on fat mass has a genetic component. Our main aim was to test whether a variation of body composition phenotypes is associated with BGLAP genomic region variants. To achieve this aim, we used an ethnically homogeneous discovery sample of 230 families consisting of 1112 apparently healthy individuals (561 males and 551 females) of European origin. We conducted association analysis between six SNPs and five obesity-related phenotypes: plasma levels of leptin, anthropometrical fat mass (FM), principal component scores of eight skinfold (SK_PC) and nine circumference (CR_PC) measurements, and body mass index (BMI). Two powerful and robust tools were applied: the pedigree disequilibrium test and variance component models, taking into account both familial and genetic effects. Significant association results were observed for all phenotypes. The most significant results were observed between the haplotype composed of three SNPs (rs2758605-rs1543294-rs2241106) and BMI (p = 8.07⁻⁷), and CR_PC (p = 5.29⁻⁵). The association with BMI was tested and confirmed in our replication study, including 2244 unrelated adult US Caucasians, who were previously assessed for whole genome SNP data. In addition, we obtained an evidence of potential non-additive interactions between the above three SNPs concerning their association with BMI. Bioinformatics sources suggest that the aforementioned interaction could originate from different genetic loci in this region; however, ascertaining the exact circumstances requires a detailed molecular-genetic study.

Introduction

Over the last decade, there has been a growing body of direct and indirect evidence suggesting complex and intimate interrelationships between adipose and bone tissues, including a specific link between body composition and serumosteocalcin [1]. It has become increasingly apparent that both adipose and bone tissues exhibit inter-related endocrine functions including production of leptin and adiponectin by adipocytes [2], as well as osteocalcin and fibroblast growth factor 23 by bone cells [3]. The published data also consistently indicate that adipose tissue can regulate bone remodeling via leptin, and that insulin influences bone metabolism via insulin-like growth factor-1 [4,5].

On the other hand, the recent data suggest that osteocalcin produced by osteoblasts is likely to be involved in regulating bone formation, and it also appears to be involved in regulating glucose and fat metabolism [6–8]. In accordance with these findings, also reports that moderate weight loss and regular exercise, as well as weight loss after bariatric surgery raise serum osteocalcin levels [9–11]. Interestingly, there are studies suggested that serum osteocalcin levels negatively correlate with the visceral fat area (VFA) and the VFA/SFA (subcutaneous fat area) ratio [8]. In addition, serum osteocalcin levels in this study were significantly reduced in obese and overweight subjects with visceral obesity (12.7 ± 3.2 ng/ml), compared with those without visceral obesity (18.6 ± 4.9). Several papers consistently reported an inverse correlation between osteocalcin plasma levels and fat mass and plasma glucose level [12–14]. These correlations are probably universal and ethnic-group independent. Tan and colleagues [15] found that osteocalcin has a significant positive correlation with HDL and a negative correlation with blood pressure, glucose, triglycerides, waist circumference, and BMI, in particular, even after adjustment for age (P < 0.001). Thus, the existing data clearly suggest a close relationship between the circulating osteocalcin and various body composition and obesity-related phenotypes.

Studying animal models has substantially impacted our understanding of the potential mechanisms underlying the interaction between adipose tissue and skeleton. This includes data that osteocalcin gene knockout mice exhibit an abnormal amount of visceral fat [16] and that these genetic mouse models display an impaired lipid and glucose metabolism, and decreased insulin secretion and sensitivity [6]. Genetic studies involving the osteocalcin gene in humans are rare. In humans osteocalcin is synthesized by the bone gamma-carboxyglutamate protein (BGLAP) gene located on chromosome 1q22, which was found to be significantly linked to type 2 diabetes [17]. However, a later study by this team [18] showed that BGLAP variants are unlikely to be major risk factors for type 2 diabetes and are unlikely to contribute to the 1q21 linkage signal in Caucasians. Regarding African Americans, this study found that the arginine to glutamine change at residue 94 of exon 4may alter glucose homeostasis traits, but this result also requires confirmation in a larger metabolic study. Thus, despite considerable accumulating data indicating a consistent correlation between the circulating osteocalcin and the obesity/energy metabolism phenotypes, we are not aware of any study that has examined associations between BGLAP polymorphisms and body composition, except for a single finding of an association between HindIII polymorphism located at the promoter region upstream from exon 1 and BMI in a modest sample of Chinese women [19]. Hence, our main objective in the present study was to test such an association in a population-based sample of ethnically homogeneous European pedigrees.

Materials and methods

Discovery sample

The basic results of this study were obtained on a cohort recruited within the framework of our project concerning the genetic epidemiology of skeletal aging in the Chuvashian population. The cohort description has been repeatedly cited by us elsewhere [20,21]. Briefly, Chuvashians are ethnic Caucasians living in numerous small villages on the Volga riverside in the Chuvashian and Bashkortostan Autonomies of the Russian Federation. The present sample includes 230 families composed of 1112 apparently healthy individuals (561 males, whose ages range from 18 to 86, and 551 females, whose ages range from 17 to 84). All participants were unaware of the specific hypotheses tested, and signed an informed consent document to participate in the study, which was conducted with the approval of the Ethics Committee of Tel Aviv University.

Anthropometrical body composition phenotypes

The following individual's measurements were used: height (cm), weight (kg), eight skinfold thicknesses (mm) (sub-scapular, chest, abdomen, hip, calf, lower arm, upper arm medial, and dorsal), and nine circumferences (mm) (chest, waist, hip, thigh, calf, ankle, wrist, upper, and lower arm). The measurements were performed using a standard anthropometric technique [22] and were described by us previously [23]. Based on these 19 measurements, the following obesity-related individual characteristics were evaluated: body mass index, BMI (kg/m²), fat mass, FM (kg), skinfold and circumference principal component analysis scores, SK_PC and CR_ PC (standardized values), respectively. The calculation formulae are detailed below, following the “Statistical and genetic analyses” section.

Biochemical measurements

Leptin plasma levels were measured by an enzyme-linked immunoassay using a commercial kit (R & D Systems, Minneapolis, Minn., USA). The results were calculated using a four-parameter curve fit and were expressed as pg/ml. The intra- and inter-assay coefficients of variation were 4% and 6%, respectively. The minimum detection dose was 7.8 pg/ml (for more details, see [24]).

SNP selection and genotyping

DNA was prepared from peripheral blood lymphocytes by standard techniques, using Nucleon™ BACC Genomic DNA Extraction Kits (Amersham International plc, UK) according to the manufacturer's protocol. The six selected SNPs were genotyped by KBiosciences (Hertsfordshire, UK) using their proprietary competitive allele-specific PCR (KASPar) method (the details are available at the company's website (www.kbioscience.co.uk/chemistry/index.htm). Based on intra-pedigree relationships, genotypes were checked for Mendelian errors using the MAN-2009 package [25].

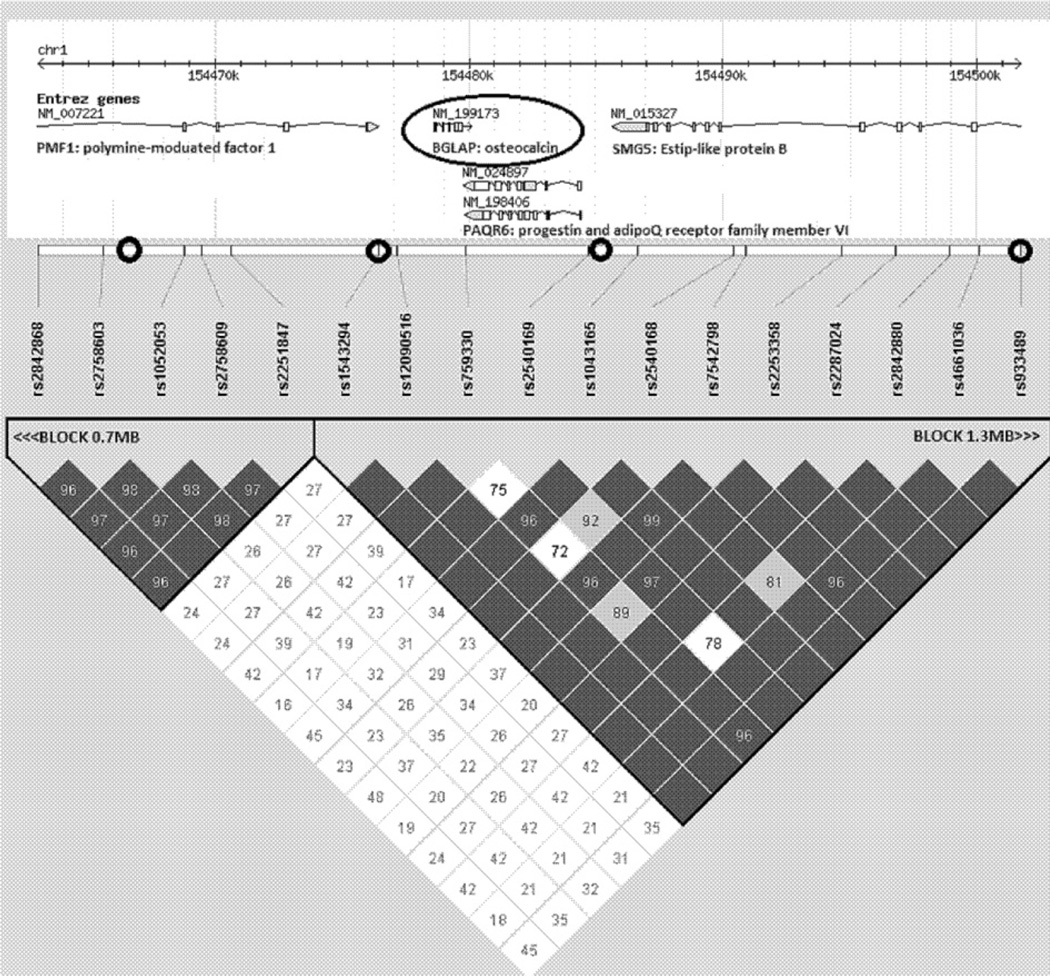
The SNPs were genotyped in a chromosomal interval of about 60 Kb covered BGLAP gene (Table 1). These SNPs belong to two broad haploblocks of 0.7 Mb and 1.3 Mb extended beyond the region of interest (Fig. 1). The quality of genotyping coverage of the region of interest was assessed on the basis of the HapMap resources (http://www.hapmap.org/). Using Haploview software we performed Tagger test, which showed that six SNPs genotyped in the present study cover the major part of the region variation, r² = 0.841. The estimation was based on all available SNPs in the interval (chromosome 1: 154,466,000–154,526,000), not including SNP deviating Hardy–Weinberg equilibrium (χ² test, p ≤ 0.05) or with MAF < 0.1.

Table 1.

Six SNPs genotyped in the BGLAP gene region.

SNP ID	Position, in bp	n, genotyped	MAF	HW (p-values)
M1: rs2758605	154467069	1096	0.320	0.232
M2: rs1543294	154476481	1097	0.251	0.180
M3: rs2241106	154485534	1087	0.341	0.185
M4: rs933489	154501744	1095	0.405	0.130
M5: rs2277872	154513352	1085	0.256	0.835
M6: rs12563631	154525577	1086	0.348	0.069

M1–M6: for the sake of simplicity, the markers’ IDs were redefined, and used in the following tables and text as M1 to M6, correspondingly; MAF: minor allele frequency; HW: the Hardy–Weinberg equilibrium test.

Fig. 1.

The BGLAP genomic region (Haploview plot). The position of the BGLAP and nearby SNPs is shown at the upper part of the figure. The triangular part of the figure shows the linkage disequilibrium pattern as measured by D′ between the SNPs. The position of SNPs (M1–M4) selected for this study are denoted by black circlets. Two additional selected SNPs (M5 and M6) are located more distantly from BGLAP, in the downstream region.

Statistical and genetic analyses

Preliminary statistical analyses of the original measurements were conducted using the STATISTICA 7.1 package (www.statsoft.com). Fat mass was estimated using skinfold measurements, body weight, and the age and sex of an individual according to Jackson et al.'s formulas [26,27]. According to the American College of Sports Medicine [28], implementation of this method for assessing body fat mass is up to 98% accurate in comparison with DXA, when performed by a trained and skilled tester. Descriptive statistics were computed separately for males and females. To avoid data redundancy due to high and significant inter-correlations between the eight skinfold thickness and nine circumference measurements, two corresponding principle components (SK_PC and CR_PC) were computed, implementing factor analysis [23], and were used in this study. Two other obesity-related phenotypes, BMI and waist-hip ratio (WHR), were calculated by ordinary: BMI (kg/m²) = weight/height² and WHR = waist circumference (mm)/hip circumference (mm).

Prior to genetic-association analysis, the studied phenotypes were adjusted for sex and age effects. This was performed by using the most parsimonious best-fitting polynomial models for each trait, as previously described in detail [29]. The adjustment procedure and further statistical-genetic analyses were conducted using the MAN-2009 package [25]. Based on intra-pedigree relationships, SNP genotypes were checked for Mendelian errors, and the individual's haplotypes were reconstructed (for details, see [21]).

Association analysis between marker allele or haplotype and the quantitative trait was performed using the pedigree disequilibrium test (PDT). PDT utilizes all available phenotypes in extended pedigrees and, as a result, possesses more statistical power than do regular transmission disequilibrium tests [30]. To take into account the potential effect of multiple testing, the false discovery rate (FDR) correction procedure was applied [31].

Since more than one SNP was significantly associated with the particular phenotype, variance component (VC) analysis was applied to test the combined effects of the SNP genotypes. The variance decomposition model assumes that a total quantitative trait variation (V_TOT) is caused by additive genetic factors (V_AD), a common family environment (V_CF), and individual, specific, unexplained residual environmental factors (V_RS). In addition, this analysis allows one to model quantitative phenotype variation as a function of covariates such as sex, age, and SNP-specific genotype. To test the SNP effect, the corresponding genotypes were coded according to the number of copies of a rare allele carried by the individual: 0 – non carrier, 1 – one dose, and 2 – two-dose carriers. Non-additive effects of alleles of interest were calculated by multiplying their number in the corresponding individual SNP-allele combination. The statistical significance of all models and the corresponding parameter estimates were assessed using the likelihood ratio test (LRT), by comparing the more general with the more restricted model (more details of the implemented method are given in [30]).

Replication sample

The main results observed in the initial sample were tested in an additional sample (replication sample), including data on 2244 unrelated adult US Caucasians (540 males, mean age 50.72 (SD = 16.05) and 1704 females, mean age 51.59 (SD = 12.92) collected randomly from apparently healthy individuals. This sample was described in detail previously [32] and consists of individuals, each of whom was assessed for BMI and who has whole genome SNP data, from which the SNPs previously mentioned were chosen. The genotype distributions at each of the selected SNPs did not deviate from the Hardy–Weinberg equilibrium expectations.

Results

The main characteristics of the selected SNPs are presented in Table 1. As shown, all six SNPs were considerably polymorphic (MAF ≥ 0.24) and their genotype frequency distributions did not deviate from the expected Hardy–Weinberg equilibrium (χ² test, p > 0.05). Close linkage disequilibrium was observed between all pairs of adjacent SNPs (D′ > 0.95), except for a pair including rs2758605 and rs1543294 (D′ > 0.48) in the upstream region.

The basic descriptive statistics of the sample phenotypes, for males and females separately, is presented in Table 2. All anthropometrical measurements as well as plasma leptin levels were significantly different between the sexes. The size phenotypes, as expected, were larger in men, whereas the adiposity-related phenotypes (BMI, FM, and PLL) were larger in women. The distribution of PLL had a significant skewness (1.78 ± 0.07) and therefore was subject to log-normal transformation to normalize the distribution in further analysis. All phenotypes, adjusted for age and sex differences, exhibited substantial familial aggregation and significant heritability estimates, ranging from 0.41 to 0.82.

Table 2.

Basic descriptive statistics of the body composition phenotypes included in the study.

Trait	h2 ± SE	Males				Females
		n	Mean	SD	r2	n	Mean	SD	r2
Age (years)		561	46.24	17.07		551	47.66	16.63
Stature (cm)	0.772 ± 0.128	549	166.4	6.77	0.242	539	154.6	5.90	0.232
Weight (kg)	0.601 ± 0.011	548	64.24	10.48	0.032	539	60.68	12.36	0.046
BMI (kg/m2)	0.484 ± 0.103	551	23.32	3.46	0.021	538	25.64	5.08	0.143
Fat mass (kg)	0.456 ± 0.129	440	8.52	3.88	0.045	413	11.59	5.69	0.075
Leptin (ng/ml)	0.409 ± 0.085	459	1.80	1.78	0.041	435	8.36	6.20	0.001

h²: heritability, the proportion of the total variance attributable to putative genetic effects; r²: the proportion of the total trait variance attributable to correlation with age; fat mass was assessed in each individual based on skinfold thickness measurements (Materials and methods).

The results of the pedigree-based association analysis (PDT) of the body composition phenotypes, adjusted for age and sex, are given in Table 3. Three SNPs, defined as M3, M4, and M6, showed significant associations with the studied phenotypes. The number of the statistically significant associations, 13, was substantially higher than expected by chance only, 1.5 (i.e. 30 tests × 0.05 type I error). Two of the p-values between M4 and BMI (p = 0.001) and CR-PC (p = 0.002) passed the expected critical levels by FDR. Therefore, we next examined the discriminating ability of the association tests utilizing the haplotypes composed from the alleles of the neighboring SNPs. In this analysis, only individuals with unambiguously reconstructed haplotypes were included. Significant associations were found for haplotypes involving SNPs from M2 to M6. As shown, the most significant results were observed for haplotypes composed of the most frequent alleles of adjacent SNPs. Hence, we next tested whether the association results could be improved by using haplotypes in which triplets of the adjacent SNPs were combined. The most impressive association results were obtained between the G-C-G haplotype, composed of the most frequent alleles in the M1–M3 markers, and all the phenotypes, but in particular, with BMI: p = 8.07⁻⁷ and CR_PC: p = 5.29⁻⁵ (Table 3). These two p-values are considerably lower than those expected from FDR: p = 0.0004 and 0.0007, respectively. The haplotypes composed of M4–M6 did not substantially enhance the association signals in comparison with the previous results.

Table 3.

Association results obtained for six selected polymorphisms in the BGLAP gene region.

Marker	na	Alleleb	Freq	BMI	CR_PC	SK_PC	Leptin	Fat mass
M1	1096	G	0.675	0.128	0.159	0.187	0.572	0.671
		G-T	0.192	0.639	0.783	0.932	0.579	0.496
M1–M2	1041	G-C	0.495	0.029	0.120	0.162	0.361	0.431
		C-C	0.275	0.187	0.431	0.202	0.569	0.912
M2	1097	C	0.754	0.480	0.348	0.938	0.689	0.841
		T-G	0.226	0.835	0.683	0.725	0.931	0.497
M2–M3	1019	C-G	0.439	0.001	0.002	0.032	0.028	0.018
		C-C	0.334	0.007	0.011	0.029	0.036	0.200
M3	1087	G	0.655	0.005	0.011	0.027	0.023	0.029
		G-G	0.280	0.682	0.819	0.750	0.862	0.642
M3–M4	994	C-G	0.328	0.004	0.006	0.024	0.025	0.137
		G-A	0.392	0.001	0.003	0.035	0.016	0.014
M4	1095	A	0.600	0.001	0.002	0.019	0.011	0.014
		G-C	0.234	0.230	0.173	0.635	0.549	0.351
M4–M5	1012	G-A	0.376	0.031	0.083	0.073	0.052	0.274
		A-A	0.390	0.002	0.003	0.023	0.015	0.015
M5	1085	A	0.749	0.498	0.446	0.984	0.624	0.671
		C-T	0.227	0.690	0.570	0.902	0.609	0.841
M5–M6	1007	A-T	0.426	0.001	0.044	0.024	0.044	0.014
		A-C	0.344	0.008	0.017	0.037	0.061	0.043
M6	1086	T	0.645	0.011	0.024	0.051	0.060	0.047
M1–M2–M3	898	G-C-G	0.259	8.07E-07	5.29E-05	0.0009	0.0028	0.0021
M4–M5–M6	829	A-A-T	0.407	0.0018	0.0090	0.0298	0.0764	0.0483

Marker designations are the same as in Table 1; the definitions of the phenotypes are given in Materials and methods. Significant results (p < 0.05) are in bold for the sake of convenience.

^an: the sample size available for the specific analysis.

^bFrequent alleles are listed for individual SNPs.

To clarify the discriminating effect of the M1–M3 markers, we conducted variance component analysis of the study phenotypes, using these SNPs as covariates. Table 4 presents the major results observed for BMI. Comparison of the competing models confirms that each of the three markers, M1, M2 and M3, has a significant effect on the BMI variation in our sample. Exclusion of any of them from the general model leads to a significant deterioration of data fitting by the likelihood ratio test (the last row in Table 4). These seemingly contradictory results with separate SNP testing (M1 and M2, Table 3) can probably be explained by the LD pattern in this genomic region and non-additive interaction of SNPs (see Discussion). It should be mentioned that when M3 was included in the VC analysis, three other SNPs, M4–M6, located more distantly from BGLAP had no additional effect on BMI variation (not shown in the table). The variance decomposition of the familial component of the BMI variation (three upper lines, Table 4) suggests that the additive genetic component explains about 46.8% of the total residual familial variance, i.e. σ_AD²/(σ_AD²+σ_SB²+σ_RS²). The shared sib environment component (σ_SB²) was small, but still significant. The VC analysis results obtained with other phenotypes were similar to those obtained for BMI but were less clear cut and therefore are not shown here.

Table 4.

Variance component analysis of the BMI variation testing effect of M1–M3.

Parameter	General model	Model 1	Model 2	Model 3
σAD2	0.451 (±0.095)	0.461	0.467	0.456
σSB2	0.063 (±0.027)	0.062	0.063	0.065
σRS2	0.449 (±0.073)	0.448	0.443	0.458
β1	−0.093 (±0.035)	(F) 0	−0.074	−0.070
β2	−0.094 (±0.038)	−0.072	(F) 0	−0.030
β3	−0.152 (±0.038)	−0.136	−0.113	(F) 0
Log(LH)	−1264.880	−1268.350	−1267.880	−1272.670
LRT(p-value)		0.0084	0.0143	0.0001

General model tested association of three SNPs (M1, M2, and M3) simultaneously with the BMI variation. Model 1 excluded the effect of M1, and models 2 and 3 excluded the effects of M2 and M3, respectively. The VC model parameters: σ_AD²: proportion of the total variance of BMI was attributable to the additive genetic effects (excluding the effect of the tested SNP), σ_SB²: common sibs’ environment, σ_RS²: residual environmental effects. β₁, β₂, β₃: regression coefficients measuring the effect of each of the SNPs on BMI variation; LH is the log-likelihood of the model. LRT is the likelihood ratio test. For markers’ definitions, see Table 1.

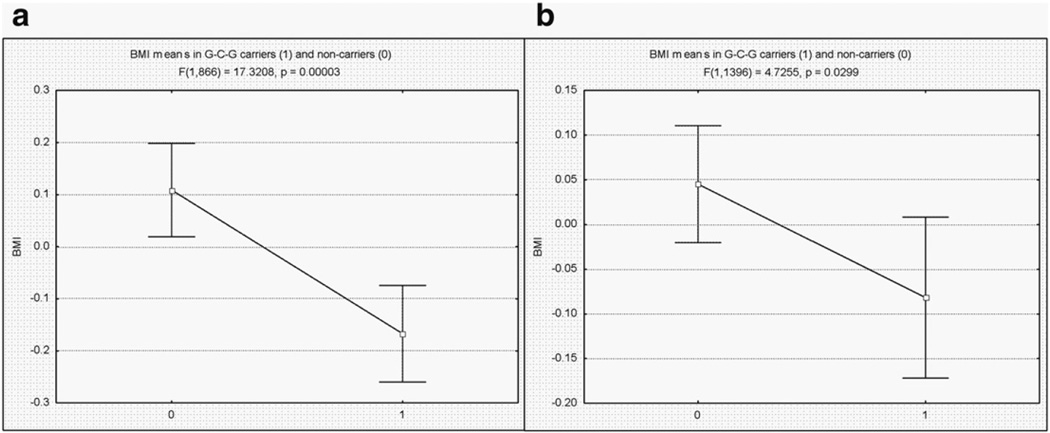
The most substantial association between BMI and the G-C-G haplotype was examined in our replication sample (see Materials and methods). In this sample, the mean BMI by sex was 28.06 (SD = 4.77) and 26.76 (SD = 5.85) in males and in females, respectively, and the differences were statistically significant (t = 4.68, p < 0.001). The BMI variation was also significantly correlated with age (r_F = 0.13 and r_M = 0.18, p < 0.0001), and was therefore adjusted for sex and age effects prior to further analysis. Since the replication sample represents unrelated individuals, an unbiased haplotype recovery could be performed only in homozygotes and single heterozygotes [33]. As a result, haplotypes composed of M1–M3 were recovered only in 1398 out of the 2244 individuals available in the total sample. The average BMI in G-C-G carriers as compared to the non-carriers is presented in Fig. 2b. As shown, the difference achieved a statistically significant level (t = 2.17, p = 0.029), and it showed the same trend as observed in the Chuvashian sample (Fig. 2a), where differences between carriers and non-carriers were highly significant, p = 0.00003.

Fig. 2.

Comparison of BMI in G-C-G haplotype carriers, group “0” and non-carriers, group “1” in (a) Chuvachian and (b) replication samples. Individual BMI values are adjusted for age and sex effects. The means are shown with their corresponding 95% CI.

Since BMI and CR_PC are complex, inter-correlated (r = 0.92) phenotypes, each including different components of body mass and not only fat mass, it was of interest to examine whether the adjustment of each of them for fat phenotypes (SK_PC, FM, and LLP) would change the association with the G-C-G haplotype. Using a modification of VC analysis, we found that this association remained statistically significant for both BMI and CR_PC (Table 5). However, adjusting the fat phenotypes for BMI diminishes the strength of the corresponding association to a negligible level (p > 0.36; not shown in the table).

Table 5.

Summary of variance component analyses of BMI and CR_PC variation with simultaneous adjustment for fat-related covariates and testing for G-C-G haplotype effect.

Parameter	M(BMI)	M0(BMI)	M(CR_PC)	M0(CR_PC)
σAD2	0.063 ± 0.014	0.066	0.113 ± 0.021	0.113
σRS2	0.092 ± 0.012	0.091	0.100 ± 0.016	0.103
α0	0.036 ± 0.018	0.037	0.075 ± 0.023	0.077
β1	0.878 ± 0.046	0.880	0.967 ± 0.054	0.969
β2	0.057 ± 0.022	0.063	0.004 ± 0.026	0.012
β3	0.085 ± 0.039	0.084	0.011 ± 0.046	0.010
β4	−0.044 ± 0.016	(F) 0	−0.054 ± 0.019	(F) 0
Log(LH)	−325.216	−328.901	−414.444	−418.453
LHR (p-value)		0.006		0.005

M(BMI) and M(CR_PC) are the general models of BMI and CR_PC variation, respectively. These two models include parameter estimates of the contribution of the fat-related (FM, PLL and SK_PC) covariates and G-C-G haplotype, as well as contribution of the putative additive genetic, σ_AD² and environmental, σ_RS² factors. M₀(BMI) and M₀(CR_PC) are the restricted models, in which contribution of the G-C-G haplotype, measured by regression coefficient β₄, was neglected (restricted to null). Contribution of fat-related covariates as measured by the regression coefficients, β₁, β₂, and β₃, respectively was allowed; α₀: regression intercept. 898 individuals, in whom the M1–M2–M3 haplotypes have been unambiguously reconstructed, were included in this analysis. The restricted models show that despite highly substantial contribution of the fat-related phenotypes to variation of BMI and CR_PC, the contribution of G-C-G haplotype to their respective variations cannot be neglected without significant loss of data fitting, and therefore these models were rejected.

Discussion

As mentioned in the Introduction section, currently there is a substantial body of evidence suggesting that osteocalcin, a major inorganic component of bone matrix and a marker of bone formation, can also regulate glucose and fat mass metabolism. Considerable uncertainty, however, remains whether the above effect on fat mass has a genetic component. In this study, our main aim was to test whether the variation in body composition phenotypes is associated with BGLAP variants. This hypothesis was tested using the ethnically homogeneous sample of families of European origin, in which each individual was anthropometrically assessed for a number of relevant phenotypes. In addition, circulating levels of leptin were also available for this project. A preliminary analysis of the study phenotypes showed that the genetic component (heritability) explains a substantial portion of their variation (Table 2), as expected from other publications on this subject, e.g. [34–36].

The phenotypes selected for this study could be roughly divided into two groups more or less specifically related to adipose tissue. The first group could be considered as fat-related phenotypes and would include SK_PC, PLL and FM; in contrast, the second group could be considered as body mass phenotypes and includes BMI and CR_PC. The last two phenotypes exhibited the most notable association with the BGLAP genomic region (Table 3). The significance of the BMI associations achieved p < 0.001 for individual SNPs, and p < 0.000001 for haplotypes composed of three neighboring SNPs (rs2758605-rs1543294-rs2241106). The association of CR_PC with these polymorphisms was of comparable magnitude: 0.002 and 0.00005, respectively. The phenotypes in the fat mass-related group exhibited a considerably lesser degree of the association with separate SNPs and haplotypes (p = 0.02–0.003), and did not survive correction for multiple testing. Importantly, the association with this above haplotype on BMI and CR_PC variation was significant in cases when the fat-related phenotypes were included as covariates in the corresponding VC models (Table 5), but not vice versa. Taking together these facts suggests that the BGLAP genomic variants are most likely associated with body mass as composite phenotypes, and less likely associated with adipose tissue itself.

The association between BMI and the G-C-G haplotype, in particular, was significant and was confirmed well in the replication sample (Fig. 2), despite very substantial cultural and economic differences between the two populations. The studied populations also differ in their BMI distributions. The BMI in the Chuvashian sample was significantly smaller in both males and females as compared with the US sample (p < 0.0001). The Chuvashian sample was collected in the former USSR, from 1998 to 2002, when the entire population lived under similar and economically severe conditions, in comparison with much more diverse and economically beneficial conditions in the US. It is therefore possible that the involvement of the environmental effects with the BMI variation may be much more substantial in the US sample, which in turn may explain the less significant association with the G-C-G haplotype in this sample.

Of particular interest is the fact that some contradiction was observed regarding the extent of association signals when considering the separately taken SNP and haplotypes composed of neighboring SNPs (Table 3). When association with individual SNPs was tested, significant associations with study phenotypes were elicited with M3, M4, and M6 located downstream of the gene's location (Fig. 1). However, in PDT involving haplotypes, significant association results were obtained with marker combinations, which in fact cover the entire BGLAP locus (Table 3, Fig. 1). The most remarkable associations were found with the G-C-G haplotype combining M1–M3. Moreover, in the variance components analysis, M4–M6 made only a negligible contribution to the BMI variation, when M3 was included in the analysis. However, M1 and M2 could not be excluded from the VC model without a significant loss in the accuracy of the data fitting (Table 4).

This controversy could probably be explained by the lack of LD between upstream SNPs (M1–M2) and downstream SNPs (M3–M6). The lack of LD increases the diversity of those haplotypes combining these markers, and therefore increases the discriminating ability of the association tests. This in turn can increase the power of association analysis using haplotype as compared with SNP. This could also partly explain the above-mentioned results of VC analysis. In addition, the combination of several SNPs in a common haplotype can generate the appearance of non-additive interactions between them. This assumption was tested in the modified VC model (Table 4), by inclusion of a non-additive effect covariate. The number of “+” alleles in each M1–M3 genotype was three additive covariates. The non-additive effect covariate was a product of these numbers, within the individual. Inclusion of this covariate to the VC model presented in Table 4 dramatically modifies the effect of each M1–M3 genotype. In the presence of the non-additive covariate, exclusion of any of the M1–M3 genotypes and even all of them does not change the model fitting by LRT (p ≥ 0.35). On the other hand, in the presence of the M1–M3 genotypes, exclusion of the non-additive covariate led to a marginally significant decrease of the model fitting (p = 0.056). Thus, it is possible that the epistatic interaction was involved in complex pattern of the associations observed by us in the BGLAP region.

It is, of course, of great interest what could be the causative variation in this genomic region and in particular in BGLAP locus. The situation is not very clear. For example, there are no HGMD reports (www.hgmd.cf.ac.uk/) on the specific disease-causing mutations or phenotype-associated/functional polymorphisms in BGLAP. On the other hand, as mentioned in the Introduction there are several publications suggesting possible association between some clinically oriented phenotypes and intra-gene BGLAP polymorphisms, such as HindIII (C/T) in promoter region and arginine/glutamine change in exon 4 (e.g. [18,19]). We can speculate that not only BGLAP gene caused the association observed in these and our studies. As seen in Fig. 1 several genes are mapped to the area where our SNPs were selected. One of them is complex locus PAQR6, encoding progestin and the adipoQ receptor family member VI. However, very limited information on a phenotype related to this locus has been reported so far, although the corresponding proteins are expected to have receptor activity [37]. Another gene that may be of relevance is the PMF1 (encoding the human polyamine-modulated factor 1). It is mapped to a BGLAP upstream region and its protein has been shown to modulate the transcription of various genes [38]. Moreover, the PMF1-BGLAP locus represents naturally occurring read-through transcriptions between neighboring genes [39]. Obviously, the currently available molecular data are not yet sufficient for drawing definite conclusions However, on the other hand, the data are substantial enough to motivate studying the next stage, which focuses on clarifying whether and which the genes in the area are involved in the epistatic interaction.

Abbreviations

BMI

body mass index

CR_PC

principal component score of nine circumference measurements

FM

fat mass

HDL

high-density lipoprotein

LH

likelihood value

LRT

likelihood ratio test

MAF

minor allele frequency

PDT

pedigree-based disequilibrium test

PCR

polymerase chain reaction

PLL

plasma level of leptin

SD

standard deviation

SFA

subcutaneous fat area

SK_PC

principal component score of eight skinfold measurements

SNP

single nucleotide polymorphism

VC

variance component

VFA

visceral fat area

WHR

waist to hip circumference ratio