Evolutionary game theory (EGT) describes dynamics in populations in which individual fitness can change because of the interactions with others, called frequency-dependent selection (1). Interactions are driven by differences in phenotype. EGT has been proposed as a framework for evolutionary dynamics of tumors (2). An underlying assumption is that different cancer cell types within a tumor engage in different heritable behavior; thus, frequency-dependent selection acts. Until now there has been little direct empirical evidence for this.
The study by Archetti et al. (3) demonstrates frequency-dependent growth rates of two phenotypically distinct cancer subclones. One clone produced the insulin-like growth factor (IGF)-II, the other did not. In a mix of producers and nonproducers, the growth rates of both clones varied with the frequency of producers. Because a similar effect was shown when varying the concentration of serum, the production of IGF-II could be viewed as a public goods game.
We welcome these experimental results but have serious concerns about the theoretical framework used for explaining them. Archetti et al. (3) use an existing model: in cell groups of size n, the growth factor (public good) was provided by producers who pay a cost and receive benefit. Nonproducers in the group simply received a benefit. The size of the group was assumed to vary between 10 and 30 individual cells and was said to relate to the diffusivity of IGF-II. Nowhere in the article is group size justified empirically. Based on an approximation of the diffusion coefficient of IGFs (10−6 cm2/s) and an estimate of system size (well radius ∼ 0.7 cm), diffusion time across the entire domain is about 1.5–3 d. This finding means that the IGF-II concentration equilibrates on roughly the same time scale as cell division occurs on, if not faster. The group among which the public good is shared should not be on the order of 10–100 cells, but rather the entire population; this would invalidate the model, because the model requires small n to result in coexistence. Contrastingly, producing is selected against in large populations (4). If IGF-II acts as a public good on the scale of the entire population we would expect producer cells to disappear in the heuristic EGT model.
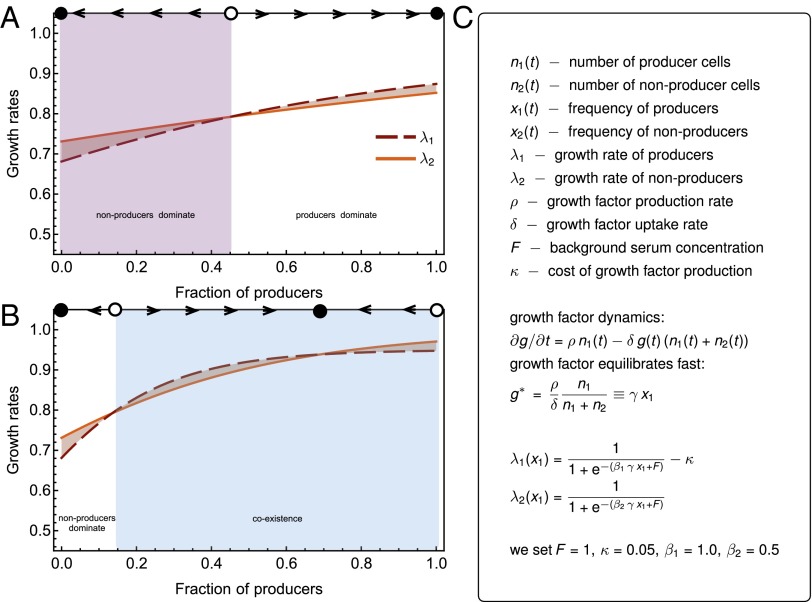
Our second concern relates to the use of the replicator equation and the birth-death process. Both assume constant population size. Although never explicitly stated in the article, the population increases more than 10-fold (figure 1A in ref. 3) during the experiments. Dynamic population size can have profound effects on the population dynamics (5). The proposed model might behave differently if the population size is allowed to increase, which definitely needs to be resolved in the future and is crucial to its application to tumor growth. In Fig. 1 we outline a model in which the public good is shared among all cells of a growing population. This model recapitulates the coexistence of producers/nonproducers observed in ref. 3. We welcome experiments that try to disentangle the complex interactions between different cancer cells. EGT has certain advantages when it comes to understanding complex interactions, but further evidence is needed for its application to growing tumors.
Fig. 1.
An illustration of the effect of differential growth rates between cancer cell phenotypes in the presence of a shared good that enhances growth. Type 1 produces and consumes a share good. Type 2 only consumes the shared good. (A) Growth rates of producers (dashed) and nonproducers (solid) when production of the shared good is only marginally higher than its rate of uptake, γ = 1.5. (B) Growth rates of producers and nonproducers when production of the shared good is five times higher than its rate of uptake, γ = 5.0. In both A and B, at the top, we show the direction of selection, with stable equilibria as full circles. (C) Mathematical model of two growing populations consuming a shared good, definitions, and equations. In this example we assume that the growth factor equilibrates fast. We do not need to assume any complex interaction patterns sometimes required by a nonlinear public goods game with population assortment. The critical parameter is the ratio of growth rate production rate over growth rate consumption rate, γ = ρ/δ. Its value determines whether the system has one unstable internal equilibrium, or two internal equilibria (one stable and one unstable).
Acknowledgments
We would like to thank the Mathematical Biosciences Institute at the Ohio State University for facilitating this work.
Footnotes
The authors declare no conflict of interest.
References
- 1.Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303(5659):793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- 2.Tomlinson IPM, Bodmer WF. Modelling the consequences of interactions between tumour cells. Br J Cancer. 1997;75(2):157–160. doi: 10.1038/bjc.1997.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Archetti M, Ferraro DA, Christofori G. Heterogeneity for IGF-II production maintained by public goods dynamics in neuroendocrine pancreatic cancer. Proc Natl Acad Sci USA. 2015;112(6):1833–1838. doi: 10.1073/pnas.1414653112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Archetti M. Evolutionary game theory of growth factor production: implications for tumour heterogeneity and resistance to therapies. Br J Cancer. 2013;109(4):1056–1062. doi: 10.1038/bjc.2013.336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chuang JS, Rivoire O, Leibler S. Simpson’s paradox in a synthetic microbial system. Science. 2009;323(5911):272–275. doi: 10.1126/science.1166739. [DOI] [PubMed] [Google Scholar]