Influence of three-dimensional nanoparticle branching on the Young’s modulus of nanocomposites: Effect of interface orientation

Significance

Currently, the effect of branching of nanoparticles tens of nanometers in size on the mechanical properties of structural composites is not well understood due to the limited availability of branched nanoscale fillers. We report that branched nanofillers have the potential for optimization of nanocomposite Young’s modulus over their linear counterparts. Lattice spring model simulations reveal that the mechanism for this improvement involves the ability of branched nanoparticles to optimize the ratio of both filler and stiff interfacial bonds aligned with the tensile axis, as opposed to linear nanoparticles, which optimize only the filler bond orientation when parallel to the stretching axis. We believe this information could inform the design of nanocomposites with optimized mechanical properties for a variety of structural applications.

Abstract

With the availability of nanoparticles with controlled size and shape, there has been renewed interest in the mechanical properties of polymer/nanoparticle blends. Despite the large number of theoretical studies, the effect of branching for nanofillers tens of nanometers in size on the elastic stiffness of these composite materials has received limited attention. Here, we examine the Young's modulus of nanocomposites based on a common block copolymer (BCP) blended with linear nanorods and nanoscale tetrapod Quantum Dots (tQDs), in electrospun fibers and thin films. We use a phenomenological lattice spring model (LSM) as a guide in understanding the changes in the Young's modulus of such composites as a function of filler shape. Reasonable agreement is achieved between the LSM and the experimental results for both nanoparticle shapes—with only a few key physical assumptions in both films and fibers—providing insight into the design of new nanocomposites and assisting in the development of a qualitative mechanistic understanding of their properties. The tQDs impart the greatest improvements, enhancing the Young's modulus by a factor of 2.5 at 20 wt.%. This is 1.5 times higher than identical composites containing nanorods. An unexpected finding from the simulations is that both the orientation of the nanoscale filler and the orientation of X-type covalent bonds at the nanoparticle-ligand interface are important for optimizing the mechanical properties of the nanocomposites. The tQD provides an orientational optimization of the interfacial and filler bonds arising from its three-dimensional branched shape unseen before in nanocomposites with inorganic nanofillers.

Polymer−nanoparticle composites have become a highly active topic of research with rapidly expanding applications (1), in part because of their high polymer−particle interfacial area and the unique shape- and size-dependent, tunable properties of nanoparticle reinforcements. For example, new polymer nanocomposites have been developed that can optically sense stress concentration (2), are responsive to magnetic, electrical, and thermal actuation (3, 4), and exhibit large changes in elastic modulus and glass transition temperature at low nanoparticle concentrations (5).

While theoretical studies show that the Young’s modulus of such polymer nanocomposites depends on nanoparticle shape (6), experimental studies are limited. Experimental studies on polymers (7) include the synergistic reinforcement effects of multiple nanocarbons (8) and the shape-dependent reinforcement effects of micrometer-sized tetrapods (9), microscale ceramic needles (10), carbon nanotubes (11), clay-based nanocomposites (12, 13), and others (14). Computational studies include the effects of nanoparticle packing and size on the nanocomposite Young’s modulus (15–17). However, the effects of increasing nanoparticle branching on the mechanical behavior of nanocomposites have not been demonstrated (18). It is possible to make nanocrystals with controlled shapes and degree of branching (19); as such, they pose an ideal system to study the effect of reinforcement branching.

Here, using nanorods (NRs) and tetrapod quantum dots (tQDs) in both electrospun fibers and solvent-cast films, we study the effect of increasing nanoparticle branching on the Young’s modulus of a common structural elastomer, poly(styrene block−ethylene−butylene block−styrene) (SEBS) (20). We chose SEBS since it is a widely used structural copolymer, has a 40% phase (ethylene−butylene) of similar chemical makeup as our nanoparticle surface ligands (although it is incompatible with 60% of the polymer, the polystyrene (PS) phase), and is amorphous, allowing for improved intercalation with the nanoparticles. In choosing polymer−filler nanocomposites, there is a critical choice to be made between the case where the polymer−filler interaction is very strong, in which case the intrinsic polymer structure is disrupted to a high degree, and the case where it is weak, leaving the native polymer structure largely unperturbed. Both limits are of significant interest, but in this first study, we focus on the latter weak interface case, as it is by far the most common case in practical composites and it is the case that is most amenable to modeling through summation of mechanically independent components. In such a case, the nanoparticles form nanoscopic aggregates distributed throughout the SEBS matrix, due to the van der Waals interactions between the native alkyl ligands on the nanoparticles and the SEBS polymer. No macrophase separation was observed, and no surface modification was performed to achieve single nanofiller dispersion. Future studies will be directed at the single-filler dispersed case, where the filler−polymer interaction is much stronger. In the stronger interface case, the nanoparticles may be selectively incorporated within one block copolymer (BCP) microdomain, and, due to their size, the intrinsic local polymer chain conformation may be more affected by the presence of the filler.

In both electrospun fibers and films, we observed nanoscopic aggregates of nanofillers (∼150 nm in diameter), and we found that the multiple-branched tQDs improved the Young’s modulus the most compared with linear shapes, i.e., nanoscale branching may optimize the Young’s modulus. Our simulated results using a 2D lattice spring model (LSM) suggest that this shape effect on the Young’s modulus is primarily due to the orientation of the strong X-type bonds (21) at the nanoparticle−ligand interface. This illustrates the importance of the orientation of both types (filler and interfacial) of bonds in increasing the stiffness of structural composites. To the best of our knowledge, our study is the first to examine this effect on the mechanical properties of composites for nanofillers in this size range, thereby providing some unique mechanistic insights. We expect that these insights can be exploited to design polymer nanocomposites with optimized mechanical properties for a variety of applications.

Results and Discussion

Nanocomposite Preparation and Uniaxial Tensile Testing.

The triblock copolymer SEBS (117,000 g/mol molecular weight, 60% PS) with a lamellar microstructure (22, 23) was used as the polymer matrix. CdSe/CdS NRs, and CdSe/CdS tQDs were prepared using established methods, and were incorporated into the polymer matrix with their native alkyl chain ligands (24). Polymer nanocomposites were prepared via electrospinning (2) of nanoparticle−polymer solutions in chloroform, while the films were processed by casting of the nanoparticle−polymer solutions into Petri dishes (see Materials and Methods). Samples were tested using quasi-static, uniaxial tensile tests to determine the Young’s modulus in the small displacement (<0.02 strain) limit. Tests were performed to failure; the average failure strain for fibers was ∼100% (for films, see SI Appendix).

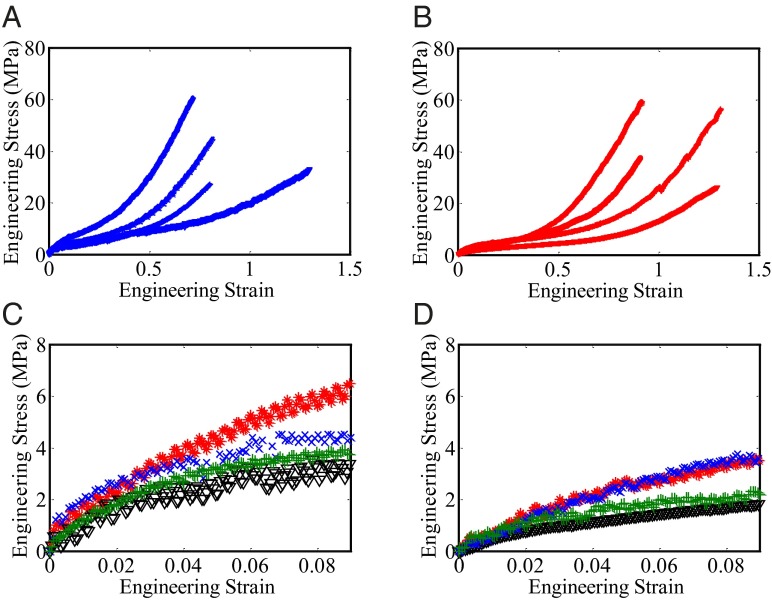
After electrospinning and fiber collection, the mechanical properties of each of the polymer nanocomposites were evaluated using uniaxial tensile tests. Fig. 1 A and B, respectively, show the tensile stress−strain curves for electrospun fibers of 20 wt.%/5 vol.% tQD-SEBS nanocomposites and 20 wt.%/5 vol.% NR nanocomposites. The curves exhibit a high strain and low stress to failure, characteristic of many elastomers. Higher magnification versions of these curves, illustrating the linear elastic regime, are shown in Fig. 1 C and D for tQD and NR nanocomposites, respectively.

Fig. 1.

Uniaxial tensile stress−strain curves of tQD and NR-SEBS polymer nanocomposites. (A) Stress−strain curves of four different 20 wt.% tQD nanocomposite samples. (B) Stress−strain curve of four different 20 wt.% NR nanocomposites. (C) Stress−strain curves of four different 20 wt.% tQD nanocomposites, shown over the first 9% strain to highlight the elastic region occurring from 0 to 2% strain. (D) Stress−strain curves of four different 20 wt.% NR nanocomposites, shown over the first 9% strain to highlight the elastic region.

As can be seen from Fig. 1, samples exhibited a processing-inherent variation in moduli and strains at failure of around ∼40% covariance for ductility and ∼30% covariance for Young’s modulus. For tQD and NR-based nanocomposites, the ductility varied minimally with concentration; for the 20 wt.% concentration, the NR composite ductility was 102.8 ± 45.9% and the tQD composite ductility was 102.4 ± 45.5%, similar to the control ductility of 96.0 ± 56.0%. Branched tQDs provide the best performance of any of the fillers, improving the Young’s modulus by 2.5 times at 20 wt.% tQD, i.e., a factor of 1.5 times more than linear NRs at the same concentration. The Young’s modulus of the unreinforced matrix was 39.7 ±11.8 MPa; for 20 wt.% reinforcement, the modulus of the composites was ∼2.5 times higher with tQDs (100.2 ± 28.4 MPa) and ∼1.5 times with NRs (66.4 ± 32.1 MPa) for both fibers and films (SI Appendix, Fig. S1).

Nanoparticle Dispersion.

When the nanoparticles are embedded into the polymer, they partially phase separate, forming aggregates distributed throughout the polymer, as seen in previous studies (2). This aggregation occurs due to the weak interface between the native alkyl chain ligands on the nanoparticles and the PS phase of SEBS, which constitutes 60% of the polymer. Although the nanoparticles experience a favorable interaction with the poly(ethylene−butylene) (PEB) phase of SEBS since they are, as mentioned above, coated with similar alkyl chain ligands, PEB makes up only 40% of the SEBS polymer in this work. The aggregation occurs not due to the favorable interactions with PEB but due to the unfavorable interactions with PS. Fig. 2 shows transmission electron microscopy (TEM) images of the NRs and tQDs before (Fig. 2 A and B) and after (Fig. 2 C and D) integration into polymers. TEM image analysis of over 150 aggregates per sample (see Materials and Methods) showed that aggregates formed in the tQD and NR nanocomposites had approximately the same size (SI Appendix, Fig. S2), indicating that the nanoparticle aggregate size differences are not responsible for the observed disparities in mechanical properties. As seen in Fig. 2D, tQD aggregates were more porous than the NR aggregates, due to their branched geometry inhibiting close packing (25, 26), evidenced by regions of lighter contrast in tQD aggregates. TEM images show very similar aggregate size and shape between tQDs and NRs. Thus, we attribute our findings on the superior Young’s modulus of tQD nanocomposites to nanoparticle shape as opposed to differences in aggregate size [see SI Appendix, Figs. S3 and S4 and section S4 for detailed studies of aggregate volume fraction (area fraction in 2D) on the nanocomposite Young’s modulus].

Fig. 2.

Transmission electron micrographs of tQD and NR Nanoparticles and nanoparticle−polymer nanocomposites. (A) Micrograph and schematic of NRs before polymer integration. (B) Micrograph and schematic of tQDs before polymer integration. (C) Micrograph of 10% NR nanocomposites. (D) Micrograph of 10% tQD nanocomposites. (Scale bars, 200 nm.)

Multiple physical factors including nanoparticle−nanoparticle interactions, polymer−nanoparticle interactions, and variations in electric field in the electrospinning process play critical roles in determining the dispersion of nanoparticles in polymer nanocomposites (18, 27).

Despite the aggregation observed, there is no degradation in any of the mechanical properties and a shape-dependent enhancement of the Young’s modulus for both tQD and NR nanocomposites in both films and fibers [films and fibers had roughly similar nanoparticle dispersion (SI Appendix, Fig. S5)].

Simulation of the Young’s Modulus of tQD and NR Nanocomposites.

To explain these results, we modeled the nanocomposites using elastic LSMs. Elastic LSMs are an alternative to finite element models (28) that model a material as an elastic spring network to estimate the Young’s modulus (see SI Appendix for more detail). Elastic LSMs have been shown to reproduce the equations of state for an isotropic elastic medium subjected to small deformations (29). The LSM used in this work was a 2D model identical in form to the LSM used in previous theoretical work on polymer composites (29, 30). Although LSMs that model plastic deformation also exist (29), the LSM used here accounted only for fully elastic deformations (30).

Because tQDs form loosely packed assemblies (26) while NRs form closely packed assemblies (25), polymer was included in tQD aggregates in the simulations but not in the NR aggregates. The bond between surface ligands and CdSe/CdS semiconductor nanocrystals is known to be a strong (relative to polymer−polymer interaction) X-type bond (21). A spring of force constant 1,000 times greater than the polymer (and half that of the nanoparticle) was thus situated at the inorganic−organic interface between ligand and polymer.

Using the literature value for the Young’s modulus of CdS [E = 90 GPa (31)], and our experimentally measured Young’s modulus of SEBS (E = 45 MPa), nanoparticle spring constants were set to be 2,000 times greater than the polymer spring constant. Because the like−like interaction between the nanoparticle ligands and the PEB domains is likely weaker than the interactions between the polymer chains, we used ligand/interfacial spring constants that were roughly half the polymer spring constant (this assumption gave the best agreement between theory and experiment; see SI Appendix, Fig. S6, for simulations and fits of other interface strengths). Once nanoparticles were assigned spring constants and placed in the matrix, the LSM calculated the minimum elastic energy of the spring network under a tensile force, reporting the Young’s modulus and Poisson’s ratio equilibrium spring configuration under stress.

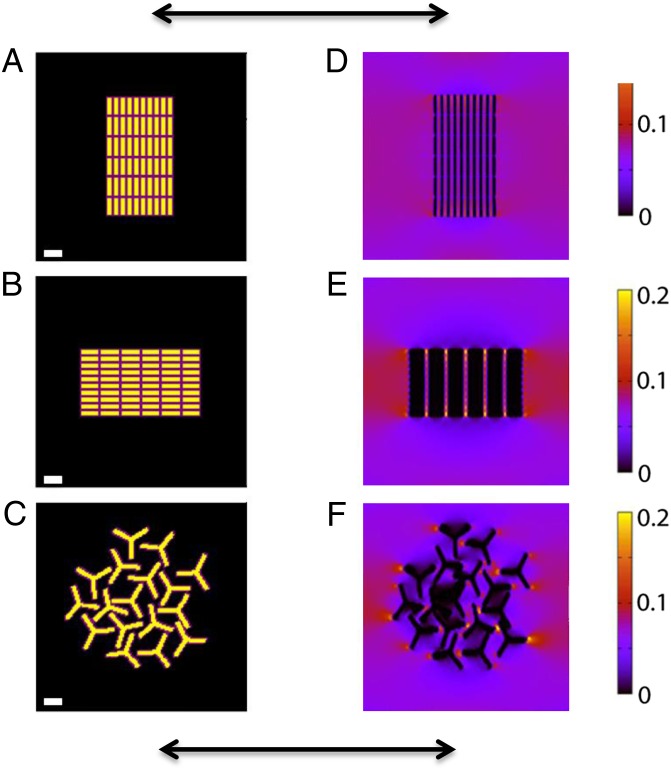
Fig. 3 shows the mask files (before strain application) (Fig. 3 A−C) and strain fields (Fig. 3 D−F) under uniaxial tension in the simulated micromechanical lattice for the 10 wt.% (2.5 vol.%) NR−polymer and tQD−polymer nanocomposites (for strain fields of other concentrations, see SI Appendix, Fig. 7). Tension was applied to the left and right of the image with equal force (see SI Appendix, SI Experimental Materials and Methods). Yellow regions correspond to highest strain, while black regions correspond to regions of zero strain.

Fig. 3.

Simulations of elastic strain fields in tQD and NR−polymer nanocomposites using a lattice spring model. LSM spring distribution images for (A) vertically aligned NRs, (B) horizontally aligned NRs, and (C) tQDs. (D−F) Corresponding elastic strain fields after stretching. Black double arrows indicate the stretching direction. [Scale bars, 25 nm (14 nodes).]

As expected, the strain in the nanoparticles is approximately zero, due to its 2,000 times higher spring constant relative to the polymer matrix (see SI Appendix, SI Experimental Materials and Methods). NR or tQD arms aligned with the tensile axis had localized regions of high strain at their apexes (yellow “hot spots” in Fig. 3 E and F). This is likely because regions of low strain are created due to the relative restriction of the polymer matrix along the long axis of an NR or tQD arm. Because of the Poisson effect, regions of high strain are created adjacent to those where the polymer is less restricted, such as at the ends of tQD arms. These yellow hot spots may be good locations for covalent anchoring of the nanoparticles to the polymer to optimize strain transfer and nanocomposite properties (1). When NRs are orthogonal to the tensile axis, stress transfer is much reduced, resulting in no hot spots of localized strain.

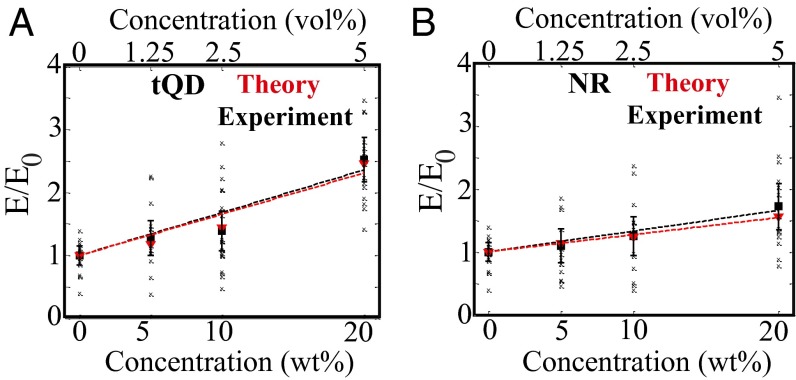
Fig. 4 shows both the disparity in Young’s modulus between tQD nanocomposites (Fig. 4A) and NR nanocomposites (Fig. 4B) and the reasonable agreement between experimentally obtained and the simulated values for the Young’s modulus at different nanoparticle concentrations. For normalization purposes, the Young’s modulus of the nanocomposites (E) was divided by the Young’s modulus of the pristine polymer (E₀) for all comparison plots. The lines of best fit for experimental and theoretical data match very closely (Fig. 4 A and B; see SI Appendix, Table S1 for details of fit) for all nanoparticle−polymer composites studied. The goodness of fit for the linear fit is slightly better for the NR than the tQD nanocomposites, indicating that tQDs follow a slightly nonlinear filler behavior. This is likely due to their branched shape, as explained in Origin of the Disparity Between tQDs and NRs as Fillers: X-Type Interface Orientation. The experimentally observed enhanced filler performance of tQDs, compared with NRs, is recovered even in a simple 2D LSM, the simplest model we could deploy that shows this effect. We see very good agreement between simulation and experiment for all filler systems studied. Importantly, this good agreement was achieved through a nonarbitrary accounting of only a few key parameters (see SI Appendix for detail), especially the nanoparticle fill factor and the ratio of polymer to particle stiffness, which are known. While the particle−polymer interface spring constant is not independently known, the results of the simulation are only weakly dependent on this quantity as long as it is within a factor of 2 of the polymer stiffness (SI Appendix, Fig. S6).

Fig. 4.

Comparison of experimental results with simulated data using lattice spring model. Top x axis is volume percent concentration, while bottom x axis is weight percent. (A) Plot of Young’s modulus, E, normalized to control modulus, E₀, versus nanoparticle concentration for tQD nanocomposites. (B) Plot of Young’s modulus, E, normalized to control modulus, E₀, versus nanoparticle concentration for NR nanocomposites. Red lines/points represent results from the lattice spring model, while black lines/points represent experimental results. Each black “x” is the result of a single experimental test. Fits are clamped to the (0,1) point, which corresponds to the normalized control modulus.

The polymer−nanoparticle interface plays a critical role in the mechanical behavior of the polymer nanocomposites (1). In fiber composites, little to no mechanical property changes are seen except in high-volume fractions (32, 33), partly due to the increased polymer−nanoparticle interface. For all nanocomposites studied here, the greatest difference in the Young’s modulus of nanocomposites containing different shapes of nanofiller was seen at the highest concentration, 20 wt.% (5 vol.%). Although the trend is clear, at lower concentrations, the experimental scatter is large enough to partially obscure the smaller differences in Young’s moduli. Variability in mechanical properties of fibers within a single synthetic batch may be due to inherent sample heterogeneity introduced by the stochastic electrospinning process (34). Studies have shown that electrospun fibers dry very rapidly as they are drawn through a spatially varying electric field (35), causing them to experience heterogeneous tensile forces and develop highly varying structures (36). The error bar in the Young’s modulus also increased with concentration, likely due to nanoparticle aggregates increasing the heterogeneity of the nanocomposite morphology and acting as nucleation sites for defects.

Origin of the Disparity Between tQDs and NRs as Fillers: X-Type Interface Orientation.

The major finding of this work is that the presence of the tQDs enhanced the Young’s modulus of the SEBS polymer to the largest extent, by 2.5 times at 20% loading, more than 1.5 times that of NRs at the same concentration. We discuss four possible explanations for this phenomenon: (i) interface orientation of X-type ligand−nanoparticle bonds, (ii) restriction of polymer chains inside porous tQD aggregates, (iii) the larger extent of interface in tQDs compared with NR clusters, and (iv) additional stress-dissipating bending modes for tQDs due to their branched shape. We conclude, based on our LSM simulations, that optimization of X-type bond interface orientation is a key explanation for the relative enhancement of the Young’s modulus of tQD nanocomposites.

One reason for the modulus enhancement can be understood by considering the influence of the filler orientation with respect to the tensile axis. Traditional isostrain and isostress predictions suggest that polymer composites with high aspect ratio ceramic fillers oriented parallel to the tensile axis should be much stiffer than those with fillers orthogonal to the tensile axis (37). Due to their linear shape (38), the NR aggregates consist of closely packed arrays in which every NR takes the same orientation. Hence, NR nanocomposites consist of NRs that are both parallel and orthogonal to the tensile axis. Due to the more branched, isotropic shape of the tQD, at least one arm is likely to have a component lying along the tensile axis, resulting in a higher Young’s modulus on average.

However, the above explanation cannot account for all of the effects observed in this study, since the simulated tQD nanocomposites still exhibited a higher elastic modulus than the simulated horizontally oriented NR nanocomposites. A second explanation likely lies in the orientation of the nanoparticle−ligand interface. In the polymer nanocomposites under study here, while the ligand is entangled with the PEB domains of the polymer via relatively weak Van Der Waals forces, as mentioned above, there is a much stronger X-type bond between the nanoparticle and its surface ligands (21). This X-type bond is represented in the LSM by a stiff spring (1,000 times stiffer than the polymer, and half the stiffness of the nanoparticle spring constant) at the nanoparticle−ligand interface.

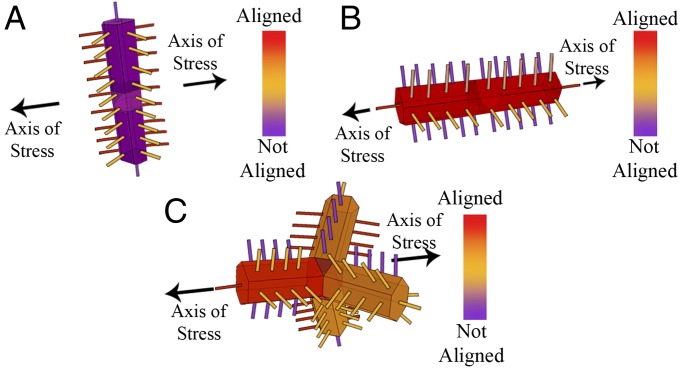
We suggest that the orientation of these strong interfacial X-type bonds plays a crucial role in the polymer nanocomposite mechanical behavior (Fig. 5). NRs perpendicular to the stretching axis have the least filler springs aligned with this axis, and hence have the lowest modulus, despite having the most interfacial springs aligned (Fig. 5A). While NRs parallel to the tensile axis have the highest number of filler springs (or bonds) aligned with the axis, they also have the least number of interfacial X-type bonds parallel to the axis (Fig. 5B) (roughly one aligned interfacial bond for every four unaligned interfacial bonds, since NRs have a width of 3 nodes and a length of 14 nodes).

Fig. 5.

Schematic of alignment of nanoparticle springs and X-type interfacial springs in NRs and tQDs with tensile axis. (A) Vertical NRs have some aligned X-type bonds but unaligned filler bonds. (B) Tetrapods have an optimization of aligned filler and interfacial bonds. (C) Horizontal NRs have no aligned interfacial bonds but aligned filler bonds.

Due to their relative isotropy, tQDs have the greatest number of interfacial X-type and filler bonds oriented with the axis (Fig. 5C) (roughly one aligned bond for every unaligned bond). The random orientation of both filler and interfacial X-type bonds in tQD composites thus may represent an orientational optimization, enhancing the Young’s modulus in tQD nanocomposites. It thus appears that to engineer a composite that maximally capitalizes on the strength of both inorganic Cd−S bonds and interfacial X-type ligand bonds, it may be highly advantageous to use a multiply branched, isotropic nanofiller such as tQDs.

These results suggest that due to the importance of these bonds for stress transfer to the filler phase, the nanoscale orientation of strong interface bonds with respect to the tensile axis can be an equally important factor in improving the small-displacement elastic mechanical properties of polymer composites as filler bond orientation. The results also suggest that certain branched nanofiller shapes are capable of optimizing the orientations of both key types of bonds to achieve overall optimal stress transfer to the filler phase. This information may be of key importance for engineering nanocomposites with tunable and maximized elastic strength for structural applications.

As shown in Fig. 2 (see SI Appendix, Fig. S2 for more details), both tQDs and NRs form similar-sized aggregates with diameters ranging from 2,000 nm² to 10,000 nm², indicating that any difference in Young’s modulus between tQDs and NRs is likely due to nanoparticle shape. Simulations of stiffness as a function of aggregate volume fraction (area fraction in 2D) on dipods, rods, and tripods with packing or area fractions ranging from ∼20% to 90% indicate that the stiffness differences are not due to shape effects on aggregate packing. These aggregate area fraction changes result in only 2–6% stiffness changes compared with ∼30–150% across nanoparticle shapes of a given concentration (see SI Appendix, section S4, Figs. S3 and S4, and Table S2 for more details). A result of the branched tQD shape is the relative porosity of tQD aggregates seen in the TEM images (Fig. 1), leading one to conclude that there is polymer inside of tQD but not NR aggregates (32). Furthermore, the chemical compatibility of the PEB phase of the block copolymer with the nanoparticle surface ligands increases the likelihood that polymer is inside the tQD aggregates. In one hypothesis, the enhanced Young’s modulus in tQD composites could be caused by restriction of polymer chains inside these relatively porous tQD aggregates, decreasing local chain mobility. However, again, our simulations indicate that the stiffness of tQD nanocomposites is not dependent on aggregate area fraction or packing density (see SI Appendix, section S4, Figs. S3 and S4, and Table S2 for more details). Experimentally, however, changing nanoparticle packing involves relatively large changes in interface strength (18), so this observation alone is not conclusive. However, restriction of chain mobility in the aggregates in the LSM simulations (by increasing stiffness of the springs inside of the tQD clusters) resulted in arbitrary Young’s modulus variations (0–90%), depending on the spring constant of the restricted polymer. Therefore, explanations based on the restriction of polymer chains are not credible as an explanation based on our simulations. The good experimental−theoretical agreement achieved in this work was based on nonarbitrary physical assumptions that did not result in large or random variations with small percent changes.

Thus, although it is likely that polymer is present inside the clusters for enthalpic reasons, we conclude that the restriction of the chains in the cluster may not be a main cause of the relative Young’s modulus improvements for our tQD composites. For entropic reasons, polymer chains tend to favor less ordering, even if enthalpic considerations cause some degree of ordering and restriction. Therefore, it is likely that the polymer chains form a relatively loosely wrapped interpenetrating network around and inside of the tQD aggregates. A similar analogy is a number of electrical wires that are loosely entangled; while pulling on the wires is easy at first as they slide past one another, it becomes increasingly difficult once a knot is encountered. In the small-displacement elastic limit under study, it is likely that the loosely wrapped polymer in the tQD aggregate is still in the sliding phase and not yet restricted enough to cause much chain mobility decrease.

Another possible explanation consists of the fact that as tQD clusters have arms protruding out of the cluster and a relatively higher porosity, they have more interface for stress transfer. Furthermore, since the tQD clusters are not densely packed, they should be much softer than those of NRs, with reasonable elasticity to further release the stresses. Indeed, packing rods less densely leads to a slight stiffness increase, leading horizontally aligned NRs to match the stiffness of the relatively isotropic tQDs at loosest packings (SI Appendix, Fig. S3). However, even very loosely packed rods oriented parallel to the stretching direction do not exceed tQDs (SI Appendix, Fig. S3) in the nanocomposite modulus, implying that, based on our simulations, this explanation alone cannot explain the discrepancy between tQDs and NRs.

Another component of this phenomenon is related to the different bending modes accessible to tQDs as opposed to NRs. The branched structure of the tQD may allow it to act as a “nano shock absorber” since its arms bend more in response to stress, unlike the rigid, linear NRs. These bending modes conferred by the tQD arms may allow the tQD to dissipate additional stress, possibly contributing to the observed increase in Young’s modulus over NR nanocomposites.

Despite the fact that the polymer−nanoparticle interactions are mainly van de Waals interactions in this study, there are still key differences in mechanical properties of nanocomposites with fillers of different shape. It is our belief that using a weak filler−matrix interfacial interaction is further beneficial so that the variation in the interfacial area among different fillers does not play a critical role. (Analytical estimates of ligand coverage differences with different sized ligands are given in SI Appendix, section S3.)

Conclusions

We have studied the effect of branching of nanoparticle fillers on the Young’s modulus of polymer nanocomposites. Films and fibers of a common structural block copolymer, SEBS, modified with tQDs of an inorganic filler, increase the Young’s modulus significantly more than in composites of linear NRs. Simple 2D lattice spring model simulations can readily recover this result, and show that the difference in the results mainly from the orientation of the strong X-type bonds at the nanoparticle−ligand interface. Our results suggest that the orientation of strong filler bonds at the inorganic−organic interface between the nanoparticle and polymer is as important a factor in tuning the Young’s modulus as the orientation of nanofiller bonds. The branched tQD, with its relatively isotropic orientation compared with NRs, optimizes both these orientations to achieve the largest enhancement of the composite Young’s modulus. This result may enable design of new nanofillers and nanocomposites of a variety of polymers with optimized mechanical properties. Multiple additional bending modes of the tQD may also contribute to the observed effect by increasing the tQD’s ability to dissipate stress over NRs and increasing overall stress transfer to the filler phase.

Materials and Methods

SI Appendix, section S6 contains the detailed experimental materials and methods (a summary is provided in text at the start of the relevant subheadings of the Results and Discussion) of the parameters and assumptions used for the LSM simulations, simulations of the effect of aggregate volume fraction (area fraction in 2D) on the stiffness, remarks on using a 2D LSM to simulate a 3D polymer nanocomposite (including references to works that have found only a 5–10% difference in the computed elastic modulus in comparing between some nine 2D and 3D LSM models), simulation results for higher and lower concentrations of nanoparticles than shown in text, analytical estimates of ligand coverage differences for tQDs and NRs, and additional information.