Force field dependent solution properties of glycine oligomers

Abstract

Molecular simulations can be used to study disordered polypeptide systems and to generate hypotheses on the underlying structural and thermodynamic mechanisms that govern their function. As the number of disordered protein systems investigated with simulations increase, it is important to understand how particular force fields affect the structural properties of disordered polypeptides in solution. To this end, we performed a comparative structural analysis of Gly₃ and Gly₁₀ in aqueous solution from all-atom, microsecond MD simulations using the CHARMM 27 (C27), CHARMM 36 (C36), and Amber ff12SB force fields. For each force field, Gly₃ and Gly₁₀ were simulated for at least 300 ns and 1 μs, respectively. Simulating oligoglycines of two different lengths allows us to evaluate how force field effects depend on polypeptide length. Using a variety of structural metrics (e.g. end-to-end distance, radius of gyration, dihedral angle distributions), we characterize the distribution of oligoglycine conformers for each force field and show that each sample conformation space differently, yielding considerably different structural tendencies of the same oligoglycine model in solution. Notably, we find that C36 samples more extended oligoglycine structures than both C27 and ff12SB.

Introduction

Over the past decade there has been considerable effort towards understanding the relationship between protein disorder and protein function and how disruptions in the primary sequences of these disordered regions abrogate protein function [1]–[5] . At the core of this effort is developing methods to characterize the ensemble of protein conformers in both native and disease states. Single molecule techniques (e.g. smFRET, FCS, etc.) have been successful in probing the conformational landscape of disordered polypeptides and entire proteins, however these methods often rely on the attachment of bulky reporter groups which may alter the native-state conformations of the polypeptide of interest [6]–[8]. These effects are difficult to experimentally control [7]. Molecular simulations are not limited by these experimental constraints and, as a result, are useful in considering the structural and thermodynamic properties of disordered polypeptides in solution. Mechanisms and structural properties hypothesized from the results of simulations can then be leveraged to develop targeted, well-designed experiments.

Classical molecular simulations depend on the functional form and corresponding parameters (i.e. force field) used to model inter- and intra-molecular interactions. While quantum mechanics (QM) can model these interactions with high accuracy, the most accurate computations in solution are intractable for biological macromolecules. A variety of force fields have been developed for protein simulations. The most commonly used force fields include CHARMM [9] and Amber [10] variants as well as OPLS [11] and GROMOS [12].

Force fields may differ in both the functional form of the energy function and its empirically adjustable parameters. Each force field is derived with a different methodology, but in general parameterization requires minimizing differences between observed and molecular mechanical energies by adjusting the energy function variables for a set of target data [13]. The target data also differ between force fields, which can lead to force field biases, and an understanding of this data used in the parameterization process should be considered when using and interpreting results from one particular force field. For example, the CHARMM36 (C36) force field optimized against a range of condensed phase experimental data (e.g. scalar and J-couplings) for full length proteins and polypeptides in combination with gas phase QM data [9].

With deficiencies noted in previous force fields, improvements in computational capabilities and newly available structural data [14]–[21], force fields are constantly undergoing systematic revisions of backbone and side chain parameters [9], [10]. For example free energy calculations with C27 (i.e. C22/CMAP) predicted a misfolded conformation of the pin WW domain to be lower in energy than the native fold, suggesting a problem with the energy function [15]. Furthermore, C27 was shown to over-stabilize helical structures [16], [17]. Towards improving the CHARMM force field, authors released C36 in 2012 where they reported new backbone CMAP and side chain potentials parameterized against a variety of data, including more accurate QM calculations and NMR couplings and shift data [9].

Amber force fields have undergone a similar evolution the result of which is a number of variants including ff99SB, ff99SB-ILDN, ff99SB*-ILDN, ff03, ff03*, among others [18], [19], [22], [23]. Most of these variants attempt to refine backbone and side chain torsion potentials, yet biases manifest in different ways. For example, ff03 and ff99SB-ILDN were shown to over- and under-stabilize helices, respectively [16]. In 2012 Amber developers released ff12SB, which is a combination of the ff99SB parameter and new backbone and side chain torsion parameters, the details of which were not published. Generally, many force fields perform similarly when modeling well-structured proteins or polypeptides; that is, many force fields maintain distributions of conformations close to the native protein fold. However, when a protein or polypeptide lacks a stable structure under specified conditions, the conformational distributions and secondary structure tendencies, or lack thereof, become increasingly more important and the differences in conformational sampling between force fields (e.g. parameterization process and target data used) may be more pronounced [16]. Here we are interested in elucidating the effects that the commonly used CHARMM and Amber force fields have on the distribution of conformations of oligoglycine. Oligoglycine was chosen because a) CHARMM and Amber developers compare with, oligoglycine conformer data, b) it has been frequently used to study structural and thermodynamic properties of the protein backbone and protein folding [7], [24], [25], and c) we anticipate its lack of structure (i.e. high degree of disorder) to capture force field dependent conformation sampling well.

In this paper we report a comparative structural analysis of Gly₃ and Gly₁₀ from results of all-atom, microsecond MD simulations using the C27, C36, and ff12SB force fields. For each force field, Gly₃ and Gly₁₀ were simulated in explicit TIP3P aqueous solvent at constant pressure and temperature for at least 300 ns and 1 μs, respectively. Simulations of two different lengths of oligoglycine also allows us to evaluate how force field effects scale with polypeptide length. Using a variety of structural metrics (e.g. end-to-end distance, radius of gyration, dihedral angle distributions), we characterize the distribution of oligoglycine conformers for each force field and show that each sample conformation space differently.

Methods

System

Oligoglycine is a model disordered peptide and has been used previously to study thermodynamic and structural properties of the protein backbone as it relates to phenomena like solvent-induced collapse and aggregation [7], [24]–[27]. Additionally, oligoglycine conformers and available structural data (e.g. NMR) were used in comparisons for both CHARMM [9], [28] and Amber force fields [19]. Here, we chose two different oligoglycines containing three (Gly₃) and ten (Gly₁₀) consecutive glycine residues to evaluate conformational sampling differences between C27, C36, and ff12SB, and how these differences change with oligomer length.

For simulations with the CHARMM force fields, extended Gly₃ and Gly₁₀ were built using VMD’s Molefacture plugin [29]. Neutral acetyl (ACE) and N-methylamide (NME) caps were added and the system was solvated with TIP3P water using VMD’s Solvate plugin. For simulations with Amber ff12SB, extended and capped Gly₃ and Gly₁₀ were built and solvated with TIP3P water using XLeap in AmberTools13 [10]. Initial box size for Gly₃ was 4 nm on a side with 1955, 1953, and 2064 water molecules for C27, C36, and ff12SB systems, respectively. Initial box size for Gly₁₀ was 6 nm on a side with 6782, 6782, and 6674 water molecules for C27, C36, and ff12SB, respectively. All simulations were then performed using NAMD 2.9 [30].

Simulations

All-atom C27, C36, and ff12SB protein parameter sets were used to simulate Gly₃ and Gly₁₀ in explicit TIP3P solvent (either CHARMM or Amber’s water parameter set) using the NAMD 2.9 molecular dynamics package [30]. Steepest descent minimization was performed followed by equilibration runs of at least 20 ns for Gly₃ or 100 ns for Gly₁₀ at constant number, temperature, and pressure (NPT ensemble). Production simulations were similarly performed in the NPT ensemble. Gly₃ and Gly₁₀ were simulated for 300 ns and 950 ns, respectively, with each force field. Temperature and pressure were maintained with a Langevin thermostat and barostat. The equations of motion were integrated with the velocity Verlet algorithm with a 2 fs time step. The van der Waals forces were truncated at 1.2 nm with NAMD’s default switching functions employed at 1.0 nm. Electrostatic forces were computed using particle mesh ewald with a grid spacing of 1.0 Å. To match Amber’s non-bonded exclusion convention, 1–4 scaling was set to 0.8333 for simulations with ff12SB only. Coordinates and system information were saved every 500 time steps corresponding to every 1 ps.

Structural Analysis

To evaluate force field dependent conformational sampling we use a variety of structural metrics to characterize the oligoglycine chains. Protein coordinates from each simulation of Gly₃ and Gly₁₀ across the three force fields were used to measure end-to-end distance, radius of gyration, solvent accessible surface area (SASA), dihedral angles, NMR J-couplings and representative structural clusters.

End-to-end distance and radius of gyration

The probability distribution of the end-to-end distance and radius of gyration provide information on tendencies to be extended or collapsed. End-to-end distance, defined as the distance between terminal carbons in the ACE and NME caps, and mass weighted radius of gyration were measured across the trajectories. These values were binned and count normalized, yielding probability distributions of end-to-end distance (bin size = 0.2 Å) and radius of gyration (bin size = 0.05 Å) for both oligoglycines across the three force fields. Error in the average estimates of end-to-end distance and radius of gyration were calculated using a block standard error (BSE) method [31]. Briefly, a series of end-to-end distance or radius of gyration calculations are broken up into blocks of a particular length such that N = MΔn, where N is the number of measurements corresponding to the number of frames analysed from a trajectory, M is the number of blocks, and n is the block length, or number of elements in one of the M blocks. For a given n the average end-to-end distance or radius of gyration is calculated within each of the M blocks. Then the BSE is calculated as the standard deviation of these M block averages normalized by the square root of the number of blocks. A series of BSE values are computed for a range of block lengths. The error in the average end-to-end distance or radius of gyration is estimated as the BSE at the point in which the BSE curve plateaus.

Inspection of the BSE suggested that errors in average end-to-end distance and radius of gyration could be sufficiently estimated with 20 ns long blocks for Gly₃ and 50 ns long blocks for Gly₁₀ across the three force fields. Probability distributions of end-to-end distance and radius of gyration for each of the 20 ns long blocks for Gly₃ or 50 ns blocks for Gly₁₀ were constructed using the same bin sizes reported above. The standard deviation of the counts in each bin was recorded and captured the within-bin spread. These are depicted as the shaded regions in the end-to-end distance and radius of gyration results in Figure 1.

Figure 1.

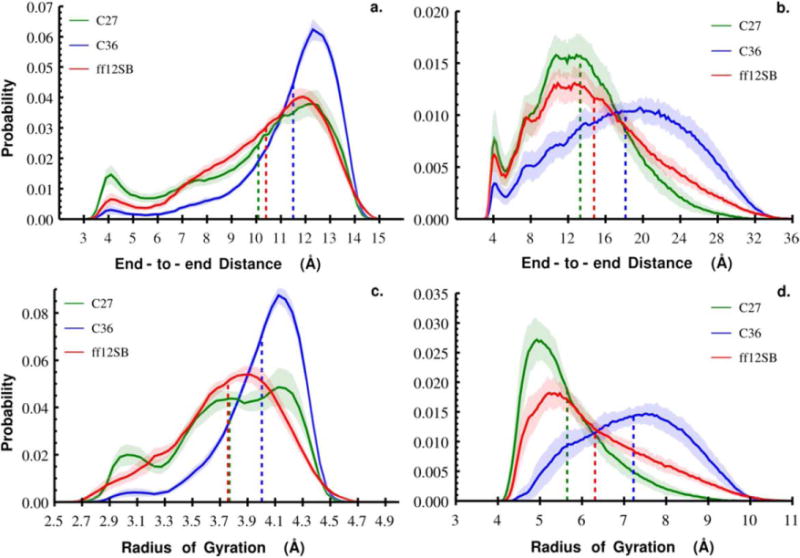
Probability distributions of end-to-end distance and radius of gyration for Gly₃ (a. and c.) and Gly₁₀ (b. and d.) as a function of force field. Results for each force field are colored: C36 (blue), C27 (green), and ff12SB (red). The colored dashed lines indicate the average end-to-end distance or radius of gyration for the corresponding force field (Table 1). The shaded regions represent the standard deviation of within-bin probabilities calculated by blocking each Gly₃ and Gly₁₀ trajectories into 20 ns and 50 ns blocks, respectively.

Comparison to random coil

Polymer models have been used to describe the behavior of disorder polypeptide segments in a variety of aqueous conditions [32], [33]. To qualitatively assess polymer behavior of Gly₁₀ and how this behavior might change when using different force fields, we compare the end-to-end distance distribution of Gly₁₀ to that predicted with an ideal, random coil polymer model. In a random coil model it is assumed that there are no self-interactions or excluded volume and that intramolecular and solvent interactions balance each other [34]. As a result, the end-to-end distance distribution for a random coil can be modeled as a 3D random walk (Eqn. 1):

$$P(r)=\frac{4\pi r^2}{{(2/3\pi \langle r^2\rangle )}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\exp [-\frac{3r^2}{2\langle r^2\rangle }]$$ (1)

where r is end-to-end distance, and r² is mean square end-to-end distance. r² was measured from the simulations of Gly₁₀ with each of C27, C36, and ff12SB and the ideal polymer end-to-end distance distributions were compared to those measured from the simulations. Polymer models were developed for high polymers containing thousands or more monomers. Gly₁₀ is thus expected to show deviations from high polymer ideality. Nonetheless, evaluating these deviations as a function of force field provides an additional way in which to compare the effects force fields have on modeling highly disordered polypeptides.

Solvent Accessible Surface Area Probability Distributions

A protein’s solvent accessible surface area (SASA) plays a major role in its solution and binding thermodynamics [2], [35]–[37]. To investigate the dependencies between SASA and force field, we measured the SASA of all Gly₃ and Gly₁₀ conformations in the C27, C36, and ff12SB trajectories with a solvent radius of 1.4 Å in VMD. SASA probability distributions were generated for each force field with bin sizes of 5 Ų.

Dihedral Angle Distributions and Free Energy Surfaces

Dihedral angles (φ,ψ) were collected along the trajectories for the internal (non-termini) residues of Gly₃ and Gly₁₀ from simulations with C27, C36, and ff12SB. Histograms of φ,ψ were generated with 2 degree bin widths. The values in each bin were converted to free energies via

$$\mathrm{\Delta }{G}_i=-\mathit{RTln}(N_i/N_{\mathit{tot}})$$ (2)

where R is the gas constant, T is absolute temperature (300 K), N_i is the count in bin i, and N_tot is the total number of counts. The free energy surface is plotted with contour levels colored according to ΔG_i (dark blue = minimum, bright red = maximum). Populations of the major secondary structure regions were assessed using the following criteria: poly-proline (PPII) with φ,ψ = (−70°±30°, 150°±30°), β-strand (β) = (−150°±30°,150°±30°), right α-helix (α_R) = (−85°±55°,−7.5°±67.5°), and left α-helix (α_L) = (85°±55°,7.5°±67.5°). The definitions of PPII and β-strand follow from [19], however we elected to use larger, symmetric areas for the right- and left-handed helical regions because of the symmetry (lack of chirality) and larger number of sterically permitted states of oligoglycine. Error in the populations of these regions was estimated with the block standard error approach detailed in the Methods section on the end-to-end distance and radius of gyration analyses. Here we used blocks of 50 ns and 125 ns for Gly₃ and Gly₁₀ respectively.

NMR Scalar Couplings

J-couplings can be related to backbone dihedral angles via the Karplus equation [38], [39]. The equation has the general form:

$$J\left(\theta \right)=A{\mathit{cos}}^2(\theta +\mathrm{\Delta })+B\mathit{cos}(\theta +\mathrm{\Delta })+C$$ (3)

where A,B, and C are parameterized against experiment or theory, θ is a backbone dihedral angle, either φ or ψ, and Δ is a phase shift for a particular J-coupling. Karplus equation parameters were taken from [21] for Gly₃. Eight J-couplings that probe the dihedral angles of the central residue were calculated across the trajectories of Gly₃ and Gly₁₀ for each force field.

Representative structure clusters

The quality threshold algorithm implemented in VMD [40] was used to classify and visualize dominant structure clusters from simulations of Gly₁₀ with the C27, C36, and ff12SB force fields. The mass weighted, root mean squared distance (RMSD) between heavy atoms was used to measure structure similarity. Five clusters containing structures within a cutoff RMSD of 2.5 Å were chosen a priori from snapshots every 50 ps. We then compared the dominant structure clusters from each trajectory using end-to-end distance and radius of gyration.

Results and Discussion

Distributions of end-to-end distance and radius of gyration exhibit force field dependency

To capture the structural properties of oligoglycine as a function of force field we calculated the distance, r, between terminal carbon atoms and the mass weighted radius of gyration, R_g, for each trajectory. Convergence and errors in our measurements were estimated using a block standard error approach (see Methods) with block lengths of 20 ns for Gly₃ and 50 ns for Gly₁₀. Considering Gly₃, we find that probability distributions of end-to-end distance and R_g vary considerably when using C27, C36, or ff12SB as depicted in Figure 1 and Table 1. C36 samples more extended, less compact structures than C27 and ff12SB with a narrower probability distribution concentrated around the mean end-to-end distance, r_C36 = 11.5 Å ± 0.04 and mean R_g, R_{g C36} = 4.0 Å ± 0.006. In contrast, both C27 and ff12SB sample more structures with short to intermediate end-to-end distances than C36 resulting in similar r′s. Although the C27 and ff12SB end-to-end distance distributions are similar, the shapes of the R_g distributions are different, suggesting different structural tendencies even though R_{g C27} and R_{g ff12SB} are essentially the same. This suggests that end-to-end distance alone may not be a sufficient metric to compare force field structure sampling and that higher order moments of end-to-end distance and R_g distributions should be considered.

Table 1.

Moments of the Gly₃ and Gly₁₀ end-to-end distance and radius of gyration distributions. In parentheses next to the mean is the estimated BSE.

		End-to-end Distance (Å)				Radius of Gyration (Å)
	Force Field	Mean	Variance	Skew	Kurtosis	Mean	Variance	Skew	Kurtosis
	C27	10.09 (0.08)	7.45	−15.87	146.69	3.77 (0.015)	0.16	−0.03	0.06
Gly3	C36	11.50 (0.04)	3.58	−10.71	77.26	4.00 (0.006)	0.08	−0.03	0.03
	ff12SB	10.40 (0.06)	5.50	−10.12	95.21	3.76 (0.010)	0.14	−0.02	0.05
	C27	13.30 (0.20)	25.78	53.17	1965.40	5.65 (0.040)	0.89	0.89	3.06
Gly10	C36	18.14 (0.24)	44.18	−21.73	4373.30	7.22 (0.050)	1.44	−0.04	4.64
	ff12SB	14.78 (0.17)	39.09	119.87	4172.69	6.31 (0.041)	1.70	1.60	8.05

To evaluate how these force field dependent properties change with oligomer length we performed the same structural analysis with trajectories of Gly₁₀ generated using C27, C36, and ff12SB. At this length of oligoglycine the differences between the force fields are accentuated. We again find C36 to sample more extended, less compact structures with a mean end-to-end distance at least 3 Å greater than C27 and ff12SB. Furthermore, both end-to-end distance and R_g distributions for C36 are skewed towards extended structures, opposite those for the other force fields (Figure 1 and Table 1). All three force fields across both oligoglycines show a small peak around ~4 Å end-to-end distance which is indicative of correlations in a loop-like formation. C27 visits these structures more than ff12SB, and considerably more than its successor C36. The question of which force field is accurately capturing the frequency with which these correlated, looped Gly₁₀ structures are formed may be resolved, in part, by single molecule methods that measure the kinetics of termini contact formation[8], [41]. The structural characteristics of ff12SB appear to be intermediate to those observed for C27 and C36.

Few experiments provide detailed structural data for longer glycine constructs making a direct comparison to experimental data challenging. This may be attributed to the increasingly low solubility of oligoglycine with respect to increasing length [25], [42]. A computational consideration of the solubility limit of Gly₅ solutions suggests a mechanism for the phase separation based predominately on non-hydrogen bonding amide dipole correlations [27]. Furthermore, experimental and computational studies disagree about the conformational preferences of the peptide backbone (extended vs. collapsed), the quality of water as its solvent, and how these change depending on chain length. Ohnishi et al. [43] used a combination of NMR and SAXS to study the conformational preferences of various oligoglycine linkers separating Acetyl-Tyr-Glu-Ser and Ala-Thr-Asp amino acid residues, which were used to decrease resonance overlap, and concluded that oligoglycines in solution prefer the extended state. For Gly₂ and Gly₆ linkers they found an R_g of 7.90 Å and 9.10 Å, respectively. Our results for Gly₁₀ with the C36 force field are not dramatically different considering that the three amino acids added to each end of the oligoglycine linker may alter the structural preferences compared to a pure glycine chain and that their polypeptide contains two additional residues.

Pappu et al. [44] constructed a potential of mean force as a function of radius of gyration for Gly₁₅ with the OPLS AA/L force field and found that Gly₁₅ collapses in water with a probability of R_g less than 7 Å to be 0.83. Consistently, Gly₁₅ was also shown to adopt a compact structure with a radius of gyration less than 6.5 Å from simulations with C27 (Karandur, submitted). These are similar to what we find for Gly₁₀ across the three force fields and also with what Ohnishi and coworkers [43] find for their shorter constructs. An experimental study, [7] determined the hydrodynamic radius of gyration of Gly₂₀ by fluorescence correlation spectroscopy to be ~10.4 Å corresponding to an R_g of ~8 Å which is less than 1 Å larger than R_{g C36} for a system of twice the chain length. The effects of the reporting groups is less certain. Recent work by Best et al. [45] suggests that current force fields poorly solvate polypeptides leading to more collapsed, unfolded states than suggested by experiment and that a better match to experiment can be achieved by modifying the short range protein-solvent interactions for disordered proteins. Given their observations and the fact that the R_g of these oligoglycine models ranging considerably in length are relatively similar, future work should aim to determine if the force fields are accurately capturing the scaling of the protein backbone’s structural properties.

Gly₁₀ deviates from random coil polymer model but depends on force field

Naturally, polymer models and theory have been extended to the study of IDPs and have proven useful in understanding how the properties depend on solvent, amino acid composition, and number of peptides [32], [33], [46], [47]. Ideal polymers, like the random coil, are modeled as a statistical random walk where monomers can occupy the same space and the positions of the monomers are uncorrelated [34]. These assumptions yield a skewed Gaussian for the end-to-end distance probability distributions (Eqn. 1). Figure 1 clearly demonstrates positional correlations, however to show that different force fields introduce different non-random coil behavior we compared the end-to-end distance distributions for Gly₁₀ obtained from simulations with C27, C36, and ff12SB to what would be expected for a random coil (Eqn. 1) with the same variance, r². Figure 2a–c shows the end-to-end distance distribution (solid) overlaid with that predicted for a random coil with the same r² (dotted). The large tails and peak locations of the C27 and ff12SB end-to-end distance distributions are captured very well by the random coil model, however it clearly does not capture these features well for C36. As a result of this “stiffer” behavior, C36 under-samples Gly₁₀ conformations with intermediate end-to-end distances compared to its random coil model. A non-linear least squares fit of Eqn. 1 to the data also clearly shows that the Gaussian functional form does not capture the distribution of long end-to-end distances for C36. Across all force fields self-interactions and other multi-body correlations result in greater populations of structures with shorter end-to-end distances (peak ~4 Å) than their random coil counterparts, but the extent to which they deviate from random depends on the force field.

Figure 2.

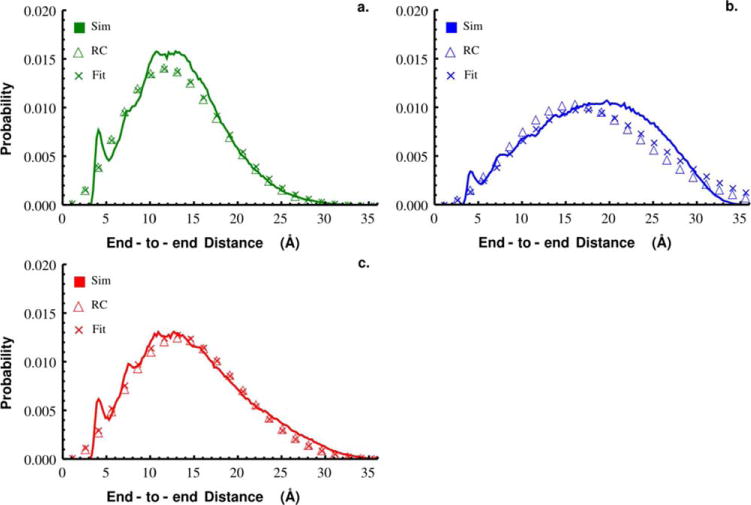
End-to-end distance distributions from simulations of Gly₁₀ (solid line) with C27 (a), C36 (b), and ff12SB (c). Overlaid is the distribution expected for a random coil with the same mean squared end-to-end distance measured from simulations (open triangle) and the distribution following a non-linear least squares fit (x’s) of Eqn. 1 to the data.

Single molecule methods, like smFRET, can be used to estimate the distribution of end-to-end distances in IDPs from measurements of the resonance energy transfer by assuming the distribution in Eqn. 1 [41], [48]. The fact that the functional form of the end-to-end distance distribution depends on force field should be considered when attempting to compare results from simulations and single molecule experiments. Which force field is most accurately modeling the distribution of end-to-end distances in Gly₁₀ remains to be seen. Single molecule experiments could be used to determine how r² scales with the length of the protein backbone and thus force field accuracy.

Solvent accessible surface area exhibits force field dependencies

Intrinsically disordered proteins (IDPs) or regions (IDRs) are often found in regulatory network hub proteins and facilitate binding to multiple partners [2]. Conformational selection and concomitant binding and folding are thought to be two of the major IDP-facilitated recognition or binding mechanisms [49]. In either case, an IDP’s conformational ensemble is likely to provide a range of available surfaces to accommodate its many binding partners. For example, Dunker and coworkers have shown that a disordered region of p53 adopts four different structures when binding four different partners and that the change in accessible surface area vary considerably [2]. Many IDPs have been shown to form extended binding surfaces with their targets [35]. The SASA for individual protein or polypeptide conformations can be easily calculated from snapshots of a molecular simulation. However, the distribution of SASA will depend on the conformational sampling and thus the model or force field used in the simulation. To highlight these dependencies we generated SASA probability distributions for Gly₃ and Gly₁₀ from the C27, C36, and ff12SB trajectories (Figure 3). The SASA distributions for Gly₃ concentrate around very similar average SASAs with Gly₃:SASA_C27 = 463 Ų, Gly₃:SASA_ff12SB = 465 Ų, and Gly₃:SASA_C36 = 470 Ų. However, clear differences between force fields emerge when we consider Gly_10. The Gly₁₀ conformations sampled by the three force fields yielded a wide range of SASA (~700–1100 Ų) and very different probability distributions (Figure 3). C36 overwhelmingly samples extended conformations with a large SASA (Gly₁₀:SASA_C36 = 1010 Ų) whereas C27 samples conformations with a broad distribution of compact, short and intermediate SASAs (Gly₁₀:SASA_C27 = 880 Ų). Again with structural properties intermediate to C36 and C27, we find a small peak at a large SASA and a broad distribution across small and intermediate SASAs, albeit less so than what we observe for C27, which yields Gly₁₀:SASA_ff12SB = 934 Ų. While consistent with what we observed from the distributions of end-to-end distance and radius of gyration, the differences in structural properties of Gly₁₀ modeled with these three force fields are further accentuated when considering SASA.

Figure 3.

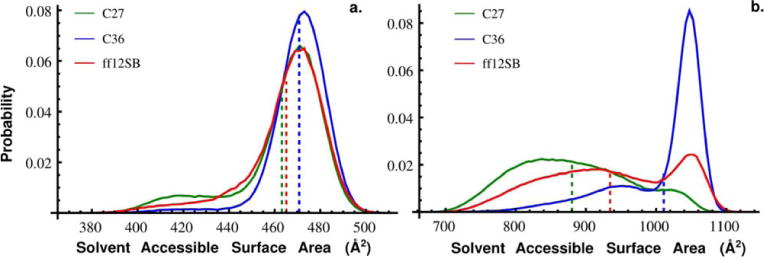
Probability distributions of solvent accessible surface area (SASA) measured from simulations of Gly₁₀ with the C27 (Green), C36 (Blue), and ff12SB (red) force fields. A solvent probe of 1.4 Å was used to calculate SASA. The mean SASA (dashed lines) for Gly₁₀ simulated with C27, C36, and ff12SB was 880 Ų, 1010 Ų, and 934 Ų, respectively.

Dihedral angle free energy surfaces

Dihedral angle distributions were constructed for internal residues of Gly₃ and Gly₁₀ from simulations with C27, C36, and ff12SB. These distributions were count normalized and converted to free energy surfaces as described in the Methods. The free energy surfaces as a function of force field and oligoglycine length are depicted in Figure 4 as contour plots using the same color scale with dark blue and red representing free energy minima and maxima, respectively. Surface plots of the corresponding probability distributions are found in Supplemental Figure 1. Comparing results for Gly₃, we find the minimum free energy in the right and left helix region for C27. This helical bias was noted previously [9], [17]. In contrast, C36 has changed this bias with the energy minima occurring in the polyproline II regions (PPII). The locations of the free energy minima match well with what MacKerell et al. observed for uncapped Gly₃ [9].

Figure 4.

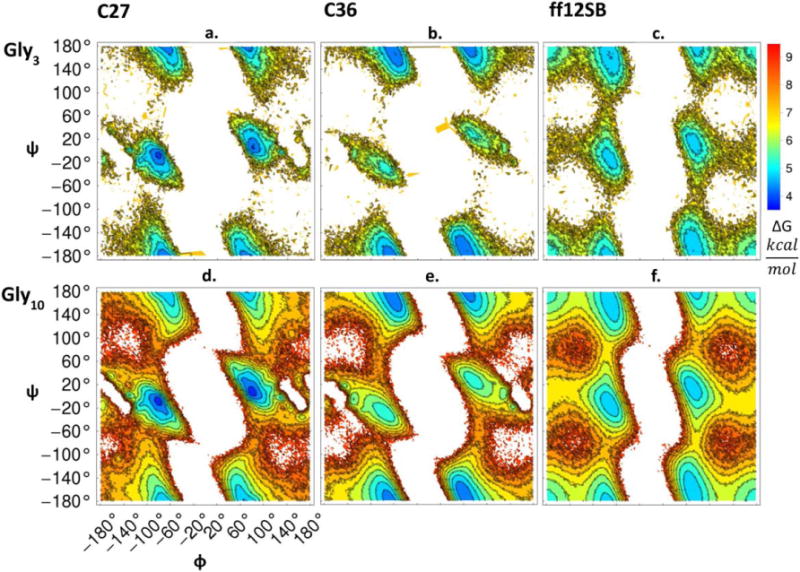
Dihedral angle free energy surfaces as a function of force field. The backbone dihedral angle pairs of internal residues were binned on a grid and the counts were converted to a free energy representation as described in the Methods. Figures 4a–c show results for Gly₃ and 4d-f for Gly₁₀ across the C27, C36, and ff12SB force fields.

With no predominantly deep energy wells, ff12SB samples the major regions of the Ramachandran map more evenly and shows a greater sampling of the β-sheet region than C27 and C36. This is consistent with the dihedral energy surfaces reported for Gly₃ and the ff99SB force field in 2006 by [19]. Upon comparison of the ff12SB and ff99SB protein parameter sets and analysis of a preliminary simulation of Gly₃ with ff99SB it appears that the backbone dihedral parameters for glycine residues have remained unchanged. For Gly₁₀, the locations of the energy minima are consistent with Gly₃ suggesting a length independence. However, due to the considerably longer simulation times and the number of internal residues for Gly₁₀, we are able to sample higher free energy regions. Overall, all force fields are sampling regions of dihedral space consistent in footprint with what is observed from a survey of the PDB (Supplemental Figure 2 and [50]). We note the PDB distribution shows correlations with non glycine neighbors, partially skewing the expected symmetry. However, it is the probability of occupying these regions that differs between force fields and the survey from the PDB, which may be considerably more important for disordered proteins than structured ones.

We also assessed the populations (Table 2) of the four major secondary structure regions. The dihedral populations of internal residues of Gly₃ and Gly₁₀ are consistent with what we observe in the free energy surfaces. We expect in the limit of sufficient sampling that α_R and α_L populations would approach equallity. Interestingly, we find a larger error and more asymmetry in sampling of these regions for Gly₃ with C27 compared to C36 and ff12SB. This asymmetry decreases as we sample over a longer period of time and more dihedrals with Gly₁₀. The relatively slower kinetics of the backbone dihedral angles for C27 are likely the cause of the asymmetrical sampling. For a simple molecule like butane, Grossfield and Zuckerman [51] found that that even after long simulations the populations of the g+ and g- states were still different by three percent. Finally, no major multi-body correlation effects on the φ,ψ surface seem to be occurring in Gly₁₀ since the patterns of dihedral populations are consistent with Gly₃.

Table 2.

Dihedral angle populations (percentages) of the central residues in Gly₃ and Gly₁₀. Regions of the Ramachandran map were defined as α_R(φ,ψ) = (−85°±55°,−7.5°±67.5°), α_L = (85°±55°,7.5°±67.5°), ppII = (−70°±30°,150°±30°), and β = (−150°±30°,150°±30°). In parentheses is the population error measured by splitting Gly₃ and Gly₁₀ trajectories into 50 ns and 125 ns blocks, respectively (see Methods for details on measuring block standard error).

	Gly3			Gly10
	C27	C36	ff12SB	C27	C36	ff12SB
αR	26.8 (1.54)	5.20 (0.45)	14.3 (1.35)	30.8 (1.93)	7.04 (0.45)	17.0 (0.29)
αL	22.2 (1.20)	4.90 (0.48)	14.6 (0.56)	32.5 (2.42)	6.31 (0.28)	16.3 (0.61)
ppII	13.4 (0.71)	25.2 (0.83)	17.4 (0.47)	8.80 (0.21)	24.2 (0.49)	16.2 (0.21)
β – strand	0.30 (0.02)	0.40 (0.02)	4.00 (0.14)	0.20 (0.008)	0.40 (0.006)	3.40 (0.048)

Our analysis of the dihedral angle distributions in each force field only reports on angles found in common secondary structures per residue and does not suggest that oligoglycine assumes a stable global secondary structure. The literature on oligoglycine conformations in solution is inconsistent. Asher and coworkers[52] used Raman spectroscopy to study the structures of Gly₅ and Gly₆ in lithium salt solutions. They concluded that in solution PPII-like conformations are stabilized and that these conformations are further stabilized as lithium concentrations are increased. This may be the case in the particular solution they used, although extrapolating these findings per residue to the global structural behavior of oligoglycine in solution is problematic. Using Raman and IR spectroscopy, [53] suggested that cationic and zwitterionic triglycine in D₂O populate a mix of PPII, right-handed α-helices, and β-turns. They interpreted their results to conclude that tripeptides in general adopt well-defined secondary structures in water. From secondary structure assignments across all trajectories using STRIDE in VMD, we find that neither Gly₃ nor Gly₁₀ form stable, common secondary structures. Rather the structures formed are transient and contain combinations of dihedral angles which contribute to the both the residue and the global equilibrium structural probability distributions.

Scalar Couplings

J-coupling constants are a measure of the local structure within a protein or polypeptide. Table 3 shows the calculated J-coupling constants for the central residues of Gly₃ and Gly₁₀ across the three force fields along with the experimentally measured values [21]. Overall the three force fields recapitulate the experimentally measured J-couplings quite well given that the uncertainty in these calculated values has been estimated to be at least ±1 Hz [54], [55]. The R² values from a linear fit between calculated and measured J-couplings were all above 0.96 for each force field. In most cases the calculated J-couplings only differ by a few tenths of one Hz between force fields and all force fields systematically either over- or under-estimate the J-couplings when compared to experiment. It is important to note that Graf et al. performed these NMR experiments in very acidic conditions (pH=2) where the carboxyl terminus of Gly₃ would be protonated. In parameterizing the C36 force field, [9] found that the calculated J-couplings from simulations of uncapped, protonated Gly₃ matched experiment well after the initial QM calculations, and so no further adjustments of the torsional correction (CMAP) were made to exactly match experiment. They did however use the measured J-coupling constant from Graf et al. as target data to optimize side chain dihedral parameters. The linear fit for uncapped Gly₃ (R²=0.988) is only slightly better than what we measure for our capped Gly₃, suggesting the neutral caps are not significantly altering the distribution of internal backbone dihedral angles. While we cannot make a direct comparison of the calculated J-couplings for the central residue of Gly₁₀, we do find that they did not change considerably compared to those for Gly₃ across all force fields.

Table 3.

J-coupling constants calculated for the central residue of Gly₃ and Gly₁₀ using the Karplus equations and parameters from (Graf et al. 2007)². The experimentally measured J-couplings for Gly₃ at a pH of 2are reported. as well as those calculated from simulations of Gly₃ with Gromos (Graf et al. 2007)² and uncapped Gly₃ with C36 (Best et al. 2012)¹

Gly3		Force-field					Exp.2 (pH = 2)
J-coupling	Dihedral	C27	C36	ff12SB	C36 Lit.1	Gromos Lit.2
J(HN,HA)	Φ2	6.327 ± 0.003	5.916 ± 0.003	5.974 ± 0.003	5.82	5.8 ± 2.7	5.89 ± 0.07
J(HN,C’)	Φ2	0.725 ± 0.002	1.203 ± 0.002	1.074 ± 0.002	1.1	1.2 ± 1.1	1.1
J(HA,C’)	Φ2	3.805 ± 0.004	4.027 ± 0.005	3.618 ± 0.005	3.73	3.3 ± 2.1	4.01
J(C’,C’)	Φ2	0.645 ± 0.001	0.599 ± 0.001	0.902 ± 0.001	0.48	1.3 ± 0.8	0.26
J(N,CA)1	Ψ2	10.957 ± 0.002	11.654 ± 0.001	11.163 ± 0.002	11.74	10.4 ± 1	12.17 ± 0.02
J(N,CA)2	Ψ1	7.934 ± 0.002	7.933 ± 0.002	7.888 ± 0.002	8.58	8.6 ± 0.2	10.45 ± 0.02
J(N,CA)2	Ψ2	7.244 ± 0.003	8.398 ± 0.002	7.803 ± 0.002	8.5	8.1 ± 0.6	9.05 ± 0.03
J(HN,CA)	Φ2 & Ψ1	0.534 ± 0	0.511 ± 0	0.602 ± 0	0.61	0.8 ± 0.2	0.78

Gly10		Force-field
J-coupling	Dihedral	C27	C36	ff12SB
J(HN,HA)	Φ5	6.289 ± 0.012	5.974 ± 0.013	5.986 ± 0.013
J(HN,C’)	Φ5	0.737 ± 0.006	1.124 ± 0.007	1.064 ± 0.007
J(HA,C’)	Φ5	3.855 ± 0.018	4.097 ± 0.019	3.65 ± 0.018
J(C’,C’)	Φ5	0.594 ± 0.002	0.618 ± 0.003	0.846 ± 0.005
J(N,CA)1	Ψ5	10.6 ± 0.006	11.590 ± 0.005	11.012 ± 0.007
J(N,CA)2	Ψ4	6.976 ± 0.01	8.274 ± 0.007	7.67 ± 0.01
J(N,CA)2	Ψ5	6.754 ± 0.009	8.313 ± 0.007	7.614 ± 0.01
J(HN,CA)	Φ5 & Ψ4	0.437 ± 0.001	0.600 ± 0.001	0.549 ± 0.002

While NMR provides valuable structural and dynamical data of polypeptides in solution that can be used to refine force field parameters, issues arise due to the ensemble averaged nature and degeneracy of NMR observables [13], [17], [54]. For example, it has been pointed out that three very unique dihedral angle distributions can yield the same J-coupling constant calculated using the Karplus equations [54]. Also, [17] noted that 8 different force fields, all sampling structures of polyalanine with different secondary structure propensities, match experimental NMR data well. Similarly, we find that although C27, C36, and ff12SB match experimental J-coupling constants well, the structural distributions and properties of oligoglycine simulated with these force fields are quite different.

Structure clustering

To further characterize the differences in conformation sampling between force fields we clustered similar structures of Gly₁₀ from the C27, C36, and ff12SB trajectories as described in the methods section above. Five dominant structure clusters were generated independently for each force field, the results of which can be seen in Figure 5. The dominant clusters sampled in C36 are much more extended and less complex than C27. Figure 5 also shows the average end-to-end distance, r, and radius of gyration, R_g, per cluster. In all clusters r_C36 is greater than 16 Å and R_{g C36} is greater than 7 Å, both of which are well above those found in C27 clusters. The dominant ff12SB clusters are more structurally diverse than C36 and C27 with r_ff12SB and R_{g ff12SB} spanning a wider range. The characteristics of the ff12SB clusters appear to be a combination of those observed for C27 and C36. Taken together, these findings are consistent with what we observed in the end-to-end and radius of gyration analysis (Figure 1).

Figure 5.

Five representative structural clusters of Gly₁₀ from C27 (top), C36 (middle) and ff12SB (bottom) force fields. Clusters were generated using the quality threshold algorithm in VMD with a cluster cutoff of 2.5 Å. Reported below each representative structure is average end-to-end distance and radius of gyration of all structures within that cluster.

Conclusions

Considerable effort over the last decade has been dedicated to understanding how structural disorder is needed for many proteins to function properly [2], [3], [5], [56]. Furthermore, the prevalence of protein disorder in various diseases has prompted numerous studies and the development of experimental and computational techniques aimed at characterizing structural properties of disordered proteins [3], [6], [7], [32]. Low solubility, among other factors, has made investigating the structural ensemble of increasingly longer disordered proteins in solution experimentally challenging.

Computer simulations are not limited by the same experimental constraints and can provide atomic resolution structural properties of the underlying models that can then be used to develop hypotheses. Classical simulations rely on a force field approximation of inter- and intra-molecular interactions. There exist a variety of classical force fields all of which have been parameterized against different QM and experimental data. Force field specific biases can result from target data used and the parameterization process [13]. Many of these force fields describe structured proteins similarly well but it is important to continually challenge these force fields with diverse systems to ensure their accuracy [16].

Here we have used oligoglycine as a protein backbone model to investigate conformational sampling biases of the commonly used C27, C36, and ff12SB force fields. A structural analysis of Gly₃ and Gly₁₀ revealed that C36 preferentially samples extended structures while C27 and ff12SB favor more compact, complex structures. The helical bias noted with C27 has been considerably reduced in C36, which more strongly samples polyproline-II regions, while ff12SB more evenly samples the major regions of Ramachandran space. We find that these force field dependent properties are more pronounced for Gly₁₀ than Gly_3. From this comparative study, we conclude that more experiments are needed to ensure that force fields are capturing the length dependence of the protein backbone’s structural properties. Interestingly we also found that the residual dipolar couplings of the central residue of Gly₃ calculated using the Karplus equation for each force field matched experiment quite well, despite each force field exhibiting some clearly different structural properties. Others have also observed this in force field comparison studies using polyalanine [17] and other alanine rich peptides [57]. While NMR provides valuable data on polypeptides in solution, the highly averaged, somewhat uncertain nature of NMR observables and the degenerate relationship between these observables and protein backbone dihedral angles may be problematic when attempting to optimize a force field against such data [13], [54], [55], [57]. Protein force fields have traditionally been used to model well-structured proteins. Our results suggest that care must be taken not only when applying these force fields to IDP systems but also when making mechanistic inferences based on the results from using a single force field.