Using Genome-Scale Models to Predict Biological Capabilities

Abstract

Constraint-based reconstruction and analysis (COBRA) methods at the genome-scale have been under development since the first whole genome sequences appeared in the mid-1990s. A few years ago this approach began to demonstrate the ability to predict a range of cellular functions including cellular growth capabilities on various substrates and the effect of gene knockouts at the genome-scale. Thus, much interest has developed in understanding and applying these methods to areas such as metabolic engineering, antibiotic design, and organismal and enzyme evolution. This primer will get you started.

Introduction

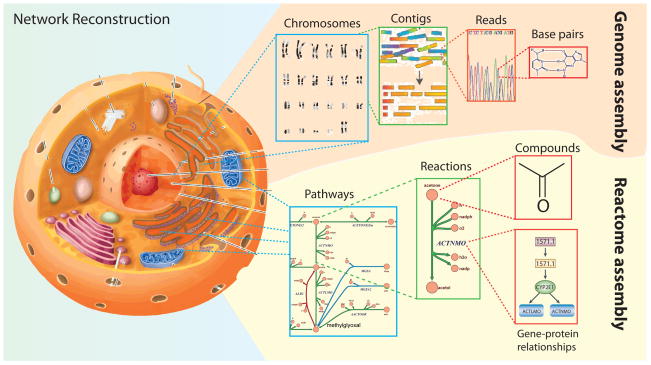
Bottom-up approaches to systems biology rely on constructing a mechanistic basis for the biochemical and genetic processes that underlie cellular functions. Genome-scale network reconstructions of metabolism are built from all known metabolic reactions and metabolic genes in a target organism. Networks are constructed based on genome annotation, biochemical characterization, and the published scientific literature on the target organism; the latter is sometimes referred to as the bibliome. DNA sequence assembly provides a useful analogy to the process of network reconstruction (Figure 1A). The genome of an organism is systematically assembled from many short DNA stubs, called reads, using sophisticated computer algorithms. Similarly, the reactome of a cell is assembled, or reconstructed, from all the biochemical reactions known or predicted to be present in the target microorganism. Importantly, network reconstruction includes an explicit genetic basis for each biochemical reaction in the reactome as well as information about the genomic location of the gene. Thus, reconstructed networks, or an assembled reactome, for a target organism represents biochemically, genetically, and genomically structured knowledge bases, or BiGG k-bases. Network reconstructions have different biological scope and coverage. They may describe metabolism, protein-protein interactions, regulation, signaling, and other cellular processes, but they have a unifying aspect: an embedded, standardized biochemical and genetic representation amenable to computational analysis.

Figure 1. Network reconstruction.

A. An organism’s reactome can be assembled in a way that is analogous to DNA sequencing assembly. From right to left: first the interacting compounds must be identified. Then, the reactions acting on these compounds are tabulated and the protein that catalyzes the reaction and the corresponding open reading frame is identified in the organism of interest. These reactions are assembled into pathways that can be laid out graphically to visualize a cell’s metabolic map at the genome-scale. Several tools for reactome assembly and curation exist including the COBRA Toolbox (Ebrahim et al., 2013; Schellenberger et al., 2011b), KEGG (Kanehisa et al., 2014), EcoCyc (Keseler et al., 2013), ModelSeed (Henry et al., 2010b), BiGG (Schellenberger et al., 2010), Rbionet (Thorleifsson and Thiele, 2011), Subliminal (Swainston et al., 2011), Raven toolbox (Agren et al., 2013) and others.

A network reconstruction can be converted into a mathematical format and thus lend itself to mathematical analysis and computational treatment. Genome-scale models, called GEMs, have been under development for nearly 15 years and have now reached a high level of sophistication. The first GEM was created for Haemophilus influenza and appeared shortly after this first genome was sequenced (Edwards and Palsson, 1999), and GEMs have now grown to the level where they enable predictive biology (Bordbar et al., 2014; McCloskey et al., 2013; Oberhardt et al., 2009). Here, we will focus on reconstructions of metabolism and the process of converting them into GEMs to produce computational predictions of biological functions.

The fundamentals of the Constraints-Based Reconstruction and Analysis (COBRA) approach and its uses are also described in this Primer, which lays out the constraint-based methodology out at four levels. First, there is a textual description of the methods and their applications. Second, visualization is presented in the form of detailed figures to succinctly convey the key concepts and applications. Third, the figure captions contain more detailed information about the computational approaches illustrated in the figures. Fourth, the primer provides a table of selected detailed resources to enable an in-depth review for the keenly interested reader. The text is organized into six sections, each one addressing a grand challenge in today’s world of “big data” biology:

1. Network Reconstructions Assemble Knowledge Systematically

A large library of scientific publications exists that describe different model organisms’ specific molecular features. Molecular biology’s focus on knowing much about a limited number of molecular events changed once annotated genome sequences became available, leading to the emergence of a genome-scale point of view. Now, putting all available knowledge about the molecular processes of a target organism in context and linked to its genome sequence has emerged as a grand challenge. Genome-scale network reconstructions were a response to this challenge.

Network reconstructions organize knowledge into a structured format

The reconstruction process treats individual reactions as the basic elements of a network, somewhat similar to a base pair being the smallest element in an assembled DNA sequence (Figure 1A). To implement the metabolic reconstruction process, a series of questions need to be answered for each of the enzymes in a metabolic network: 1) What are the substrates and products? 2) What are the stoichiometric coefficients for each metabolite that participates in the reaction (or reactions) catalyzed by an enzyme? 3) Are these reactions reversible? 4) In what cellular compartment does the reaction occur? 5) What gene(s) encode for the protein (or protein complex) and what is (are) their genomic location(s)? Genes are linked to the proteins they encode and the reactions they catalyze using the gene-protein-reaction relationship (GPR). All of this information is assembled from a range of sources including organism specific databases, high-throughput data, and primary literature. Establishing a set of the biochemical reactions that constitute a reaction network in the target organism culminates in a database of chemical equations. Reactions are then organized into pathways, pathways into sectors (such as amino acid synthesis), and ultimately into genome-scale networks, akin to reads becoming a full DNA sequence. This process has been described in the form of a 96-step standard operating procedure (Thiele and Palsson, 2010).

Today, after many years of hard work by many researchers, there exist collections of genome-scale reconstructions (sometimes called GENREs) for a number of target organisms (Monk et al., 2014; Oberhardt et al., 2011) and established protocols for reconstruction exist (Thiele and Palsson, 2010) that can be partially automated (Agren et al., 2013; Henry et al., 2010a).

Recapitulation

Network reconstructions represent an organized process for genome-scale assembly of disparate information about a target organism. All this information is put into context with the annotated genome to form a coherent whole that, through computations, is able to recapitulate whole cell functions. The grand challenge of disparate data integration into a coherent whole is achieved through the formulation of a GEM. A GEM can then compute cellular states such as an optimal growth state. This process is further explored in the next section. A detailed reading list is available in Supplemental Table 1 on the network reconstruction process and software tools used to facilitate it.

2. Converting a Genome-scale Reconstruction to a Computational Model

Before a reconstruction can be used to compute network properties, a subtle, but crucial step must be taken in which a network reconstruction is mathematically represented. This conversion translates a reconstructed network into a chemically accurate mathematical format that becomes the basis for a genome-scale model (Figure 2A). This conversion requires the mathematical representation of metabolic reactions. The core feature of this representation is tabulation, in the form of a numerical matrix, of the stoichiometric coefficients of each reaction (Figure 2B). These stoichiometries impose systemic constraints on the possible flow patterns (called a flux map, or flux distribution) of metabolites through the network. These concepts are detailed below. Imposition of constraints on network functions fundamentally differentiates the COBRA approach from models described by biophysical equations, which require many difficult-to-measure kinetic parameters.

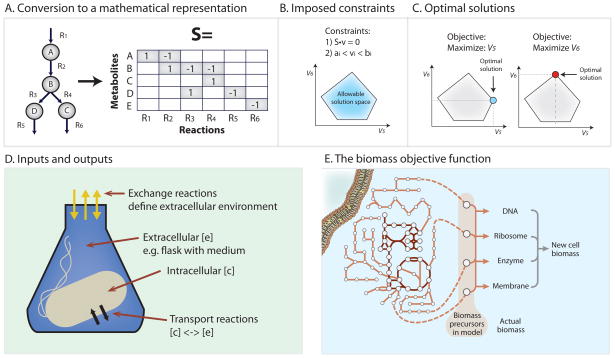
Figure 2. Formulation of a computational model.

A. After the metabolic network has been assembled it must be converted into a mathematical representation. This conversion is performed using a stoichiometric (S) matrix where the stoichiometry of each metabolite involved in a reaction is enumerated. Reactions form the columns of this matrix and metabolites the rows. Each metabolite’s entry corresponds to its stoichiometric coefficient in the corresponding reaction. Negative coefficient substrates are consumed (reactants), and positive coefficients are produced (products). Converting a metabolic network reconstruction to a mathematical formulation can be achieved with several of the toolboxes listed in Supplemental Table 1.

B. Constraints can be added to the model such as 1) enforcement of mass balance and 2) reaction flux (v) bounds. The blue polytope represents different possible fluxes for reactions 5 and 6 consistent with stated constraints. Those outside the polytope violate the imposed constraints and are thus ‘infeasible.’

C. Constraint-based models predict the flow of metabolites through a defined network. The predicted path is determined using linear programming solvers and termed Flux Balance Analysis (FBA). FBA can be used to calculate the optimal flow of metabolites from a network input to a network output. The desired output is described by an objective function. If the objective is to optimize flux through reaction 5, the optimal flux distribution would correspond to the levels of flux 5 and flux 6 at the blue point circled in the figure. The objective function can be a simple value or draw on a combination of outputs, such as the biomass objective shown in Fig 2E. It is important to note that alternate optimal flux distributions may exist to reach the optimal state as discussed in Figure 4C.

D. Once a network reconstruction is converted to a mathematical format, the inputs to the system must be defined by adding consideration of the extracellular environment. Compounds enter and exit the extracellular environment via ‘exchange’ reactions. The GEM will not be able to import compounds unless a transport reaction from the external environment to the inside of the cell is present.

E. In addition to exchange reactions, the biomass objective function acts as a drain on cellular components in the same ratios as they are experimentally measured in the biomass. In FBA simulations the biomass function is used to simulate cellular growth. The biomass function is composed of all necessary compounds needed to create a new cell including DNA, amino acids, lipids and polysaccharides. This is not the only physiological objective that can be examined using COBRA tools.

Constraints are mathematically represented as equations that represent balances or as inequalities that impose bounds (Figure 2C). The matrix of stoichiometries imposes flux balance constraints on the network, ensuring that the total amount of any compound being produced must be equal to the total amount being consumed at steady state. Every reaction can also be given upper and lower bounds, which define the maximum and minimum allowable fluxes through the reactions, that in turn are related to the turnover number of the enzyme and its abundance. Once imposed on a network reconstruction, these balances and bounds define a space of allowable flux distributions in a network; the possible rates at which every metabolite is consumed or produced by every reaction in the network. The flux vector, a mathematical object, is a list of all such flux values for a single point in the space. The flux vector represents a ‘state’ of the network that is directly related to the physiological function that the network produces. Many other constraints such as substrate uptake rates, secretion rates, and other limits on reaction flux can also be imposed, further restricting the possible state that a reconstructed network can take (Reed, 2012). The computed network states that are consistent with all imposed constraints are thus candidate physiological states of the target organisms under the conditions considered. The study of the properties of this space thus becomes an important subject.

Flux balance analysis (FBA) calculates candidate phenotypes

FBA is the oldest COBRA method. It is a mathematical approach for analyzing the flow of metabolites through a metabolic network (Orth et al., 2010). This approach relies on an assumption of steady-state growth and mass balance (all mass that enters the system must leave). The constraints discussed above take the form of equalities and inequalities to define a polytope (blue area within the illustration in Figure 2C) that represents all possible flux states of the network given the constraints imposed. Thus, many network states are possible under the given constraints and multiple solutions exist that satisfy the governing equations. The blue area is therefore often called the ‘solution space’ to denote a mathematical space that is filled with candidate solutions to the network equations given the governing constraints. FBA uses the stated objective to find the solution(s) that optimize the objective function. The solution is found using linear programming, and, as indicated in Figure 2D, the optimal solution lies at the edges of the solution space impinging up against governing constrains.

The utility of FBA has been increasingly recognized due to its simplicity and extensibility: it requires only the information on metabolic reaction stoichiometry and mass balances around the metabolites under pseudo-steady state assumption. It computes how the flux map must balance to achieve a particular homeostatic state. However, FBA has limitations. It balances fluxes, but cannot predict metabolite concentrations. Except in some modified forms, FBA does not account for regulatory effects such as activation of enzymes by protein kinases or regulation of gene expression. More details are found in the caption of Figure 2, and computational resources are summarized below that can be deployed to find the optimal state and to study its characteristics.

Models impose constraints and allow prediction

One of the most basic constraints imposed on genome-scale models of metabolism is that of substrate, or nutrient, availability and its uptake rate (Figure 2E). Metabolites enter and leave the systems through what are termed “exchange reactions” (i.e., active or passive transport mechanisms). These reactions define the extracellular nutritional environment and are either left ‘open’ (to allow a substrate to enter the system at a specified rate) or ‘closed’ (the substrate can only leave the system). Measurements of the rate of exchange with the environment are relatively easy to perform and they prove to be some of the more important constraints placed on the possible functions of reaction networks internal to the cell. More biological- and data-derived constraints can also be imposed on a model. These advanced constraints are detailed in sections 4, 5 and 6.

The next step in converting a network reconstruction to a model is to define what biological function(s) the network can achieve. Mathematically, such a statement takes the form of an ‘objective function.’ For predicting growth, the objective is biomass production, that is, the rate at which the network can convert metabolites into all required biomass constituents such as nucleic acids, proteins, and lipids needed to produce biomass. The objective of biomass production is mathematically represented by a ‘biomass reaction’ that becomes an extra column of coefficients in the stoichiometric matrix. One can formulate a biomass objective function at an increasing level of detail: Basic, Intermediate, and Advanced (Feist and Palsson, 2010; Monk et al., 2014). The biomass reaction is scaled so that the flux through it represents the growth rate (μ) of the target organism.

It is important to note that the biomass objective function is determined from measurements of biomass composition, the uptake and secretion rates from measuring the nutrients in the medium, and the model formulation is based on a network reconstruction that is knowledge-based. Thus, the growth rate optimization problem represents “big data” integrated into a structured format and the hypothesis of a biological objective; grow as fast as possible with the resources available. This is a well-defined optimization problem.

GEMs are input-output “flow models”

The inner workings of a GEM are readily understood conceptually. In a given environment (i.e., where the nutritional inputs are defined) GEMs can be used to compute network outputs. Flux balance analysis (FBA) can computationally trace a fully balanced path through the reactome from the available nutrients to the prerequisite output metabolite. Such calculations are performed as detailed above with an objective function that describes the removal of the target metabolite from the network. The synthesis of biomass in a cell requires the simultaneous removal of about 60–70 different metabolites. Using FBA, a GEM can also compute the balanced use of the reactome to produce all the prerequisite metabolites for growth simultaneously, and does so in the correct relative amounts while accounting for all the energetic, redox, and chemical interactions that must balance to enable such biomass synthesis. This exercise is one of genome-scale accounting of all molecules flowing through the reactome.

Recapitulation

Given its simplicity and utility, FBA has become one of the most widely employed computational techniques for the systems-level analysis of living organisms (Bordbar et al., 2014; Lewis et al., 2012). It has been successfully applied to a multitude of species for modeling their cellular metabolisms (Feist and Palsson, 2008; McCloskey et al., 2013; Oberhardt et al., 2009), and therefore, enabled a variety of applications such as metabolic engineering for the over-production of biochemicals (Yim et al., 2011), (Adkins et al., 2012), identification of anti-microbial drug-targets (Kim et al., 2011), and the elucidation of cell–cell interactions, (Bordbar et al., 2010). Further reading and detailed descriptions of FBA and sources for existing genome-scale models are available in Supplemental Table 1.

3. Validation and reconciliation of qualitative model predictions

Ensuring the consistency and accuracy of all the information available for a target organism is a grand challenge of genome-scale biology. Since model predictions are based on a network reconstruction that represents the totality of what is known about a target organism, such predictions are a critical test of our comprehensive understanding of the metabolism for the target organism. Incorrect model predictions can be used for biological discovery by classifying them and understanding their underlying causes. Performing targeted experiments to understand failed predictions is a proven method for systematic discovery of new biochemical knowledge (Orth and Palsson, 2010b). This section will focus on evaluating qualitative model predictions, their outcomes, underlying causes of incorrect predictions, and how to go about correcting them. Section 4 discusses the same process for quantitative model predictions.

Genetic and environmental parameters

Genome-scale models have many genetic and environmental parameters that can be experimentally varied. Altering the composition of the growth media changes environmental parameters. Alteration of genetic parameters is achieved through genome editing methods. Both environmental and genetic parameters are explicit in GEMs and thus the consequence of both types of perturbations can be computed, predicted, and analyzed. The scale of such predictions has grown steadily since the first genome-scale model of E. coli appeared in 2000 (Edwards and Palsson, 2000).

Genome-scale gene essentiality data are available from specific projects or organism-specific databases. One can systematically remove genes from a reconstruction, and thus the corresponding reactions from the reactome, and repeat the growth computation to predict gene essentiality; i.e., if a growth state cannot be computed without a particular gene, the GEM predicts it to be essential (Figure 3A). Such growth rate predictions of gene deletion strains have gone from a hundred predictions in the year 2000 (Edwards and Palsson, 2000), to over 100,000 predictions in 2012 (Yamamoto et al., 2009), and may be heading for over a million predictions in just a few years (Monk and Palsson, 2014).

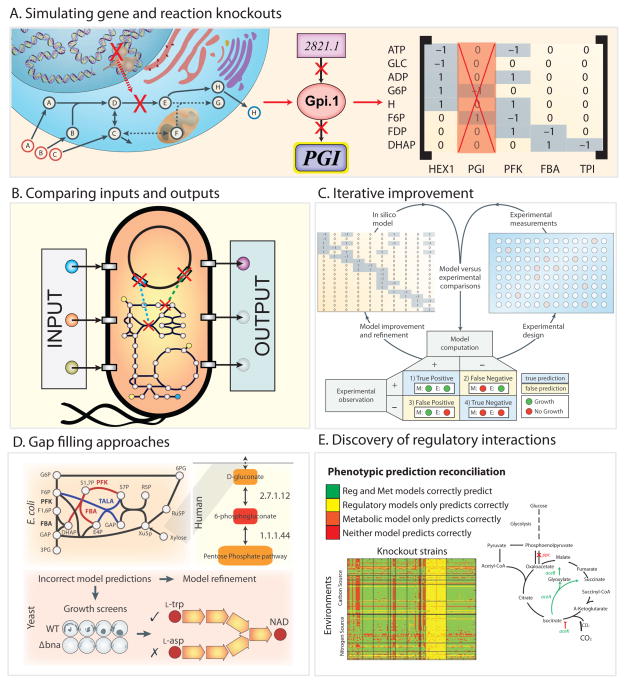
Figure 3. Using models for qualitative predictions and iterative improvement.

A. Each reaction in the network is linked to a protein and encoding gene through the gene-protein-reaction (GPR) relationship. Because each reaction in the network corresponds to a column in the stoichiometric matrix, simply removing the column association with a particular reaction can simulate gene knockouts. Thus, multiple KO simulations can be performed. For example, it is easy to delete every pairwise combination of 136 central carbon metabolic E. coli genes to find double gene knockouts that are essential for survival of the bacteria.

B. The simplicity of altering inputs to change cellular growth environments and removing genes in silico allows one to perform simulations in millions of experimental conditions quickly. Even on a modest laptop computer a single FBA calculation runs in a fraction of a second, thus simulating the effect of all gene knockouts in E. coli central metabolism can be run in less than 10 seconds.

C. Incorrect model predictions are an opportunity for biological discovery because they highlight where knowledge is missing. Targeted experiments can be performed to discover new content that can then be added back to a model to improve its predictive accuracy. Missing model content can be discovered using automated approaches known as ‘gap-filling’ (Orth and Palsson, 2010a) that query a universal database of potential reactions to restore in silico growth to a model.

D. Gap-filling approaches have been used to discover new metabolic reactions in several organisms. E. coli: Two new functions for two classical glycolytic enzymes phosphofructokinase (PFK) and fructose-bisphosphate aldolase (FBA) were discovered (red) (Nakahigashi et al., 2009a). Human: Gluconokinase (EC 2.7.1.12) activity was discovered based on the known presence of the metabolite 6-phosphogluconolactonate in the human reconstruction (Rolfsson et al., 2011b) (red). Yeast: Automated model refinement suggested modifications in the NAD biosynthesis pathway. Experiments demonstrated that a parallel pathway from aspartate thought to exist in yeast was not present (Szappanos et al., 2011).

E. False positive predictions can be reconciled by adding regulatory rules derived from high throughput data (Covert et al., 2004), for example, a recent study was able to reconcile 2,442 false model predictions from the E. coli GEM by updating the function of just 12 genes (Barua et al., 2010). Additionally, a false positive growth inconsistency in the metabolic model of S. Typhimurium was reconciled by updating regulatory rules for the iclR gene product’s transcriptional repression of aceA encoding isocitrate lyase. Transcriptional repression can also often be relieved via adaptive laboratory evolution. Such evolution drives experimental phenotypes to achieve model predictions. Several experimental studies have shown that an organism can evolve to achieve model-predicted optimal growth state (Ibarra et al., 2002).

Both environmental and genetic parameters can be varied when performing FBA. The simplicity of computing growth states (i.e., an output) as a function of media composition (i.e., the nutritional inputs) with the selective removal of genes (Figure 3B) has led to a number of studies that cross environmental parameters with gene deletions. The explicit relationship between a gene and a reaction makes the deletion of genes and their encoding reactions straightforward. You can readily do this for your target organism, provided that you can construct a library of gene deletion strains. Improved molecular tools for generating knockout collection libraries (Tn-seq, CRISPR systems, etc.) and improved high-throughput methods for measuring knockout phenotypes have enabled a massive scale-up in the number of phenotypes that can be measured.

Classification of model predictions

Computational predictions of outcomes fall into four categories: true-positives, true-negatives, false-positives and false-negatives. The true-positive and true-negative predictions, where computational predictions and experimental outcomes agree, have generally exceeded 80% to 90% for well-characterized target organisms. Going beyond single gene knockouts to double genes knockouts and more, true negative predictions are particularly significant as they indicate model predictions of true genetic, or epistatic, interactions. In a screen of double-gene yeast knockouts, Szappanos et al. found that models could predict 2.8% of negative genetic interactions (Szappanos et al., 2011). While this indicates poor recall of prediction, of these, 50% were correct, indicating that model predictions are highly precise, but may miss several interactions. These missed predictions represent cases that are currently difficult for functional geneticists to understand. For applications where the goal is to have true predictions, such as for antibiotic design, precision is more important than recall.

FBA based models are highly precise because they are good at predicting impossible states (such as when a gene knockout leads to death). This assumes that the network structure is complete, an assumption that can be a problem when promiscuous enzyme activity arises, leading to a reaction with an encoding gene that is not captured in the model. Models have lower accuracy because FBA assumes that all reactions can happen at maximum rates. Model false positives often occur because an enzyme is either transcriptionally repressed or does not catalyze the designated reaction at a high enough rate (Supplemental Table 2, Evaluation of Model Predictions). Predictive failure is perhaps of more interest than success as it represents an opportunity for biological discovery. False negative predictions occur when a GEM predicts the inability to grow in a given environment without the deleted gene, but the experiments show growth. This discrepancy indicates that the reconstructed reactome is incomplete. In contrast, false positive predictions occur when a GEM predicts growth but the experiment results in no growth. This outcome indicates possible errors in the knowledge on which the reactome was based, or that a regulatory process is missing that prevents the use of a gene product factored in the computed solution. An example would be regulation that either represses gene expression or a metabolite-enzyme interaction that inhibits the function of an enzyme that the GEM used to compute the predicted growth state.

Prediction failures can be used to systematically (i.e., algorithmically) generate hypotheses addressing the failures. Such hypotheses have been shown to direct experimentation to improve our knowledge base for the target organism. Computations that vary environmental and genetic parameters become part of a workflow (Figure 3C). The outcome of the workflow is a set of qualitative model predictions of growth or no growth that are then compared to the experimental outcome of a growth screen. Correct predictions align with experimental results, while incorrect predictions do not. The two are then compared and classified into four categories as shown in Figure 3C. The failure modes lead to systematic experimentation.

Discovery using model false negatives

Reconciling such discrepancies between predicted and observed growth states is now a proven approach for biological discovery. A series of algorithms have been developed that have been shown to compute the most likely reasons for failure of prediction that in turn led to a model-guided experimental inquiry and discovery. Furthermore, high-throughput tools such as phenotypic microarrays and robotic instruments are becoming available to screen cells at high rates. Such discoveries are then incorporated into the reconstruction, leading to its iterative improvement.

The discrepancies between GEM predictions and experimental data have been used to design targeted experiments that correct inaccuracies in metabolic knowledge. In this subsection we provide three illustrative examples that detail how reconciliation of model errors led to the discovery of new metabolic capabilities in three model organisms.

Human

The activity of open reading frame 103 on chromosome 9 (C9orf103) of the human genome was discovered (Rolfsson et al., 2011a) using established gap-filling protocols (Orth and Palsson, 2010b; Reed et al., 2006). The authors focused on unconnected, “dead end” metabolites in the human metabolic network reconstruction, Recon 1 (Duarte et al., 2007). Dead end metabolites lead to model errors by creating blocked reactions due to a violation of mass balance. Any flux leading to them cannot leave the network. In an attempt to connect these dead end metabolites, a universal database of metabolic reactions was used to predict the fewest reactions required to fully connect all metabolites in the network. Focusing on gluconate, which is a disconnected metabolite, the authors experimentally characterized (C9orf103), previously identified as a candidate tumor suppressor gene, as the gene that encodes gluconokinase, thereby consuming this metabolite and connecting it to the rest of the human metabolic network.

E. coli

Gap-filling methods combined with systematic gene knockouts in E. coli (Nakahigashi et al., 2009b), were used to discover new metabolic functions for the classic glycolytic enzymes phosphofructokinase and aldolase. Single, double, and triple knockout strains of central metabolic genes were grown on 13 different carbon sources. Concurrently, the same gene knockouts and growth conditions were simulated using the E. coli GEM. Several discrepancies between model predictions and experimental results were related to talAB interactions in the pentose phosphate pathway and could not be reconciled. A metabolomic analysis identified a new metabolite, sedoheptulose-1,7-bisphosphate, that had not been previously characterized. Using metabolic flux analysis and in vitro enzyme assays, the investigators confirmed that phosphofructokinase carries out the reaction and that glycolytic aldolase can split the seven-carbon sugar into three- and four-carbon sugars, glyceraldehyde-3-phosphate (G3P) and D-erythrose 4- phosphate (E4P) respectively.

Yeast

An analysis of synthetic lethal screens and gap-filling methods were used to correct incorrect pathways leading to NAD⁺ synthesis in yeast (Szappanos et al., 2011). The study compared an experimental set of genetic interactions for metabolic genes against interactions that were predicted by FBA. Using machine-learning techniques, key changes to the metabolic network that improved model accuracy were identified. Model refinement identified one of the two NAD⁺ biosynthetic pathways from amino acids in the GEM as a source of inaccurate predictions. Using growth screens with mutant strains, the authors validated that the synthesis of NAD⁺ from amino acids was only possible from L-tryptophan (L-trp) but not from L-aspartate (L-asp).

Adaptive laboratory evolution in the discovery process

In contrast to false negatives, false positives arise when the model predicts growth, but experiments show no growth (Figure 3D). False positives occur in cases where experimental data show a particular gene to be essential but model simulations do not. Metabolic models can be used to predict efficient compensatory pathways, after which cloning and overexpression of these pathways are performed to investigate whether they restore growth and to help determine why these compensatory pathways are not active in mutant cells.

Discovering context-specific regulatory interactions using false positive predictions

Cloning and overexpression of a false positive associated gene has been demonstrated for a ppc knockout of Salmonella enterica serovar Typhimurium (Fong et al., 2013). A metabolic model of S. Typhimurium predicted that the cells could route flux through the glyoxylate shunt when ppc is removed due to the backup function of isocitrate lyase encoded by aceA. However, the Δppc cells were nonviable experimentally. The protein IclR is a transcription factor that regulates the transcription of genes involved in the glyoxylate shunt, including aceA. Therefore a dual knockout ΔppcΔiclR mutant was constructed. Growth was restored in this double mutant at ~60% of the wild type growth rate. Therefore, the prediction of the metabolic model of S. Typhimurium failed because it erroneously allowed flux through the glyoxylate shunt when ppc was deleted due to the absence of regulatory information in the model.

Adaptive laboratory evolution can also be used to reconcile false positive predictions. Often, cell populations may need time to adapt to a genetic change or shift in media conditions, giving them the appearance of slow or no growth, despite a model prediction of growth. However, it has been shown that incorrect predictions of in silico models based on optimal performance criteria may be incorrect due to incomplete adaptive laboratory evolution under the conditions examined. It has been shown that E. coli K-12 grown on glycerol over 40 days (or about 700 generations) and subjected to a growth rate selection pressure (passing a small fraction of the fastest growers) achieves a final growth rate that is predicted by the GEM (Ibarra et al., 2002). The quantitative prediction of growth rates is discussed in section 4. Thus, a false positive result may indicate that the model is in fact correct and a researcher should be patient while the cell adapts to achieve the model-predicted growth.

Recapitulation

Given that our knowledge of any target organism is incomplete, its network reconstruction will also be incomplete. Thus, failures in GEM prediction of qualitative outcomes of growth capability are informative about the completeness of a network reconstruction and the consistency of its content. Furthermore, these approaches can be extended beyond model improvement. As genome editing techniques improve, in silico prediction of the effect of multiple gene-knockouts will be vital for contextualizing results of knockout studies and engineering genomes to achieve a desired phenotype (Campodonico et al., 2014). Additionally, reconciliation of model false negatives have been used to explore the role that underground metabolism plays in adapting to alternate nutrient environments (Notebaart et al., 2014). The algorithmic procedures that have been developed to address failure of prediction have led to some computer-generated hypotheses resulting in productive experimental undertaking. Further reading about the gap-filling process and algorithms for its implementation are available in Supplemental Table 1.

4. Quantitative phenotype prediction through optimality principles

The previous section treated qualitative predictions that relate to the presence or absence of parts from a reconstruction. Quantitative predictions of phenotypic functions are more challenging, but possible. The ability to compute quantitative organism functions from a genome-scale model represents a grand challenge in systems biology. Quantitative predictions are achievable with GEMs (even if they are based on incomplete reconstructions) by deploying cellular optimality principles. Evolutionary arguments underlie the deployment of optimality-based hypotheses. Phenotypes maximizing a hypothesized fitness function (as represented by an objective function) can be computed with constrained-optimization methods (Orth et al., 2010).

As for qualitative binary predictions of possible growth states, incorrect quantitative predictions often lead to new biological hypotheses and understanding. However, the discoveries arising from quantitative phenotype predictions are typically of a different nature than qualitative predictions. Rather than relating to missing reconstruction content (Section 3), the discoveries from quantitative phenotype prediction often relate to broad, fundamental organismal constraints (Beg et al., 2007; Zhuang et al., 2011b) and evolutionary objectives and trade-offs (Shoval et al., 2012).

Quantitative phenotype prediction has also proven to be a useful capability for bioengineering applications. By optimizing an engineering (instead of evolutionary) objective, the best possible performance of an engineered biological system can be determined. Furthermore, the specific flux states needed to achieve high performance can guide engineering design {King, 2015 #145}.

Workflow for quantitative phenotype prediction

Quantitative phenotypes can be predicted through the same computational procedures used for qualitative growth predictions (Figure 4A). An objective (either evolutionary or engineering) is assumed, and maximized computationally (subject to flux balance and other constraints). The flux state(s) that maximize the objective are then the predicted quantitative fluxes. These predictions can then be compared to experimental measurements. In cases of agreement, the evolutionary hypothesis is supported. In cases of a disagreement between experimental and theoretical predictions, either the biological system has not been exposed to the selection pressure to reach the theoretical optimum (i.e., the assumed evolutionary objective is incorrect or partially correct), or there are missing biological constraints that affect the theoretical predictions (i.e., the relevant biological constraints are incomplete).

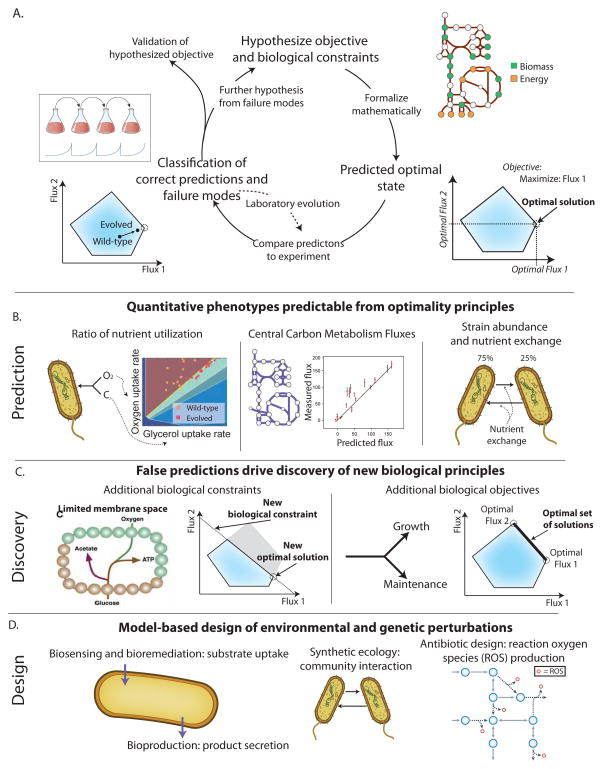
Figure 4. Quantitative phenotype prediction using optimization.

A. Quantitative phenotype prediction is an iterative workflow. First, hypothesized biological constraints and objectives are formulated mathematically, and computational optimization is used to determine optimal phenotypic states (see Section 2). The predicted phenotypic states can then be compared to experimental measurements to identify where predictions are consistent. When consistent, the hypothesized evolutionary objective and constraints are validated. When inconsistent, laboratory evolution can be used to gain further insight as to why the computed and measured states differ. Examples of validation of quantitative phenotypes are detailed in 4B and further hypotheses derived from incorrect predictions are detailed in 4C.

B. The generic workflow in 4A has been successfully applied to several classes of phenotypes. i) Nutrient utilization ratios can be predicted by maximizing biomass flux (Edwards et al., 2001). ii) Central carbon metabolism fluxes can be predicted; for some organisms, much of the variability in flux can be attributed to biomass flux maximization (Schuetz et al., 2012). iii) The ratio of organism abundances and nutrient exchanges can be predicted for both natural and synthetic communities. Note that one important feature of quantitative phenotype predictions is that optimal flux solutions are often not unique. To address this, flux variability analysis (FVA) (Mahadevan and Schilling, 2003) can be used to identify the ranges of possible fluxes. It should be noted that non-uniqueness is not necessarily a handicap of COBRA as biological evolution can come up with alternate solutions (Fong et al., 2005).

C. Inconsistencies with model predictions have led to the appreciation of new constraints and objectives underlying cellular phenotypes. i) Inconsistent predictions in by-product secretion have led to the hypothesis that membrane space limits membrane protein abundance and metabolic flux (Zhuang et al., 2011b). ii) The range of metabolic fluxes observed across different environments have led to the realization that fluxes can be understood as simultaneously satisfying multiple competing objectives, such as growth and cellular maintenance. Multi-objective optimization algorithms find solutions that maximize multiple competing objectives.

D. Accurate prediction of quantitative phenotypes has led to prospective design of biological functions. A number of algorithms have been developed that predict genetic and/or environmental perturbations required to achieve a bioengineering objective. Relevant bioengineering objectives have included biosensing, bioremediation, bioproduction, the creation of synthetic ecologies, and the intracellular production of reaction oxygen species (ROS) to potentiate antibiotic effects.

Experimental evolution can discriminate these alternatives (Ibarra et al., 2002; Schuetz et al., 2012) by exposing the biological system to the appropriate selection pressure, leading it to evolve towards the stated optimum. For example, in one study, strains carrying deletions of one of six metabolic genes were evolved on four different carbon sources. A total of 78% of strains tested reached the metabolic model predicted optimal growth rate after adaptive laboratory evolution after 40 days of passage (Fong and Palsson, 2004).

Flux variability analysis (FVA) calculates possible flux states

Flux balance analysis computes an optimal objective value and a flux state that is consistent with that objective (and all of the imposed constraints). While the objective value is unique, multiple flux states can typically support the same objective value in genome-scale models. For this reason, flux variability analysis (FVA) is used to determine the possible ranges for each reaction flux (Mahadevan and Schilling, 2003). With FVA, the objective value is set to be equal to its maximum value, and each reaction is maximized and minimized. For some fluxes, their maximum value will be equal to their minimum, enabling a specific prediction. For others, there may be a wide range of possible values due to alternative pathways. Often, a parsimonious flux state is also assumed and computed with parsimonious-FBA (pFBA) (Lewis et al., 2010a). With pFBA, the sum of fluxes across the entire network is minimized (again, subject to the optimal objective value determined); pFBA will eliminate some alternative pathways. Typically, many reaction fluxes can by uniquely predicted with optimality and parsimony assumptions. Additional biological constraints in next-generation models (Section 6) reduce the possible flux states further (Lerman et al., 2012).

Types of possible (evolutionarily optimal) quantitative predictions

The simplest type of quantitative phenotype predictable with constraint-based models is nutrient utilization. While metabolic models do not predict absolute rates of nutrient uptake, they predict the optimal ratios at which nutrients are utilized. For example, metabolic models predict an optimal oxygen uptake rate relative to the carbon source uptake rate (resulting in a predicted optimal ratio between the two nutrients). In an early study, the ratios of oxygen and carbon uptake were shown to be predictable for a number of carbon sources in E. coli (Edwards et al., 2001). In a later study, E. coli was evolved in the laboratory on a carbon source (glycerol) for which the wild-type strain did not match the predicted nutrient utilization; after evolution, the strain exhibited the optimal uptake rates predicted theoretically (Figure 4B) (Ibarra et al., 2002). Comparison of experimental and predicted phenotypes therefore reveals the environments to which an organism has been evolutionary exposed.

Metabolic fluxes for central carbon metabolism can be estimated with ¹³C carbon labeling experiments, making them candidates for quantitative prediction (Figure 4B). Since the dimensionality of carbon labeling data is larger than that for nutrient uptake, there is more opportunity to dissect the differences in computed and measured fluxes to better understand the multiple objectives and constraints underlying microbial metabolism. Impressively, the biomass objective function can explain a large amount of the variability of fluxes (Schuetz et al., 2007). Failure modes in prediction have led to the appreciation of the importance of protein cost (O’Brien et al., 2013), and membrane (Zhuang et al., 2011b) and cytoplasmic spatial constraints (Beg et al., 2007), which affect the optimal flux state (Figure 4C). Furthermore, failure modes have led to the understanding that metabolism is simultaneously subject to multiple competing evolutionary objectives, resulting in trade-offs (e.g., growth versus maintenance) employed by different species (Figure 4C). In this way, outliers in quantitative predictions can improve the understanding of constraints and objectives underlying a particular organism’s metabolism.

Optimality principles from stoichiometric models have also been expanded from single populations of cells to microbial communities. To model microbial communities, multiple species are linked together through the exchange of nutrients extra-cellularly (Stolyar et al., 2007) or through direct electron transfer (Nagarajan et al., 2013). The secretion rate from one species limits the uptake rate for others, resulting in balanced species interactions. For a number of cases of communities composed of two or three members, the optimal rate of nutrient exchange and the ratio of the species in the population (Wintermute and Silver, 2010) can be predicted. The effects of spatial organization of community members are also being uncovered (Harcombe et al., 2014). The constraints on nutrient flow between organisms (e.g., diffusion) have proven to be important for predicting community composition and behavior, highlighting the importance of abiotic constraints and community structure in the behavior of biological communities.

Evolution is a natural counterpart to optimality-based predictions with constraint-based methods. Constraint-based optimality predictions have focused on predicting the endpoints of short-term experimental evolution. However, this scope of application has increased in recent years to study long-term phenotypic and enzyme evolution (Nam et al., 2012; Plata et al., 2015).

From optimality principles to prospective design

Quantitative phenotype prediction via optimization is also commonly used for bioengineering applications (Figure 4D). For example, in metabolic engineering, optimal pathway yields are used to prioritize pathways to be built into a production strain and to benchmark their performance. Furthermore, the flux states required to achieve these optima (and how they differ from wild-type growth states) can guide strain design (Cvijovic et al., 2011).

A number of design algorithms have been built to work with metabolic models and predict the genetic and environmental modifications to increase performance (Burgard et al., 2003; Ranganathan et al., 2010). While many design algorithms and applications have been focused on metabolite production (e.g., for production of fuels and chemicals), metabolic models have also been utilized for the design of biosensors (Tepper and Shlomi, 2011) and biodegradation (Scheibe et al., 2009; Zhuang et al., 2011a). Also, design has expanded beyond single populations to microbial communities/ecosystems (Klitgord and Segre, 2010).

Recapitulation

Quantitative phenotype predictions initially focused on simple physiological predictions and are still expanding to more complex phenotypes, biological systems (Levy and Borenstein, 2013), and environments. Although there have been notable successes of quantitative phenotype prediction, certain phenotypes are still difficult to predict. Historically, difficult predictions have led to the development of new computational methods and an appreciation of new biological constraints. Supplemental Table 2 (Evaluation of Model Capabilities) summarizes several types of predictions and the approximate performance of constraint-based methods utilized to date. The expansion in the scope and accuracy of predictions continues today with models of increased scope (Chang et al., 2013a; O’Brien et al., 2013), discussed in section 6.

Thus far, quantitative phenotypes have been limited primarily to microbial systems and, more recently, plants (Collakova et al., 2012; Williams et al., 2010). For multi-cellular organisms, specialized cell types support the fitness of the entire organism. Cell-type specific ‘objectives’ have been constructed (Chang et al., 2010), though they typically are used for qualitative (Section 3) instead of quantitative phenotype prediction. Instead, quantitative phenotypes in multi-cellular organisms are typically determined through model-driven analysis of experimental data, discussed in Section 5.

5. Multi-omic data integration: constraining and exploring possible phenotypic states

With the expanding quantity of omics and other phenotypic data, there is an increasing need to integrate these datasets to drive further understanding and hypothesis generation. Phenotypic data types can be integrated with metabolic GEMs to determine condition-specific capabilities and flux states in the absence of assumed objectives (Section 4). Computational methods that identify the possible range of phenotypic states given the measured data allow one to quantify the degree of (un)certainty in metabolic fluxes. Some types of data are quantitative and directly indicative of metabolic fluxes, whereas other data are qualitative or indirectly related to metabolic fluxes. By layering different data types, the true state of a biological system can be determined with increased precision. The need for formal integration of disparate data types represents a grand challenge that has been termed Big Data to Knowledge (BD2K, bd2k.nih.gov).

Workflow for multi-omic data integration

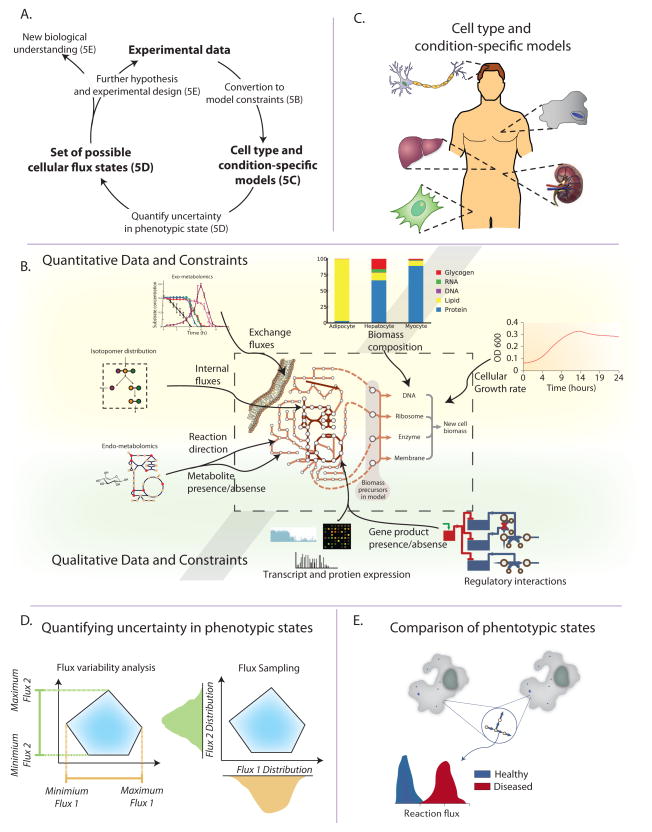
The overall procedure for multi-omic integration with genome-scale models is an iterative workflow (Figure 5A). Once experimental data from the particular biological system under study is obtained, it is converted into constraints on model function (Figure 5B). The successive application of experimentally derived constraints to the reaction network results in the generation of a cell-type and condition-specific model (Figure 5C). Several computational procedures can then be used to explore the metabolic capabilities and achievable phenotypes of the experimentally constrained model (Figure 5D). Evaluation of these phenotypic capabilities and comparison of different cells or environments leads to identification of their molecular differences (Figure 5E), providing biological insight and driving further hypotheses.

Figure 5. Data integration and exploration of possible cellular phenotypes.

A. The general workflow for multi-omic data integration begins with the conversion of the experimental data into model constraints (see Figure 5B). This procedure results in cell-type (e.g. neuron, macrophage) and condition-specific (e.g. healthy vs. diseased) models that represent the metabolic capabilities of those specific cells (see Figure 5C). Several computational procedures can then be used to explore the metabolic capabilities and determine achievable phenotypes systematically (see Figure 5D). Evaluation of these phenotypic capabilities and comparison of different cells or environments leads to identification of their molecular differences (see Figure 5E). Additionally, if the original experimental data cannot precisely distinguish between certain metabolic states, additional targeted experiments can be designed and integrated as further constraints.

B. Numerous data types can be integrated into metabolic models. Some directly affects model structure and variables (e.g. growth rate, biomass composition, exchange fluxes, internal fluxes and reaction directionality). Standard processing of these data types allows for integration into the model. Other data types affect metabolic fluxes more indirectly. As such, different computational methods exist for formulating the appropriate constraints (Table 1).

C. Experimental data is integrated to construct cell-type and/or conditionspecific models. These models represent the metabolic capabilities in a certain state, and are then used for further inquiry (see Figures 5D,E). Specific algorithms for building cell-type specific models from gene expression data include MBA (Jerby et al., 2010) and GIMME (Becker and Palsson, 2008).

D. After adding constraints to the model, computational procedures are used to assess the implication of the experimental data on metabolic fluxes. The two main methods for querying the consequences of the measured data on a cell’s phenotypes are flux variability analysis (FVA) and Markov-chain Monte-Carlo (MCMC) sampling. i) FVA determines the maximum and minimum values of all metabolic fluxes. ii) MCMC sampling randomly samples feasible metabolic flux vectors (usually resulting in tens to hundreds of thousands of flux vectors). These sampled flux vectors can then be used to derive the distribution of possible flux values for a given metabolic reaction.

E. Often a comparative approach is employed in which experimental data from two conditions are used to generate two condition-specific models. Then, the achievable phenotypes of the two states are compared (e.g. though MCMC sampling, see Figure 5D).

Converting data to model constraints

Successive imposition of constraints is a basic principle of COBRA (Palsson, 2000). Some data types can be directly converted into constraints on model variables. Biomass composition and growth rate affect the metabolic demands of cellular growth (Feist and Palsson, 2010). Time-course exo-metabolomics can be used to set the uptake and secretion rates of nutrients (Mo et al., 2009). Intracellular quantitative metabolomics combined with reaction free energies can discern condition-specific reaction directionalities (Henry et al., 2007). Isotopomer distributions from cellular biomass or metabolite pools can be used to infer and constrain intracellular fluxes (Zamboni et al., 2009). These data can be used separately or combined to identify with increasing precision the true state of the cell.

Other data types affect metabolism more qualitatively. In theory, quantitative metabolite, transcript, and protein levels can be used to constrain metabolism quantitatively, but in practice this requires many parameters that are hard-to-measure and are organism-specific. Instead, these data types can be used as qualitative constraints relating to gene product or metabolite presence/absence; that is, if a metabolite is present, a reaction must be active that produces it (Shlomi et al., 2008), and if a gene product is absent, it’s catalyzed reactions cannot carry flux (Jerby et al., 2010; Schmidt et al., 2013). Similarly, regulatory interactions can be added to affect the presence/absence of a gene product based on condition-specific activity of a transcription factor (Chandrasekaran and Price, 2010).

Cell-type and condition-specific models

Starting from a large reconstructed reaction network (e.g., representing all metabolic reactions encoded in the human genome (Thiele et al., 2013)), the imposition of experimental data results in the generation of cell-type and condition-specific models. Experimentally derived constraints pare down the achievable phenotypes from those encoded by the totality of the cell’s genome. By eliminating phenotypes that cannot be achieved, this new model represents the capabilities of the particular cell-type and environment assayed. This model summarizes the experimental data in a self-consistent and integrated format, and forms the starting point for further computational and biological inquiry (Agren et al., 2012; Shlomi et al., 2008) (see Figure 5D,E).

Quantifying uncertainty

Once a cell-type and condition-specific model is created, computational methods are used to determine the possible flux states of the cell. Flux variability analysis (FVA, which is described in section 4) (Mahadevan and Schilling, 2003) can be used to determine the range of fluxes that are consistent with the experimental data. A more refined approach is flux sampling (Schellenberger and Palsson, 2009) (typically with Markov Chain Monte Carlo, MCMC, methods), which determines the distribution of fluxes for all reactions (instead of simply the range). When no cellular objective is assumed, the feasible flux space is very unconstrained and a particular reaction could be operating at nearly any flux value. As more data is layered, the feasible flux space decreases. When no objective is assumed, fluxes are rarely precisely known, and many will remain completely unknown. However, an imprecisely known flux space is often sufficient to discern differences between two environments/states as discussed in the following subsection.

Using computed states to drive discovery

Once the range of possible phenotypic states is quantified, they must be analyzed to gain biological insights. Often a comparative approach is employed, in which two experimental states (e.g., neurons from Alzheimer’s disease patients compared to healthy controls (Lewis et al., 2010b)) are compared. Reactions that have a non-overlapping FVA range must be different between the two states, and can be indicative of important metabolic changes. In cases where the FVA ranges are overlapping, the flux distributions from MCMC sampling can still be different – that is, the reactions are likely different between the two states, but the current experimental data is insufficient to guarantee it.

Pathway visualization is also helpful in gaining insight into changes in cell states—fluxes (or flux ranges) are most comprehensible in a network context. A few tools exist for the visualization of metabolic fluxes; some are based on static maps (Schellenberger et al., 2010), whereas others create auto-generated layouts and new tools allow for the drawing of maps based on flux solutions (King and Ebrahim, 2014). Finally, identifying reactions or subsystems that remain partially identified (e.g., based on a large FVA range) can guide further experimentation, resulting in an iterative computational and experimental elucidation of a cell’s state.

Recapitulation

GEMs can be used to integrate numerous data types. In fact, as more experimentally derived constraints are successively imposed, analysis often becomes easier (as the range of possible solutions shrinks (Reed, 2012)), instead of more challenging as often occurs with statistically based data integration procedures. A current challenge with metabolic GEMs is the explicit integration of data types that do not directly reflect metabolic fluxes (e.g., transcriptomics, proteomics, and regulatory interactions). This challenge is primarily due to the fact that these processes are not explicitly described in metabolic models. Expansions of metabolic models to encompass gene expression hold promise to address this challenge and are discussed in section 6.

6. Moving beyond metabolism to molecular biology

Up to this point, this Primer has focused on metabolic models, or M-Models. M-models have reached a high degree of sophistication after 15 years of development, resulting in standard operating procedures for their construction (Thiele and Palsson, 2010) and use (Schellenberger et al., 2011a). However, M-Models are limited in their explicit coverage to metabolic fluxes. Thus, a grand challenge in the field has been to expand the concepts of constraint-based models of metabolism to other cellular processes to formally include more disparate data types in genome-scale models (Reed and Palsson, 2003).

Computing properties of the proteome

The process of addressing this grand challenge has begun (Figure 6A). Recently, genome-scale network reconstructions have expanded to encompass aspects of molecular biology. Two significant expansions are genome-scale models integrated with protein structures, GEM-PRO, and integrated models of metabolism and protein expression, ME-Models. GEM-PRO allows for structural bioinformatics analysis to be performed from a systems-level perspective, and have those results in turn affect network simulations. ME-Models allow for the simulation of proteome synthesis, and account for the capacity and metabolic requirements of gene expression.

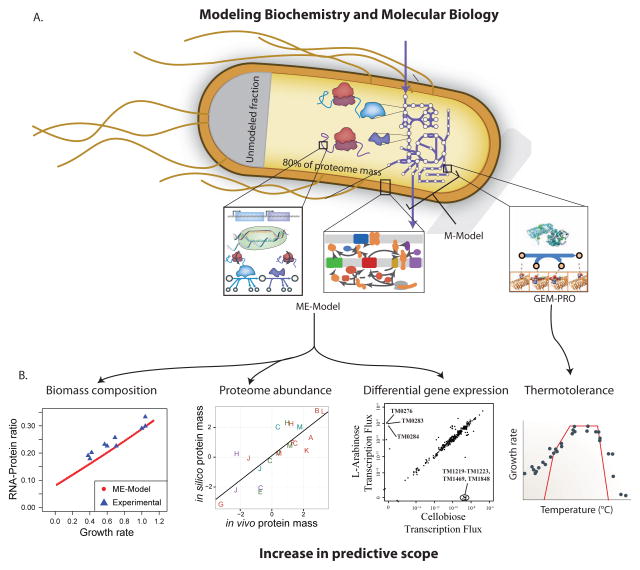
Figure 6. Expansion of genome-scale models to encompass molecular biology.

A. Metabolic models have been expanded to encompass the processes of proteome synthesis and localization as well as data on protein structures. Models including protein synthesis and localization are referred to as ME-Models, which stands for metabolism and gene expression. GEM-PRO refers to genome-scale models integrated with protein structures. For GEM-PRO, a combination of structural data directly references the GPRs in the metabolic reconstruction; structures can be obtained from experimental databases or homology modeling. The E. coli ME-Model mechanistically accounts for ~80% of the proteome mass in conditions of exponential growth and 100% of other major cell constituents (DNA, RNA, cell wall, lipids, etc).

B. Addition of cellular processes vastly increases the predictive scope of models. ME-Models can predict biomass composition, abundances of protein across subsystems, and differential gene expression in certain environmental shifts (in addition to the predictions possible with M-Models); like FBA these were predicted by assuming growth maximization as an evolutionary objective, though the specific optimization algorithm differs due to the addition of coupling constraints. GEM-PRO has been used to predict the metabolic bottlenecks and growth defects of changes in temperature on protein stability and catalysis; protein stability is predicted with structural bioinformatics methods and then used to limit the catalyzed metabolic flux. The uses of these integrated models are just beginning to be explored.

A structural biology view of cellular networks

GEM-PRO reconstructions can have varying degrees of detail, which affects the types of analysis possible. So far, GEM-PRO reconstructions have been created for T. maritima (Zhang et al., 2009) and E. coli (Chang et al., 2013a; Chang et al., 2013b). Initial reconstructions have focused on single peptide chains (Zhang et al., 2009), and utilized homology modeling to fill in gaps where organism-specific structures have not been identified. Further reconstruction detail has included protein-ligand complexes (Chang et al., 2013a) and quaternary protein assemblies (Chang et al., 2013b). To link the structures to the metabolic model, structural data directly references the GPRs in the metabolic reconstruction. For cases of protein-metabolite complexes, the metabolites also need to be properly annotated in the structural data. The structural reconstruction therefore provides a physical embodiment of the gene-protein-reaction relationship.

There are a few notable cases demonstrating the unique analysis possible with the combination of protein structures and network models. In T. maritima, network context and protein fold annotations were combined to test alternative models for pathway evolution (Zhang et al., 2009). The T. maritima GEM-PRO supported the patchwork model for genesis of new metabolic pathways. In E. coli, the effect of temperature on protein stability and enzyme activity was simulated at the systems level, recapitulating the effects of temperature on growth (Chang et al., 2013a). Also in E. coli, protein-ligand interactions were combined with gene essentiality predictions to discover new antibiotic leads and off-targets (Chang et al., 2013b). These examples just scratch the surface of analyses made possible with the integration of network and structural biology.

Modeling molecular biology and metabolism

ME-Models formalize all of the requirements for biosynthesis of the functional proteome (Figure 6B). They compute the proteome composition and its integrated function to produce phenotypic states and all the metabolic processes needed for its synthesis. This represents an integrated view of metabolic biochemistry and the core processes of molecular biology. As with GEM-PRO, the first ME-Models were formulated for T. maritima (Lerman et al., 2012) and E. coli (O’Brien et al., 2013; Thiele et al., 2012).

The reconstruction of a ME-Model starts with the formation of reactions for gene expression and enzyme synthesis (Thiele et al., 2009). The processes explicitly accounted for in ME-Models are very detailed, including transcription units and initiation and termination factors for transcription, tRNAs and chaperones needed for translation and protein folding, and metal ion and prosthetic group requirements for catalysis. In other words, the reconstructions strive to match as closely as possible all the biochemical processes required to synthesize fully functional enzymes. To create a ME-Model, the reactions for enzyme synthesis are coupled to the totality of metabolic reactions with pseudo-kinetic constraints, termed ‘coupling constraints’ (Lerman et al., 2012; Thiele et al., 2010). These constraints relate the abundance of an enzyme (or any ‘recyclable’ chemical species, e.g., mRNA, tRNA), to its degradation rate and catalytic capacity.

ME-Models thus significantly expand the scope of phenotype predictions possible to include aspects of transcription and translation. RNA and protein biomass composition are variables in ME-Models, and are no longer set a priori (as in the biomass objective function of M-Models). ME-Models predict the experimentally observed linear changes in the ratio of RNA-to-protein mass fractions as a consequence of changes in protein synthesis demands (O’Brien et al., 2013). Furthermore, the mass fractions of protein subsystems agree well with those predicted by the ME-Model. This shows that the broad distribution of protein subsystem abundance is predictable using optimality principles and the comparison reveals that some subsystems were under-predicted, thus identifying them as gaps in knowledge and targets for further reconstruction and model refinement (Liu et al., 2014). While the quantitative prediction of individual protein abundances is currently out of scope of the ME-Model (as these demands depend on enzyme-specific kinetics) the ME-Model has been shown to accurately predict differential expression across certain environmental shifts, due to the differential requirements of proteins across conditions (a more qualitative than quantitative prediction) (Lerman et al., 2012).

A recent expansion to the ME-Model includes the addition of protein translocation, allowing for the localization of protein to be computed (Liu et al., 2014) (i.e., into cytoplasm, periplasm, inner and outer membrane). Translocase abundances and compartmentalized proteome mass was accurately predicted from the bottom-up based on optimality principles. Addition of compartmentalization also allows for membrane area and cytoplasmic volume constraints to be formalized, which, if combined with GEM-PRO, approaches a digital embodiment of a three-dimensional cell.

Recapitulation

Metabolic models are limited in their predictive ability dictated by the scope of the reconstruction. Nearly all of the predictions of metabolic models outlined in the previous sections can be refined and expanded with GEM-PRO or ME-Models. Advances to include protein structures and protein synthesis open new vistas for constraint-based modeling.

The scope of genetic perturbations (Section 2) that can be simulated is significantly larger due to the inclusion of genes for gene expression (and accounting for protein cost) and the effects of coding mutations on protein structures; GEM-PRO also expands the scope of environmental perturbation to enable simulation of changes in temperature. GEM-PRO allows for new gap-filling approaches (Section 3) based on structural bioinformatics methods. ME-Models expand the scope of quantitative molecular phenotypes to include transcript and protein levels (Section 4), and transcriptomics and proteomics can be analyzed in mechanistic detail (Section 5).

With the added capabilities of GEM-PRO and ME-Models also come additional computational challenges. While single optimization calculations with M-Models take less than a second on a modest laptop computer, growth-maximization with a ME-Model can take over an hour. The ME-Model also requires specialized high-precision solvers. Many promising applications of GEM-PRO will require simulation of protein dynamics with molecular dynamics (MD) and hybrid quantum mechanics/molecular mechanics (QM/MM) simulations on protein structures. High-performance computing environments are required for such simulations, and there is a pervasive trade-off between the precision of simulations and the scope of structural coverage. However, advances in high-precision solvers for ME-Models (Sun et al., 2013) and structural simulations for GEM-PRO are rapid and are likely to ameliorate these challenges.

Like discoveries enabled by comparing M-Model predictions to experimental data, we anticipate much biology can be learned from comparing in silico and in vivo proteome allocation (O’Brien and Palsson, 2015), leading to increasingly predictive models. The E. coli ME-Model currently encompasses many key cellular functions, covering ~80% of the proteome by mass in conditions of exponential growth; the remaining proteome mass outside of the scope of the model can guide model expansion. In addition to DNA replication and cell division (Karr et al., 2012), much of the remaining proteome mass involves cellular stress responses (e.g., pH, osmolarity, osmotic); like with temperature, GEM-PRO will aid in modeling these cellular stresses.

Perspective

Genome-scale models have been under development since the first annotated genomesequences appeared in the mid to late 1990s. For most of this history, the focus of GEMs has been on metabolism. After initial successes with metabolic GEMs it became clear that the same approach could be applied to other cellular process that could be reconstructed in biochemically accurate details. Thus, a vision was laid out in 2003 that the path to whole cell models was conceptually possible and that such models could be used as a context for mechanistically integrating disparate omic data types (Reed and Palsson, 2003). This vision is now being realized. This Primer shows how six grand challenges in cell and molecular and systems biology can be addressed using GEMs. A surprising range of cellular functions and phenotypic states can be now dealt with.

We now have the tools at hand to develop quantitative genotype-phenotype relationships from first principles and at the genome-scale. Current models of prokaryotes account for metabolism, transcription, translation, protein localization, and protein structure. Processes not described in the current ME models will be systematically reconstructed over the coming years to gain a more and more comprehensive description of cellular functions. Biology can thus look forward to the continued development and use of a mechanistic framework for the study of biological phenomena as physics and chemistry have enjoyed for over a century.