An analysis of asthma hospitalizations, air pollution, and weather conditions in Los Angeles County, California

Abstract

There is now a large body of literature supporting a linkage between exposure to air pollutants and asthma morbidity. However, the extent and significance of this relationship varies considerably between pollutants, location, scale of analysis, and analysis methods. Our primary goal is to evaluate the relationship between asthma hospitalizations, levels of ambient air pollution, and weather conditions in Los Angeles (LA) County, California, an area with a historical record of heavy air pollution. County-wide measures of Carbon Monoxide (CO), Nitrogen Dioxide (NO₂), Ozone (O₃), Particulate Matter < 10 μ m (PM₁₀), Particulate Matter < 2.5 μ m (PM_2.5), maximum temperature, and relative humidity were collected for all months from 2001 to 2008. We then related these variables to monthly asthma hospitalization rates using Bayesian regression models with temporal random effects. We evaluated model performance using a goodness of fit criterion and predictive ability. Asthma hospitalization rates in LA County decreased between 2001 and 2008. Traffic-related pollutants, CO and NO₂, were significant and positively correlated with asthma hospitalizations. PM_2.5 also had a positive, significant association with asthma hospitalizations. PM₁₀, relative humidity, and maximum temperature produced mixed results, whereas O₃ was non-significant in all models. Inclusion of temporal random effects satisfies statistical model assumptions, improves model fit, and yields increased predictive accuracy and precision compared to their non-temporal counterparts. Generally, pollution levels and asthma hospitalizations decreased during the 9 year study period. Our findings also indicate that after accounting for seasonality in the data, asthma hospitalization rate has a significant positive relationship with ambient levels of CO, NO₂, and PM_2.5.

1. Introduction

Long term exposures to NO₂, O₃, and PM₁₀ have been associated with chronic respiratory impairments (Wilhelm et al., 2008) and a large body of literature supports an association between increased levels of ambient air pollution and negative effects on human health (for a review, see Samet and Krewski 2007). A number of recent studies have shown that rates of asthma incidence, exacerbation, and/or mortality rise with increased exposure to various air pollutants (Gehring et al., 2010; Ho et al., 2007; Ko et al. 2007; Szyszkowicz 2008), although others have reported highly mixed results by pollutant (Burra et al. 2009; Mar and Koenig 2009; Moore et al. 2008), inconclusive results (Chan et al. 2009; Wilson et al. 2005), or no definitive relationship (Abe et al. 2009). Variation in study design and modeling methods possibly contribute to the lack of consistency in results (Akinbami et al. 2010), whereas the choice of outcome (e.g., prevalence, emergency department visits, hospitalizations, mortality), spatio-temporal scale (e.g., data aggregation level, temporal resolution), and exposure modeling (e.g., ambient monitor data, personal exposure data) have the potential to influence the observed relationship.

We examine the relationship between asthma morbidity, air pollution, and weather conditions at a county-scale of analysis. Monthly observations of asthma hospitalizations are compared with ambient levels of criteria air pollutants regulated by the Environmental Protection Agency (EPA), temperature, and relative humidity in a time-series analysis. After adjusting for confounding due to seasonal variation in the data, we formulate single and multi-pollutant linear regression models with parameter and predictive inference following a Bayesian framework. The addition of temporal random effects to the linear regression models accounts for dependence between observations that was not explained by predictor variables or seasonal trends. This enables comparison with traditional regression models that do not account for temporal dependence between observations.

This study yields three outcomes: i) identifies the models that best predict monthly asthma hospitalization rates; ii) reports the directionality and significance of the observed relationships between ambient air pollution, weather conditions, and asthma hospitalizations, and; iii) examines the differences in model fit, predictive performance, and inference between comparable models with and without temporal random effects.

2. Study Area

California is often viewed as a leader in state-wide efforts to reduce emissions from transportation activities (Boies et al. 2009). At the state level, improved technologies in vehicular emissions, due to both government regulation and manufacturer innovation, have led to substantial reductions in ambient air pollution in spite of a growing population and increases in total miles driven per year (Kahn and Schwartz 2008). However, Los Angeles (LA) County is consistently one of the most polluted counties in the United States, ranking as the 6 ^th worst for short-term particle pollution (24 hour PM_2.5), the 12 ^th worst for year-round particle pollution (annual PM_2.5), and 5 ^th worst for O₃ pollution from 2006 to 2008 (American Lung Association 2010). During the 1970s and 1980s, the city of Los Angeles implemented the most encompassing regulatory air pollution control program in the nation and the region has seen dramatic and consistent declines in pollution levels (Mazmanian 2009). Since 1985, few regions with similar population and economic growth have improved their PM₁₀ and O₃ pollution levels as much as the Los Angeles region, however unhealthy air persists despite these gains (Hall et al. 2010). Su et al. (2009) report that the quality of the air continues to have a major impact on the residents of LA County due to a heavy reliance on automotive travel, a large number of goods moved through the Long Beach/Los Angeles port complex, a regional susceptibility for atmospheric inversion (trapping air near the land surface), and little chance for precipitation removal of pollutants.

3. Materials

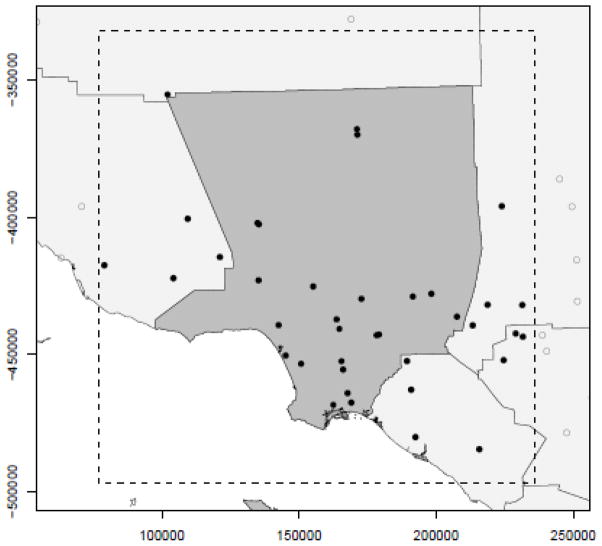
Average daily levels of criteria pollutants were collected from the Environmental Protection Agengy (EPA) AQS Datamart (http://www.epa.gov/ttn/airs/aqsdatamart) for all dates between January 1, 2001 and December 31, 2008 and all monitoring stations falling within 20 km of the outermost boundaries of LA County. San Clemente Island and Santa Catalina Island were not included due to their small populations and the lack of a monitoring station on either island. Although 20 km is an arbitrary distance, it was chosen based on previous research in southern California where data from ambient monitoring stations were used to measure pollutant exposure, e.g., 5 miles (Wilhelm et al. 2008), 20 miles (Neidell 2004), and 50 km (Moore et al. 2008). Figure1 shows the county bounds, study area bounds, and locations of monitoring stations that measured the pollutants of interest at least once between 2001 and 2009.

Figure 1.

Los Angeles County, Califoria with larger study area bounds (dashed line) and ambient pollution measurement locations (black circles) collecting data between 2001 and 2009. 1cm (ppm). 1cm

We collected daily hospital admission counts for LA County in which the primary diagnosis was extrinsic, intrinsic, or other asthma from the Healthcare Information Resource Center, which is within the purview of the Office of Statewide Health Planning and Development (OSHPD). The subset of the database provided to us included information on:

• Daily admission (counts) for patients with asthma for the calendar years 1983–2008.

• County of Patient Residence.

• Principal Diagnosis.

• Secondary Diagnosis (i.e., the diagnosis of asthma was made in any of the secondary diagnosis variables).

• Types of asthma:

  • Extrinsic (ICD-9-CM codes 493.0x);

  • Intrinsic (ICD-9-CM codes 493.1x);

  • Other (ICD-9-CM codes 493.8x);

Any daily admission count falling between 1 and 4 was masked and reported as a dummy value. The extrinsic and intrinsic asthma categories contained a large number of masked values, accounting for 81% and 100% of their non-zero daily entries, respectively. Considering the high level of uncertainty associated with the masked values, these two categories were removed prior to analysis. The vast majority of the overall asthma admissions were diagnosed under other asthma. Given the range of the masked value (1–4), other asthma admissions constitute between 89% and 94% of the total asthma admissions. Therefore, we believe that removing these admissions did not significantly affect the results of the analysis. PRISM (from http://www.prism.oregonstate.edu/) monthly maximum temperature (labeled as Tmax in tables and figures) data were downloaded for the conterminous US. The raster grids were clipped to the boundaries of LA County and a county-wide mean was calculated using the clipped grid cells. Relative humidity measurements are not available from PRISM, therefore daily measurements of mean temperature, mean wet bulb temperature, and mean atmospheric pressure were downloaded from the National Climatic Data Center (http://www.ncdc.noaa.gov) for all weather stations locations inside the previously mentioned study area bounds. At each weather station, mean daily relative humidity (labeled as RH in tables and figures) was calculated using mean temperature, wet bulb, and atmospheric pressure readings.

4. Methods

1. Pre-processing

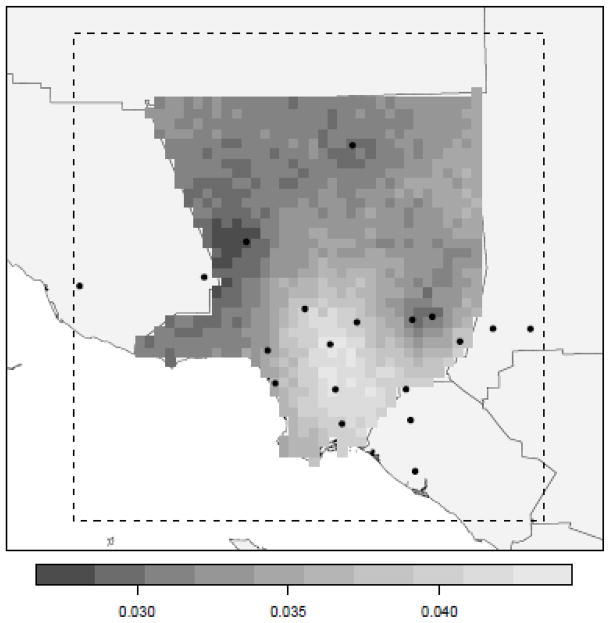
Daily pollution and relative humidity were predicted at a high spatial resolution (i.e., 3×3 km grid) over the study area using a Bayesian kriging model (Banerjee et al. 2004) and point-referenced data collected at the monitoring stations within the larger study area boundaries. In an effort to balance the robustness of theses predicted surfaces and data availability, a daily surface was created only if 10 stations collected a reading on that day. The daily number of stations collecting SO₂ data did not meet the requirements for number of point observations per day at any time during the study period, therefore this pollutant was not included in our study. The predicted surfaces were then clipped to the county boundaries and the mean value of the clipped surfaces were recorded as the county-level daily values (see Figure 2). Monthly values were created by averaging these daily values within the given month.

Figure 2.

Example of predicted daily pollution surface for NO₂

We calculated monthly rate of asthma hospitalizations (expressed as mean daily rate) using the hospital admission counts from OSHPD and population data collected from the State of California (www.dof.ca.gov/research/demographic). The county-level population data were only available in yearly increments, therefore they were interpolated linearly to monthly increments in an effort to match the temporal units of the hospitalization data. The interpolated monthly data offer a more realistic scenario of population change compared to the alternative of a more dramatic population shift occurring on January 1st of every year. Using the monthly population data and the daily hospitalization counts, we calculated the mean daily hospitalization rate for each month. The use of mean daily rate in lieu of overall monthly rate accounts for the inconsistent number of days in each month. Each month’s mean daily hospitalization rate was natural log transformed and set as the outcome variable in the regression analysis detailed in Section 3. This transformation produced an approximately normally distributed variable, which meets model assumptions. Further, the transformation ensured the correct support following back-transformation of model fitted and predicted values.

2. Data preparation

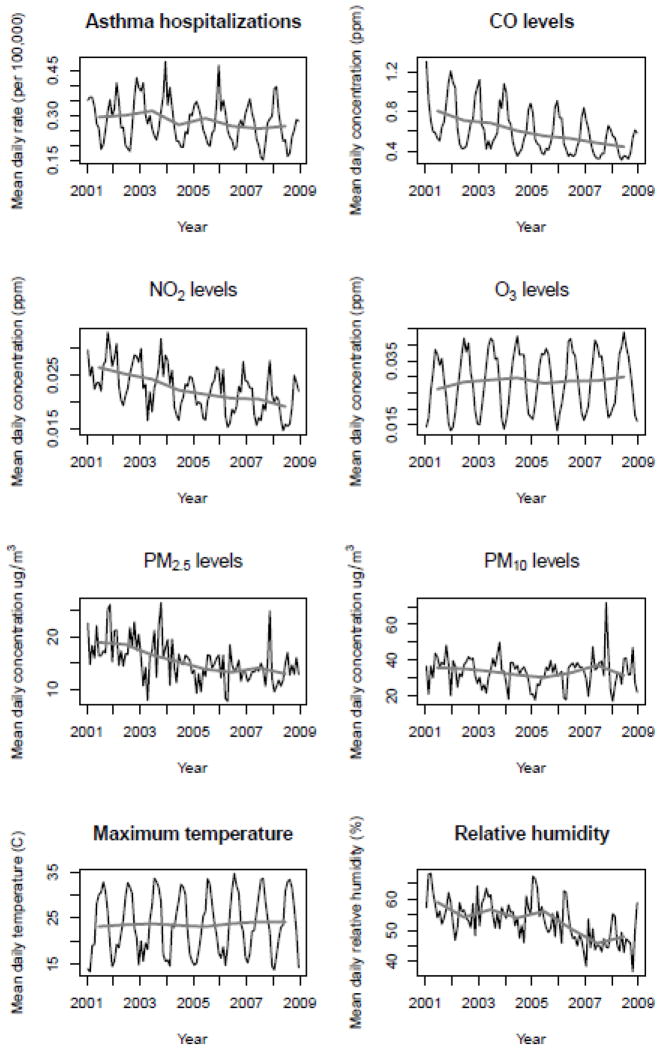
Preliminary investigations of the data revealed high correlation between predictor variables due to strong seasonal oscillation (see Figure 3). Seasonality was removed prior to modeling, thereby accounting for the potential confounding due to the temporal cycles within the variables (Burnett et al. 2001). For each variable, a two-sided moving average filter was used to identify the yearly and seasonal trends in the data using a two step process (Peng and Dominici 2008). First, the yearly trend was identified and removed from the data. Then, using the yearly de-trended data, the seasonal oscillation was identified. Due to the nature of the moving average filter, the results deviated slightly from a regular oscillating cycle. Therefore, we calculated the monthly mean values of the original seasonal trend over all years resulting in a regular, repeating cycle consistent throughout the entire study period. The estimated seasonal trend was then removed from the original data resulting in the de-trended data product containing both the long and short term variability in the data without the collinearity between variables due only to seasonal fluctuations. Supplemental Material, Figure 1 illustrates the individual data preparation steps. Supplemental Material, Tables 1 and 2 report the Pearson Correlation Coefficients between all of the predictor variables before and after seasonal trend removal. High correlation (> 0.5) was found in 8 of 21 pair wise comparisons prior to de-trending and 6 of 21 afterward.

Figure 3.

Monthly (black) and yearly (gray) trends for all variables prior to seasonal de-trending. 1cm

Prior to regression analysis, the predictor variables were natural log transformed. The transformation produced approximately normally distributed variables.

3. Regression analysis

Assuming that the transformed mean hospitalization rate, y(t), is normally distributed, we assume a regression model

$$y(t)=\mathbf{x}{(t)}^{\prime }\beta +u(t)+\epsilon (t),$$ (1)

where x(t) is a p×1 vector of temporally referenced predictors, β is a p×1 vector of regression coefficients, u(t) is a temporal process, and (t) an independent white noise process capturing residual variation not captured by the temporal process – for example, variation that occurs at a temporal resolution finner than that of the observed data. With any collection of n observations, say T = {t₁,…,t_n}, we assume that the ε(t_i) ’s are identically and independently distributed as N (0, τ²).

Turning to u (t_i) ’s, one approach would be to seek out parametric forms such as cyclical trends or growth curves that model increasing trends. These, however, are usually much less flexible and do not fit the data well in most cases. Furthermore, inference on residual temporal correlation structures is no longer easily available. A richer and more versatile approach models the u (t_i) ’s as zero-centered temporal random effects. There is no loss of generality in assuming mean zero as any trend or structure in large scale variation can be incorporated in x(t)′ β. These random effects, therefore, are a part of the residual from the regression and provide local adjustment (with structured dependence) to the mean. They can also be interpreted as capturing the effect of unmeasured or unobserved predictors with temporal pattern.

The joint distribution of these effects will depend upon our specification for u(t). In particular, we posit that the u (t_i) ’s should be correlated with each other. In other words, random effects arising from time points closer to each other would tend to cluster more than those arising from time points farther away. A rich and flexible modeling choice for this purpose is the Gaussian process (e.g.,Rasmussen and Williams 2006), u (t) ~ GP(0, C(·,·;θ)), specified by a valid covariance function C (t, s;θ) = Cov(u(t),.u(s)) that models the covariance corresponding to a pair of time points t and s. The process realizations over T are collected into an ntimes1 vector u = (u(t₁),…, u(t_n))′, which follows a multivariate normal distribution N (0, Σ_u), where Σ_u is the n×n covariance matrix of u with (i, j) -th element given by C(t_i, t_j;θ) . From a Bayesian perspective, the Gaussian process can be regarded as a prior on a function. Rather than specify a function parametrically and use priors on those parameters, the Gaussian process provides a more flexible non-parametric alternative to modeling an unknown function in this case, u(t). In this sense, model 1 can be regarded as a semi-parametric regression model (Ruppert et al. 2003), where x(t)′ β is the parametric part and u(t) is the nonparametric part.

Clearly C(t, s;θ) cannot be just any function; it must ensure that the resulting Σ_u matrix is symmetric and positive definite. Such functions are known as positive definite functions and are characterized as precisely characteristic functions of symmetric random variables. Classes of such functions have been studied extensively in machine learning contexts (e.g., Rasmussen and Williams 2006) and in spatial statistics (e.g., Gneiting and Guttorp 2010). The most flexible such class is the Matérn family of covariance functions that involve both a process range parameter as well as a smoothness parameter. While popular in spatial analysis, this class is computationally more demanding and possibly more complex than needed for our purposes. In addition, not all of these parameters are identifiable or consistently estimable.

Focusing upon computational scalability and simplicity in interpretation, we specify C (t, s;θ) = σ² ρ(t, s;θ φ) where θ = {σ², φ} and ρ(·;φ) is a correlation function with the φ parameter controlling the rate of correlation decay. Then Var(u(t)) = σ² represents a temporal variance component in model (1). Given the fixed intervals of our data, a convenient, yet flexible, specification of the correlation function is ρ (t, s;θ) = exp(−φ | t − s |), where | t − s |) is the separation between the time points. This is known as the Ornstein-Uhlenbeck (OU) process whose realizations over t₁ < t₂ < … <t _n yield a multivariate normal distribution with a tridiagonal inverse correlation matrix. To be precise, Σ_u = σ² R(φ) with the (i, j) -th element of R⁻¹(φ) equal to 0 whenever | i − j |>1, equal to $\frac{-{\rho }_{i,j}^2(\phi )}{(1-{\rho }_{i,j}^2(\phi ))}$ when | i − j |=1 and with i-th diagonal element equal to

$$1+I[i=1]\frac{{\rho }_{i+1,i}^2(\phi )}{1-{\rho }_{i+1,i}^2(\phi )}+I[i=n]\frac{{\rho }_{i,i-1}^2(\phi )}{1-{\rho }_{i,i-1}^2(\phi )}+I[1<i<n]\sum _{j=0}^1\frac{{\rho }_{i-j,i-j+1}^2(\phi )}{1-{\rho }_{i-j,i-j+1}^2(\phi )},$$

where ρ_ij(φ) = exp(−φ | t_i − t_j |).. The tridiagonal inverse implies a Markovian structure for the u(t_i) ’s since the (i, j) -th element of R⁻¹(φ) equals zero if and only if u(t_i) and u(t_j) are conditionally independent given the remaining u(t_k) ’s. Therefore, the conditional distribution of u(t_i) given the remaining variables will depend only upon its two “neighbors” u(t_i−1) and u(t_i+1). This closed form inverse of Σ_u (i.e., isplaystyle $\frac{R{(\phi )}^{-1}}{{\sigma }^2}$) allows for computationally efficient evaluation of model (1)’s multivariate normal likelihood, which is required for parameter estimation.

As noted in Section 1, we have adopted a Bayesian approach to inference. To complete the Bayesian specification we assign prior (hyperprior) distributions to the model parameters (hyperparameters) and inference proceeds by sampling from the posterior distribution of the parameters (see, e.g., Gelman et al. 2004). For instance, the Gaussian process above induces a N (0, σ² R(φ)) prior distribution on u. For the remaining parameters, β was assigned a multivariate Gaussian prior N(μ_β, Σ_β), which subsumes a non-informative flat prior when ${\mathrm{\sum }}_{\beta }^{-1}=O$ is the matrix of zeroes. The temporal variance component σ² and the measurement error variance τ² were assigned inverse-Gamma (IG) priors. The process correlation parameter, φ, was assigned an informative prior uniform prior over a finite time interval. The proposed MCMC sampler and prediction algorithms for model (1) are detailed in Supplemental Material, p. 1.

4. Model selection and evaluation

Given L posterior samples ${\{{\mathrm{\Omega }}^{(l)}\}}_{l=1}^L$ where Ω = { β, σ², φ, τ² }, we assess model performance using independent replicates for each observed outcome: for each t_i ε T, we draw y_rep(t_i)^(l) from N(x(t_i)′ β^(l) + u(t_i)^(l), τ^2(l)), one for one for the posterior samples. Letting μ_rep,i and ${\sigma }_{\mathit{rep},i}^2$ be the posterior predictive mean and variance for each y_rep(t_i), we compute $G={\sum }_{i=1}^n{(y(t_i)-{\mu }_{\mathit{rep},i})}^2$ and $P={\sum }_{i=1}^n{\sigma }_{\mathit{rep},i}^2$. The former acts as a measure of goodness of fit, while the latter penalizes complexity. We use D = G + P (e.g., Gelfand and Ghosh 1998) as a model selection criteria, with lower values of D indicating preferred models. For models wherein all predictor variables were statisticaly significant at a 90% credible level, we used a holdout set (10% of the observations selected at random) to assess predictive performance by computing the mean squared prediction error (MSPE), $\frac{1}{q}{\sum }_{i=1}^q{(y(t_i)-y(t_{0,i}))}^2$, and bias, $\frac{1}{q}{\sum }_{i=1}^{q}y(t_i)-y(t_{0,i})$, where y(t_0,i) is the predicted outcome at the i-th holdout time and q is the number of observations withheld. Those observations comprising the holdout set are indicated with an open circle symbol along the x-axes in Figure 4. The MCMC sampler and routines for prediction and model performance criterion were implemented in R (http://www.R-project.org).

Figure 4.

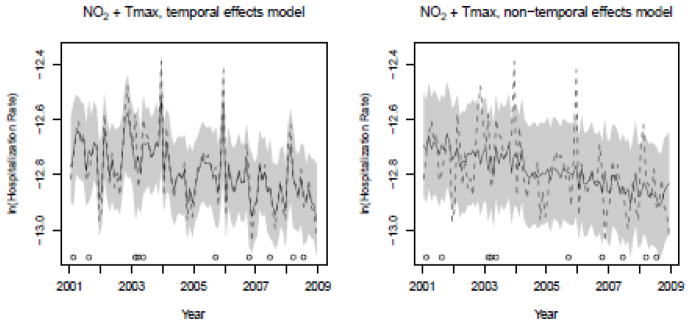
Predicted values (solid line), actual values (dashed line), and 90% credible intervals (gray region) for NO₂ + maximum temperature. The open circle symbols along the x-axes indicate those dates included in the holdout set.

5. Results

1. LA County trends

The yearly average of daily hospitalization rate for LA County decreased by 10.23% between 2001 and 2008. The year with the highest mean rate was 2003 (0.3162 per 100,000) and the lowest was 2007 (0.2572 per 100,000). The monthly data display a strong seasonal variation with peaks in winter months and valleys in summer months. The highest monthly rates were December 2003, December 2005 November 2002, and February 2002 at 0.481, 0.468, 0.427, and 0.41 (admissions per 100,000), respectively, Figure 3. Here too, the lowest monthly rates were August 2007, July 2007, July 2008, and August 2008 at 0.153, 0.162, 0.164, and 0.175 (admissions per 100,000).

Figure 3 shows that monthly values of ambient levels of the two traffic-related pollutants, CO and NO₂, also have strong seasonal cycles and a general decline in their mean yearly value over the study period. In general, CO and NO₂ levels are highest in the cooler months (October February) and lowest in late spring and early summer (May August). The yearly mean of CO level dropped nearly half between 2001 and 2008, from 0.7621 ppm to 0.4057 ppm. These results were consistent with strategies implemented in CA to reduce the amount of traffic-related pollution during this time period. Ambient levels of O₃ display a strongly seasonal pattern with peaks in mid-late summer months and lows from November to January. The yearly mean values of O₃ were consistent from 2001 to 2008 whereas levels did not fluctuate greatly and showed a small increase. Monthly levels of PM₁₀ and PM_2.5 showed less regular seasonal oscillation than the other 3 pollutants. Generally, the levels of PM are higher in summer and fall months and lower in winter and spring.

Maximum monthly temperature displayed a strong seasonal oscillation, whereas relative humidity did not vary with a regular seasonal pattern. The annual mean of maximum temperature increased slightly over the study period while relative humidity generally decreased. The decrease in relative humidity was likely due to a persistent drought in CA throughout much of the study period (Keeley et al. 2007).

2. Candidate models and variable significance

Initially, all possible combinations of predictor variables were considered in forming potential models for evaluation, which resulted in 128 unique models. Due to high collinearity between predictor variables (absolute Pearson Correlation Coefficient greater than 0.5), 93 models were removed from consideration. Thus, 35 models were evaluated and listed in Supplemental Material, Table 3 (7 single variable, 15 two variable, 11 three variable, and 2 four variable models).

To explore what benefits, if any, the addition of temporal random effects might fetch, both the full model (1) and its counterpart with the temporal random effects removed are considered. Within the subsequent tables and figures, the results from the full model (1) and its non-temporal counterpart are identified as the temporal effects and non-temporal effects models respectively. Because of the large number of models evaluated, we initially report only a summary of the results. Table 1 contains an overview of the directionality and significance of the regression coefficients for each of the predictor variables in all 35 models. The predictor variables CO, NO₂, and PM_2.5 were positive and significantly associated with asthma hospitalizations in all models, whereas PM₁₀ was positive and significant in 2 of 12 models, relative humidity was positive and significant in 6 of 14 temporal effects models and all non-temporal effects models, and maximum temperature was negative and significant in 2 of 14 models. O₃ was not a significant predictor of asthma hospitalizations in any of the models evaluated.

Table 1.

Directionality and statistical significance of predictor variables in all models. The number of models that included the given variable are recorded in the column labeled #. Values under the columns labeled Positive and Negative indicate the number of time a variable was statistically significant at the 0.1 level.

Variable	Temporal effects			Non-temporal effects
	#	Positive	Negative	Positive	Negative
CO	10	10	0	10	0
NO2	10	10	0	10	0
O3	18	0	0	0	0
PM10	12	2	0	2	0
PM2.5	6	6	0	6	0
Tmax	8	0	2	0	2
RH	14	6	0	14	0

3. Model evaluation

Fit scores for all models evaluated can be found in Supplemental Material Table 3. Of these 35 models, 7 models produced results wherein all predictor variables were statistically significant at the 0.1 level. These models along with corresponding fit scores, MSPE, and bias are listed in Table 2. Here, the consistently lower D scores suggest that the addition of the temporal random effects improve model fit in all cases. Although the addition of the temporal random effects result in only marginal improvement of MSPE, they do increase the precision of the posterior predictive distributions. This precision is summarized by calculating the holdout set’s mean 90% posterior predictive credible interval (C.I.) width, which is given in Table 2. Here too, we included the coverage rate, which is the number of times the true holdout value is within the 90% posterior predictive C.I., divided by the number of observations in the holdout set. Despite the temporal models’ marginally narrower mean posterior predictive C.I. widths, their coverage rates are comparable to those of the non-temporal models. This is a desirable quality and can be more clearly seen in a graphical representation of the models’ fitted and predicted values. For example, Figure 4 illustrates the accuracy and precision of the fitted and predicted estimate for the temporal and non-temporal NO₂ + Tmax models. Here, comparison between the two subplots clearly shows that the addition of the temporal effects results in a more accurate and precise representation of hospitalization rates. These same advantages, afforded by the addition of the temporal random effects, can be seen in all of the other candidate models.

Table 2.

Model fit and holdout set MSPE, bias, mean 90% posterior predictive credible interval width, and coverage rate for candidate models with all significant predictor variables.

	Temporal effects							Non-temporal effects
Model	G	P	D	MSPE	Bias	C.I. Width	Coverage rate	G	P	D	MSPE	Bias	C.I. Width	Coverage rate
CO	0.22	0.79	1.01	0.010	0.018	0.36	0.9	1.21	1.22	2.44	0.010	0.015	0.37	0.9
NO2	0.22	0.79	1.01	0.009	0.017	0.36	0.9	1.20	1.21	2.41	0.009	0.017	0.38	0.9
NO2 + RH	0.26	0.82	1.09	0.008	0.015	0.38	0.9	1.14	1.17	2.31	0.008	0.015	0.39	0.9
PM2.5 + RH	0.27	0.88	1.15	0.010	0.021	0.36	0.9	1.27	1.31	2.58	0.011	0.022	0.37	0.9
PM10 + RH	0.28	0.90	1.17	0.008	0.015	0.36	0.9	1.30	1.34	2.64	0.009	0.014	0.36	0.9
NO2 + Tmax	0.33	0.89	1.23	0.008	0.013	0.38	1	1.16	1.19	2.35	0.008	0.013	0.39	0.9
PM2.5	0.32	0.93	1.24	0.011	0.024	0.37	0.9	1.34	1.35	2.70	0.013	0.026	0.38	0.9

The parameter estimate for those model listed in Table 2 are detailed in Tables 3 and 4. Specifically, Table 3 provides the parameter summaries for the single variable temporal random effects models. Here, CO, NO₂, and PM_2.5 were positively associated with asthma hospitalizations and statistically significant at a 0.1 level, i.e., the 90% C.I. do not include zero. Although a number of individual variables were statistically significant in the multivariable models, only the 4 models detailed in Table 4 produced results in which all predictor variables were statistically significant. Comparing Tables 3 and 4, we see that the regression coefficients in the single and multi-variable models were consistent in significance and sign. Here too, we can see the addition of temporal random effects apportions the total residual variance nearly equally between the temporal and non-temporal components, i.e., σ² / τ² ≈ 1. Finally, the temporal decay parameter φ estimates suggest an effective temporal range of at least 1 month for any given model. We define the effective temporal range as the period of time beyond which the temporal correlation drops below 0.05. For instance, from Table 3, the median and 90% CI for in φ the CO single variable model is 1.46 (0.54, 2.69) and is equivalent to an effective temporal range of 2.05 (1.11, 5.56) months.

Table 3.

Parameter credible intervals, 50 (5, 95) percentiles, for single variable temporal effects models.

Coefficient	CO	NO2	PM2.5
β0	−12.67 (−12.72, −12.61)	−11.37 (−11.96, −10.81)	−13.09 (−13.35, −12.82)
βCO	0.22 (0.13, 0.31)
β NO2		0.37 (0.22, 0.52)
β PM2.5			0.11 (0.01, 0.21)
φ	1.46 (0.54, 2.69)	1.60 (0.53, 2.79)	0.94 (0.09, 2.4)
σ2	0.007 (0.001, 0.013)	0.008 (0.001, 0.013)	0.007 (0.001, 0.014)
τ2	0.004 (0.001, 0.015)	0.004 (0.001, 0.016)	0.006 (0.001, 0.013)

Table 4.

Parameter credible intervals, 50 (5, 95) percentiles, for multi-variable temporal effects models.

Coefficient	NO2 + RH	PM2.5 + RH	PM10 + RH	NO2 + Tmax
beta;0	−12.25 (−13.14, −11.36)	−13.9 (−14.62, −13.11)	−14.38 (−15.37, −13.25)	−8.98 (−11.13, −6.83)
βNO2	0.36 (0.21, 0.5)			0.44 (0.28, 0.6)
βPM2.5		0.12 (0.02, 0.21)
βPM10			0.12 (0.01, 0.23)
βRH	0.21 (0.05, 0.37)	0.20 (0.01, 0.38)	0.30 (0.07, 0.49)
βTmax				−0.28 (−0.52, −0.04)
φ	1.65 (0.51, 2.8)	1.49 (0.41, 2.74)	1.28 (0.16, 2.7)	1.46 (0.37, 2.75)
σ2	0.006 (0.001, 0.012)	0.007 (0.001, 0.014)	0.008 (0.001, 0.014)	0.005 (0.001, 0.012)
τ2	0.005 (0.001, 0.012)	0.005 (0.001, 0.013)	0.005 (0.001, 0.013)	0.006 (0.001, 0.012)

The apportioning of the residual variances and substantial effective temporal ranges further support the use of the temporal random effects and suggests that models that do not accommodate residual dependence, e.g., the non-temporal models in Tables 2 and Supplemental Material Table 3, violate the assumption of independent and identically distributed residuals and could, as a result, produced erroneous inference.

6. Discussion

The findings presented here are similar to those reported by Linn et al. (2000) in a study of metropolitan Los Angeles using daily time-series data. In single pollutant models, the authors found significant associations between asthma hospital admissions and CO, NO₂, and PM₁₀ levels and a non-significant association with O₃ (PM_2.5 was not included in their study). Recent studies exploring asthma and air pollution in southern California have focused largely on children’s health outcomes. Willhelm et al. (2008) found that children living in areas with higher levels of O₃ and PM₁₀ experienced more frequent asthma symptoms while children living near to heavy traffic experienced a higher amount of emergency department visits and hospitalizations. In Moore et al. (2008), a time series analysis showed that increased O₃ levels were associated with a higher number of asthma hospitalizations for children. Although O₃ was not a significant predictor of asthma hospitalizations in any single or multivariable models in this analysis, the previously mentioned studies do lend credence to an association between O₃ levels and asthma exacerbation and symptoms in southern California. However, doubt exists to whether O₃ causes asthma exacerbation (e.g., Donnay 2004; Giovannini et al. 2010). The results presented here suggest that O₃ is not associated with asthma hospitalizations at this scale of analysis. Sun et al. (2006) also showed that the relationship between asthma-related emergency department visits and air pollution may be quite different for adults and children. Because the entire population of LA County was evaluated simultaneously, these age-specific relationships may have not been detected. Our decision to conduct the analysis at a monthly time scale, rather than daily, was guided by two considerations. First, in a similar study conducted by Moore et al. (2008), that looked at the relationship between childhood asthma and ozone in Southern California, they point out that given the variation in time spent outdoors in a large population, such as that in LA County, monthly aggregation (or in their study three month aggregation) could “provide a more stable population-level estimate than would be the case for shorter time intervals, such as days or weeks.” Similar rational for analysis of monthly asthma hospitalizations were used in recent studies in Greece (Priftis et al. 2006) and Taiwan (Chen et al. 2006; Sun et al. 2006). Second, in our initial exploratory analysis of the asthma data we created autocorrelation function plots that showed a strong temporal correlation at a 30 day lag (i.e., a correlation of 0.5), and even at a 60 day lag the correlation was m 0.3. Therefore we felt there would not be a substantial loss of information by working at a monthly time scale.

Many studies examining the effects of air pollutants and health outcomes observe high correlation between the pollutants measurements themselves and are often highly temporally correlated with seasonal changes and/or climatic variables (e.g., Cao et al. 2009). We attempted to account for these correlations by using both traditional methods (moving average seasonal adjustment) and a flexible Bayesian modeling framework to accommodate residual temporal dependence. High correlation between predictor variables was accounted for using the seasonal adjustment, while the temporal dependence was addressed within the models using temporal random effects. Accounting for these correlations allow for confidence that the resulting relationships between asthma hospitalizations, pollutants, and weather conditions did not result from temporal dependence between observations.

Of the 7 models with all statistically significant variables, D scores were best for single variable models CO and NO₂ and multi-variable model NO₂ + relative humidity. However, the model with the lowest MSPE and bias, thus the most accurate predictor of asthma hospitalizations, was NO₂ + Tmax. Interestingly, this model had the largest average C.I. width of the 7 models evaluated. We do note, however, that given the relatively small holdout set only 10 observations the ordering of the models based on MSPE could change, perhaps significantly, if other holdout sets were considered.

Associations between health outcomes and air pollution have, in many cases, relied on pollution data gathered at a single monitoring station or an average value from multiple monitoring stations (Chen et al. 2007). When using regional or aggregated data, calculating the arithmetic mean of station measurements has been the prevailing approach for assigning a single pollution measurement to the area under study (Lee and Shaddick 2010; Wilson et al. 2006). In these methods, the spatial variability of air pollution is often addressed by incorporating a buffer distance from the monitoring station or a simple distance-weighted measure between the monitoring station and observation. Although these methods have produced significant results in the past, their use may lead to exposure assignment errors and possible weakening of the observed relationship between health outcomes and air pollution exposure (Beelen et al. 2009). We believe that efforts to incorporate the spatial variability of air pollution within a study area are necessary, even in cases where the data is summarized over the study area. Chen et al (2007) compared the results of non-spatial and spatial methods of linking air pollution data (PM₁₀) to health outcome data (respiratory hospital admissions) in a metropolitan area and found that the non-spatial method underestimated the relative risk of hospitalization compared to the spatial method. County-level air pollution predictors were generated using surfaces of pollutants predicted using spatial Bayesian regression models and the monitoring station locations and observations.

7. Limitations

Ecological and time series studies have well known limitations and are subject to a number of biases. Due to the spatial resolution of the asthma hospitalization data and its lack of patient demographic and residential location information, we were compelled to make assumptions that potentially influenced the results of our study.

Hospitalization data are a measure of confirmed cases that can be tethered spatially and temporally to a specific location and time, allowing them to be linked to measures of air pollution. However, we acknowledge the possibility that residents from another county visited a hospital in LA county (and vice versa) allowing for over- or under-representation of cases when using hospitalizations as a outcome variable. Because we do not possess the residential locations of the individuals hospitalized, we assume that the number of nonresidents of LA county admitted to LA county hospitals equal the number of residents of LA county admitted to non-LA county hospitals.

Time-series studies are generally limited by lack of individual data, which can greatly influence personal exposure to pollutants (Mar and Koenig 2009). However, measuring personal exposures is not feasible in large populations over long study periods and therefore exposure estimates are necessary (Rose et al. 2009; Vienneau et al. 2009). The use of ambient pollution measurements as a surrogate for exposure data limits the ability to establish a causal link between air pollution and asthma outcomes. Also, utilizing ambient levels likely results in some misclassification of air pollution exposure as it does not account for the presence of confounding factors such as time spent outdoors, second hand smoke presence, indoor air pollution, or avoidance behavior. Neidell (2009; 2004) studied avoidance behavior due to air quality warnings in southern California and showed that omitting the responses to air quality warnings could lead to underestimated effects of pollution on asthma outcomes. Accounting for this factor could potentially strengthen the observed relationships between pollutant levels and hospitalizations in this study, however measuring and/or describing the avoidance behavior of an aggregated population over a long study period could prove difficult in practice.

Although we accounted for changes in the overall population of LA county, we did not account for changes in the demographic structure of the population or other risk factors for asthma exacerbation. By restricting the study area to one county, we attempted to control for the confounding effects of demographic variation present in regional or state-wide studies and allow for testing of our methods in a initial, manageable setting. Mar and Koenig (2009) note that for time-series studies, these variations need no control as they remain relatively constant throughout the study period.

This study utilized the 24-hour mean concentration in lieu of the EPA regulated measures of 8 hour and 1 hour O₃ concentration. Although recent research supports the use of EPA regulated measures for O₃ (Darrow et al. 2011), others report high correlation between 24-hour and 8-hour measurements (Akinbami et al. 2010; Woodruff et al 2008). Because of the large study area, long time series, and lack of exposure data, we believe this measure introduced less potential for exposure misclassification. The use of 24-hour mean also ensured consistency in the temporal scales for all pollutants included.

8. Conclusions

We explored the relationship between asthma morbidity, ambient levels of air pollutants, and weather conditions at a county level using a monthly time series analysis. In LA County, we found that asthma hospitalizations were significantly associated with CO, NO₂, and PM_2.5 levels in single variable regression models and NO₂ + relative humidity, PM_2.5 + relative humidity, PM₁₀ + relative humidity, and NO₂ + maximum temperature in multi-variable models. Although ecological and time series studies are subject to a number of potential shortcomings, they allow for associations to be revealed at a population level. Understanding the relationship between air pollution levels, weather conditions, and asthma hospitalization rates for the entire county population over a long study period may help to inform future policy decisions aimed at reducing LA County’s total asthma burden. Using Bayesian linear regression with temporal random effects, we accounted for residual dependence between observations that was not removed by the seasonal adjustment or predictor variables. These temporal random effects models were compared to their non-temporal counterparts using objective measures of model fit and predictive performance. The addition of temporal random effects resulted in improved model fit, more accurate and precise prediction, and reduced potential for violating the basic model assumption of independent and identically distributed residuals.

Because hospitalization for asthma generally only occurs in situations where a person experiences a severe asthmatic event, asthma hospitalizations only measure a portion of the total asthma burden. However, the size of LA County’s population (estimated at nearly 10 million by the US Census Bureau (2010)) and large number of hospitalizations highlight the importance of the results presented here.

The general decline in average levels of NO₂, CO, and PM_2.5 in LA county were consistent with the aforementioned strategies implemented to reduce traffic related and other air pollution in California. However, LA County continues to be classified as a “maintenance area” by the EPA for each of these pollutants. Considering the results of our analysis, we believe that further reduction would lead to fewer asthma hospitalizations.

Highlights.

• Asthma hospitalization rates in Los Angeles County, CA, decreased between 2001 and 2008.

• CO, NO₂, PM_2.5, were significant and positively correlated with asthma hospitalizations.

• O₃, PM₁₀, relative humidity, and maximum temperature produced mixed results.

• Inclusion of temporal random effects met model assumptions, improves fit and predictive ability.