TNF-α increases endothelial progenitor cell adhesion to the endothelium by increasing bond expression and affinity

Abstract

Endothelial progenitor cells (EPCs) are a rare population of cells that participate in angiogenesis. To effectively use EPCs for regenerative therapy, the mechanisms by which they participate in tissue repair must be elucidated. This study focused on the process by which activated EPCs bind to a target tissue. It has been demonstrated that EPCs can bind to endothelial cells (ECs) through the tumore necrosis factor-α (TNF-α)-regulated vascular cell adhesion molecule 1/very-late antigen 4 (VLA4) interaction. VLA4 can bind in a high or low affinity state, a process that is difficult to experimentally isolate from bond expression upregulation. To separate these processes, a new parallel plate flow chamber was built, a detachment assay was developed, and a mathematical model was created that was designed to analyze the detachment assay results. The mathematical model was developed to predict the relative expression of EPC/EC bonds made for a given bond affinity distribution. EPCs treated with TNF-α/vehicle were allowed to bind to TNF-α/vehicle-treated ECs in vitro. Bound cells were subjected to laminar flow, and the cellular adherence was quantified as a function of shear stress. Experimental data were fit to the mathematical model using changes in bond expression or affinity as the only free parameter. It was found that TNF-α treatment of ECs increased adhesion through bond upregulation, whereas TNF-α treatment of EPCs increased adhesion by increasing bond affinity. These data suggest that injured tissue could potentially increase recruitment of EPCs for tissue regeneration via the secretion of TNF-α.

endothelial progenitor cells (EPCs) are a rare population of cells that that participate in postnatal neovascularization (angiogenesis) (3, 4, 46). EPCs have been found to exist primarily in the bone marrow but have also been isolated from peripheral blood and vascular walls (24, 59). EPCs have been shown to participate in angiogenesis directly by incorporating into areas of vessel growth and indirectly by secreting proangiogenic factors (27, 35). Impaired angiogenesis is a major component of many cardiovascular diseases including diabetes, angina pectoris, and atherosclerosis (55, 56). Additionally, clinical studies have associated decreased numbers of circulating EPCs in patients with cardiovascular disease (44).

Shortly after the discovery of EPCs in 1997, many groups used autologously isolated EPCs as a cellular-based regenerative therapy to treat cardiovascular disease in humans (58). Results have been promising but inconsistent. Ineffective EPC therapy could be due to one or more factors: impaired EPC mobilization from the bone marrow or resident tissue, failure of EPCs to “home” to the target site, reduced production/secretion of angiogenic factors at the target site, and/or impaired EPC engraftment. The purpose of this study was to dissect the physical mechanisms governing EPC binding to the inner most vascular layer, the endothelium. Binding to the endothelium is the first step in the process of EPC engraftment. Understanding the mechanisms of EPC adhesion to the vascular endothelium is important for determining the mechanisms of EPC-induced angiogenesis as a successful cellular-based therapy (9).

When studying the mechanisms of EPC function, it is important to consider the specific subtype of the isolated EPC population as the parental lineage and site of isolation can have a strong effect upon several phenotypes. EPCs in this study were isolated from the bone marrow (BM). All BM cells are derived from hematopoietic stem cells (HSCs). HSC derivatives often exhibit similar properties of activation, adhesion, and integration (13). Thus, when studying the mechanisms of EPC adhesion to the vascular endothelium, it is important to consider mechanisms of binding and integration that EPCs may share with other HSC derivatives, for example, B-cells and monocytes.

Tumor necrosis factor-α (TNF-α) is a proinflammatory cytokine primarily produced by activated macrophages (8). TNF-α acts to regulate immune cell function including rolling, adhesion, proliferation, and apoptosis (49, 57). To increase localized recruitment of leukocytes during an inflammatory response, TNF-α stimulation of the endothelium increases the number of integrins expressed on the cell surface, increasing the adhesion and recruitment of leukocytes to an active site (38). Because TNF-α has known roles in cellular recruitment, adhesion, and remodeling, it was hypothesized that an acute, low-dose TNF-α treatment to EPCs would increase the adhesive properties of EPCs to vascular endothelial cells (50).

It has been shown by Dentelli et al. (11) that adhesion of EPCs to vascular endothelial cells is mediated by vascular cell adhesion molecule 1 (VCAM1) and its ligand, very-late antigen 4 (VLA4). VCAM1 and VLA4 are part of the protein family of integrins. Integrins are transmembrane proteins that mediate intercellular attachment. There are two known mechanisms by which TNF-α can increase adhesion between cells using integrins. The first is to increase the number of integrin-based bonds formed between two cell types by upregulation of plasma membrane integrin expression. The other is to increase the rupture force of the bond by increasing the affinity of the integrin for its ligand. VLA4 has been shown to have the ability to switch between a low and high affinity state in response to cytokines (12, 31). Bond expression and affinity are two distinct processes that are difficult to separate without isolating individual bonds at the molecular scale. Litvinov et al. (36) conducted a micromanipulation study to measure the rupture force of individual integrins by allowing platelets to form a single bond to a coated glass plate and then disrupting the interaction using laser tweezers. Litvinov et al. generated the probabilistic distribution of integrin rupture forces for platelets with integrins in a low affinity state and integrins activated to a high affinity state. While an impressive study, this experimental setup would not allow for the measurement of cell/cell interactions, because it would be impossible to control for the number of bonds formed between two cell types. To study the EPC/endothelial cell (EC) interaction, it is necessary to use techniques other than micromanipulation assays.

There are several techniques that exist to measure cell/cell detachment forces using microfluidic devices. Studies have measured detachment forces by “peeling” bound cells using laminar flow, quantifying the wall shear stress (WSS) required to detach cells from another cell or a coated surface (15, 16, 53). After the number of adherent cells were measured after exposure to fluid-induced WSS, these data can be used in a descriptive statistical analysis to isolate differences in treatment groups. However, this technique cannot mechanistically distinguish between an increase in adhesion from bond upregulation versus an increase in bond affinity. This is because an increase in bond affinity and bond upregulation both will increase the number of attached cells. In this study, to account for these two similar yet distinct processes, a Monte Carlo-based mathematical model was created that predicts the number of adherent cells based upon the relative number of bonds formed between the two cell types, the affinity of the bonds, and the magnitude of the exposed fluid shear stress. To determine the mechanism of EPC/EC adhesion, biophysical simulations were compared with experimental data.

This study had several goals: 1) to develop an assay measuring cellular detachment under conditions of laminar fluid flow (Fig. 1); 2) to develop a mechanistic biomechanical model predicting cellular adhesion under conditions of laminar fluid flow as a function of integrin expression and affinity; 3) to determine mathematically how TNF-α affects the expression and affinity of integrin-based bonds between EPCs and vascular endothelial cells; and 4) to determine the mechanism that TNF-α affects the adhesive properties of the VCAM1/VLA4 integrin in an in vitro model of EPC/EC adhesion.

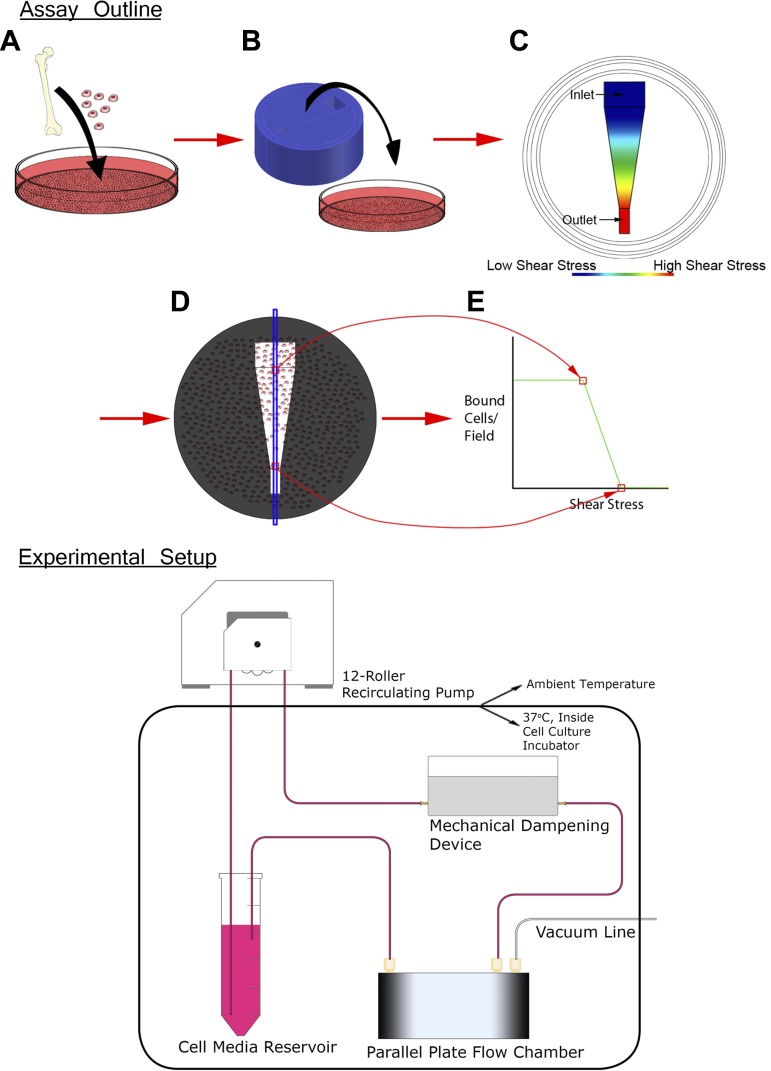
Fig. 1.

Outline of binding strength experimental assay. Top: endothelial progenitor cells (EPCs) were isolated and cultured from a rat femur (A) and allowed to bind under static conditions to an endothelial cell (EC) monolayer (B). The device then induced a disruptive shear-stress gradient (C). After cell media was passed over the monolayer, an area of interest (D) was imaged and the number of cells bound per field was determined (E). Bottom: entire experimental setup was contained within a cell culture incubator, with the exception of the 12-roller recirculating pump. The media flow from the pump was pulsatile, so the dampening device served as a mechanical capacitor steadying the media flow into the parallel plate flow chamber (PPFC). After leaving the PPFC, the cell media returned to the supply reservoir where it was recirculated.

METHODS

Design, drawings, and construction.

A parallel plate flow chamber (PPFC) was designed, built, characterized, and validated according to the following criteria: 1) the device is biocompatible; 2) the device induces a uniform shear stress gradient that is accurately characterized; 3) the device is compatible with 60-mm cell culture dishes; and 4) the fluid flow through the device induces a shear stress that is laminar and biologically relevant. The device was built because no device existed commercially that met all of these criteria. Several devices have met some of these criteria; for example, Usami et al. utilized the first PPFC that induced a shear stress gradient across cultured cells (53). Additionally, C&L Instruments was the first to design a PPFC that could attach to commercially available cell culture plates; however, this device induced a constant shear stress field, as opposed to a gradient that would be necessary for this study (43). Elements from these two designs were used to develop a device that would be optimally suited for the proposed experiments.

The PPFC was initially designed using Eq. 1 (described below) and later refined used computational fluid dynamics (CFD) simulations. For a PPFC with a chamber height (h) and chamber width (b), where h << b, and where the PPFC was perfused by fully developed, steady laminar Newtonian fluid flow, it is safe to assume (when away from walls, inlet, and outlet of the PPFC) that flow within the PPFC can be described as flow between two infinitely parallel plates:

$${\mathrm{\tau }}_{\mathrm{w}}=\frac{6\mu \mathrm{Q}}{b{h}^2}$$ (1)

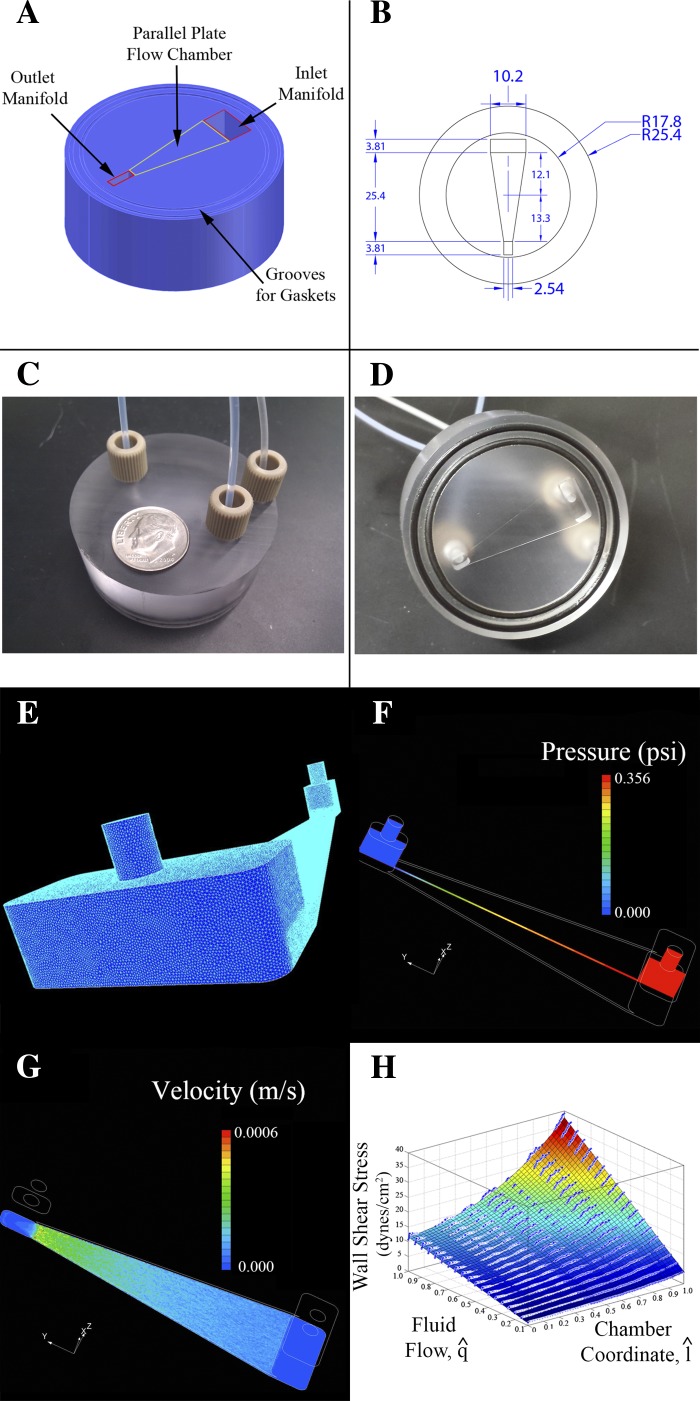
where τ_w is wall shear stress, μ is fluid viscosity, Q is fluid flow (53). The viscosity of the cell media was approximated to the same as water at 37°C. The area of the PPFC was maximized within the vacuum seals. Equation 1 shows τ_w is inversely proportional to h² so the device was constructed to be as thin as possible (minimizing h) in order that the recirculating pump could generate a high enough fluid flow Q to maintain the desired shear stress (Fig. 1). The PPFC was designed to be supplied and emptied by manifolds with large cross-sectional area compared with that in the PPFC. Using this design, the majority of resistance to fluid flow in the device would be in the PPFC, allowing fluid with a uniform velocity to enter the PPFC. To determine the initial geometry, it was determined the maximal shear stress that would be necessary for this study would be below 40 dyn/cm², so the PPFC exit dimensions were calculated according to Eq. 1 using τ_{w =} 40 dyn/cm². The inflow dimensions were then maximized within the constraints of the device allowing a fourfold change in shear stress from inlet to outlet. The device needed to have an overall diameter that was compatible with 60-mm cell culture dishes. The device attached to the cell culture dish using a vacuum suction between two O-ring gaskets placed on the outer edge of the device. The space left on the surface of the device resulted in construction of a PPFC where h = 200 μm while the height of each manifold was 3.8 mm (Fig. 2).

Fig. 2.

Design, construction, and computational fluid dynamics (CFD) characterization of PPFC, including three-dimensional rendering (A), where the device bottom is facing up. The two outer circular grooves are gasket slots. A vacuum line connects to the outer port on the top of the device to create a vacuum seal with the cell culture plate. B: top view drawing (dimensions in millimeters) demonstrating that the inlet portion of the chamber is 4× as wide as the outlet. C: photograph of device, top view, including the vacuum line, fluid inlet, and fluid outlet. D: photograph of device, bottom view. E–H: results of CFD simulation including mesh of 1 × 10⁶ elements (E). Element density in PPFC is increased with respect to manifold. PPFC element density is the most crucial area for increasing element density; it was found that increasing the elemental thickness to greater than 10 elements ensured a reproducible result. F and G: example outputs from the SC/Tetra solver that found numerical solutions for the variables “pressure” and “velocity.” H: CFD simulation summary. Scatter data represents wall shear stress predictions that were calculated using SC/Tetra CFD software. Scatter data plotted in the graph represents wall shear stress values from a line bisecting the long axis of the chamber. The surface is a function that was generated from three-dimensional scatter data using best-fit polynomial (3^rd order for fluid flow and chamber coordinate) to smooth noise introduced via numerical differentiation (as seen in G).

The device was designed using AutoCAD 2011 (Autodesk; San Rafael, CA) and constructed out of polycarbonate using a model 2000 mill (Sherline; Vista, CA).

CFD analysis.

Fluid flow was analyzed with a computational fluid dynamics (CFD) model that was developed using the commercially available SC/Tetra V8 suite (Cradle Software; Osaka, Japan). A mesh of 1 × 10⁶ elements was created based on the geometry of the fluid flow path created in AutoCAD (Fig. 2). Nineteen simulations were run based on the fluid flows at which the Ecoline VC-360 recirculating pump was calibrated (Harvard Apparatus; Holliston, MA). The simulation assumed nonslip boundary conditions and fluid properties of water at 37°C (density equal to 993.3 kg/m³, viscosity equal to 6.965 × 10⁻⁴ Pa·S). The CFD model treated the fluid as Newtonian and simulated the steady-state laminar fluid dynamics. The solver was set to converge after reaching a relative fluctuation of <1 × 10⁻⁴ between iterations. The CFD solver calculated fluid velocity, pressure, and shear stress as a function of chamber position. CFD data were exported from SC/Tetra into MATLAB R2010a (The MathWork; Natick, MA) for analysis with custom scripts (Fig. 2H).

Device validation.

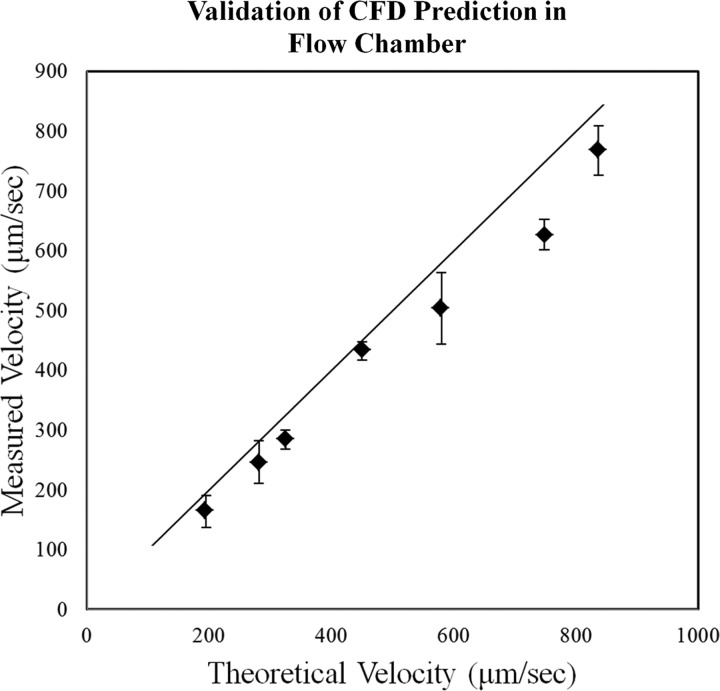
CFD results were validated by pumping 5 μm diameter neutrally buoyant fluorescent beads (Spherotech, F1CP-50-2; Lake Forest, IL) through the chamber using a PHD 22/2000 syringe pump (Harvard Apparatus) to compare CFD velocities (theoretical predictions) with the measured bead velocities (Fig. 3).

Fig. 3.

Device validation. Fluorescent beads of 5 μm were pumped through the chamber while tracking them using fluorescent microscopy. Data are plotted as the average ± SD. The black line is reference of 1:1 measured:theoretical, where the CFD-predicted velocities agree measured velocities. This exact relationship was not demonstrated, likely due to the fact that the measured microscope plane was a finite thickness. Therefore, beads traveling less than the maximal velocity were measured as well; hence, the measured velocities were slightly less than the predicted velocities.

Cell culture.

Rat cardiac microvascular endothelial cells (RCMVECs) were plated, expanded (P3–P8) in 60-mm dishes (R1111; Cell Biologics; Chicago, IL), and cultured to confluence in endothelial cell-specific media (MCDC131, E3000-01B; US Biological; Swampscott, MA) with the microvessel cell EGM-MV pack (CC-4147; Lonza; Basel, Switzerland). The hydrocortisone supplement from the EGM-MV pack was omitted.

The Medical College of Wisconsin (MCW) Institutional Animal Care and Use Committee approved all animal protocols. Animals were maintained on water and a low-salt ad libitum diet (0.4% NaCl) within the MCW Animal Resource Center. EPCs were isolated from 9-wk-old Sprague-Dawley rats (Charles Rivers, Wilmington, MA) as described previously (10). Briefly, bone marrow from the tibia and femur was isolated. Using density gradient centrifugation (Histopaque 1083; Sigma-Aldrich; St. Louis, MO), red blood cells were removed from the mononuclear fraction. The mononuclear fraction was then seeded (1 × 10⁷ cells/plate) on to fibronectin (33010-018; Invitrogen; Carlsbad, CA)-coated plates in endothelial cell-specific media (MCDC131, E3000-01B; US Biological) supplemented with the endothelial progenitor cell EGM-2 pack (CC-4176; Lonza). At day 3, nonadherent cells were rinsed off, and the remaining EPCs were cultured until day 10. Previous studies have characterized this specific population for surface markers (CD34⁺/VEGFR2⁺/CD31⁺/CD45⁺) and function (react with BS-1 lectin, uptake LDL) (10, 22, 25). Specifically, these markers and properties are consistent with early outgrowth EPCs.

Adhesion experiments.

RCMVECs were grown to confluence and were treated with recombinant rat TNF-α or vehicle (1 ng/ml; PRC3015; Invitrogen) added to the culture media for 12 h before binding experiments. EPCs were treated with TNF-α (1 ng/ml) or vehicle for 3 h before binding experiments. EPCs were then stained with DAPI (40 μg/ml; D9542, Sigma-Aldrich) and lifted using an enzyme-free cell dissociation buffer (S-014-B; Merck Milipore; Billerica, MA). EPCs were counted using a Countess cell counter (C10311; Invitrogen), and then 2.5 × 10⁵ EPCs were plated on endothelial cells (ECs) and allowed to bind for ∼2 h.

After binding was completed, a shear-stress gradient was induced using the PPFC. The pump was turned on, and the system was given ∼5 min to achieve steady-state flow. The PPFC was then attached to the cell plate. After 30 min of shear stress, the PPFC was removed from the cell culture plate, and a series of images were acquired (TS100 Inverted Microscope; Nikon; Shinjuku, Japan) along a line (16 microscope fields) bisecting the long axis of the induced shear-stress field. The average shear stress in each microscope field was calculated based on the CFD data. Images were analyzed using MetaMorph (Molecular Devices; Sunnyvale, CA) image processing software to determine the relative EPC binding.

Confocal microscopy.

To measure the shape of the EPCs after adhesion to an EC monolayer, EPCs were lifted by washing the cells 2× with Dulbecco's PBS at 4°C (14190-144, Life Technologies) and then lifting the EPCs using 4 ml of enzyme-free dissociation buffer (S-014-B, Millipore). To ensure the shape of the lifted EPCs was the same as in the adhesion experiments, this lifting protocol was identical to that used in the PPFC experiments. Cells were washed and then resuspended in 4 ml of 2.5 mM of NHS-SS-Biotin for 60 min while rocking on ice. Cells were washed 2× and then resuspended in streptavidin conjugated with AlexaFluor-488 diluted 1:100 in PBS (S32354, Invitrogen) for 60 min while rocking on ice. Labeled EPCs were then washed 2× with ice-cold PBS and placed on a glass-bottom cell culture dish (P35G-0-20; MatTek; Ashland, MA) coated with a monolayer of RCMVECs and cells. After 2 h of incubation, a Z-stack of images were generated in the X-Y plane in 1-μm increments with a Leica TCS SP5 using a ×40 objective.

Mathematical model.

A Monte Carlo simulation was created to generate theoretical adhesion curves based on the experimental design. More specifically, the simulation generates EPC/RCMVEC interactions by adding bonds between two simulated cells in silico. Because individual integrins can break and form under no load, a Monte Carlo mathematical model was built that randomly creates integrin bonds between EPC/RCMVECs within model parameters that specified integrin expression and affinity. The model can increase EPC/RCMVEC adhesion by increasing the bond expression (number of bonds) or bond rupture force (bond affinity). The model simulated the adhesion between 1 × 10⁵ EPC/RCMVEC interactions by creating integrin bonds between EPCs/RCMVECs. Rupture strengths of bonds were defined by a probability distribution function experimentally measured by Litvinov et al. (36). The study by Litvinov et al. measured the rupture strength of the αIIβIII integrin. The interaction modeled in this study was that of the VLA4 integrin which is made up of the αIVβI subunits (6, 47). While these integrins are not identical, the components αII and βIII are splice variants of the αIV and βI components, and thus it is a reasonable assumption to use the data from Litvinov et al. as no similar data exists for the VLA4 interaction.

After 1 × 10⁵ EPC/RCMVEC interactions were generated with a parameter-defined expression and affinity, the simulation then determined what fraction of these cell-to-cell interactions would detach for a given shear stress. The fraction of adherent cells was then scaled to the number of EPCs originally seeded onto the cell culture plate in vitro and plotted. The variability in bond expression and affinity can be expressed by three model parameters. Bond expression, or the number of bonds (N) simulated between the two cell types was randomly selected from a Gaussian probability distribution function (P) defined by two parameters, a mean μ_bonds and standard deviation σ_bonds. The Gaussian distribution was selected as a parsimonious assumption given no data exists describing the distribution of bond expression for a given population of cells.

$$P\left(N\right)=\frac{1}{{\sigma }_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\sqrt{2\pi }}{e}^{-\frac{{\left(N-{\mathrm{\mu }}_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\right)}^2}{2{{\sigma }_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}}^2}}$$ (2)

1 × 10⁵ EPC/RCMVEC interactions were simulated; the number of bonds generated between the two cell types in each individual interaction was determined from Eq 2. The third variable that accounts for bond variability is a bond affinity parameter. The number of bonds determined to be high affinity is defined as M, which is determined from the percent activation γ parameter as outlined by Eq. 3.

$$M=\gamma N$$ (3)

The remaining bonds are defined as low affinity bonds. Because a bond can switch from a low affinity to a high affinity state, the number of high affinity bonds is simply the fraction of the total number of expressed bonds known as N. The rupture force of each bond generated (high or low affinity) in the simulation was randomly selected using the MATLAB random number generator from a low or highaffinity array of possible bond strengths defined by a probability distribution function that was determined experimentally by Litnov et al. (Fig. 4A) (36). One additional model parameter included in the model described the number of cells that will not detach even in the presence of very high shear stress and was defined as the nonspecific adhesion α parameter.

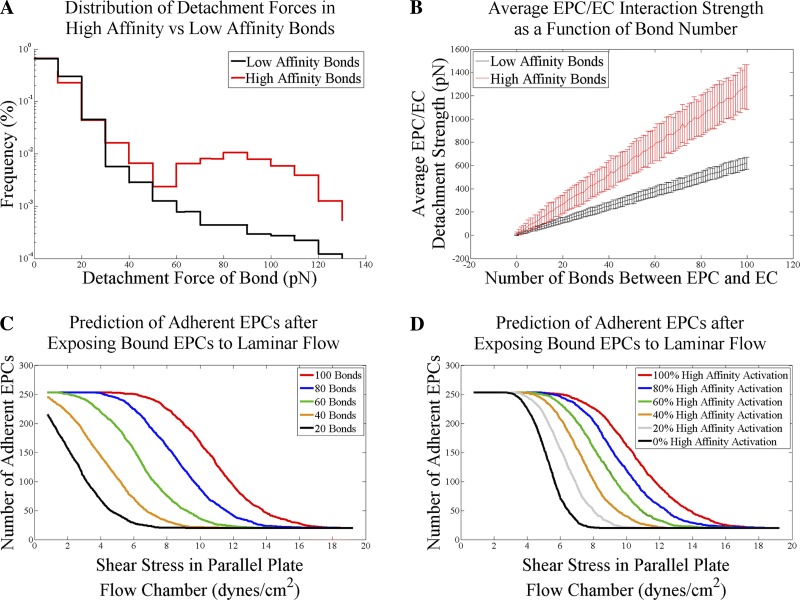
Fig. 4.

Biophysical model of EPC adhesion based on bond affinity and number. A: experimental distributions of high and low affinity bonds [from Litvinov et al. (36). Copyright 2002, National Academy of Sciences, USA]. B: demonstration of the force required to disrupt EPC/EC interaction as a function of the number of bonds created between the two cell types. Detachment strength and each number of bonds was simulated 250 times based on random sampling of the distributions in A. Data shown are the averages of 250 simulations (error bars are means ± SD). C: predicted adhesion curves for EPC/EC interactions with expressions of 20, 40, 60, 80, or 100 relative bonds (bond affinities held constant for all curves). D: predicted adhesion curves for EPC/EC interactions of a fixed bond expression with a mixture of low and high affinity bonds. Predicted adhesion curves for 0, 20, 40, 60, 80, or 100% high affinity bonds (bond expression held constant for all curves).

The fraction of adherent cells (f_a) was determined by generating cell/cell interactions as a function of bond mean (μ_bonds), standard deviation (σ_bonds), percent activation (γ), nonspecific adhesion (α), and shear stress (τ):

$$f_{\mathrm{a}}(\tau )=f\left({\mu }_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}},{\sigma }_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}},\gamma ,\alpha ,\tau \right)$$ (4)

The total number of predicted adherent cells (AC_P) was determined from the fraction of predicted f_a scaled to the average seeding density of the plate:

$$\mathrm{A}{\mathrm{C}}_{\mathrm{P}}=f_{\mathrm{a}}\left\{N_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d}}\frac{{\Lambda }_{\mathrm{f}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d}}}{{\Lambda }_{\mathrm{f}\mathrm{i}\mathrm{e}\mathrm{l}\mathrm{d}}}\right\}$$ (5)

where N_plated is the number of EPCs seeded onto the cell culture plate, A_field is the area of a single microscope field, and A_total is the area of the entire cell culture plate.

It was assumed that the intercellular bonds are arranged in parallel. This allowed for the total detachment strength of the EPC/RCMVEC interaction to be calculated by simply summing the rupture forces of all the integrin rupture forces. The force applied to the EPC/RCMVEC interaction was calculated using Eq. 6 derived by Gallant et al. (14).

$$F_{\mathrm{\tau }}=32R^2\mathrm{\tau }\sqrt{1+{\left(\raisebox{1ex}{$0.8R$}\!\left/ \!\raisebox{-1ex}{$a$}\right.\right)}^2}$$ (6)

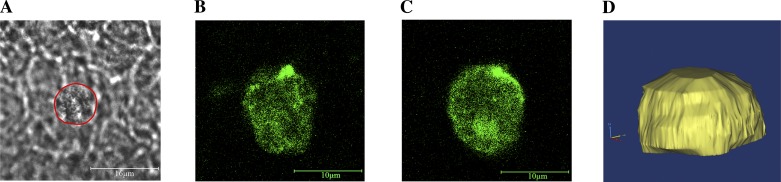
where F_T is the minimum force required to resist detachment, R is the average radius of the cell, τ is the wall shear stress induced by fluid flow through a PPFC, and a is the contact radius of the cell. R was held constant at 5 μm and a was assumed to be 75% of R. In the simulation, if the sum of the strengths of the randomly chosen population of bonds is not equal to or greater than FT, the cell will be considered “nonadherent.” This equation represents the minimum shear stress required for detachment of a spherical cell that is pressed against and adherent to a flat surface. To confirm this equation was a reasonable approximation for the experimental conducted in vitro, EPCs were labeled with a nonspecific biotin/AlexaFluor 488 stain and allowed to bind to an endothelial monolayer. An axial stack of confocal fluorescent images was acquired and the shape of the cell was reconstructed (Fig. 5). After three-dimensional reconstruction, it was apparent that the EPC was spherical with exception of the deformed surface that was adherent to the endothelial cell monolayer.

Fig. 5.

Geometry of adherent EPCs. Fluorescently stained EPCs were placed on top of an EC monolayer, allowed to bind, and imaged using confocal microscopy. A: brightfield image of EPC adherent to an endotheial cell monolayer. Red outline determined from fluorescent overlay. B: XY slice of EPC at the level of the EC monolayer (Z = 0 μm). C: XY slice of EPC 5-μm above the EC monolayer (Z = 5 μm). D: three-dimensional rendering of adherent EPC, demonstrating an approximate spherical geometry.

Figure 4B demonstrates how increasing the number of bonds between the two cell types will increase the minimum detachment force. Figure 4, C and D, are simulated detachment assay experiments that show how increasing the expression or affinity of bonds can shift the predicted adhesion curve. Additionally, these panels demonstrate the model sensitivity to bond expression and affinity.

Solution optimization.

To determine the optimal model parameters to fit the experimentally obtained adhesion data the sum of the squared errors (SSE) between theoretical, AC_th and experimental data AC_ex was minimized. Equation 7 is the squared error (SE) between the theoretical and experimental counts of adhesive cells.

$$\mathrm{S}{\mathrm{E}}_{\mathrm{\tau }}={\left(\mathrm{A}{\mathrm{C}}_{\mathrm{t}\mathrm{h}}-\mathrm{A}{\mathrm{C}}_{\mathrm{e}\mathrm{x}}\right)}^2$$ (7)

Because the relationship between τ and position within the parallel plate flow chamber was nonlinear, the sum of the SE was binned as a function of shear stress and normalized for n_τ the number of experimental points per bin. Equation 8 normalizes the contribution of skewed sampling to the total error function.

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}={\displaystyle \sum _{\mathrm{\tau }=1}^{14}\frac{\mathrm{S}\mathrm{S}{\mathrm{E}}_{\mathrm{\tau }}}{{\mathit{n}}_{\mathrm{\tau }}},\hspace{0.17em}}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{S}\mathrm{S}{\mathrm{E}}_{\mathrm{\tau }}={{\displaystyle \sum _i^{n_{\mathrm{\tau }}}\left(\mathrm{A}{\mathrm{C}}_{\mathrm{t}\mathrm{h}}\mathrm{-}\mathrm{A}{\mathrm{C}}_{\mathrm{e}\mathrm{x}}\right)}}^2$$ (8)

The purpose of this function was to equally weight experimental adhesion data as a function of shear stress. The weighting function was divided into 14 equal-sized bins as this was the maximum number of bins that could be generated while maintaining a nonzero number of points in each bin. This ensured the experimental data were weighted equally as a function of shear stress. For example, if many more bins were used and those containing zero data points were excluded from the weighting function, data points from low shear stress values would then be weighted more heavily as these points were oversampled relative to the high shear-stress values.

Mechanistically, the most informative portion of the adhesion curve is the transient section. The SE was weighted more heavily along the transient portion of the curve by scaling the SE by the weighting coefficient w_τ Eq. 8, the equally weighted error function, was multiplied by w_τ that was calculated (Eqs. 10–12) by taking the absolute value of the derivative of a Sigmoid curve fit to each experimental data set, yielding Eq. 9. The limits of the derivative were scaled from 1 to 6.

$$\mathrm{S}\mathrm{S}{\mathrm{E}}_{\mathrm{\tau }\mathrm{,}\mathrm{w}}={\displaystyle \sum _i^{n_{\tau }}{\mathrm{w}}_{\mathrm{\tau }}{\left(\mathrm{A}{\mathrm{C}}_{\mathrm{t}\mathrm{h}}\mathrm{-}\mathrm{A}{\mathrm{C}}_{\mathrm{e}\mathrm{x}}\right)}^2}$$ (9)

For example, the raw data was best fit to the Sigmoid curve as a function of shear stress in the form of Eq. 10 where a, b, c, and d are best fit parameters.

$$f\left(\mathrm{\tau }\right)=\frac{d}{1+e^{\mathit{c}\mathit{·}\tau -b}}+a$$ (10)

Equation 11, the derivative of Eq. 10, is:

$$f\mathrm{\prime }\left(\mathrm{\tau }\right)=-c·d\frac{e^{c·\mathrm{\tau }-b}}{{\left(1+e^{c·\mathrm{\tau }-b}\right)}^2}$$ (11)

To scale Eq. 11 from 1 to 6, weighting function becomes Eq. 12.

$${\mathrm{w}}_{\mathrm{\tau }}=5·\left|\raisebox{1ex}{$f\mathrm{\prime }\left(\mathrm{\tau }\right)$}\!\left/ \!\raisebox{-1ex}{$f\mathrm{\prime }{\left(\mathrm{\tau }\right)}_{\max }$}\right.\right|+1$$ (12)

With the combination of Eqs. 8 and 9, the final error function becomes Eq 13.

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}{\mathrm{r}}_{\mathrm{w}}={\displaystyle \sum _{\tau =1}^{14}\frac{\mathrm{S}\mathrm{S}{\mathrm{E}}_{\tau \mathrm{+}\mathrm{w}}}{n_{\tau }}}$$ (13)

Equation 13 was minimized using the genetic algorithm (GA) within the MATLAB Global Optimization Toolbox. The GA is an optimization routine that uses artificial intelligence designed to mimick biological evolution. This routine was chosen to avoid user bias by inputting a starting point. Ranges for each parameter were provided and the GA randomly generated 1,000 initial guesses. The error for each initial guess was determined (by comparison to measured data), and subsequent generations were selected based on parameter set “fitness.” The GA was run for 20 generations with 1,000 offspring in each generation. Solutions were verified visually.

Immunoblot to determine VLA4 regulation.

EPCs were isolated and cultured as described above. Cells were treated with TNF-α (1 ng/ml; PRC3015; Invitrogen) or vehicle and isolated in a membrane isolation buffer (255 mM sucrose, 1 mM EDTA, 20 mM HEPES) containing protease inhibitors (Roche Diagnostics no. 11697498001; Indianapolis, IN). Cells were lysed using a cooled glass dounce. Cell lysates were concentrated using 10-kDa membrane filtration columns (UFC901024; Milipore). Protein concentrations were quantified using the Micro BCA Protein Assay Kit (no. 2325, Thermo Fisher Scientific; Rockford, IL). Protein was loaded on a 10% polyacrylamide gel (no. 456-1034; Bio-Rad; Hercules, CA) and blotted onto a PVDF membrane. Protein standard used was the Precision Plus Protein Kaleidoscope Standards (no. 161-0375; Bio-Rad). Membranes were blocked overnight with a 10% milk nonfat dry milk (NFDM) in TBS-T (no. 170-6404XTU; Bio-Rad) solution. Membranes were then incubated overnight with the Rabbit VLA4 antibody (no. 251867, dilution 1:1,000 in 1% NFDM; Abbiotec, San Diego, CA) at 4°C. After serial washes, the membrane was incubated for 2 h with the secondary antibody (horseradish peroxidase-conjugated goat anti-rabbit, 1:1,000 in 1% NFDM; no. 170-6515, Bio-Rad) at 4°C. Immunoblots were visualized using chemiluminesence followed by autoradiography. The membrane was stained with Coomassie (Bio-Rad) to confirm proper loading and normalization. The results were quantified using MetaMorph (Molecular Devices) one-dimensional gel analysis and expressed as relative densitometry.

FACS to determine VLA4 regulation.

EPCs were isolated and cultured in the same manner as Western blot preparation. After TNF-α/vehicle treatment, cells were scraped, washed and fixed in 2% paraformaldehyde for 10 min and 37°C. Cells were permeabilized using 0.1% triton for 30 min and incubated using an anti-VLA4 antibody (cat. no. 251867; Abbiotec) according to the manufacturers recommendations. Cells were washed three times and incubated with a goat anti-rabbit Alexa-Fluor 488 2° for 60 min (Invitrogen, catalog no. A-11008), washed, and resuspended. Labeled EPCs were analyzed on an LSRII Flow Cytometer (Becton Dickinson). Each sample included 50,000 events.

RESULTS

Device construction, characterization, and validation.

To develop a device that could attach to the cell culture dish while forming a PPFC, a design similar to the VC-LFR-25 (C&L Instruments) (43) was constructed that uses a vacuum clamping system. The VC-LFR-25 is a constant shear stress PPFC (nontapered). Such devices attach to a cell culture plate through a vacuum chamber created by placing two gaskets around the perimeter of the device. When a vacuum is applied, it causes the device to adhere to the cell culture dish, forming a PPFC. The PPFC formed when the device is attached to a cell culture plate is thin (200 μm). The width of the PPFC exit is smaller than the entrance by a factor of 4 (Fig. 2). This change in PPFC geometry forces an increase in fluid velocity. As the fluid velocity increases, the fluid-induced WSS along the bottom of the PPFC increases proportionally.

The device was designed to induce a WSS gradient according to Eq. 1. However, several assumptions of Eq. 1 were not met; namely, flow between infinite parallel plates, so a CFD analysis of the fluid flow path was conducted. Steady-state CFD analyses were performed on the fluid path from 1 to 10 ml/min at 0.5 ml/min increments. The WSS from these analyses were plotted as a function of chamber position and fluid flow (Fig. 2). These data were filtered using a low-pass filter to remove high-frequency noise introduced by numerical differentiation. The filtered data were fit to a nondimensionalized polynomial where $\widehat{l}$ is normalized chamber length and $\widehat{q}$ is normalized chamber fluid flow (Eq. 14).

$${\tau }_w=f\left(\widehat{l},\widehat{q}\right)=-4.157+51.51\widehat{l}+12.0\widehat{l}\widehat{q}-132.4{\widehat{l}}^2-0.5269\widehat{l}\widehat{q}-0.0043{\widehat{q}}^2+90.4{\widehat{l}}^3+25.94{\widehat{l}}^2\widehat{q}-{0.003839\widehat{l}\widehat{q}}^2-1.127\times {10}^{-4}{\widehat{q}}^3$$ (14)

Model sensitivity.

As discussed, the mathematical model contains four parameters that can affect the predicted adhesion curves. The main parameters investigated in this study are those affecting bond expression (μ_bonds, σ_bonds) and bond affinity (γ). Because parameter sensitivity is dependent on the shear stress delivered to the cells (e.g., in Fig. 4C increasing expression from 80 to 100 at 2 dyn/cm² does not alter the predicted adhesion), the specific sensitivities were not calculated for each parameter. Instead, a demonstration of increasing both expression and affinity was conducted in Fig. 4, C and D, showing how increasing both of these parameters can shift the curve to the right in both instances. The final variable, nonspecific adhesion (α) simply shifts the curve up or down, depending on the value. For example, an α value of 15 would set a baseline adhesion of 15 cells per field. Although it is possible that there exists an adhesive mechanism that results in the adhesion curve exhibiting a relationship that is a long decay in response to shear stress rather than a simple shifting of the curve, it is unlikely that this would alter the predictions made by the mathematical model as the majority of the expression/affinity changes shifted the adhesion curves left/right as opposed to up/down.

Endothelial progenitor cell peeling/adhesion.

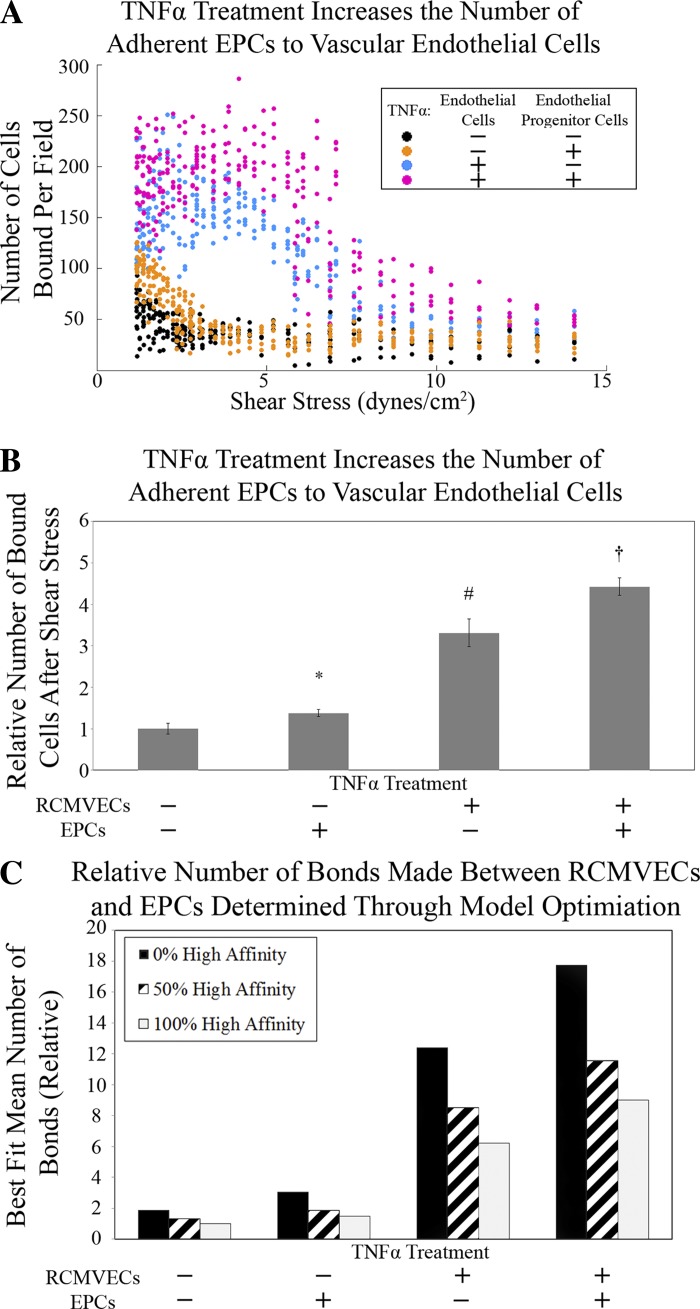
To test the effects of TNF-α on EPC adhesion, RCMVECs and EPCs were independently cultured. TNF-α or vehicle-treated EPCs were lifted, stained, and allowed to adhere statically in vitro to TNF-α or vehicle-treated RCMVECs. After allowing 2 h for EPCs to bind to RCMVECs, the PPFC (Fig. 1) was attached to this culture dish and cell culture media was pumped through the PPFC over the interacting cells to provide a force to detach bound EPCs. After 30 min of fluid flow, the PPFC was detached and a series of fluorescent images was acquired along a line bisecting the area subjected to laminar flow. The number of cells was quantified in each image as a function of chamber position. The average WSS exerted by the PPFC in each image was quantified using the CFD model. For all groups, the number of adherent cells was plotted as a function of average WSS within the image (Fig. 6A). Treatment to both EPCs and RCMVECs with TNF-α demonstrated the highest number of adherent cells, whereas treating both EPCs and RCMVECs with a vehicle had the lowest number of adherent cells (Fig. 6B). All treatment groups segregated into statistically distinct groups.

Fig. 6.

Experimental EPC/rat cardiac microvascular endothelial cells (RCMVECs) adhesion data. A: raw data from adhesion experiments. Colors represent the treatment conditions for tumor necrosis factor-α (TNF-α) treatment to RCMVECs/EPCs. Black circles, vehicle/vehicle; orange circles, vehicle/TNF-α; blue circles, TNF-α/vehicle; pink circles, TNF-α/TNF-α. B: adhesion data from A integrated with respect to shear stress and averaged (6 runs per group, error bars indicate means ± SD). A two-way ANOVA demonstrated that all four groups were statistically distinct (P < 0.05). *TNF-α treatment to RCMVECs increases adhesion with respect to no treatment. #TNF-α treatment to EPCs increases adhesion with respect to no treatment or TNF-α treatment only to RCMVECs. †TNF-α treatment to EPCs and RCMVECs increases adhesion with respect to no treatment or single TNF-α treatment to RCMVECs or EPCs. C: average bond number expression (relative to 100% high affinity activation, vehicle/vehicle-treated EPC/RCMVEC group) in each experimental group determined by a best-fit mathematical model for low affinity, high affinity, and a 50/50 low/high affinity population.

Optimized solutions.

The data in Fig. 6A are the number of cells per image that were able to resist detachment from fluid shear stress. Figure 6B represents the total number of adherent cells following shear stress from each treatment group. With Eq. 6, one can determine the minimum total bond force required for EPCs to maintain adhesion to RCMVECs. Under the assumption that bonds can be in a “high affinity” or “low affinity” state, bond expression could vary depending on the number of bonds that are in each state. The biomechanics of this assay can determine the minimum forces required to maintain adhesion under laminar flow, but because an increase in bond expression or affinity can increase adhesion, the in vitro experiment cannot distinguish increases in adhesion as a result of these two distinct mechanisms. Therefore, optimized solutions were determined indicating the relative bond expression required to best model the experimental data under the condition that the percentage of bonds selected from the high affinity state was fixed at 0%, 50%, or 100%. In each solution the number of bonds created between each EPC/RCMVEC interaction was allowed to vary. The probability of the number of bonds created in each interaction was defined by a Gaussian probability distribution function. The optimized mean number of bonds required to best fit the model to the experimental data was plotted in Fig. 6C for each treatment group. If numbers generated in the simulation became negative, the portion of the distribution that was negative was discarded and the simulation continued with the skewed distribution. It should be noted that this was the case for simulations that were analyzing experimental groups without TNF-α treatment to endothelial cells. This treatment was responsible for the largest increase in adhesion between the cell types.

Simulations.

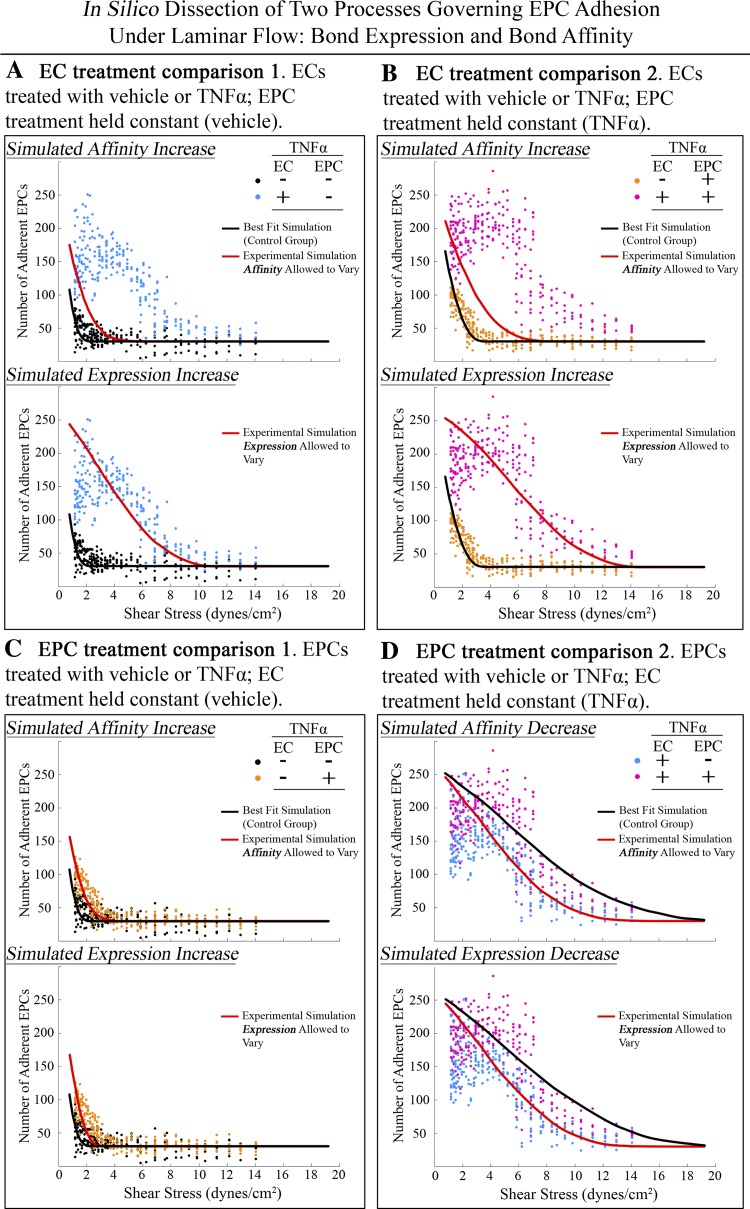
TNF-α treatment can increase the expression and/or affinity of integrins (40, 42). To separate these processes in silico, the optimized bond number (expression) results from Fig. 6C were used as controls for experiments run in silico (Fig. 7) to test two hypotheses representing potential mechanisms of increased EPC adhesion in response to TNF-α treatment. Hypothesis 1 was that TNF-α treatment increased adhesion solely by shifting bond affinity from a low to high state. Hypothesis 2 was that TNF-α treatment increased adhesion solely by increasing the relative expression of bonds. To conduct these experiments in silico, experimental data sets were compared two at a time to isolate TNF-α treatment to a single cell type. For each simulation, one experimentally measured group was assigned to be the “control” and the other was assigned to be the “experimental” group. The parameter set for each “control” group was determined by fitting the mathematical model to the experimental data, obtaining an optimum parameter set for each experimental group. Because direct measurement of the affinity distributions of bonds on these cell types was outside the scope of this study, it was assumed the vehicle/vehicle-treated group would have a high affinity activation of 0% and the TNF-α/TNF-α-treated group would have a high affinity activation of 100%. These two parameter set were used as controls in the simulations (Fig. 6C).

Fig. 7.

Monte Carlo analysis of experimental EPC/RCMVEC adhesion results. Two data sets were compared for each simulation to determine the mechanism of TNF-α increased adhesion in endothelial cells (A and B) or endothelial progenitor cells (C and D). Symbols are the raw data replotted from Fig. 5; lines represent mathematical model fit to experimental data under conditions described. For each cell type, two hypotheses were tested. Hypothesis 1 was that a shift from low to high affinity bonds could adequately explain the increased adhesion observed from TNF-α treatment. Hypothesis 2 was that an increase in the number of bonds (expression) could adequately explain the increased adhesion observed from TNF-α treatment. In A the vehicle/vehicle-treated EPC/RCMVEC group was compared with the vehicle/TNF-α-treated group. The best-fit result from the vehicle/vehicle group was obtained from Fig. 3C and only the affinity activation parameter (γ) was allowed to vary to adequately fit the data in from the vehicle/TNF-α group. The model was not able to adequately fit the data, rejecting hypothesis 1. Hypothesis 2 was tested by only allowing the bond expression parameters to vary to adequately fit the data. The model was able to adequately fit the data, supporting hypothesis 2 and rejecting hypothesis 1 for TNF-α treatment of RCMVECs. The same analysis and conclusion was drawn in B when comparing the TNF-α/vehicle group with the TNF-α/TNF-α group. Both hypotheses were tested in C to determine the mechanism of increased adhesion by TNF-α treatment to endothelial progenitor cells. When the vehicle/vehicle and TNF-α/vehicle groups are compared, support for both hypotheses was found. By only allowing bond expression of affinity to increase both simulations were able to adequately fit the data. This mechanism was also tested in D by comparing the TNF-α/TNF-α group with the vehicle/TNF-α group. It was assumed that treating both cell types with TNF-α would only create high affinity bonds so the best-fit parameters used as the control set was the 100% high affinity activation set (Fig. 3C). To allow these data to fit the vehicle/TNF-α data set only the affinity or expression parameters were allowed to decrease. Support for both hypotheses was found.

Figure 7, A and B, investigates potential mechanisms of TNF-α treatment to RCMVECs. To test hypothesis 1, that TNF-α treatment to RCMVECs can increase EPC adhesion solely by increasing the bond affinity, the optimum solution obtained for the Monte Carlo simulation of the vehicle/vehicle-treated EPC/RCMVEC data set at 0% high affinity activation (Fig. 6C) was fit to the vehicle/TNF-α-treated EPC/RCMVEC data set by only allowing the percentage of high affinity bonds to increase (γ). This simulation was not able to adequately fit the data as the best-fit solution saturated the γ parameter at 100% (Fig. 7A) rejecting the hypothesis that TNF-α treatment to RCMVECs increased EPC adhesion solely by increasing the affinity of existing bonds. Hypothesis 2, that TNF-α treatment to RCMVECs increased EPC adhesion by increasing the number of bonds between the cell types was tested (Fig. 7A) and confirmed, demonstrating that upregulation of bond expression is sufficient to explain increased adhesion of EPCs when treating RCMVECs with TNF-α. In Fig. 7B, a similar analysis was conducted to further investigate the mechanism of TNF-α to RCMVECs comparing the TNF-α/vehicle and the TNF-α/TNF-α sets. After simulations were conducted as in Fig. 7A, the same conclusions were reached. These results suggest that TNF-α treatment to endothelial cells increases adhesion of EPCs through upregulation of bond expression, which is consistent with other published data in the literature (20, 38).

Figure 7, C and D, investigates potential mechanisms of TNF-α treatment to EPCs. To test hypothesis 1, that TNF-α treatment to EPCs increases the adhesion of EPCs to RCMVECs solely by increasing the affinity of existing bonds, the optimum solution obtained for the Monte Carlo simulation of the vehicle/vehicle-treated EPC/RCMVEC data set at 0% affinity was fit to the TNF-α/vehicle data set by only allowing the affinity parameter to increase. This hypothesis was confirmed when the solution obtained at 0% high affinity activation for the vehicle/vehicle-treated EPC/RCMVEC data set was fit to the TNF-α/vehicle-treated EPC/RCMVEC data set by increasing the high affinity parameter from 0% to 59% (Fig. 7C). This hypothesis was further supported when the TNF-α/TNF-α-treated EPC/RCMVEC data at 100% high affinity activation was fit to the vehicle/TNF-α-treated EPC/RCMVEC data set by only allowing the percentage of high affinity bonds to decrease to the low affinity state. The simulation was able to fit the data by decreasing the high affinity parameter from 100% to 35% further supporting hypothesis 1 (Fig. 7D) that TNF-α treatment to EPCs increases the adhesion of EPCs to RCMVECs solely by increasing the affinity of existing bonds. Hypothesis 2 was also tested in Fig. 7, C and D, that increased adhesion from TNF-α treatment to EPCs is mediated through an increase in the expression of bonds. In Fig. 7, C and D, the model was able to fit the data so this hypothesis was also supported. These results showed that the observed increase could be mediated through either an increase in bond expression or an increase in bond affinity, warranting additional analysis. Optimally solved model parameters and best-fit weighted errors are listed in Table 1. Ranges of independent variables within simulations were obtained by performing a bootstrapping analysis of the experimental data. Ranges reported in Table 1 are the highest and lowest parameter values obtained from doing this analysis. It should also be noted that when performing these simulations, an α = 30 was used for all simulations to only allow variables to change in the simulation that specifically related to bond expression or affinity. This value was used as initial best-fit simulations for all data sets averaged to ∼30, thus it was reasonable to use this value for simulations performed in Fig. 7.

Table 1.

Optimized parameter fits

Model Parameter	μbonds	σbonds	γ	α	Error	R2 Value
A: EC treatment comparison 1
Best fit (to control data set)	3.1 [2.0–4.6]	15.1 [13.4–19.1]	0%	30 [27.5–31.4]	5.7 × 103	0.8121
Affinity experimental simulation	3.1	15.1	100% [100–100%]	30 [26.9–36.9]	1.5 × 105	0.1618
Expression experimental simulation	57.1 [51.9–74.4]	70.3 [65.3–87.1]	0%	30 [28.1–35.8]	5.1 × 104	0.8192
B: EC treatment comparison 2
Best fit (to control data set)	1 [1–4.9]	27.8 [22.0–30.1]	0%	30 [29.4–34.2]	7.3 × 103	0.8524
Affinity experimental simulation	1	27.8	100% [100–100%]	30 [29.0–41.4]	2.5 × 105	0.0766
Expression experimental simulation	105 [91.5–121.6]	80.4 [71.3–92.7]	0%	30 [28.5–43.2]	9.0 × 104	0.7730
C: EPC treatment comparison 1
Best fit (to control data set)	3.1 [2.0–4.6]	15.1 [13.4–19.1]	0%	30 [27.5–31.4]	5.7 × 103	0.8121
Affinity experimental simulation	3.1	15.1	59% [51–64%]	30 [26.0–33.5]	5.6 × 103	0.8135
Expression experimental simulation	14.6 [12.1–17.3]	16.9 [15.1–24.3]	0%	30 [25.1–34.8]	5.6 × 103	0.7037
D: EPC treatment comparison 2
Best fit (to control data set)	61.3 [55.1–74.4]	55.6 [51.0–62.6]	100%	30 [28.1.–42.3]	7.5 × 104	0.9380
Affinity experimental simulation	61.3	55.6	35% [28–40%]	30 [28.9–41.4]	1.2 × 105	0.7368
Expression experimental simulation	35.8 [29.0–40.9]	39.4 [33.4–45.9]	100%	30 [29.5–45.2]	1.0 × 105	0.7872

Best-fit parameter sets were solved for in Fig. 6.

EC, endothelial cells.

Simulations were conducted to determine whether increased adhesion could be explained through tumor necrosis factor-α (TNF-α)-mediated affinity or expression increase. In comparisons A and B, it was found that only increased expression could explain the increased adhesion as the affinity parameter maxed out at 100% and did not adequately fit the data. In comparisons C and D both increased expression and affinity could explain the increased adhesion as the error generated in each simulation was similar. Bolded numbers indicate parameters that were allowed to change in the simulation (with respect to the “best-fit” control set). Results from each simulation are plotted in Fig. 7 See text for Greek symbol definitions.

Analysis of VLA4Expression using FACS and immunoblot.

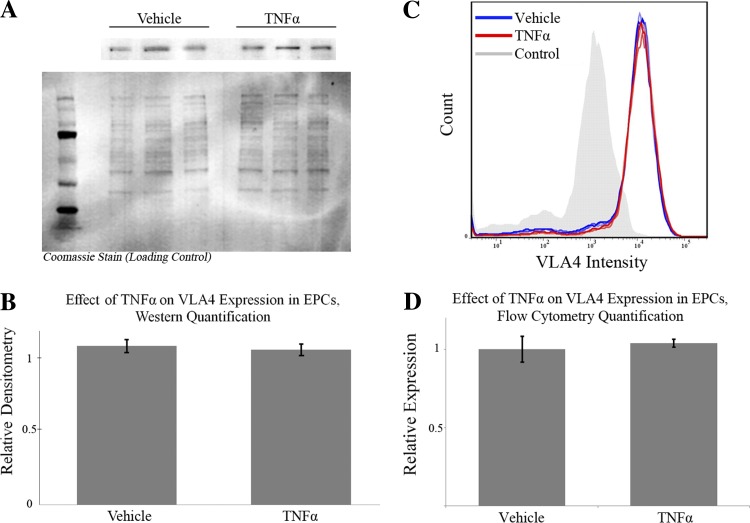
Simulations demonstrated that TNF-α treatment of EPCs could increase adhesion to RCMVECs either by increasing bond expression or affinity. To differentiate between these two remaining explanations for the experimental data, VLA4 expression was measured using an immunoblot and fluorescence-activated cell sorting (FACS) to test the hypothesis that increased integrin expression was the mechanism of increased TNF-α-stimulated adhesion. It has been demonstrated that EPC adhesion to endothelial cells is mediated through the VCAM1 on endothelial cells and VLA4 on EPCs (11). Quantification of VLA4 expression via Western blot analysis and FACS demonstrated no differential regulation of VLA4 in TNF-α-treated EPCs, suggesting that the mechanism of increased adhesion of EPCs to RCMVECs by TNF-α treatment is mediated by an increase in the affinity of VLA4 for VCAM1 (Fig. 8).

Fig. 8.

Immunoblot and fluorescence-activated cell sorting (FACS) analysis of very-late antigen 4 (VLA4) in EPCs. Differential expression of VLA4 in response to TNF-α was quantified using Western blot analysis (A) relative to the membrane Coomassie stain. Ladder lane is the Precision Plus Protein Kaleidoscope Standard. B: an unpaired t-test could not refute the null hypothesis (P = 0.54) rejecting the hypothesis that an acute, low dose of TNF-α differentially regulates VLA4 in EPCs (error bars indicate means ± SD). C: differential expression of VLA4 in response to TNF-α was quantified using FACS. EPCs treated with TNF-α/vehicle demonstrated nearly identical fluorescent histograms. D: when quantified, an unpaired t-test could not refute the null hypothesis (P = 0.47) rejecting the hypothesis that an acute, low dose of TNF-α differentially regulates VLA4 in EPCs (error bars indicate means ± SD).

DISCUSSION

This study described the construction, characterization, and validation of a PPFC designed to induce a spatial shear-stress gradient on cultured cells. The PPFC was used to conduct a detachment study that measured the adhesive forces created with integrin bonds between EPCs and RCMVECs. The results show that TNF-α stimulation of EPCs and RCMVECs causes an increase in adhesion between EPCs/RCMVECs. A Monte Carlo mathematical model was created to estimate the fraction of EPCs that would remain adherent to endothelial cells following a period of laminar flow based on the number of bonds made between the two cell types and their relative affinities representing the VCAM1/VLA4 interaction. Monte Carlo simulations demonstrated that the mechanism of increased adhesion by TNF-α treatment to RCMVECs is mediated through an upregulation of the expression of bonds (VCAM1) as opposed to an increase in affinity. Monte Carlo simulations demonstrated increased adhesion by TNF-α treatment to EPCs could be adequately explained through an increase in bond affinity or expression (VLA4), demonstrating the need for further analysis. Using an immunoblot, the expression of VLA4 was measured in response to TNF-α, showing no differential regulation and supporting the hypothesis that TNF-α treatment to EPCs is increased through an increase in VLA4 affinity.

Differential detachment in response to hydrodynamic flow is a technique to measure bond formation between cells where the mechanism of cellular adhesion is unknown.

Several detachment assays exist to measure the strength of cellular adhesion in vitro. The main categories of adhesion assays are 1) washing assays, 2) micromanipulation assays, 3) centrifugation assays, and 4) microfluidic assays in a PPFC (17). Many different PPFC designs have been used in adhesion assays. This study, to our knowledge is the first study where the detachment force between EPCs and ECs was measured in a variable shear-stress microfluidic assay.

Previous studies have investigated the ability of cells to bind to a biologically relevant substrate. Using a variable shear-stress PPFC, Usami et al. (53) conducted a detachment study on activated platelets attached to a fibrinogen-coated glass slide demonstrating a linear relationship between platelet detachment and shear stress finding that 50% of platelets had detached by 40 dyn/cm². Garcia et al. (16) conducted a detachment assay of osteosarcoma cells to cell culture plates demonstrating 50% of initially seeded cells detached at ∼60 dyn/cm². Both of the measurements in these studies are considerably higher than any of the values obtained in the current study; however, it was expected that adhesion between fibronectin and osteosarcoma cells as well as platelets and fibrinogen would be greater than the adhesive forces between EPCs and RCMVECs for two reasons. First, cell culture plates coated homogeneously with fibronectin/fibrinogen represent the most ideal surface to induce maximum adhesion resisting detachment under very high levels of shear stress. Second, osteosarcoma cells and activated platelets once bound are nonspherical. The torque induced from laminar flow on the cell will be greatly diminished if the cell is flattened from a spherical geometry. Because of this, the 40–60 dyn/cm² range should be considered an “upper bound” for detachment studies.

Lawrence and Springer (33) measured the shear stress required to detach neutrophils from a surface homogenously coated with a variety of surface receptors in vitro. They found that detachment occurred between 0.5 and 2.5 dyn/cm², a result much more consistent with that of this study (33). It has been hypothesized that EPCs leave the circulation by binding in the postcapillary venules as is the primary binding site for leukocytes (18). In the postcapillary venules in vivo, fluid pulsatility is low and shear stresses have been estimated to range from 2.5 to 10.0 dyn/cm², a range much more relevant to this study (32). In the present study 50% of EPCs remained attached at 7.5 dyn/cm² when endothelial cells were treated with TNF-α, suggesting the inflammatory processes can decrease the ability of circulating blood to detach bound cells. It should be noted that allowing cells to bind in static culture before performing an in vitro detachment assay will determine an artificially high detachment force compared with cells binding in conditions of dynamic flow. Cells that have the time to bind statically in vitro are likely to form more bonds that an interaction taking place statically, explaining why some of the cells in this study were able to resist detachment at relatively high shear-stress values. In vivo, it has been demonstrated that leukocytes quickly bind with high affinity after being subjected to varying shear stress associated with conjoining and bifurcating segments (23). In this study, cells were given a long time relative to in vivo conditions to bind in vitro in the absence of flow. It is likely that the binding interaction takes longer to complete in vitro due to the absence of varying stresses that occur with dynamic flow. The current studies demonstrated that the binding kinetics of the EPC/EC interaction is comparable to that of other leukocytes under similar conditions in vitro (32, 33). Follow-up studies should address whether the EPC/EC interaction in vivo is weaker than other leukocyte/EC interactions and whether or not the same mechanisms are responsible for binding in vitro versus in vivo. Results from this investigation could provide insight as to the mechanism behind clinically impaired EPC-mediated repair.

EPCs vary functionally based on the isolation method and lineage of origin.

After the discovery of EPCs in 1997 (4), many methods of EPC collection and culture have yielded cells of similar form and function. There exist many classifications and subclassifications of EPCs based on location of cell fraction, cellular lineage, and associated phenotypes. EPCs have been isolated from the bone marrow, blood mononuclear fraction, and vascular wall (5, 24, 51, 59). EPCs isolated from the bone marrow have been derived from a hematopoietic lineage, whereas EPCs isolated from the vascular wall are thought to have been derived from the periphery, perhaps another nonhematopoietic stem cell (2).

A major difference in these two types of EPCs is the difference in expression of the CD45 marker, otherwise known as leukocyte common antigen. Expression of CD45 is found on EPCs isolated from the bone marrow, but expression of CD45 on circulating EPCs (otherwise known as “late EPCs”) is typically reported to be “dim” and expression of CD45 is not present in EPCs that are native to the vascular walls (54). The EPC population in this study was isolated from the bone marrow of the rat. On the basis of the review by Hirschi et al. (21), this population is classified as “early EPCs.” Controversially, EPCs with CD45 expression have been reported as not being EPCs, but rather a subclassification of HSC. This is a difficult but important distinction to make because the phenotypes of the different EPC subclassifications vary greatly. Hoffmann et al. (22) demonstrated that early EPCs do not form tube-like structures on a Matrigel surface, a phenotype associated with HSCs. Karcher et al. (28) demonstrated early EPCs induce angiogenesis in skeletal muscle, a phenotype associated with EPCs, but not HSCs. The current study demonstrated that the adhesion of early EPCs are detached under similar levels of shear stress as are neutrophils (15), a phenotype further associating early EPCs with HSCs and HSC derivatives.

For this study, it was hypothesized that TNF-α treatment of early EPCs would increase adhesion to vascular endothelial cells, similar to other HSC-derived cells. For example, TNF-α has been shown to increase adhesion of neutrophils, monocytes, and mesenchymal stem cells to the vascular endothelium (29, 39). Additionally, TNF-α treatment to endothelial cells has been demonstrated to increase the number of adherent EPCs in vitro (37, 52). Therefore, it was expected that TNF-α would increase the adhesion of early EPCs to endothelial cells, increasing the known characteristics shared with HSCs and HSC-derived cells.

TNF-α signaling is complex; effects are dependent on cell type, dosage, and timing.

TNF-α is primarily produced by macrophages and regulates immune cell function. For example, in some cell types, 10 ng/ml TNF-α will induce apoptosis after 12 h, whereas in other types, it will induce maximal adhesion (48). TNF-α can signal through two receptors, p55 and p75 (30). Signaling through p55 induces apoptosis through the caspase pathway, whereas signaling through p75 induces a variety of functions including survival, inflammation, adhesion, migration, and angiogenesis (7, 26, 34, 45). In this study, it is likely that the predicted switch from a low to high affinity VLA4 integrin is mediated by TNF-α signaling through the p75 receptor as p75 signaling leads to gene transcription through the NF-kB pathway.

In summary, this study describes the development and validation of an in vitro detachment assay designed to measure the adhesive forces between EPCs and vascular endothelial cells. By using a mechanistic Monte Carlo-based simulation, it was determined that TNF-α-induced adhesion between EPCs/RCMVECs in vitro is mediated through upregulation of VCAM1 expression in RCMVECs and a shift from low to high VLA4 binding affinity in EPCs. Regulation of bonds in this manner represents the optimal mechanism for recruiting EPCs to an ischemic site in vivo to induce reparative angiogenesis. An ischemic site in a proinflammatory state subjected to acutely high TNF-α levels would upregulate integrins to recruit regenerative EPCs from the circulation. However, the exposure of a circulating EPC to a proinflammatory environment would be much more brief than the exposure of endothelial cells, so a conformational shift form a low to high affinity bond would represent the optimal mechanism to increase EPC recruitment out of the blood into areas of ischemia. It is important to note that a key difference between this study and behavior of cells in vivo is that in vivo, cells do not bind to endothelial cells in a static environment (in absence of flow). Follow-up studies should investigate how TNF-α affects the ability of EPCs to bind to the endothelium in the presence of laminar fluid flow. Additional consideration should be paid to whether or not the endothelial cells have been aligned due to the influence of laminar fluid flow. When comparing TNF-α/vehicle-treated EPCs adherent with TNF-α-treated endothelial cells, it appears that the model does not faithfully reproduce a Sigmoid-shaped curve in the TNF-α-treated EPC group. We hypothesize that the low-dose TNF-α treatment induces expression of protective genes preventing apoptosis associated with harsh lifting conditions. Cells that undergo apoptosis will not bind, effectively decreasing the maximum plateau at low shear stresses. Subsequent models will be able to further characterize and investigate this phenotype.

It has been hypothesized that early EPCs are mobilized out of the bone marrow into the periphery to repair areas of ischemia (41). Many groups have studied the stimuli that increase and decrease the number of peripheral EPCs. The rationale behind studying EPC mobilization is that in response to an event, EPCs mobilize out of the bone marrow, enter the circulation, and migrate to areas of ischemia. The implications of this study are most directly applicable to the migration stage. After migration, EPCs bind and engraft into a target tissue ultimately inducing repair by a direct or indirect mechanism (although this has been debated) (27, 35). Acute events such as myocardial infarction, stroke, and dilated cardiomyopathy increase the number of peripheral circulating EPCs (a common feature of all of these diseases is production of TNF-α) (19, 60, 61). In these studies, patients with increased levels of peripheral EPCs typically exhibited better outcomes than patients with a lower number of peripheral EPCs. Therefore, we hypothesize that TNF-α generation associated with organ damage could potentially involved in the physiology of tissue regeneration. More specifically, we hypothesize damaged organs secrete TNF-α to pull circulating EPCs from the circulation into damaged tissue. The implications of this proposed mechanism could have important clinical ramifications as most antiinflammatory agents reduce TNF-α production, a process that could be detrimental to EPC adhesion and engraftment (1).

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant HL082798 and a gift from the Kern Family Foundation. A. Prisco was supported in part by an MSTP Institutional Training Fellowship from National Institute of General Medical Sciences (T32 GM80202).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.R.P., M.R.P., B.E.C., and A.S.G. conception and design of research; A.R.P. performed experiments; A.R.P., M.R.P., and A.S.G. analyzed data; A.R.P., B.E.C., and A.S.G. interpreted results of experiments; A.R.P. prepared figures; A.R.P. drafted manuscript; A.R.P., M.R.P., B.E.C., and A.S.G. edited and revised manuscript; A.R.P., M.R.P., B.E.C., and A.S.G. approved final version of manuscript.