Evaluating surrogate endpoints, prognostic markers, and predictive markers — some simple themes

Abstract

Background

A surrogate endpoint is an endpoint observed earlier than the true endpoint (a health outcome) that is used to draw conclusions about the effect of treatment on the unobserved true endpoint. A prognostic marker is a marker for predicting the risk of an event given a control treatment; it informs treatment decisions when there is information on anticipated benefits and harms of a new treatment applied to persons at high risk. A predictive marker is a marker for predicting the effect of treatment on outcome in a subgroup of patients or study participants; it provides more rigorous information for treatment selection than a prognostic marker when it is based on estimated treatment effects in a randomized trial.

Methods

We organized our discussion around a different theme for each topic.

Results

“Fundamentally an extrapolation” refers to the non-statistical considerations and assumptions needed when using surrogate endpoints to evaluate a new treatment. “Decision analysis to the rescue” refers to use the use of decision analysis to evaluate an additional prognostic marker because it is not possible to choose between purely statistical measures of marker performance. “The appeal of simplicity” refers to a straightforward and efficient use of a single randomized trial to evaluate overall treatment effect and treatment effect within subgroups using predictive markers.

Conclusion

The simple themes provide a general guideline for evaluation of surrogate endpoints, prognostic markers, and predictive markers.

Introduction

Providing an overview of methods for evaluating surrogate endpoints, prognostic markers, and predictive markers is a challenging because of the large number of approaches. Rather than trying to provide a comprehensive exposition, we focus on a particular theme for the evaluation of each endpoint or biomarker, with examples based on our work in these areas. Each endpoint or biomarker involves particular goals and data that motivate its method of evaluation. Therefore, we present three sections addressing these distinct uses of biomarkers.

Surrogate endpoints: fundamentally an extrapolation

A surrogate endpoint is an endpoint that is (i) observed earlier than an unobserved true endpoint, which is the health outcome of interest and (ii) is used to draw conclusions about the effect of a new treatment on the unobserved true endpoint. The primary goal of using surrogate endpoints is to shorten the trial duration, eliminating follow-up for the true endpoint. Our theme is that the evaluation of treatment using surrogate endpoints fundamentally involves extrapolation to the unobserved true endpoint. This theme has two key consequences. First, assumptions needed for this extrapolation must be considered. In this article we specify these assumptions. Second, it is important to consider how the conclusions based on the surrogate endpoint will be used. More confidence in the extrapolation is needed for treatment decisions than if the decision is simply whether or not to implement a trial with a true endpoint.

Surrogate endpoint versus auxiliary variable

Sometimes the terms “surrogate endpoint” and “auxiliary variable” are used interchangeably but it helps to make a distinction. Both are observed before the true endpoint and used to draw conclusions about treatment effect on the true endpoint. However, with a surrogate endpoint, the true endpoint is unobserved among all persons, but, with an auxiliary variable, the true endpoint is unobserved in some (but not all) participants. Thus, with auxiliary variables there is no shortening of the duration of the trial because follow-up to true endpoint is needed in some participants. Instead, the goal of using an auxiliary variable is to either increase efficiency or remove bias when estimating treatment effect. If the missing-data mechanism for true endpoint depends only on baseline variables, adjusting for the auxiliary variable can increase the efficiency of estimates of treatment effect.^1,2 If the missing-data mechanism for true endpoint depends on the auxiliary variable (and possibly baseline variables), adjusting for an auxiliary variable can avoid bias in estimating the effect of treatment on the true endpoint.³

Surrogate endpoint trial without relevant historical trials

We first consider the situation of a new trial with a surrogate endpoint (and no observed true endpoint) with no historical trials of treatments involving the same surrogate and true endpoints as in the new trial. Such a situation often arises in studies of new agents for cancer prevention. For example, before considering a definitive lung cancer trial (which can involve perhaps 30,000 persons and last 5 years⁴) to evaluate a new chemoprevention agent, investigators often evaluate a new agent in a small trial (for example a trial of 112 persons with a surrogate endpoint of bronchial dysplasia at only 6 months).⁵

Absent relevant historical trials, there are no data for predicting treatment effect on true endpoint, and the basic analysis involves hypothesis testing for extrapolation. The underlying premise is that rejecting a null hypothesis of no treatment effect on the surrogate endpoint implies rejecting the null hypothesis of no treatment effect on the true endpoint. ^6,7 In a landmark paper, Prentice introduced a set of criteria for valid hypothesis testing extrapolation.⁸ The key criterion, later called the Prentice Criterion, is that the probability of the true endpoint given the surrogate endpoint does not depend on randomization group.⁸ In other words, the Prentice Criterion says that treatment affects true endpoint only by influencing the surrogate endpoint, which then influences the true endpoint – a very high bar requiring an in-depth understanding of biological mechanism. With a binary surrogate endpoint, an additional criterion needed for hypothesis testing extrapolation is an association between the surrogate and true endpoints⁹ – which is easily satisfied. If the sample size of the surrogate endpoint and true endpoint trials are similar, a small deviation from the Prentice Criterion will not seriously affect the hypothesis testing extrapolation. However, if the size of the surrogate endpoint trial is much smaller than that of the true endpoint trial, hypothesis testing extrapolation is sensitive to small deviations from the Prentice Criterion.^8,9

An alternative to the Prentice Criterion for hypothesis testing extrapolation is the Principal Stratification Criterion,⁶ based on a principal stratification model for surrogate endpoints.¹⁰ With binary surrogate endpoints, the principal strata are the pairs (surrogate endpoint if randomized to group 0, surrogate endpoint if randomized to group 1), which take values (0,0), (0,1), (1,0), and (1,1). The appeal of principal stratification is that the surrogate endpoint becomes a baseline variable, thereby avoiding post-randomization confounding; however the “price” is assumptions needed to estimate parameters. The Principal Stratification Criterion, which is analogous to the two standard assumptions for principal stratification with all-or-none compliance^11-13, states (i) no principal stratum (0,1) and (ii) the probability of true endpoint given principal stratum (0,0) or (1,1) does not depend on the randomization group. As with the Prentice Criterion, the Principal Stratification Criterion makes assumptions about biological mechanism requiring in-depth knowledge not likely to be present. Also, hypothesis testing extrapolation is sensitive to small deviations from the Principal Stratification Criterion in small trials.⁶

Surrogate endpoint trial with relevant historical trials

Sometimes investigators have data from historical trials with both surrogate and true endpoints, where the historical trials and new trial each involve different treatments, but all treatments are thought to affect outcomes through similar biological mechanisms. Examples include (i) 10 historical trials of early colon cancer with a surrogate endpoint of cancer recurrence within three years and a true endpoint of overall mortality by five years¹⁴, (ii) 10 randomized trials for advanced colorectal cancer with a surrogate endpoint of cancer regression by 6 months and a true endpoint of overall mortality by 12 months,¹⁵ and (iii) 27 randomized trials of advanced colorectal cancer with a surrogate endpoint of tumor response status at 3-6 months and a true endpoint of overall mortality by 12 months.¹⁶

To analyze these data, a researcher could perform hypothesis-testing extrapolation and check the Prentice Criterion and the Principal Stratification Criterion using historical trials. Here, we discuss a more informative extrapolation involving the prediction of treatment effect on true endpoint in a new trial using a successive leave-one-out analysis.¹⁷ We use as the outcome the difference in survival at a pre-specified time. Use of an absolute difference avoids assumptions associated with hazard ratios¹⁸ and is often easier for clinicians to interpret than a ratio.^19-22 Let true and surr denote binary true and surrogate endpoints of survival to a given time. We computed survival probabilities using Kaplan-Meier estimates.

Let pr(surr | group)_NEW denote the estimate of pr(surr | group) in the new trial, and let pr(true | surr, group)_HIST denote the estimate of pr(true| surr, group) based on historical trials. Let pr(true| group)_NEW denote the predicted estimate of pr(true| group) in the new trial. The effect of treatment on true endpoint in the new trial based on the fitted model and the surrogate endpoints in the new trial is

$$\left(modelresult\right)=pr{(true\mid group1)}_{NEW}-pr{(true\mid group0)}_{NEW}.$$ (1)

The mixture model estimate, which does not require the Prentice Criterion²³, is

$$pr{(true\mid group)}_{NEW}-{\Sigma }_{surr}pr{(true\mid surr,group)}_{HIST}pr{(surr\mid group)}_{NEW}.$$ (2)

A principal stratification estimate has the form

$$pr{(true\mid group)}_{NEW}={\Sigma }_{ps}pr{(true\mid ps,group)}_{HIST}pr{\left(ps\right)}_{NEW},$$ (3)

and invokes the assumptions of the Principal Stratification Criterion. An estimate using a random effects linear model^24,25 has the form

$$\{pr{(true\mid group1)}_{NEW},pr{(true\mid group0)}_{NEW}\}=f_{HIST}\left(\{pr{(surr\mid group1)}_{NEW},pr{(surr\mid group0)}_{NEW}\}\right),$$ (4)

where f_HIST( ) involves a product of variance component matrices. An estimate under a proportional difference model is

$$pr{(true\mid group1)}_{NEW}-pr{(true\mid group0)}_{NEW}=k_{HIST}\{pr{(surr\mid group1)}_{NEW}-pr{(surr\mid group0)}_{NEW}\},$$ (5)

where k_HIST is estimated from weighted least squares.

A major analytical challenge is the “labeling dilemma,” namely deciding whether to label a randomization group as either group 0 or group 1, which is particularly problematic when a treatment is a control in one trial and experimental in another trial. Among the aforementioned models, only the proportional difference model is invariant to the choice of labels.^26,27

For historical trial j, let (model result)_j denote the model result computed using the surrogate endpoint in trial j and a model fit to the remaining historical trials. Let (observed result)_j denote the estimated effect of treatment on the true endpoint based on data on the true endpoints in trial j. Let (extrapolation error) _j = (model result)_j – (observed result)_j. In this framework the predicted result for a new trial is

$${\left(predictedresult\right)}_{NEW}={\left(modelresult\right)}_{NEW}+mean{\left(extrapolationerror\right)}_j,$$ (6)

$$var{\left(predictedresult\right)}_{NEW}=var{\left(modelresult\right)}_{NEW}+var{\left(extrapolationerror\right)}_j,$$ (7)

where var(model result) is a function of the survival probabilities.

A summary of model performance is the standard error multiplier which equals se(predicted result) _j /se(observed result)_j averaged over the left-out trials. A standard error multiplier of k says that surrogate endpoint analysis requires a sample size k² times that of the observed endpoint analysis to achieve same the precision as the true endpoint analysis. For the three data sets, the standard error multipliers were most reasonable for the mixture, principal stratification, and proportional difference models (Table 1).

Table 1.

Comparison of standard error multipliers. Results from Baker, Sargent, Buyse, et al.¹⁷

Data set	Mixture model	Principal stratification model	Linear random effects	Proportional difference
early colorectal cancer: 10 trials	1.24	1.21	1.39	1.35
advanced colorectal cancer: 10 trials	1.36	1.34	1.81	1.33
advanced colorectal cancer: 27 trials	1.51	1.50	2.06	1.25

Other approaches to surrogate endpoint analysis

Perhaps the most commonly used surrogate endpoint analysis involves the aforementioned random effects linear model,^24,25 but not in a leave-one-out analysis. With this approach, a summary measure of model performance in historical trials is R²_Trial which equals one minus the ratio of the estimated variances of the observed result adjusting versus not adjusting for the surrogate endpoint. A problem with using R²_Trial is deciding on the value that would be sufficient for validation.²⁸ A more useful measure, that can be used for extrapolation, is the surrogate threshold effect, which is the minimum treatment effect on the surrogate endpoint to yield a non-zero treatment effect on the true endpoint.²⁸

Extrapolation issues

Importantly, regardless of the analytic approach and the performance of the surrogate endpoint in historical trials, drawing conclusions in a new trial is still fundamentally an extrapolation that involves the following issues: ^6,7,29

• (1)whether the treatment in the new trial and the treatments in the historical trials affect outcome through the same biological mechanism,
• (2)whether the effect of patient management following the surrogate endpoint would likely be similar in the new trial and the historical trials,
• (3)whether serious detrimental side effects can arise between the time of observation of the surrogate endpoint and the time of observation of the true endpoint.

In other words, non-statistical considerations associated with extrapolation can easily outweigh statistical considerations when proposing use of a surrogate endpoint.

Prognostic marker: decision analysis to the rescue

A prognostic marker^30,31 (sometimes called a risk prediction marker)³² is a marker for predicting the risk of an event given a control treatment or no treatment. A prognostic marker informs treatment decisions when there is information on anticipated benefits and harms if a new treatment were applied to persons at high risk. An important question is whether collecting data on an additional prognostic marker is worthwhile. A commonly used measure for addressing this question is the difference in the area under the receiver operating characteristic curve (AUC) for a baseline risk prediction model (Model 1) versus an expanded risk prediction model that includes an additional prognostic marker (Model 2). Typically, the inclusion of an additional marker with a large odds ratio only slightly increases the AUC,³³ which suggests to some investigators that a change in AUC poorly measures the value of an additional marker.^34,35 But why should the odds ratio trump AUC? To circumvent this dilemma, we recommend a decision analysis approach using costs and benefits. We briefly review one such approach based on relative utilities.^36-38 A related approach involves decision curves.³⁹

We revisit a previous evaluation of the addition of breast density to a risk prediction model for invasive breast cancer among asymptomatic women receiving mammography.³⁷ The data come from published risk stratification tables.^32,40 Let Tr0 denote treatment in the absence of risk prediction (no chemoprevention) and Tr1 denote treatment (chemoprevention) for those at high risk. Model 1 estimates the risk of invasive breast cancer as a function of age, race, ethnicity, family history, and biopsy history. Model 2 adds breast density to Model 1.

Tice et al.⁴⁰ randomly split the aforementioned breast cancer data into training and test samples. They fit Models 1 and 2 to the training sample and evaluated them in the test sample. To investigate generalizability some investigators use a test sample from a different population. A first step in our decision analysis is to compute predicted risks for each person in the test sample based on the model fit to the training sample. These predicted risks are biased when there is overfitting in the training sample (i.e., too closely matching random fluctuations when the model contains many parameters) or because the test sample involves a population different from that in the training sample. To circumvent these biases, we construct intervals of predicted risk in the test sample and compute estimated risks (fraction with an unfavorable event) in these intervals. The use of risk estimates based on intervals facilitates reproducibility because the count data used to construct these estimates can be presented when individual-level data cannot be shared.

ROC curve in test sample

Let J index the ordered risk intervals in the test sample. Let FPR_j (the false positive rate) denote the probability that J ≥ j when the outcome under Tr0 (in this example invasive breast cancer with no chemoprevention) does not occur. Let TPR_j (the true positive rate) denote the probability that J ≥ j when the outcome under Tr0 does occur The quantities FPR_j and TPR_j are functions of the observed risks in the intervals.^37,38 Our ROC curve plots TPR_j versus FPR_j with lines connecting the points. If the ROC curve is not concave, we create a concave ROC curve using a concave envelope of points, a procedure with optimal decision analytic-properties.³⁸ Figure 1 shows the concave ROC curves for breast cancer example.

Figure 1.

ROC and relative utility (RU) curves for predicting the risk of invasive breast cancer among asymptomatic women. Model 1 uses baseline variables. Model 2 uses baseline variables and breast density. The dashed vertical lines in the plot for the RU curve represent the range of risk thresholds in Tables 2 and 3. The figures are similar to those in Baker.³⁷

Risk threshold

To formally define the risk threshold we need to define utilities. Let U_{Tr0:NoEvent|Tr0} denote utility of Tr0 when the unfavorable event (invasive breast cancer) would not occur given Tr0. In an analogous manner, we define U_{Tr1:NoEvent|Tr0}, U_{Tr0:Event|Tr0}, and U_{Tr1:Event|Tr0}. Let B = U_{Tr1:Event|Tr0} – U_{Tr0:Event|Tr0} denote the benefit of Tr1 instead of Tr0 in a person who would experience the unfavorable event under Tr0. In our example, B is the benefit of reduced risk of invasive breast cancer due to chemoprevention. Let C= U_{Tr0:NoEvent|Tr0} − U_{Tr1t:NoEvent|Tr0} denote the cost or harm of side effects from Tr1 instead of Tr0 in a person who would not experience the unfavorable event under Tr0. In our example, C is the harm from side effects of chemoprevention. It is not necessary to specify B and C, as only the ratio is needed.

The risk threshold T= (C/B) / (1+C/B) = C/(C+B) is the risk at which a person would be indifferent between Tr0 and Tr1.^38,41 The risk threshold is the value of T such that expected utilities under Tr0 and Tr1 are equal, namely T U_{Tr1:Event|Tr0} + (1−T) U_{Tr1:NoEvent|Tr0} = T U_{Tr0:Event|Tr0} + (1−T) U_{Tr0:NoEvent|Tr0}. Thus, the risk threshold accounts for costs and benefits of treatment.

Net benefit

Let C_Test denote the cost of ascertaining the variables in the risk prediction model. The net benefit of risk prediction relative to no treatment in the absence of prediction^35,37 is

$$N{B}_j=PTP{R}_{j}B-(1-P)FP{R}_{j}C-C_{Test}.$$ (8)

A classic result in decision analysis^42,43 is that the optimal cutpoint, which maximizes net benefit, is j = j(T) such that ROCSlope_j(T) = {(1−P) / P}{C / B} = {(1−P) / P}{T / (1−T)}. The maximum net benefit of risk prediction at the optimal cutpoint j(T) equals

$$maxNB\left(T\right)=PTP{R}_{j\left(T\right)}B-(1-P)FP{R}_{j\left(T\right)}C-C_{Test}.$$ (9)

Relative utility curve

The relative utility^36-38 is the maximum net benefit of risk prediction divided by the net benefit of perfect prediction (ignoring for now the costs of marker testing). The net benefit of perfect prediction equals equation (1) with TPR_j = 1 and FPR_j = 0 and C_Test =0 to yield P B. For no treatment in the absence of prediction, the relative utility curve has the form

$$\begin{array}{cc}\hfill RU\left(T\right)=& \{PTP{R}_{j\left(T\right)}B-(1-P)FP{R}_{j\left(T\right)}\}∕\left(PB\right),\text{for}T\ge P\hfill \\ \hfill =& TP{R}_{j\left(T\right)}-ROCSlop{e}_{j\left(T\right)}FP{R}_{j\left(T\right)},\text{for}T\ge P.\hfill \end{array}$$ (10)

For treatment in the absence of risk prediction, the relative utility curve has the form (derived elsewhere^36-38),

$$RU\left(T\right)=(1-FP{R}_{j\left(T\right)})-(1-TP{R}_{j\left(T\right)})∕ROCSlop{e}_{j\left(T\right)},\text{for}T<P.$$ (11)

A relative utility curve is a plot of RU(T) versus T. Figure 1 shows the relative utility curves for the breast cancer example.

Test tradeoff

The test tradeoff summarizes the value of ascertaining an additional marker. Let ΔRU(T) = RU_Model2 (T) − RU_Model1(T) denote the difference in relative utility curves at risk threshold T. Let C_Marker = C_Test(Model2) – C_Test(Model1) denote the cost of ascertaining the additional marker. The test tradeoff is

$$TestTradeoff\left(T\right)=1∕\left\{\Delta RU\right(T\left)P\right\}.$$ (12)

For an additional marker to be worthwhile, maxNB_Model2(T) − maxNB_Model1(T) > 0, which implies

$$TestTradeoff\left(T\right)<B∕C_{Marker}.$$ (13)

In a decision-analytic viewpoint, investigators need to consider trading the harm of additional testing against the net benefit of improved risk prediction. The test tradeoff formalizes this notion. Based on equation (13), the test tradeoff is the minimum number of persons tested for an additional marker that needs to be traded for one correct prediction to yield an increase in net benefit with the additional marker. In this example, the test tradeoff is the minimum number of women in whom breast density is measured that needs to be traded for a correct prediction of invasive breast cancer. Determining if the test tradeoff is acceptable depends on the invasiveness and costs of the test. In our example, the test tradeoff for Model 2 versus Model 1 ranged from about 2500 to about 3900 over various risk thresholds (Table 2), which means that breast density must be collected on 2500 to 3900 persons for every correct prediction of invasive breast cancer -- which may be reasonable because collecting breast density data is non-invasive and not a costly addition to mammography. We also computed the test tradeoff for Model 1 versus chance which ranged from about 500 to 1100 over various risk thresholds (Table 3) .

Table 2.

Test tradeoffs comparing Model 2 versus Model 1 (with 95% bootstrap confidence intervals.

	Test tradeoffs
Risk threshold	Estimate	Lower bound	Upper bound
0.014	2701	1625	7492
0.016	2573	1826	4203
0.017	2457	1967	3246
0.019	2797	2191	3834
0.021	3891	2819	6072

Table 3.

Test tradeoffs comparing Model 1 versus chance (with 95% bootstrap confidence intervals.

	Test tradeoffs
Risk threshold	Estimate	Lower bound	Upper bound
0.014	510	463	562
0.016	612	571	662
0.017	767	717	826
0.019	959	858	1085
0.021	1149	1006	1336

Applying the risk prediction model

Once investigators select the appropriate risk prediction model (if any) based on the test tradeoff, application to decision making is straightforward. Physicians use patient markers to compute a predicted risk; they then report an observed risk (possibly interpolated) based on the interval of the predicted risk. The clinician and patient base treatment decisions on this observed risk and their anticipation of costs and benefits. The use of risk prediction models for treatment selection is most suitable when there is good information on anticipated costs and benefits; otherwise predictive markers are more desirable for making treatment decisions.

Predictive markers: the appeal of simplicity

A predictive marker (or treatment selection marker)⁴⁵ is a marker for predicting the effect of treatment on outcome in a subgroup of patients or study participants.³¹ Predictive markers can include both high throughput results and clinical variables. Our theme is “the appeal of simplicity,” referring to the straightforward and efficient use of a single randomized trial to evaluate overall treatment effect and treatment effect in a subgroup determined by predictive markers.

Evaluating a single predictive marker

Various designs have been proposed to evaluate a pre-specified predictive marker.^45-47 In one study design, one arm of the trial is marker-based treatment selection (new treatment if the marker is positive, old treatment if negative) and the other arm is old or new treatment; although not its original intent, this design fundamentally evaluates treatments in subgroups defined by the marker,^47-49 A simpler design that achieves this same goal (and also estimates overall treatment effect) is randomization to old or new treatment with marker data collected in all persons.^47-49 A way to reduce marker testing costs is to ascertain the marker in a random sample of stored specimens stratified by outcome and group.⁵⁰

Identifying and evaluating multiple predictive markers

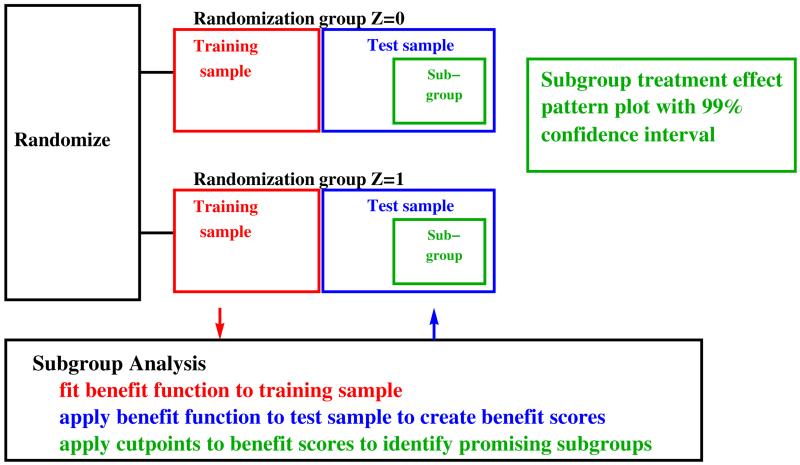
Sometimes investigators may wish to search through multiple candidate predictive markers (sometimes high-dimensional), identify the most promising markers, and evaluate the effect of treatment on outcome in a subgroup determined by these markers. One approach is a modified version of the adaptive signature design,^47,51,52 depicted in Figure 2. First, investigators compute a 96% confidence interval for overall treatment effect among all participants. If this confidence interval excludes zero and the treatment effect outweighs harm of side effects, investigators recommend the treatment to all eligible participants. Otherwise, investigators implement a second step, a subgroup analysis based on splitting the participants in the trial into training and test samples.

Figure 2.

Schematic for modified adaptive signature design.

In the subgroup analysis investigators fit to the training sample a benefit function to predict treatment effect.⁴⁷ Among the large literature of benefit functions,^51-67 one simple benefit function is the risk difference,^53-58 which is the probability of outcome given markers in the experimental group minus the probability of outcome given markers in the control group. Motivation for the risk difference benefit function comes from decision analysis.⁴⁷ There is no consensus on the best way to fit the risk difference benefit function particularly with large numbers of markers. We use the following simple method that is motivated by two results in the classification literature: (i) simple approaches often perform as well as more complicated approaches⁶⁸ and (ii) classification performance often improves little after around five best-fitting variables have been included in the model.^68-70 For each randomization group, we select a preliminary set of markers based on a univariate filter and use stepwise logistic regression on these markers, including only variables that increase AUC by more than 0.05.

The second phase of the subgroup analysis is applying the risk difference benefit function to marker values from each participant in the test sample to obtain a benefit score. Using the benefit scores, we create a tail-oriented subpopulation treatment effect pattern plot^71-73 to determine if there is a promising subgroup. A subgroup is considered promising if the lower bound of the estimated subgroup treatment effect plot is greater than zero (or a threshold based on harms and benefits^47,55,59) and the optimal subgroup is the largest promising subgroup.

Because we lacked high-dimensional data from a randomized trial we illustrate the method using an artificial example based on a microarray data from 52 prostate cancer and 50 non-tumor specimens.⁷⁵ We designated the first 6300 genes to be markers from a hypothetical randomization group 0 and the last 6300 to be the same markers from a hypothetical randomization group 1. In other words, group is an arbitrary construct used here for illustration. The reason for this approach is that we wanted a realistic association among the markers. The subpopulation treatment effect pattern plot is shown in Figure 3 along with a simultaneous 99% confidence interval. The vertical axis is the estimated treatment effect in the subgroup, which is difference in probabilities of outcomes in the two groups. The horizontal axis is the benefit score that forms the lower bound of the subgroup. The optimal subgroup occurs at a cutpoint of the benefit score near zero.

Figure 3.

Subpopulation treatment effect pattern plot using data from prostate cancer classification (tumor or not), designating the first 6300 genes to be markers from a hypothetical randomization group 0 and the last 6300 genes to be the same markers from a hypothetical randomization group 1. The upper and lower dashed lines indicate the simultaneous 99% confidence interval.

Summary

We have covered selected practical aspects of biomarker use for clinical investigations. The applications require both statistical and clinical decisions and are enhanced by a team approach between statistician and clinical investigator Mathematica⁷⁵ software packages are available at http://prevention.cancer.gov/programs-resources/groups/b/software.