Diffuse transition state structure for the unfolding of a leucine-rich repeat protein

Abstract

Tandem-repeat proteins, such as leucine-rich repeats, comprise arrays of small structural motifs that pack in a linear fashion to produce elongated architectures. They lack contacts between residues that are distant in primary sequence, a feature that distinguishes them from the complex topologies of globular proteins. Here we have investigated the unfolding pathway of the leucine-rich repeat domain of the mRNA export protein TAP (TAPLRR) using Φ-value analysis. Whereas most of the tandem-repeat proteins studied to date have been found to unfold via a polarised mechanism in which only a small, localised number of repeats are structured in the transition state, the unfolding mechanism of TAPLRR is more diffuse in nature. In the transition state for unfolding of TAPLRR, three of the four LRRs are highly structured and non-native interactions are formed within the N-terminal α-helical cap and the first LRR. Thus, the α-helical cap plays an important role in which non-native interactions are required to provide a scaffold for the LRRs to pack against in the folding reaction.

Introduction

Tandem repeat proteins, such as ankyrin, tetratricopeptide (TPR), HEAT and leucine-rich repeats, are composed of tandem arrays of 20-40 amino acid structural motifs that pack together in a roughly linear fashion to produce elongated non-globular architectures. They present extended surfaces for molecular recognition and thereby mediate diverse functions within the cell. Unlike globular proteins, which have complex topologies involving many interactions between sequence-distant residues, tandem repeat proteins are stabilised solely by short-range interactions between residues close in sequence. Therefore the formation of the structures of these elongated proteins during the folding process can be studied in a segmented fashion^1-11.

Leucine-rich repeat (LRR) proteins are characterised by repetition of a ~20 amino acid sequence motif with the consensus sequence L_in-X_out-L_in-X_out-L_in-X_out-X_out-N_in where L is a leucine residue, X is any amino acid and N is an asparagine residue. The subscripts “in” and “out” refer to whether the side chain of the residue points in to the hydrophobic core of the structure or out to the solvent. The repeats form a concave surface of short (6 or 7 residue) β-strands and a concave surface of α-helices that run approximately anti-parallel to the β-strands (Fig. 1). The consensus sequence corresponds to the β-strand of each repeat, with the leucine residues making stacking interactions that maintain the hydrophobic core of the domain. Whereas ankyrin repeats and TPRs have been extensively characterised^{1-3, 5-11,12-18}, much less is known about the folding mechanisms of LRR proteins^19-23. Residue-specific information about folding mechanisms, obtained using the Φ-value approach, is available for only one LRR protein to date, Internalin B²¹. The results showed that the N-terminal α-helical capping motif polarises the folding mechanism by acting as a nucleus upon which the repeats assemble.

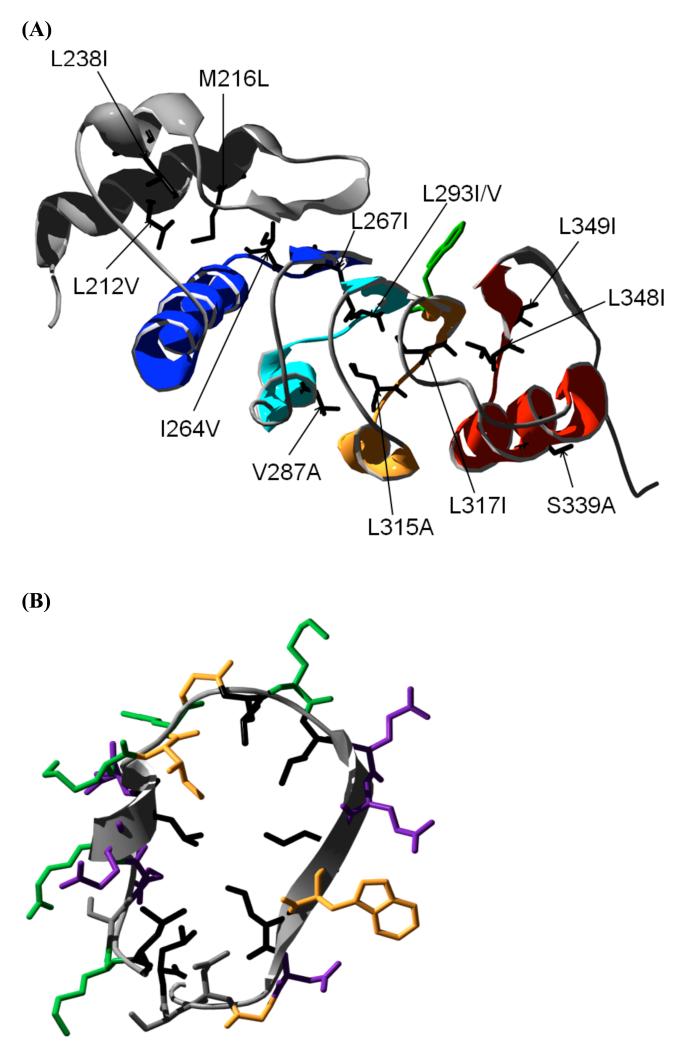
Figure 1. Structure of the LRR domain of TAP (TAPLRR).

(A) The four leucine-rich repeats are shown coloured from N- to C- terminus in blue (repeat 1), turquoise (repeat 2), gold (repeat 3) and red (repeat 4). The N-terminal helical cap is shown in grey. The side chain of the single tryptophan residue (W321) is shown in green. The side chains of the residues mutated in this study are shown in black. (B) Structure of repeat 3 of TAPLRR showing the side chains of all the residues, coloured according to their properties. Leucine residues are coloured black. Polar, hydrophilic residues (Asn, Ser) are in grey, non-polar hydrophobic residues (Ile, Trp, Gly) are in gold, acidic residues (Asp, Glu) are coloured purple, basic residues (Lys, Arg) are in green.

The LRR domain of the nuclear export factor TAP (referred to subsequently as TAPLRR) is responsible for binding the constitutive transport element of the RNA^24,25. It comprises four tandem LRRs and an α-helical cap at the N-terminus. Here we have investigated the unfolding mechanism of TAPLRR using Φ-value analysis, in which single-site, conservative substitutions are made throughout the structure and the effects on the folding/unfolding kinetics are compared with those on the stability, thereby allowing structural information about the transition-state ensemble to be obtained. For all natural repeat proteins studied to date, structure in the folding/unfolding transition states has been found to be localised to a small subset of the repeats ^1,6,11,26. In contrast, the transition state structure for TAPLRR is rather diffusely distributed, with interactions being well formed in three of the four repeats. As observed for Internalin B²¹, the α-helical cap of TAPLRR appears to play an important role in the folding. However, in the case of TAPLRR, non-classical Φ-values indicate that residues in the cap form non-native interactions in the transition state.

Results

TAPLRR unfolds at equilibrium via an apparent two-state mechanism

The TAPLRR construct used in this work consists of 179 residues. A non-cleavable hexa-Histidine tag at the C-terminus is followed by the N-terminal helical cap comprising 49 residues, the LRR domain is 104 residues, and the unstructured C-terminal tail is 20 residues. The stability of TAPLRR was measured using the fluorescence of the single tryptophan residue (W321 located in β4 of LRR3) and by circular dichroism (CD). The fluorescence-monitored urea denaturation curve can be fitted to a two-state equation, giving an m-value (a constant of proportionality that is related to the change in solvent exposure of hydrophobic side chains upon unfolding) of 3.21 ± 0.25 kcal mol⁻¹ M⁻¹ and a midpoint of unfolding (D^50%) of 1.64 ± 0.02 M urea. The same results were obtained when the data were plotted at different emission wavelengths. The free energy of unfolding in water ($\Delta G_{D-N}^{H_{2}O}$) was 5.26 ± 0.42 kcal mol⁻¹. The refolding denaturation curve superimposes on the unfolding denaturation curve, with the same midpoint and m-value within error, indicating that the unfolding of TAPLRR is reversible in these experimental conditions. The denaturation curve monitored by ellipticity at 222 nm to probe α-helical structure can also be fitted to a two-state transition but the m-value is different from that obtained by fluorescence. If the fluorescence- and CD-monitored denaturation curves are fitted by fixing m to the weighted-average value of the wild type and mutants as monitored by fluorescence (2.66 ± 0.14 kcal mol⁻¹ M⁻¹), the midpoints of unfolding obtained are the same within error (1.60 ± 0.03 M and 1.64 ± 0.02 M for the fluorescence and CD data, respectively) (Fig. 2A). Therefore the equilibrium unfolding of TAPLRR can be approximated to a two-state model. The m-value is similar to that of another small LRR domain, Internalin B.²⁰

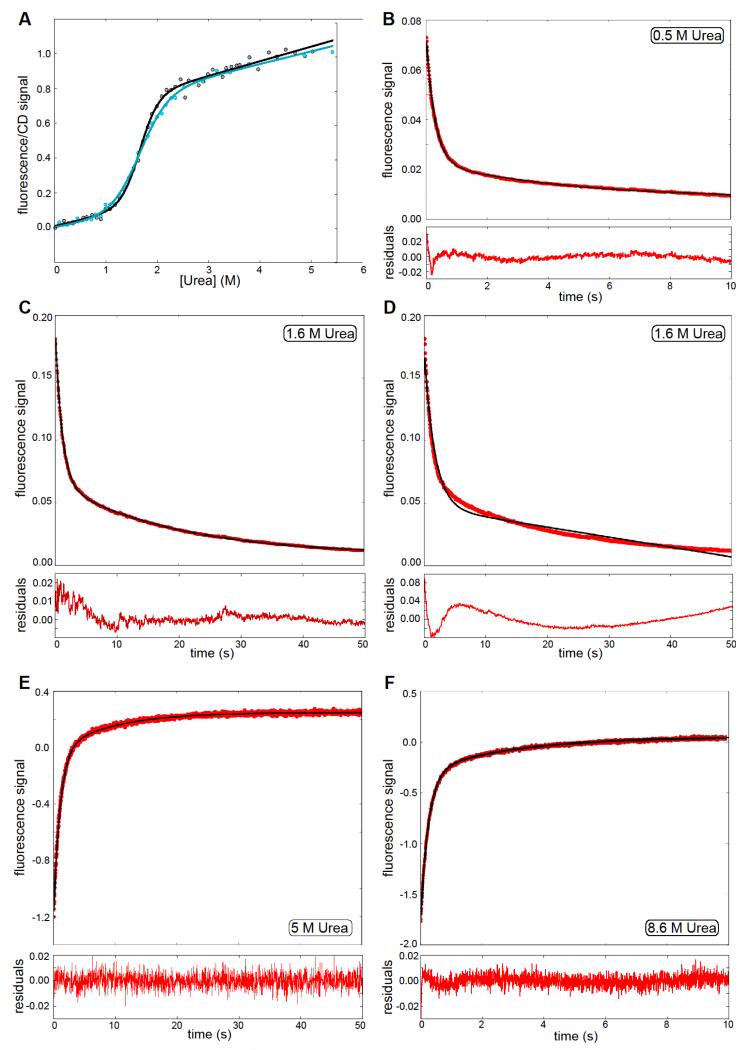
Figure 2. Equilibrium and kinetic folding of wild-type TAPLRR.

(A) Denaturation curves for wild-type TAPLRR, monitored by fluorescence (black) and CD (blue). The data were fitted to a two-state equation, represented by the solid line in the same colour. (B), (C) Kinetic traces for refolding at 0.5 M and 1.6 M urea, the solid line is the fit of a double exponential. (D) Kinetic trace for refolding at 1.6 M urea, the solid line is the fit of a single exponential, with linear instrumental drift. Clearly this does not reproduce the observed kinetic trace and hence justifies the fitting of a double exponential. (E), (F) Kinetic trace for unfolding at 5M and 8.6 M urea. In both cases the solid black line is a fit to a double exponential decay. In figures (B) to (F) the residuals are shown below the plot, normalised by the maximum fluorescence value of the corresponding kinetic trace; the fluorescence intensity is in arbitrary units.

Both the refolding kinetics and the unfolding kinetics of TAPLRR are biphasic

The refolding and unfolding kinetics of wild-type TAPLRR were measured by stopped-flow fluorescence. The kinetic traces for both reactions were not well described by single exponential phases (see Figure 2D) but they could be fitted to the sum of two exponential phases, as shown in Figure 2. The fast phase of unfolding accounts for ~85% of the total amplitude and the slow phase for ~15%. The fast phase of refolding accounts for ~80 % of the total amplitude and the slow phase for ~20%. The urea dependence of the observed rate constants and amplitudes is shown in Figure 3B. Formation of oligomers or aggregates can retard the folding reaction; however for TAPLRR no protein concentration dependence of the rate constants of refolding or their relative amplitudes was observed in the range of 0.5 μM to 30 μM, indicating that oligomerisation is not the cause of the slow refolding phase. Alternatively, the slow refolding phase could be limited by proline isomerisation (TAPLRR has nine proline residues), although the presence of the peptidyl-prolyl cis/trans isomerase cyclophilin did not speed up the refolding kinetics, or it could correspond to one step of a multi-step reaction.

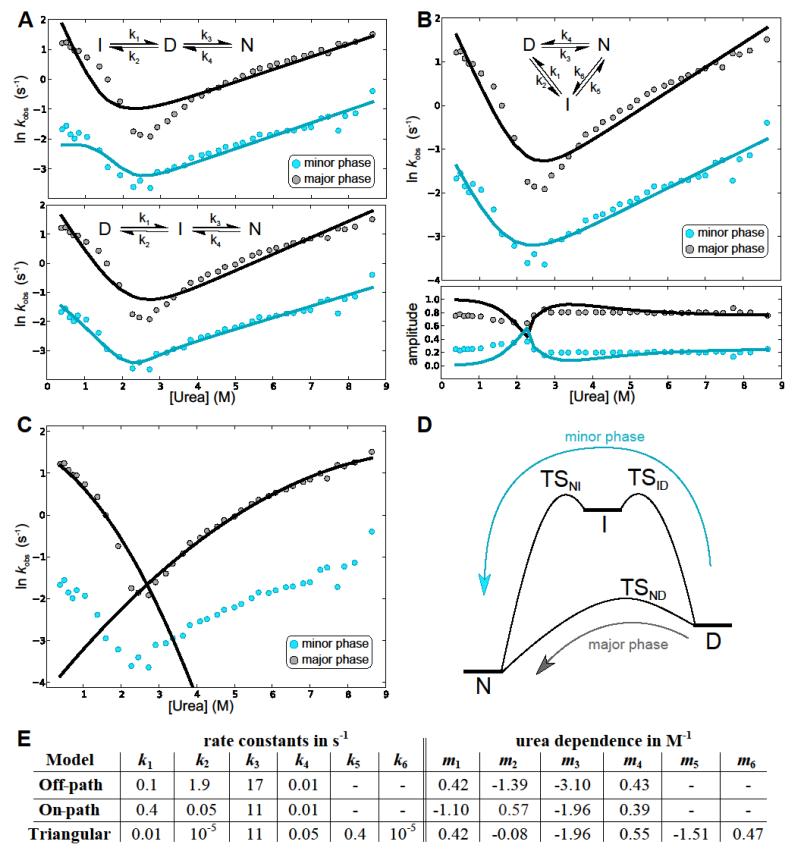
Figure 3. Fitting to microscopic rates of folding in 3-state mechanisms.

(A) Best fit to the off-pathway (top) and on-pathway (bottom) model. Whereas the on-path fit is comparable to the triangular fit in B, the off-path fit is significantly worse. (B) Best global fit of the rates (top) and amplitudes (bottom) to the triangular mechanism. The rates are shown in grey for the major phase and blue for the minor phase; the solid line in the same colour is the best fit. (C) Fits of the curvature in the urea dependence of the logarithms of the rate constants, due to Hammond behaviour, for both the unfolding arm and the refolding arm of the major phase. (D) A schematic of the energy landscape of folding. This schematic is for illustration purposes only, and the heights of the barriers and energies of the species are not intended to accurately reflect the experimentally observed rates. (E) The microscopic rates and their urea dependences for the best fits as shown above. Note that the rates to the intermediate for the triangular case are very small compared to the rates from the intermediate, suggesting a high-energy intermediate, which is in accordance with its absence in the equilibrium denaturation curves. Due to the small rates these transitions have little effect on the overall behaviour so their rates and m values may only be accurate to within an order of magnitude.

The urea dependence of the rate constant of unfolding clearly shows downward curvature over the wide range of urea concentrations assayed. Similar non-linearity has been observed for many other proteins and it can be rationalised as follows: unfolding can be viewed as taking place over a broad energy barrier with a smooth movement across it as the denaturant concentration is increased, in accordance with Hammond behaviour.^{27, 28} The data can be fitted to a quadratic equation to describe this behaviour:

$$\ln k_{\mathrm{u}}\left[U\right]=\ln k_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}+m_{\mathrm{u}}\left[U\right]+m^{\ast }{\left[U\right]}^2$$ 1

where $k_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}$ is rate constant of unfolding in water, m_u is a constant that is proportional to the increase in solvent accessible surface area between the native state and the transition state, and m* is the denaturant dependence of m_u. The fitting of the kinetic data is discussed in detail in the next section.

Modelling of the kinetic data

A double exponential decay, as observed for both the refolding and unfolding kinetic traces, is indicative of a system involving three species²⁹. The most general model for a three-species system is a triangular mechanism, wherein each of the species is connected to the other two by a forward and reverse rate. In the limit that the rates between two species are vanishingly small, the more common cases of on-pathway intermediate (I) (if the rate between the native state (N) and the denatured state (D) is small) and off-pathway intermediate (if the rate between native state and intermediate is small) are obtained. In a Φ-value analysis the changes in the folding and unfolding rates upon mutation of specific residues are used to infer the structure in the transition state. For systems involving three interconnected species, there will in general be three transition states, which define six rate constants connecting the three species, and for a meaningful Φ-value analysis one needs to ensure that only one transition state contributes to the results and establish which species it connects. One can solve the kinetic equations for a general system of three interconverting species and relate the results to observables²⁹ such as fluorescence. The observed rates are, in general, determined by a combination of all the microscopic rate constants, but often the larger of the two observed rates is found, to a good approximation, to be dominated by one microscopic rate. In that case the observed rate constant can be assigned to a specific microscopic rate and thereby a specific transition state in the system, which is crucial if a Φ-value analysis is to be attempted. The rate constant for the minor phase often shows a dependence on several microscopic rates and its interpretation in terms of specific reaction steps is less straightforward.

In an effort to delineate the folding pathway, a double exponential was used to fit the time courses of the fluorescence for the folding and unfolding experiments, giving two amplitudes and two observed rate constants at each denaturant concentration; these observed data were fitted to three different models: on-pathway intermediate, off-pathway intermediate and a triangular mechanism, as shown in Figure 3A,B. As is commonly the case, we assumed that the natural log of the microscopic rates (ln(ki)) varies linearly with denaturant concentration, with slope mi (refer to the Methods section for the detailed equations). Using the equations derived in ²⁹ and as applied in ^30,31, this assumption then allows us to fit the full dataset with 8 free parameters (4 rates, 4 slopes) in the case of the on- and off-pathway mechanisms, or 10 free parameters in the case of the triangular mechanism.

The best fits of the data to the linear mechanisms are shown in Figure 3A. An off-pathway mechanism can be discarded when considering the wild-type TAPLRR data, on the grounds that it gives a poor fit to the exponents. The fits to the on-pathway mechanism were as good as the fits to the more general triangular mechanism, but the on-pathway mechanism could be discarded by looking at the behaviour of the minor phase upon mutation (discussed further in the next sections; see also Figure 6): In the on-pathway fits the major rate was, to a good approximation, determined only by the rate constants between the intermediate and the native state, whereas the minor phase was determined by the rate constants between the denatured state and the intermediate. This arrangement of the rate-determining transition states in series is not consistent with the fact that the major and minor phases respond in a very similar way to mutation. Consider, for example, the mutant I264V (Fig. 6): The fact that the observed rates for the minor unfolding phase of this mutant are much faster than those of wild type suggests that the structure is fully broken in the transition state going from I and D, whereas the faster rates for the major unfolding phase of this mutant compared with wild type suggest that the structure is fully broken in the transition state going from N to I. It is not possible in a linear on-pathway-intermediate mechanism for structure to be fully broken twice. Therefore a triangular mechanism must instead be considered. A global fit of the observed rates and amplitudes to the triangular mechanism is shown in Figure 3B.

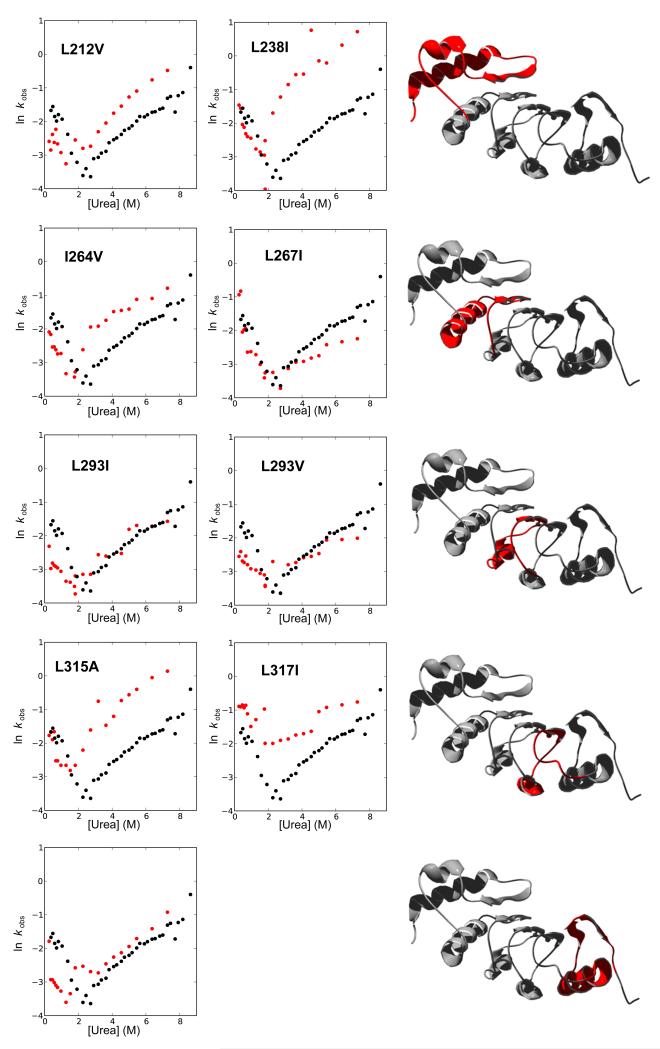
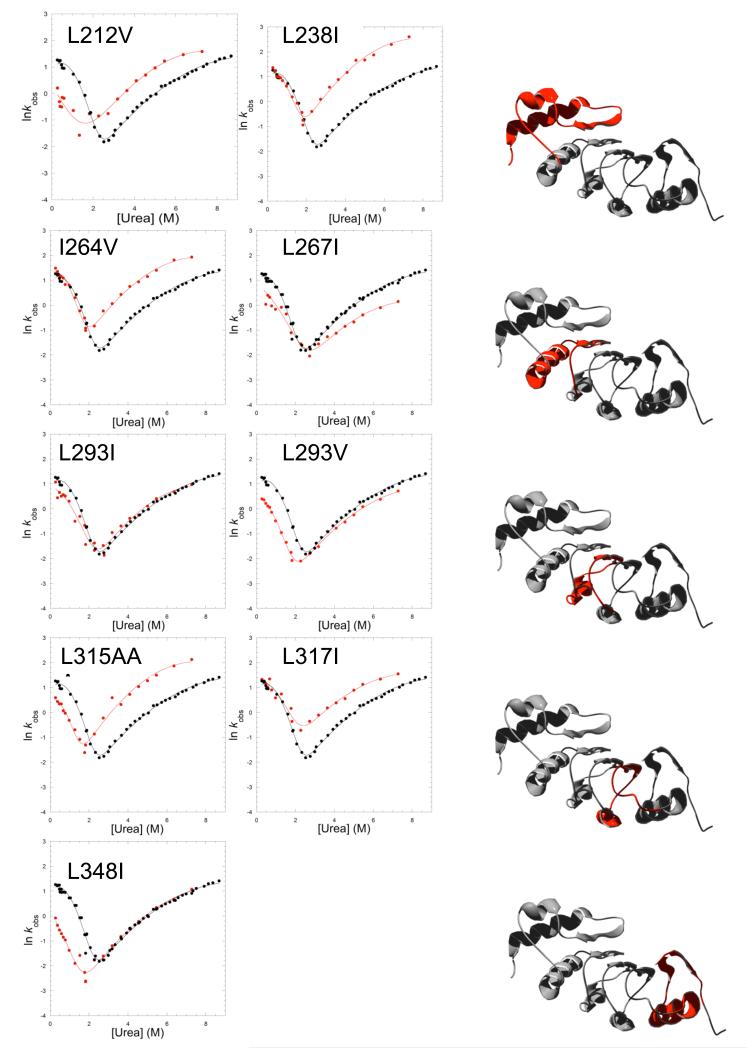
Figure 6.

Plots of the rate constants of the minor phase of refolding and unfolding for TAPLRR mutants. Each panel shows the urea dependence of the rate constants for wild type (black) and mutant (red). The schematic shows in red the location of each pair of mutants.

The parameters obtained in the fits are summarised in the table in Figure 3E, and in the triangular mechanism the major phase is determined by the rates k3 (at low denaturant) and k4 (at high denaturant) over the entire range of denaturant concentrations. This means that the dominant transition state remains the same at different denaturant concentrations, namely the transition state between D and N, making a Φ-value analysis possible using the major phase. The minor phase is determined by rates k₁ and k₅ and hence the behaviour upon mutation can be explained if the intermediate and the transition states leading to it (TS_NI and TS_ID) are similar in structure to the transition state (TS_ND) determining the major phase (see Figure 3D).

As was mentioned above, the urea dependence of the logarithm of the rate of the major phase displays negative curvature. This can not be explained assuming a linear dependence of ln(ki) on the denaturant concentration and the deviation from the experimental data is evident in the fits. We therefore assumed a quadratic dependence of the two rates dominating the major phase, as given in Equation 1, and fitted the major phase as shown in Figure 3C. Only the major phase was fitted with this quadratic dependence, as including this factor in the fitting of both phases would require an additional parameter for each rate and therefore would result in an unfeasibly large number of fitting parameters. The fits to the whole data set in Figure 3B should therefore be considered mainly as a means of relating the macroscopically observed phases to specific microscopic steps on the folding pathway. A quadratic fit to the major phase was used for all mutants in order to extract the rates and thereby the Φ-values of the major phase. The Φ-value analysis of TAPLRR is described below.

Single-site substitutions greatly destabilise TAPLRR

A first round of mutations was designed at solvent-exposed sites throughout the structure. Given the low stability of the TAPLRR, it was hoped that these mutations would perturb the structure sufficiently to allow Φ-value analysis but not so much as to cause unfolding or misfolding. The parameters obtained from fitting the equilibrium unfolding data of the mutants to a two-state model are shown in Table 1. Four proteins (M216L, V287A, S339A and L349I) were expressed in this first round of mutagenesis. However, none of them had significant effects on the equilibrium and kinetics of the protein, and hence they could not be used for Φ-value analysis.

Table 1. Equilibrium denaturation parameters for wild type and mutants of TAPLRR.

The m-values and midpoints of unfolding ([U]^50%) listed are those obtained by fitting the individual denaturation curves to a two-state equation. The weighted-average of the m-values of wild type and those mutants with long pre-transition baselines in the denaturation curves (<m> = 2.66 ± 0.14) was then used to refit the denaturation curves. The midpoints of unfolding obtained from these fits were used to calculate the changes in the free energy of unfolding upon mutation, $\Delta \Delta G_{D-N}^{H_{2}O}=<m>({{\left[U\right]}^{50\%}}_{\text{wild type}}-{{\left[U\right]}^{50\%}}_{\text{mutant}})$. The errors are the standard deviations from the fits of the data.

Protein	Location	Location of interacting residues	m-value (kcal mol−1 M−1)	[D]50% (M)	$\Delta \Delta G_{\mathrm{U}-\mathrm{N}}^{{\mathrm{H}}_2\mathrm{O}}$ (kcal mol−1)
WT			3.21 ± 0.25	1.64 ± 0.02	-
L212V	α1 cap	LRR1	-	1.08 ± 0.11*	1.38 ± 0.31
M216L	α1 cap	LRR1	2.56 ± 0.14	1.70 ± 0.02	−0.27 ± 0.10
L238I	α2 cap	Cap	3.44 ± 0.44	1.51 ± 0.03	0.35 ± 0.13
I264V	α3-β2 strand LRR1	Cap	3.40 ± 0.21	1.41 ± 0.02	0.64 ± 0.10
L267I	α3-β2 strand LRR1	Cap LRR2	2.27 ± 0.23	1.52 ± 0.05	0.11 ± 0.11
V287A	α4 LRR2	LRR3	2.66 ± 0.24	1.54 ± 0.03	0.16 ± 0.11
L293I	α4-β3 strand LRR2	LRR1 LRR3	2.92 ± 0.23	1.33 ± 0.03	0.80 ± 0.12
L293V	α4-β3 strand LRR2	LRR1 LRR3	-	1.07 ± 0.06*	1.41 ± 0.19
L315A	α5-β4 strand LRR3	LRR2 LRR4	-	0.98 ± 0.09*	1.65 ± 0.27
L317I	α5-β4 strand LRR3	LRR2 LRR4	2.52 ± 0.22	1.26 ± 0.04	0.85 ± 0.12
S339A	α6 LRR4	LRR4	2.85 ± 0.55	1.73 ± 0.06	−0.32 ± 0.18
L348I	α6-β5 strand LRR4	LRR3 C-terminus	2.88 ± 0.41	1.42 ± 0.05	0.53 ± 0.14
L349I	β5 LRR4	LRR3	2.38 ± 0.30	1.60 ± 0.05	−0.05 ± 0.13

^*The pre-transition baseline was absent or very short for three highly destabilising mutations, L212V, L293V and L315A, resulting in poor fits of the data. Therefore, for these mutants the values of [U]^50% listed are those obtained by fitting the denaturation curves with the m-value fixed at <m>.

Next, mutations were made at sites in the hydrophobic core. Many of these sites are leucine residues, and mutation of subset of these (L296, L298, L303, L309, all located in repeat 3) to alanine was found to destabilise the protein to such an extent that the mutants could not be obtained in a soluble folded form in sufficient quantities. A similar sensitivity to mutation was observed previously for the LRR domain of Internalin B.²¹ Mutation to alanine of L267 in repeat 2, L293 in repeat 3 and L348 in repeat 4, was attempted, as well as mutation to glycine of A290 in repeat 2, but only very small quantities of the proteins could be produced in soluble form. The following were successfully expressed and purified and found to be folded like the wild type, as judged by gel filtration and CD: two mutations were made at equivalent positions in repeat 2 (I264V) and repeat 3 (L315A) (Fig. 4), and five mutations were made at equivalent positions in the loop at the end of each repeat between the α-helix and the β-sheet, in repeat 1 (L267I), repeat 2 (L293I and L293V), repeat 3 (L317I) and repeat 4 (L348I) (Fig. 4). In common with other LRR proteins TAPLRR has a helical cap at one end that is thought to protect the overall repeat structure by shielding the hydrophobic core. The cap in TAPLRR is at the N-terminus and comprises a long α-helix followed by a β-sheet and a shorter α-helix; two mutations were made in the N-terminal cap (L212V and L238I (Fig. 4)). All but two of the hydrophobic core mutations showed changes in stability that are within the range compatible with accurate Φ-value determination (i.e. $\Delta \Delta G_{D-N}^{H_{2}O}>0.5$ kcal mol⁻¹). For the two exceptions, L238I and L267I, the values of $\Delta \Delta G_{D-N}^{H_{2}O}$ were very small but the mutations had significant effects on the kinetics. These two mutants are therefore also included in the discussion below.

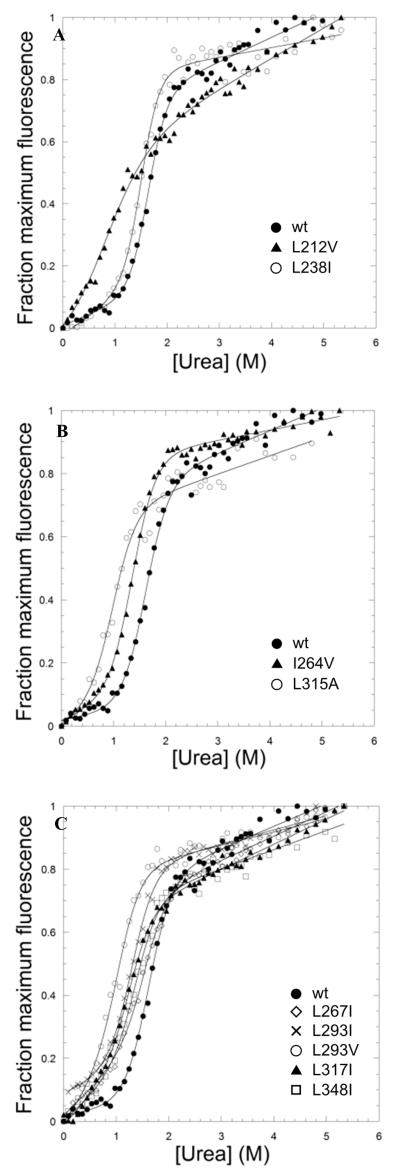
Figure 4. Equilibrium denaturation curves of TAPLRR mutants.

(A) Mutations in the N-terminal helical cap, L212V (triangles) and L238I (open circles). (B) Mutations in equivalent positions of repeat 1 (I264V) and repeat 3 (L315A) shown by triangles and open circles, respectively. (C) Mutations in equivalent positions of all repeats. L267I in repeat 1 is shown by open diamonds, L293I and L293V in repeat 2 are shown by crosses and open circles, respectively. L317I in repeat 3 is shown by triangles. L348I in repeat 4 is shown by squares. The denaturation curve of wild-type TAPLRR is shown by closed circles in all panels for comparison. The data were fitted to a two-state equation as for Figure 2.

Φ-value analysis

The V-shaped plots for the major phase in the kinetics of the TAPLRR mutants are shown in Figure 5. Curvature is evident in the unfolding and refolding limbs for most of the mutants, as was observed for the wild type. To calculate the Φ values, we fitted the unfolding limbs, outside the transition region, to a quadratic equation (Equation 1). The values of m_u and m* obtained for the mutants were similar to those of the wild type, indicating that the mutations do not cause a gross change in the transition state structure. To minimise the errors, the data were then refitted to a quadratic equation using a weighted-average value of the curvature, calculated from wild type and all the mutants. Φ values were determined at a urea concentration of 5.5 M, which is in the middle of the urea range used for the unfolding studies, in order to avoid the need for a long extrapolation back to 0 M denaturant and thereby minimise the errors. The kinetic parameters, including the Φ values, are listed in Table 2.

Figure 5. Plots of the refolding and unfolding rate constants for TAPLRR mutants.

Each panel shows the urea dependence of the rate constants for refolding and unfolding of wild type (black) and mutant (red). The data are fitted as for Figure 2. The schematic shows in red the location of each pair of mutants.

Table 2. Kinetic parameters for the unfolding of wild type and mutants of TAPLRR.

$\ln k_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}$ and $m_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}$ were obtained by fitting the unfolding data to a quadratic equation. To minimise the errors, a weighted-average value of the curvature was calculated using the wild type and mutants (<m*> = −0.052). The data were then refitted to a quadratic equation with m* fixed to the weighted-averaged value. The data were also fitted to give the rate constants for unfolding at 5.5 M urea, in the middle of the denaturant concentration range used for the unfolding kinetics, in order to avoid the need for large extrapolation back to 0 M urea and thereby reduce the errors. The errors listed are the standard deviations from the fits of the data. The Φ values were calculated at 5.5 M urea and they have errors of 5-10%.

	$\ln k_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}$	mu (M−1)	$\ln k_{\mathrm{u}}^{5.5M}$	Φ 5.5M
WT	−4.18 ± 0.03	1.09 ± 0.01	0.26 ± 0.01
L212V	−2.74 ± 0.12	0.99 ± 0.02	1.13 ± 0.03	0.63 ± 0.13
L238I	−2.08 ± 0.12	1.02 ± 0.02	1.93 ± 0.03	< 0
I264V	−2.48 ± 0.07	0.99 ± 0.01	1.39 ± 0.02	−0.05 ± 0.17
L267I	−4.07 ± 0.09	0.95 ± 0.02	−0.42 ± 0.03	> 1
L293I	−3.65 ± 0.11	1.01 ± 0.02	0.33 ± 0.03	0.95 ± 0.04
L293V	−4.18 ± 0.10	1.05 ± 0.02	0.01 ± 0.03	1.11 ± 0.03
L315A	−2.74 ± 0.09	1.05 ± 0.02	1.47 ± 0.02	0.57 ± 0.07
L317I	−2.57 ± 0.93	0.94 ± 0.02	1.04 ± 0.03	0.46 ± 0.09
L348I	−4.04 ± 0.06	1.07 ± 0.01	0.29 ± 0.02	0.97 ± 0.04

L293V in repeat 2 and L348I in repeat 4 have Φ values close to 1, indicating that these regions are fully structured in the transition state, and residues in repeat 3 have high fractional Φ values, indicating that this region is also highly structured in the transition state. The N-terminal region of the protein is less well structured in the transition state: L212V in the N-terminal cap has a fractional Φ value and I264V in repeat 1 has a Φ value of 0, indicating that this region is unstructured in the transition state. Interestingly, the mutation L267I (repeat 1) has a negligible effect on the equilibrium stability but its unfolding kinetics is significantly slower than that of the wild-type protein. The consequence of this behaviour is a non-classical Φ value of greater than 1. Likewise, the mutation L238I (in the cap) has a negligible effect on the equilibrium stability but significantly speeds up the unfolding kinetics. The consequence is a non-classical Φ value of less than 0. These non-classical Φ values indicate the presence of non-native interactions in the transition state.

Discussion

The thermodynamic stability of TAPLRR is very sensitive to mutation of the consensus leucine residues

The low thermodynamic stability of TAPLRR ($\Delta \Delta G_{D-N}^{H_{2}O}=5.3$ kcal mol⁻¹) limited the number of mutant proteins that could be expressed in soluble form. In the hydrophobic core, the conserved leucine residues of repeat 3 were first selected for mutation to alanine but only one mutant could be expressed in a soluble form to sufficient quantities (L315A). The large truncation of the leucine side chain to alanine may disrupt the core packing interactions to such an extent as to cause unfolding of the protein. A similar sensitivity to mutation was observed for the small LRR domain of Internalin B.²¹ More conservative mutations were therefore made in the other repeats. Conversely, many of the substitutions at surface sites in the LRR structure could be expressed in a soluble form but did not destabilise the structure sufficiently to allow Φ-value analysis.

Φ-value analysis of the major kinetic unfolding phase shows a more diffusely structured unfolding transition state than those of other repeat proteins

Both the refolding and unfolding kinetics of TAPLRR can be fitted to the sum of two exponential phases (Figure 2). The urea dependence of the rate constants for these phases, shown in Figure 3, appears to describe two distinct V-shaped plots. We show that the wild-type data can be modelled reasonably well using a 3-state mechanism. Most of the mutations affect the minor refolding/unfolding phase in a similar way to the major refolding/unfolding phase (Figures 5 and 6). For example, for L293I and L348I, the major and minor unfolding rates of the mutant are similar to those of the wild-type; for I264V, the major and minor unfolding rates of the mutant are much faster than those of the wild type. One possible reason for this could be that the reaction can proceed via two parallel pathways, one including an intermediate and one going directly from D to N. These pathways proceed via similar transition states and are therefore affected by mutations in a similar way.

There has been some discussion in the literature in recent years regarding the structural and mechanistic interpretation of Φ values and to what extent the magnitude of a Φ value is dependent on the equilibrium stability change associated with the mutation^32,33; uncertainty may sometimes arise when the stability change is small, and the Φ value obtained can then appear to be erroneously high. Therefore, care must be taken when carrying out this type of analysis and particularly when interpreting the observation of a very small number of high Φ values amongst otherwise low Φ values in terms of a nucleation-type folding mechanism. In this regard it is interesting to look at repeat proteins. For this class of proteins, polarised folding and unfolding mechanisms have generally been observed to date (see for example^{1, 6, 21}), in which structure in the transition state is localised to a subset of repeats. It is important to emphasise, however, that this behaviour corresponds to a large rather than a small number of high Φ values, and they are not associated with small stability changes.

A different picture is obtained here for the transition state of TAPLRR compared with those of previously studied repeat proteins. The transition state is rather diffusely structured, with three of the four LRRs having residues with high Φ values of between 0.5 and 1. The difference in the unfolding mechanism of TAPLRR compared with other repeat proteins may be a consequence of the small number of repeats combined with a relatively large cap, causing TAPLRR to behave more like globular proteins that tend to have diffuse transition state structures. Interestingly, we find that two residues, one located in the N-terminal helical cap and one in the first leucine-rich repeat, have anomalous Φ values of less than 0 or greater than 1, indicating the presence of non-native interactions in the transition state. The formation of non-native structure by the cap may be required early in the reaction to protect the LRRs while they fold; the cap must then rearrange to the native structure late in the folding reaction.

Experimental Procedures

Molecular biology and protein purification

TAPLRR (residues 199-372) in plasmid pQE60 (Qiagen) with a C-terminal non-cleavable 6-residue histidine tag was a generous gift from E. Conti (EMBL, Heidelberg, Germany). Site-directed mutagenesis was performed using the QuikChange kit (Agilent Technologies) and mutant plasmids identified by sequencing. E. coliC41(DE3) cells were transformed with plasmid and a small number of colonies picked from the plate into flasks containing 1 L 2xTY medium plus ampicillin. The cells were grown at 37°C to O.D._600nm ~0.6 then induced with 0.5 mM IPTG overnight at 28°C. Cells were harvested by centrifugation at 5000 g for 10 minutes at 4°C and resuspended in 50 mM Tris-HCl buffer, pH 8.1, 500 mM NaCl, 10% glycerol, 5 mM imidazole. Cells were lysed in an Emulsiflex C5 high-pressure homogeniser (GC Technology) and soluble protein purified by Ni-NTA affinity chromatography followed by size-exclusion chromatography (Superdex 75, GE Healthcare Life Sciences). Purified protein was dialysed into 5 mM Tris-HCl buffer, pH 8.1, and was judged to be >95 % pure by SDS-PAGE and mass spectrometry. Protein aliquots were flash frozen and stored at −80 °C.

Equilibrium denaturation

0.8 mL aliquots containing various concentrations of urea in buffer (50 mM sodium phosphate, pH 7, 1 mM EDTA) were dispensed using a Hamilton MicroLab dispenser. 100 μL protein was added to each aliquot to a final concentration of 4 μM and samples equilibrated at 25 °C for 4 hours. For refolding experiments, the protein was first denatured in 3 M urea and incubated for 1 hour at 25 °C, then dispensed as above. The fluorescence was monitored using an Aminco-Bowman series 2 luminescence spectrofluorimeter using a quartz cuvette with a 10 mm pathlength. The excitation wavelength was 280 nm and emission was measured between 345 nm and 355 nm at a rate of 1 nm/second. CD spectra were recorded on a Jasco J720 spectrapolarimeter using a quartz cuvette with a 10 mm pathlength at 25 °C. Three scans from 240 nm to 217 nm were acquired and averaged for each urea concentration at a scan rate of 50 nm/min. The final protein concentration for the CD measurements was 15 μM. Equilibrium denaturation curves were fitted to a two-state model as described³⁴ using Kaleidagraph 4.1 (Synergy software).

Stopped-flow fluorescence

Stopped-flow fluorescence measurements were performed using an Applied Photophysics SX-18MV instrument. The final protein concentration after mixing was 4 μM. Six traces were acquired and averaged for each urea concentration. Refolding experiments were performed by mixing one volume of protein unfolded in 3 M urea with 10 volumes of buffer (50 mM sodium phosphate buffer, pH 7, 1 mM EDTA) at 25 °C. Unfolding experiments were performed by mixing one volume of protein in buffer with 10 volumes of solutions of buffer and urea. The averaged traces were fitted to the sum of two exponential phases using Kaleidagraph 4.1. The V-shaped plots were fitted to a quadratic equation to describe the denaturant-dependent movement of the transition state according to Hammond behaviour.

Calculation of Φ values

Φ-value analysis is used to characterise the structures of folding transition states and intermediates at a residue-specific level³⁵. By making single-site, conservative mutations that delete an interaction or a small number of interactions without introducing new interactions, the effect on the energy of the transition state can be determined. If a mutation destabilises the transition state by the same amount as it destabilises the native state then it indicates that that region is as structured in the transition state as it is in the native state (Φ = 1). Conversely, if a mutation destabilises the native state but has no effect on the stability of the transition state then the region can be said to be as unstructured in the transition state as it is in the denatured state (Φ = 0). Fractional values are most simply interpreted as resulting from partial structure formation in the transition state. Φ values were calculated for TAPLRR from the unfolding rate constants using the following equation:

$$\Phi =1-\frac{\mathit{RT}\ln \left(\frac{k_u^{\mathit{mut}}}{k_u^{\mathit{wt}}}\right)}{\Delta \Delta G_{D-N}}$$

where T is the temperature in Kelvin, R is the gas constant, and $k_{\mathrm{u}}^{\mathrm{wt}}$ and $k_{\mathrm{u}}^{\mathrm{mut}}$ are the rate constants for unfolding of wild-type and mutant proteins, respectively. ΔΔG_D–N is the change in the free energy of unfolding upon mutation as measured by equilibrium denaturation experiments.

Modelling

The data were fitted using the following equations, derived in 30:

$${\lambda }_{1,2}=\frac{1}{2}\left({\beta }_1\pm \sqrt{{\beta }_1^2-4{\beta }_2}\right)$$

with

$$\begin{array}{cc}\hfill {\beta }_1=k_1& +k_2+k_3+k_4+k_5+k_6\hfill \\ \hfill {\beta }_2=k_1(k_3+k_4+k_6)& +k_2(k_4+k_5+k_6)+k_3(k_5+k_6)+k_4{k}_5\hfill \end{array}$$

where λ_1,2 are the two experimental rates and the k_i are the microscopic rates as defined in Figure 3. The on- and off-pathway mechanisms can be obtained from the above general expression by setting the relevant rates to zero. In addition to these equation an exponential dependence of the k_i on the denaturant concentration was assumed:

$$k_i=k_{{\mathrm{H}}_2\mathrm{O}}\mathrm{Exp}\left(m_i\right[U\left]\right)$$

where k_H2O is the rate without denaturant and [U] is the denaturant concentration.

The amplitudes for the triangular mechanism are given by:

$$\begin{array}{cc}\hfill A_{\text{unfolding}}& =\frac{(k_4{\lambda }_1-{\gamma }_3+a(k_6{\lambda }_1-{\gamma }_2\left)\right)}{{\lambda }_1({\lambda }_1-{\lambda }_2)}\hfill \\ \hfill A_{\text{refolding}}& =\frac{(k_3{\lambda }_1-{\gamma }_1+(1-a\left)\right(k_2{\lambda }_1-{\gamma }_2\left)\right)}{{\lambda }_1({\lambda }_1-{\lambda }_2)}\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill {\gamma }_1& =k_5{k}_3+k_5{k}_2+k_1{k}_3\hfill \\ \hfill {\gamma }_2& =k_6{k}_3+k_6{k}_2+k_4{k}_2\hfill \\ \hfill {\gamma }_3& =k_6{k}_1+k_4{k}_5+k_4{k}_1\hfill \\ \hfill a& =\frac{F_I-F_D+(m_I-m_D)\left[U\right]}{F_N-F_D+(m_N-m_D)\left[U\right]}\hfill \end{array}$$

where F_N, F_U, F_I, m_N, m_U, m_I are the fluorescence intensities and their change with urea of the native, and denatured states (which can be obtained from the equilibrium denaturation) and of the intermediate. For further details see Ref. 29 and 30.

We moreover added Hammond behaviour in the eventual fits of the major phase, i.e. the dependence of the rates on urea was changed to:

$$\ln k_{\mathrm{u}}\left[U\right]=\ln k_{\mathrm{u}}^{{\mathrm{H}}_2\mathrm{O}}+m_{\mathrm{u}}\left[U\right]+m^{\ast }{\left[U\right]}^2$$

We found this was necessary as a 3-state model without Hammond behaviour is not capable of fitting both phases and still produce the correct curvature for the major phase. The resulting system, a 3-state reaction with Hammond behaviour, is rather complex, but was the simplest mechanism consistent with the observed data.