Semiparametric Estimation of the Impacts of Longitudinal Interventions on Adolescent Obesity using Targeted Maximum-Likelihood: Accessible Estimation with the ltmle Package

Abstract

While child and adolescent obesity is a serious public health concern, few studies have utilized parameters based on the causal inference literature to examine the potential impacts of early intervention. The purpose of this analysis was to estimate the causal effects of early interventions to improve physical activity and diet during adolescence on body mass index (BMI), a measure of adiposity, using improved techniques. The most widespread statistical method in studies of child and adolescent obesity is multi-variable regression, with the parameter of interest being the coefficient on the variable of interest. This approach does not appropriately adjust for time-dependent confounding, and the modeling assumptions may not always be met. An alternative parameter to estimate is one motivated by the causal inference literature, which can be interpreted as the mean change in the outcome under interventions to set the exposure of interest. The underlying data-generating distribution, upon which the estimator is based, can be estimated via a parametric or semi-parametric approach. Using data from the National Heart, Lung, and Blood Institute Growth and Health Study, a 10-year prospective cohort study of adolescent girls, we estimated the longitudinal impact of physical activity and diet interventions on 10-year BMI z-scores via a parameter motivated by the causal inference literature, using both parametric and semi-parametric estimation approaches. The parameters of interest were estimated with a recently released R package, ltmle, for estimating means based upon general longitudinal treatment regimes. We found that early, sustained intervention on total calories had a greater impact than a physical activity intervention or non-sustained interventions. Multivariable linear regression yielded inflated effect estimates compared to estimates based on targeted maximum-likelihood estimation and data-adaptive super learning. Our analysis demonstrates that sophisticated, optimal semiparametric estimation of longitudinal treatment-specific means via ltmle provides an incredibly powerful, yet easy-to-use tool, removing impediments for putting theory into practice.

Introduction

Adolescent obesity has become a major concern in public health due to its increasing prevalence [1, 2]. Overweight and obese adolescents often become overweight and obese adults, and are at increased risk for chronic diseases such as heart disease, diabetes and cancer [3–6]. Physical activity and diet are established determinants of obesity development [7–11]. At a physiological level, obesity occurs when there is energy imbalance, specifically when energy intake exceeds energy expenditure. Energy needs vary considerably for the growing child/adolescent, and there is considerable variability in energy intake and expenditure patterns throughout childhood and adolescence.

Multivariable linear or logistic regression has often been used to model the effect of energy intake and expenditure patterns on body mass index (BMI) or other indicators of obesity using observational data, and the parameter of interest is the coefficient attached to certain variables [8]. An alternative approach, which can utilize data adaptive estimation, is based upon the so-called G-computation formula, from which a substitution-type estimator can be derived [12, 13]. In the longitudinal settings, G-computation is an identifiability result derived from the sequential randomization assumption implied by a causal graph or the nonparametric structural equation (NPSEM) model of the data-generating mechanism [12, 14]. The parameters of interest returned by these substitution estimators are chosen so that they can be interpreted, under assumptions, of the treatment (or exposure) effects one typically estimates in a randomized controlled trial appropriately adjusted for time-dependent confounders. Since these estimators are functions of portions of the data-generating distribution (such as conditional means), rather than byproducts of a parametric regression model, they put little constraints on the form of the data-generating distribution. Thus, one can use data-adaptive (machine learning), flexible algorithms in order to search among a large class of models to find the one that fits the model optimally. If this fit, according to some loss function, is estimated in an unbiased way (using cross-validation), then one can derive a better fit to the data than say an arbitrary linear regression model, and so derive estimates of the parameter that both have less bias, and lower variance. In addition, because the model selection is done to maximize the fit (minimize the cross-validated risk) of the prediction models, and not targeted towards the parameter of interest, significant reductions in bias are possible via an augmentation to the estimated statistical model based on targeted maximum likelihood estimation (TMLE) [14].

The purpose of this article was to quantify the longitudinal effects of energy intake and expenditure patterns on BMI in adolescence using data from the National Heart, Lung, and Blood Institute Growth and Health Study (NGHS), a 10-year prospective cohort study of preadolescent white and African American girls designed to assess factors associated with the onset and development of obesity [15]. In particular, we assessed the impact of early interventions on physical activity level and caloric intake on BMI by estimating parameters defined by the G-computation formula. Our objectives were to compare, in this setting of longitudinal studies of obesity, the use of standard regression models for estimating the relevant components of the data-generating distribution with semi-parametric, data-adaptive methods and discuss practical implementation of latter methods using the ltmle R package [42].

Methods

Data structure

For this analysis we used a subset of the NGHS data consisting of the participants recruited by the University of California at Berkeley center, one of three recruitment sites for NGHS (n = 530). The participants were 9–10 years of age at study entry and followed for 10 years; 887 girls enrolled at baseline. The study collected anthropometric measurements annually and an extensive set of variables potentially relevant to weight gain, including physical, behavioral, socioeconomic and mental health factors such as pubertal maturation stage, diet, physical activity, parental education, and perceived self-worth [10, 15–20].

The time-dependent outcome variable of interest was BMI-for-age z-score, which indicates BMI relative to other girls of the same age on a standard deviation scale [21]. We focused on physical activity and total calories as the exposures/potential interventions of interest, with the hypotheses that increasing physical activity would result in a lower 10-year BMI and that increasing total calories would have the opposite effect. Physical activity was measured using a Habitual Activity Questionnaire that was adapted from a questionnaire developed by Ku et al. (1981) [22], and compared against two other assessment methods [18]. Total calories were estimated from 3-day food diaries [7]. Potential confounding variables were selected based primarily upon previously reported associations with BMI [10, 16–24]. These included baseline race (white or African American), and the time-dependent variables pubertal maturation stage (four levels: prepuberty, early maturity, midpuberty, maturity), number of hours of television watched per week, perceived stress scale [23], global self-worth score (an indicator of self-esteem measured using a Harter’s Self Perception Profile for Children) [18, 24], as well as the outcome, BMI, at previous measurements.

We focused on three time points after enrollment: years 0 (age 9–10 years), 5 and 10 (19–20 years); selection of these time points was based on preliminary work indicating that these were the most relevant for capturing BMI trajectories. We restricted the sample to the subset of participants who had total calories, physical activity, and BMI z-score measured at years 0, 5, and 10 (n = 530) since this is the level of resolution such that there would be relatively little missing data. However, even at this resolution, there were still missing data for some of the time-varying covariates (confounders), and we imputed missing values by using a local average of the years around the time point of interest within the subject, rather than omitting the girls with missing values completely. This did not appreciably change the overall summary statistics for the covariates when compared to a complete case analysis.

Parameter of interest

The research question we endeavored to answer concerned the potential causal effect of intervening to set longitudinal profiles of physical activity level or caloric intake amount on BMI z-score at year 10 of the study, when the girls were aged 19–20 years. An ideal experiment that would answer this question would be to randomize a cohort of girls at baseline to each potential longitudinal pattern of physical activity and diet, then follow up with the girls, ensuring perfect adherence and no attrition. The causal inference estimation framework makes transparent the identifiability assumptions necessary to estimate such parameters from observational data. The structural causal model (SCM) reflecting our belief about the time-ordering and relationships between the exposure, covariates, and outcome of interest was

$$\begin{array}{l}{L}_0=f_{L_0}(U_{L_0})\\ A_0=f_{A_0}(L_0,U_{A_0})\\ L_5=f_{L_5}(A_0,L_0,U_{L_5})\\ A_5=f_{A_5}(L_5,A_0,L_0,U_{A_5})\\ L_{10}=f_{L_{10}}(A_5,L_5,A_0,L_0,U_{L_{10}})\\ A_{10}=f_{A_{10}}(L_{10},A_5,L_5,A_0,L_0,U_{A_{10}})\\ Y\equiv L_{10+}=f_Y(A_{10},L_{10},A_5,L_5,A_0,L_0,U_Y)\end{array}$$ (1)

where the subscripts denote the three time points of interest (years 0, 5 and 10), A_j, denotes the exposure of interest (physical activity or total calories) within time interval j, L_j are the vector of time-varying confounders (variables that affect both future exposure and the outcome of interest, including intervening measurements of BMI) within interval j, Ydenotes the outcome process of interest (BMI at year 10), and the Us denote unmeasured, independent (exogenous) variables, so that the variables that make up our data set are deterministic (but unknown) functions of the measured history, and some unmeasured error term. Now, we can represent the data as an independent, and identically distributed sample of $O=(\overline{A},\overline{L},Y)$, where the over-bar notation denotes the history of the variable, e.g. Ā = (A₀, A₅, A₁₀, and. Ā₅=(A₀, A₅).

Intervening on the exposure of interest at a certain time point corresponds to deterministically setting (A₀, A₅, A₁₀) = (a₀, a₅, a₁₀), resulting in a modified set of structural equations. The counterfactual outcome is denoted $Y_{\overline{a}}$ and is interpreted as the value that Y would have taken under universal application in the population of the hypothetical intervention Ā = ā. The modified SCM, based on intervening by setting nodes to fixed values, is

$$\begin{array}{l}{L}_0=f_{L_0}(U_{L_0})\\ A_0=a_0\\ L_5(a)=f_{L_5}(a_0,L_0,U_{L_5})\\ A_5=a_5\\ L_{10}(a)=f_{L_5}(a_5,L_5,a_0,L_0,U_{L_{10}})\\ A_{10}=a_{10}\\ Y(a)=f_Y(a_{10},L_{10},a_5,L_5,a_0,L_0,U_Y)\end{array}$$ (2)

where the (1) notation represents counterfactuals indexed by specific treatment regimes, a. Once the SCM is specified, the next step is to specify the counterfactuals indexed by interventions on A. The interventions simulated in this analysis were ones that deterministically set values of the vector ā = {a₀, a₅, a₁₀}. The variables intervened on were physical activity level (1 denotes a high level defined as > 20 METS-times/wk, 0 denotes a low level defined as ≤ 20 METS-times/wk), caloric intake (1 denotes a total caloric intake of 2,000 kcal/day or less and 0 denotes a total caloric intake more than 2,000 kcal). The cutoff for the total calories intervention was determined based on average energy requirement recommendations for women [25]. The physical activity cutoff was determined based on the distribution of physical activity during the first five study years, before physical activity began to decline steeply [26]. The counterfactuals of interest were therefore denoted as Y(a₁, a₅, a₁₀), which can be interpreted as the BMI z-score that participants would have had under interventions on physical activity and total calories. A value a_j = 1 means that a person can be considered “treated” at time point j, while a value a_j = 0 means that they were “untreated” at that timepoint j. The intervention ā = {1, 1, 1} was chosen because it represents good physical activity behavior and/or eating habits being instilled at a young age and continued through adolescence. In contrast, the early intervention of ā = {1, 0, 0} was chosen to represent a decline in physical activity and/or eating habits with age. The late intervention ā = {0, 0, 1} represents the opposite.

Identifiability assumptions – G-computation

In order to estimate the marginal distribution of different counterfactuals from observed data, identifiability assumptions must be asserted. In longitudinal data, one such assumption, the sequential randomization assumption [14, 27] corresponds to

$$A(k)\perp Y(\overline{a})|\text{Parents of }A(k),$$

where Parents indicates all preceding measured variables, and in this case Y(ā) are the set of counterfactuals defined by the combinations of possible interventions. Under this assumption (as well as others outlined below), we can write the counterfactual as an estimand that is a function only of the observed data-generating distribution, P₀:

$$\begin{array}{c}E[Y(\overline{a})]={\displaystyle \sum _{\overline{l}=(l_0,l_5,l_{10})}E[Y|\overline{A}=\overline{a},\overline{L}=\overline{l}]P{[L_{10}=l_{10}|{\overline{A}}_{10}={\overline{a}}_{10},{\overline{L}}_5={\overline{l}}_5]}^{\ast }}\\ P[L_5=l_5|{\overline{A}}_5={\overline{a}}_5,L_0=l_0]P[L_0=l_0].\end{array}$$ (3)

This result is the longitudinal G-computation formula, which allows specification of parameters of the observed data distribution. The parameters we specified depended on the different intervention patterns contained in ā. The parameters of interest are functions of the marginal mean under longitudinal treatment regimes, E[Y(a₀, a₅, a₁₀)], or:

$$\begin{array}{l}{\psi }_1=E[Y(1,1,1)-Y]\\ {\psi }_2=E[Y(1,1,1)-Y(0,0,1)]\\ {\psi }_3=E[Y(1,0,0)-Y(0,0,1)]\\ {\psi }_4=E[Y(1,0,0)-Y]\\ {\psi }_5=E[Y(1,1,1)-Y(0,0,0)]\end{array}$$ (4)

where ψ₁ can be interpreted as the mean difference of BMI z-scores within a population of universal, early sustained intervention versus the mean BMI z-score in the population without any intervention; ψ₂ is a comparison of early sustained intervention to late intervention; ψ₃, compares early intervention, that is not sustained, versus late intervention; ψ₄ is equivalent to ψ₁, but now comparing early, but not sustained intervention to a population without any intervention. Finally, ψ₅ compares sustained intervention to a population where everyone follows relatively high caloric intake or relatively low physical activity.

In order for one to be able to estimate these causal parameters, there needs to be sufficient natural experimentation of the variable of interest (the A_j) within groups defined by the history of covariates, ${\overline{L}}_j$ and previous levels of the A_j−. This is the so-called positivity assumption. There cannot be combinations of covariate and exposure histories, for which all participants are only “treated” or “untreated”, since this would make the right-hand side of eq. (2) undefined. Positivity is especially problematic when the covariates and treatment are continuous and in these data, there were many covariates. Thus we discretized the covariates by creating groupings defined by reasonable cutoffs. Specifically, we dichotomized the number of hours of television according to the recommendations from the American Academy of Pediatrics as “high” if the individual watched more than 2 hours/wk and “low” if they watched two or fewer hours per week. Stress was dichotomized as “high” if the stress score was above 25 and “low” if the score was equal to or less than 25. Race, pubertal stage, and self-worth score did not require discretization to address the positivity requirement. Energy intake was used as a confounder in the analysis of an intervention on physical activity and vice versa, using the cutoffs defined above.

The substitution estimator is then given by

$$\begin{array}{c}\widehat{E}[Y(\overline{a})]={\displaystyle \sum _{\overline{l}=(l_0,l_5,l_{10})}\widehat{E}[Y|\overline{A}=\overline{a},\overline{L}=\overline{l}]\widehat{P}{[L_{10}=l_{10}|{\overline{A}}_{10}={\overline{a}}_{10},{\overline{L}}_5={\overline{l}}_5]}^{\ast }}\\ \widehat{P}[L_5=l_5|{\overline{A}}_5={\overline{a}}_5,L_0=l_0]P_n[L_0=l_0].\end{array}$$ (5)

This estimator requires the estimates of the relevant regressions and joint distribution of intermediates, given the past. Typically, one derives the mean via time-sequential simulation of the L-process, setting the treatment history to the desired rule. Thus, the standard formulation of this substitution estimator requires often challenging estimation, since it requires estimation of joint densities.

Van der Laan and Gruber [28] present a different representation of eq. (3) that avoids having to estimate the joint conditional density of intermediate variables, e.g. the $P[L_t=l_t|{\overline{A}}_{t-1}={\overline{a}}_{t-1},{\overline{L}}_{t-1}={\overline{l}}_{t-1}]$ Specifically, by invoking the tower rule, one can represent E[Y(ā) as an iterative conditional expectation (ICE). The approach is based on the G-computation representation of the density of the covariate process, L, which can be written as:

$$P^a(\overline{l})={\displaystyle \prod _{j=0}^{J+1}{Q}_j^a}(\overline{l}(j)),$$

where $Q_j^a(\overline{l}(j))=P(l(j)|\overline{L}(j-1)=\overline{l}(j-1),\overline{A}(j-1)=\overline{a}(j-1))$ is shorthand notation for defining the conditional distribution of a covariate process given a treatment process at a particular time j; equivalently define ${\overline{Q}}_j^a$ to be the associated conditional expectation implied by $Q_j^a$. In addition, introduce notation for a set of random variables, L^a = (L(0), L^a(1),…, L^a(J), Y = L^a(J + 1)) which has distribution, P^a, that is counterfactual random vectors of the covariate process generated under a specific treatment regime, a. The ICE representation is based on an equality which is formed from ICEs relative to these counterfactual distributions, or:

$$\begin{array}{l}E[Y(\overline{a})]=E_{L(0)}\left[E({\overline{Q}}_1^a(L^a(1)|L(0))\right]\\ =E_{L(0)}\left[E\left[E({\overline{Q}}_2^a(L^a(2))|L^a(1)\right]|L(0)\right]\\ =E_{L(0)}\left[E\left[\dots E({\overline{Q}}_{J+1}^a(Y)|L^a(J))\right]|\dots L(0)\right]\end{array}$$

The substitution estimator, following eq. (6), starts with estimating the innermost conditional expectation, $E[{\overline{Q}}_{J+1}^a(Y)|L^a(J))]$, and then moves outward, estimating the relevant regressions to generate the estimated conditional expectations, until at the end, one simply gets an average across all observations. The obvious computational virtue is that unlike the estimator (5), one does not have to estimate conditional densities of the covariate process, L, but only a set of conditional expectations (regressions) that can be done much more straightforwardly, using data-adaptive (semiparametric) techniques. This is an enormous advantage over the estimator based on eq. (5). The one small disadvantage, is these set of regressions must be run for each desired treatment rule, a, whereas using the original formulation, one only has to estimate the conditional densities once. However, this is a very small price to pay when the covariate process is high dimensional, i.e. consists of many variables, so any practical joint conditional density estimation requires either very strong assumptions (conditional independence, or joint normality, etc.) or a very large degree of smoothing (e.g. histogram density with very large bins). Table 1 contains the steps for defining the parameter of interest, as well as the associated estimation steps, for our specific obesity study.

Table 1.

Steps of defining parameter and estimate in the ICE formulation

Step	Definition of parameter in ICE formulation	Estimation step in the obesity study
1	Define the conditional expectation of the outcome with covariate history set to observed, and the treatment history to the desired intervention, or: ${{\overline{Q}}_{Y,10+}^a}^{\underset{¯}{\underset{¯}{\text{def}}}}E(Y|{\overline{A}}_{10}={\overline{a}}_{10},{\overline{L}}_{10})$	Regress the final BMI z-score, Y, given its parents: ${\overline{Q}}_{n,Y,10+}({\overline{A}}_{10},{\overline{L}}_{10})$, get the predicted value at the treatment history of interest: ${\overline{Q}}_{n,Y,10+}({\overline{a}}_{10},{\overline{L}}_{10})$
2	Take the expectation of ${\overline{Q}}_{Y,10+}^a$ based on the covariate and intervention of interest up to 10 years (in our ordering treatment comes after L-process measured within the same interval), ${{\overline{Q}}_{L,10+}^a}^{\underset{¯}{\underset{¯}{\text{def}}}}E({\overline{Q}}_{Y,10+}^a|{\overline{A}}_5={\overline{a}}_5,{\overline{L}}_5)$	Regress ${\overline{Q}}_{n,Y,10+}({\overline{a}}_{10},{\overline{L}}_{10})$ against parents of ${\overline{L}}_{10}$ and then predicted at ${\overline{A}}_5={\overline{a}}_5,{\overline{L}}_5:{\overline{Q}}_{n,L,10}^a({\overline{a}}_5,{\overline{L}}_5)$.
3	Repeat to define ${{\overline{Q}}_{L,5}^a}^{\underset{¯}{\underset{¯}{\text{def}}}}E({\overline{Q}}_{L,10+}^a|A_0=a_0,L_0)$	Regress ${\overline{Q}}_{n,L,10}^a({\overline{a}}_5,{\overline{L}}_5)$ against the parents of ${\overline{L}}_5$ and predict at $a_0,{\overline{L}}_5:{\overline{Q}}_{n,L,5}^a(a_0,L_0)$
4	The parameter of interest is: ${{\overline{Q}}_{L,0}^a}^{\underset{¯}{\underset{¯}{\text{def}}}}{E}_{L_0}({\overline{Q}}_{L,5}^a)=E[Y(\overline{a})]$	Derive the estimate of the treatment-specific mean by taking an average of the $Q_{n,L,5}^a$, or $\widehat{E}Y(\overline{a})=\frac{1}{n}{\displaystyle {\sum }_{i-1}^n{\overline{Q}}_{n,L,5}^a}(a_0,L_{0,i})$

Because the ${\overline{Q}}_{n,L,t}^a({\overline{A}}_{t-},{\overline{L}}_{10})$ are defined via particular treatment regime of interest, a, this procedure is repeated for each particular regime of interest. This formulation offers a very compelling alternative to a substitution based on the standard representation (4). However, using the estimator based on the ICE approach still requires estimates of very high-dimensional regression, outcomes versus often many variables, potentially measured at several times in the past), in a very big, semi-parametric model. We discuss below how to target the estimation towards our particular parameter of interest, but before we do so, we discuss a general data-adaptive approach for deriving the regression models required for the estimate listed in Table 1.

Estimation via SuperLearner

Given little theory to guide one on the functional form of the regressions that comprise our ICE estimator, and the impossibility of nonparametric estimation because of the high dimension of the predictors, a potentially consistent approach requires a data-adaptive, semiparametric modeling method. Traditional approaches would fit the regressions based on a potential simplification (dimension reduction) of the predictors (e.g. the conditional means given the entire history are only functions of the most recent history), and/or the assumption of a simple parametric forms (e.g. regression with only main effects). Because doing so will almost certainly result in a misspecified model, such arbitrary (non-targeted) simplifications will result in an arbitrarily biased estimator. Thus, we used the data-adaptive, ensemble machine learning algorithm known as the SuperLearner (SL) [29]. The SL takes a library of algorithms and uses cross-validation to create a convex combination of the algorithms with weights based on the ability of each algorithm to minimize the cross-validated risk (expected value of the user-supplied loss function) in the cross-validation procedure. The optimality properties of cross-validation and super learning are detailed in van der Laan and Polley [29] and van der Laan et al. [30]. If k algorithms are competitors, the Oracle Selector is the one that chooses the algorithm that minimizes the true risk as if the true underlying distribution of the data was known. The Oracle Inequality suggests that the number of candidates algorithms considered can be polynomial in size without hindering the performance of SL. Thus, many algorithms can be considered and the combination will perform asymptotically as well as the Oracle selector. Therefore, it is a good choice for estimating the required models since one can include both more agnostic algorithms, and particular models favored by the researchers. Although sample size might indicate a variance-bias trade-off towards a smaller model (and thus more biased model), theory indicates that this trade-off will be in an optimal direction.

Since the SL is an ensemble learner, the candidate algorithms from which it chooses and utilizes in the combination are not indicated. We used the SL package available in R [31] and our library of candidate learners included generalized linear models (GLM), generalized additive models (GAM) [32], Bayesian generalized linear models (bayesGLM) [33], generalized linear models using coordinate-wise descent (glmnet) [34, 35], and the mean function. In addition, one must specify the number of splits (folds); 10-fold cross-validation was used to estimate the final model.

Targeted maximum likelihood estimation

The data-adaptive fitting of the models that make up Step 1 above are targeted to optimizing the ability of models to predict the outcome, and not towards estimating the parameter. One can improve the estimator by “targeting” these fits towards the parameter of interest. Specifically, we used Targeted Maximum-Likelihood Estimation (TMLE), a two-stage estimator that augments the estimated models that comprise the ICE-inspired algorithm discussed in Table 1. This results in a bias-reduction step, which will remove residual bias relative to the substitution estimator if the treatment mechanism can be estimated consistently [14]. The TMLE augmentation [28] involves adding a so-called clever covariates to each of these regressions, which requires estimation of the treatment mechanism. Specifically, for each time point, it requires estimates of the probability of being in the treatment group (e.g. high physical activity) given the past (that is, all past covariates, treatments, and outcomes) [36].

Specifically, we use the same formulation as discussed above, but now based on $Q_{n,L,J}^{\ast a}$, which is obtained, as a regression, treating the initial estimator, $Q_{n,L,J}^a$ as an offset, of Y against covariate:

$$c_j(\overline{A},g)=\frac{I(\overline{A}(j-1)=\overline{a}(j-1))}{{\displaystyle {\prod }_{k=0}^{j-1}{g}_{n,k}}}$$

where g_k, ≡ P(A_k = a_k|Parents(A_k)). To derive the clever covariate one needs an estimate of g_k (g_n,k) and in this case, we used simple main terms logistic regression, both for the outcome of current treatment given the past. This is done as a compromise to ameliorate the residual bias that could result from the original SL fits, which are designed to minimize the risk of the prediction but avoid adding problems with creating large outliers via these clever covariates that can result from models that estimate probabilities of censoring or treatment either close to 1 or 0 (see chapter on CTMLE in Van der Laan et al. for a less ad hoc approach to model selection for the treatment/censoring models in the context of TMLE).

As discussed above, one of the virtues of TMLE over the initial substitution estimator is that it reduces bias due to the fact that the original statistical models are chosen based on minimizing expected loss with regards to prediction of the outcomes (intermediate and final), and not with regards to minimizing the mean-squared-error of the estimate of the parameter of interest. Relatedly, the TMLE estimate is consistent if either the original models or the treatment/censoring models are consistently estimated (doubly-robust). If they both are consistently estimated, the estimator is semi-parametrically (locally) efficient. Finally, the TMLE can be thought of a smoothing of the original substitution estimator, and thus can have more predictable sampling distributional properties; it is an asymptotically linear estimator with a known influence function, and this can be used to derive robust asymptotic inference [14]. Thus, one can derive an approximate SE by simply taking the sample standard deviation of the estimated IC of a subject divided by the sample size, or $\mathrm{SE}\left(\widehat{\psi }\right)=\sqrt{\frac{\widehat{\mathrm{var}}(\text{IC})}{n}}$ (see van der Laan and Gruber [28] for the form of the IC).

The required calculations would seem a daunting task to code, and thus the effort required could inhibit taking such an approach. However, an R package, ltmle, provides a one-stop, user-friendly implementation of the ICE, TMLE estimator. One can either use the defaults available for estimating the prediction and treatment models, or one can specify particular algorithms, including SL with an associated library of learners. Though not discussed here, the package incorporates the possibility of missing data and not just fixed treatments of interest, but treatment rules. The package also returns, in addition to the TMLE estimate, the ICE based on non-augmented model, the so-called inverse probability of treatment weighted (IPTW) estimators, as well as a “naïve” estimate based on no dependent confounding. Finally, the package will also return estimates of marginal structural models if one wants to model the treatment-specific mean as a potentially smooth function of the history of intervention (e.g. the total number of time intervals with treatment). Thus, the powerful ltmle packages makes estimating a relatively complex suite of estimators amazingly straightforward, which opens the door to estimation of targeted casual parameters based on potentially complex interventions to a much wider audience.

Data analysis results

Characteristics of the sample of NGHS participants at the three time points in the analysis are provided in Table 2. All participants were aged 9 or 10 at Year 0. There was a noticeable decrease in physical activity at Year 10. Additionally, by the end of the study, all participants had reached pubertal maturation. Table 3 contains the numbers and percent of individuals who followed the relevant patterns of interest in total calories and physical activity.

Table 2.

Characteristics of the sample of NGHS participants (N = 530) at three time points

Variable	Year 0	Year 5	Year 10
	mean (SD1)	mean (SD)	mean (SD)
BMI z-score	0.41 (1.1)	0.72 (1.0)	0.53 (1.1)
Total calories (kcal)	1,953 (607)	1,894 (699)	1,972 (717)
Physical activity (METS-times/wk)	29.1 (17.9)	19.7 (14.1)	11.4 (17.2)
Hours of TV/video per week	33.0 (18.4)	35.5 (20.6)	30.6 (24.4)
Perceived stress2	25.3 (6.8)	24.0 (6.4)	23.4 (8.0)
Global self-worth score3	3.1 (0.6)	3.1 (0.7)	3.2 (0.6)
	N (%)	N (%)	N (%)
Race
White	270 (51%)
Black	262 (49%)	–	–
Pubertal stage
Prepuberty	334 (63%)	0 (0%)	0 (0%)
Early maturity	172 (32%)	32 (6%)	0 (0%)
Midpuberty	24 (5%)	400 (75%)	0 (0%)
Maturity	0 (0%)	98 (18%)	530 (100%)

Notes:

¹Standard deviation

²A 10-item scale developed by Cohen with scores ranging from 0 to 40 (1983)

³A 6-item scale developed by Harter with scores ranging from 1 to 4 (1982).

Table 3.

Number and percent following the early interventions on physical activity and total calories

	1, 1, 1	1, 0, 0	0, 0, 1	0, 0, 0
Physical activity	102 (19%)	132 (25%)	10 (2%)	45 (8%)
Energy intake	130 (25%)	63 (12%)	35 (7%)	54 (10%)

The results of estimation of the marginal means of interest by four estimators are in: a “naïve” estimator, and a series of ICE substitution estimators based on different models for the relevant regressions: (a) based on multivariate regressions with only main effect terms, (b) on SL fits, and (c) based on augmented SL fits, or TMLE. We fit these to compare, in order, an estimators that (1) simply assumed no confounding at all, but in that context makes no modeling assumptions (naïve), (2) adjusts for confounding, but in a parametric model (MTLR for multivariable linear regression), (3) adjusts for confounding in a much bigger (and therefore less biased) statistical model, but where the estimator is not targeted towards the particular parameter of interest (and thus, contains no “smoothing” adjustment of the estimate of the data-generating distribution towards that parameter – SL), and (4) is targeted for estimation in a large (semiparametric) model and, but specifically for the parameter of interest (TMLE). Statistical inference was based on the influence curve for the TMLE estimators, but on the nonparametric bootstrap for all others (we also re-did the inference for one of the TMLE estimators using the bootstrap as a check on the IC-based inference).

There are often substantial differences between the adjusted estimates based on the SL (TMLE and SL) and the, naïve, suggesting that these are confounded by the included covariates. For example, the naive point estimate of E(Y(0,0,1)) is very different from the estimates generated from the SL and TMLE estimators (Table 4). The point estimates serve as the inputs for the various intervention comparisons (4) shown in Table 5. One can see some significant differences between the simple substitution estimator based on parametric regression and that based on SL (the equivalent substitution estimator and TMLE). For instance, for physical activity, the estimate of ψ₄ using MTLR is −0.44 and apparently statistically significant. However, given the model used was no doubt misspecified, no doubt the estimator is also biased, whereas both the estimators based on an initial SuperLearning fit (SL and TMLE) are close to the null. This represents a fairly serious bias that could have resulted in the estimate of a misspecified, parametric regression model was used. If looking at the TMLE estimates, there are no significant estimated intervention comparisons for physical activity; the most “extreme” comparison for total caloric intake (longitudinally consistent low versus consistently high) suggests a modest but significant reduction in BMI standardized units (−0.192; 95% CI −0.374, −0.010). To make sure that this estimate and inference was stable, we also derived the inference of this estimate using the nonparametric bootstrap and got very similar results (95% CI −0.410−0.011), with a symmetric bootstrap distribution (see Figure 1). The corresponding estimate before the TMLE augmentation (the SL estimator) shows a more modest reduction in BMI from consistently low caloric intake of −0.123. The difference between the two is driven mainly by the difference in the TMLE estimate versus the SL estimate of E[Y(0,0,0)], that is around 0.7 vs. 0.6 standardized units (and both estimates are much larger than the naïve estimate of around 0.5). Thus, the significant TMLE-based association appears to be a result, not just of fitting a semiparametric model adjusting for time-dependent and time-independent confounding, but also by the augmentation of these original models to account for potential residual confounding.

Table 4.

Comparison of the point estimates for each intervention using 4 different estimators

Intervention	Estimation method	Intervention
		Physical activity	Energy intake
E(Y(0,0,0))	NAÏVE	0.747	0.526
	MTLR	0.636	0.662
	SL	0.590	0.599
	TMLE	0.548	0.695
E(Y(0,0,1))	NAÏVE	0.400	0.638
	MTLR	0.729	0.582
	SL	0.636	0.561
	TMLE	0.641	0.508
E(Y(1,0,0))	NAÏVE	0.526	0.433
	MTLR	0.490	0.549
	SL	0.505	0.535
	TMLE	0.528	0.597
E(Y(1,1,1))	NAÏVE	0.399	0.555
	MTLR	0.522	0.434
	SL	0.531	0.476
	TMLE	0.597	0.503
E(Ybar)	NAÏVE	0.533	0.533
	MTLR	0.533	0.533
	SL	0.531	0.531
	TMLE	0.540	0.528

Notes: A simple naïve (unadjusted) estimator (NAÏVE), ICE-based substitution estimates using (a) main effects multivariable linear regression (MTLR), (b) SL, and (c) SL augmented via Targeted Maximum-Likelihood Estimation (TMLE). Values are based on BMI z-scores.

Table 5.

Estimates for specific intervention comparisons with different estimation methods

	Method	Intervention
		Physical activity (95% CI)	Energy intake (95% CI)
Ψ1	NAÏVE	−0.134 (−0.429, 0.100)	−0.056 (−0.254, 0.212)
	MTLR	−0.010 (−0.122, 0.103)	−0.099 (−0.166, −0.027)
	SL	0.0001 (−0.115, 0.086)	−0.055 (−0.167, −0.047)*
	TMLE	0.057 (−0.520, 0.634)	−0.026 (−0.458, 0.406)
Ψ2	NAÏVE	−0.002 (0.617, 0.497)	0.161 (−0.471, 0.237)
	MTLR	−0.206 (−0.382, −0.032)*	−0.148 (−0.298, 0.019)
	SL	−0.106 (−0.345, 0.043)	−0.085 (−0.306, −0.018)*
	TMLE	−0.044 (−0.304, 0.216)	−0.005 (−0.227, 0.217)
Ψ3	NAÏVE	0.125 (−0.481, 0.582)	−0.103 (−0.628, 0.163)
	MTLR	−0.239 (−0.436, −0.057)	−0.032 (−0.206, 0.145)
	SL	−0.131 (−0.363, −0.064)*	−0.0261 (−0.200, 0.100)
	TMLE	−0.114 (−0.330, 0.103)	0.089 (−0.157, 0.335)
Ψ4	NAÏVE	−0.007 (−0.226, 0.149)	0.002 (−0.426, 0.174)
	MTLR	−0.437 (−0.110, 0.022)	0.017 (−0.087, 0.114)
	SL	−0.025 (−0.093, 0.020)	0.004 (−0.080, 0.095)
	TMLE	−0.012 (−0.620, 0.596)	0.068 (−0.354, 0.491)
Ψ5	NAÏVE	−0.348 (−0.646, −0.095)*	−0.056 (−0.325, 0.307)
	MTLR	−0.114 (−0.312, 0.083)	−0.228 (−0.388, −0.065)*
	SL	−0.059 (−0.271, 0.076)	−0.123 (−0.400, −0.108)*
	TMLE	0.049 (−0.170, 0.269)	−0.192 (−0.374, −0.010)*

Notes: Naïve corresponds to an unadjusted comparison under different interventions. MTLR corresponds to main effects multivariable linear regression. SL corresponds to a simple substitution estimator based on SL. TMLE corresponds to targeted maximum-likelihood estimates. Values are differences in BMI z-scores, and

^*indicates statistically significant association.

Figure 1.

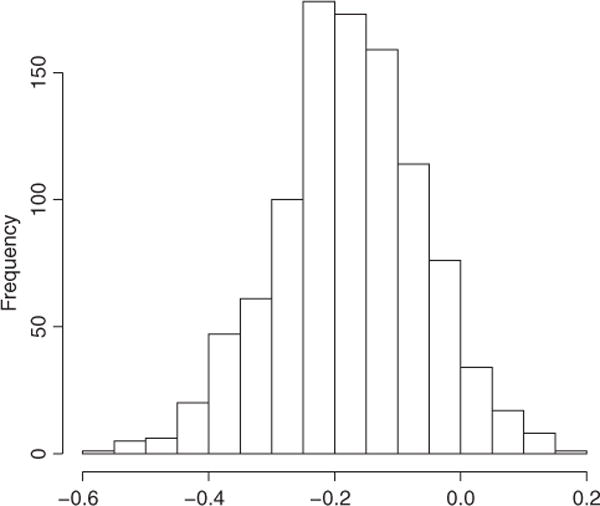
Nonparametric bootstrap distribution of TMLE estimator of ψ₅

Discussion

One should always estimate the data-generating distribution within a statistical model that only is constrained by what one actually knows about the distribution. In most circumstances, such as longitudinal studies of obesity, little if anything is known about the form of the data-generating distribution, so the true statistical model is semiparametric. In addition, the parameters of interest should be based upon the specific scientific/policy questions of interest, and not as a convenient byproduct of a parametric statistical model. In this article, we have applied advances in data-adaptive estimation (SuperLearning) combined with a targeted bias reduction (TMLE) to estimate parameters targeting the impact of longitudinal interventions in both caloric intake and physical activity on BMI in the study of adolescent obesity.

In our case, we defined the parameters of interest as marginal means of BMI at different fixed longitudinal intervention profiles, and differences of those means related to specific questions regarding how a potential pattern of intervention could affect BMI at age 19–20 years old. Then, we compared the use of data-adaptive super learning and a targeted (TMLE) augmentation to this initial fit to estimates of the same parameter using both parametric linear regression analyses, as well as a simple naïve (unadjusted) analysis.

The estimated impacts of physical activity and total calories on year 10 (ages 19–20) mean BMI z-score in this population were not significant, with total calories having a larger effect regardless of the estimation method used. Specifically, looking at the TMLE estimates, only the most extreme comparison (that is ψ₅, representing the difference of means if having continuously reported relatively high versus low caloric intake) was the only comparison to remain significant (or close to significant), though the impact on mean BMI is rather slight. We were concerned about the stability of this estimate, so we also used the nonparametric bootstrap (as opposed to the influence-curved based inference) and found the resulting estimates of the sampling distribution were nearly identical, indicating the robustness of this finding. There significant differences in the estimates of some parameters (see ψ₄ for physical activity), but not for others (the estimate of ψ₅ for total caloric intake). However, one never knows a priori when using a semiparametric TMLE estimator will “matter” and when it makes little difference in the estimation/inference, and this analysis suggests it is unwise to assume the difference will not be important. Thus, augments are made on behalf of simpler approaches as opposed to a more rigorous and more complicated procedure are charitably, naïve. In summary, the TMLE based on SL provided an estimate that appears to have a (close to) normal sampling distribution as estimated by the bootstrap (Figure 1), less asymptotic bias since it is estimated in a much larger model, but in this case apparently little sacrifice regarding sampling variability. We note that there are estimating equation based alternatives for estimating these parameters include inverse probability of treatment weighting (IPTW) and augmented IPTW (A-IPTW) [12, 27, 37]. However, as discussed in van der Laan and Rose [14] and several other articles involving applications, TMLE has both the double-robustness of the A-IPTW in this case, but also has the additional benefit of more potential robustness in this case by making sure the model for the relevant components of P₀ falls within the natural boundaries of the outcome variable (in this case, between the minimum and maximum of observed BMI z-scores).

To suggest that we can identify the causal effect of the proposed interventions from the data requires strong assumptions, and we acknowledge that many of them will not be precisely true. We also acknowledge that examining the longitudinal effects of total caloric intake and physical activity on BMI is a complex problem and that other variables could be considered in future studies. For instance, accurate measurement of diet and physical activity, especially in children, is challenging, and measurement error could have been a major issue in this application. Additionally, deterministically setting diet and physical activity to certain levels may not be realistic since, for example, girls who are very physically active may consume more calories. Dynamic regimes assign the exposure value based on the value of covariates. In this case, for example, physical activity could be set to a certain level depending on the total calories consumed. Rather than forcing everyone in the study population to the same exposure value, this allows for more realistic interventions. Finally, we limited our analysis to a relatively small set of potential confounders. Some other potential confounders of interest that warrant future investigation with regard to the development of adolescent obesity include genetic factors, self-perception, and exposures to mental health stressors, endocrine disruptors, and community-level variables such as aspects of the built environment [38–40]. Though there is clearly a benefit to reducing the bias of residual confounding, new challenges arise, such as greater potential for the violating positivity assumption, which requires that there be variation of the exposure variable within strata of the covariates; this assumption generally becomes harder to meet as more covariates are included in the analysis [41]. In our application, even with a relatively small set of covariates, some dimension reduction measures, such as dichotomizing continuous variables, was needed. Of course, that is one of the challenges of estimating ambitious parameters with relatively small sample sizes.

Recognizing the limitations of this analysis, we have provided a framework for estimation of longitudinal interventions related to childhood obesity from observational data. This analysis has demonstrated how a very flexible, and yet user-friendly implementation of estimation of intervention rules via longitudinal TMLE (ltmle) [28, 42] provides a powerful way of estimating parameters with direct public health relevance within a large (honest) statistical model.