Abstract
Cell motility relies on the continuous reorganization of a dynamic actin-myosin-adhesion network at the leading edge of the cell, in order to generate protrusion at the leading edge and traction between the cell and its external environment. We analyze experimentally measured spatial distributions of actin flow, traction force, myosin density, and adhesion density in control and pharmacologically perturbed epithelial cells in order to develop a mechanical model of the actin-adhesion-myosin self-organization at the leading edge. A model in which the F-actin network is treated as a viscous gel, and adhesion clutch engagement is strengthened by myosin but weakened by actin flow, can explain the measured molecular distributions and correctly predict the spatial distributions of the actin flow and traction stress. We test the model by comparing its predictions with measurements of the actin flow and traction stress in cells with fast and slow actin polymerization rates. The model predicts how the location of the lamellipodium-lamellum boundary depends on the actin viscosity and adhesion strength. The model further predicts that the location of the lamellipodium-lamellum boundary is not very sensitive to the level of myosin contraction.
Keywords: cell motility, lamellipodium, adhesion
1. INTRODUCTION
Cell migration results from a cycle of protrusion, adhesion, and contraction. The cell leading edge is protruded by the polymerizing front of a broad and flat network of F-actin filaments called the lamellipodium [1]. Near the leading edge, the polymerization of the lamellipodium only partially translates into protrusion, because the network also undergoes retrograde motion toward the cell center. The retrograde flow of actin is slower in the lamellum (actomyosin network that begins 2–4μm away from the leading edge). While the faster retrograde flow near the leading edge is driven mainly by growing actin filaments pushing against the membrane [2], the slower flow in the lamellum is caused by myosin II-generated contraction of the actin network [2] (figure 1). In addition to driving the actin network backward, actomyosin contraction pulls the cell rear forward and is also involved in maturation of adhesion sites [3–4]. The adhesion sites are initiated in a myosin force-independent manner within the lamellipodia as very dynamic nascent adhesions [5]. The nascent adhesions become partly stabilized, forming dot-like focal complexes, and then grow, elongate, and become further stabilized producing elongated mature focal adhesions [6].
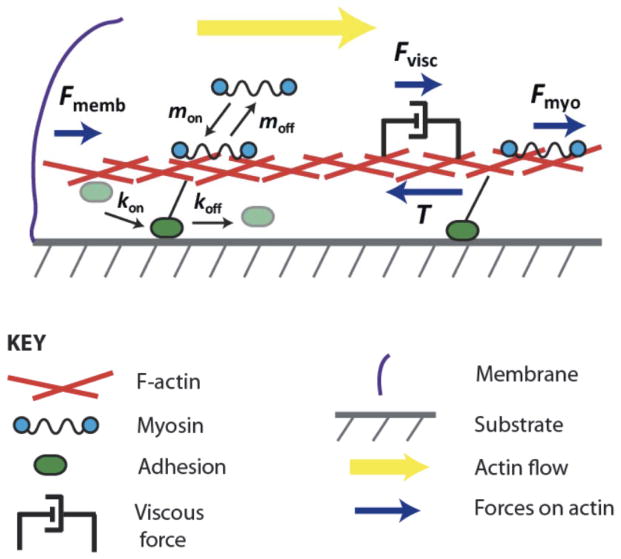
Figure 1. Schematic of model.
The viscous actin network undergoes the retrograde flow pushed by the membrane tension and pulled by the myosin-generated stress balanced by the traction stress. Both myosin and adhesion units engage/disengage with/from the actin network, the latter with the rates affected by the flow rates and myosin forces.
Adhesions connect the actin network to the extracellular matrix (ECM) [7] and transmit stresses generated in the actin network by the actin pushing against the membrane and by the myosin contraction to the ECM. These traction stresses generally orient away from the leading edge, in the same direction as the flow of actin, allowing the polymerizing actin network to exert protrusive force on the leading edge membrane [8–9]. The mechanical role of the adhesions is often likened to a molecular clutch, which slows actin retrograde flow and allows the actin polymerization to contribute to leading edge protrusion [10–12]. Thus, mechanical properties of the adhesions are crucial for cell motility.
While the mechanics of single adhesive molecules is being actively investigated [13], experimental understanding of adhesion complex mechanics is very poor. So far, the only, relatively crude, way to estimate the adhesive strength is to measure simultaneously the actin flow and traction stress [14–15], and to interpret the ratio of the stress and flow speed as an effective adhesive viscous drag. To fill this gap in our knowledge, recent modeling studies [16–19] borrowed ideas from the theories of molecular friction [20] and simulated adhesions as sticky springs dynamically binding and unbinding to the deformable surfaces that these springs connect. Even these simple models revealed a great wealth of mechanics of the dynamic adhesion, including, among other possibilities, biphasic and stick-slip force-velocity relations, so that the adhesive strength can be great at slow actin flow rate and weak at faster rates. These models focused largely on the dynamics and mechanics of individual adhesions. On the other hand, a number of other models considered coupling of adhesion-generated forces to active contractile forces generated by myosin and passive resistance of the lamellipodial actin network to deformations [21–23] assuming constant uniform adhesion strength across the cell. Two recent modeling studies [24–25] went further: in Welf et al. [24], a balance of four sources of stress – originating from contraction, membrane ‘recoil’, adhesion clutch and retrograde flow – was considered. Notably, the adhesion force had viscous character – it was proportional to the product of the density of nascent adhesions and the retrograde flow rate, and the number of engaged adhesions was a decreasing functions of the force applied to them. In addition, positive feedbacks from protrusion to adhesion, and from tension on the clutch adhesions to myosin, were introduced. In another study [25], adhesions were modeled as elastic springs between the actin network of the cell and the deformable substrate, which disengage at a critical force. The focus of these two studies was not on the spatial self-organization of the adhesions, actin flow, myosin and traction force. Complex and stochastic temporal leading edge dynamics was investigated in [24], while myosin and stresses and flow in actin network were not modeled in [25], besides, the very special case of wide and fast keratocyte’s lamellipodium was addressed in [25].
A recent paper by Shemesh et al [26] considered the interactions of the F-actin network and force-sensitive adhesion dynamics in a coordinated, spatially explicit way for the first time. In [26], the actin network is modeled as an elastic gel. Adhesions detach at a rate that increases with local force, grow if the force is above a certain force threshold and shrink if the force is below another force threshold. These dynamics lead to separation between the leading edge and a band of adhesions, because adhesions too close to the front experience so much local force that the gel momentarily detaches from the adhesion, switching from a sticking mode (bound to adhesion) to a slip mode. In the slip mode, the adhesions do not apply traction on the gel, but they re-stick at some rate. The adhesions near the leading edge experience more time in the slip mode, but the average traction forces over time cause them to grow slowly. At a greater distance, adhesions grow faster because they share the applied force, which allows them to grow but rarely induces the stick-slip transition. At yet greater distance, adhesions are screened from the elastic forces and decay. Thus, the model predicted that the band of the stable adhesions develops at some distance from the leading edge, and the authors of [26] proposed, following experimental study [27], that this band demarcates the lamellipodium – lamellum boundary.
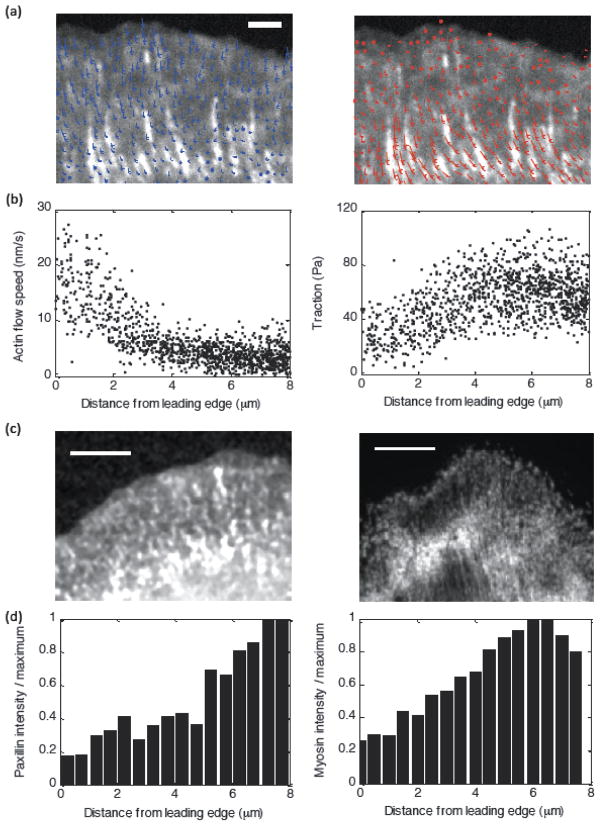
Simultaneous measurements of the traction stress and actin flow rate in Ptk1 epithelial cells [14] revealed that this adhesion band at the lamellipodium – lamellum boundary also is slightly distal to a peak in the traction stress, which is smaller both at the front, in the lamellpodium, and at the rear, in the lamellum (figure 2). On the other hand, the actin flow rate decreases away from the leading edge (figure 2), revealing a biphasic spatial relationship between F-actin retrograde flow speed and traction stress. To understand this complex spatial organization of the actin, myosin, and adhesions underlying the adhesion clutch and the resultant regions of inverse and direct correlation between actin flow and traction, we build on the ideas of [24, 26] and develop a continuous mechanical model for coupled actin flow, myosin contractility, adhesion dynamics and traction stress.
Figure 2. Sample experimental data from Ptk1 cells.
(a) Left: Actin flow vector field overlaid on paxillin intensity image for a Control Ptk1 cell. Right: Traction vector field overlaid on same image. (b) Actin flow speed and traction magnitude as a function of distance from the leading edge for a sample control cell. (c) Fluorescent images of paxillin intensity (left) and myosin intensity (right) for sample control cells. (d) Intensity as a function of distance from the leading edge for the sample cells in (c).
Such a model is necessary for the following reasons: First, [24–26] did not focus on the spatial distribution of the actin flow and traction stress. Second, [26] assumed that the actin network is mechanically elastic (studies [24–25] did not explicitly model the spatial distribution of stress in the actin network). However, at characteristic values of the lamellipodial width and actin flow speed in slow motile epithelial cells, it would take on the time scale of minutes for an actin filament to traverse the lamellipodial width, while actin filaments turn over many times on this time scale [28]. This turnover makes the elastic deformations dissipate and the actin network becomes mechanically viscous [29–30]. (We also demonstrate in the appendix that a model based on elastic deformations predicts an actin flow distribution qualitatively different from that observed.) Third, [26] did not consider myosin contraction in their work, which was justified by the idea that myosin does not influence the lamellipodial dynamics. Here we explicitly consider myosin dynamics; Its weak (but not negligible) role in the lamellipodium is one of the predictions of the model. Finally, the continuous and deterministic character of our model complements the discrete, computational and stochastic nature of the study [26], providing further insight into how key mechanical parameters determine lamellipodial-lamellar geometry, forces and movements.
We demonstrate that a model in which adhesion clutch engagement is strengthened by myosin force but weakened by actin flow (or traction force) quantitatively explains the experimentally observed biphasic traction force distribution and decreasing actin flow (figure 2) [14], and also qualitatively reproduces measured distributions of myosin and adhesion density (figure 2). The model further predicts that, for cells with slow uniform retrograde flow speed across the lamella, the traction peak is located at the leading edge and the lamellar actin flow speed is relatively insensitive to myosin-generated stress. We confirm these predictions by measuring actin flow and traction stress in U2OS epithelial cells, which exhibit relatively slow uniform flow in contrast to the steeply decaying retrograde flow speed distribution observed in Ptk1 cells. We treated the U2OS cells with varying concentrations of the Rho-kinase inhibitor Y-27632 compound, which leads to reduced myosin forces, and we observe relatively unchanged actin flow speed in the lamella over a broad range of total myosin force [31]. The insensitivity of lamellar actin flow to myosin-generated stress in U2OS cells is explained in our model by the myosin-dependent adhesion strengthening: Greater myosin pulling increases the adhesion strength, and so the flow (which is the ratio of the former and the latter) does not change. We also discuss the predicted dependence of the lamellipodial width on mechanical parameters of the cell.
2. MODEL
Figure 1 illustrates the physics of our model of the leading edge adhesion clutch system. Because the relevant forces and flows are directed radially inward, we consider a one-dimensional (1D) description of the system, where the variable x denotes the inward distance from the cell leading edge. We treat the F-actin network as an isotropic gel [32], and we assume that internal network stresses are viscous. There is evidence in biophysical literature [30–31] that on time scales longer than a few seconds, the actin gel, even cross-linked heavily, is mostly viscous. This is because actin-binding proteins attach to and detach from actin filaments on the second scale, and over a few seconds most of the elastic bending energy dissipates. The characteristic rate of the actin flow is ten nm per second, and over a few seconds, the actin displacement is less than one-hundred nm. This is not only smaller than the scale of several microns over which characteristic features of actin flow and traction are observed, but it is even smaller than the usual filament size. Thus, the actin network has to be modeled as a viscous or viscoelastic fluid (with flowing viscous and elastic elements in series). Also, in the appendix, we demonstrate that the assumption of an elastic nature of the actin network predicts an actin flow profile qualitatively different from that observed.
2.1 Model equations
There are three forces that are balanced throughout the actin network [33]: passive deformation force, traction force between the cell and the ECM and myosin contractile force (figure 1). The balance of these forces (more appropriately, balance of linear momentum) that assumes the viscous nature of the actin gel has the form:
| (1) |
Here, μ is the actin gel’s viscosity coefficient and V(x) is the actin retrograde flow speed. The spatial derivative of the velocity is the rate of strain. Assuming that the actin network is a Newtonian fluid, μdV/dx is the viscous stress, and the force is proportional to its derivative. The same assumptions were used before in many modeling papers including [21–22]. In the appendix, we consider the cases of elastic and viscoelastic rheology of the actin network. T(x) is the traction force between the adhesions and the ECM, and Fmyo(x) is the myosin contractile force within the actin network. The second and third model assumptions are reflected in the expressions for the traction and myosin forces in equation (1). Namely, we assume, following previous models [19, 21–22, 24], that the traction between the F-actin network and the ECM has a viscous character and thus is proportional to the actin flow speed. At relevant slow rates of the actin flow, representation of adhesions with sticky springs leads to this model [18–19]. Furthermore, experiments in which a single molecule is dragged along a filament or a surface demonstrate effectively viscous protein friction [34]. The parameter ζ represents an effective viscous drag per adhesion unit, and Nadh(x) is the local density of the adhesion units. The expression for Fmyo is based on the assumption that near the leading edge most of myosin is distributed throughout the isotropic actin gel, rather than concentrated in the stress fibers connecting mature adhesions and the actin network. We further assume that the myosin exerts isotropic stress, fM, proportional to the local myosin density M. Effectively, f is the force per myosin motor. Then, the contractile force is proportional to the local gradient of the density of myosin in the actin network [22, 35].
Note that the membrane tension in our model is generated by the force of actin polymerization: presumably, the rate of actin flow at the leading edge is less than the free polymerization rate, which means that the membrane is tensed and loads the growing actin filaments slowing them down. The membrane tension (equal to ) therefore balances the viscous stress at the very leading edge, because both myosin and traction forces are negligible at x = 0. As a result, the implicit assumption of this model is that the membrane tension is equal to −μ∂V/∂x(0). As we have the measured value of ∂V/∂x(0), and have estimates of the actin viscosity from the literature (see below), we can estimate the membrane tension (see Discussion). Finally, if the myosin force is very small througout the lamellipodium, which the model predicts (see below), the traction force has to be equal to the integral of the traction stress across the lamellipodium, which provides another testable prediction.
Based on experimental observations, we choose the following two boundary conditions for equation 1: (1) V(0) = V0: constant leading edge actin flow speed. We focus on the characteristic case for slow motile epithelial cells in which the net protrusion is much slower than the retrograde flow at the front, and so parameter V0 is the polymerization rate. (2) Another boundary condition is based on the observation (figure 2) that the actin flow speed becomes uniform in the lamellum. This likely means that the traction and myosin forces equilibrate in the lamellum and viscous deformation of the actin gel disappears. Thus, we use the condition ∂V/∂x(L) = 0 at distance L = 8μm from the leading edge – farther than the observed lamellipodium-lamellum boundary. In fact, the model then predicts that the flow speed becomes constant closer to the leading edge than L. Note that this boundary condition indirectly predicts that the membrane tension is determined by the integral of the traction stress minus the integral of the myosin force.
To model the myosin distribution, we assume that myosin in the cytoplasm attaches to the actin network with rate mon and detaches from it with rate moff, and that attached myosin flows inward with actin, such that the density of attached myosin, M(x), is given by:
| (2) |
Based on fluorescent measurements of myosin density in Ptk1 cells (figure 2 and [14]), we choose the boundary condition M(0) = 0. In the appendix, we discuss mass continuity equation for actin and demonstrate that the actin dynamics does not explicitly affect the dynamics of flow and myosin and adhesion density distributions.
Similarly, the local density of adhesion units, Nadh(x), is determined by the rates of assembly (kon) and disassembly (koff). How forces and actin flow affect growth of adhesions is still not entirely clear, but both of these factors do influence the adhesion dynamics [13]. Here we test the hypothesis that the adhesion clutch is strengthened by an indirect effect of local myosin force but weakened by fast flow of actin:
| (3) |
Here, is the adhesion assembly rate in the absence of myosin, and is the disassembly rate in the absence of actin flow. Based on fluorescent imaging of paxillin as an indicator of adhesion density in Ptk1 cells (figure 2 and [14]), we choose the boundary condition Nadh(0) = 0. The parameter β characterizes the effect of adhesion strengthening, and V* is a characteristic actin flow speed above which adhesions rapidly detach and disassemble.
The data in [36] show that the adhesion complexes near the leading edge are first attached to the actin network and slip relative to the substrate, and then at a critical stress attach to the substrate and slip relative to the actin network. However, these movements are on a very short, sub-micron spatial scale, and so we do not include them in the model. Adhesions are multi-component protein complexes, whose content and properties depend on many factors and on the stage of their dynamics [5, 36–37]. However, the detailed morphological cycle of adhesion maturation and turnover is beyond the scope of the current study, as there is little understanding of respective mechanical changes. We focus simply on the density of the generalized adhesion units and its influence on the forces.
Two key assumptions of the model, which we will test by comparison to experimental data, are introduced in equation 3: (1) The adhesion disassembly rate, koff, increases with actin flow speed. This hypothetical property is sometimes referred to as “stick-slip” behavior [19, 26, 38]. A qualitative microscopic explanation for this mechanism is that at fast actin flow speeds, the bonds between actin and the ECM are quickly stretched to their breaking point, whereas at slower sliding speeds weak or broken bonds have time to reform. The stick-slip mechanism for adhesion weakening may explain the experimentally observed biphasic relationship between actin flow and traction strength. Note also that assuming that the rate of detachment is a function of the retrograde flow velocity is mathematically equivalent to assuming it to be a function of the traction force. Indeed, the traction stress is T = ζNadhV, so the force per adhesion complex is equal to T/Nadh = ζV because local stress imposed on the adhesions in any small area is distributed, on the average, equally among them. In fact, the functional form for the detachment dependence on the force, , where f = ζV, f* = ζV* is the characteristic force of breaking an adhesion, is equivalent to the Bell equation used often to describe the force-dependent breaking of molecular bonds [24]. (2) The growth rate of adhesions, kon, increases with a factor proportional to the local myosin density gradient. It was suggested in the past that force application at adhesion sites helps stabilize new adhesive contacts [37, 39] and promotes adhesion maturation and growth [6, 38–40]. However, recently it was shown that absolute values of the intracellular forces do not correlate directly with the adhesion growth rate [31]. Rather, this study suggested that adhesion growth depends sensitively on structure and dynamics of the actin network which adhesions engage with [31]. Besides, while the traction force is applied to adhesions directly, the local myosin force is generated by myosin clusters contracting actin filaments that are part of the actin lamellipodial network. Some of these filaments interact with adhesion molecules, and so the adhesion complexes are unlikely to feel the local myosin force directly. What we propose is that myosin density gradient could induce structural changes in the actin network leading to growth of actin templates favorable for adhesion strengthening. In effect, there is not a direct effect of the myosin-generated force on the adhesion assembly, but rather an indirect effect of this force on the actin network dynamics and structure, which in turn affects the adhesion assembly.
We also examine the possibility of the assumption that the adhesion assembly rate is proportional not to the gradient of the myosin density, but to the myosin density itself. Consequences of this assumption are reported in supplemental figure 7 and show that if adhesion growth is proportional to the myosin density, the predicted flow and traction distributions are different from those observed experimentally. On the other hand, if adhesion growth is proportional to the myosin density gradient (as in equation 3), the model reproduces all experimental observations.
The model equations can be expressed in the following simplified dimensionless form in steady state:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where V = V0Ṽ ≡ V(x = 0)Ṽ, , and x = L0x̃ ≡ (1μm)x̃. The steady-state distributions are defined by the five dimensionless free parameters: , b ≡ βT0, and . Note that λ is the measure of actin viscosity, F is the measure of myosin strength, γ is the measure of the myosin rate of detachment from the actin network, b is the measure of myosin force influence on the adhesion strengthening, and v* is the measure of how much smaller is the flow rate at which adhesions are weakened by the flow than the polymerization rate at the front.
2.2 Characteristic model parameters
In the definition of parameter γ, the ratio L0/V0 is the time over which the actin flow carries myosin molecules across a small part of the lamellipodium. The only way the model reproduces the experimental observations is if myosin molecules do not detach before the flow moves them to the lamellum’s boundary; otherwise, myosin would be distributed much more evenly between the lamellipodium and lamellum than observed. Thus, we assume that the rate of myosin detachment is orders of magnitude smaller than the ratio L0/V0. Good agreement with the data is achieved if γ ~ 1000. Note that comparison of the myosin distribution model with the data in keratocyte cells earlier led to a similar estimate [22]. To explain the experimental relationship between flow speed and traction, the actin flow speed at which the flow no longer weakens adhesions must be somewhat slower but on the same order of magnitude as the characteristic flow speed V0. Therefore, the parameter v* is less than 1, but not by an order of magnitude. In the simulations, we use v* ~ 0.3. Note that in the case of U2OS cells when parameter V0 is much smaller, parameter v* is much greater (supplemental figure 1). Parameter b has to be significantly greater than 1 for adhesions to be sensitive to the indirect effect of the myosin force, so in the simulations, we use b ~ 10. Parameter F is the measure of the ratio of the maximal myosin stress to the characteristic traction stress. The characteristic traction stress and myosin force are of the same order of magnitude, because the myosin stress and membrane tension are two factors contributing to the traction, and both are either likely to be of the similar order of magnitude or the membrane tension is much less than the myosin force. Maximal myosin stress, however, is likely much greater than the resulting myosin force because of relatively smooth myosin distribution in space leading to pulling from neighboring myosin clusters largely canceling each other and generating smaller force. Thus, parameter b is likely significantly greater than 1. Comparison of the data and simulations show that they compare well if F ~ 10. Finally, the order of magnitude of the parameter λ can actually be estimated from the published data. From [14], . On the other hand, the reported actin network viscosity is of the order of 2 × 103 pN×s/μm2 [29]. Parameter μ can be obtained from the measured viscosity by multiplying the latter by the lamellipodial thickness of the order of a micron. Thus, parameter λ ~ 2. This value actually gives a very good qualitative agreement with the data for PtK1 cells. For U2OS cells, we have to use much greater values (supplemental figure 1).
We explore the dependence of the model on each of these parameters in figure 4 and supplemental figures 2–4. We constrain the model parameters by determining values that can simultaneously fit the actin flow and traction distributions for cells under several different experimental perturbations. We note that there is a significant amount of cell-cell variation in the experimental data, and our goal is to illustrate how the hypothetical clutch mechanism produces the qualitative spatial organization observed experimentally, rather than to obtain precise numerical values for each of these parameters.
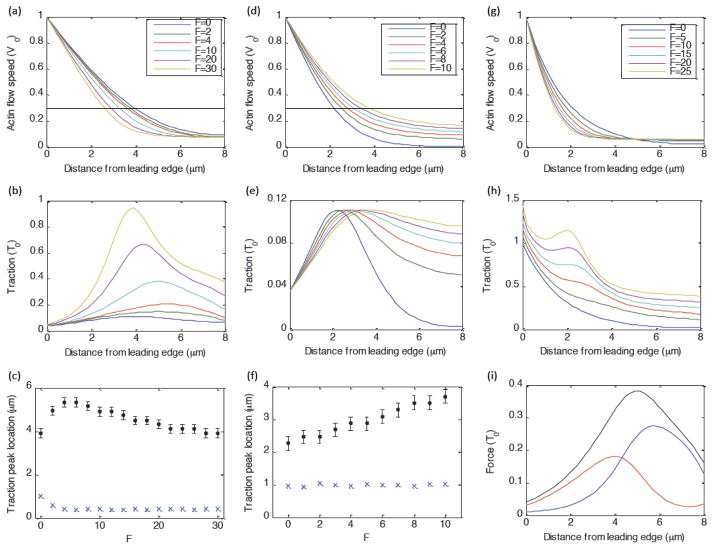
Fig. 4. Role of myosin-dependent and actin-flow-dependent adhesion dynamics.
Unless otherwise stated, parameters are: λ=3, b=15, v*=0.3, and γ=1000. (a–c) Full model with myosin-dependent adhesion strengthening and flow-dependent adhesion weakening. (a, b) Actin flow speed and traction as a function of distance from the leading edge. (c) Position of traction peak in mm (black dots) and actin flow speed (in units of v*) corresponding to traction peak (blue exes) as a function of F. (d–f) Same as (a–c), except without myosin-dependent adhesion strengthening (by setting b = 0). (g–h) Actin flow and traction as a function of distance from the leading edge, in the absence of actin-flow-dependent adhesion weakening (by setting v* ≫ 1). (i)Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=10, b=15, v*=0.3.
We obtained numerical solutions to model equations using MATLAB (The MathWorks, Natick, MA) codes that were based on finite difference numerical methods. We solved the partial differential equations of the model using an explicit stepping method with the first-order upwind scheme for the advection terms. The spatial domain was divided into 40 equal segments, and the time steps were set sufficiently small to guarantee numerical stability. Computational time was on the order of several minutes on a personal computer.
2.3 Experimental data used to test the model
The experimental data from Ptk1 epithelial cells in figures 2–3 were originally published in [14], and are included here for the purpose of illustration and direct comparison with the predictions of our theoretical model. Traction and actin flow data in human osteosarcoma (U2OS) epithelial cells (supplemental figure 1) used to test the model predictions were originally published in [31].
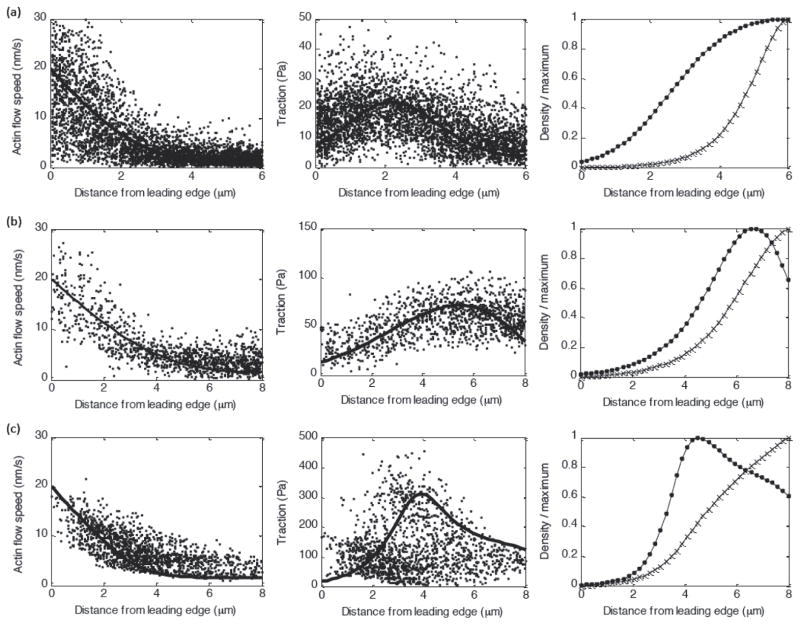
Figure 3. Model fits to sample experimental Ptk1 data.
(A–C) Actin flow speed (left) and traction (middle) and predicted myosin density and adhesion density (right) for a Blebbistatin-treated cell (A), a control cell (B), and a CA-Rho treated cell (C).
3. RESULTS
3.1 Bimodal flow-traction relationship arises from competing mechanisms of adhesion dynamics regulation: flow-dependent detachment and myosin-dependent attachment
As first reported in [14], correlation between actin dynamics and traction in Ptk1 epithelial cells reveals an inverse relationship between actin flow speed and traction magnitude in the lamellipodium and a direct correlation in the lamellum (figure 2). These cells exhibit rapid actin flow at the leading edge (~20nm/s) that decays across the lamellipodia, and relatively uniform slow flow (~2nm/s) in the lamella. The corresponding traction stress magnitude increases with distance across the lamellipodium and decreases with distance across the lamellum. Interestingly, the location of the traction peak depends in a non-trivial way on the strength of myosin contractility (figure 3; [14]): The peak is closer to the leading edge in blebbistatin-treated cells (where myosin contractility has been inhibited) than in control cells. However in CARho-treated cells, which exhibit increased myosin contractility, the location of the traction peak shifts back toward the leading edge relative to control cells. The actin flow speed corresponding to maximal traction is relatively similar under each of these conditions [14].
Our model for the adhesion clutch reproduces the bimodal relationship between actin flow speed and traction magnitude observed in Ptk1 cells (figure 3). The spatial distributions for individual cells can be reproduced by tuning the myosin strength parameter F to correspond to experimental changes in myosin contractility (increasing F for Blebbistatin, Control, and CARho-treated cells, respectively), and using a lower effective viscosity λ to fit Blebbistatin data (figure 3). Note that it is reasonable to expect that actin networks with reduced myosin contractility are less stiff [41]. Other system parameters were not varied from one cell to the next. Our model also reproduces the experimental observations that adhesion and myosin densities (as identified by microscopic tracking of fluorescent markers [14]) are relatively small in the lamellipodia, and dramatically increase near the lamellipodia/lamella boundary (figures 2, 3).
The bimodal flow-traction relationship observed in Ptk1 cells can be explained by considering the interplay between velocity-dependent adhesion detachment and myosin-dependent adhesion strengthening (equation 3). Near the leading edge, actin polymerization against the membrane produces a fast retrograde flow speed, resulting in a low adhesion density. For a very rigid actin network (high λ), retrograde flow is uniform throughout the network. On the other hand, for a deformable viscous network (lower λ), the retrograde flow speed decays with distance from the leading edge (as observed in Ptk1 cells, figures 2 and 3). As retrograde flow decays, adhesions detach less frequently, according to the stick-slip mechanism in equation 3, leading to an increase in adhesion density. For the region near the leading edge where Ṽ > v*, the adhesion density increases more rapidly with distance than the flow speed decays, so that the traction (T̃ = ÑadhṼ) increases with distance. This effect is responsible for the observed trend near the leading edge for traction to increase as retrograde flow decreases.
In the lamella region further from the leading edge, the trend for traction to decrease with distance can be explained by the force-dependent adhesion strengthening mechanism described in equation 3. Myosin attaches to the actin network and is swept back with actin retrograde flow, producing a steep increase in attached myosin density where the flow speed levels off (figure 3). The peak in myosin force at this location creates a corresponding peak in adhesion density. Beyond this peak, traction decreases with distance due to the decrease in adhesion density, which becomes smaller due to the decreasing myosin force beyond the peak, as well as a slight continued decay in retrograde flow speed (figure 3).
3.2 Myosin contractility regulates traction peak location by modulating adhesion distribution
Our model also reproduces the experimental observation (comparing Blebbistatin, Control, and CARho-treated cells) that increasing myosin contractility initially shifts the traction peak to higher x values, but further increasing myosin contractility shifts the peak back toward the leading edge (figures 3, 4). This is because, in the absence of myosin force (as in Blebbistatin-treated cells), the traction distribution is given by T̃ exp(−Ṽ/v*)Ṽ (equation 9), which is maximal when Ṽ = v*. In this case, the balance of internal viscous forces and external traction determine the location of the peak (supplemental figure 2). In the presence of myosin forces (as in the Control and CARho-treated cells), the traction distribution also depends on the location of the myosin force peak (equation 9). As myosin strength F initially increases from zero, the location of the traction peak shifts in the +x-direction toward the location where the myosin gradient is highest (in the region where the flow speed levels off). Further increasing F shifts the traction peak back toward the leading edge, because higher adhesion density causes the flow speed to fall off more steeply (figure 4).
3.3 Traction is highest at leading edge for cells with slow uniform flow
As discussed above, the bimodal traction-flow relationship observed in Ptk1 epithelial cells results from the interplay between velocity-dependent adhesion detachment and myosin-dependent adhesion strengthening. However, in cells with very slow leading edge polymerization speed and corresponding retrograde flow speed (V0 ≪ V*), adhesion disassembly is insensitive to actin flow speed and adhesion density is no longer kept small near the leading edge. In this case, the predicted traction distribution is (equation 9), and we predict that traction will decay with distance from the leading edge if the myosin force contribution is relatively small, and that the traction distribution will mirror the myosin force distribution for increasing myosin strength (supplemental figure 1 (d,e)). For cells with slow spatially uniform actin flow (V(x) = V0 ≪ V*), the balance of forces on the actin network becomes F̃myo = T̃ (equation 5). The steady-state myosin density predicted by equation (7) is , and the resulting myosin contractile force is , and the traction is predicted to decay with distance from the leading edge for all values of myosin strength.
This prediction is consistent with our measurements of actin flow and traction in U2OS epithelial cells (supplemental figure 1 (d,e)). These cells exhibit relatively uniform flow (~2–4nm/s) across the lamellipodia/lamella, with the leading edge speed only slightly higher than the speed of flow in the lamella. The corresponding traction profile in these cells is highest near the cell membrane and decays with distance from the leading edge.
3.4 Actin flow speed insensitive to myosin strength in regions of uniform flow
A second prediction we can make for cells with slow uniform flow is the dependence of this flow speed on the magnitude of the myosin force. If myosin turnover is slow compared to the rate of transport across the lamellipodia (γ ≫ 1), then the myosin force and corresponding traction in the lamella are approximately uniform, T̃ = F̃myo ≈ F. In this case, the steady-state traction distribution (equation 9) yields:
| (10) |
An increase in the myosin force driving actin flow is canceled out by increased traction due to myosin-dependent adhesion strengthening. For saturating levels of myosin strength, we predict that the actin flow speed will be insensitive to myosin strength. Assuming that the total traction force between the cell and the surface is proportional to the local myosin stress (Ftot ∝ F), we can re-express equation 10 as a Hill-like relationship between total force and lamellar flow speed, VLM:
| (11) |
We test this prediction by treating U2OS cells with various concentrations of the Rho-kinase inhibitor Y-27632 compound [31], which interferes with actomyosin-based contractility, allowing us to tune the magnitude of myosin contractile force. In agreement with the model, despite significant changes in the measured total contractile force magnitude, the actin flow speed in the lamella is relatively unchanged for all but the highest concentrations of Y-27632 compound tested (supplemental figure 1).
4. DISCUSSION
We have shown that mechanical feedback between F-actin flow and focal adhesion dynamics allows the leading edge of motile cells to self-organize into distinct regions of inverse and direct correlation between actin flow and sub-cellular traction, as observed in epithelial cells [14]. These characteristic distributions arise from a balance of viscous stress in the actin network, acto-myosin contraction, membrane tension and adhesive traction. This ability to self-organize into functionally distinct spatial regions allows the cell to undergo rapid actin polymerization near the leading edge while adhering firmly to the surface near the lamellipodia/lamella boundary. Although we consider several plausible actin-adhesion feedback mechanisms (appendix), the model that reproduces experimental distributions of actin flow and traction is one in which the adhesion “clutch” engagement is strengthened by an effect of myosin contractility on actin templates favorable for adhesion assembly and weakened by actin retrograde flow. The spatial distributions predicted by our model result from a balance of internal forces in the actin network (myosin contraction and internal viscosity) and external traction forces exerted on the network. The model predicts that viscous deformation is the major factor generating the traction stress near the front, while myosin force is the main contributor to the traction stress farther than a few microns from the leading edge. While there is substantial cell-cell variation, as expected, we find that our model reliably predicts characteristic features of the data including the location of the traction peak, dependence of traction magnitude on myosin strength, and the spatial distribution of the actin retrograde flow.
Our model also reproduces qualitative features of cells that have very different leading edge actin flow and traction profiles from the Ptk1 epithelial cells discussed above. We looked at simultaneous actin flow and traction stress measurements in human osteosarcoma (U2OS) epithelial cells and in contrast to the Ptk1 cells, and these cells exhibit slow relatively uniform retrograde flow across the lamellipodia/lamella and traction that is highest at the leading edge. The slower more uniform flow in these cells may be the result of physiological differences such as a more rigid actin network, slower actin polymerization due to lower available G-actin pool, or differences in leading edge membrane tension. In the framework of our model, cells with slow uniform flow are effectively utilizing only one of our hypothetical adhesion regulation mechanisms (myosin-dependent clutch strengthening), but are in a physical regime where they do not experience the other hypothetical mechanism (“stick-slip”, or flow-dependent clutch weakening). The myosin-dependent mechanism alone reproduces key observations in U2OS cells: (1) traction is highest at the leading edge; and (2) lamellar flow speed is relatively insensitive to myosin strength. The insensitivity of actin flow speed to perturbations in myosin contractility may allow the cell to maintain robust protrusive activity in the presence of fluctuating molecular concentrations.
Our model makes a very simple prediction for the lamellipodial width. Our simulations show that this width is not sensitive to myosin strength because myosin is largely ‘swept away’ from the leading edge and starts affecting the flow and traction only close to the lamellum’s boundary where the flow already slows down. Near the leading edge, the viscous force largely balances the traction: . The boundary conditions at the lamellipodium-lamellum boundary at distance X from the leading edge are V(X) ≈ 0, . Solving this equation for the distance-dependent actin flow velocity yields . The condition gives . Furthermore, the traction stress can be estimated as T̄ ~ ζ̃V(0) where is the characteristic adhesion strength. Thus, we arrive at the very simple result: , and we predict that the lamellipodial width is proportional to the square root of the actin viscosity, and inversely proportional to the square root of the average adhesion strength at the leading edge. This is the spatial scale that seems to be fundamental for cell mechanics: the effect of a force applied to the actin network at a point dissipates over this distance [22,42]. At realistic values of parameters, the characteristic lamellipodial width is predicted to be on the order of a few microns, as observed. Importantly, this scale is largely insensitive to parameters other than the viscosity and adhesion strength.
Another interesting prediction of our model is that, because the myosin force in the lamellipodium is small, the membrane tension roughly balances the average traction stress multiplied by the lamellipodial width, which in turn is approximately equal to the actin viscosity multiplied by the flow rate gradient. The traction stress, lamellipodial width and the flow rate gradient were measured in [14], which allows us to predict a viscosity value of μ ~ 103 pN×s/μm2 This agrees with the viscosity measured in [29], and the membrane tension magnitude (~ 60 pN/μm), which is also of the same order of magnitude normally measured in slow-moving cells [30, 43].
Our model is, of course, ignoring many complexities of the cell motile machinery. We did not consider potentially very complex dynamic feedbacks between actin, adhesion and myosin [44]. There are more complex dynamics of adhesion growth and turnover that depend not only on force but on signaling [45–46] as well as spatial-temporal history [47]. Behind the steady-state distributions of the cytoskeletal elements, flows and forces at the cell leading edge, there are many non-steady processes on various spatial-temporal scales [48]. We also did not investigate the effects of complex kinetics of lamellipodial and lamellum actin networks and respective actin binding proteins [49–50]. We did not consider the discrete character of the actin networks on the micron scale or the anisotropic nature of the contractile network. All these factors, however, have to be included only after more coarse-grained models of the type that we propose here are sufficiently tested.
Supplementary Material
(a) Actin flow speed in the lamella as a function of Y-compound concentration. (b) Total measured traction force as a function of Y-compound concentration. (c) Lamellar flow speed as a function of total force (black dots), fit to model prediction (eq. 11, Vmax=6.6nm/s, Fk=23nN). (d) Model fit (black line) to experimental data (blue dots) for actin flow speed in a U2OS cell treated with 2mM Y-compound. Parameters: λ=50, γ=1000, v*=100, b=1.5, F=300 (e) Model fit to traction data for same cell as in (d).
Unless otherwise stated, parameters are: F=b=0, v*=0.3, γ=1000. (A) Position of traction peak (black dots) and actin flow speed (in units of v*) corresponding to traction peak (blue exes) as a function of λ. (B–E) Actin flow, traction, myosin density, and adhesion density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*.
Unless otherwise stated, parameters are: F=b=0, v*=3, γ=1000. (We set F=0, in order to illustrate the dependence of the myosin distribution on γ for the same flow profile in each case, rather than for changing flow profiles that would occur for F>0). (A) Actin flow speed (black) and traction (red) as a function of distance from the leading edge. (B) Myosin distribution for different values of γ. (C) Myosin gradient for same values of γ as in (B).
Unless otherwise stated, parameters are: λ=3, F=1, v*=0.3 and γ=1000. (A) Position of traction peak in μm (black dots) and actin flow speed (in units of v*) corresponding to traction peak (blue exes) as a function of b. (B–F) Actin flow, traction, myosin density, myosin force, and adhesion density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (G–I) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for myosin strength b=10 (G), b=40 (H), and b=100 (I).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=0.2 (e) and F=0.4 (f).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=0.2 (e) and F=0.4 (f).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=2 (e) and F=4 (f).
Acknowledgments
We thank Jun Allard and Kun-Chun Lee for useful discussions. The study was funded by the National Institute of Health GM068952 to A.M. and Burroughs Welcome Career Award and Packard Fellowship to M.L.G.
Appendix
1. Characterizing each adhesion regulation mechanism separately
In the main text, we consider a model for adhesion dynamics regulation that relies on two mechanisms: (1) Flow-dependent adhesion disassembly; and (2) Myosin-dependent adhesion assembly. Here we discuss each of these mechanisms separately.
a. Myosin-dependent adhesion assembly (supplemental figure 1)
Here we consider a variation of the model in the main text in which the assembly rate for adhesions is given by the myosin-dependent expression in equation 3, but the disassembly rate is kept constant instead of the flow-dependent expression in equation 3 (i.e., we set v* ≫ 1).
In the absence of flow-dependent adhesion disassembly, the steady-state adhesion density distribution mirrors the myosin force distribution (Ñadh = 1 + bF̃myo). For increasing values of myosin strength F, the adhesion density and corresponding traction magnitude increase. This causes the actin flow speed to decay more steeply with distance, which results in the myosin force peak location moving closer to the leading edge with increasing F. Because myosin is swept away from the leading edge by actin flow, the adhesion density near the leading edge is uniform and the resulting traction is directly proportional to the decaying actin flow speed.
This mechanism alone creates a spike in traction at a location that is sensitive to myosin strength, and can reproduce lamellar flow insensitivity to myosin strength for high F, similar to experimental observations. However, the traction and actin flow near the leading edge are directly proportional, in contrast to the experimental observation of inverse flow-traction near the leading edge.
b. Actin flow-dependent adhesion disassembly (supplemental figures 2–3; and figure 4 (d–f) in the main text)
Here we consider a variation of the model in the main text where the disassembly rate for adhesions is given by the flow-dependent expression in equation 3, but the assembly rate is kept constant instead of the myosin-dependent expression in equation 3 (i.e., we set b=0).
In this case, the steady-state traction distribution is given by T̃ = exp(−Ṽ/v*)Ṽ (equation 9), which is maximal for Ṽ = v* independent of other system parameters. The location of the traction peak depends on the internal viscosity of the actin network, λ, which determines the decay rate of actin flow speed as a function of distance from the leading edge (supplemental figure 2).
The myosin distribution is determined by the parameter γ, which characterizes the time scale for myosin to stay attached to the actin network (supplemental figure 3). For low γ, such that myosin turnover is fast compared to the timescale for actin retrograde flow across the lamellipodia, the myosin distribution is spatially uniform. For higher γ, such that myosin stays attached long enough to be transported by actin across the length of the leading edge, the myosin distribution is small near the leading edge and increases rapidly as the actin flow speed levels off, in agreement with fluorescent images of myosin distributions.
Although this variation of the model can produce the experimentally observed bimodal relationship between actin flow and traction, there are some experimentally observed features it fails to reproduce: (1) The location of the traction peak increases monotonically with myosin strength (see figure 4(f) in the main text), in contrast to experimental results comparing Control, Blebbistatin-treated, and CARho-treated cells (figure 3 in the main text). In these experiments, the traction peak location initially increases with increasing myosin strength, but moves back toward the leading edge for higher myosin strength. (2) This mechanism alone cannot explain the insensitivity of lamellar actin flow speed to myosin inhibition observed in U2OS cells (supplemental figure 1).
2. Model dependence on strength of myosin-dependent assembly parameter b (supplemental figure 4)
Because the adhesion density simply depends on the product bF, the model dependence on b is similar to the dependence on F (see figure 4 in the main text), with the following exception: For increasing F, the myosin contractile driving force increases along with the adhesion density, so the corresponding flow speed is independent of F at saturating levels (supplemental figure 4b). For increasing b, the adhesion density increases with no corresponding increase in driving force, so the actin flow speed at the traction peak approaches zero for high b.
3. Model variations and alternative models (supplemental figures 5–7)
a. Uniform myosin force distribution (supplemental figure 5)
If we assume that myosin contractile force is spatially uniform, many of the qualitative features predicted by the model in the main text are reproduced. In particular, the bimodal relationship between actin flow and traction distributions is not dependent on the particular myosin force distributions predicted by the dynamic equation for myosin (equation 2). However, for uniform myosin force, the location of the traction peak is relatively insensitive to myosin force strength F and depends primarily on actin network viscosity λ. Given this limitation, this form of the model cannot simultaneously reproduce the actin flow and traction profiles measured experimentally. If λ is chosen high enough to produce a traction peak at the experimentally observed distance from the leading edge, the corresponding actin flow speed falls off less steeply than experimentally observed.
b. Step function myosin distribution (supplemental figure 6)
If we treat the myosin force as a step function (zero near the leading edge and constant beyond a threshold distance), adhesion density is very small near the leading edge due to a lack of myosin-dependent assembly in combination with rapid disassembly resulting from fast flow. For this reason, the traction peak spikes at the step-function boundary and then rapidly decays with increasing distance due to continuing decay in flow speed. As in the case of uniform myosin force distribution discussed above, this version of the model does not reproduce experimental flow and traction distributions as well as the full model with myosin force calculated based on the predicted myosin distribution (equation 7).
c. Myosin force directly proportional to myosin density (supplemental figure 7)
Here, we consider a variation of the model in which myosin force is directly proportional to myosin density, instead of proportional to the gradient of the myosin density as in the main text (equation 1). In this case, adhesion density is close to zero near the leading edge, and increases in proportion to myosin density away from the leading edge. The resulting traction increases with distance from the leading edge, rather than having a distinct peak as observed in Ptk1 cells and predicted by the model in the main text.
4. Note about actin density
Unlike equations 2 and 3 that deal with conservable densities of myosin and adhesions, respectively, equation 1 is the force balance equation. The velocity that this equation describes is the velocity of the actin network, and the mass conservation law has to be satisfied for actin. The equation for actin density A has the form: . Here z1(A) is the non-dimensionless term describing the actin assembly rate, which can be dependent on the actin density, and z2(A) is the non-dimensionless term describing the actin disassembly rate, which also can be dependent on the actin density. Dimensional parameter r is the dimensional characteristic rate of actin turnover. The usual rates of actin turnover are 0.1/sec. Introducing the time scale equal to 1/r and spatial scale equal to the lamellipodial length L0, we can re-scale and non-dimensionalize the actin density equation as: . Here t̃ = rt; x̃ = x/L0; ε = V0/(rL0); v = V/V0. Small parameter ε ~ (0.02μm/s)/(0.1/s × 2μm) ~ 0.1 therefore the transport term can be neglected, and approximately, . Thus, assuming there is a unique stable steady state for the actin turnover, the model predicts a constant in space actin density. Figure 1E of [14] shows actin fluorescent signal in the lamellipodium, and other than increasing patchiness away from the front, the average actin density is roughly constant, in agreement with the model. On the relevant time scale of 10 sec, the actin network displacement is but 0.1 micron, orders of magnitude less than the lamellipodial width. Therefore, the actin flow is likely irrelevant for the actin density, which is determined by the balance of assembly and disassembly. Therefore, in the model, we did not include possible assumptions about a) myosin viscosity being proportional to actin density, b) attachment rate for adhesions and/or myosin being proportional to actin density.
5. Assumption that actin network is elastic leads to predicted distribution of actin flow qualitatively different from the observed spatial flow profile
Let us assume that the lamellipodial actin network is elastic and consider two material points at time t = 0 – one at the very leading edge, with coordinate x = 0, another a small distance away from the front, with coordinate x = δ. We investigate the case when the retrograde actin flow is steady and its velocity distribution is given by the function V(x) where the velocity is positive and directed to the rear, away from the leading edge. Over a small time increment, a material point displacement at x = s would be ds = V(s)dt, then, , where x(t) is the coordinate of the first material point (with coordinate x = 0 at time t = 0). Similarly, for the second material point (with coordinate x = δ at time t = 0), , where y(t) is the coordinate of this second material point.
Then, and . Comparing these two expressions and considering that , we find: . In the limit of very small values of δ, we have: , or . At the very leading edge, the actin network is compressed by the membrane tension. Let us define the width of the network between the two considered material points without this compression as Δ. Then, we can define the strain ε of the network between the two considered material as . If Y is the Young modulus of the network (which we will consider constant for simplicity, as well as rescaled for the 1D problem), and Fmemb is the membrane tension (similarly rescaled for the 1D problem), then the strain at the leading edge is: . Therefore, the elastic stress is equal to . On the other hand, the spatial derivative of this stress (in 1D problem) is equal to the difference between the traction force and the myosin force: .
Thus, . The constant in the bracket, , is positive because in the framework of the linear elasticity theory that we use, the force at the boundary has to be significantly smaller than the Young modulus. In the case of the blebbistatin-treated case, Fmyo(x) ≈ 0, and the traction force, T(x) > 0 (this force is directed to the leading edge, compressing the network). Therefore, : the retrograde flow velocity should increase toward the rear, contradicting the experimental measurements showing that the flow rate decreases toward the rear (figure 2). The explanation of the theoretical result is very simple: at the very front, the network is compressed maximally by the membrane tension balanced by the distributed traction force. As we go away from the leading edge to the rear, smaller and smaller part of the total traction compresses the network. This is similarly physically to the elastic rod standing vertically in the gravitation field: at the floor, the material is compressed maximally by the total gravitational force balanced by the counter-force from the floor. As we go higher, the rod material is compressed less and less and finally the top of the rod is uncompressed at all. We conclude that the elastic rheology of the actin network is incompatible with the observation that the retrograde velocity decreases toward the rear.
It is similarly easy to demonstrate that if the network is viscoelastic (Kelvin model with spring and dashpot in parallel), then the prediction is the same, and this is not a viable approximation in the sense that the model prediction would not agree with the data. However, if the network is described by the Maxwell viscoelastic model (with spring and dashpot in series), then equation 1 in the main text has to be modified as follows [22]:
Where parameter α determines a non-Newtonian fraction of viscosity, σve is the viscoelastic part of the stress tensor (scalar in the 1D case), and τ is the relaxation time. In the case of the steady actin flow, . Let us consider the case when elastic deformations relax fast compared to the characteristic time of flow across the lamellipodial domain: τ ≪ L0/V(0). Then, using the rescaled relaxation time τ̃ = τV(0)/L0 as the small parameter, we can expand the velocity and stress into the perturbation series and retain only linear terms with respect to the small parameter: V = v0 + τ̃v1, σve = σ0 + τ̃σ1. In the zeroth order, , and in the first order: and . From the last equation, . Substituting this expression into the previous equation, we obtain: . From the observations, we can approximate the flow rate as decreasing exponentially on the spatial scale L : v0 = V(0)exp(−x/L). Then, , and we finally obtain the approximate formula for the flow rate distribution:
The result is intuitive: the elastic and non-Newtonian part of the stress in the actin network causes modest increase of the flow rate everywhere. Simply speaking, elastic resistance to deformation tends to diminish the spatial gradient of the flow rate. However, qualitatively, the velocity still decreases away from the leading edge, and its spatial profile is qualitatively the same as in the viscous Newtonian case. Thus, the viscoelastic Maxwell model is a possible description of the actin network rheology.
References
- 1.Pollard TD, Borisy GG. Cellular motility driven by assembly and disassembly of actin filaments. Cell. 2003;112:453–65. doi: 10.1016/s0092-8674(03)00120-x. [DOI] [PubMed] [Google Scholar]
- 2.Ponti A, Machacek M, Gupton SL, Waterman-Storer CM, Danuser G. Two distinct actin networks drive the protrusion of migrating cells. Science. 2004;305:1782–6. doi: 10.1126/science.1100533. [DOI] [PubMed] [Google Scholar]
- 3.Parsons JT, Horwitz AR, Schwartz MA. Cell adhesion: integrating cytoskeletal dynamics and cellular tension. Nat Rev Mol Cell Biol. 2010;11:633–43. doi: 10.1038/nrm2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chrzanowska-Wodnicka M, Burridge K. Rho-stimulated contractility drives the formation of stress fibers and focal adhesions. J Cell Biol. 1996;133:1403–15. doi: 10.1083/jcb.133.6.1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Choi CK, Vicente-Manzanares M, Zareno J, Whitmore LA, Mogilner A, Horwitz AR. Actin and alpha-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat Cell Biol. 2008;10:1039–50. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bershadsky AD, Balaban NQ, Geiger B. Adhesion-dependent cell mechanosensitivity. Annu Rev Cell Dev Biol. 2003;19:677–95. doi: 10.1146/annurev.cellbio.19.111301.153011. [DOI] [PubMed] [Google Scholar]
- 7.Gardel ML, Schneider IC, Aratyn-Schaus Y, Waterman CM. Mechanical integration of actin and adhesion dynamics in cell migration. Annu Rev Cell Dev Biol. 2010;26:315–33. doi: 10.1146/annurev.cellbio.011209.122036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kaverina I, Krylyshkina O, Small JV. Regulation of substrate adhesion dynamics during cell motility. Int J Biochem Cell Biol. 2002;34:746–61. doi: 10.1016/s1357-2725(01)00171-6. [DOI] [PubMed] [Google Scholar]
- 9.Gupton SL, Waterman-Storer CM. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 2006;125:1361–74. doi: 10.1016/j.cell.2006.05.029. [DOI] [PubMed] [Google Scholar]
- 10.Mitchison T, Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1:761–72. doi: 10.1016/0896-6273(88)90124-9. [DOI] [PubMed] [Google Scholar]
- 11.Lin CH, Forscher P. Growth cone advance is inversely proportional to retrograde F-actin flow. Neuron. 1995;14:763–71. doi: 10.1016/0896-6273(95)90220-1. [DOI] [PubMed] [Google Scholar]
- 12.Jurado C, Haserick JR, Lee J. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol Biol Cell. 2005;16:507–18. doi: 10.1091/mbc.E04-10-0860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Margadant F, Chew LL, Hu X, Yu H, Bate N, Zhang X, Sheetz M. Mechanotransduction in vivo by repeated talin stretch-relaxation events depends upon vinculin. PLoS Biol. 2011;9:e1001223. doi: 10.1371/journal.pbio.1001223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gardel ML, Sabass B, Ji L, Danuser G, Schwarz US, Waterman CM. Traction stress in focal adhesions correlates biphasically with actin retrogtrade flow speed. J Cell Biol. 2008;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fournier MF, Sauser R, Ambrosi D, Meister JJ, Verkhovsky AB. Force transmission in migrating cells. J Cell Biol. 2010;188:287–97. doi: 10.1083/jcb.200906139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Macdonald A, Horwitz AR, Lauffenburger DA. Kinetic model for lamellipodal actin-integrin ‘clutch’ dynamics. Cell Adh Migr. 2008;2:95–105. doi: 10.4161/cam.2.2.6210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–91. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 18.Li Y, Bhimalapuram P, Dinner AR. Model for how retrograde actin flow regulates adhesion traction stresses. J Phys: Condens Matter. 2010;22:194113. doi: 10.1088/0953-8984/22/19/194113. [DOI] [PubMed] [Google Scholar]
- 19.Sabass B, Schwarz US. Modeling cytoskeletal flow over the adhesion sites: competition between stochastic bond dynamics and intracellular relaxation. J Phys: Condens Matter. 2010;22:194112. doi: 10.1088/0953-8984/22/19/194112. [DOI] [PubMed] [Google Scholar]
- 20.Urbakh M, Klafter J, Gourdon D, Israelachvili J. The nonlinear nature of friction. Nature. 2004;430:525–8. doi: 10.1038/nature02750. [DOI] [PubMed] [Google Scholar]
- 21.Kruse K, Joanny JF, Jülicher F, Prost J. Contractility and retrograde flow in lamellipodium motion. Phys Biol. 2006;3:130–7. doi: 10.1088/1478-3975/3/2/005. [DOI] [PubMed] [Google Scholar]
- 22.Rubinstein B, Fournier MF, Jacobson K, Verkhovsky AB, Mogilner A. Actin-myosin viscoelastic flow in the keratocyte lamellipod. Biophys J. 2009;97:1853–63. doi: 10.1016/j.bpj.2009.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ziebert F, Swaminathan S, Aranson IS. Model for self-polarization and motility of keratocyte fragments. J R Soc Interface. 2012;9:1084–92. doi: 10.1098/rsif.2011.0433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Welf ES, Johnson HE, Haugh JM. Bidirectional coupling between integrin-mediated signaling and actomyosin mechanics explains matrix-dependent intermittency of leading-edge motility. Mol Biol Cell. 2013;24:3945–55. doi: 10.1091/mbc.E13-06-0311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ziebert F, Aranson IS. Effects of adhesion dynamics and substrate compliance on the shape and motility of crawling cells. PLoS One. 2013;8:e64511. doi: 10.1371/journal.pone.0064511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shemesh T, Bershadsky AD, Kozlov MM. Physical model for self-organization of actin cytoskeleton and adhesion complexes at the cell front. Biophys J. 2012;102:1746–56. doi: 10.1016/j.bpj.2012.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Alexandrova AY, Arnold K, Schaub S, Vasiliev JM, Meister J-J, Bershadsky AD, Verkhovsky AD. Comparitive dynamics of retrograde actin flow and focal adhesions: formation of nascent adhesions triggers transition from fast to slow flow. PLoS One. 2008;3:e3234. doi: 10.1371/journal.pone.0003234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Watanabe NI, Mitchison TJ. Single-molecule speckle analysis of actin filament turnover in lamellipodia. Science. 2002;295:1083–6. doi: 10.1126/science.1067470. [DOI] [PubMed] [Google Scholar]
- 29.Bausch AR, Ziemann F, Boulbitch AA, Jacobson K, Sackmann E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys J. 1998;75:2038–49. doi: 10.1016/S0006-3495(98)77646-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Betz T, Koch D, Lu YB, Franze K, Käs JA. Growth cones as soft and weak force generators. Proc Natl Acad Sci U S A. 2011;108:13420–5. doi: 10.1073/pnas.1106145108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Beckham Y, Vasquez RJ, Stricker J, Sayegh K, Campillo C, Gardel ML. Arp2/3 inhibition induces amoeboid-like protrusions in MCF10A epithelial cells by reduced cytoskeletal-membrane coupling and focal adhesion assembly. PLoS One. 2014;9:e100943. doi: 10.1371/journal.pone.0100943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stricker J, Falzone T, Gardel M. Mechanics of the F-actin cytoskeleton. J Biomech. 2010;43:9–14. doi: 10.1016/j.jbiomech.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Danuser G, Allard J, Mogilner A. Mathematical modeling of eukaryotic cell migration: insights beyond experiments. Annu Rev Cell Dev Biol. 2013;29:501–28. doi: 10.1146/annurev-cellbio-101512-122308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bormuth V, Varga V, Howard J, Schäffer E. Protein friction limits diffusive and directed movements of kinesin motors on microtubules. Science. 2009;325:870–3. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- 35.Bois JS, Jülicher F, Grill SW. Pattern formation in active fluids. Phys Rev Lett. 2011;106:028103. doi: 10.1103/PhysRevLett.106.028103. [DOI] [PubMed] [Google Scholar]
- 36.Aratyn-Schaus Y, Gardel ML. Transient frictional slip between integrin and the ECM in focal adhesions under myosin II tension. Curr Biol. 2010;20:1145–53. doi: 10.1016/j.cub.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vicente-Manzanares M, Choi CK, Horwitz AR. Integrins in cell migration – the actin connection. J Cell Sci. 2009;122:199–206. doi: 10.1242/jcs.018564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wolgemuth CW. Lamellipodial contractions during crawling and spreading. Biophys J. 2005;89:1643–9. doi: 10.1529/biophysj.105.066720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Geiger B, Spatz JP, Bershadsky AD. Environmental sensing through focal adhesions. Nat Rev Mol Cell Biol. 2009;10:21–33. doi: 10.1038/nrm2593. [DOI] [PubMed] [Google Scholar]
- 40.Roca-Cusachs P, Gauthier NC, del Rio A, Scheetz MP. Clustering of alpha5beta1 integrins determines adhesion strength whereas alphavbeta3 and talin enable mechanotransduction. Proc Natl Acad Sci. 2009;106:16245–50. doi: 10.1073/pnas.0902818106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Koenderink GH, Dogic Z, Nakamura F, Bendix PM, MacKintosh FC, Hartwig JH, Stossel TP, Weitz DA. An active biopolymer network controlled by molecular motors. Proc Natl Acad Sci U S A. 2009;106:15192–7. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mayer M, Depken M, Bois JS, Jülicher F, Grill SW. Anisotropies in cortical tension reveal the physical basis of polarizing cortical flows. Nature. 2010;467:617–21. doi: 10.1038/nature09376. [DOI] [PubMed] [Google Scholar]
- 43.Raucher D, Sheetz MP. Cell spreading and lamellipodial extension rate is regulated by membrane tension. J Cell Biol. 2000;148:127–36. doi: 10.1083/jcb.148.1.127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Shutova M, Yang C, Vasiliev JM, Svitkina T. Functions of nonmuscle myosin II in assembly of the cellular contractile system. PLoS One. 2012;7:e40814. doi: 10.1371/journal.pone.0040814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Boettiger D. Mechanical control of integrin-mediated adhesion and signaling. Curr Opin Cell Biol. 2012;24:592–9. doi: 10.1016/j.ceb.2012.07.002. [DOI] [PubMed] [Google Scholar]
- 46.Cirit M, Krajcovic M, Choi CK, Welf ES, Horwitz AF, Haugh JM. Stochastic model of integrin-mediated signaling and adhesion dynamics at the leading edges of migrating cells. PLoS Comput Biol. 2010;6:e1000688. doi: 10.1371/journal.pcbi.1000688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Stricker J, Aratyn-Schaus Y, Oakes PW, Gardel ML. Spatiotemporal constraints on the force–dependent growth of focal adhesions. Biophys J. 2011;100:2883–93. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Machacek M, Hodgson L, Welch C, Elliott H, Pertz O, Nalbant P, Abell A, Johnson GL, Hahn KM, Danuser G. Coordination of Rho GTPase activities during cell protrusion. Nature. 2009;461:99–103. doi: 10.1038/nature08242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Stuhrmann B, Huber F, Käs J. Robust organizational principles of protrusive biopolymer networks in migrating living cells. PLoS One. 2011;6:e14471. doi: 10.1371/journal.pone.0014471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Iwasa JH, Mullins RD. Spatial and temporal relationships between actin-filament nucleation, capping, and disassembly. Curr Biol. 2007;17:395–406. doi: 10.1016/j.cub.2007.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(a) Actin flow speed in the lamella as a function of Y-compound concentration. (b) Total measured traction force as a function of Y-compound concentration. (c) Lamellar flow speed as a function of total force (black dots), fit to model prediction (eq. 11, Vmax=6.6nm/s, Fk=23nN). (d) Model fit (black line) to experimental data (blue dots) for actin flow speed in a U2OS cell treated with 2mM Y-compound. Parameters: λ=50, γ=1000, v*=100, b=1.5, F=300 (e) Model fit to traction data for same cell as in (d).
Unless otherwise stated, parameters are: F=b=0, v*=0.3, γ=1000. (A) Position of traction peak (black dots) and actin flow speed (in units of v*) corresponding to traction peak (blue exes) as a function of λ. (B–E) Actin flow, traction, myosin density, and adhesion density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*.
Unless otherwise stated, parameters are: F=b=0, v*=3, γ=1000. (We set F=0, in order to illustrate the dependence of the myosin distribution on γ for the same flow profile in each case, rather than for changing flow profiles that would occur for F>0). (A) Actin flow speed (black) and traction (red) as a function of distance from the leading edge. (B) Myosin distribution for different values of γ. (C) Myosin gradient for same values of γ as in (B).
Unless otherwise stated, parameters are: λ=3, F=1, v*=0.3 and γ=1000. (A) Position of traction peak in μm (black dots) and actin flow speed (in units of v*) corresponding to traction peak (blue exes) as a function of b. (B–F) Actin flow, traction, myosin density, myosin force, and adhesion density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (G–I) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for myosin strength b=10 (G), b=40 (H), and b=100 (I).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=0.2 (e) and F=0.4 (f).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=0.2 (e) and F=0.4 (f).
Unless otherwise stated, parameters are: λ=3, v*=0.3, b=15 and γ=1000. (a–d) Actin flow, traction, adhesion density, and myosin density as a function of distance from the leading edge. Black dashed line in (b) corresponds to v=v*. (e–f) Balance of forces on actin network (traction (black), myosin force (blue), internal viscous force (red)), for F=2 (e) and F=4 (f).