Assessment of Chemical Exchange in Tryptophan-Albumin Solution through ¹⁹F Multicomponent Transverse Relaxation Dispersion Analysis

Abstract

A number of NMR methods possess the capability of probing chemical exchange dynamics in solution. However, certain drawbacks limit the applications of these NMR approaches, particularly, to a complex system. Here, we propose a procedure that integrates the regularized nonnegative least squares (NNLS) analysis of multiexponential T₂ relaxation into Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion experiments to probe chemical exchange in a multicompartmental system. The proposed procedure was validated through analysis of ¹⁹F T₂ relaxation data of 6-fluoro-DL-tryptophan in a two-compartment solution with and without bovine serum albumin. Given the regularized NNLS analysis of a T₂ relaxation curve acquired at the CPMG frequency ν_CPMG = 125, the nature of two distinct peaks in the associated T₂ distribution spectrum indicated 6-fluoro-DL-tryptophan either retaining the free state, with geometric mean */multiplicative standard deviation = 1851.2 ms */1.51, or undergoing free/albumin-bound interconversion, with geometric mean */multiplicative standard deviation = 236.8 ms */1.54, in the two-compartment system. Quantities of the individual tryptophan species were accurately reflected by the associated T₂ peak areas, with an interconversion state-to-free state ratio of 0.45 ± 0.11. Furthermore, the Carr-Purcell-Meiboom-Gill relaxation dispersion analysis estimated the exchange rate between the free and albumin-bound states in this fluorinated tryptophan analog and the corresponding dissociation constant of the fluorinated tryptophan-albumin complex in the chemical-exchanging, two-compartment system.

Protein dynamics, referring to temporal and spatial changes in protein properties from the biophysical perspective, plays an essential role in determining protein functions (Baldwin and Kay 2009; Kleckner and Foster 2011). Thus, it is of importance to gain insight into the dynamic process to understand, predict or manipulate the biological function and behavior of a particular protein (Kleckner and Foster 2011). Chemical exchange, one of the particular dynamic processes, indicates coexistence of two or more distinct chemical environments or states for the molecule(s) investigated, of which the properties can be assessed by an array of NMR-based modalities (Kleckner and Foster 2011). Although a number of existing NMR methods possess the capability of probing the chemical exchange properties on defined timescales (Kleckner and Foster 2011), these methods are barely applied to samples not prepared in solution due to their lack of notable differences in specified parameters between the exchange states, such as degeneracy in chemical shift and peak overlap caused by broad linewidths.

It has been increasingly applied to several disciplines that the nonnegative least squares (NNLS) algorithm accompanied by a regularization term is used to analyze the multiexponential ¹H transverse relaxation data of H₂O, from which identified T₂ components were attributed to different H₂O compartments, for example, 1) cerebrospinal fluid, intra/extracellular water and water trapped between myelin bilayers in healthy human brain, 2) mobile water and proteoglycan-bound water in bovine patellar cartilage, and 3) intracellular and extracellular water compartments in hypertonic saline-injected masseter muscle (Gambarota et al. 2001; Laule et al. 2007; Reiter et al. 2011). Furthermore, the Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion experiment has been widely used to quantitate the features of kinetics, thermodynamics and structures of proteins or nucleic acids in exchange processes. Examples include studies of the multi-site folding/unfolding exchange process in the ¹⁵N-labeled deuterated Gly48Met Fyn SH3 domain by measuring T₂ relaxations of backbone amide ¹H and ¹⁵N nuclei, the conformational exchange of ribose backbone groups in the GCAA RNA tetraloop by detecting ¹³C relaxation dispersion on the C2′ and C4′ resonances, and the kinetic, thermodynamic and structural properties of basic pancreatic trypsin inhibitor by analyzing transverse relaxation dispersions of the associated backbone ¹⁵N spins (Grey et al. 2003; Johnson and Hoogstraten 2008; Korzhnev et al. 2005; Korzhnev et al. 2004). In the present work, we propose an affordable procedure that incorporates the regularized NNLS analysis of multiexponential T₂ relaxation curves into the CPMG relaxation dispersion experiment to study chemical exchange in a two-compartment system. By gathering a set of the regularized NNLS fits of T₂ relaxation curves at various CPMG frequencies in a tryptophan-albumin model to generate transverse relaxation dispersion curves, this approach demonstrated the potential for not only distinguishing T₂ components associated with the effective compartments separated by a semi-permeable membrane but also characterizing chemical exchange occurring in the millisecond time frame in a specified compartment.

A simple model of tryptophan binding serum albumin was selected to validate the NMR procedure of detecting the interconversion in a two-site exchange system. Serum albumin is the most abundant protein in blood plasma and is frequently used to investigate the strength of protein-ligand interaction due to owning a principal binding site for drugs, while tryptophan is one of a few endogenous substances bound to serum albumin (Cao et al. 2003; Fielding et al. 2005). Given the favorable NMR properties of ¹⁹F nuclei that provide a convenient label for NMR studies, we employed 6-fluoro-DL-tryptophan (6F-Trp), a fluorine-labeled tryptophan analog, to monitor its kinetic interaction with bovine serum albumin (BSA) (Jenkins and Lauffer 1990). In contrast to ¹³C or ¹⁵N CPMG relaxation dispersion experiments that may require a relaxation compensation element to equate evolution between in-phase and anti-phase transverse magnetizations, ¹⁹F-¹H couplings do not evolve significantly during the echo-spacing interval, 2τ_CPMG, if a restriction of τ_CPMG < 1/4J_FH is imposed (Loria et al. 1999). Thus, without concerning in-phase/anti-phase evolution, the relaxation compensation was simply neglected and the CPMG echo train was implemented to acquire the ¹⁹F transverse relaxation data of 6F-Trp with a concentration of 45 mM at 20 ± 1 °C. All the individual points collected at the tops of the respective echoes were assembled to form a decay curve for estimating the T₂ relaxation times (detailed in the Supporting Information). Through varying 2τ_CPMG, the interval between successive 180° pulses, a set of CPMG experiments with the interleaved value of ν_CPMG, i.e. the reciprocal of 4τ_CPMG, ranging from 10–1250 Hz were recorded for the ¹⁹F transverse relaxation dispersion analysis. The same manner was respectively performed on the transverse relaxation data collected in the solution of BSA-6F-Trp complex and in the two-compartment system constituting sole 6F-Trp and BSA-6F-Trp complex solutions (abbreviated to two-compartmental 6F-Trp system), of which the sole 6F-Trp and the BSA-6F-Trp complex were separated into the respective layers by a semi-permeable dialysis membrane (Figure 1). More details can be found in the Supporting Information.

Figure 1.

Skematic of the two-compartmental 6F-Trp system. A 3-mm inner diameter tube made of semi-permeable dialysis membrane was inserted into a 5-mm NMR tube to separate the BSA-6F-Trp complex solution from the sole 6F-Trp solution for the ¹⁹F transverse relaxation experiments.

The acquired ¹⁹F transverse decay curves were introduced into the multiexponential T₂ relaxation analysis by using the NNLS algorithm equipped with the Tikhonov regularization (Graham et al. 1996; Reiter et al. 2009):

$${\mathrm{\sum }}_{n=1}^N{\mid {\mathrm{\sum }}_{m=1}^M{A}_{nm}{S}_m-y_n\mid }^2+\mu {\mid {\mathrm{\sum }}_{m=1}^M{S}_m\mid }^2$$ (1)

in which y_n contains N echo amplitudes on a transverse relaxation curve (N is 192 at echo-spacing τ_CPMG = 25 ms up to 20480 at echo-spacing τ_CPMG = 0.2 ms), A_nm denotes a matrix composed of N × (M-1) kernels exhibiting exponential relaxations and N × 1 entries of value 1, and S_m consists of M-1 unknown amplitudes associated with the M-1 transverse relaxation times and one unknown amplitude responding to baseline offset adjustment (detailed in the Supporting Information) (Reiter et al. 2009). In addition, μ is referred to as an NNLS regularizer that endures a certain degree of misfit to balance overfitting and underfitting of experimental data (Graham et al. 1996; Whittall and MacKay 1989). In this study, a set of 80 (= M-1) possible T₂ relaxation values were equally spaced over the logarithmical scale between 0.1 and 5000 ms. The number of estimated T₂ values, M-1, is much less than the number of data points, N, referring to large degrees of freedom for the regularized NNLS analysis of each decay curve. The outcome of the regularized NNLS analysis of a transverse relaxation curve was typically presented as a distribution of the continuous spectrum constructed by a subset of the 80 possible T₂ values. In fact, the regularized NNLS analysis bypassed a classical paradigm for exponentially ill-posed problems that render no unique solution to, for example, exponential analysis of a multicomponent transverse relaxation curve (Istratov and Vyvenko 1999). Figure 2 exhibits an example of T₂ distribution results attributed to the regularized NNLS analysis of ¹⁹F transverse relaxation data acquired at ν_CPMG = 125 Hz in the 6F-Trp solution, the BSA-6F-Trp complex solution, and the two-compartmental 6F-Trp system, respectively. The fits of the corresponding T₂ relaxation curves performed by the regularized NNLS analysis were evaluated by the χ² goodness-of-fit test, with the corresponding p values reported. The test indicated that high correlations were performed between the T₂ relaxation data and the fits resulting from the regularized NNLS approach, as shown in Fig. S1 and Table S2 in the Supporting Information.

Figure 2.

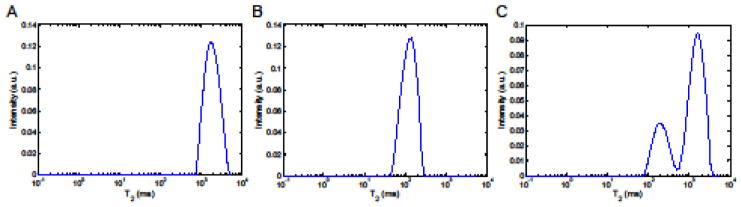
T₂ distributions resulting from the regularized NNLS analysis of ¹⁹F T₂ relaxation curves. The echo time present in the CPMG pulse sequence was τ_CPMG = 2 ms. A single T₂ component was depicted in (A) the 6F-Trp solution and (B) the BSA-6F-Trp complex solution, respectively, while (C) two T₂ components were observed in the two-compartmental 6F-Trp system. The χ² statistics for goodness-of-fit tests of the regularized NNLS-derived fits of T₂ relaxation curves exhibited χ² = 2317, p = 0.41 for the 6F-Trp solution (Figure S1A), χ² = 2370, p = 0.16 for the BSA-6F-Trp complex solution (Figure S1B), and χ² = 2206, p = 0.92 for the two-compartmental 6F-Trp system (Figure S1C), all with degrees of freedom = 2303.

The T₂ distribution results consisting of either one or two T₂ peaks were further fitted by a 4- or 7-parametric lognormal model (detailed in the Supporting Information). The statistic of the every fit was reported as the geometric means and multiplicative standard deviations (MSD) of the lognormal distributions accordingly. While a T₂ distribution consisted of two distinct peaks, the weight fractions of the 6F-Trp compartments associated with the peaks were determined by integrating the peak areas under the corresponding histogram bins, the amplitudes of which were estimated by the lognormal function. In Fig. 2A, the fit exhibited a single T₂ component of 1912.0 ms */1.31 in geometric mean */MSD, referring to free 6F-Trp in the 6F-Trp solution. Fig. 2B shows a T₂ peak with reduction in its average of 149.6 ms */1.52, indicating an indiscernible state made up of free and BSA-bound 6F-Trp in the BSA-6F-Trp complex solution. The indistinct pattern of the free and bound states, presented by a sole peak in the T₂ distribution, was due to occurrence of chemical exchange during acquisition of transverse relaxation data (Baldwin and Kay 2009). In contrast, the regularized NNLS analysis of relaxation data obtained from the two-compartmental 6F-Trp system revealed a T₂ distribution composed of two distinct peaks of 1851.2 ms */1.51 and 236.8 ms */1.54 in average, respectively (Fig. 2C). Through peak identification by reference to Figs. 2A and 2B, the outcome evidenced coexistence of the free 6F-Trp state and the interconversion of free and BSA-bound 6F-Trp in the two-compartmental 6F-Trp system. This result shows that the regularized NNLS algorithm is capable of conducting the multiple T₂ component analysis in different types of nuclei but not limited to ¹H transverse relaxations acquired mostly for water compartment analysis.

As noted, two distinct/resolvable peaks shown in the T₂ distributions in the two-compartmental 6F-Trp system refer to a free 6F-Trp state and an interconversion between free and BSA-bound 6F-Trp, respectively. This two-peak feature was observed as the corresponding transverse decay curves acquired at ν_CPMG ranging from 10 to 200 Hz (Table 1). The averaged T₂ values in interconversional 6F-Trp exhibited an increasing trend when ν_CPMG elevating. Such ν_CPMG-dependent T₂ relaxations indicated the presence of chemical exchange, and further analysis through implementing the CPMG relaxation dispersion was required. A minute relaxation dispersion was observed in T₂ distributions obtained from free 6F-Trp (Figure 3), which was mainly due to underestimation of the relaxation times while using the NNLS algorithm to analyze the transverse decay curves with low single-to-noise ratios (Reiter et al. 2009). In addition, Table 1 shows the ratios of the fractional weight associated with the exchanging 6F-Trp to that associated with the free 6F-Trp in the two-compartment system, with an arithmetic average of 0.45 ± 0.11 at ν_CPMG varying between 10 and 200 Hz. The ratios reflected the quantities of 6F-Trp inside the semi-permeable dialysis membrane (i.e., 6F-Trp in the exchange state) and outside the membrane (i.e., free 6F-Trp), respectively. Briefly, by fitting the T₂ distributions with lognormal distributions the estimated 6F-Trp quantitation provides a sensible outcome, compared to the quantity of 6F-Trp determined in the sample preparation with a BSA-6F-Trp complex-to-sole 6F-Trp ratio of 0.45.

Table 1.

Regularized NNLS-derived T₂ distributions in the two-compartmental 6F-Trp system

νCPMG (Hz)	200	175	150	125	100	75	50	37.5	25	18.75	12.5	10
T2,long (ms)	1944.6	2140.5	1920.4	1851.2	1773.5	1737.0	1630.4	1558.5	1528.9	1528.2	1308.6	1211.7
σlong	(1.47)	(1.67)	(1.43)	(1.51)	(1.42)	(1.43)	(1.54)	(1.40)	(1.52)	(1.45)	(1.42)	(1.32)
[T2,long/σlong, T2,long*σlong]	[1321.8, 2860.9]	[1285.3, 3564.7]	[1345.1, 2741.8]	[1222.6, 2802.9]	[1251.4, 2513.4]	[1212.6, 2488.2]	[1057.3, 2514.0]	[1112.3, 2183.6]	[1004.1, 2328.1]	[1050.6, 2222.8]	[920.5, 1860.2]	[919.4, 1597.0]
T2,short (ms)	268.6	315.2	325.2	236.8	250.1	232.7	160.8	154.2	168.7	176.6	160.7	164.4
σshort	(1.42)	(1.80)	(1.70)	(1.54)	(1.44)	(1.38)	(1.86)	(1.58)	(1.49)	(1.46)	(1.39)	(1.52)
[T2,short/σshort, T2,short*σshort]	[189.0, 381.7]	[174.8, 568.6]	[191.4, 552.7]	[153.7, 364.7]	[174.1, 359.3]	[157.5, 343.6]	[86.3, 299.4]	[97.6, 243.5]	[113.0, 251.9]	[121.3, 257.0]	[115.7, 223.4]	[108.1, 250.0]
Area ratio (w2,short/w2,long)	0.45	0.46	0.51	0.38	0.38	0.42	0.50	0.54	0.21	0.50	0.43	0.67

^*T₂,_long (or T₂,_short) and σ_long (or σ_short) are the geometric mean and the multiplicative standard deviation for long (or short) T₂ component, respectively.

^**Data acquired at ν_CPMG = 250 to 1250 Hz are not shown due to the T_{2, long} and T_{2, short} components are indistinct.

Figure 3.

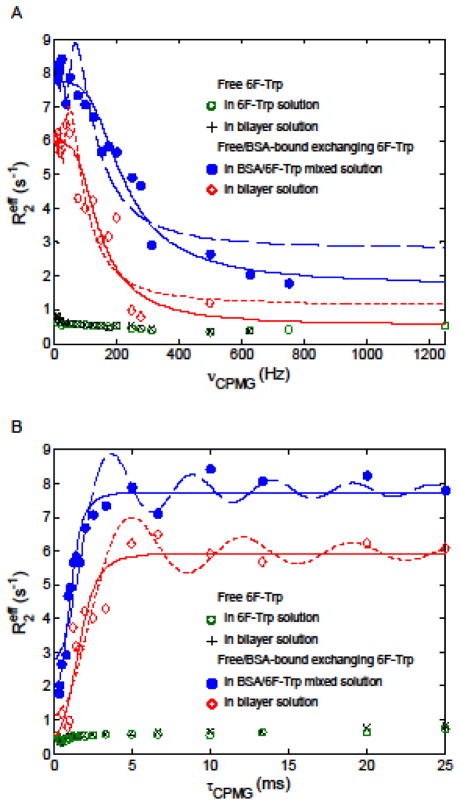
¹⁹F effective transverse relaxation rates as a function of CPMG field strength for 6F-Trp compartments. Relaxation dispersion data collected in free/bound exchanging 6F-Trp are presented with the associated fitting curves. The fitting curves to relaxation dispersion data using Eq. 2 (slow exchange expression) are displayed in dash lines, while those using Eq. 3 (skewed population P_A > P_B approximation) are in solid lines. The relaxation dispersions are plotted in (A) $R_2^{\mathit{eff}}$ vs. CMPG frequency and (B) $R_2^{\mathit{eff}}$ vs. half of echo-spacing τ_CPMG.

Chemical exchange in slow (k_ex ≪ δω; δω: chemical shift difference of the associated peaks between the exchanging states), intermediate (k_ex ≈ δω), or fast regime (k_ex ≫ δω) is detectable via a CPMG-based NMR experiment in which the spin-echo pulse train serves to refocus transverse magnetization dephasing and to lessen non-chemical-shift-derived relaxations including exchange broadening (Ishima and Torchia 1999; Kleckner and Foster 2011; Kloiber et al. 2011; Palmer et al. 2001). Through alternating the echo-spacing, 2τ_CPMG, between successive 180° pulses, the effective transverse relaxation rate constant, $R_2^{\mathit{eff}}$, i.e. the reciprocal of effective T₂, was conducted to estimate the exchange parameters, such as exchange rate k_ex, fractional spin population p_i on site A or B, and chemical shift difference δω_AB between sites A and B (Kovrigin et al. 2006). Quantitative estimation of the parameters in the exchanging system can be achieved by analyzing the change in the $R_2^{\mathit{eff}}$ relaxation rates, which were derived from the regularized NNLS fits of the associated T₂ decay curves, responding to varying ν_CPMG frequency (Figure 3). As shown in Fig. 3A, the $R_2^{\mathit{eff}}$ of free 6F-Trp in the 6F-Trp solution slightly fluctuated between 0.33 and 0.75 s⁻¹ at the ν_CPMG measured. A similar $R_2^{\mathit{eff}}$ profile of free 6F-Trp in the outer layer of the two-compartmental 6F-Trp system was observed, with the value alternating from 0.35 to 0.83 s⁻¹. In contrast, the observed $R_2^{\mathit{eff}}$ of the 6F-Trp under exchange process varied from 1.79 s⁻¹ at ν_CPMG = 750 Hz up to 8.42 s⁻¹ at ν_CPMG = 10 Hz in the BSA-6F-Trp complex solution as well as from 0.80 (ν_CPMG = 500 Hz) to 6.67 s⁻¹ (ν_CPMG = 10 Hz) in the inner layer of the two-compartmental 6F-Trp system. This indicates that the sense of chemical exchange process was predominated by the binding and unbinding behavior of 6F-Trp on the BSA binding site. Thus, investigation of exchange process focuses primarily on the interconversion of free and BSA-bound 6F-Trp.

To examine a two-site exchange process in the slow exchange regime, the CPMG-based relaxation dispersion curves characterizing interconvensional 6F-Trp were fitted into an analytical function of $R_2^{\mathit{eff}}$ expressed on the more populated site A (Tollinger et al. 2001):

$$R_{2A}^{\mathit{eff}}=R_{2A}+k_A-k_A\frac{sin(\delta \omega {\tau }_{\mathit{CPMG}})}{\delta \omega {\tau }_{\mathit{CPMG}}}$$ (2)

where R_2A, k_A and δω denote the transverse relaxation rate without exchange on site A, the first-order forward rate constant and the chemical shift difference between two sites A and B, respectively. By considering the free state of 6F-Trp the more populated site A based on preparation of the BSA-6F-Trp complex solution, the relaxation dispersion fitting for interconvensional 6F-Trp between the free and BSA-bound states can project the exchange parameters R_2A, k_A and δω. The estimated δω was 1231 ± 155 Hz (or 3.27 ± 0.41 ppm) in the solution of BSA-6F-Trp complex, compared with the observation of a 3.45-ppm drift from the free peak to the BSA-bound peak for 6F-Trp in the ¹⁹F spectra (Cao et al. 2003). In addition, a dispersion curve described in the slow exchange regime retained a particular damped oscillation feature near the low-frequency end of ν_CPMG (Fig. 3A), from which δω can be estimated by identifying the frequency leading to the local extremum in the second term of Eq. 2, i.e., δω= tan(δωτ_CPMG)/τ_CPMG (Tollinger et al. 2001). Accordingly, δω was calculated by locating the first local maximum observed from the high-frequency end of the dispersion curve (δωτ_CMPG ≈3π/2); however, the estimated δω of 2.51 ppm did not match the direct measure on the ¹⁹F NMR spectra. This is likely due to the designed ν_CMPG frequencies not close enough to the loci of actual extrema on the dispersion curve (Fig. 3B).

In addition to profiling the damped oscillation on the relaxation dispersion curve, the curve fitting using Eq. 2 obtained the estimated R_2A and k_A of 2.80 ± 0.77 s⁻¹ and 4.94 ± 1.01 s⁻¹, respectively, for 6F-Trp undergoing chemical exchange in the BSA-6F-Trp complex solution. Still, this fitting analysis untangles neither an exchange rate nor fractional populations in an exchange system (Kloiber et al. 2011). Alternatively, a simpler approximation of the Carver-Richards analysis that tackles prediction of the exchange rate and the spin populations is applicable to the condition of skewed populations P_A > P_B from slow to fast exchange regimes (Ishima and Torchia 1999; Palmer et al. 2001):

$$R_2^{\mathit{eff}}=R_2+\frac{P_A{P}_B\delta {\omega }^2{k}_{ex}}{k_{ex}^2+{(P_A^2\delta {\omega }^4+\frac{144}{16{\tau }_{\mathit{CPMG}}^4})}^{1/2}}$$ (3)

in which R₂ and k_ex are the exchange-free transverse relaxation rate and the exchange rate constant, respectively. Through implementing Eq. 3 to fit the relaxation dispersion curve collected in the BSA-6F-Trp complex solution, the estimates of k_ex = 249.8 s⁻¹, P_A = 97.54% of 6F-Trp (or 43.98 mM) in the free state and P_B = 2.46% of 6F-Trp (or 1.11 mM) in the bound state, which are expected becaues of the molar ratio of BSA to 6F-Trp being 2.51% as the sample prepared. The populations P_A and P_B estimated, referring to the dissociation constant K_D = 912 μM, are comparable to P_A = 97.49 to 97.65% (P_B 2.51 to 2.35%) calculated from the dissociation constant K_D = ~10 to 3000 μM reported in literature and the sample concentrations used in this study (Cao et al. 2003; Chanut et al. 1992; Fielding et al. 2005). Further, the estimates of R₂ and δω were obtained from the same analysis, with the values of 1.72 s⁻¹ and 1205 Hz (3.20 ppm), respectively. Here we simply demonstrated that the fits of the multiexponential-T₂-analysis-derived CPMG relaxation dispersions were sensibly comparable to the results obtained from different approaches (Cao et al. 2003; Chanut et al. 1992; Fielding et al. 2005), although it is well known that the absolute values of the derived parameters including the dissociation constant in an exchange process are usually inaccurate and require multi-field relaxation dispersion data for faithful estimation (Cao et al. 2003; Kovrigin et al. 2006; Palmer et al. 2001).

In the two-compartmental 6F-Trp system, the same maner of fitting analyses using Eqs. 2 and 3 were also applied to the ¹⁹F transverse relaxation dipserison curve associated with 6F-Trp undergiong exchange process. The fit via Eq. 2 estimated R_2A of 1.15 ± 0.96 s⁻¹, k_A of 4.81 ± 1.20 s⁻¹ and δω of 904 ± 142 Hz (2.40 ± 0.38 ppm), while k_ex of 249.5 s⁻¹, P_A of 97.61%, R₂ of 0.82 s⁻¹ and δω of 693 Hz were obtained by the simpler approximation with a prerequisite of P_A ≫ P_B (Eq. 3). The results indicate that the regularized NNLS analysis permits valid characterization of transverse relaxation dispersion of a given compartment in the presence of an uninteresting, “contaminating” compartment. Morevoer, the regularized NNLS-integrated CPMG relaxation dispersion analysis provides a potential approach to investigation of exchanging kinetics, for example, in the nature of a monomer-oligomer equilibrium with overlapping MR resonances, which precludes conventional NMR analyses.

In summary, investigation of chemical exchange process in a complex system, such as a two-compartment system, can be achieved through using a procedure that integrates the regularized NNLS analysis of multiexponential T₂ decay curves into the CPMG relaxation dispersion analysis. By exploiting the fluorinated amino acid as a ¹⁹F NMR label, the procedure exhibited the capabilities of distinguishing two 6F-Trp species, quantitating these two species in the two-compartmental 6F-Trp system and rationally estimating the chemical exchange parameters for the interconversional 6F-Trp.