Growth and hemodynamics after early embryonic aortic arch occlusion^*

Abstract

The majority of severe clinically significant forms of congenital heart disease (CHD) is associated with great artery lesions, including hypoplastic, double, right or interrupted aortic arch morphologies. While fetal and neonatal interventions are advancing, their potential ability to restore cardiac function, optimal timing, location, and intensity required for intervention remain largely unknown. We here combine computational fluid dynamics (CFD) simulations with in vivo experiments to test how individual pharyngeal arch artery hemodynamics alters as a result of local interventions to obstruct individual arch artery flow. Simulated isolated occlusions within each pharyngeal arch artery were created with image derived three-dimensional (3D) reconstructions of normal chick pharyngeal arch anatomy at Hamburger-Hamilton (HH) developmental stages HH18 and HH24. Acute flow redistributions were then computed using in vivo measured subject-specific aortic sinus inflow velocity profiles. A kinematic vascular growth-rendering algorithm was then developed and implemented to test the role of changing local wall shear stress patterns in downstream 3D morphogenesis of arch arteries. CFD simulations predicted that altered pressure gradients and flow redistributions were most sensitive to occlusion of the IV^th arches. To evaluate these simulations experimentally, a novel in vivo experimental model of pharyngeal arch occlusion was developed and implemented using two-photon microscopy guided femtosecond laser based photodisruption surgery. The right IV^th arch was occluded at HH18, and resulting diameter changes were followed for up to 24 hours. Pharyngeal arch diameter responses to acute hemodynamic changes were predicted qualitatively but poorly quantitatively. Chronic growth and adaptation to hemodynamic changes however were predicted in a subset of arches. Our findings suggest that this complex biodynamic process is governed through more complex forms of mechanobiological vascular growth rules. Other factors in addition to wall shear stress, or more complex WSS rules are likely important in the long-term arterial growth and patterning. Combination in-silico/experimental platforms are essential for accelerating our understanding and prediction of consequences from embryonic/fetal cardiovascular occlusions, and lay the foundation for non-invasive methods to guide CHD diagnosis and fetal intervention.

Introduction

Pharyngeal arch artery (PAA) morphogenesis involves complex transformations of the generalized vertebrate template of six symmetric pairs of embryonic PAA into species-specific patterns that include the mature and asymmetric aortic arch, pulmonary arteries and great vessels. Concurrent with PAA morphogenesis, outflow tract (OT) morphogenesis transforms the common outlet of the embryonic heart into the separate great vessels and semilunar valves. This delicate sequence of vascular and cushion/primitive valve remodeling takes place within an active biomechanical environment that includes changes in ventricular function, vascular impedance and vessel geometry, as well as finely orchestrated changes in cellular and matrix biology. The regulation of such outflow (PAA and OT) morphogenesis has been an area of intense interest for nearly a century (Bremer, 1928; Elzenga and Gittenberger-de-Groot, 1985; Kirby, 2002; Yashiro et al, 2007). Errors in PAA and OT morphogenesis occur in more than 50% of infants with congenital heart disease (CHD) (Go et al. 2013). Defects associated with malformation of the OT and PAA include hypoplastic left heart syndrome with arch atresia, aorticopulmonary septation defects with arch anomalies such as tetralogy of Fallot (25% with right pharyngeal arch), double outlet right ventricle with arch interruption, transposition of the great vessels and vascular rings.

Although the etiologies of congenital heart defects are not yet fully understood, they are thought to result in part from changes in hemodynamics (Culver and Dickinson, 2010; Hove et al., 2003; Jaffee, 1965; Kamiya and Togawa, 1980; Langille, 1996; le Noble et al., 2005; Thoma, 1893), with wall shear stress (WSS), being a major extrinsic mechanical stimulus for vascular remodeling (Culver and Dickinson, 2010; Rodbard, 1975). Changes in WSS patterns are detected through endothelial cells, which convert mechanical stimuli into intracellular signals, leading to an increase or decrease in vessel diameter (Bayer et al., 1999; Girerd et al., 1996; Langille and O’Donnell, 1986). Recent studies of the Hamburger-Hamilton (HH) stage 18, 21, and 24 PAA have revealed clear relationships between PAA flow, WSS, and luminal growth (Kowalski et al., 2013; Wang et al., 2009). While the asymmetric PAA regression pattern has been shown to occur by differential apoptosis (Molin et al., 2002), the expression of genes that normally orchestrate left/right asymmetry has not been observed in the PAA (Liu et al., 2002; Yashiro et al., 2007). Whereas the right lateral PAA IV diameter increases significantly (p<0.05) from stage 18 to 21 to 24, the left lateral diameter remains the same from stage 21 to 24 (Kowalski et al., 2013). This asymmetric growth correlates with the asymmetric flow distribution, in which the right lateral consistently receives >65% of all flow directed to PAA pair IV – the largest imbalance among all PAA pairs.

The vertebrate chick embryo undergoes PAA and OT morphogenesis similar to humans and is amenable to imaging and manipulation (Clark et al., 1989; Hu et al., 2009; Pexieder, 1986). It has been extensively used to study the role of hemodynamics in embryonic cardiovascular development, where acute and chronic perturbations in blood flow have produced a spectrum of cardiovascular defects (deAlmeida et al., 2007; Gessner, 1966b; Hogers et al., 1999; Lucitti et al., 2005; Reckova et al., 2003; Sedmera et al., 1999; Tobita et al., 2005). Vascular interventions such as chronic left atrial ligation (LAL) and unilateral vitelline vein ligation (VVL) result in a redistribution of blood flow to the individual PAAs, generating a variety of abnormalities (Hogers et al., 1999; Hu et al., 2009; Rychter and Lemez, 1965). Distinct PAA perfusion patterns were demonstrated by Rychter and Lemez, who further showed that these patterns were disrupted by transection or ligation of vitelline veins. The VVL model was extended by Hogers et al. (Hogers et al., 1999), revealing a change in intra-cardiac flow patterns as well. Fully hatched embryos displayed multiple defects in PAA development, including hypoplastic right brachiocephalic artery, interrupted aortic arch, double aortic arch, and hypoplastic pulmonary artery. The LAL model also produced changes in PAA flow, which was significantly reduced in all PAA, as measured by laser Doppler velocimetry (Hu et al., 2009). Defects such as absent PAA III and IV and PAA hypoplasia were present in stage 27 LAL embryos. More recently, we developed and applied a femtosecond laser ablation technique to the embryonic heart to perturb prevalvular cushion and ventricular development (Yalcin et al., 2010a; Yalcin et al., 2010b). Compared to LAL and VVL that alter the “upstream” intra-cardiac flow streams, these contemporary embryonic vascular interventions have been shown to generate more drastic effects in blood flow and hemodynamics, primarily due to the low Reynolds number flow regimes of the early embryo damping the upstream differences in intra-cardiac flow streams (Kowalski et al., 2013).

In this manuscript, the femtosecond pulsed laser photoablation technique has been extended to occlusion of the PAA of the early chick embryo, together with a detailed comparative PAA-by-PAA computational hemodynamic analysis of its consequences at multiple developmental time-points. We explore the alteration of neighboring arch hemodynamics due to targeted arch occlusion. Using the WSS field computed from computational fluid dynamics (CFD) analysis, we implement a simple proportionality model to test its ability to forecast downstream shear-mediated three-dimensional PAA growth. As experimental tools and simulation strategies improve and integrate, this combinatorial strategy will inform how PAA development may progress under clinically relevant structural abnormalities.

Methods

In silico pharyngeal arch occlusion and flow modeling

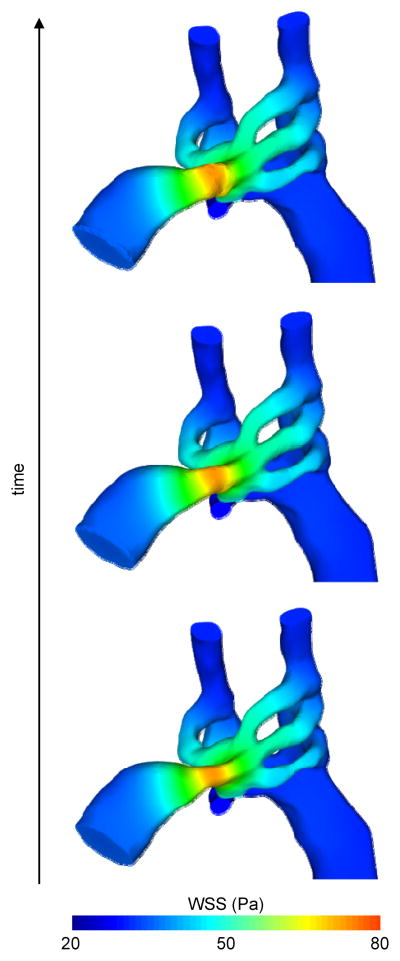
Subject-specific 3D geometries of the HH18 and HH24 PAA are generated using microinjected polymerizing resin (diluted MICROFIL® Silicone Rubber Injection Compounds MV-blue, Flow Tech Inc., Carver, MA) and micro computed tomography (micro-CT) as previously described (Butcher et al., 2007; Wang et al., 2009). PAA geometries extended from the distal outflow tract to the dorsal aorta and paired cranial aortae. Occlusion of a single PAA was modeled in silico by creating a geometric discontinuity with flat cut surfaces at two locations symmetrically positioned from a central plane bisecting the PAA. In silico occlusion and preparation of 3D geometries for CFD was performed in Geomagics Studio 10 (Geomagic Inc., Durham, NC). For comparison with our in vivo experiment, we modeled occlusion of the right lateral PAA IV (denoted “PAA^IV-R” and similar hereafter) in the HH18 model. We further modeled occlusions of the PAA^III-R in the HH18 model and each of the six PAA present in the HH24 model (right and left laterals of PAA pairs III, IV, and VI), totaling eight in silico occlusion test cases (Figure 1).

Figure 1.

Control and occluded HH18 (a–c) and HH24 (d–j) PAA models. The peak WSS indicated by surface color. In the control models (a and d), the PAA and relevant vascular structures are labeled. R – right, L – left.

For each PAA occlusion and the control HH18 and HH24 geometries, we modeled 3D blood flow using an in-house pulsatile cardiovascular flow solver incorporating a validated 2^nd order accurate multi-grid artificial compressibility numerical method (Menon et al., 2013). Blood was treated as a Newtonian fluid with constant hemodynamic properties (ρ = 1060 kg/m³, μ = 3.71 × 10⁻³ Pa.s) and rigid, impermeable vessel walls were assumed with no slip boundary conditions. Flow was simulated in terms of inlet normalized spatio-temporal units, on a high-resolution unstructured Cartesian immersed boundary grid with finite-difference numerical treatment. Grid sensitivity analysis was conducted in the control PAA models in order to ensure consistency and reliability of the numerical solutions and also identify an appropriate spatial resolution (0.01 mm, 500,000 fluid nodes) for all simulations presented in this study, beyond which resulting mass-flow redistributions were insensitive to further Cartesian grid refinements.

As per recent studies, (Bharadwaj et al., 2012), Poiseuille flow inlet boundary profiles were applied in the HH18 model, while plug flow profiles were applied in the HH24 model. A fixed mass flow-split type outflow boundary condition was imposed in each model in order to maintain distribution of the total cardiac output to dorsal aorta and cranial vessels in the ratio of 90/10. Pulsatile flow was simulated based on outflow tract cardiac output waveforms selected from our previously published studies (Wang et al., 2009; Yoshigi et al., 2000). Pulsatile flow was modeled in order to more realistically account for the inertial effects of the accelerating flow fields on pressure and velocity, but for practical purposes hemodynamic parameters were reported only for peak systole.

CFD simulations were conducted at Pittsburgh Supercomputing Center’s Blacklight supercomputing cyber-infrastructure. Each simulation was terminated after 5 cardiac cycles and cost an average of 22 hours at 32 core parallelism. Convergence of the transient CFD solution was monitored using the time-evolution of mass-flow split distributions between the PAA at the instant of peak systole. Simulation data from the 5^th cardiac cycle was analyzed in order to ensure damping of initial transients.

Computational model of shear driven pharyngeal arch growth

We developed a WSS driven three-dimensional luminal growth kinematics model of the short-term response to altered hemodynamics after PAA occlusion. This numerical model was applied to the control and right lateral PAA IV (PAA^IV-R) occluded HH18 models, corresponding to our experiment. WSS at the immersed boundary nodes of the mesh was computed at the instant of peak systole flow from the CFD solution. Kriging interpolation (Davis, 1986) was then used to sample WSS on the PAA wall surface (Tecplot, Bellevue, WA). For each wall surface node, a vector comprising the principal diagonal elements of the shear stress tensor was calculated based on the local growth rule. A simple local growth rule is specified where the wall displacement (Δx) was computed by offsetting the wall surface along the vector direction indicated by the principal diagonal shear stress vector (τ), assuming a linear relation between shear stress and displacement. The basic growth law is defined in Eq 1, where α is the proportionality constant, valued at 8.1×10⁻⁶ μm/Pa·s for all PAA. The proportionality between shear-stress and displacement was calibrated based on relationships approximated from our previous study, which monitored natural PAA growth between HH18 and HH21(Kowalski et al., 2013).

$$d\mathit{x}/dt=\alpha \mathit{\tau }$$ (1)

In order to avoid effects of artificial peaks and plateaus in the WSS field as well as to smooth the region of influence predicting wall displacements, the peak systole WSS field was smoothed using a function solving an iterative solution to the Laplace equation. The smoothed WSS was arrived at from the solution to a difference equation for WSS, using generalized coordinates (Anderson et al., 1984), defining a diffusive smoothing parameter, D, set between 0 and 0.95 to determine the extent of smoothing. The number of point-Jacobi iterations used to solve this equation for WSS (i.e. smoothed WSS) was an additional input variable, which smoothed the region of influence of the WSS field. Each pass of smoothing (i.e. each iteration) shifted the value of the variable at a data point towards an average of the values at its neighboring data points. In this study, we examine the likely displacement effects of WSS using D=0.90 and 100 smoothing iterations. The choice of these smoothing parameters and their effects in light of true shear-mediated response is a subject of presently ongoing studies.

We computed wall displacement for eight time points from HH18 to HH24 (a 24 hour period) in both a normal and PAA^IV-R occluded model. Wall displacement at each time point was based on the WSS computed from the initial CFD solution. As a first approximation and to limit computational expense, we did not re-solve the flow-growth algorithm between growth steps after the initial step. Therefore, in our growth model, the WSS field was independent of time, and Eq 1 was simplified to Δx = ατΔt. The hydraulic diameter of the PAA at every time point was computed based on the cross sectional area at the PAA midpoint to assess net luminal growth and compare with the experiment.

Experimental pharyngeal arch occlusion

Embryo culture and preparation

Fertile white Leghorn chicken eggs were incubated blunt-side up for three days in a continuous rocking incubator at 37.5°C. Embryos were then open cultured as previously described (Yalcin et al., 2010a; Yalcin et al., 2010b). Briefly, HH18 embryos were transferred onto a polyurethane (Saran Wrap) membrane and placed atop a plastic cup partially filled with water. Injection micro-needles were fashioned from pulled capillary tubes (0.75 mm ID) cut to 20 μm inner diameter via a microforge (Glassworx, St. Louis, MO). A micromanipulator (model M3301L, World Precision Instruments, Sarasota FL) positioned the needle into a vitelline vein (usually >100 μm in diameter), and 1–1.5 μl of Texas red dextran (70,000 MW, neutral Sigma-Aldrich D1830) diluted in Earle balanced salt solution (5% w/v) was slowly injected. The embryos were returned to the incubator and monitored until the dye could be seen throughout the vasculature.

Two-photon microscopy and femtosecond pulsed laser ablation

A custom built two-photon excited fluorescence (2PEF) microscope was modified to include a path for a femtosecond pulsed photoablation laser, as described previously (Nishimura et al. 2006; Yalcin et al., 2010a). Laser pulses from a 1040-nm fiber laser (μJewel-FCPA, IMRA America, Inc, 1MHz, 350-fs pulses) or a Ti:Sapphire laser tuned to 900 nm (Chameleon, Coherent, 80 MHz, 75-fs pulses) were used for two-photon excitation. Pulses were scanned by galvonometric scanners (3 frames per second) and focused into the sample using a 1.0 numerical aperture, 20x water immersion objective (Zeiss). Fluorescence emission from the Texas red dextran was reflected by a dichroic mirror, collected through a 645 nm bandpass filter, and relayed to photomultiplier tubes. Laser scanning and data acquisition were controlled by ScanImage (Pologruto et al, 2003).

A 1-kHz high-pulse-energy Ti:Sapphire amplified laser system with 50-fs pulse duration (Legend-USP, Coherent, Santa Clara, CA, 800-nm central wavelength) was used to perform the targeted vessel disruption. This laser beam was focused into the center of the imaging plane to induce clotting in vessels (see (Yalcin et al., 2010a) for experimental set-up). Incident laser energy and exposure time was controlled through the use of neutral density filters and a fast mechanical shutter (2-ms minimum opening time, Uniblitz Rochester, NY).

Targeted vessel occlusion

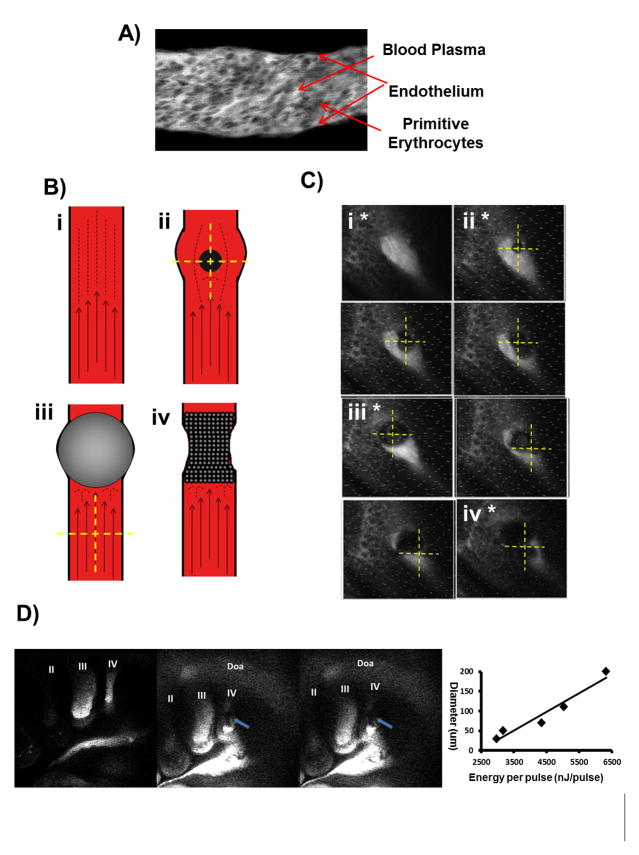
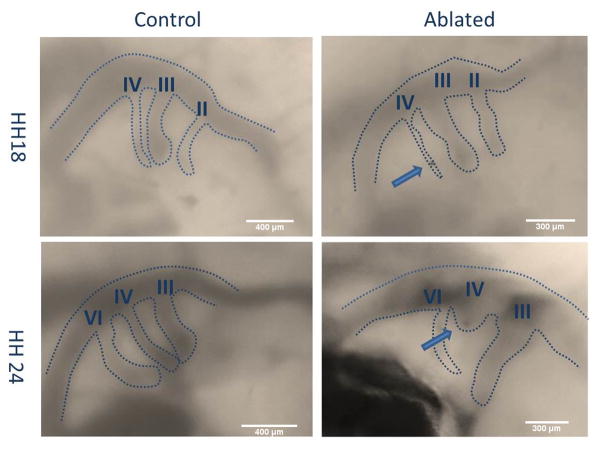
The PAA^IV-R was identified and occluded in HH18 (Day 3) embryos. HH18 embryos with smaller PAA^IV-R were specifically chosen to facilitate faster occlusion experiments, as it is easier to occlude arteries with smaller cross sectional areas. Femtosecond pulses were tightly focused into the center of the PAA lumen causing nonlinear absorption of laser energy that drives photodisruptive damage. This absorption separates positively and negatively charged ions, which quickly recombine to form a gas bubble that expands and contracts in size based on an equilibrium between the laser energy input and its external environment (Vogel and Venugopalan 2003; Nishimura et al. 2006). Photodisruption was confined to the volume focused by the two-photon microscopy optics. Laser pulse energies of 3–4.5 μJ were required to grow and maintain a cavitation bubble that temporarily stopped flow in vessels ranging from 30–70 μm in diameter (Figure 2D). HH18 embryos (Day 3) with smaller PAA^IV-R were therefore specifically chosen to facilitate faster occlusion experiments. Occlusion was further facilitated by pre-cooling embryos in an ice bath in order to slow the heart rate ~50% (and thereby the blood flow rate), resulting in greater persistence of cavitation bubbles that mark the beginning of the occlusion process. Following the creation of this cavitation bubble, laser energy was directed to the increasingly more stagnant flow directly behind the cavitation bubble, accumulating damage and cohesion in the lumen (Figure 2B). This process was adjusted and/or repeated as needed until a stable occlusion was formed. Stable occlusions were taken to be those that persisted for 5 minutes without laser perturbation. Figure 2C illustrates the process as observed with the two-photon microscopy. Embryos were imaged in their ice bath no longer than one hour, and then promptly returned to the incubator. Embryos quickly returned to 37.5°C and normal heart rate was restored within 20 minutes. Previous studies demonstrated no adverse effects of this temporary hypothermia (Yalcin et al., 2010a). Sham control embryos were placed in a similarly cooled water bath outside of any beam path for the duration of an occlusion cycle. The location and degree of vessel occlusions were confirmed through intravital microscopy, India ink and/or thin section histology. Occlusions were created either at the base or head of the arch artery (Figure 3).

Figure 2.

A) Two-photon image of flow inside of an HH18 vessel. Blood plasma is visible as bright fluorescence while primitive erythrocytes remain dark spheres. B) Schematics representing occlusion process. Identification of vessel in question (i), creation of cavitation bubble (ii), temporary blockage of vessel flow via a large cavitation bubble (iii) and formation of permanent vessel occlusion (iv). C) Two photon fluorescent images of vessel occlusion process with roman numerals and asterisks marking occlusion process as defined by schematic. Yellow crosshairs mark ablation laser focal point. D) Full vessel view at baseline (left) during (middle) and after (right) the occlusion process as seen through two-photon fluorescence. Blue arrows indicate occluded vessel. On right is a plot of cavitation bubble diameter as a function of laser energy.

Figure 3.

Stereoscope images of H18 and HH24 PAAs for a control and ablated embryo. Dashed lines mark vessel diameters. Roman numerals identify PAA branches. Arrows point to vessel occlusion.

Measurement of vessel diameter

Embryonic pharyngeal arch artery diameters were visualized using India ink injections, and measured at their midpoints with a calibrated stereomicroscope (Zeiss stereo Discovery) immediately following occlusion (HH18), 3 hours post occlusion (HH19), and 24 hours following occlusion (HH22/23). Additional embryos were maintained for 48 hours after vessel occlusion (HH28), then fixed in 4% paraformaldehyde. These embryos were then paraffin processed, cut into 10μm sections, and stained with hematoxylin and eosin (H&E). Experimental results are based off a set of 3 occlusion embryos and 4 control embryos.

Statistics

Statistical comparisons were made through the use of GraphPad Prism (GraphPad Software, Inc San Diego, CA) statistical software. Linear regressions were performed on experimental and simulation control and occlusion subsets for the diameter of each of the three arch pairs (II, III, IV) as a function of time. Two-tailed analysis of covariance (ANCOVA) was then performed comparing experimental control to experimental occlusion curves, experimental control to simulation control curves, and experimental occlusion curves to simulation occlusion curves. These analyses tested the null hypothesis that the curves were identical, comparing slopes first and then the curve as a whole, using P<0.05 to assign significance.

Results

Wall shear stress based PAA vessel 3D growth simulation

As expected, the highest values for WSS were noted at sites of narrowest PAA diameters, which in-turn were the locations which experienced the maximum displacement as per our short-term PAA growth prediction model. The WSS based growth model was expected to reduce peak WSS by dilating such narrowed regions. However, since our first-approximation WSS-based growth model does not anticipate the naturally occurring disappearance of the PAA^II arches or the generation of the PAA^VI arches, the proposed predictive kinematics approach is focused on ascertaining short-term growth effects attributable only to current hemodynamic and anatomical conditions, but doesn’t account for ongoing biological programs.

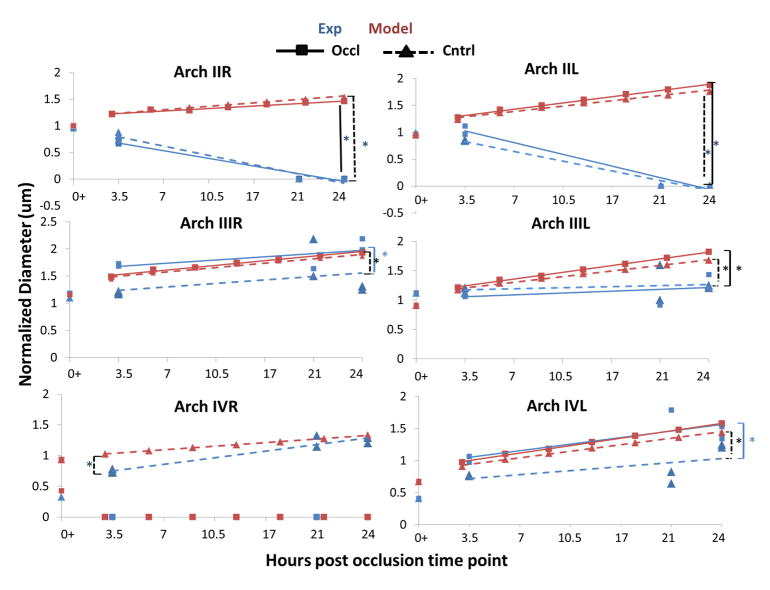
WSS created wall-displacement model results for the control HH18 models are presented in Figure 4. Cross-sectional ovalization of each PAA was predicted correctly using the WSS dependent growth model, supporting local WSS based PAA remodeling. Simulated incremental changes in PAA diameter were then plotted over eight equally-spaced developmental time intervals from HH18 to HH24 (Figure 7). Diameters are normalized to the initial value at HH18. Videos of the growth of PAA are available in the supplementary material.

Figure 4.

WSS-based short term growth prediction in the normal HH18 model.

Figure 7.

Graphs representing diameter changes as a result of HH18 right IV vessel occlusion imposed flow redistributions for both experimental and computational data over a 24 hour period. Each data set has been fit with linear trend lines. A) PAA^II-R B) PAA^III-R C) PAA^IV-R. D) PAA^II-L E) PAA^III-L F) PAA^IV-L. Both control (dashed line, triangles) and occluded (solid line, squares) trends are shown for experimental (blue) and computational (red) data. Brackets with asterisks couple significantly different trends. Black lines indicate comparison of simulation and model subsets, dashed lines indicate comparison between control subsets. Blue brackets indicate a comparison between model subsets. Diameters are normalized to an initial HH18 PAA^II-R value within each subset.

Given that our inflow boundary condition (total cardiac output waveform) remained constant, the flow into an occluded PAA must be re-distributed among the remaining vessels. This effect is shown in Table 1, which presents the peak flow in each PAA at HH18. In the control geometry, the flow distribution aligns well with the hydraulic resistances of the PAA vessels, i.e. PAA^III-R is the largest diameter and receives the highest flow and PAA^IV-L is the smallest diameter and receives the least flow. In the case of simulated PAA^IV-R occlusion at HH18, the flow distribution pattern is retained (Table 1). Following PAA^III-R occlusion, PAA^II-R emerges as the vessel with the greatest flow (.22 mm³/s), followed closely by PAA^III-L and PAA^IV-R (Table 1). In the case of III-R occlusion, PAA^II-R is positioned to become the hemodynamically dominant arch. Though the right lateral PAA^IV-R is predetermined to become the aorta, at HH18 the PAA^IV pair has only recently formed and is nearly 40% smaller than PAA^III. By HH24, however, PAA^IV pair enlarge significantly (especially the right lateral) and eclipses PAA^III in diameter (Wang et al., 2009). Therefore, occluding the presumptive aorta at this early stage is likely to result in a variety of PAA defects. Our simulations suggest that the PAA^III-R would then become the dominant PAA and may compete to become the mature great vessel during later stages of development.

Table 1.

Stage HH18 PAA mean flow distribution

	flow (mm3/s)		% change from occlusion		% of cardiac output
	R	L	R	L	R	L
No Occlusion
PAA II	0.14	0.14	0.00%	0.00%	16%	16%
PAA III	0.26	0.16	0.00%	0.00%	30%	18%
PAA IV	0.14	0.045	0.00%	0.00%	16%	5.1%
Right Lateral PAA IV Occluded
PAA II	0.17	0.16	21%	14%	19%	18%
PAA III	0.31	0.18	19%	13%	35%	21%
PAA IV	0.00	0.051	−100%	13%	0.00%	5.8%
Right Lateral PAA III Occluded
PAA II	0.22	0.18	57%	29%	25%	21%
PAA III	0.00	0.21	−100%	31%	0.00%	24%
PAA IV	0.20	0.062	43%	38%	23%	7.1%

Flow rate, cardiac output, and percent change of occluded HH18 subsets with respect to the control or non-occluded HH18 model. Note how PAA^II-R received the largest percent increase with PAA^III-R occlusion (57% increase) and PAA^IV-R occlusion (21% increase). In both cases PAA^II-R and PAA^III-L are brought to be within 0.1 mm³/s from each other.

HH24 PAA in silico occlusion cases

The flow changes after in silico PAA occlusions at HH24, shown in Table 2, further demonstrate the importance of the PAA^IV-R. Similar to the HH18 occlusion cases, all but two HH24 PAA occlusions result in the PAA^IV-R experiencing the largest relative increase in blood flow. In the cases of PAA^VI-L occlusion and right lateral PAA^IV-R occlusion, flow to the PAA^III-R increased the most. Although PAA^IV-R is the largest in diameter at HH24, the occlusion based redistribution pattern is not always as simple as the geometry may suggest. In particular, we expected left sided occlusions to shift flow toward the remaining left sided vessels in order to maintain equal distribution between the paired cranial aortae. However, as each cranial aorta receives just 5% of the total cardiac output, maintaining equal right and left sided PAA ratio may not be a strong requirement. Our previous CFD model suggested that the PAA^IV-R is placed in an optimal position due to outflow tract orientation, which may be a reason for its preference during flow re-distribution after PAA occlusion (Kowalski et al., 2012). However, as in the HH18 model, simulated occlusion of the PAA^IV-R at HH24 resulted in the largest flow increase to PAA^III-R. This pattern suggests that PAA^III-R is positioned to take on the role of the mature aorta after such occlusion.

Table 2.

Stage HH24 PAA flow distribution

	flow (mm3/s)		% cardiac output		% change from occlusion		flow (mm3/s)		% cardiac output		% change from occlusion
	R	L	R	L	R	L	R	L	R	L	R	L
Right Lateral PAA III Occluded							Left Lateral PAA III Occluded
PAA III	0.00	0.18	0.00%	12%	−100%	20%	0.25	0.00	17%	0.00%	8.7%	−100%
PAA IV	0.42	0.47	29%	32%	24%	15%	0.38	0.45	26%	31%	12%	9.8%
PAA VI	0.28	0.11	19%	7.6%	17%	11%	0.27	0.11	19%	7.6%	13%	11%
Right Lateral PAA IV Occluded							Left Lateral PAA IV Occluded
PAA III	0.31	0.19	21%	13%	35%	27%	0.31	0.21	21%	14%	35%	40%
PAA IV	0.00	0.52	0.00%	36%	−100%	27%	0.47	0.00	32%	0.00%	38%	−100%
PAA VI	0.31	0.12	21%	8.2%	29%	21%	0.34	0.14	23%	9.6%	42%	41%
Right Lateral PAA VI Occluded							Left Lateral PAA VI Occluded
PAA III	0.27	0.18	19%	12%	17%	20%	0.25	0.16	17%	11%	8.7%	6.7%
PAA IV	0.41	0.49	28%	34%	21%	20%	0.36	0.43	25%	30%	5.9%	4.9%
PAA VI	0.00	0.12	0.00%	8.2%	−100%	21%	0.26	0.00	18%	0.00%	8.3%	−100%
No Occlusion
PAA III	0.23	0.15	16%	10%	0.00%	0.00%
PAA IV	0.34	0.41	23%	28%	0.00%	0.00%
PAA VI	0.24	0.099	16%	6.8%	0.00%	0.00%

Flow rate, cardiac output, and percent change of HH24 occluded subsets with respect to the control or non-occluded HH24 model. Note how PAA^IV-R occlusion leads to the largest percent increase in PAA^III-R (35% increase), the most cranial right arch artery at this stage, while PAA^III-R occlusion leads to the largest percent increase in PAA^IV-R, the most cranial right arch artery available at this stage.

In vivo PAA photo-occlusion

Live multi-photon microscopy was used to visualize the vasculature of embryos injected with fluorescent dye. The pharyngeal arch arteries (PAA) were located and the imaging plane was adjusted so that the entire profile of the selected arch was clearly visible. Blood plasma was fluorescent and circulating cells appeared as dark disks against the fluorescent background (Figure 2A). Tightly-focused femtosecond laser pulses were used to cause targeted damage inside the vessel lumen, forming a transient cavitation and upstream aggregation of circulating cells that blocked blood flow. The minimum energy per pulse required to produce a stable occlusion increased linearly with vessel diameter from 3 μJ at 30 μm to 6.5 μJ at 200 μm (Figure 2D). The time required to form a stable occlusion (5–20 minutes) varied in part based on embryo size, vessel size, and the initial flow rate through the vessel. Permanent vessel occlusion was confirmed post photoablation acutely via two photon microscopy and long-term via histological sections. Figure 5 depicts a sagittal view of a control and ablated embryo in their natural orientation, right side up, with the arches and dorsal aorta visible upstream of the heart.

Figure 5.

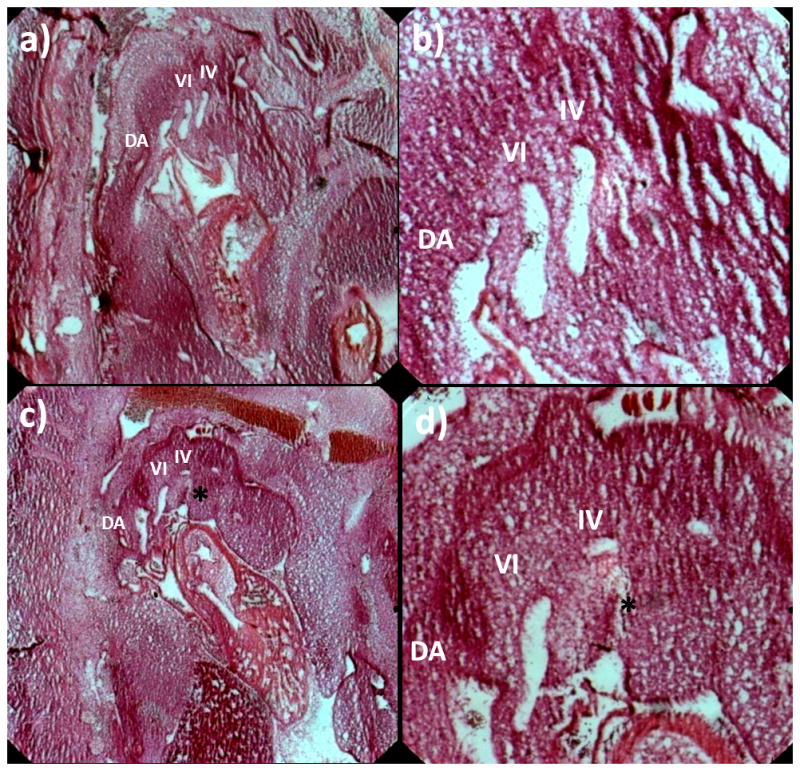
H&E section of HH28 control embryo (a) and ablated embryo (HH18 R IV occluded) (c) with roman numerals marking PAA branches in plane. Note PAA III is out of the plane slice. (b) and (d) show close up of PAA. Asterisks marks occluded embryo. DA – dorsal aorta.

Acute diameter changes after PAA occlusion

A comparison between experimental results and computational model predictions of PAA diameters at HH19 is shown in Figure 6. Bars represent percent change in “occluded” diameters (meaning embryos whose PAA^IV-R arch was occluded) with respect to control diameters. Because overall embryo size varies at HH19, initial diameters have been normalized to the PAA^II-R mean HH19 value within their respective experimental and simulation subsets. However, notable differences between simulations and experimental conditions were found. Simulated PAA^IV-R arch occlusion predicted nearly homogeneous changes in diameter across the other arch arteries, while the actual experimental changes in vessel diameter varied considerably between arch arteries. Four of the six arch artery diameters increase or decrease in the same direction as that predicted by simulations, though the magnitude of that change differs greater than 75%.

Figure 6.

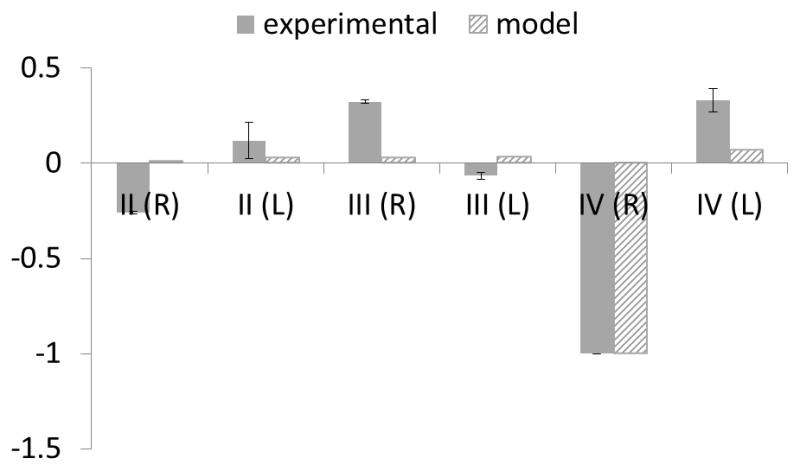
Change in diameter upon occlusion graphs for experimental PAA diameters (solid) and WSS-based model embryos (hashed). Diameters are normalized to an initial HH19 PAAII-R value within each subset.

While our simplified, linear WSS-driven growth model was able to capture some qualitative trends in PAA growth in control and PAA^IV-R occluded embryos, more rigorous quantitative agreement between the experimental and model-predicted PAA diameters is desired. Quantitative disparity was particularly large in the short-term period (<12 hours) following occlusion (Figure 7). We examine several sources of this disagreement, including limitations of the CFD model, the role of additional mechanical factors, developmental trends not incorporated in our growth prediction, and biological alterations and responses ignored by our model. The latter is addressed in the Discussion of this manuscript, while the remaining three points are considered here.

Most importantly, the present CFD model makes several assumptions related to the flow boundary conditions. We specify a 90/10 flow split between the trunk and cranial vessels, which is consistent across the investigated timeframe (Hu and Clark, 1989). We maintain this 90/10 trunk/cranial ratio in the occluded model as well, however we did not measure flow in any occluded experiments, and therefore cannot determine if the flow split is maintained post-intervention. Furthermore, a 50/50 right/left cranial aorta flow split was assumed in the occluded model. As occlusion of an entire PAA vessel changes the left/right lumped resistances and impedances of the PAA network, it is possible that the cranial aortae flow split changes after occlusion. Growth of the PAA may restore the flow distribution, but in the short term, the cranial boundary condition may be inaccurate. Experiments to measure flow distributions after PAA occlusion would provide better data for the outflow conditions of our model, which may improve agreement with experimental trends. The above reasoning is supported since the disparity between our model and experiment is larger in the short term. Occlusion of the PAA^IV-R increases afterload on the embryonic ventricle. We do not incorporate this type of feedback into our model, instead maintaining a constant outflow tract waveform. Coupling a lumped-parameter ventricle model to our 3D PAA CFD model would allow incorporation of cardiac responses (such as change in CO and heart rate), and may improve the predictive capabilities of our growth model. Finally, our model specifies no-slip, rigid walls. This assumption is made to simplify the CFD solution, but ignores importance mechanical aspects of the PAA. These are discussed further in the next paragraph.

During the HH18-24 timeline of this study, the walls of the PAA are comprised of a single endothelium surrounded by 1–2 cell layers of mesenchyme and externally constrained by the surrounding mesoderm-derived pharyngeal arches. (Waldo et al., 2005; Waldo et al., 1996). While the material properties are unknown at these early stages, these soft tissues are likely able to elastically deform under pressure, generating impedance to flow. For simplicity and due to the lack of appropriate material models, we applied a rigid wall assumption to our model. This boundary condition can over-estimate WSS values as it ignores vascular compliance. Since our proportionality constant was based on similar rigid-wall models, we feel that this assumption has little effect on the predicted WSS-growth response. Without a PAA wall model, however, we are unable to compute transmural stresses and thus had to exclude them from our growth model. Growth and remodeling of blood vessels requires both WSS at the endothelium and stress within the vascular wall (Culver and Dickinson, 2010; Huang et al., 2003; Lucitti et al., 2007; May et al., 2004). The inclusion of only one of these biomechanical factors (WSS) as the sole driver of PAA growth limits our ability to simulate the in vivo environment, leading to the quantitative disparity between our model and the experimental results. Incorporating an arterial wall component and formulating more sophisticated growth laws would enhance our model and its predictive capacity. Structural models of adult arteries have been combined with integrative growth laws to examine growth and remodeling in cardiovascular disease (Figueroa et al., 2009; Humphrey and Rajagopal, 2002; Valentin et al., 2011). Modeling the development of embryonic vessels is more challenging, as the properties and composition of the vascular wall change as differentiation, proliferation, and genetic state progress. Growth and remodeling of the embryonic and postnatal aorta has, to date, only been performed on cylindrical, axisymmetric geometries (Taber, 1998; Taber and Eggers, 1996; Wagenseil, 2010). The extension to complex networks such as the PAA will require more sophisticated computational strategies as well as greater data on the structural properties of embryonic blood vessels.

The initial geometry of our model is a representative HH18 PAA network, which we based on micro-CT scans and verified by comparing PAA diameter and length to experimentally measured values (Wang et al., 2009). However, by HH24, which acts as the endpoint of our model timeline in this study, the PAA geometry changes dramatically, including the regression of PAA^II and emergence of PAA^VI, elongation of the PAA, migration of the outflow tract, and localized enlargements and reductions in dorsal and cranial aortae diameters (Wang et al 2009). We previously performed a parametric study of 2D PAA models to investigate the effects of PAA length and curvature on flow and WSS, and found that WSS was maintained within 20% when PAA length increased 50% and varied 10% when PAA tortuosity increased 10% (Kowalski et al., 2013). Therefore, we may be able to ignore small changes in PAA length in our model. However, the importance of outflow tract migration and rotation in the asymmetric morphogenesis of the PAA has been demonstrated by several studies (Bajolle et al., 2006; Bremer, 1928; Dor and Corone, 1985; Gessner, 1966a; Liu et al., 2002; Yashiro et al., 2007). Additionally, cardiac function is changing rapidly during this period; in particular, cardiac output increases exponentially (Broekhuizen et al., 1993; Ursem et al., 2001). These morphologic and hemodynamic trends create a dynamic biomechanical environment within the PAA, and adaptation to new mechanical loads, in part, drives their growth. For simplicity, our model does not include these developmental trends, and instead assumes a constant WSS field throughout the 24 hour timeline. Applying time-dependent morphological changes to the outflow tract and cranial and dorsal aortae, as well as the inflow waveform, is required to fully simulate the biomechanical environment over a long-term period. The quantitative disparity between our model and the experimental results demonstrates the importance of these developmental trends in shaping the PAA.

Chronic vessel growth data comparisons

Simulation predictions and occlusion experiments both confirmed significant overall PAA growth over 24 hours for both the right and left side (P < 0.0002 for control embryos and P < 0.0038 for occlusion embryos). Growth rate differences in individual arches between occlusion and control conditions occurred within the experimental and simulation datasets (Figure 7).

Experimental comparisons

PAA^II-L and PAA^II-R both regress completely in the experimental embryos (occlusion and control, P<0.004), while no significant growth trend was measured in PAA^III-R and PAA^III-L under control conditions. PAA^IV-R grew at a rate of 13.5% per hour (P = 0.007; R² = 0.9168) in control conditions, while PAA^IV-L displayed no significant change in growth over time (occlusion or control conditions).

Computational comparisons

In contrast, our simple wall shear stress based PAA growth simulations predicted that with the exception of the occluded PAA^IV-R, all vessels would increase significantly in diameter in both control and “occlusion” (meaning PAA^IV-R occlusion) subsets. Specifically, simulated PAA^II-R increased 6.7% per hour (P<0.0001, R² = 0.9=7) within the control subset but only increased 4.7% per hour (P = 0.0002, R² = 0.95) within the occlusion subset. Likewise, simulated PAA^III-R control and occlusion subsets increased by 8.3 % and 8.8% respectively, (P= 0.002, R² = 0.95; P < 0.0001, R² = 0. 89). PAA^IV-R was predicted to increase by 6% per hour in control conditions. PAA^II-L was predicted to increase by 10.3% per hour (P < 0.0001, R² = 0.98) in the control case and 12% (P< 0.0001, R² = 0.98) per hour in the occlusion case. Similarly, PAA^III-L increased 10% (R² = 0.98, P < 0.0001) in the control case and 12% (R² = 0.99) in the occluded case. PAA^IV-L was predicted to increase by 12% per hour in the occlusion case (R² = 0.99, P < 0.0001), and only 10.6% per hour (R² = 0.99, P < 0.0001) in the control case. Table 3 summarizes the equations of each arch artery growth curve, it’s R² value and significance in terms of slope.

Table 3.

Summary Arch Artery Equations

	equation	R2 value	slope significatly non-zero?	P-Value		equation	R2 value	slope signifantly non-zero?	P-value
exp (occl)					Model (occl)
II	Y = −0.1804*X + 4.099	0.9576	Yes	0.0038	II	Y = 0.04720*X + 0.3375	0.9496	Yes	0.0002
III	Y = 0.07810*X + 0.1867	0.4725	No	0.1997	III	Y = 0.08796*X − 0.1481	0.9716	Yes	< 0.0001
IV	----------------------------------------				IV	-------------------------------------------------
IIL	Y = −0.2727*X + 6.198	0.9518	Yes	0.0046	IIL	Y = 0.1197*X − 0.9651	0.9852	Yes	< 0.0001
IIIL	Y = 0.04138*X + 0.2681	0.1949	No	0.4567	IIIL	Y = 0.1197*X − 1.039	0.9932	Yes	< 0.0001
IVL	Y = 0.1259*X − 1.331	0.5945	No	0.1269	IVL	Y = 0.1208*X − 1.300	0.9933	Yes	< 0.0001

	equation	R2 value	slope significatly non-zero?	P-value		equation	R2 value	slope signifantly non-zero?	P-value
exp (cntrl)					Model (cntrl)
II	Y = −0.2207*X + 4.981	0.9458	Yes	0.0002	II	Y = 0.06731*X − 0.04047	0.9664	Yes	< 0.0001
III	Y = 0.07535*X − 0.1823	0.1591	No	0.3753	III	Y = 0.08326*X − 0.08899	0.9538	Yes	0.0002
IV	Y = 0.1350*X − 1.809	0.9168	Yes	0.0007	IV	Y = 0.06117*X − 0.1315	0.9973	Yes	< 0.0001
IIL	Y = −0.2280*X + 5.147	0.9421	Yes	0.0013	IIL	Y = 0.1033*X − 0.6809	0.9779	Yes	< 0.0001
IIIL	Y = 0.02256*X + 0.7484	0.04341	No	0.692	IIIL	Y = 0.09950*X − 0.6854	0.9885	Yes	< 0.0001
IVL	Y = 0.08583*X − 0.9238	0.3944	No	0.1818	IVL	Y = 0.1058*X − 1.073	0.989	Yes	< 0.0001

Statistics for the lines made to fit arch artery trends. The equation of the curve, R² value, significance of the slope and P-value are displayed. Note how not all the experimental curves are significantly non-zero while the model curves are all significantly non-zero. Exp- experiment, Occl- Occluded, Cntrl – control.

Computational vs experimental growth

We employed Analysis of covariance (ANCOVA) to compare the differences between control and PAA^IV-R occlusion (“occlusion”) growth trends for both experimental and simulation conditions. As expected, the experimental occlusion and the control PAA^II changes were significantly different from their simulation counterparts. Vessel diameter growth for the PAA^IV-R experimental control condition differed significantly from its simulation (P = 0.016). Interestingly, there were no other differences in growth rate (slope) between the simulations and experimental conditions for any other vessels, but we did find significant differences in elevations between the growth curves (Table 4). These results support that after the initial adaptation to the occlusion, follow on vessel growth was generally predictable by proportionality to wall shear stress.

Our simulations also predicted that growth of the left arch arteries would be significantly different from that of their right-sided pair for the majority of cases. In control conditions, PAA^II and PAA^IV were predicted to grow significantly from their side-matched counterpart, (P = 0.002 and P = 0.04 respectively). Simulations predicted all three pairs within the occlusion subgroup to exhibit different growth patterns when compared to their side-matched counterpart (P = 0.0003). The experimental results, however, showed that growth of the left arch arteries were statistically similar to their respective vessel on the right side regardless of whether the PAA^IV-R arch was occluded. Apart from the obvious difference PAA^IV-R and PAA^IV-L arch in occluded conditions, only PAA^II-R and PAA^II-L of the experimental occlusion subgroup also grew differently from each other over time (P = 0.04).

Together, these findings suggest that PAA^IV-R occlusion causes significant acute changes in initial vessel diameters that are poorly predicted by simple shear stress driven growth simulations. Apart from the PAA^II however, post-occlusion vessel growth trends were predicted well by the simulations, which suggests follow-on PAA growth is largely proportional to wall shear stress. Interestingly, in two cases (PAA^III-R and PAA^IV-L) the predicted vessel growth post-occlusion converges over time with the experimental data. This limited agreement supports a morphogenetic role for wall shear stress in PAA vessel remodeling. Our results also reveal the necessity of a highly influential but yet unaccounted programming that helps drive PAA morphogenesis and hemodynamic adaptation.

Discussion

Arch artery malformations underlie many clinically significant heart defects, but the dysmorphogenetic mechanisms are poorly understood. This study expands upon our previous intra-cardiac hemodynamic investigations while at the same time highlighting the need for a better understanding of the biological programming that underlies PAA growth and morphogenesis. These strides are necessary in order to begin to reconstruct continuous series of three-dimensional vascular anatomies for abnormal flow and pressure distributions. With this knowledge, scientists could begin to tackle cardiac malformations not directly linked to particular genetic dispositions. We examine the results of abnormal arch artery flow in contrast with those obtained in normal (healthy) 3D PAA morphologies during critical periods of development and highlight the impact of altered arch artery geometry on PAA perfusion. Analysis of redistributed flows indicates that some PAA occlusion can lead to configurations where PAA^IV no longer carries the dominant proportion of the flow, leading to possibly altered PAA growth or regression. The present study predicted that PAA^IV-R occlusion would create the greatest flow alteration across the entire network. This finding is notable since this vessel matures to become the adult aortic arch in the chick.

The poor accordance of acute diameter changes with that predicted from our simple linear WSS growth model suggests that these vessel growth and adaptation likely follow more complex fluid dynamics principles, at least at this stage in development. Their growth can only be partially predicted by simple proportionality to wall shear stress. This discrepancy may also be related to the fact that these primitive vessels are completely surrounded by stiff pharyngeal mesenchyme. The best-fit computational to experimental models were that of PAA^III-R and PAA^IV-L occluded subsets, which converge to similar values over the course of the 24 hour post occlusion time period. Significant changes in flow distribution revealed the importance of local hydrodynamic resistance of the PAA manifold over the peripheral vascular resistance. Intriguingly, flow redistribution after occlusion did not align well with hydraulic resistances of the PAA vessels, which meant that the largest diameter vessel did not receive the largest amount of flow. The fact that flow redistribution and subsequent vessel remodeling again highlights the existence of additional hemodynamic and biological factors in PAA remodeling. Cardiac output and upstream OT morphology can drastically alter the initial hemodynamic conditions of the PAA network (Hu et al., 2009; Wang et al., 2009).

It is well known that morphogenesis of the pharyngeal arches and their corresponding arch arteries is a complex system of events involving precise timing and integration of multiple progenitor infiltrations and biological signaling networks (Graham, 2003; Macatee et al., 2003; Waldo and Kirby, 1993; Waldo et al., 1996). The present in silico computations were unable to account for the regression of PAA^II or the appearance of PAA^VI, as these features are not solely determined by hemodynamics. Indeed, by HH24 PAA^II has completely regressed, while PAA^IV is now patent. Pharyngeal arch arteries III, IV and VI persist throughout the rest of development. As Waldo et al have stipulated, a difference between a vessel which regresses and one that persists may be in the associated mesenchyme (Waldo et al., 1996). Indeed in their 1997 paper Kirby, et al. showed that antisense targeted to a paralogous group of Hox messages caused PAA^III to regress in a manner similar to PAA^II, while antisense targeted to another paralogous group Hox message caused the appearance of an additional pharyngeal arch containing a novel and completely independent pharyngeal arch artery (Kirby et al., 1997). At this stage in their development (HH18/19), the PAA are comprised of endothelium and surrounded by an externally supportive mesenchyme which separates the primitive vessels from the ectodermal and endodermal epithelium (Le Lièvre and Le Douarin 1975; Bockman, Redmond, and Kirby 1989). Subsequent stages (HH18+) are characterized by a gradual increase in medial cell layers and maturation of the tunica media (Bergwerff et al. 1996). The stiffness of the surrounding mesenchyme may therefore be a key parameter regulating acute vessel expansion, as it represents the primitive vessel’s first mechanical support. Indeed, the pharyngeal arches don’t begin to express soluble tropoelastin until day 5 or 6 (Rosenquist et al. 1990; Rosenquist et al. 1988), indicating a stiffer phenotype may be possible prior to this time period. The onset of elastogenesis corresponds with a period of rapid cardiac growth and morphogenesis (Hu and Clark 1989) and coincides with loss of alpha smooth muscle actin (aSMA) expression from the proximal part of the arterial tree (Bergwerff et al. 1996).

The development of the pharyngeal arches and their corresponding arch arteries is a complex system of events that also involves neural crest migration as well as endoderm signaling (Macatee et al. 2003; Graham 2003; Waldo and Kirby 1993; Waldo, Kumiski, and Kirby 1996). Local hemodynamic forces likely affect early differentiation of smooth muscle cells (SMCs) through changes in endothelium characteristics (Bergwerff et al. 1996). Around the onset of our study, at HH17/18, early markers of SMC differentiation are present in the form of aSMA positive myoblasts in the aortic sac. By HH21 (roughly 12 hours post the occlusion time point) actin expression has spread further and completely surrounds the dorsal aorta, pharyngeal arteries and aortic sac. At HH24 (24 hours post occlusion time point) the pulmonary arteries acquire aSMA expression at their junction with the sixth arch arteries, a time point that coincides with the initiation of flow through these vessels. Throughout this time (HH18-HH24 time period), the ability for the arch arteries to functionally communicate with their environment is increasing. Vinculin, a representative component of cellular adhesion complexes, was present in aSMA-positive cells of the dorsal aorta at HH18. At HH21, the aortic sac, pharyngeal arch arteries, and dorsal aorta all express high levels of vinculin, suggesting the existence of an early functional relationship between the cell’s cytoskeleton and its environment (Bergwerff et al. 1996). Through the use of our targeted vessel occlusions, future studies may examine the role of hemodynamics in maintaining this functional relationship and the timing of SMC differentiation in response to controlled changes in flow and WSS levels.

Through our analysis of redistributed flow it was possible to model pathological situations where the left and right PAA^IV no longer transport the dominant proportion of PAA flow. In an earlier work Rychter experimentally ligated each individual PAA at HH24 (Rychter, 1962). Ligations were performed through the insertion of a silver microclip into the branchial clefts. Unlike the occlusion experiments presented in this paper, Rychter’s ligation also disrupted local tissue mesenchyme, so the effects are not flow specific. Upon PAA^IV-R ligation, a variety of mature great vessels patterns were produced. In the majority of Rychter’s PAA^IV-R arch ligations (performed at HH24) cases (~75%), the PAA^III-R became the dominant arch artery or “main substitute channel”, taking part in formation of the definitive arch of aorta alone or in combination with others. Our CFD and in vivo results agree with Rychter’s observations in that the PAAIII-R received the largest flow redistribution and the largest change in diameter. However, our PAA^IV-R occlusions at HH18 were highly lethal (100% lethality before HH30), while Rychter’s HH24 occlusions were able to grow to hatching. These findings suggest that PAA^IV-R flow disruptions between HH18 and HH24 highly influence outflow tract and great vessel morphogenesis and gestational viability. Stage specific flow distribution and downstream morphogenetic consequences remain unclear, but at least between those stages PAA^IV-R occlusion appears to favor PAA^III-R dominance.

The results of CFD flow changes following PAA occlusion can inform Rychter’s observations. With Rychter’s PAA^III-L ligation, the portion of the left carotid artery normally formed by the left lateral PAA^III-L is instead derived from the persistence of the ventral portion of PAA^IV-L. There is no left brachiocephalic artery, but rather the left subclavian and left carotid arteries have separate origins. This result can be explained in part using our CFD simulations: if the net gain of flow in each PAA is examined after PAA^III-R occlusion, then PAA^IV-L received the most of the occluded PAA’s flow and caused a portion of PAA^IV-L to persist when the entire vessel normally degenerates. Similarly, in Rychter’s PAA^VI-R ligation experiment, the right ductus arteriosus doesn’t form. In some cases, a short thin cord, a persistent remnant of PAA^IV-L was present. Our CFD occlusion of PAA^VI-L showed PAA^IV-R had the greatest percentage increase in flow. PAA^IV-L received the most of the occluded PAA’s flow, which may explain why a portion of PAA^IV-L persists when the entire vessel normally degenerates. These occlusion experiments highlight the importance of unobstructed flow through the right lateral fourth arch artery.

In the embryo, PAA^IV-R carries the greatest amount of flow and has unique histogenesis as well as neurological innervation (Molin et al., 2002). Experimental models in which PAA fail to persist are often associated with valvular abnormalities (Molin et al., 2004). The increase in afterload and altered morphology caused by PAA occlusion may also have upstream effects, disrupting flow across the OT cushions, leading to valve defects. Based on our in-silico results, a hypoplastic or atretic PAA^IV in the embryo may be a critical factor in the development of congenital heart disease (Ilbawi et al. 2007). Complex molecular mechanisms and pathways have been identified to support embryonic endothelial mechanosensitivity (Molin et al., 2002). In vascular development, according to the flow-dependency principle, low WSS is empirically known to lead to chronic vessel regression; whereas, the physiological WSS inhibits apoptosis, contributing to vessel enlargement after flow increase (Roman and Pekkan, 2012).

Our In silico analysis of WSS based growth in HH18 controls may serve as a reference for surgical guidance to counteract the progression of arch artery malformations. Our study suggests that if a patient-specific PAA model is reported to have peak flow in an arch artery other than the predetermined dominate right IV, restorative interventions may include PAA flow alterations, either directly (using WSS fields as a guide) or indirectly (through changes in OT orientation. To our knowledge, this study presents the first 3D growth kinematics predictions of a complex vascular system. We also present here, for the first time, experiments in which PAA flow is obstructed at a specified time point without disrupting the containing vessel or surrounding tissue. Such experiments allow us to differentiate the effects of altered flow from that of local tissue deformation and delineate the effects of disease formation. With the use of this targeted femtosecond laser ablation technology, we can begin to understand how altered hemodynamics initiates changes on both the whole tissue and molecular scale. Once comparable quantitative data in human great vessel development is established the same technology can be applied to predict and plan surgical cardiac interventions of congenital heart patients in utero.

During the recent decade, the clinical experience in fetal surgical cardiac interventions in human patients has steadily advanced (McElhinney et al., 2010), however the extremely complex vascular morphodynamics processes require new tools so that these advanced surgical interventions can be timed and planned precisely for the best outcome. Fundamental studies that define key regulatory mechanisms and the limits for in vivo adaptation to altered cardiovascular loading conditions is relevant to optimizing fetal management for CHD including the timing of fetal cardiac intervention for critical aortic stenosis and left heart hypoplasia (Emery et al., 2007) as well as other forms of CHD associated with altered biomechanics. The embryo’s response to altered flow patterns during critical periods of development is one which scientists have been working to characterize for decades. This study invigorates this investigation by combining a minimally invasive technique to produce occlusions with new computational fluid dynamics mechanisms. While we are not yet able to fully capture and account for in vivo results, we have begun to capture key players and highlight areas that necessitate further exploration. A precise understanding of the factors involved in abnormal hemodynamics perturbations will prove to be powerful tool in clinical diagnosis and intervention of congenital heart defects.