A pre-computed brain response atlas for instantaneous strain estimation in contact sports

Abstract

Finite element models of the human head play an important role in investigating the mechanisms of traumatic brain injury, including sports concussion. A critical limitation, however, is that they incur a substantial computational cost to simulate even a single impact. Therefore, current simulation schemes significantly hamper brain injury studies based on model-estimated tissue-level responses. In this study, we investigate the feasibility of a pre-computed brain response atlas (pcBRA) to substantially increase the simulation efficiency in estimating brain strains using isolated rotational acceleration impulses parameterized with four independent variables (peak magnitude and duration, and rotational axis azimuth and elevation angles) with values determined from on-field measurements. Using randomly generated testing datasets, the partially established pcBRA achieved a 100% success rate in interpolation based on element-wise differences in accumulated peak strain (ε^p) according to a “double-10%” criterion or average regional ε^p in generic regions and the corpus callosum. A similar performance was maintained in extrapolation. The pcBRA performance was further successfully evaluated against responses directly simulating two independently measured typical real-world rotational profiles. The computational cost to estimate element-wise whole-brain or regional ε^p was 6 sec and <0.01 sec, respectively, vs. ~50 min directly simulating a 40 ms impulse. These findings suggest the pcBRA could substantially increase the throughput in impact simulation without significant loss of accuracy from the estimation itself and, thus, its potential to accelerate the exploration of the mechanisms of sports concussion in general. If successful, the pcBRA may also become a diagnostic adjunct in conjunction with sensors that measure head impact kinematics on the field to objectively monitor and identify tissue-level brain trauma in real-time for “return-to-play” decision-making on the sideline.

Introduction

Sports-related concussion is a major public health and socio-economical problem in the United States estimated to occur in 1.6–3.8 million individuals annually, and is particularly common in football and ice hockey.¹¹ However, concussions are frequently under- or undiagnosed in a competitive athletic environment because signs of cognitive alterations may be mild and masked, unrecognized, or ignored by the athletes.³⁶ Both concussive and subconcussive head impacts have been associated with acute brain injury as well as chronic neurodegeneration.³⁷ Growing evidence suggests that a substantial group of athletes without clinically diagnosed concussion also exhibits measurable neurocognitive and neurophysiological impairment present on diffusion tensor imaging (DTI)^2,34 and functional magnetic resonance imaging (fMRI).^6,51 In addition, these athletes experience significantly more impacts, especially to the top-front of the head.^6,51 A recent study analyzing head impact exposures (HIEs)¹⁵ in a cohort of concussed athletes suggests that those with delayed diagnosis of concussion sustained significantly more impacts on the day and within seven days of injury than those with immediate diagnosis of concussion.³ These studies underscore the importance of the cumulative effects of repetitive head impacts on the risk of concussion and associated neurodegeneration.

To better understand the mechanisms of sports-related concussion, on-field measurements of HIE have provided important insights on the kinematics involved.^3–5,15 Various kinematics-based injury metrics have been proposed to assess the risk of concussion, including the head injury criterion (HIC), a generalized acceleration model for brain injury threshold (GAMBIT),⁴⁰ head impact power (HIP),⁴¹ and the HIT severity profile (HITsp).¹⁷ Because many believe rotational acceleration to be a primary mechanism for diffuse axonal injury (DAI), including loss of consciousness and concussion,^21,28 more recent efforts such as the rotational injury criterion (RIC) and power rotational head injury criterion (PRHIC) based on the HIC and HIP counterparts, respectively,²⁷ and the brain injury criterion (BrIC),⁴⁹ are solely composed of head impact rotational components. These efforts are in-line with the work by Rowson and colleagues who investigated head rotational kinematics as an injury risk function in football,⁴⁷ while later they extended their work by combining both linear and rotational kinematics to assess the probability of concussion.⁴⁶ Despite these efforts, no consensus has been reached on an appropriate kinematics-based injury metric or a concussion tolerance threshold to date. In part, this may be because these injury metrics, alone, do not provide region-specific brain mechanical responses that are presumed to be directly responsible for initiating the injury at the tissue level.

To understand how external energy in head impact is converted into regional brain mechanical responses sufficient to initiate the injury at the microstructural level, finite element (FE) models of the human head play a unique and important role in estimating tissue-level brain mechanical responses such as strain, stress, and pressure that are otherwise infeasible or challenging to obtain in live humans.⁵⁷ For example, several research groups have attempted to establish a concussion threshold based on model-estimated regional brain responses from analyses of reconstructed NFL impacts,^30,33,59 pedestrian and motorcycle accidents,⁵⁵ and instrumented helmets from collegiate football players.⁵⁰ Recent work evaluating model-estimated strain and strain rate in the corpus callosum also showed promise in correlating regional brain responses directly with longitudinal changes in neuroimaging parameters.³⁵ Further, the consistency between model-estimation and neuroimaging findings was significantly improved in terms of the spatial distribution and group-wise extent of potential white matter damage when using strains along white matter fiber directions instead of isotropic maximum principal strains.^2,25 Because brain strains are significantly correlated to rotational (a_rot) but not linear (a_lin) acceleration,²⁶ parametric studies have also investigated the significance of a_rot directionality and pulse shapes.^29,43,54,58

However, a critical limitation in these head FE models is that they incur a substantial computational cost to simulate even a single head impact (hours on a modern multi-core computer or even a super computer).^{13,24,25,30,42,49,50,59} In large part, therefore, these models have been limited to studies that focus on single head impacts to date, and current FE simulation schemes are likely impractical to handle the amount of computations to study the cumulative effects of repetitive head impacts especially on a large scale (e.g., hundreds of players where each athlete typically sustains hundreds of impacts in a single season of play).^3,4,6,53 In addition, the extensive computational cost and demand in high performance computational hardware also significantly hamper the establishment of injury risk metrics based on model-estimated tissue-level mechanical responses such as strain or stress as opposed to global kinematic measures or their variants alone.⁴⁹ A substantial increase in the efficiency in head impact simulation is, therefore, necessary and much desired to address the computational challenges in model-based brain injury studies in order to accelerate the exploration of the mechanisms of traumatic brain injury (sports concussion in particular) in the future.

In this study, we investigate the feasibility of a pre-computed brain response atlas (pcBRA) to enable an efficient estimation (within seconds or instantaneously as opposed to hours) of brain strain responses without significant loss of accuracy from the pcBRA estimation itself. Critical to its potential success is the ability to use isolated a_rot alone instead of full degrees-of-freedom (DOFs) head impact as model input to estimate brain strain responses,²⁶ thereby substantially reducing the dimensionality of model input parametric space. Ultimately, the practical utility of the technique depends on a systematic and quantitative comparison of pcBRA-estimated brain strain responses with their counterparts directly simulated from actual full DOFs head impacts. In our current study, however, we focus on assessing the pcBRA performance (accuracy and efficiency) using parameterized or idealized a_rot impulses. A preliminary evaluation of the pcBRA performance was also conducted using two independently measured typical real-world a_rot profiles as input to gain an initial confidence of the technique. If successful, the pcBRA could substantially increase the throughput in head impact simulation and, thus, accelerate the exploration of the biomechanical mechanism of sports-related concussion.

Methods

The Dartmouth Head Injury Model (DHIM)

All brain responses were simulated using the recently developed and validated Dartmouth Head Injury Model (DHIM; Fig. 1).^25,26 Briefly, the DHIM was created with high mesh quality and geometrical accuracy based on high-resolution magnetic resonance images (MRI) of an athlete. When neuroimaging is available for other individuals, the DHIM also allows the creation of a geometrically accurate subject-specific head FE model. The DHIM is composed of solid hexahedral and surface quadrilateral elements with a total of 101.4 k nodes and 115.2 k elements (56.6 k nodes and 55.1 k elements) and a combined mass of 4.562 kg (1.558 kg) for the whole head (brain). The average element size for the whole head and the brain is 3.2±0.94 mm and 3.3±0.79 mm, respectively. The material properties for the brain and other head components are reported previously.^25,26 Because no consensus has been reached on how best to characterize brain material properties and experimental observations conflict on the relative stiffness of grey and white matter,²² the entire brain was modeled as a homogenous medium without incorporating the possible inter-regional differences in material properties or material property anisotropy using a hyperelastic material model identical to the “average model” in Kleiven (2007).³⁰ DHIM achieved an overall “good” to nearly “excellent” validation performance against relative brain-skull displacement and pressure responses from cadaveric impacts,^19,20,39,52 as well as full-field brain strains in a live human volunteer,⁴⁸ as previously reported.^25,60

Fig. 1.

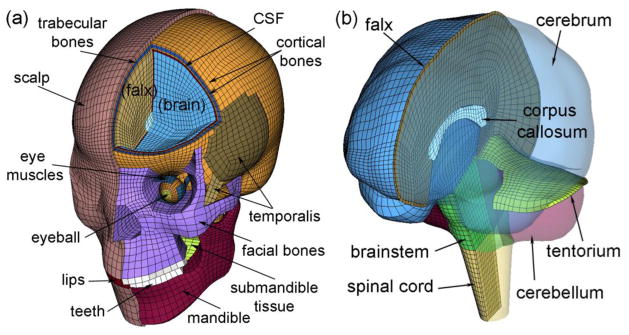
The DHIM with color-coded regions of interest showing the head exterior (a) and intracranial components (b). The model includes part of the spinal cord to improve its biofidelity in the inferior region, which was excluded from analysis in this study.

Reduction in Model Input Parametric Dimension

Conceptually, a head FE model is simply a mathematical function mapping impact kinematic parameters (i.e., time-varying a_lin and a_rot accelerations relative to the head center of gravity, CG) into regional brain mechanical response variables such as strain, stress and pressure as well as their derivatives either for an individual element or a specific region of interest (ROI; e.g., the entire white matter, the cerebrum, or the corpus callosum). The functional mapping for a response distribution within the FE domain is abstracted as the following equation:

$$\mathbf{F}=\mathbf{F}({\mathbf{a}}_{\mathit{lin}},{\mathbf{a}}_{\mathit{rot}}),$$ (1)

where the model-specific function, F, is composed of material properties of various components, interfacial boundary conditions, meshes, element formulations, and numerical simulation solver, etc. Because a given head impact leads to a unique set of output responses, F is deterministic; thus, allowing a set of brain responses to be pre-computed by systematically varying the input parameters to build a “library” or “look-up table” to enable a highly efficient “interpolation” for brain response estimates using solutions already computed. A similar pre-computation strategy has already been successfully employed in image-guided neurosurgery,¹⁶ but has not been applied in brain dynamic simulations before. A brute-force approach is likely infeasible here because of the input’s high dimensionality (a total of 12 DOFs since each component of the 6-DOFs accelerations can be an independent function of time) in head impact that would require an exponential computational complexity of O(M^N), where N and M are the number of parametric dimensions and the number of samples along each dimension, respectively. Therefore, reduction in the dimension of model input parametric space or the number of independent variables required to pre-compute the response atlas is essential.

It is well known that brain strain responses are significantly correlated to a_rot but not to a_lin.^24,30,50,59 Using two independently established and validated head FE models, the DHIM and SIMon, brain strain-related responses (strain, strain rate and stress) are found to be significantly correlated to both the magnitude and duration of a_rot, but not to a_lin,²⁶ because of brain’s high bulk modulus. These results establish the feasibility of using isolated a_rot-only to estimate brain strain responses, F_strain, without significant loss of accuracy. Therefore the following functional mapping is obtained that effectively halves the number of parametric dimensions required to establish the brain strain response atlas:

$${\mathbf{F}}_{\mathit{strain}}\approx \mathbf{F}({\mathbf{a}}_{\mathit{rot}}).$$ (2)

Further reduction in the parametric dimension is necessary and possible because the temporal characteristics of on-field head impacts are similar where a single largest acceleration peak dominates (typically with much smaller secondary peaks) and is similar to a triangular waveform.^8,10 Using the largest rotational acceleration peak, a_rot can be parameterized with four independent variables including its peak magnitude ( $a_{\mathit{rot}}^p$) and duration (Δt), as well as the azimuth and elevation angles, θ and α, characterizing the instantaneous rotational axis, Ω. In practice, Ω is determined by the a_rot components along the three major axes when the resultant $a_{\mathit{rot}}^p$ is reached. The strain response functional mapping is re-written into:

$${\mathbf{F}}_{\mathit{strain}}\approx \mathbf{F}({\mathbf{a}}_{\mathit{rot}})={\mathbf{F}}_1(a_{\mathit{rot}}^p,\mathrm{\Delta }t,\theta ,\alpha )+{\mathbf{F}}_{\mathit{err}},$$ (3)

where F₁ is the response from the parameterized a_rot symbolizing a 1^st-order approximation, while F_err is the residual error representing the element-wise difference distribution between pcBRA-estimated responses and the ground-truth directly from the full DOF a_rot. In sum, these idealization and parameterization of a_rot allows using four instead of as many as 12 DOFs to generate model inputs, which is the basis of the pre-computation in this study.

Rotational Axis Sampling Space

The rotational axis sampling space can be further halved because of the head geometrical symmetry relative to the mid-sagittal plane (i.e., xz-plane in Fig. 2a). For a given Ω(θ, α) passing through the head CG, the head rotates counter clock-wise (CCW) by convention. A clock-wise (CW) rotation with an identical magnitude temporal profile with respect to the xz-plane mirroring axis, Ω′(−θ, α), or equivalently, a CCW rotation with respect to the its negative axis, Ω″(180° −θ, −α), produces a symmetric brain response relative to the mid-sagittal plane compared to that using Ω as the rotational axis. When Ω traverses through the shaded hemisphere shown in Fig. 2b and c, Ω″ traverses through the other un-shaded hemisphere. In combination, therefore, Ω and Ω″ sample the entire rotational axis parametric space.

Fig. 2.

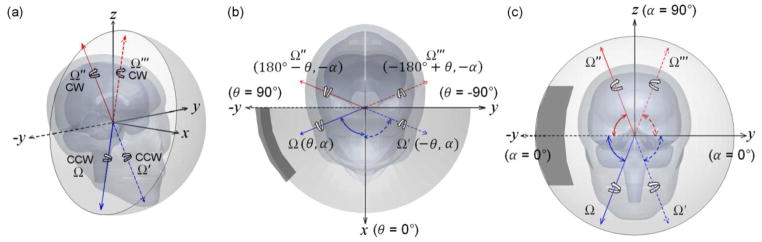
Schematic of head rotational axes and the sampling space in iso- (a), top (b), and frontal (c) views. Brain responses using Ω and Ω″ (solid), or Ω′ and Ω‴ (dashed), as the rotational axes are symmetric about the mid-sagittal or xz-plane. When Ω traverses through the shaded hemisphere, its counterpart, Ω″, traverses through the other un-shaded hemisphere. In combination, they sample the entire rotational axis parametric space. The dark area corresponds to the same identified parametric space in Fig. 3.

To further illustrate the rotational axis sampling space, Fig. 3 shows pairs of rotational axes that produce mirroring or symmetric brain responses when the head is subjected to rotational impulses of an identical magnitude temporal profile. The shaded hemisphere in Fig. 2b and c corresponds to the shaded area in Fig. 3 (i.e., area defined by θ range [−90°, 90°] and α range [−90°, 90°]; including the boundary). For a rotational axis in the unsampled region (e.g., Ω″ and Ω‴ in Fig. 3), the brain responses can be easily obtained by mirroring the responses from the corresponding rotational axis in the sampled region (e.g., Ω and Ω′, respectively, in Fig. 3) about the mid-sagittal plane.

Fig. 3.

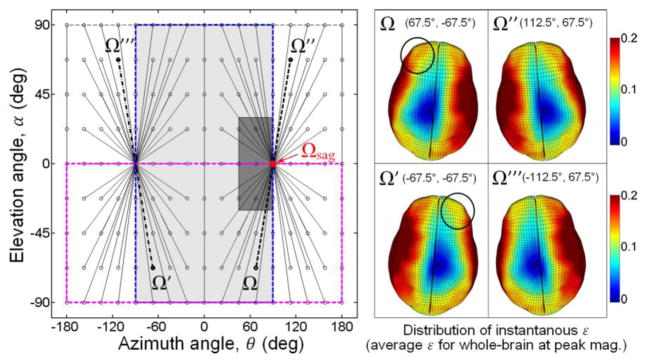
Schematic of head rotational axis sampling space (left). Each pair of sampling points connected by a line segment generates brain responses symmetric about the mid-sagittal plane when using an identical resultant a_rot profile. Brain strain responses in deformed states are shown for two pairs of rotational axes (right). Symmetric responses about the mid-sagittal plane were evident for those generated by Ω and Ω″, and by Ω′ and Ω‴, respectively. However, responses generated by Ω and Ω′, and by Ω″ and Ω‴, were not (see circled regions). Both the shaded area (θ range [− 90°, 90°] and α range [−90°, 90°]) and the lower half bounding box (θ range [−180°, 180°] and α range [−90°, 0°]) can be used to sample half of the parametric space (the former was chosen in this study, which is identical to the shaded hemisphere in Fig. 2).

Generation of pcBRA for Brain Strain Responses

Triangulated a_rot-only impulses parameterized by four independent variables, $a_{\mathit{rot}}^p$, Δt, θ, and α, were generated as model inputs by combining selected values of each variable with their respective ranges determined from on-field measurements. Because higher $a_{\mathit{rot}}^p$ values are likely more relevant to potential injury but occur less frequently,^9,45 we have constrained ${\mathrm{a}}_{\mathit{rot}}^p$ to 1500–4500 rad/s², or approximately between the 50^th and the 95^th percentile of $a_{\mathit{rot}}^p$ in on-field ice-hockey.²⁴ The lower and upper bounds were also comparable to the 75^th percentile subconcussive and (slightly below) the 50^th percentile concussive $a_{\mathit{rot}}^p$ magnitudes in collegiate football, respectively (Fig. 4).⁴⁷ The range of the impulse duration, Δt, was based on the temporal characteristics of high school football on-field measurements (mean plus and minus twice the standard deviation according to the reported duration of 10±3 ms for a_lin),⁷ which encompassed the average a_lin impact duration of 14 ms reported in collegiate football.⁴⁵ The full ranges of θ and α were both [−90°, 90°], as explained earlier (Fig. 3). To further limit the amount of computation in this study, they were restricted to [45°, 90°] and [−30°, 30°], respectively (dark area in Fig. 3), effectively simulating rotational impulses near a sagittal rotation corresponding to (oblique) frontal impacts in the parametric space. The empirically determined range, step size, and the number of samples for each variable are summarized in Table 1. Combining each unique value for each individual variable, a total of 500 (5×5×4×5) rotational impulses were generated to serve as the pcBRA training dataset, which effectively formed a four-dimensional (4D) regular grid data structure (their orthogonal two-dimensional (2D) projections are shown in Fig. 4).

Fig. 4.

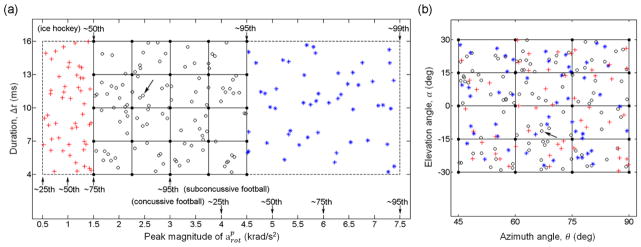
Distribution of the training (black dots) and testing (circles, crosses and stars for in-range interpolation and below- and above-range extrapolation, respectively) datasets as orthogonal 2D projections of the 4D data points on the $a_{\mathit{rot}}^p-\mathrm{\Delta }t$ (a) and θ-α planes (b). Locations for representative $a_{\mathit{rot}}^p$ values that approximately correspond to characteristic on-field measurements are also shown. Kinematic variable values for one representative interpolation testing data point are: $a_{\mathit{rot}}^p=2647.1\text{rad}/{\mathrm{s}}^2$, Δt = 11.1 ms, θ = 66.9°, α = − 11.4° (arrows).

Table 1.

Summary of the rotational impulse parameterization variables and their ranges, step sizes and numbers of samples used to establish the pcBRA.

Variable	$a_{\mathit{rot}}^p(\text{rad}/{\mathrm{s}}^2)$	Δt (ms)	θ (deg)	α (deg)
Range	[1500, 4500]	[4, 16]	[45, 90]	[−30, 30]
Step size	750	3	15	15
# of samples	5	5	4	5

For all parameterized a_rot impulses, an additional 25 ms zero acceleration was appended to ensure reaching brain peak responses in simulation; Fig. 5). The resulting a_rot profile was used to simulate a rigid skull rotation about the given axis passing through the head CG (the skull, scalp and face were all simplified as rigid bodies). Maximum principal engineering strain (ε; Abaqus output variable “NEP”) was extracted for each brain element at every temporal point (resolution of 1 ms) to obtain the peak value (ε^p) regardless of the time of occurrence.

Fig. 5.

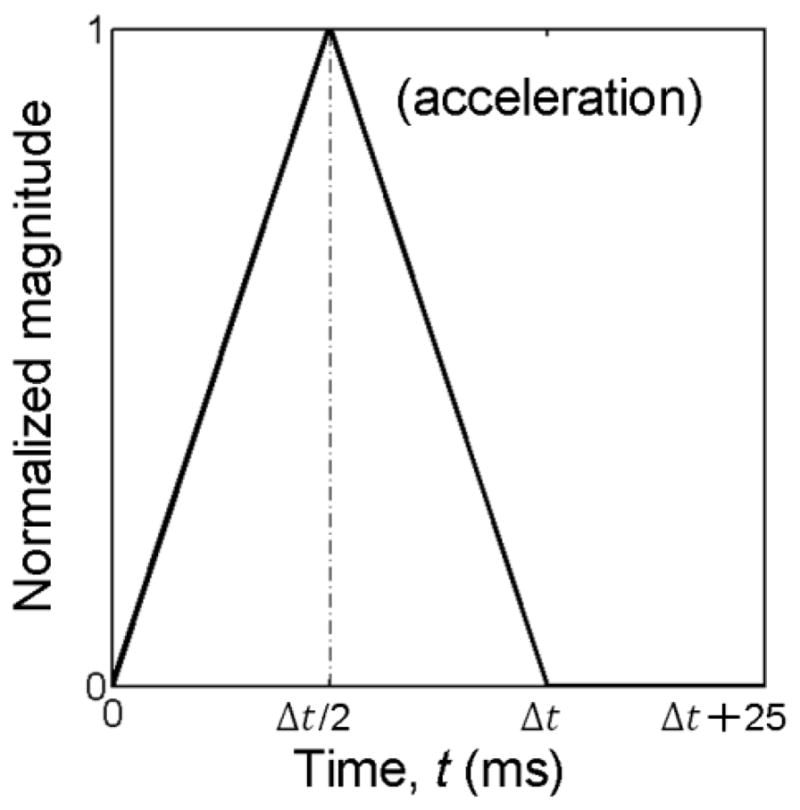
The normalized, triangulated head rotational impulse temporal profile (Δt range 4–16 ms).

Performance Evaluation Using Idealized a_rot

Interpolation

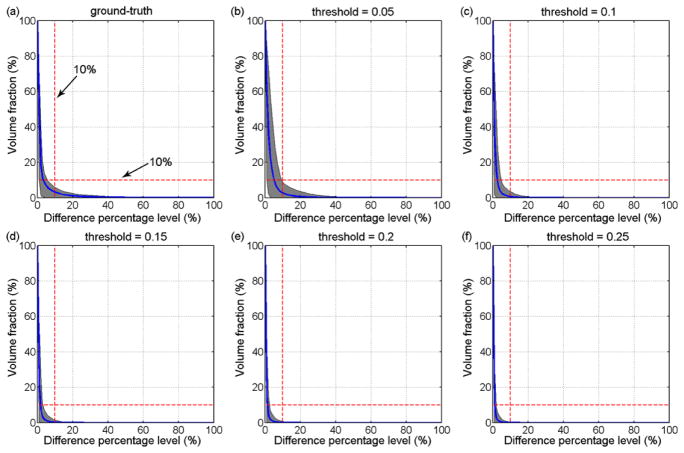
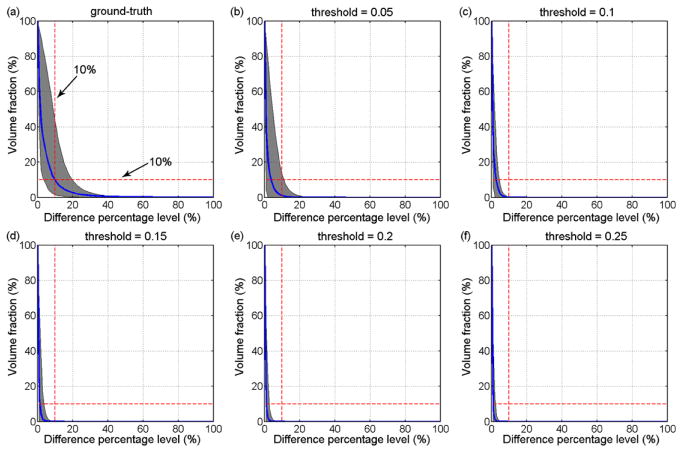
A testing dataset of 100 rotational impulses were created by randomly generating values for each individual variable within the corresponding range (Table 1) following a uniform distribution and then randomly combining them with the generated values (Fig. 4).²⁶ The ground-truth ε^p at each element was obtained via a direct simulation using each impulse as model input. By comparison, the pcBRA-interpolated ε^p was obtained through a multivariate linear interpolation (via Matlab function “interpn.m”) operated independently for each element using values at neighboring 4D grid points in the atlas.¹⁸ Element-wise absolute differences in ε^p were obtained and further normalized by the directly simulated ground-truth counterparts to calculate the relative difference. Because the resulting normalized, element-wise differences constituted a spatial distribution within the FE domain, we reported the volume fractions of brain experiencing ε^p element-wise differences relative to the directly simulated ground-truth above a range of percentage levels (varied from 0 to 100% at a step size of 1%) to characterize their response differences.

The normalized differences relative to the ground-truths, alone, however, did not necessarily reflect any clinical significance relative to injury-causing thresholds (e.g., the relative difference could be large in percentage but its magnitude may be sufficiently small and clinically irrelevant).²⁶ Therefore, the element-wise response differences were further normalized by a range of injury thresholds (0.05–0.25 with a step size of 0.05) to evaluate their relative differences against each injury threshold values for potential real-world injury risk assessment. The range selected virtually encompassed thresholds established from an in vivo animal study (Lagrangian strain range 0.09–0.28 with an optimal threshold of 0.18, or equivalently, engineering strain range 0.086–0.249 with an optimal threshold of 0.166)¹ and FE-based analyses of real-world injury cases (e.g., 0.19 in the grey matter,⁵⁹ 0.21 (0.26) in the corpus callosum (grey matter).³⁰ Similarly, we reported the volume fractions above a range of percentage differences for each injury threshold.

For each testing rotational impulse evaluated, we defined that the pcBRA-interpolated response was sufficiently accurate when the volume faction of large element-wise differences in ε^p (i.e. >10% relative to the ground-truth or a given injury threshold) for the whole-brain was less than 10% (dubbed the “double-10%” criterion). A success rate as the percentage of the testing impulses for which the pcBRA-interpolation was sufficiently accurate was used to evaluate the overall pcBRA interpolation accuracy.

Finally, because tissue-level regional responses can be conveniently used to assess region-specific risk of injury for a given ROI,^30,50,59 we also computed the volume-weighted regional average ε^p for generic brain regions (whole-brain, cerebrum, cerebellum and brainstem) and the corpus callosum to evaluate the pcBRA estimation performance. Similarly, the pcBRA estimate was considered sufficiently accurate when the absolute difference between the pcBRA-estimated response and the ground-truth was within 10% relative to the ground-truth or the same range of injury thresholds. Analogously, a success rate was used to assess the overall pcBRA performance in regional response estimate.

Extrapolation

Because the training dataset input variables were constrained within their ranges (Table 1) and did not encompass the entire sampling space, it was necessary to evaluate the pcBRA extrapolation performance. This was especially true for $a_{\mathit{rot}}^p$ because only a relatively small range of on-field measurements (50–95^th percentile values in on-field ice hockey; Table 1) was covered. We did not evaluate the extrapolation performance for other variables because for Δt, twice the standard deviation covered approximately 95.4% of occurrences (assuming a normal distribution). Although θ and α were also restricted to a small range, they were intentionally limited and could easily be expanded to cover the entire sampling space in the future.

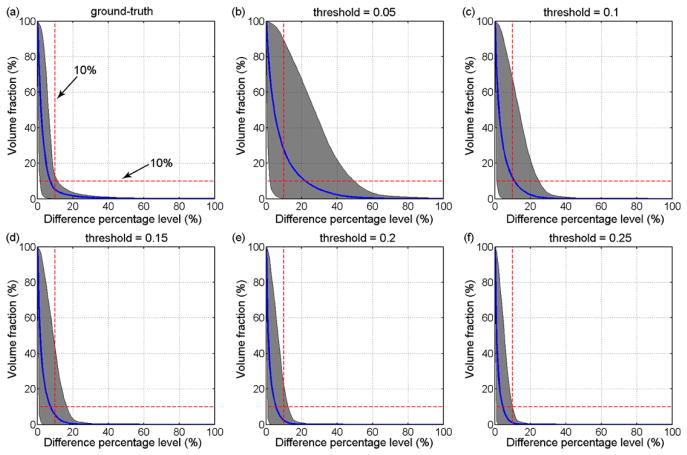
Two separate testing datasets (N=50 each) were randomly generated by constraining $a_{\mathit{rot}}^p$ to a range either immediately below (500–1500 rad/s²) or above (4500–7500 rad/s²) that in the training dataset (Fig. 4) while maintaining the same ranges for other variables using the same approach described previously. The lower and upper end of $a_{\mathit{rot}}^p$ for the below- and above-range extrapolation approximately corresponded to the 25^th percentile subconcussive and the 95^th percentile concussive $a_{\mathit{rot}}^p$ values for collegiate football, respectively (Fig. 4).⁴⁷ Element-wise whole-brain strain responses were obtained via a spline-based extrapolation (via Matlab function “interpn.m”) using values at neighboring grid points in the pcBRA.¹⁸ Similarly, we computed the volume fractions above a range of percentage differences in ε^p relative to the directly simulated ground-truth and the same range of injury thresholds, and further reported the success rates based on the “double-10%” criterion. In addition, the success rates for pcBRA-extrapolated regional strain responses for generic regions and the corpus callosum were also reported.

Performance Evaluation Using Two Typical Real-world a_rot Profiles

The pcBRA performance was further assessed by comparing against the directly simulated results using two typical a_rot profiles independently measured from anthropomorphic test device (ATD) as inputs.^10,44 Because only the resultant profiles were available, mono-axis sagittal rotations were simulated using the corresponding entire a_rot profile (Ω_sag in Fig. 3). By comparison, the major a_rot peak was parameterized into a triangular impulse by maintaining an identical rotational velocity, $v_{\mathit{rot}}^p$, and Δt resulting from the corresponding major peak, as detailed in Fig. 6 for the two profiles. The resulting parameterized impulses were used to interpolate element-wise ε over time as well as ε^p from the pcBRA. Similarly, we reported the element-wise ε^p differences and whole-brain average ε as a function of time between the two brain responses for each a_rot profile.

Fig. 6.

Parameterization of two independently measured typical real-world resultant a_rot profiles into triangular impulses (dark lines) by maintaining an identical $v_{\mathit{rot}}^p$ and Δt determined from the corresponding major peak (shaded area). Note that the parameterized $a_{\mathit{rot}}^p$ values in (a)¹⁰ and (b)⁴⁴ were 9.2% lower and 20.2% higher than the corresponding measured counterparts, respectively. Although the measured $a_{\mathit{rot}}^p$ in (b) was 25.2% lower than that in (a), its $v_{\mathit{rot}}^p$ was 22.7% higher.

Significance of a_rot Parameterization Impulse Shape

Our pcBRA was established based on triangulated a_rot impulses. To investigate the significance of a_rot parameterization impulse shape, a sine and a haversine impulse resulting in an identical $v_{\mathit{rot}}^p$ (of 15 rad/s) from a typical triangular impulse ( $a_{\mathit{rot}}^p=3000\text{rad}/{\mathrm{s}}^2$, Δt =10 ms) were further generated as model inputs to simulate a sagittal rotation (Ω_sag in Fig. 3). The resulting ε^p was similarly compared against that from the triangular impulse.

Data Analysis

For all simulations, brain strain responses were obtained from the DHIM with the given a_rot profile as model input via Abaqus/Explicit (Version 6.12; Dassault Systèmes, France). The typical runtime for a 40 ms impulse was ~50 minutes on a multi-core Linux cluster using 8 CPUs with available Abaqus tokens (Intel Xeon X5560, 2.80 GHz, 126 GB memory). Element-wise ground-truth ε^p was obtained for each impulse simulated. Element-wise ε^p and regional average ε^p for generic brain regions and the corpus callosum were also interpolated or extrapolated using the pcBRA. With 12 CPUs executing in parallel, the computational cost to estimate an element-wise ε^p and a regional average ε^p for one impulse was 6 sec and <0.01 sec, respectively. All data analyses were performed in MATLAB (R2014a; Mathworks, Natick, MA).

Results

Performance Using Idealized a_rot

The average volume fraction for the whole-brain at a difference percentage level of 10% in ε^p was calculated for each testing impulse relative to either the ground-truth or a range of injury thresholds to compute an average and a range for the corresponding interpolation or extrapolation testing dataset. Regardless of the normalization denominator, the pcBRA in-range interpolation had a 100% success rate. When normalized by the ground-truths, an 80% success rate was achieved for the below-range extrapolation, and it was nearly 100% for the above-range extrapolation except for one failed case with the highest v_rot. When normalized by the range of injury thresholds, higher success rates were achieved at larger injury thresholds, as expected. The below-range extrapolation achieved a 100% success rate except at the lowest threshold of 0.05. For the above-range extrapolation, however, the accuracy performance depended on the magnitude of $a_{\mathit{rot}}^p$ as nearly a 100% success rate was achieved when $a_{\mathit{rot}}^p$ was low even at the lowest threshold (only one case failed), while it significantly degraded when $a_{\mathit{rot}}^p$ was high (Table 2). At the largest threshold of 0.25, however, all above-range extrapolations achieved a 100% success rate.

Table 2.

Summary of the average and range of volume fractions (VF) for element-wise differences relative to the ground-truths and a range of injury thresholds at the 10% difference level for pcBRA in-range interpolation and below- and above-range extrapolations, together with the corresponding success rates based on the “double-10% criterion”. The above-range extrapolation was sub-divided into three groups based on $a_{\mathit{rot}}^p$ to better categorize the pcBRA performance.

Normalization denominator			Ground-truths	Injury thresholds
				0.05	0.1	0.15	0.2	0.25
				Interpolation (N=100)		Avg. VF (%)	3.19	2.65	0.65	0.20	0.00	0.00
VF range (%)	0.00–5.99	0.00–8.85	0.00–3.63			0.00–1.48	0.00–0.64	0.00–0.29
Success rate (%)	100	100	100			100	100	100
Below-range extrapolation (N=50)		Avg. VF (%)	6.22	1.08	0.06	0.00	0.00	0.00
		VF range (%)	0.00–28.89	0.00–13.44	0.00–0.99	0.00–0.09	0–0.01	0.00–0.00
		Success rate (%)	80	96	100	100	100	100
Above- range extrap.	4.5–5.5 krad/s2 (N=16)	Avg. VF (%)	3.24	5.55	1.76	0.63	0.23	0.00
		VF range (%)	0.00–5.21	0.21–10.16	0.00–4.29	0.00–1.96	0.00–0.86	0.00–0.32
		Success rate (%)	100	93.75	100	100	100	100
	5.5–6.5 krad/s2 (N=18)	Avg. VF (%)	4.56	21.49	5.47	1.98	0.95	0.47
		VF range (%)	0.84–8.39	2.06–55.99	0.28–22.32	0.00–6.40	0–3.17	0–1.85
		Success rate (%)	100	38.90	94.40	100	100	100
	6.5–7.5 rad/s2 (n=16)	Avg. VF (%)	6.94	54.24	28.67	13.89	6.00	2.41
		VF range (%)	2.61–13.2	6.75–89.18	1.40–67.48	0.35–43.49	0.05–22.21	0.01–9.83
		Success rate (%)	93.75	12.50	37.50	43.75	81.25	100

Whole-brain volume fractions for response differences exceeding the full range of percentage difference levels (0–100%) are shown in Fig. 7–Fig. 9 when normalized by either the ground-truths or the range of injury thresholds for pcBRA in-range interpolation, below- and above-range extrapolations, respectively.

Fig. 7.

Volume fractions for element-wise differences in ε^p relative to the ground-truths and a range of injury thresholds (0.05–0.25) for in-range pcBRA interpolation. Curves and shaded areas represent the average and the range of volume fractions at each difference percentage level for all testing impulses. When normalized by the range of injury thresholds, the volume fractions at each difference percentage level decreased with the increase in the threshold value, as expected.

Fig. 9.

Volume fractions for element-wise differences in ε^p relative to the ground-truth and the same range of injury thresholds for above-range pcBRA extrapolation (all testing impulses clustered).

To investigate the location where large relative differences occurred, a Pearson correlation test between the element-wise differences in ε^p relative to the directly simulated ground-truth and the ground-truth ε^p, itself, was performed for all impulses. We found a consistently significant negative correlation between the two (average correlation coefficient of −0.165 (range −0.077 to −0.344); p<0.0001), suggesting that large differences mostly occurred in regions with low ε^p responses.

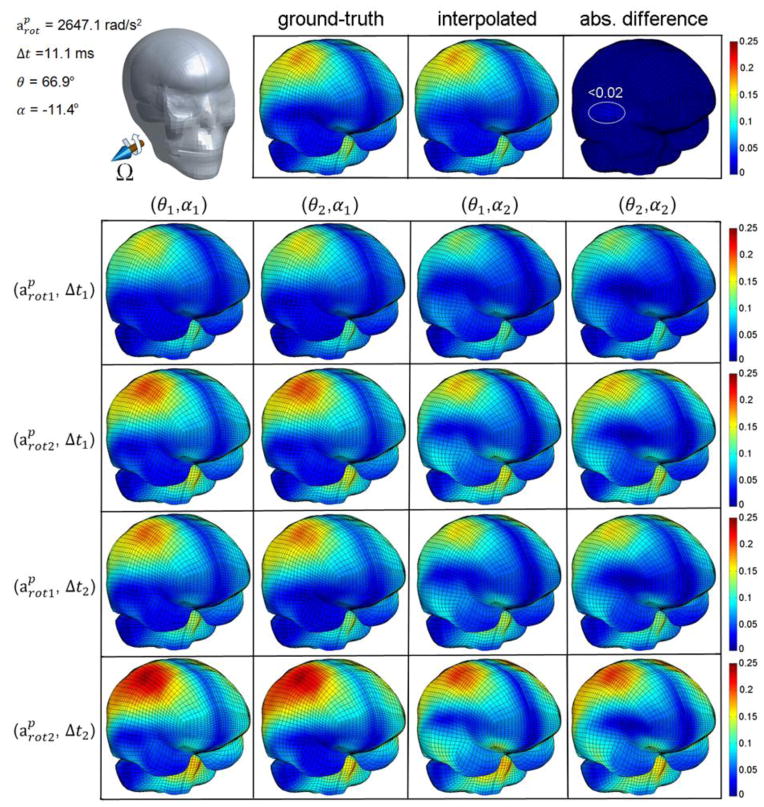
A representative impulse was chosen to visually compare the magnitude and distribution of the ground-truth ε^p and the nearly identical pcBRA-interpolated counterpart (Fig. 10, top panel). The responses at the 16 (2⁴) neighboring grid points are also shown, which essentially provided the response “modes” for interpolation (Fig. 10, bottom panel).

Fig. 10.

Comparison between the pcBRA-interpolated ε^p and the ground-truth from the directly simulated along with their absolute difference (top panel; location for largest differences identified) for a representative rotational impulse in the testing dataset (impulse parameters identified in Fig. 4). The corresponding pcBRA responses at the 16 (2⁴) neighboring grid points are also shown (bottom panel; variable values are: $a_{\mathit{rot}1}^p=2250\text{rad}/{\mathrm{s}}^2$, Δt₁ = 10 ms, θ₁ = 60°, α₁ = − 15°; $a_{\mathit{rot}2}^p=3000\text{rad}/{\mathrm{s}}^2$, Δt₂ = 13 ms, θ₂ = 75°, α₂ = 0°). Each row of the 4-by-4 grid represents a comparable response magnitude with an identical $v_{\mathit{rot}}^p$, while each column represents a similar distribution pattern with an identical rotational axis.

The pcBRA-estimated regional average ε^p achieved a 100% success rate regardless of the normalization denominator or ROI except when $a_{\mathit{rot}}^p$ was more than 1 krad/s² larger than the upper bound in the training dataset (Fig. 11). When normalized by the ground-truth, a 100% success rate was achieved even for the highest $a_{\mathit{rot}}^p$ regardless of the ROI. However, when normalized by the injury thresholds, the success rate degraded especially for larger $a_{\mathit{rot}}^p$, although a 100% success rate was still maintained at threshold levels ≥0.2.

Fig. 11.

The pcBRA success rates for the above-range extrapolation when $a_{\mathit{rot}}^p$ was within (a) 5.5–6.5 krad/s² and (b) 6.5–7.5 krad/s² in terms of regional average ε^p in generic regions and the corpus callosum using a range of normalization denominators. The pcBRA achieved a 100% success rate for all other $a_{\mathit{rot}}^p$ values, and are not shown.

Performance Using Typical Real-world a_rot Profiles

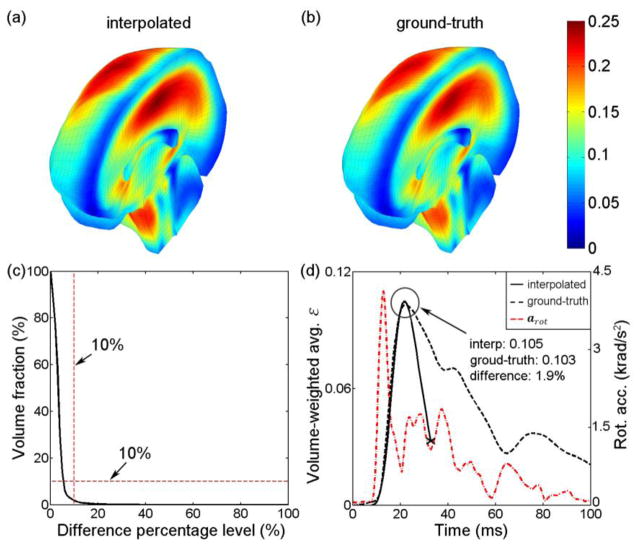
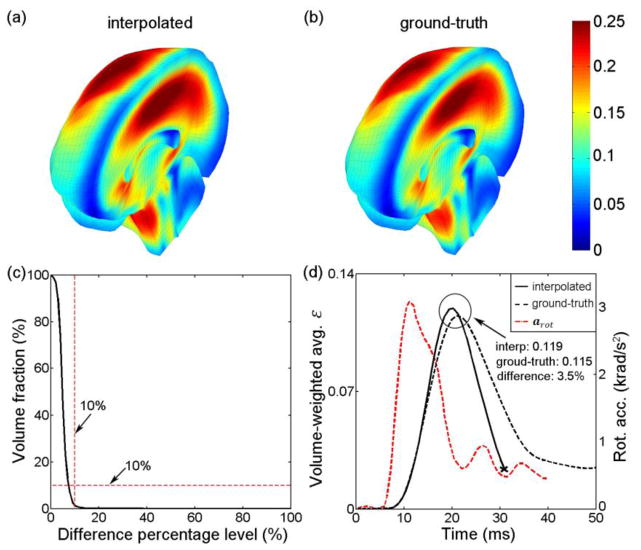
The pcBRA-estimated ε^p magnitude and distribution were nearly identical to those generated from the “ground-truth” ε^p obtained directly from the simulation using each given a_rot profile as input (Fig. 12 and Fig. 13; top panels). The nearly identical ε^p response was further confirmed by the volume fraction of their whole-brain ε^p differences (volume fraction of 1.80% and 1.31% at a difference percentage level of 10%; Fig. 12c and Fig. 13c) and the nearly identical whole-brain average peak values (circled regions in Fig. 12d and Fig. 13d).

Fig. 12.

Comparison of the (a) pcBRA-estimated and (b) the directly simulated ground-truth ε^p (i.e., element-wise peak responses during the entire impact regardless of time of occurrence) for a typical real-world a_rot profile.¹⁰ (c) Volume fractions for ε^p differences relative to the ground-truth. (d) Comparison of volume-weighted whole-brain average ε as a function of time between the pcBRA-estimated and the ground-truth counterpart. The pcBRA-estimated and ground-truth whole-brain ε^p averages in (a) and (b) were 0.116 and 0.114, respectively, which served as the upper bounds for the corresponding whole-brain average ε peak values, shown in (d), because not all elements reached their respective peak responses at the same time.

Fig. 13.

A similar comparison between the pcBRA-estimated result and that directly simulated for another independently measured a_rot profile (see Fig. 12 for caption).⁴⁴ The pcBRA-estimated and the ground-truth whole-brain ε^p averages for this case were 0.130 and 0.124, respectively. Although $a_{\mathit{rot}}^p$ was 25.2% lower than that in Fig. 12, its $v_{\mathit{rot}}^p$ was 22.7% higher, leading to an 8.8% increase in whole-brain average ε^p.

Significance of a_rot Parameterization Impulse Shape

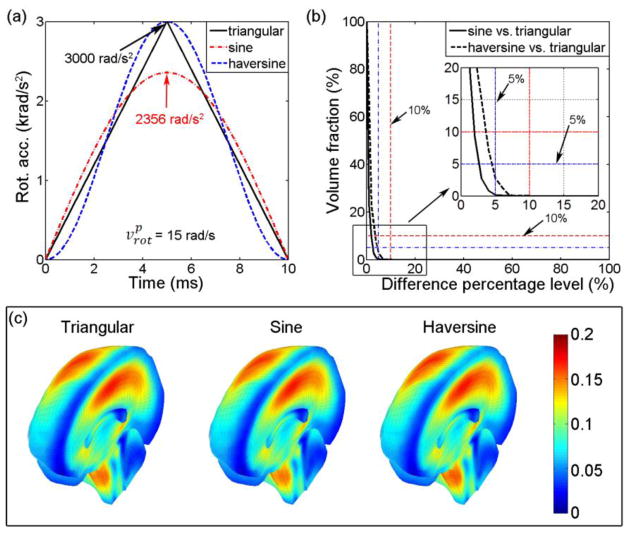
The three a_rot profiles (Fig. 14a) of an identical $v_{\mathit{rot}}^p$ and Δt led to nearly identical ε^p responses (a volume fraction of 0.19% (2.76%) exceeded a 5% difference percentage level when comparing ε^p from the sine (haversine) impulse relative to that from the triangular impulse; Fig. 14b), which was further confirmed by their nearly identical ε^p magnitudes and distributions (Fig. 14c).

Fig. 14.

(a) Illustration of a triangular, a sine, and a haversine a_rot impulse with an identical $v_{\mathit{rot}}^p$ and Δt. (b) Volume fractions for element-wise ε^p differences relative to that from the triangular impulse. (c) Comparison of the ε^p distributions from the three impulses. The sine impulse had an $a_{\mathit{rot}}^p$ 21.5% lower than that of the others.

Discussion

A substantial increase in head impact simulation efficiency is likely critical to ultimate deploy computational models of the human head for large-scale brain injury studies, particularly in contact sports. Using parameterized, triangulated a_rot impulses as training dataset (N=500), we have successfully established a subset of a pre-computed brain response atlas (pcBRA) partially sampling the 4D parametric space based on the DHIM to accurately and efficiently estimate brain strain responses. Using randomly generated in- (N=100), below- (N=50) and above-range (N=50) testing datasets, we have demonstrated excellent pcBRA accuracy performance for element-wise response estimation especially for in-range interpolation as a 100% success rate was achieved based on the “double-10%” criterion regardless of the normalization denominator (directly simulated ground-truths or injury-causing thresholds). An excellent performance (100% success rate) was also achieved when interpolating regional average ε^p for all generic ROIs and the corpus callosum, regardless of the normalization denominator. For extrapolation, excellent or nearly excellent performance was maintained for element-wise or regional average ε^p as long as $a_{\mathit{rot}}^p$ was within 1 krad/s² relative to its bounds in the training dataset, again, regardless of the normalization denominator. The slightly lower success rate for the below-range extrapolation (80%) was likely because of the rather small ε^p due to extreme low $a_{\mathit{rot}}^p$ in input. Even with much higher $a_{\mathit{rot}}^p$ for the above-range extrapolation, excellent or nearly excellent performance was still maintained when normalized by the ground-truth or larger injury-causing thresholds (Table 2). Further, relatively larger element-wise differences were mostly located in regions with low ε^p values (i.e., in corridors along the rotational axes), suggesting more accurate estimates to occur with higher ε^p values that are likely more injury-relevant.

The pcBRA dramatically reduced the computational cost required to achieve element-wise whole-brain responses over that from direct simulation (6 sec using 12 CPUs as opposed to ~50 min for a 40 ms impulse using 8 CPUs (the number of CPUs for Abaqus simulation was limited by the available license tokens)). Because regional ε^p values can be pre-computed for any arbitrary ROI (generic or targeted, e.g., corpus callosum) based on the established atlas responses, an instantaneous pcBRA estimate of brain regional strain levels is readily achievable (<0.01 sec for each individual interpolation/extrapolation) to assess region-specific injury risk. These results suggest the potential for the pre-computation strategy to substantially increase the throughput in head impact simulation without significant loss of accuracy relative to responses directly simulated from the parameterized impulses. Therefore, the pcBRA could have the capability to enable a large-scale tissue-level, model-based investigation of the mechanisms of traumatic brain injury in the future (e.g., to evaluate brain responses from repetitive head impacts in contact sports).

While it may be possible to reduce FE model simulation time via simplified models with coarser meshes, the degradation in solution accuracy is never desirable and is against the general trend of model development. More powerful computers are certainly effective in reducing simulation time. However, with the ever-growing model sophistication and mesh resolution, the computational challenge persists. Regardless, none of these techniques would be capable of providing an instantaneous regional response in an arbitrary ROI that the pcBRA readily offers, even on a low-end computer. These findings clearly underscore the significant advantages of pcBRA over other conventional, alternative approaches.

Essentially, the pcBRA technique is an end-to-end sampling of a smooth and continuous parametric hyperspace, which has not been applied to brain dynamic simulation before. Additional approximation errors can occur especially for extreme out-of-range extrapolations. While this may seem undesirable, it is critical to consider the utility of model simulation from a system’s perspective in a concerted effort (as opposed to an isolated technique by itself) for brain injury studies, especially when (potentially even larger) uncertainties or variations exist in head impact kinematics, neuroimaging, cognitive measures and concussion diagnosis.²⁵ On the other hand, increasing the training dataset sampling density and range (i.e., to avoid “extrapolation”) could easily reduce the unwanted errors. Further, because the accuracy of each simulated pcBRA solution solely depends on the head model, any error in kinematic inputs (e.g., under- or over-estimation of $a_{\mathit{rot}}^p$ or $v_{\mathit{rot}}^p$) could also be easily compensated for without rerunning the pcBRA simulations. These observations highlight the unique scalability of the pcBRA technique.

It must be recognized that the pcBRA feasibility comes at the cost of idealizing full DOFs head impact kinematics into a reduced system by parameterizing the largest single peak of isolated a_rot-only with the minimum number of DOFs (4 as opposed to as many as 12), which would likely result in further loss of accuracy. However, our validations against the directly simulated results using two independently measured typical real-world a_rot profiles suggest that the pcBRA could achieve an excellent performance when simulating mono-axis rotations, which established an important confidence of our technique. While subsequent secondary a_rot peaks did influence brain strain response history, they did not significantly alter the peak responses induced by the first major peak (see Fig. 12ab and Fig. 13ab for element-wise ε^p and circled regions in Fig. 12d and Fig. 13d for whole-brain average ε peaks). Importantly, because current tissue-level injury metrics including strain, strain rate, their product,²⁸ as well as their variants such as cumulative strain damage measure (CSDM)⁵⁰ are all based on tissue-level accumulated peak responses rather than their response history during the 40–100 ms impact, the nearly identical element-wise peak strain magnitudes between the pcBRA-estimated and the ground-truth counterparts well justify the use of pcBRA for any real-world, practical application.

The a_rot peak parameterization impulse shape (triangular, sine, or haversine) appears unimportant even when their $a_{\mathit{rot}}^p$ could differ by as much as 21.5% (Fig. 14). As long as they maintain an identical $v_{\mathit{rot}}^p$ and Δt, they lead to almost the same ε^p level. This could be conceptually explained using a dimensional analysis because the transformed brain strain energy is likely proportional to the rotational kinetic energy while they are each proportional to the square of ε^p and $v_{\mathit{rot}}^p$, respectively.²⁶ Therefore, although the parameterized $a_{\mathit{rot}}^p$ was nearly ~10% lower (Fig. 6a) or 20% higher (Fig. 6b) than the measured counterpart for the two real-world profiles, the pcBRA-estimated and ground-truth ε^p magnitudes and distributions were nearly identical (Fig. 12ab and Fig. 13ab). More interestingly, while the measured real-world $a_{\mathit{rot}}^p$ in Fig. 6b was more than 25% lower than that in Fig. 6a, the corresponding $v_{\mathit{rot}}^p$ was nevertheless nearly 23% higher, leading to a ~9% increase in whole-brain average ε magnitude (Fig. 12b and Fig. 13b). While these findings clearly suggest that $v_{\mathit{rot}}^p$ as opposed to $a_{\mathit{rot}}^p$ may be more informative for injury risk assessment as previously recognized,^{20,26,29,30,49,50,58} a longer Δt lowers ε^p (e.g., whole-brain average ε^p magnitude decreased by more than 15% when Δt was varied from 4 to 16 ms with $v_{\mathit{rot}}^p$ of 25 rad/s), as similarly observed before.²⁹ The decrease in ε^p is likely a result of increased energy dissipation over a longer Δt due to the brain viscoelastic property. Therefore, we have chosen to parameterize $a_{\mathit{rot}}^p$ and Δt separately instead of using $v_{\mathit{rot}}^p$ directly, albeit the latter could allow using three as opposed to four independent variables to establish the pcBRA (and hence, to further significantly reduce the computational cost and atlas storage space).

It should be noted that our current pcBRA performance evaluations were limited to mono-axis, mono-phasic (i.e., acceleration-only) rotations because only resultant a_rot profiles were available.^10,44 However, a real-world full-DOF a_rot profile could be much more complicated involving multiple rotational axes in time, or more likely, continuous change of instantaneous rotational axis during impact. In addition, deceleration will inevitably follow the acceleration to avoid an unbounded but unphysical head motion in real world. Parametric studies using multi-axis, multi-phasic impulses would be valuable to gain insights into their significance on brain responses. However, most studies are limited to mono-axis, mono-phasic rotations to-date,^29,43,54 except for one studying mono-axis, bi-phasic rotations using an idealized 2D model.⁵⁸ Nevertheless, it is important to further investigate the loss of accuracy or the residual error, F_err in Eqn. 3, against responses from real-world full-DOF a_rot to assess the pcBRA utility for real-world injury analysis in the future.

Further, when secondary a_rot peaks become increasingly dominant that may violate the assumption of a single major a_rot peak, the pcBRA may become invalid (e.g., some brain regions may experience higher responses at a later time but are not captured). Interesting, the pcBRA in these cases may still serve as an upper- or lower-bound of the true responses (e.g., upper-bound as suggested by a 2D parametric study;⁵⁸ albeit, further studies using a validated and realistic 3D head model are still warranted). It must also be recognized that these rather complicated impact conditions will most likely invalidate other kinematics-based injury metrics as well that similarly focus on a single major a_rot peak. An accurate direct simulation of the true brain strain responses (peak and history) will inevitably place a more stringent scrutiny on head impact measurement systems that provide the required model input in the first place. These observations, once again, highlight the importance of a concerted effort necessary to elucidate the biomechanical etiology of sports-related concussion.

Regardless, to account for these inherent limitations with the pcBRA strategy (i.e., mono-axis, mono-phasic rotations that only capture the single major a_rot peak), it is possible to further compensate for F_err due to model input idealization and parameterization. However, injecting additional perturbation parameters of the time-varying a_rot profile (e.g., mono- vs. biphasic and mono- vs. multi-axis acceleration profile) into the model input parametric space is ill-advised because it would necessarily increase the pcBRA computational complexity, exponentially. Therefore, it may be advisable to statistically probe the relationship between the perturbation in input and the variation in response. Analogously, a statistical model could also be used to probe the relationship between model geometrical/anatomical perturbations and variation in response to account for brain individual variability. By statistically quantifying F_err in element-wise or regional strain responses (e.g., through a linear regression model),³² a higher order and hence, a more accurate approximation of F_strain is likely attainable. Additionally, individualized pcBRA could also be established if so desired using subject-specific models that can be developed with existing techniques.^23,25

Despite these accuracy concerns, because the pcBRA instantly provides regional tissue-level brain strain responses that are presumed to be directly responsible for initiating region-specific injury, even the 1^st-order approximation appears to be a significant step forward in investigating the mechanisms of sports concussion as compared to other studies using isolated $a_{\mathit{lin}}^p$ and/or $a_{\mathit{rot}}^p$ alone, for injury risk assessment that do not otherwise incorporate regional brain mechanical responses.^{3,4,9,46,47,53} Because it is possible to compare model-estimated tissue-level brain peak responses directly with injury thresholds established from in vivo and in vitro micro-scale injury studies to assess the risk of injury,^1,38 the pcBRA potentially offers a unique capability to efficiently design and evaluate the utility of injury risk metrics based on regional tissue-level responses as opposed to solely depending on global kinematic variables or their variants (e.g., GAMBIT,⁴⁰ HIP,⁴¹ HITsp,¹⁷ RIC and PRHIC,²⁷ and BrIC)⁴⁹. These findings suggest that the pcBRA does indeed have the potential to accelerate the exploration of the biomechanical mechanisms of traumatic brain injury in the future. Because brain strain-related responses, including strain itself, are significantly correlated to the product of $a_{\mathit{rot}}^p$ and Δt instead to $a_{\mathit{rot}}^p$ only,²⁶ a systematic investigation of how best to parameterize real-world a_rot impulses must be performed in the future to ensure accurate representation of brain strain responses. Interestingly, our simple parameterization strategy by maintaining both the identical $v_{\mathit{rot}}^p$ and Δt from the major a_rot peak as outlined in Fig. 6 appeared to perform sufficiently well for the two independently measured real-world a_rot resultant profiles (albeit, further work is necessary to verify its utility in real-world full-DOF head rotations).

Besides the pcBRA accuracy and efficiency performances, the ultimate utility of the technique for real-world injury studies also relies on model simulation fidelity because the response approximation function, F₁ in Eqn. 3, is model-dependent. The DHIM validation performance has been categorized as “good” to nearly “excellent” when simulating relative brain-skull displacements and pressure responses in cadaveric head impacts according to a fidelity rating based on correlation scores.^25,26,60 Further, DHIM also achieved an “excellent” performance when validating against full-field brain strain responses in a live human (as opposed to discrete displacement data in cadavers) under a mild head rotational acceleration based on correlation scores.⁴⁸ These model response verifications at the low (~250–300 rad/s² for a volunteer), mid (~1.9–2.3 krad/s² for cadaveric impact tests C755-T2 and C383-T1), and high (~11.9 krad/s² for test C393-T4) levels of $a_{\mathit{rot}}^p$ provide an important insight on the confidence in DHIM-estimated regional brain strain responses for a large spectrum of on-field impacts.

The range of $a_{\mathit{rot}}^p$ evaluated for pcBRA estimation performance in this study was sufficiently large (500–7500 rad/s², approximately from the 25^th percentile subconcussive to 95^th percentile concussive $a_{\mathit{rot}}^p$ in college football, or up to ~99^th percentile in ice-hockey; Fig. 4). We have limited the $a_{\mathit{rot}}^p$ sampling range in this study to evaluate the pcBRA extrapolation accuracy at higher $a_{\mathit{rot}}^p$ levels, which is important for its performance characterization. However, due to the reduced extrapolation accuracy when $a_{\mathit{rot}}^p$ was sufficiently high (e.g., >5500 rad/s²), arguably it may be necessary to further extend the range of $a_{\mathit{rot}}^p$ in the training dataset to improve the pcBRA estimation accuracy (i.e., to avoid extrapolation). On the other hand, it may actually be computationally more sensible to simply simulate the few high $a_{\mathit{rot}}^p$ impulses directly instead because of the skewed distribution of on-field $a_{\mathit{rot}}^p$,^9,45 unless a (near) real-time feedback is critical (e.g., when possibly using the model-estimated responses to aid the “return-to-play” decision-making on the field). Although Δt was based on measured a_lin instead of a_rot, the temporal characteristics of the two acceleration components are likely similar,¹⁰ and the training dataset covered a large range of occurrences (~95.4% assuming a normal distribution). The azimuth and elevation angles, θ and α, were also limited in this study, which can be easily extended to cover the entire parametric space for the rotational axis, Ω (Fig. 3). Because on-field data distribution of Ω is likely clustered instead of being random or uniformly distributed (e.g., see for head impact locations in Breedlove et al. (2012),⁶ although on-field distribution of Ω appears not available yet), sampling the Ω parametric space accordingly will likely be more economical in computation than a simple brute-force approach. Further, the accuracy of pcBRA estimation apparently depends on the sampling density of each parameterization variable; however, we did not investigate their individual significance on the pcBRA performance. Regardless, extending the partially established pcBRA to increase the parametric coverage space or sampling resolution for any of the independent variables is straightforward.

While we have only evaluated pcBRA performance for engineering strain in this study, the technique would most likely be applicable as well to other strains (e.g., Lagrangian or logarithmic strain), strain components (e.g., white matter fiber strain,²⁵ or alternatively, referred to as “axonal strain”),^12,14,31,56 or strain-related responses such as strain rate and stress. Because the pcBRA model inputs were generated using generic kinematic variables that do not rely on the specific technique used in actual impact measurement (e.g., through laboratory reconstruction, instrumented helmet, mouthguard, or ATD),^10,17,42 the pcBRA is applicable as long as it remains feasible to parameterize the isolated a_rot profile into a triangular impulse to estimate brain strain responses. In addition, once fully established, the pcBRA could also serve as an efficient engine to conduct parametric studies, for example, to investigate the distribution and extent of potential white matter damage using randomly generated rotational impulses based on the distribution of actual on-field impact measurements.²⁵ These investigations will be the subjects of future publications.

Finally, an analogous brain pressure response atlas can also be established. Because brain pressure responses in a translational/direct head impact are causally determined by a_lin itself (magnitude and directionality), brain size and shape,⁶⁰ only two (as opposed to four for the strain response atlas in this study) independent variables (i.e., the azimuth and elevation angles, θ and α, for the translational axis) are necessary. However, further study is necessary to assess whether pressure can be estimated from isolated a_lin, alone, without significant loss of accuracy. Nevertheless, it may be necessary to ultimately combine these brain response atlases to fully capture the potential risk of brain injury induced by either a_lin, a_rot, or their combination for practical applications,⁴⁶ especially given the rather low correlation found between the two acceleration components that suggests impacts with low a_rot but high a_lin magnitudes are possible on the field.⁴⁵ These atlases designed for (near) real-time tissue-level estimation of both strain and pressure responses may provide the computational tools necessary and critical to accelerate the exploration of the biomechanical mechanisms of traumatic brain injury (including, but not limited to, sports-related concussion) in the future.

Conclusion

We have successfully demonstrated the feasibility of using a pre-computed brain response atlas (pcBRA) to substantially increase the efficiency in head impact simulation for brain strain responses without significant loss of accuracy from the estimation itself using idealized, parameterized rotational impulses as well as two typical real-world rotational profiles. The typical computational cost of pcBRA was 6 sec and <0.01 sec for element-wise or average regional peak responses, respectively, vs. ~50 min simulating a 40 ms impulse directly. Future studies include systematic investigation of rotational profile parameterization and more extensive performance evaluation using real-world data. Once fully established, the pcBRA could have the potential to accelerate the exploration of the mechanisms of brain injury (sports-related concussion in particular) in the future. If successful, the pcBRA may also become a diagnostic adjunct in conjunction with sensors that measure head impact kinematics on the field to objectively monitor and identify tissue-level brain trauma in real-time for “return-to-play” decision-making on the sideline.

Fig. 8.

Volume fractions for element-wise differences in ε^p relative to the ground-truth and the same range of injury thresholds for below-range pcBRA extrapolation.