Sloppiness in Spontaneously Active Neuronal Networks

Abstract

Various plasticity mechanisms, including experience-dependent, spontaneous, as well as homeostatic ones, continuously remodel neural circuits. Yet, despite fluctuations in the properties of single neurons and synapses, the behavior and function of neuronal assemblies are generally found to be very stable over time. This raises the important question of how plasticity is coordinated across the network. To address this, we investigated the stability of network activity in cultured rat hippocampal neurons recorded with high-density multielectrode arrays over several days. We used parametric models to characterize multineuron activity patterns and analyzed their sensitivity to changes. We found that the models exhibited sloppiness, a property where the model behavior is insensitive to changes in many parameter combinations, but very sensitive to a few. The activity of neurons with sloppy parameters showed faster and larger fluctuations than the activity of a small subset of neurons associated with sensitive parameters. Furthermore, parameter sensitivity was highly correlated with firing rates. Finally, we tested our observations from cell cultures on an in vivo recording from monkey visual cortex and we confirm that spontaneous cortical activity also shows hallmarks of sloppy behavior and firing rate dependence. Our findings suggest that a small subnetwork of highly active and stable neurons supports group stability, and that this endows neuronal networks with the flexibility to continuously remodel without compromising stability and function.

Introduction

Neuronal networks continuously remodel through changes in synaptic strength and number (Okabe et al., 1999; Holtmaat et al., 2005; Minerbi et al., 2009) and changes in neural excitability (Desai et al., 1999; Daoudal and Debanne, 2003). These changes are driven both by spontaneous activity (Maletic-Savatic et al., 1999; Okabe et al., 1999; Minerbi et al., 2009) and by experience-dependent plasticity during development and in the adult brain (Trachtenberg et al., 2002; Holtmaat et al., 2005). The presence of such changes is generally expected to destabilize stored information over time (Fusi and Abbott, 2007). However, functional representations in neural populations are consistently found to be very stable, despite continuous changes of the behavior of single neurons (Carmena et al., 2005; Chestek et al., 2007; Huber et al., 2012; Margolis et al., 2012; Ziv et al., 2013). These observations suggest that networks have considerable flexibility to reorganize structure without affecting previously established function. However, the relationship between plasticity of individual neurons and collective network stability is currently not well understood (Turrigiano, 2011).

Similar issues in systems biology relating to the interplay of robustness and evolvability were recently addressed by the theory of sloppiness in multiparameter models (Daniels et al., 2008). Within this framework, robustness of a model system stems from a highly anisotropic parameter space, where large regions of parameter values map onto very similar system behavior (sloppy parameters), and only few parameters or parameter combinations exert significant influence over collective activity (stiff parameters). Thus, local changes need not result in global changes, and global stability can be achieved through homeostatic regulation of only a few crucial parameters. A range of systems biology models have been found to indeed exhibit such properties (Brown and Sethna, 2003; Machta et al., 2013). Here we examine whether this concept can explain collective stability in networks of neurons.

We investigated this hypothesis using spontaneously active dissociated neural preparations, cultured on high-density multielectrode arrays. Such in vitro cultures are globally stable (Slomowitz et al., 2015) and at the same time undergo significant restructuring of synaptic connections (Maletic-Savatic et al., 1999; Okabe et al., 1999; Minerbi et al., 2009; Slomowitz et al., 2015), accompanied by changes in the activity of single neurons (Slomowitz et al., 2015). Importantly, these preparations allow for reliable recordings of hundreds to thousands of individual neurons over several days (Berdondini et al., 2009). We recorded from three hippocampal cultures and, similar to in vivo reports (Mizuseki and Buzsáki, 2013), we found highly skewed distributions of firing rates that were stable between consecutive recordings (Slomowitz et al., 2015). At the same time, the activity of single neurons and individual correlations changed substantially, indicating the presence of local fluctuations of neuronal properties.

To parametrically describe obtained multiunit spike trains, we used pairwise maximum entropy models (Schneidman et al., 2006; Shlens et al., 2006; Tang et al., 2008). This parametric form enabled us to use a recently introduced method to quantify the influence of parameter fluctuations on the collective network behavior (Machta et al., 2013). Interestingly, the model parameter sensitivity was highly uneven, implying sloppiness. This is, to our knowledge, the first demonstration of sloppiness in models directly fit to neuronal data. Our analysis further revealed that the most rapid and significant changes in neural activity occurred along the insensitive, sloppy parameter dimensions. In contrast, a small number of neurons, which had highly sensitive stiff parameters, exhibited slower and smaller fluctuations.

We further confirmed that also in vivo data and simulations of cortical activity in the asynchronous regime both exhibit sloppiness. Together, these results are consistent with the hypothesis that a small but stable subnetwork of neurons is responsible for global stability, allowing considerable plasticity to take place in the remaining majority of cells.

Materials and Methods

Dissociated cultures preparation.

All procedures involving experimental animals were approved by the institutional IIT Ethic Committee and by the Italian Ministry of Health and Animal Care (Authorization ID 227, Prot. 4127 March 25, 2008). Neural cultures were obtained by dissociating hippocampal neurons from brain tissue of embryonic rats (both sexes) at day E18 and plating the cells (35,000–40,000 cells) on microelectrode arrays pretreated with adhesion factors (PEI/poly-l-lysine). Subsequently, cultures were incubated in Neurobasal supplement with 1% glutamax 2% B-27 Neurobasal medium, in a humidified atmosphere 5% CO₂ at 37°C. Fifty percent of the medium was changed every 3–4 d. Three sets of recordings were obtained from three cultures from 24 d in vitro (DIV) onward over the course of 3–5 d. As the recordings took place outside of the incubator, the dishes were closed with sterilized custom designed polydimethylsiloxane (PDMS) caps that prevent media evaporation and osmolarity changes while permitting gas exchange. After each recording, the chips were returned to the incubator after removal of the PDMS cap under a sterilized hood.

High-resolution multielectrode array recordings.

High-resolution extracellular recordings were performed on the BioCam4096 platform with active pixel sensor multielectrode array (APS MEA) with chips type BioChip 4096S (3Brain), providing 4096 square microelectrodes of 21 × 21 μm in size on an active area of 2.67 × 2.67 mm and with interelectrode separation of 21 μm. The platform records at a sampling rate of 7.022 kHz and 12 bits resolution per channel when measuring from the full 64 × 64 channel array. Raw data were visualized and recorded with the BrainWave software application provided with the BioCam4096 platform. Activity was recorded at 12 bits resolution per channel, low-pass filtered at 5 kHz with the on-chip filter and high-pass filtered by a digital high-pass filter at 0.1 Hz. Recordings, 15 min each, were performed at 0, 2, 20, 50, 68, and 92 h in Culture 1 and at 0, 2, 20, and 44 h in cultures 2 and 3.

Spike detection.

Spikes were detected with a custom algorithm (O. Muthmann, H. Amin, E. Sernagor, A. Maccione, D. Panas, L. Berdondini, and U. S. Bhalla, M. H. Hennig, unpublished data). In short, putative spikes were identified as negative voltage deflections crossing a specified threshold and satisfying simple signal shape constraints (minimum peak width of 2 frames, no other minimum in the following 1 ms, partial repolarization). The threshold was defined in units of local noise estimate v relative to baseline b as follows: b − 5v. Baseline was defined as the local estimate of voltage tertile, incrementally updated in each time step. In a similar vein, the noise estimate was increased or decreased by a set value in each frame to reflect whether voltage was within v of the baseline or not. Subsequently, a correlation-based analysis was performed to separate out the false-positives exploiting the random nature of random, uncorrelated electrode noise. To this end, the distribution of correlated channels for each putative spike was compared with a corresponding distribution of surrogate data of randomly generated spikes.

Because spike sorting on the full APS MEA system is not feasible due to the high neural density and limited acquisition rates, isolation of single units was not attempted. Given the small size of electrodes and limited signal spread between electrodes in in vitro cultures, each electrode was assumed to report the activity of a separate, single neuron, as was observed in previous work using cultured cortical neurons with comparable density (Berdondini et al., 2009). In rare cases of a spike appearing simultaneously (±1 frame) on neighboring electrodes, the lower amplitude event was ignored; however, such events were not common (<3% in test recordings).

In vivo data.

Single 15 min recording of in vivo activity of 140 neurons from primary visual cortex was obtained from the CRCNS.org on-line data repository, and was used here with permission from the authors. The dataset (Chu et al., 2014) and its description are available from the website. All experimental procedures are reported in detail in the original study (Chu et al., 2014). In short, a multishank multielectrode array (64 electrodes) was inserted normal to the cortical surface into the primary visual cortex (V1) of Macaca cyclopsis, and spontaneous activity was recorded under light anesthesia. Potential spikes were detected through filtering the recorded voltage (400–5000 Hz, 28 Db/octave), digitalized and stored. Single units were isolated off-line using superparamagnetic clustering (Quiroga et al., 2004) with manual corrections.

Pairwise maximum entropy models.

To avoid counting errors and extremely sparse pattern probability distributions, only channels >0.1 Hz were considered. Channels active across all recordings from a single culture were identified and then 100 groups of 10 neurons each were randomly chosen for analysis. To this end, channel indices were permuted and first 10 neurons were chosen; channels that were selected more than four times were removed from further permutation runs. This procedure resulted in a homogeneous sampling over available population.

For each group, a pairwise maximum entropy model was fit to the data (Schneidman et al., 2006; Shlens et al., 2006; Tang et al., 2008). To this end, spike trains were binned, creating binary matrices X = {x_j^t} with +1 representing a spike and −1 silence of unit j in bin t. In each time bin, the state X^t of the group could be 1 of 2¹⁰ possible spiking patterns X_s (e.g.; 1,−1, 1, 1,−1, 1,−1, 1, 1, 1). The fraction of how often state X_s occurred in the data yielded the probability distribution of spiking patterns in the group P_obs(X_s). This distribution will typically depend on the choice of a time bin, as larger time bins are more likely to include more simultaneous spikes and thus exhibit more synchrony, possibly including spurious higher-order correlations. On the other hand, too small time bins will ignore existing and pertinent synchrony. The particular choice we made in this work was dictated by consideration of the time scale of latency of a monosynaptic connection. As reported previously (Fitzsimonds et al., 1997; Erickson et al., 2008), the majority of latencies between a presynaptic and postsynaptic spike in a dissociated hippocampal culture fall within 1–5 ms. We therefore chose a time bin of 5 ms.

The distribution obtained from the data can be approximated by a maximum entropy model under first and second order constraints, i.e., a model that reproduces the following marginals:

and is otherwise unconstrained, i.e., is maximized with respect to entropy. The model that satisfies those criteria takes the parametric form of the Boltzmann distribution:

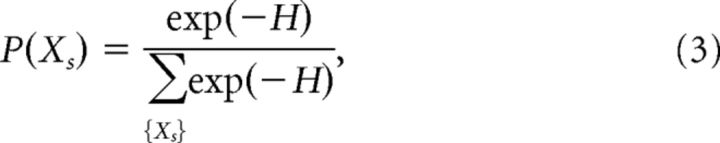where H is a measure closely related to energy:

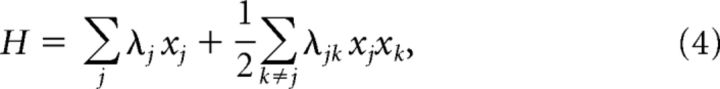with parameters, λ_j and λ_jk, describing the functional excitability and the functional interactions of neurons. To obtain a model fit, the parameters were adjusted by an iterative scaling algorithm as follows:

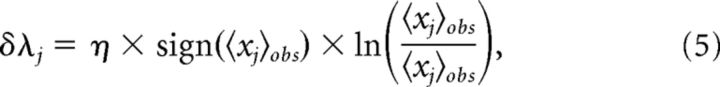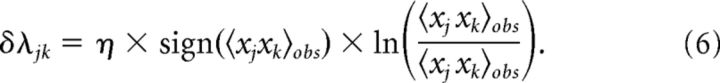A constant learning rate η < 1 was used for each set of neurons. Adjustments continued until the relative difference between model and observed marginals was on the order of 10⁻⁵, which corresponds to reproducing spike and coincident spike numbers with the precision of ∼1 spike. If a group did not converge within a prescribed number of iterations (typically 50,000), alternative value of η was used, to obtain the desired convergence. In the rare cases of incomplete convergence, the precision dropped to ∼1.5–2.5 spikes.

Comparison measures.

To compare the pattern probability distributions between consecutive days and between the model and the data, the Jensen–Shannon divergence was used:

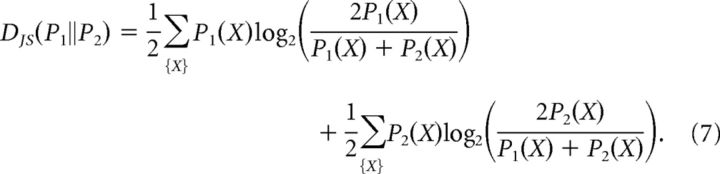To compare group parameters between time points while allowing for overall fluctuations in excitation or coupling, we used the coefficient of determination r². To this end, for two sets of parameter values of a group i, Λ_{i, t1} = {λ_jⁱ, λ_jkⁱ}_t1 at time t₁ and Λ_{i, t2} at time t₂, linear regression was performed, fitting the following:

The r² of this fit was used as a measure of similarity between parameter groups. The comparisons were calculated in reference to the baseline recording, unless otherwise noted.

Fisher information matrix.

The Fisher information matrix (FIM) for a probabilistic model with observables x, and parameters Λ = {λ_l} is defined as follows:

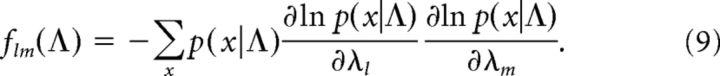In the particular case of a pairwise maximum entropy model, l, m ϵ {j, jk}, and so for 10 neurons the FIM has the following form:

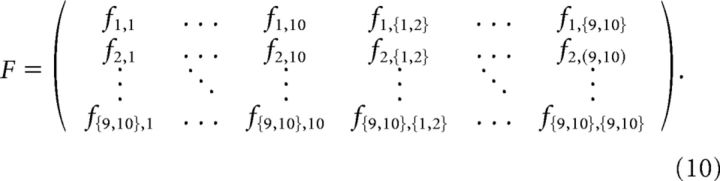The FIM provides a measure of the curvature of the log-likelihood landscape with respect to the model parameters, and as such it quantifies the sensitivity of the model to parameter changes. For the pairwise maximum entropy model the matrix entries can be directly computed from the model, taking on the form of the covariance matrix of the random variables associated with all parameters in turn:

where X_l = x_j for the parameters λ_j and X_m = x_jx_k for the couplings λ_jk. The matrix can also be computed from the data, by taking expectations with respect to the measured probability distribution. Direct comparison showed that these two versions of the FIM were almost identical. Moreover, for a statistical physics model such as Equation 3, the FIM can equivalently be expressed as the free entropy change of a system with respect to model parameters, which has the Riemannian property of a metric tensor (Crooks, 2007).

Gini coefficient analysis.

The Gini coefficient is a commonly used and robust (Hurley and Rickard, 2009) measure of sparsity. For a distribution of N values f_i, it is defined as follows:

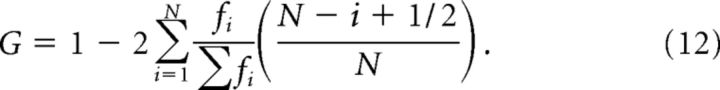As a control, we also computed Gini coefficients for two artificially generated maximum entropy models. The first was a maximum entropy model with will all interactions λ_jk set to 0, and the fields λ_j set to a value that reproduces the firing rates of the data (Culture 1, recording at 0 h, and in vivo recording). This model provides an estimate of sparsity under the assumption of an independent model, where neurons do not interact, and the number of relevant parameters is reduced from 55 to 10. The second model used was an entirely artificial 'toy' model, with fields and interactions set as follows

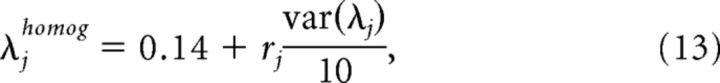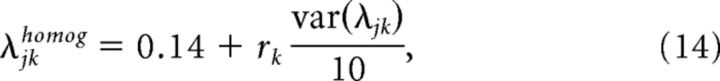where r_j and r_jk were randomly drawn numbers from a uniform distribution, variance was set to one-tenth of that of the fitted models, and the mean was arbitrarily chosen. This model was aimed to provide an example of how nonsparse a maximum entropy model can be if the fields and interactions are homogeneous, and therefore there is little differentiation in their sensitivity.

Shuffling and resampling procedures.

To verify that presented results are not due to overfitting data of limited sample size nor random effects, shuffling and resampling procedures were used to generate surrogate data for comparisons. In the shuffling procedures neurons or groups of neurons (see Figs. 2E,F, 5B, respectively) had their indices permuted before computing comparison measures against original, unshuffled data. For group shuffling, this was repeated N_shuf = 50 times. In the resampling procedure, for each group of neurons an artificial spike matrix X = {x_j^t} was generated by randomly sampling from the model distribution P_mod(X). Subsequently, a pairwise maximum entropy model was fit to the artificial data, exactly as for the observed spike trains. This was repeated N_res = 50 times. Fisher Information Matrices were calculated, and eigendecompositions were conducted as for the data, and the resulting resampled FIMs, parameters, and eigenparameters could then be compared against the original true data in parallel to comparisons between recordings. The differences against original data were averaged across resamples in each group.

Figure 2.

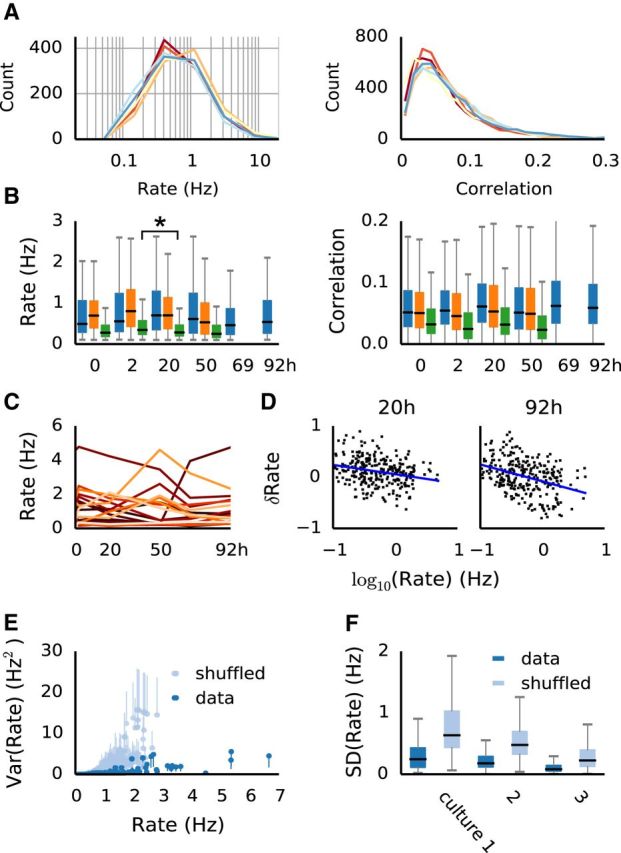
The distributions, but not individual firing rates are preserved over several days in neural cultures. A, Stable distributions of firing rates (left; Kolmogorov–Smirnov test reported no significant differences at α = 0.05) and similar distributions of pairwise correlations (right; significantly correlated between recordings at p < 0.01) in a single preparation over several days. B, Distributions (median and interquartile ranges) of firing rates (left) and correlations (right) in all three preparations. Firing rate distributions remained stable (Kolmogorov–Smirnov test yielded p > 0.05 in 8, and p > 0.01 in 10 of the 11 pairs; the outlier pair marked by an asterisk). C, Example of firing rates across recordings of 20 randomly selected individual neurons. D, Rate changes are not entirely random, but exhibit a bias of neurons with low firing rate to increase activity, and neurons with higher activity to decrease firing (blue lines). Graphs show the relative changes, δRate = (R_t2 − R_t1)/(R_t1 − R_t2) between time points t₁ and t₂. E, The relationship between the mean firing rate and the variance of firing rate in individual neurons across recordings (blue dots; error bars shown only on one side for clarity). For comparison, the same is plotted for shuffled data (gray; unit rates were randomly shuffled within recording), as an estimate of the behavior of population variance. F, Distributions (median and interquartile ranges) of firing rate SD of individual neurons, compared with shuffled data, for all recordings.

Figure 5.

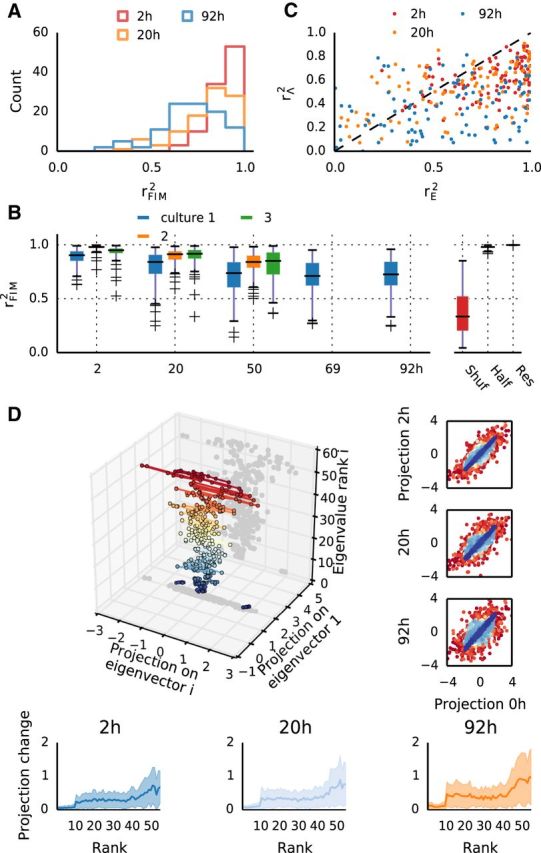
Fluctuations in network parameters predominantly occur in sloppy dimensions with weak influence on collective dynamics. A, Distributions of FIM similarity r_FIM² for different intervals (Culture 1). Note much higher similarity than for model parameters. B, FIM similarities r_FIM² for all experiments at different intervals. For comparison, r_FIM² is also shown for shuffled groups (Shuf), for models fit independently to two halves of the same recording (Half) and to models fit to data resampled from previously fit models (Res). C, Comparison of parameter similarity in each group, versus eigenparameter similarity, for three pairs of recordings in Culture 1. D, Eigenvector decomposition allows for subspace projections for each group's parameters. Here a single group is imaged across six recordings (same group as A, B). Projections onto the principal and i′th eigenvector are in the x–y plane, and the z-axis denotes the rank i of the eigenvector (also indicated by different colors). Dots represent projections of one parameter set at different time points. These become progressively wider with increasing eigenvector rank, indicating stronger changes along sloppy dimensions. Right, Scatter-plots of projections between two time points, pooled across all groups, in the same color code as the 3D figure. Bottom, The average magnitude of change in parameter projections as a function of eigenvector rank.

Network simulations.

Four separate networks of 3200 excitatory and 800 inhibitory randomly connected leaky integrate and fire neurons were simulated for 900 s. The resting potential was set to −49 mV, the membrane time constant to 20 ms, the spike threshold to −50 mV and the reset potential to −60 mV. Current-based synapses were modeled as low-pass filters with time constants 5 ms for excitatory and 10 ms for inhibitory connections. The weight of inhibitory synapses was set such that it resulted in an IPSP of −9 mV. The weight of the excitatory synapses was different for each of the four networks, resulting in EPSPs of 1.6, 2, 2.25, and 2.5 mV for “lif 1”–“lif 4,” respectively. The networks were randomly initialized with voltages from a uniform distribution ranging from −60 to −50 mV. These simulations were run with the Brian Simulator v1.4.1 (Goodman and Brette, 2009). Randomly selected groups of neurons were analyzed as described above.

Code and data availability.

The code for reproducing the results shown in the paper, as well as a sample dataset, are provided online as a GitHub repository at: https://github.com/dpanas/SloppyIsing.

Results

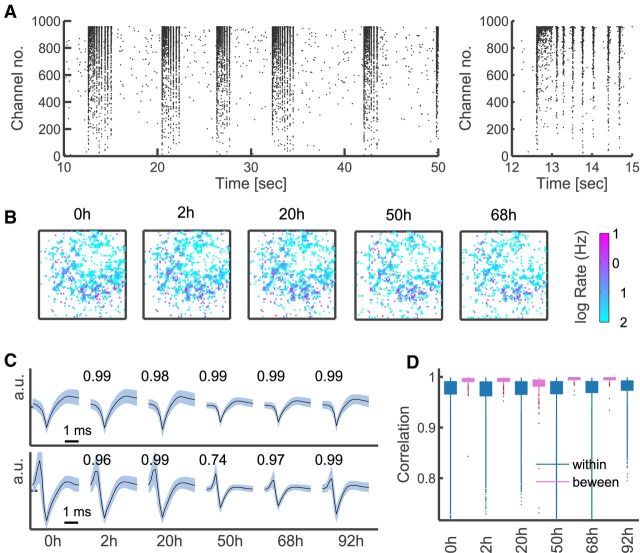
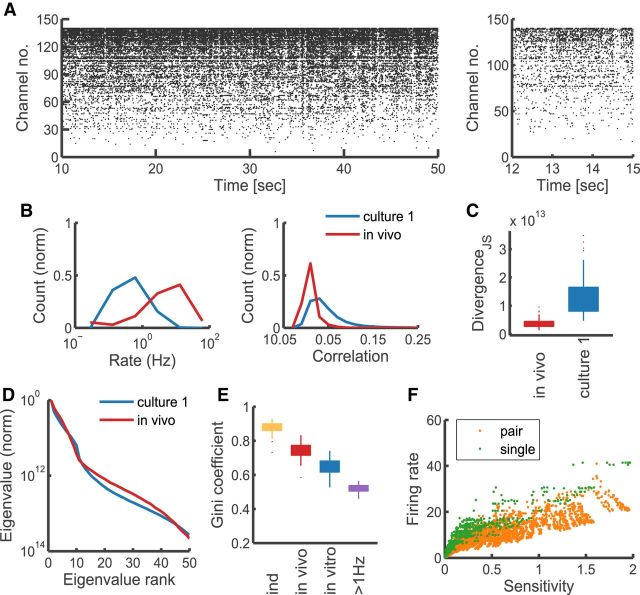
Neural activity from cultured dissociated hippocampal neurons was recorded with a high-density 4096 channel MEA (Fig. 1A,B) starting from the 24 DIV, where synaptogenesis and other developmental processes are complete (Lesuisse and Martin, 2002; Wagenaar et al., 2006). Fifteen-minute-long recordings were taken from three cultures at different time points over several days (Fig. 1B). Intervals between recordings ranged from 2 to 30 h, a time scale on which spontaneous synaptic remodeling was reported in cultured neurons (Minerbi et al., 2009). Typically, 1500–3500 channels reported spiking activity, with most neurons spiking at rates <1 Hz. Because estimation of spike shapes, rates, and correlations is unreliable for low spike rates, we restricted our analysis to units with rates >0.1 Hz, leaving between 400 and 1600 viable channels.

Figure 1.

High-resolution recordings from cultured neurons and monitoring single units over time. A, Example raster plot of culture activity (left), and a close-up of a superburst (right); all channels >0.01 Hz shown for illustration. B, Distribution of firing rates on the array monitored over time (color-coded log firing rate of each channel arranged on a 64 × 64 lattice corresponding to the physical layout of the MEA); all channels >0.01 Hz shown for illustration. C, Example spike shape voltage traces of two electrodes at different time points; mean (black) and SD (pale blue), averaged across detected spikes within a recording. Overlaid are values of the correlation coefficients between the presented mean spike shapes. D, The distributions (median and interquartile ranges and outliers) of spike-shape correlation values between consecutive recordings in Culture 1 (pink); only channels >0.1 Hz shown, as used in the main analysis. Shown for comparison (blue) are the distributions of correlations between average spike shapes of different units within a recording.

As established in previous research (Berdondini et al., 2009), the APS MEA allows for stable recordings from single units, due to high density and small size of the electrodes, and the typical shunt resistance in high-density cultures. To further verify that the single-unit resolution was preserved across time, we compared average spike shapes between consecutive recordings. As depicted in Figure 1C, even the least correlated waveforms (bottom) appear to retain their characteristic features across recordings (despite the fact that a media change at 42 h affected all channels and reduced signal strength across the array). Furthermore, examining the distribution of the correlation coefficients between spike shapes shows that waveforms are highly correlated between recordings, significantly more so than waveforms from different electrodes (Fig. 1D).

The activity showed the typical spontaneous, nonrandom bursting patterns observed in mature cultures (Segev et al., 2004; van Pelt et al., 2005; Wagenaar et al., 2006), with 50–100 short and highly synchronized bursts per minute, and almost no spiking between bursts (Fig. 1 A). Notably, although the appearance of highly synchronous bursts might suggest otherwise, pairwise correlations were generally weak (Fig. 2A). At a fine time resolution of 5 ms, on which synaptic events take place (Fitzsimonds et al., 1997; Erickson et al., 2008), the median correlation coefficient was ∼0.05 or less (Fig. 2B), and correlation matrices were dense and unstructured. The presence of these weak yet significant correlations motivated the use of maximum entropy models in this study (Schneidman et al., 2006; Shlens et al., 2006).

Dense culture recordings are stable despite significant individual fluctuations

First we examined the overall stability of the population activity over time. Firing rate distributions remained largely unchanged from day to day in all preparations (Fig. 2 A,B), as indicated by a Kolmogorov–Smirnov test between consecutive pairs of recordings (p values, Culture 1: 0.298, 0.464, 0.851, 0.18, 0.609; Culture 2: 0.064, 0.027, 0.516; Culture 3: 0.028, 0.004, 0.075). Pairwise correlations were less stable, but always significantly rank-correlated from recording to recording (average Kendal tau correlation coefficient 0.51, ranging from 0.37 to 0.69). In contrast to the overall population activity, the activity of single neurons showed clear and significant changes, as illustrated in Figure 2C. Between two recordings, individual firing rates could increase or decrease by >100% (relative to the first), with most changes approximately ≤25% and one-quarter of the population changing by >50%. These firing-rate changes revealed a tendency of slowly firing neurons to increase their activity, and of neurons with high rates to decrease activity (Fig. 2D). This bias became more pronounced over time and was consistent over different preparations. Importantly, this could not simply be accounted for by random fluctuations, as the estimated variance of firing rates in single channels was significantly lower than the population variance estimated from shuffled data, particularly for neurons with higher firing rates (Fig. 2E,F). Pairwise correlations between neurons changed even more prominently (often one-half of the correlations changed by >50%), but less consistently than firing rates when compared over time and across preparations. Together, these results demonstrate the presence of significant fluctuations in the activity of single neurons, although overall the networks maintained stable firing-rate distributions, in accordance with other reports (Slomowitz et al., 2015).

Changes in populations of neurons

To analyze the impact of single-neuron fluctuations on group behavior, we turned to a parametric model of multineuron activity. Pairwise maximum entropy models were fit to a 100 randomly selected groups of 10 neurons. Groups were selected from channels with activity in all recordings, to allow for systematic comparison across an entire experiment. These models aim to reproduce the probabilities of each pattern of silence and spiking by fitting a Boltzmann distribution with matching first and second order marginals, where each group i has a set of parameters Λ_i: local biases λ_j, controlling independent spiking of each neuron j; and interactions λ_jk, representing functional couplings between neurons j and k, required to model their joint firing. The models captured on average 70–90% of the multineuron correlation structure, similar to reports from other studies (Schneidman et al., 2006; Tang et al., 2008; Ohiorhenuan et al., 2010). Furthermore, comparison of Jensen–Shannon divergences shows that the model predicts the data on a comparable level with prediction of one-half of the dataset from the other half (Fig. 3A).

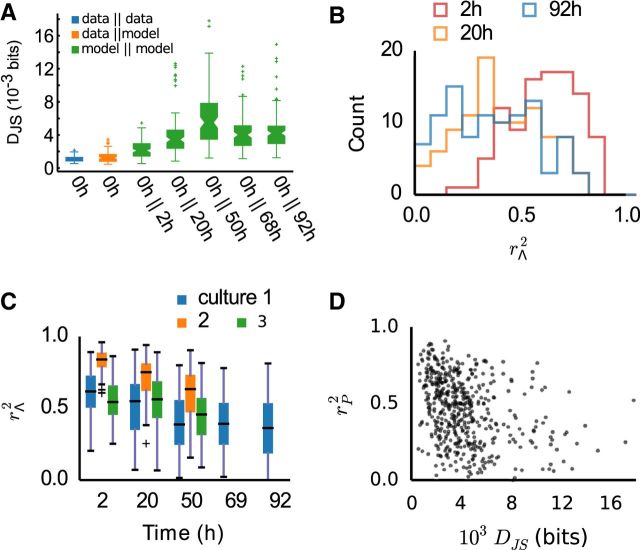
Figure 3.

Pairwise maximum entropy models reflect changes in network activity over time. A, Jensen–Shannon divergence D_JS between models at different time points from the same neuron groups. The probability distributions predicted by the models became increasingly dissimilar over time. For reference and indication of model fit quality, also shown are representative D_JS between probability distributions obtained from two halves of a single recording, and between model and data. B, Distributions of model parameter similarity r_Λ² between recordings at different time points, in a single preparation. For longer intervals, the differences between the models become more pronounced. C, Summary of the average parameter similarity at different time points, for all preparations. D, Parameter similarity between recordings is not predictive of distribution similarity; a scatterplot of r_Λ² of each group against the D_JS of the same group.

We then proceeded to compare the models between each recording taken at different time intervals. Over time, activity distributions became increasingly dissimilar, as measured by the Jensen–Shannon divergence D_JS,_i (Fig. 3A). To assess single-neuron fluctuations, we directly compared the model parameters of each group i between time points, using the coefficient of determination r² of the linear regression between the parameter values of each group at two different time points (see Materials and Methods). In-line with the results shown so far, significant and increasing changes between recordings were apparent as a decreasing average and broadening distribution of r_Λ,i² values (Fig. 3B,C). Yet, there was only a weak relationship between parameter dissimilarity and D_JS,i (r² < 0.15, p < 0.05; Fig. 3D). This result is due to the nonlinear relationship between single-neuron parameters and multineuron group behavior, and illustrates that the local changes do not predictably translate into global changes.

Sloppiness in populations of neurons and implications for stability

To understand the effects of local changes and systematically examine their impact on model similarity, we used the FIM. The FIM measures the curvature of the model log-likelihood with respect to the parameters, thus characterizing the parameter sensitivity of the model. Additionally, it provides a true metric for the model class used here, and therefore enables a direct comparison of models between recordings (for details, see Materials and Methods).

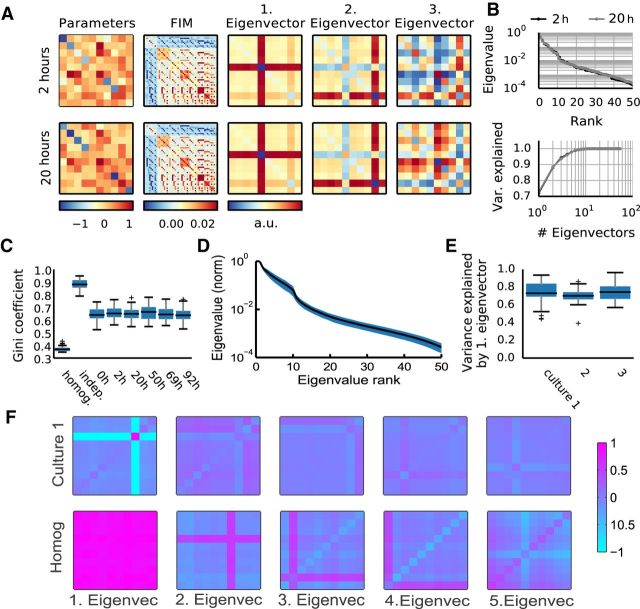
In a first step, we obtained the FIM for each group of neurons (Fig. 4A, second panel), and following the approach of Machta et al. (2013), we performed eigenvector decomposition of the FIMs (Fig. 4A). Because the form of the FIM is such that each entry corresponds to a pair of parameters (see Materials and Methods), the matrix does not map in a straightforward manner onto parameters themselves. However, in analogy with principal component analysis of a covariance matrix, an eigenvector decomposition of FIM can be performed to obtain the dimensions in parameter space providing the dominant contribution to the matrix. For sloppy models, this eigendecomposition should result in rapidly decreasing eigenvalues, reflecting the anisotropy of the model space and revealing the sloppy (insensitive to changes) and stiff (sensitive) dimensions in the space of parameters. As in other sloppy systems (Daniels et al., 2008; Machta et al., 2013), we observed rapidly decreasing eigenvalues (Fig. 4B, representative example, D, average behavior). The principal eigenvector explained on average ∼80% of the variance (Fig. 4E), hence yielding the most relevant contribution to parameter sensitivity and defining the stiffest direction in parameter space. On the other hand, eigenvectors associated with low eigenvalues correspond to sloppy dimensions, along which parameters can change without significantly affecting the spike pattern distributions (Fig. 4F, illustrative example). Thus we obtained a remapping of parameter space that allowed us to project the parameter vectors of each model onto eigenvectors and examine whether the observed changes between recordings happen along sloppy or stiff dimensions (see next section; Fig. 5D).

Figure 4.

The FIM of maximum entropy models reveals a sloppy parameter space for neural activity. A, For each model (left; diagonal elements are local fields, upper triangle represents interactions, lower triangle filled to visualize that couplings between neurons are symmetric) the FIM is computed (second left). FIM is a 55 × 55 matrix, as there are 55 independent parameters in the model, 10 fields, and 45 symmetrical interactions. Next, the FIMs eigenvalues and eigenvectors are determined (middle to right; arrangement corresponding to the arrangement of parameters). This example shows the same group of neurons recorded 18 h apart (top vs bottom row). Although the parameters differ, the two FIMs and their first two eigenvectors are almost indistinguishable. For these two models, D_JS(M₁|M₂) ≈ 0.007, r_E² = 0.99 for the principal eigenvector and r_Λ² = 0.61 for the parameters. B, Eigenvalues of the example two models (top) and fraction of FIM variance explained by adding consecutive eigenvectors (bottom). C, Gini coefficients for the FIM computed for nonsparse Ising models (homogeneous; local fields and interactions both drawn from normal distributions with mean 0.14, and variance 1/10 of fitted fields and interactions), independent models (matching the firing rates of the data), and from six datasets recorded at different time points (same preparation as A). D, The shape of average eigenvalue distribution across groups in the first recording of Culture 1, with SD in blue. Note, log scale used for the eigenvalues; the disparity between eigenvalues and fast saturation of explained variance both suggest that the models are sloppy. E, FIM variance explained by the principal eigenvector across all groups in each of the cultures (first recording only, as it is representative). F, The first five eigenvectors (scaled by eigenvalues relative to the first) of a random group of neurons from Culture 1 (top row), against first five eigenvectors of a random group of neurons from the toy homogeneous model (bottom row).

To further examine the parameter space anisotropy, and in particular to assess how many parameters were relevant to the stiff dimensions in our models, we turned to sparsity analysis. This was motivated by the fact that a FIM that is both sloppy and sparse indicates that the model is sensitive to only a small number of model parameters and their combinations. In contrast, a FIM that exhibits sloppiness but not sparseness indicates that the stiff dimensions involve more complicated combinations of many parameters. Therefore, as a measure of sparseness, we computed Gini coefficients (Hurley and Rickard, 2009) for each FIM. To provide a frame of reference, we also calculated Gini coefficients for sets of FIMs obtained from models without interactions and models with more homogeneous activity than the data. The first set came from maximum entropy models with null interactions and fields set to reproduce the firing rates of the data. This created much sparser FIMs than the data (Fig. 4C, “indep”), and provided an estimate of the upper limit of sparsity given the observed firing rates. The second set was from an Ising model with parameters more homogeneous than the fitted models (see Materials and Methods), to illustrate that sparsity is not an intrinsic feature of this model class. This resulted in very uniform FIMs (Fig. 4C, “homog”), reflecting a hypothetical scenario where all neurons' fields and interactions are very similar, and therefore little differentiation of sensitivity is expected. For our data-fitted models, the FIMs of all groups across all time points were always significantly sparser than those of the homogeneous models (Fig. 4C). This indicates that many parameters in our models do not contribute to sensitivity and therefore do not contribute to the stiff dimensions. This is illustrated in Figure 4F, where only a subset of parameters defines the principal eigenvector, in contrast to what occurs in a homogeneous model. On the other hand, a significantly lower FIM Gini coefficient compared with independent indicates that the sparsity is not simply due to a smaller number of parameters where the interactions are irrelevant.

Networks change faster along insensitive dimensions

Having established that our models of neural activity are sloppy, we then proceeded to examine whether sloppiness contributes to stability. First, a comparison of FIMs between recordings indicated that, despite substantial differences in model parameters and resulting observables, the sensitivities of the models remained relatively stable, with median coefficient of determination remaining >0.7 even for an interval of 92 h (Fig. 5A,B, compare with Fig. 3B,C; a case where the FIM is identical over an interval of 18 h is illustrated in Fig. 4A). At the same time, the activity of groups of neurons slowly changed over the recordings, an effect that clearly exceeded noise levels estimated by cross-validation or resampling from models (Figs. 3A, 5B), evident both in pattern distributions and FIMs. However, examining the projections of parameters onto the eigenvectors (Fig. 5D) revealed that the majority of changes between recording sessions occurred along the sloppy dimensions in parameter space (Fig. 5D). Scatterplots of parameter projection values from a given time point against the baseline (Fig. 5D, right) indicate that the projections onto stiff dimensions (blue) remain nearly unchanged, whereas the most pronounced changes are confined to projections onto the sloppiest dimensions. In line with this, the average (across groups) of the absolute projection changes clearly shows an increase with eigenvector rank (Fig. 5D, bottom).

To provide a complimentary view on the relationship between changes and sloppiness, and to be able to link parameter sensitivity to direct neural measures, we conducted further analysis, focusing on the stiffest dimension. Because the dominant eigenvector informs us of the relative contribution of individual parameters to the stiff dimension, and those contributions are sufficiently differentiated, we adopted the principal eigenvector entries (referred to as eigenparameters, v_ij) as sensitivity measures of corresponding parameters. We then analyzed the relationship between parameter sensitivity and changes in the activity, parameters, and eigenparameters of corresponding neurons. As shown in Figure 6A,B (top), the largest fluctuations consistently occurred along the least sensitive dimensions in model parameter space. These parameter changes were accompanied by corresponding changes in spike counts, which were stronger for insensitive associated parameters, at least for short intervals (Fig. 6A,B, middle). However, this relationship became less prominent after 2 d, suggesting that slow network remodeling took place. This is in line with decreasing similarity of model distributions (Fig. 3A) and FIMs (Fig. 5A,B), as these results indicate that on longer time scales increased remodeling takes place. To further understand this phenomenon, we also examined the behavior of eigenparameters over time. As for the parameters, here initially the changes occurred mostly in insensitive regions, but after the second day concerted and significant changes became apparent in sensitive regions as well (Fig. 6A,B, bottom). A comparison with shuffled data demonstrates that the trend we observe could not be explained by random effects (Fig. 6B, red lines), and modeling resampled data indicates no influence of uncertainties in parameter estimation from finite amounts of data (Fig. 6B, light green lines).

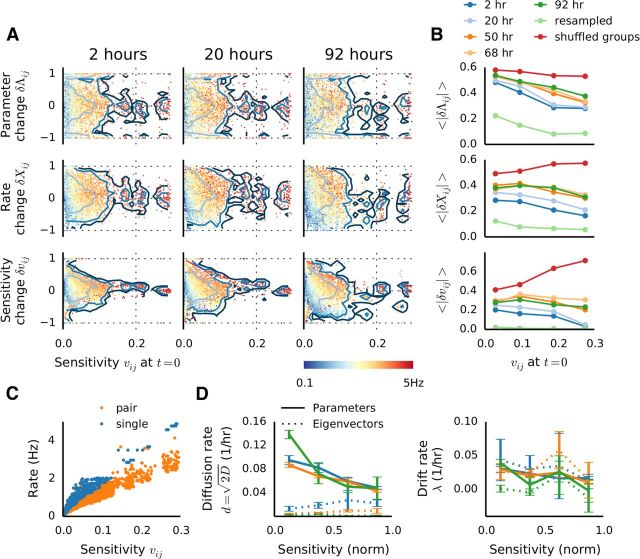
Figure 6.

Sensitivity to changes, high-firing neurons, drift and diffusion. A, Relative changes of model parameters (top, δΛ_ij), data marginals (middle, δΧ_ij) and eigenparameters (bottom, δv_ij) at different time points in one experiment, plotted as a function of the eigenparameters (which are used here as a measure of parameter sensitivity). Marginals were estimated as the spike counts and counts of coincident spikes. Relative changes were calculated as δ = (A₂ − A₁)/(|A₁| + |A₂|). Colors indicate the average firing rate of each neuron pair at the corresponding time points. Contour lines indicate 1, 2, and 3 SD. B, Degree of relative change of parameters (top), marginals (middle), and eigenparameters (bottom), expressed as the absolute mean of the distributions in C, as binned into quarters according to the sensitivity. For comparison, resampled data (light green) and shuffled data (dark red). C, The relationship between firing rate and sensitivity shows a clear dependence of sensitivity on the firing rate of corresponding neuron(s). D, Ornstein–Uhlenbeck model parameters estimated for the parameters (straight lines) and eigenparameters (dashed lines). Diffusion coefficients d (left) and drift constants λ (right) were estimated by fitting Var(ΔJ_ij)_Δt = $\frac{D}{\lambda }$ (1 − e^−2λΔt), where D is the diffusion constant and λ the drift rate. The curves were generated by dividing the sensitivity into four bins, and normalizing the range to enable comparison across recordings. Error bars indicate SEM of the least-squares fit.

Altogether, these results indicate that stability between recordings is associated with stability in sensitive neurons. Furthermore, we also found a tight positive relationship between parameter sensitivity and firing rates of the corresponding neuron pairs (Fig. 6A, colors, C); in all preparations, the correlation between those measures was >85%, and in most >91%. This implies that highly active neurons generally have a disproportionally strong influence on the collective network activity, much more so than functionally strongly coupled neurons, as there was no significant relationship between parameter sensitivity and correlations. We further explored the notion of high-firing units influence by conducting additional sparsity analysis. To this end, we again randomly sampled groups of neurons, this time however restricting the choice of units to those with firing rates >1 Hz. As shown in Figure 7E, FIMs of high-firing groups were significantly less sparse than those of random groups. This indicates that sensitivity is more uniform for groups comprised solely of highly active neurons.

Figure 7.

Spontaneous activity of in vivo neurons is sloppy and sparse. A, Example raster plot of spontaneous in vivo activity recorded from primary visual cortex of macaque monkey. B, Distributions of firing rates and correlations in the spontaneous cortical activity, compared with those of in vitro data (first recording, Culture 1). C, Jensen–Shannon divergence D_JS between model and the data, compared with same from in vitro data (first recording, Culture 1). D, Comparison of the average eigenvalue distributions (scaled to the first eigenvalue, averaged across all groups) between in vivo and in vitro models. E, Comparison of the distributions of model sparsity between different models. “Ind,” Independent model reproducing the firing behavior of in vivo data; “in vivo,” pairwise model fit to in vivo data; “in vitro,” example of pairwise model fit to in vitro data (first recording, Culture 1); “>1 Hz,” pairwise model fit to in vitro data filtered by firing to include only channels >1 Hz. F, Relationship between parameter sensitivity and the firing rate (“single” denotes the “field” parameter, “double” refers to the “interaction” parameter between two neurons; for a pair of neurons the firing rate is the average of the two).

Finally, to obtain a quantitative estimate of the rates of the parameter and eigenparameter fluctuations, we turned to their description by a mean-reverting stochastic process. Because their distributions were stable over time and the variance of their fluctuations closely approximated Var$\left(\frac{x_{t2}-x_{t1}}{\Delta t}\right)$∝(Δt)⁻² (not illustrated), an Ornstein–Uhlenbeck, which combines diffusion with a mean-reverting drift, is an appropriate model. This model has been used before to describe synaptic weight dynamics (van Rossum et al., 2000; Minerbi et al., 2009; Loewenstein et al., 2011), and enabled us to estimate quantities characterizing the fluctuations, and their dependency on parameter sensitivity.

We estimated the diffusion rate δ = $\sqrt{2D}$, where D is the diffusion constant, and the drift rate λ separately for the coupling parameters, and corresponding eigenparameters for four ranges of sensitivities. Consistent with the results shown so far, diffusion was fastest for insensitive and slowest for the most sensitive parameters (Fig. 6D, left, straight lines). In contrast, and consistent with the small effect of parameter fluctuations along sloppy dimensions, the diffusion rate for eigenparameters was significantly smaller (Fig. 6D, left, dashed lines). The drift rates, on the other hand, showed a weak dependency on sensitivity, were similar for parameters and eigenparameters, and consistently smaller than the diffusion rates, and are therefore likely associated with actual network remodeling (Fig. 6D, right).

Sloppiness and sparsity in vivo

The above analysis of in vitro recordings suggests sloppiness as a candidate mechanism contributing to stability in networks of neurons, organizing neuronal activity such as to not rely uniformly on all network parameters. However, although cultured neurons might reveal innate tendencies of self-organizing neural circuits, their activity is not representative of the activity observed in vivo (compare Figs. 7A, B, 1A, B,). Therefore, to test the relevance of our hypothesis for intact functional circuits, we performed additional analysis on 15 min spike-sorted spontaneous V1 activity recorded in vivo under light anesthesia from 140 isolated units in Macaca cyclopsis (Chu et al., 2014). We performed model fitting and FIM sparsity analysis following the same protocol as used for the cultured neurons. As illustrated in Figure 7C, model fits were very accurate in predicting the activity statistics, more so in fact than the in vitro maximum entropy models. This result likely reflects the effect of bursting observed in cultures, which leads to excess synchrony. We then computed the FIMs for each group and performed their eigenvector decomposition. The distributions of eigenvalues indicated that the models were sloppy (Fig. 7D), similarly to the models of cultured neuronal activity. However, as illustrated by the comparison of Gini coefficients of model FIMs (Fig. 7E), there was a significant difference in sparsity between the in vivo and in vitro data. As with model fit quality, this effect likely reflects the difference in synchrony between those two types of data, with cortical recordings being more asynchronous and spanning a wider range of firing frequencies. This asynchrony, however, was significantly different from what would be expected of an independently firing population (Fig. 7E). Thus it appears that in cortical networks fewer of the connections are significant than in cultures, and stiff dimensions are even more aligned with the original parameters. Finally, we investigated the relationship between firing rates and sensitivity of individual parameters. As illustrated in Figure 7E, the trend observed in cultures of high dependency of sensitivity on firing rates is preserved also in vivo. This would suggest that also in vivo the synaptic connections between highly active neurons are the most tightly regulated and most relevant for patterning the network activity.

Sloppiness and sparsity in simulated networks

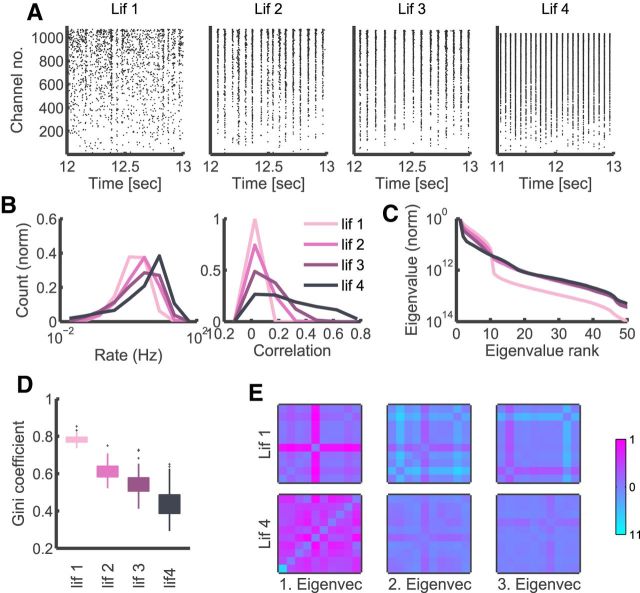
To further understand the interplay of sloppiness and sparsity in different models we also performed our analysis on simulated neural activity. We used randomly connected sparse networks of excitatory and inhibitory leaky integrate and fire neurons (LIF; see Materials and Methods for details) with increasing excitatory synaptic strengths, where the activity becomes progressively more correlated and synchronized (Fig. 8A,B). This analysis underscores the importance of examining not only how sloppy the spectrum of the decomposed FIM is, but also the sparsity of the matrix.

Figure 8.

Varying sloppiness and sparsity in simulated data. A, Example raster plots of the activity of four simulated LIF networks, “lif 1”–“lif 4”, in order of increasing excitatory strength. B, Distributions of firing rates and correlations in the four types of simulated activity. C, Comparison of the average eigenvalue distributions (scaled to the first eigenvalue, averaged across all groups) between models fit to four different types of simulated activity. D, Comparison of model sparsity between models fit the four different types of simulated activity. E, First three eigenvectors (scaled by eigenvalues relative to the first) of a random group of neurons from two different simulations, the least (“lif 1,” top row) and most (“lif 4,” bottom row) synchronous.

As shown in Figure 8C, increasing the synchrony in the simulated data results in eigenvalues that decrease rapidly in the first few ranks, and then flatten out. In contrast, less synchrony is associated with less prominent dominance of first eigenvector over others. This apparent anisotropy in dimensions in parameter space should not, however, be confused with reliance on few parameters only. Although the first eigenvector of the strongly correlated network is “stiffer” than for other simulated networks, it is not guaranteed to be sparse and have its sensitivity aligned with original parameter dimensions. In Figure 8D it becomes apparent that the trend is, in fact, the opposite. Comparison of Gini coefficients of model FIMs indicates that the more synchronous the activity, the less sparse the model FIMs are. An illustrative example in Figure 8E clarifies why this is the case. For the most synchronous LIF network, the activity of neurons is more homogeneous and all neurons exhibit very similar behavior. As a result, the stiff dimension is composed of a combination of nearly all individual parameters. In the least synchronous LIF network, neurons are on the other hand more differentiated and influence of some parameters is more prominent than others.

Although the LIF model was not intended here to reproduce the different types of data, only as a very simplified analogy, it provides interesting suggestions for interpreting our results and inspiration for further research. The decreasing sparsity in our LIF models (Fig. 8D) mimics the decreasing sparsity in the data (Fig. 7E, “in vivo,” “in vitro,” and “>1 Hz”). The accompanying increase in correlations both in LIF models (Fig. 8B) and in the data (Fig. 7B) falls in line with the expectation that increased synchrony between neurons will result in more uniform behavior and less differentiation in sensitivity. Because the LIF networks varied only in the excitatory connection strength, this suggests that the cultured neurons might exhibit stronger, on average, synaptic strengths than encountered in vivo. However, it has to be noted that the behavior of rates is different in the simulated data and in recordings, and more detailed and biologically realistic simulations are needed for firmer conclusions.

Discussion

Here we demonstrate that cultured hippocampal neurons and in vivo cortical networks are well described as sloppy systems. We present a novel framework for stability analysis in application to neurons, which combines two approaches, maximum entropy modeling (Schneidman et al., 2006; Ohiorhenuan et al., 2010) and FIM analysis (Machta et al., 2013). We further show that, in cultured neurons, the activity and coactivity of single neurons undergo considerable spontaneous fluctuations, and these tend to occur along sloppy dimensions in parameter space on the time scale of hours and tens of hours. In contrast, changes along stiff dimensions become prominent only at longer time intervals of days. Finally, we show that sensitivity to changes is highly correlated with firing rate, both in vitro and in vivo. Based on these results we propose that a relatively sparse subnetwork of stable highly active neurons could be supporting operational and possibly functional stability of neuronal networks (Mizuseki and Buzsáki, 2013; Cossell et al., 2015). At the same time, plasticity can take place along sloppy dimensions without compromising stability, thus equipping the network with considerable flexibility to remodel. This is, to our knowledge, the first evidence of sloppiness from models directly fit to neuronal data. Together with our findings on sparsity, this might be related to the anisotropy in neuronal representation reported by Hung et al. (2014). Moreover, these results mirror the degeneracy discovered in single neuron expression profiling indicating sloppiness also at the single neuron level (Schulz et al., 2006), which can result in significant flexibility in maintaining neural phenotypes (Prinz et al., 2004).

The particular choice of the parametric description of group behavior was motivated by the fact that pairwise maximum entropy models offer a meaningful, readily interpretable description of neuronal data. The fitted distributions capture the probabilities of binary spike patterns, and thus measure the capacity of the network to code information in those patterns. Furthermore, parameters correspond to local functional properties of neurons and their interactions. However, although the models exactly reproduce the pairwise correlations and individual firing, they fail to account for the full higher-order correlation and temporal structure in the activity (Ohiorhenuan et al., 2010; Yu et al., 2011), and tend to overestimate multineuron firing probabilities (Tkačik et al., 2014). Although we obtained good fits that could account for a large fraction of the correlation structure (Fig. 3B), the small networks used here are not informative about the relative importance of higher-order interactions in the full circuit (Roudi et al., 2009). Yet inferences about higher order structure in an entire population are generally limited, both computationally, because probability distributions grow exponentially with the number of neurons, and by the availability of data, particularly in the case of sparse activity as observed here. Although full analysis for bigger group sizes is not feasible, it is still possible to compute FIMs directly from the data correlations (see Materials and Methods). A comparison of different group sizes up to 40 neurons showed no systematic differences to the results reported here (not illustrated); we note however, that this data-driven approach implicitly ignores the problem of higher-order correlations, and therefore it can only be viewed as an extension of our results. It is an interesting question whether the same approach could be exploited to narrow down the parameter space and aid the interpretation of larger spatiotemporal models (Marre et al., 2009; Cofré and Cessac, 2014).

Our findings are in part based on analysis of spontaneously active and randomly wired cultured networks, which enabled us to reliably and repeatedly perform simultaneous recordings from hundreds to thousands of neurons with high spatial resolution. This served to avoid the sampling bias expected from conventional recording methods, where typically neurons with low activity are not reliably detected and the very few highly active neurons are undersampled (Mizuseki and Buzsáki, 2013; Wohrer et al., 2013). Moreover, the use of cultured preparations allowed us to reliably track single neurons over days, which was crucial for the purpose of assessing individual fluctuations. While different from the highly structured networks of the cerebral cortex or hippocampus, cultures on the other hand provide insight into the innate properties of self-organized circuits. To test the generality of our findings, we also analyzed an in vivo recording from the visual cortex and confirmed the presence of sloppiness and sparsity in functional networks. Thus, our results suggest that sloppiness and sparsity could be basic inherent properties of neural networks, which are also used as needed in the intact brain. Whether fluctuations over time follow the same principles we discovered in cultured neurons has to be investigated in stable long-term in vivo recordings.

In parallel to observations from cultures (Maletic-Savatic et al., 1999; Okabe et al., 1999; Minerbi et al., 2009), the adult cortex appears to slowly, but continuously remodel its connectivity with variable rates (Trachtenberg et al., 2002; Holtmaat et al., 2005). These changes resemble our observation that the rate of change of the coactivity of single neurons varied substantially. Furthermore, in vivo imaging has shown that spine size fluctuations could be modeled as an Ornstein–Uhlenbeck stochastic process (Loewenstein et al., 2011), which could also account for changes in our data. It is, however, unclear to what extent functional and structural connectivity are related, so more pertinent are the examples from a functional perspective. First, chronic recordings in motor cortex also revealed changing firing rates of individual neurons over the course of days, which however had little influence on decoding performance (Chestek et al., 2007). Second, chronic imaging showed that selectivity of place cells is not generally, but only in subsets of neurons, stable over time, but decoding from the population was again stable over time (Ziv et al., 2013). Both of these studies are consistent with our finding that single neurons can change their activity substantially along insensitive dimensions, without significantly influencing the population activity. Finally, chronic imaging has shown that a small fraction of highly active and selective neurons in barrel cortex were particularly stable over time (Margolis et al., 2012), resembling our finding that highly active neurons and neuron pairs had the highest parameter sensitivity and exhibited only slow remodeling. Together, these results are consistent with the hypothesis that few highly active neurons are critical for stable functional representations.

Thus, although neural coding is typically sparse and distributed and relies on neurons with low activity and high selectivity, the collective functional representations might be held stable by a backbone of highly active, functionally interacting, and perhaps less-selective neurons (Mizuseki and Buzsáki, 2013). Our results predict that these stiff neurons have higher spontaneous rates, and their synapses are less susceptible to plasticity. Such neurons may correspond to a relatively small number of “choristers,” which preferentially respond to stimulus categories in primate IT (Hung et al., 2014), and may inherit correlations through direct synaptic contacts (Cossell et al., 2015). Because these neurons play an important role in shaping the overall pattern repertoire of the circuit, changes in their connections are predicted to have a disproportionally large influence on the network response. The remaining sloppy neurons (the “soloists”), on the other hand, are likely much more susceptible to plasticity, and may change their activity more rapidly, for instance to explore a large region of parameter space without a strong effect on collective dynamics and stability. What mechanisms underlie these differences is not clear; a possibility is the weaker LTP reported in neurons with stronger background conductances (Delgado et al., 2010), which may be present in the more highly active stiff neurons. We speculate that this flexibility increases the ability of networks to learn or adapt to novel inputs, because it opens paths between regions in parameter space that would be unavailable in networks with a uniformly high-parameter sensitivity. This form of enhanced evolvability through exploitation of sloppy parameter space domains may be a general property of biological systems (Daniels et al., 2008).