Shared Sensory Estimates for Human Motion Perception and Pursuit Eye Movements

Abstract

Are sensory estimates formed centrally in the brain and then shared between perceptual and motor pathways or is centrally represented sensory activity decoded independently to drive awareness and action? Questions about the brain's information flow pose a challenge because systems-level estimates of environmental signals are only accessible indirectly as behavior. Assessing whether sensory estimates are shared between perceptual and motor circuits requires comparing perceptual reports with motor behavior arising from the same sensory activity. Extrastriate visual cortex both mediates the perception of visual motion and provides the visual inputs for behaviors such as smooth pursuit eye movements. Pursuit has been a valuable testing ground for theories of sensory information processing because the neural circuits and physiological response properties of motion-responsive cortical areas are well studied, sensory estimates of visual motion signals are formed quickly, and the initiation of pursuit is closely coupled to sensory estimates of target motion. Here, we analyzed variability in visually driven smooth pursuit and perceptual reports of target direction and speed in human subjects while we manipulated the signal-to-noise level of motion estimates. Comparable levels of variability throughout viewing time and across conditions provide evidence for shared noise sources in the perception and action pathways arising from a common sensory estimate. We found that conditions that create poor, low-gain pursuit create a discrepancy between the precision of perception and that of pursuit. Differences in pursuit gain arising from differences in optic flow strength in the stimulus reconcile much of the controversy on this topic.

Introduction

The mammalian brain interprets widespread cortical activity to derive information about the environment that can be used to generate perceptions and actions. We wondered how sensory estimates for movement behavior and perception are decoded and communicated within the brain. One possibility is that sensory activity is decoded centrally and then passed to multiple processing streams. Another possibility is that decoding is accomplished by the multiple recipients of sensory activity themselves, perhaps in the very interconnections between areas, and thus might be private to different processing streams. Testing these hypotheses requires interrogating sensory estimation through the behaviors that it generates. In cases in which motor behavior is a loyal readout of a sensory signal, we expect that shared sensory estimates should give rise to covariation in movements and perception. If sensory estimates for perception and action are formed independently, then there is no reason to expect covariation above chance. Here, we explored the nature of sensory representation by analyzing both perceptual reports and sensory-driven movement behavior in human subjects.

Our approach was to compare perceptual reports with smooth pursuit eye movements. Pursuit is a tracking behavior, initiated by retinal image motion, which rotates the eyes to stabilize the image of a moving target (Rashbass, 1961). Two factors make pursuit an excellent test bed for this investigation: (1) the eye movement is initiated from feedforward visual estimates of target direction and speed (Rashbass, 1961; Lisberger and Westbrook, 1985; Tychsen and Lisberger, 1986; Krauzlis and Lisberger, 1994) and (2) fluctuations in eye velocity during this “open-loop” interval appear to be dominated by errors in motion estimation (Osborne et al., 2005, 2007; Stephens et al., 2011).

Motion information is shared between perceptual and motor processing streams. The middle temporal cortical area (MT) provides visual inputs for the initiation of pursuit via a descending pontine pathway to the cerebellum, as does the medial superior temporal area (MST) (Newsome et al., 1985; Komatsu and Wurtz, 1988; Komatsu and Wurtz, 1989; Groh et al., 1997; Born et al., 2000; Ilg and Thier, 2008; Mustari et al., 2009). MT also mediates motion perception (Britten et al., 1996, Zohary et al., 1994; Liu and Newsome, 2003) and it projects to parietal association areas such as the lateral interparietal area (LIP) that are not known to contribute to presaccadic pursuit initiation (O'Leary and Lisberger, 2012). Several LIP/MT comparison studies support a distinction between sensory and perceptual activity. For example, Assad and colleagues found that MT responses were most strongly correlated with fluctuations in the visual stimulus, whereas LIP activity was most strongly correlated with the monkey's response regardless of whether that response correctly or incorrectly reported the stimulus (Williams et al., 2003). The implication is that, whereas many cortical areas carry information about sensory stimuli, downstream activity may be more strongly related to behavioral outcome. We compare variation in visually driven pursuit with perceptual variation within subjects, testing the hypothesis that upstream sensory estimates are shared between perception and action pathways. Our findings reconcile differing results from past inquiries into the relationship between motion estimates in eye movements and perception.

Materials and Methods

Data acquisition

Eye movements and perceptual reports were recorded in five human adult subjects (three male, two female) with normal or corrected-to-normal vision following procedures approved in advance by the Institutional Review Board of the University of Chicago. All subjects (identified by their initials: T.M., M.B., A.C., C.S., and G.Z.) provided informed consent and three of the subjects were authors (T.M., M.B., and C.S.). All but one subject (C.S.) were initially inexperienced with tracking but received substantial practice by study conclusion. Subjects were seated in a dimly lit room in front of a CRT display (100 Hz at 1024 × 768 pixels, 32.38° by 21.02°) at a viewing distance of 60–85 cm. To minimize contamination from head movement, subjects used a personalized bite bar and forehead rest. A Dual-Purkinje Infrared Eye Tracker (Ward Electro-Optics, Gen 6) provided an analog output proportional to horizontal and vertical position of the right eye with 1 arcminute resolution and a 1 ms response time. Tracker output was passed through an analog filter/differentiator that output signals proportional to eye position and low-pass filtered signals proportional to eye velocity at frequencies <25 Hz with a 20 dB/decade roll-off. Position and velocity signals were sampled at 1 kHz and the digitized data stored. Perceptual reports were indicated by a button press that generated a voltage signal that was stored along with the eye movement record. We used Maestro version 2.5.2 (https://sites.google.com/a/srscicomp.com/maestro/home), an open-access visual experiment control application (S. Ruffner, S. Lisberger, developers), to control stimulus display and data acquisition. Experimental sessions typically lasted 30–45 min with breaks. During each session, subjects would perform ∼500 trials that were each 2–3 s in duration. Before analysis, each pursuit trial record was inspected visually. We excluded trials if a saccade or blink occurred within the time window chosen for analysis, the tracker lost its lock on the eye signal during the trial, or eye velocity during the initial fixation interval exceeded 2°/s. Datasets, pooled across sessions, consisted of eye velocity responses to at least 60 and typically >100 repetitions of target motion for each condition for a total of ∼1000 trials.

Experimental design

Pursuit experiments.

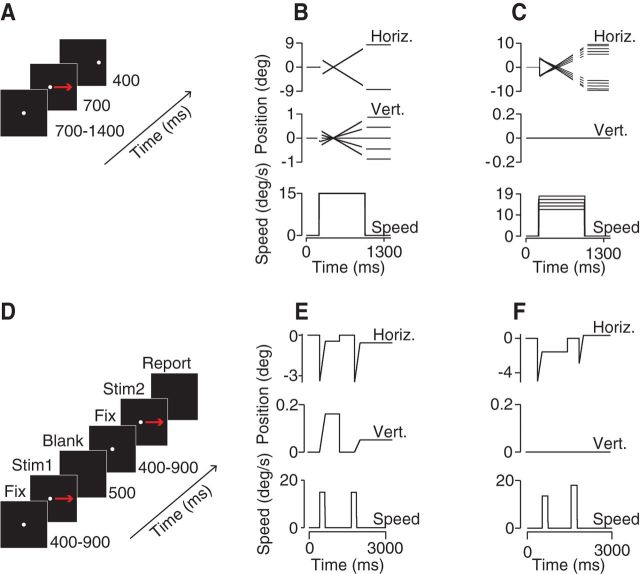
Pursuit experiments consisted of a set of trials each representing a single target form and motion trajectory. Each trial included an initial fixation interval, a pursuit interval, and a final fixation interval. To minimize anticipatory eye movements, we randomized the initial fixation duration by 700 ms and presented target directions (and/or speeds) in a pseudorandomly interleaved fashion such that blocks of trials had equal frequencies of the different target motions. Target directions were always balanced about the origin, including leftward and rightward motions and upward and downward components on direction discrimination tasks. The typical task design for pursuit experiments is shown in Figure 1, A–C. Trials began by fixating a central spot target for a random interval, typically 700–1400 ms, of which the last 200 ms were recorded. The fixation point would then extinguish and the target would appear ∼3° eccentric to screen center (varied for each subject) and then immediately move toward the former position of the fixation point with a constant direction and speed. The size of the position step was chosen for each subject to minimize the frequency of saccades in the first 250 ms of pursuit. For pursuit experiments, target motion continued for at least another 700 ms, after which time the target jumped by 1° along the direction of motion and stopped for a final fixation interval of 400 ms.

Figure 1.

Motion discrimination tasks. A, Schematic representation of events during a pursuit trial sequence. B, Pursuit direction discrimination task. Top, Horizontal target position. Middle, Vertical position. Bottom, Target speed over time. C, Pursuit speed discrimination task. Shown are the target position and speed components over time. D, Perception (2AFC) discrimination task. Subjects reported whether a second motion interval was CW/CCW (faster/slower) than the first. E, F, Target motion over time in a perceptual direction discrimination task (E) and a speed discrimination task (F).

For pursuit direction discrimination experiments (Figs. 1A,B, 2A,B), target directions ranged from −9° to +9° from rightward or leftward in 3° increments. Target speeds were typically 10–15°/s, but ranged from 4 to 30°/s as noted in the text. For pursuit speed discrimination experiments, targets moved left and right and target speeds were spaced by 10% increments around a base speed of 10 or 15°/s (Figs. 1C, 2C).

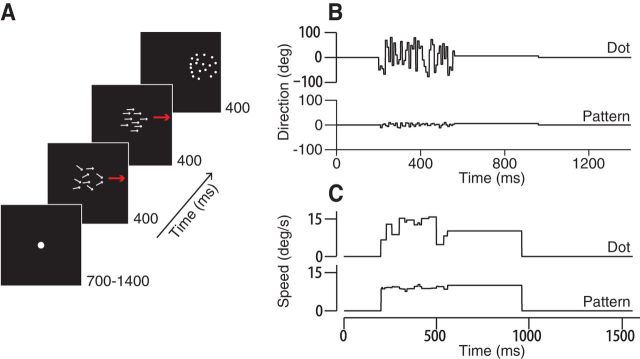
Figure 2.

Spatial-temporal noise targets and experimental design. A, Schematic representation of the “noisy dots” pursuit direction discrimination task. The dots move with a fixed speed but different directions, randomly chosen anew at each update interval. Trials consisted of a fixation interval, a noise interval, a coherent motion interval, and a final fixation interval. B, Direction noise targets. Top, Direction of a single dot over time. Bottom, Average direction of all dots in the pattern. Dot speeds are uniform and constant. C, Speed noise targets. Top, Speed of a single dot over time. Bottom, Average speed of all dots. Dot directions are uniform and constant.

Perception experiments.

Perceptual discrimination experiments (Fig. 1D–F) were configured as two-alternative forced choice tasks to try to recreate the sensory discrimination required in the pursuit task while not providing extraneous cues. After a randomized fixation interval, two stimuli were presented sequentially with a 500 ms blank period designed to minimize any phosphor persistence from the previous stimulus (Fig. 1D–F). Otherwise, target forms and motions were identical to the companion rightward pursuit tasks except that coarser and finer spacing in target motions were required to produce good psychometric curves for threshold estimates. For direction discrimination tasks, additional directions were added to create angular spacing from 0 to 8°. For speed discrimination tasks, target speeds differed by 0,1, 1.5, 2.25, 3, 3.75, up to 10°/s. Subjects indicated by a button press whether the second stimulus was clockwise or counterclockwise (or faster/slower) relative to the first. Motion duration for both direction and speed perceptual discrimination tasks was randomized by ±10 ms of the desired time. An additional design change was made to the speed discrimination task to minimize the use of nonmotion cues. The target starting position was randomized within 3°.

Combined pursuit-perception task.

We used a task design quite similar to our perception-only task to measure pursuit and perceptual judgment of target direction on the same trial. After a random fixation interval of 800–1600 ms, a spot target underwent step-ramp motion to translate at 15°/s. The target moved for 450 ms and was then extinguished. There was a brief blank interval, followed by another fixation interval and a motion interval with the same durations. After the second motion interval, the subjects indicated by button press whether the second direction was clockwise or counterclockwise with respect to the first. Targets moved leftward or rightward on each trial, randomly interleaved. Target directions were within −6° to +6° of horizontal with 1° spacing. The first motion segment was either horizontal or ± 3°. Using the dataset as a whole (all directions), we corrected any vertical bias arising from calibration errors before analyzing eye movements. Trials with saccades during open-loop pursuit (before 240 ms after pursuit onset) were excluded from analysis. We found that eye direction stabilized well before the close of the open loop interval (see below). We therefore could recover eye direction on single trials by fitting a line through the vertical eye velocity time vector during fixation and another line through the last 50 ms of the open loop interval. We used the angle formed by these lines as the eye direction for that motion interval on that trial. The difference in eye direction between the two motion intervals was converted to a sign value (upward/downward) to compare with the perceptual reports.

Measurement of open-loop interval.

We performed experiments with two subjects to estimate the duration of the open-loop interval, the period after pursuit onset when pursuit is driven by visual inputs alone. Subjects pursued spot targets in the step-ramp paradigm as described above, but we randomly interleaved trials in which we kept the motor control loop open electronically by adding eye velocity to target velocity (Lisberger and Westbrook, 1985; Osborne et al., 2007). Until pursuit begins, the target velocity and retinal image velocity are identical on both the stabilized and normal trials, but when the eyes begin to move, the retinal image velocity falls in the normal trials but remains constant in the stabilized trials. The point at which the pursuit responses to the two trial types diverge indicates the point at which altered visual input affects the eye movement. This is a lower bound on the time interval when extraretinal signals contribute to pursuit.

Visual stimuli.

Visual stimuli were bright, high-contrast targets presented against the dark background of the CRT display. We focused on two different target forms, spot targets and random dot kinetograms. The spot targets were uniformly illuminated circles of 0.25° diameter. The random dot kinetograms were randomly drawn “dots,” typically 3 adjacent pixels illuminated at full intensity within a circular aperture sized from 2 to 10° in diameter. We refer to these as “pattern” targets when the motion is fully coherent and each dot moves with the same direction and speed. Dots and aperture translated together with the same vector velocity such that the stimulus looked like a pattern that simply translated across the screen.

Noisy dots stimuli.

We used a second type of random dot kinetogram target modeled on those developed by Williams and Sekuler (1984) and used by Watamaniuk and Heinen (1999) and others. We refer to these targets colloquially as “noisy dots” targets (Osborne et al., 2007). The noisy dot target had a 5° diameter circular aperture with 100 “dots,” trios of adjacent illuminated pixels presented against the dark background of the screen. Each dot in the pattern had a fixed vector velocity plus an added stochastic perturbation in either direction or speed that we generated every 40 ms. For direction discrimination experiments, each dot had a fixed speed and time-averaged direction of motion, but each dot's instantaneous direction changed every four frames when we updated the stochastic direction value independently for each dot in the pattern. The distribution of dot directions around the mean was uniform within the selected range with 1° spacing. Therefore, for four frames (40 ms), each dot was painted to move smoothly along a different direction and, on the subsequent frame, the dice are rolled again to update each dot's direction. If a dot's updated position were to fall outside of the aperture, it would be randomly repositioned along the opposite edge of the aperture. We avoided conditions in which dots could move in directions opposed to the aperture direction. The greater the range of dot directions, the slower the apparent motion of the pattern along the mean direction. Slower translational motion of the pattern lowered eye speed during pursuit, a potential confound for our study. We therefore increased dot speed slightly in order for the dots pattern to move at the same apparent speed as the aperture and, importantly, to maintain the same eye velocity throughout the analysis period for every direction noise level. We found that the expected correction by the cosine of the dot direction range worked well. To ensure that variation in pursuit and perception arose from internal sources rather than trial-to-trial differences in stimuli, we fixed the seed of the random number generator from which dot directions (or speeds) were chosen. Therefore, the dots moved in the same way on every repetition of a given target trajectory. Noisy dots target motion followed the same step-ramp task design that we used for spot targets. In some experiments, we initiated dot motion within a stationary aperture for 160 ms before starting to move the aperture with the dots for the rest of the trial. This created a brief interval when the texture moved behind a stationary window, followed by a translating stimulus. Our analysis interval was chosen to ensure that we measured the response to dot motion rather than aperture motion when the dots started moving within a stationary aperture. We found no difference in the data between immediately translating and briefly stationary aperture conditions.

We also created “speed noise” targets in which all dots moved in the same direction, but dot speeds ranged logarithmically about a central value. The speed of each dot, S, at each update step was chosen by S = S₀ · 2^x/E, where S₀ is the mean speed of the target and x is a random value drawn from a uniform distribution from −N to N with a granularity of 0.05; to obtain different ranges of speed noise, N took on values from 0 (no noise) up to 7 in integer steps. E represents the expected value of 2^x given by ∑_xp(x)2^x where p(x) is the probability of each value of x. The average value of the individual dot and pattern speed approached S₀ after sufficient time steps. We updated each dot's speed independently every 40 ms, as we did for the direction noise targets. Like the direction noisy dot targets, the speed noise targets had a 5° circular aperture with 100 dots.

Motion cloud stimuli.

We used an additional type of motion stimulus, “motion clouds,” which had a limited Fourier bandwidth. Task design was the same as for other target forms. In a previous study, these stimuli produced differing changes in sensitivity (1/σ) in eye movements and speed perception (Simoncini et al., 2012). Motion clouds are a class of band-pass-filtered white noise stimuli (Schrater et al., 2000; Leon et al., 2012). In Fourier space, the envelope of the filter is a Gaussian in the coordinates of the relevant perceptual axis, which in this study is direction. The stimulus is fully characterized by its mean spatial and temporal frequencies (Sf₀ and Tf₀) and bandwidth (B_sf). Therefore, a given image (I) is defined by the following equations:

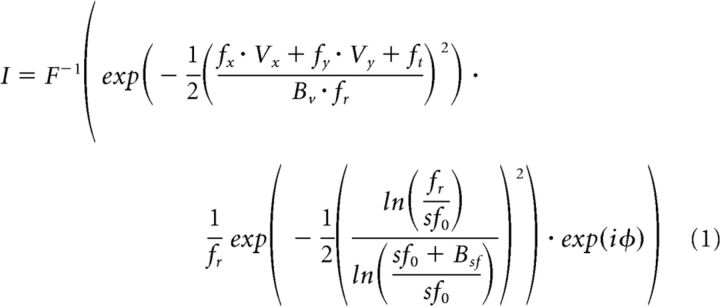Where F⁻¹ is the inverse Fourier transform, v = (v_x, V_y) is the central motion, fr = $\sqrt{f_x^2+f_y^2+f_{xt}^2}$ is the radial frequency, and φ is a uniformly distributed phase spectrum in (0,2π). This equation acts as a filter on a random Gaussian grayscale texture that is generated anew each frame. We parameterize bandwidth by the envelope's SD. Central Sf₀ and Tf₀ were set to define a mean speed V = (Tf₀/Sf₀) of 20°/s. We defined the Gaussian envelope on a logarithmic frequency scale and used three different B_sf values (0.1, 0.4, or 0.8 cpd) with the same mean Sf₀ (0.3 cpd). The motion stimulus was presented in an 18° diameter aperture that remained stationary for 200 ms and then translated across the screen with the motion cloud. Base directions for the discrimination task were rightward and leftward.

Analytical methods

Pursuit threshold calculation.

To analyze the precision of direction and speed discrimination in pursuit and perception, we computed thresholds based on the signal-to-noise ratio (SNR) in the responses to different target motions. We used the same approach used in previous analyses of nonhuman primate pursuit to give the most complete and statistically stable estimates of threshold (Osborne et al., 2007). We repeat the essential features of those methods here.

First, we aligned trial data on pursuit motion onset, the average latency for each target condition. In our data, eye velocity is a vector with horizontal and vertical components of length T where each element is spaced by 1 ms. In the direction discrimination experiments, target motions were concentrated near the horizontal and so the vertical components of target velocity dominate direction discrimination. In speed discrimination experiments, the vertical velocity is negligible and differences in the horizontal velocity components dominate speed discrimination. Therefore, we were able to simplify the eye velocity response as a collection of T time points of the appropriate component: s⃗ = {s_i} where i indexes time.

For each speed (v) and direction (θ) of target motion within an experiment, we subtracted the average signal across trials for that target motion 〈s⃗(θ, v)〉 from the eye velocity on each trial s⃗(θ, v) to form an eye velocity noise vector, δs⃗ = s⃗(θ, v) − 〈s⃗(θ, v)〉. We found that the noise statistics did not change over the range of directions and speeds that we tested. We could therefore use noise vectors from all trials to estimate the covariance matrix of fluctuations about the mean eye velocity vector in time as follows:

Where i and j index points in time and 〈…〉 denotes an average over all trials.

Although the covariance matrix describes the noise in pursuit, the signal is defined by the difference in the trial averaged velocity vectors for each pair of target motions. We represent the mean eye velocity signals at a given time (i) for target motion of a given direction (θ) and speed (v) as m_i(θ, v) = 〈s_i(θ, v)〉. We define the signal-to-noise ratio for discrimination between, for example, two different target directions θ and θ′ as follows:

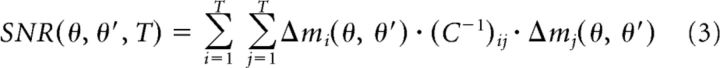Here, C⁻¹ denotes the inverse of the covariance matrix, i and j index time, and Δm_i(θ, θ′) = m_i(θ) − m_i(θ′) indicates the difference in the mean eye velocity at time i for target motion in two different directions.

Equation 2 is the definition of the SNR, but in practice, computing the inverse of the full covariance matrix could introduce errors arising from the finite size of our datasets. To minimize these errors, we reduced the matrix dimensionality. We found, as we had in previous work with nonhuman primate pursuit, that the covariance matrix of human pursuit noise is well represented by three dominant modes that together account for >90% of velocity variation (Osborne et al., 2005). We therefore approximated the inverse covariance matrix as follows:

Where v⃗_μ are the eigenvectors that correspond to the three largest eigenvalues, λ_μ. The use of a covariance-based method for SNR calculation provided the most stable estimates of threshold over time (Osborne et al., 2007).

In experiments with targets moving in different directions, the angular difference between motions was small and our data showed that eye direction by the end of the open-loop interval rotated nearly perfectly with the target direction such that Δm⃗(θ, θ′)∝θ − θ′. Given Equation 2, this predicts a relationship that we also found experimentally, namely that the signal-to-noise ratio for pairs of angles (θ, θ′) scales as the square of the angular separation of the pair as follows:

Where K_θ(T) is a function of time that does not depend on the pair of angles. We used this relationship to rewrite the SNR as an effective threshold for reliable discrimination of target direction from the eye movement vector, defining threshold as the direction difference |θ − θ′| = Δθ_thresh(t) that would generate SNR = 1 (equivalent to 69% correct in a two-alternative forced choice paradigm) as follows:

Similarly, for small differences of target speed about some reference speed v₀, we find that the difference in the mean pursuit response for two target speeds scales with fractional target speed (Weber's Law): Δm⃗(v, v′)∝(v − v′)v₀. Therefore:

and

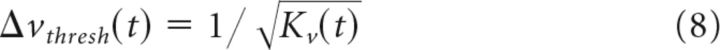Where Δν_thresh(t) is measured as a fraction of the base speed and K_v(T) is a function of time that does not depend on target speed. Applying these equations to the data sample, we computed the SNR for each pair of target motions. In practice, SNR values varied across different motion pairs with the same spacing and we used the SD of those values to compute the uncertainty in our threshold measurements for pursuit.

Perceptual threshold calculation.

To estimate a perceptual threshold for motion discrimination, we recorded subject's reports in a two-alternative forced choice (2AFC) task in which they indicated whether a second stimulus was clockwise (CW) or counterclockwise (CCW) (or faster/slower) than the first (Fig. 1D–F). We measured the percentage of correct responses as a function of motion parameter difference (direction or speed) for each subject. Stimuli included rightward trials and the motion directions of the pursuit experiments, with additional directions added as needed to produce a well defined psychometric curve. We then used probit analysis (Finney, 1971; Lieberman, 1983; McKee et al., 1985), a maximum likelihood regression method that minimized the χ² error between the sigmoid fit and the data, to find the parameters of the underlying cumulative normal distribution, φ(μ,σ) that best described the percentage of correct responses as follows:

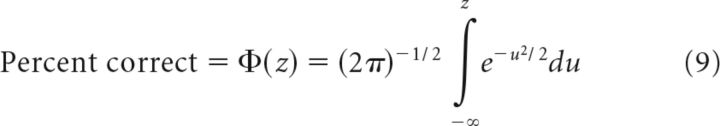Where z = (x − μ)/σ is the z-scored stimulus data and u is a dummy variable representing the direction difference. Specifically, we used the negative log-likelihood MATLAB function negloglike in an unconstrained nonlinear error minimization search fminsearch to return the mean and SD of the distribution φ. We defined threshold as σ/√2 where the √2 normalization arises from the fact that two stimuli were observed to make the judgment (Krukowski and Stone, 2005). This yields a 69% correct performance at threshold, which is in agreement with the pursuit threshold analysis.

Optic flow score.

In addition to the targets described above, we collected limited data using a variety of different target forms (see Results) for which we observed differences in eye acceleration, pursuit gain, and therefore threshold value. To account for these differences, we quantified the total optic flow for each motion stimulus. We used an algorithm based on Sun et al. (2010) that computes a vector field describing the translations of pixels from one frame to the next. We created 1024 × 768 pixel, 100 Hz frame rate videos for each target type and ran the algorithm on each video to generate a scalar flow value for each experiment. For all but one of our targets, the pixels were either on or off and moved at a constant speed, so the optic flow was simply the fraction of illuminated pixels per frame times pixel speed summed over frames. For a drifting Gabor sine wave grating target, which was presented with background illumination as in Gegenfurtner et al., 2003, the flow is the speed-weighted difference in pixel intensity with respect to the background for each pair of frames normalized by the total pixel number. We quantified the flow in degrees/s for the first 200 ms of target motion, corresponding to our analysis window.

If we used this metric of optic flow alone, then a random dot pattern moving within a stationary aperture would have the same flow value as a dot pattern that translated across the screen at the same speed. To distinguish translational from nontranslational target motion, we also computed the center of mass (COM) motion to include in the optic flow score. We computed the COM position in each frame by spatially averaging the location of each illuminated pixel. We computed COM motion speed from the position values across frames, converting to degree/s.

We defined a total optic flow score by adding the pixel flow and COM flow values. For example, a target comprised of a 2° nontranslating aperture and 8 3-pixel dots moving at 10°/s has a total optic flow score of 7°/s, whereas a 0.25° spot target translating at 15°/s has a total flow score of 150°/s.

Simulations.

To explore the behavior of single decoder versus coupled decoder models with respect to the correlation of the two behavioral outputs, pursuit and perception, we created two simple models. Because our goal was not to test decoding models per se, nor to account for the threshold values we observed, we did not use spiking, feature-selective model neurons as a starting point. Rather, we modeled a population of units that each provided an estimate of the motion direction. Direction estimates were drawn randomly from a Gaussian distribution with an SD of 15–30° to match MT experimental data (Osborne et al., 2004) and had a mean equal to the actual target direction. We simulated a uniform level of neuron-neuron stimulus conditioned (noise) correlations, ρ(neuron − neuron|θ, v), where ρ is the Pearson correlation coefficient for the covariance in direction estimates for each pair of neurons, ρ = $\frac{\mathrm{cov}\left(\Delta \theta \left(neuron1\right),\Delta \theta \left(neuron2\right)\right)}{{\sigma }_1{\sigma }_2}$, Δθ is the fluctuation from the mean direction for that neuron and trial, and σ is the SD of the direction estimate. Our idealized decoder simply averaged direction estimates across the population. We could set the output variance of the decoder by changing population size and the level of noise correlation, but our results comparing correlation between the behavioral outputs did not depend on matching the model variance to experimental data.

For the dual decoder model (see Fig. 8D), we created two populations with equivalent within-population noise correlations and unit direction variances. We simulated different levels of both between-population correlation and within-population correlation using the MATLAB function mvnrnd (The Mathworks). In this model, no other noise was added. The output of each decoder was converted to a sign value (up/down) and then the fraction of sign agreement was computed. The conversion was necessary to compute correlations between binary perceptual reports and eye movements.

Figure 8.

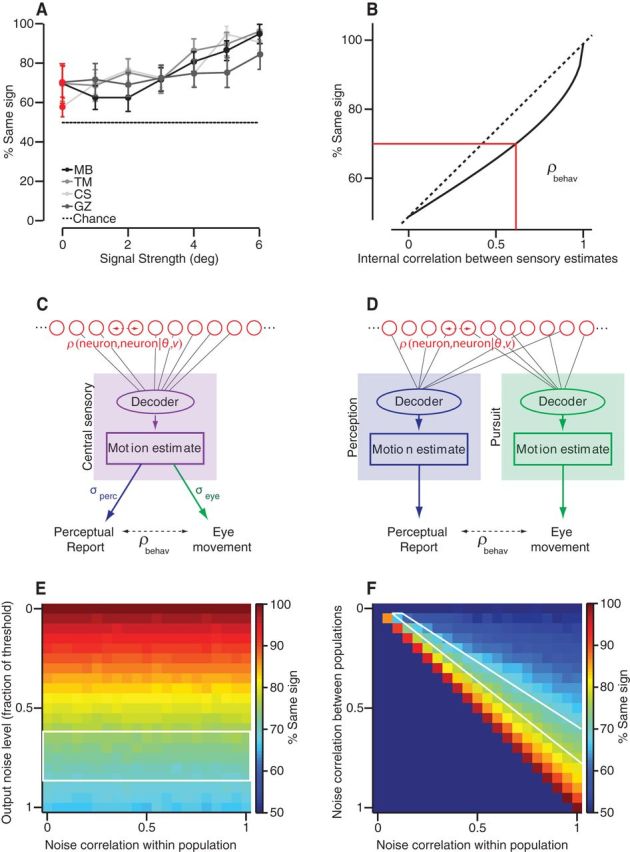
Correlation of direction estimates between pursuit and perception, data and model. A, Percentage of trials for which perceptual reports had the same rotational sign as the pursuit eye movement plotted as a function of the absolute direction difference between stimuli. B, Relationship between percentage sign agreement and the underlying correlation between perceptual report and eye movement. C, D, Conceptual models representing two decoding schemes for neural population activity to derive target direction estimates for perception and pursuit. Red circles represent inputs from a homogeneous sensory population with equal variance direction estimates and a uniform level of noise correlation. Decoders average direction estimates. C, A single decoder (purple box) forms a direction estimate that is shared between perceptual and pursuit processing streams. Each stream adds noise independently to its output (σ_E, σ_P). D, Two identical decoders (blue perception, green pursuit) estimate target direction from two closely related populations (identical variance and within-population noise correlations as in C); between-population correlations vary. No additional noise was seen. E, Percentage sign agreement expected from the model in C. Data are plotted as a function of the noise correlation within the neural population and the output noise level as a fraction of the decoder threshold. F, Percentage sign agreement in behavioral outputs from model in D. Data are plotted with respect to within- and between-population levels of noise correlation.

The single decoder model (Fig. 8C) had one decoder (as above) such that direction estimates were formed upstream of the split between perception and pursuit pathways. We then added independent random variables to each behavioral output with equivalent variance. We simulated different noise levels in terms of fractions of the variance in the direction estimate. Calculation of the fractional sign agreement across simulated trials was identical to the twin decoder model.

Results

The visual activity driven by a target moving in the visual field creates perceptual awareness and becomes the drive for pursuit eye movement. Even under carefully controlled conditions, the perceptual report of that motion and the eye movement it elicits will differ each time it is presented. We exploited that variation to investigate the relationship between sensory estimates for perception and for motor behavior. The internal estimate of the target's movement arises from image slip on the retina. The pursuit system responds to that slip by smoothly accelerating the eye until it approximately matches the target's direction and speed, stabilizing the retinal image. Before pursuit begins, retinal image motion is substantial, giving rise to estimates of target direction and speed that guide the subsequent eye movement. Although, on long time scales, pursuit operates as a closed-loop, negative feedback system in which residual retinal image motion is minimized to keep the eye on the target (Lisberger et al., 1987), the initiation of pursuit is under open-loop control, arising from feedforward sensory estimates of target motion begun during the latency period (Lisberger and Westbrook, 1985). The duration of the open-loop interval provides an appropriate time scale over which to compare visually driven pursuit and perceptions of target motion arising from the same sensory source.

We measured the duration of the open-loop interval by comparing the eye velocity responses with two different target motion conditions. In the first, normal motion case, a spot target underwent leftward or rightward “step-ramp” target motion at 15°/s after a random duration fixation interval. The step-ramp paradigm, developed to reduce the frequency of saccades, involves a fixation target undergoing a position step and then immediately ramping back toward the former fixation location with a constant velocity (Rashbass, 1961). Therefore, the target nears the foveal gaze position just as the eye begins to accelerate (Fig. 3A). The second motion condition was identical to the first, but we held the pursuit control loop open electronically by adding the eye velocity back into the target velocity as the eye accelerated (Lisberger and Westbrook, 1985; Osborne et al., 2007). This feedback manipulation holds the control loop open such that the eye movement cannot influence the retinal signals generated by the target. The benefit of this method is that the retinal image velocity is held at 15°/s no matter how and when the eye moves from trial to trial. We measured the time at which the enforced open-loop eye velocity diverged from normal step-ramp pursuit. The trial-averaged eye speeds in the two conditions diverge at 236 and 239 ms for subjects M.B. and T.M. The point at which the means are separated by one SD was 260 and 320 ms relative to pursuit onset (430 and 480 ms with respect to target motion onset). To standardize across subjects, we will use 240 ms to define the open loop interval with respect for pursuit onset for our subjects for subsequent analyses. Human pursuit open-loop intervals are substantially longer than those observed in nonhuman primates, as are human pursuit latencies (170 and 160 ms for the same two subjects, respectively).

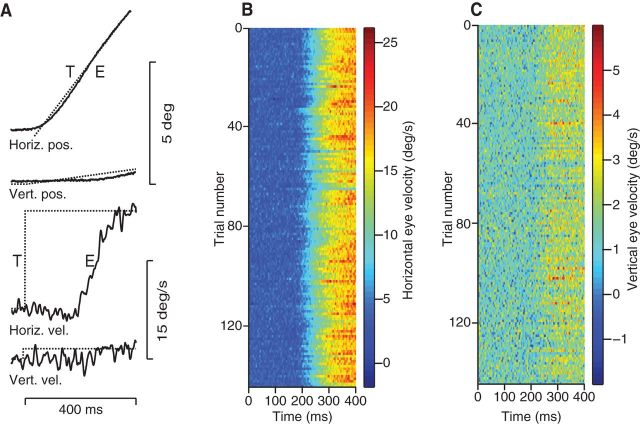
Figure 3.

Pursuit response to a step in target motion. A, Pursuit response to a spot target moving at 15°/s in a direction of 6°. Shown are the horizontal and vertical components of eye (E) position and velocity in response to target (T) motion. Top to bottom, Superimposed horizontal target and eye position (Horiz. pos.), superimposed vertical target and eye position (Vert. pos.), horizontal target and eye velocity (Horiz. vel.), and vertical target and eye velocity (Vert. vel.). The x-axis represents time with respect to target motion onset. B, C, Density plots in which colors indicate horizontal and vertical eye velocities and each line represents a response to the same target motion. Time is relative to target motion onset.

Eye movements are slightly different each time a motion stimulus is presented. Figure 3 shows the response to a 15°/s step in rightward target motion on a single trial (Fig. 3A) and the horizontal and vertical components of eye velocity for 144 repeats (Fig. 3B,C) of the same target motion, drawn from an experiment with 13 other target directions. Fluctuations in eye velocity, shown as different colors in Figure 3, B and C, limit how precisely pursuit eye movements report target motion. To investigate the temporal structure of pursuit variation, we analyzed the covariance of velocity fluctuations for the initial 240 ms of the vertical and horizontal components of pursuit eye velocity compared with velocity variation during 240 ms of fixation. We find that pursuit variation differs substantially from variation during fixation. During fixation, eye velocity fluctuations are small, Gaussian distributed, have a short correlation time of ∼10 ms, and are high dimensional (>150 of 480 dimensions significant). Therefore, fixation noise is dominated by “jitter.” Although this velocity jitter is present during pursuit as well, it is swamped by variation of a much different temporal structure. Pursuit variation has a long time scale and is low dimensional. The covariance matrix of eye velocity fluctuations is dominated by just three of 500 possible dimensions that together describe >91% of the variance. Trial-to-trial variation in human pursuit is well described as a rotation, scaling, and time shift relative the trial-averaged pursuit response for each target condition (Osborne et al., 2005; Stephens et al., 2011). The low-dimensional structure of pursuit variation motivates the use of a simplified version of the covariance matrix as a model of variation in open-loop pursuit (Eq. 4).

Direction estimation in pursuit and perception

To measure pursuit's discrimination of target direction differences, we performed experiments in which target directions differed by small angles. To determine whether two different target motions are discriminated by the pursuit system, we use an SNR-based metric termed an oculomotor threshold (Kowler and McKee, 1987; Watamaniuk and Heinen, 1999; Krukowski and Stone, 2005; Osborne et al., 2007). The threshold defines the smallest target direction or speed difference that can be read out from the pursuit response correctly on 69% of trials (Eq. 2–8). Threshold values change over time. Before pursuit begins, thresholds are very large and essentially undefined, but as the eye accelerates, the vector difference between the eye velocity responses to different target motions increases and thresholds fall (Fig. 4A). For each pair of target directions, we compute the vector difference in the trial-averaged eye velocity using the whole time vector from target motion onset to a time T sampled at millisecond resolution. We define noise as the covariance matrix across time of fluctuations in the eye movements about those mean trajectories (Eq. 2). In practice, because velocity fluctuations had no direction dependence, we pooled all trials to estimate the covariance and keep only the three dominant modes of variation to improve statistical power. We find that the SNR(T) scales with the squared target direction separation, which allows us to find the direction separation that would yield SNR = 1 (Eq. 5–6), which we define as threshold Δθ(T) (Osborne et al., 2007). This method provides a smooth and statistically stable estimate of pursuit thresholds over time.

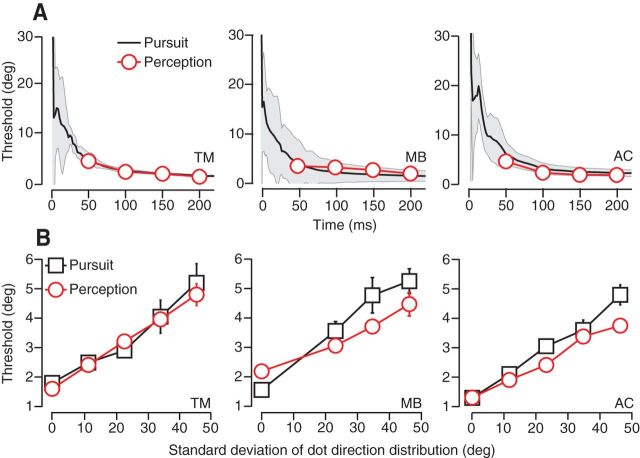
Figure 4.

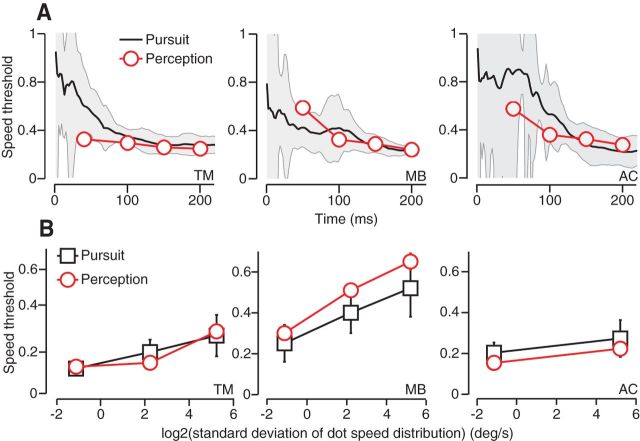
Direction discrimination in pursuit and perception in three subjects. A, Threshold time course for discrimination of small differences in direction of a target moving at 10°/s. Pursuit threshold values (black), calculated from eye velocity, represent the angular difference in target direction that yields 69% correct discrimination. Time is defined with respect to pursuit onset. The gray regions indicate SDs. Perceptual thresholds (red symbols) are calculated via probit analysis and are plotted as a function of viewing duration. Error bars indicate SD. B, Direction discrimination thresholds for pursuit and perception are plotted as a function of the SD of dot directions within fixed-seed noisy-dots targets. Thresholds correspond to a viewing duration of 240 ms or the first 240 ms of pursuit.

Pursuit direction thresholds drop rapidly as the eye begins to accelerate to reach a more or less stable value by the end of the open loop interval (1.9° for T.M., 1.5° for M.B., and 1.6° for A.C.). Figure 4A shows the direction thresholds for three subjects (black traces) plotted as a function of time since pursuit onset. Thresholds before pursuit onset are not defined. The error bars (gray shading) represent SD. Direction discrimination thresholds in the three human subjects are similar to those measured in monkeys at the close of their open loop interval (1.6–6.6° after 125 ms of pursuit; Osborne et al., 2007). As with nonhuman primates, human pursuit thresholds are not substantially improved by the availability of extraretinal feedback signals that contribute to eye movements during closed-loop, steady-state pursuit.

To compare the sensory estimates underlying pursuit to estimates underlying a second type of behavioral report, we measured the perceptual threshold for motion discrimination. We used the same target types and motions that we had in the pursuit experiments, but reconfigured the trials into a 2AFC task (see Materials and Methods, Fig. 1D,E). Subjects would see two motion intervals, interleaved with a fixation interval, and indicated by button press whether the second target motion was rotated clockwise or counterclockwise with respect to the first. To minimize the use of nonmotion cues for this task, we randomized the start position of the target within a 3° window. No difference in percentage of correct choices was noted as a function of the direction of the first target, so we pooled data across directions for the same angular spacing. Using probit analysis, we found the best cumulative Gaussian function fit to all responses and, from that fit, defined the threshold (Eq. 9). Figure 4A plots the perceptual direction discrimination thresholds for the same three subjects used in the pursuit experiments (red symbols). The time points for the perceptual thresholds correspond to the viewing time (i.e., target motion duration), which ranged from 50 to 200 ms. The error bars in perceptual threshold estimates are occluded by the size of the symbols plotted. Pursuit and perceptual discrimination thresholds are within error bars of each other across time in all three subjects.

To test whether direction discrimination thresholds for pursuit and perception agree over a wide range of conditions, we manipulated the difficulty of the direction discrimination task to parametrically increase threshold values. We used random dot kinetograms in which each dot had an added stochastic direction component (Fig. 2B) modeled on targets developed by Sekular and colleagues (Williams and Sekuler, 1984; Watamaniuk et al., 1989; Watamaniuk and Heinen, 1999; Osborne et al., 2009). These “noisy dots” targets had a visual appearance like a swarm of tiny bees such that each dot moved randomly yet remained in the swarm (Fig. 2A,B; Materials and Methods). For a low direction noise target, dot directions might remain within ±20° of the base direction, whereas for the highest noise targets, they remained within ±80° of the base direction. Unlike the experiments by Watamaniuk and Heinen (1999), the aperture translated across the screen along with the dots in the step-ramp trial design that we described for the spot targets. As the range of dot directions increases, the component of motion along the aperture direction decreases, lowering the translational speed of the target and along with it the eye velocity during pursuit. To keep the eye movements as similar as possible across noise levels and to keep contributions from motor noise constant, we increased dot speed slightly with the dot direction range to maintain the same eye speed. The pursuit and perceptual discrimination tasks and data analyses were otherwise the same as for the previous experiments.

Because each dot is moving independently, the overall direction of pattern movement becomes more difficult to estimate, as evidenced by an increase in thresholds with noise level for both pursuit and perception. We plot pursuit (black symbols) and perception thresholds (red symbols) as a function of direction noise level in Figure 4B. Each symbol represents the direction discrimination threshold measured 240 ms after pursuit onset or with a perceptual viewing time of 240 ms. We find that both pursuit and perceptual direction discrimination thresholds rise with increased randomization of dot motion within the target. For subject T.M., the agreement between pursuit and perceptual direction discrimination thresholds is excellent for all noise levels, and this was somewhat less so for our other two subjects. However, in all cases, manipulating noise level in the visual stimulus while keeping the motor response the same across conditions increased pursuit and perceptual thresholds together. Variation arising from the stimulus must therefore dominate any private noise sources in both behaviors.

Speed estimation in pursuit and perception

Producing effective eye-tracking behavior requires estimating target speed as well as direction, so we performed a companion series of experiments to measure speed discrimination in pursuit and perception. In the speed experiments, a spot target moved at a base speed of 15°/s rightward or leftward, with additional speeds that differed from the base by ±10%. Data collection and analyses were similar to those in the direction experiments. Figure 5A shows the speed discrimination thresholds over time relative to pursuit onset for each of the same three subjects shown in Figure 4. We report speed discrimination thresholds as a fraction of the mean speed; therefore, a threshold of 0.1 would indicate that 10°/s could be discriminated from 11°/s as reliably as 20°/s could be discriminated from 22°/s. Speed thresholds fall sharply as pursuit gets under way to reach a fairly stable value by the close of the open-loop interval (20% for T.M., 18% for M.B., and 17% for A.C.). We designed the companion speed perception tasks to be similar to the direction discrimination perception tasks. Spot targets moved rightward at different speeds in a randomly interleaved fashion. Each trial presented two motion intervals with a 500 ms blank period in between (Fig. 1F). Subjects reported whether the second target motion was faster or slower than the first. We computed perceptual thresholds for speed discrimination using the same method described for direction. The results for all three subjects are plotted as a function of viewing duration in Figure 5A (red symbols). Consistent with the results for direction discrimination, we found excellent agreement between pursuit and perceptual thresholds for speed discrimination for all three subjects over time.

Figure 5.

Speed discrimination in pursuit and perception in three subjects. A, Threshold time course for discrimination of small differences in target speed expressed as a fraction of base speed (15°/s). For pursuit traces (black), time is relative to pursuit onset; for perception (red), time represents viewing duration. Error bars in pursuit (gray regions) and perception (not visible) indicate SDs. B, Fractional speed discrimination thresholds (base speed, 10°/s) for noisy-dots speed targets plotted as a function of log2 of the SD of dot speeds, a measure of noise level. Perceptual thresholds (red circles) were measured at a 240 ms viewing duration; pursuit thresholds (black squares) at 240 ms after pursuit onset.

We created “speed noise” targets analogous to the randomized direction dot kinetogram targets described above to manipulate the fidelity of internal sensory estimates of target speed (Watamaniuk and Duchon, 1992; Osborne et al., 2007). In the speed case, all dots in a texture moved in identical directions, but dot speed was randomized over an interval of V*2^−N to V*2^N, where N ranged from 0 (no noise) to 7 around a base speed of 10°/s. The logarithmically scaled spacing of dot speeds reflects the logarithmic dependence of both perceptual sensitivities to motion speed (Orban et al., 1984; McKee and Nakayama, 1984; de Bruyn and Orban, 1988) and the speed tuning in motion sensitive neurons in MT (Maunsell and Van Essen, 1983; Churchland and Lisberger, 2001; Liu and Newsome, 2003; Priebe et al., 2003; Nover et al., 2005). The eye speed was very similar over time for all noise levels. We found that, even while keeping the motor response fixed, pursuit thresholds for speed discrimination increased with increasing variation in dot speeds within the pattern. Figure 5B (black symbols) plots pursuit thresholds measured 240 ms after eye movement onset as a function of speed noise level for the same subjects. Noise levels represent the SD of dot speeds within the pattern. Overlayed are the perceptual thresholds for speed discrimination (red symbols) measured with the same targets. Like the results for direction discrimination, we found that both pursuit and perceptual thresholds increase together with noise level in the visual stimulus.

Optic flow, eye acceleration, and pursuit thresholds

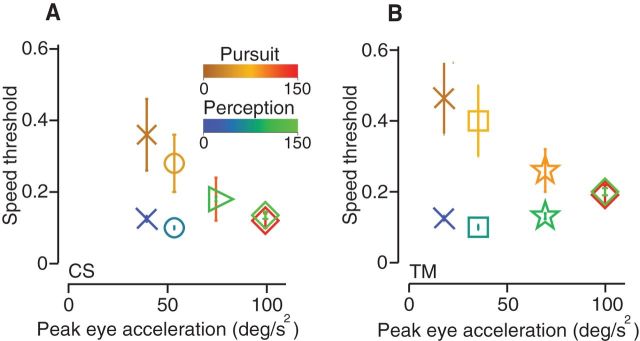
Some previous studies comparing pursuit and perception have found sizeable discrepancies between threshold values for speed or direction discrimination (Watamaniuk and Heinen, 1999; Krukowski and Stone, 2005; Rasche and Gegenfurtner, 2009; Simoncini et al., 2012) and some have found similar threshold values (Kowler and McKee, 1987, Stone and Krauzlis, 2003; Gegenfurtner et al., 2003; Osborne et al., 2005; Osborne et al., 2007). To understand the differences in the literature, we approximated some of the visual stimuli used in past studies and retested direction discrimination in two subjects. The visual stimuli included one drifting sinusoidal grating (Gabor patch) and several random dot kinetograms of differing aperture sizes, dot numbers, and dot and aperture speeds. We plotted the pursuit and perceptual thresholds for each new target form in Figure 6, A and B, along with spot, dot pattern, and noisy dots data that we presented in previous figures. We tested a sinusoidal grating suggested by a target used in Gegenfurtner et al. (2003). The grating (•) had a diameter of 5°, a contrast of 12%, and a spatial frequency of 1 cycle/°. The space constant of the Gaussian spatial filter was set to 1° and the target speed was 4°/s. This target was presented against a uniformly illuminated screen set to the average intensity of the target. After Watamaniuk and Heinen (1999), we used a variant of the noisy dots targets described previously, but instead of translating across the screen, the aperture remained stationary while the dots moved within it. Target (□) had a 10° circular aperture with 200 single-pixel dots that moved at 8°/s. The direction of each dot was chosen randomly with replacement from a uniform distribution from −40 to 40° around a central direction and updated every 40 ms. We made two additional variants of the above target to study how manipulating the optic flow score affected thresholds. For one variant (○), dot number increased to 400 in the same sized, stationary aperture. For the second variant (★), the target was otherwise the same, but aperture also translated across the screen at 8°/s. The remaining two dot pattern targets were a small 2°, 8 dot (3 pixels each) pattern moving at 10°/s in a stationary aperture (*) and a 5°, 50 dot (3 pixels each) pattern moving along with the aperture at 10°/s (×). We have also replotted spot target (▷) and direction noisy dots target (♢) data we presented in Figure 4. We used the same data analyses described previously to compute direction thresholds and collected datasets of comparable size. In each case, we measured differences between pursuit and perceptual threshold values that were comparable to those presented in previous studies. To determine whether the target-dependent differences between pursuit and perception derived from a difference in pursuit quality, we measured the peak eye acceleration during the open-loop interval elicited by each target type. Figure 6, A (subject M.B.) and B (subject T.M.), plot pursuit threshold values measured at 240 ms after eye movement onset and perceptual threshold values measured with 240 ms viewing time for each target form as a function of peak eye acceleration during the open loop interval, a measure of pursuit gain (Lisberger and Westbrook, 1985). Replotting the results against pursuit gain measured as the ratio between eye and target speed at the end of the open-loop interval gave very similar results (data not shown). With stimuli that elicit the highest gain pursuit responses, like those used in our study (♢, ▷ symbols), the agreement between pursuit and perceptual threshold values is nearly exact; however, for visual stimuli that produce weak pursuit with low eye acceleration, pursuit thresholds are substantially larger. Differences in target type also affected perceptual reports of target direction. Among this collection of targets, those that produce higher eye accelerations are also more easily discriminated perceptually such that differences between pursuit and perception are smallest when pursuit is strong.

Figure 6.

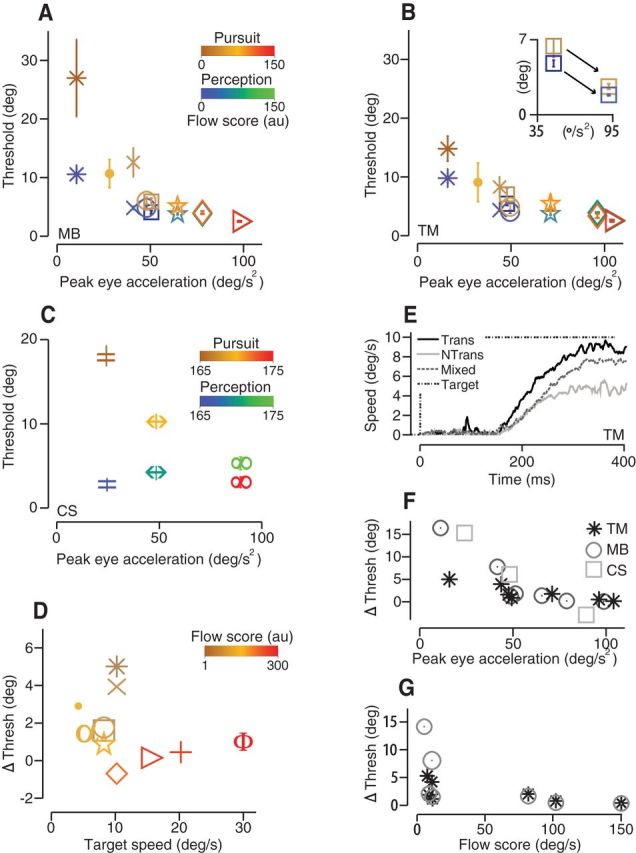
Threshold values and pursuit gain depend on optic flow score in the visual stimulus. A, Direction discrimination thresholds for pursuit (red-brown) and perception (blue-green) plotted against peak eye acceleration (°/s²) for subject M.B. for eight different targets. Symbol color corresponds to relative optic flow score scaled for clarity. Target forms (symbols) are defined in Results. B, Same data for subject T.M. Inset, Threshold versus eye acceleration for a nontranslating 10° dot pattern before and after a manipulation to increase its optic flow score. C, Pursuit (brown-red) and perception (blue-green) direction thresholds for 0.1 (=), 0.4 (↔), and 0.8 (∞) cpd motion cloud stimuli, subject C.S. D, Threshold difference plotted as a function of target speed, data from subjects T.M. and C.S. Threshold difference depends more strongly on optic flow score than on target speed per se. E, Trial-averaged eye speed time course differed when the dots and aperture moved together (Trans, black line) versus dots moving in a stationary aperture (N Trans, gray line). Randomly interleaving both targets produced intermediate eye speeds (Mixed, dotted gray line). F, Threshold differences between pursuit and perception plotted as a function of peak eye acceleration for three subjects. Data are replotted from A–C. G, Threshold differences replotted from A and B as a function of optic flow score (a.u.).

Many features of target form and motion can affect pursuit. Eye acceleration scales linearly with target speeds up to about 45°/s, so slow target speeds will produce low eye acceleration (Lisberger and Westbrook, 1985). Targets (●, □, ○, ★) all had speeds of 8°/s or less, but they produced a range of threshold results. Other factors known to affect pursuit gain include the size and density of illuminated pixels in the pattern (Heinen and Watamaniuk, 1998; Osborne et al., 2007). To account for the differences in eye acceleration among the variety of tested target forms, we computed an optic flow score for each stimulus that we used to color each symbol in Figure 6, A and B. We define the optic flow score as a normalized sum of all illuminated pixel speeds plus the COM translational speed of the target (see Materials and Methods). We included the COM term to distinguish targets that translate across the screen from those that had motion within a stationary aperture. Targets with higher dot numbers, larger dot pixel sizes, higher speeds, and translating apertures have higher flow scores. We took one particular target form (□, 10° stationary aperture, 200 single-pixel dots, 8°/s) and increased its flow score by increasing the dot size from 1 to 3 pixels and the dot speed from 8 to 10°/s. The flow score increased from 8°/s in the original target configuration to 11°/s. Using the new target, we found that peak eye acceleration increased from 48 to 92°/s² and the difference between pursuit and perceptual thresholds for direction discrimination decreased from 1.6° to 0.7° (Fig. 6B, inset). This result underscores that many features of the visual stimulus that affect optic flow contribute to the precision of both pursuit and perception.

We performed a similar threshold comparison using motion cloud stimuli with controlled spatial and temporal frequency bandwidths (see Materials and Methods). Dot pattern targets have a Fourier bandwidth with infinite asymptote, so they contain all spatial and temporal frequencies (Schrater et al., 2000). A recent study compared the sensitivity (i.e., 1/std) in motion perception to ocular following (OFR), a cortically mediated postsaccadic smooth eye movement with wide-field optic flow (Simoncini et al., 2012). They found that, for high spatial frequency (s.f. > 0.1 cpd) motion cloud stimuli, the sensitivity (1/std) in eye speed was high and perceptual sensitivity was low; sensitivities were similar at low s.f. bandwidths (<0.1 cpd). To reconcile the seeming conflict between their results and ours, we synthesized motion cloud targets with s.f. bandwidths of 0.1 (=), 0.4 (↔), and 0.8 (∞) cpd that had yielded discrepant performance in eye movements and perception in Simoncini et al. (2012) (Fig. 6C). To match the eye accelerations of the dot pattern target data and to display the motion cloud within a moving aperture (also 20°/s; see Materials and Methods), we increased the speed of motion to 20°/s. Our results confirm three features of the results of Simoncini et al., 2012. First, that peak eye velocity or acceleration increases with spatial frequency bandwidth. Second, that eye movement precision increases (sensitivity increases and threshold decreases) with increasing bandwidth. Third, that perceptual precision has a weak dependence on s.f. bandwidth that opposes pursuits such that perceptual precision decreases as motion cloud s.f. bandwidth increases. The net result, in our study, is that motion clouds that yield higher eye accelerations also yield similar thresholds for pursuit and perception, consistent with our results using dot-pattern target forms. The trend in threshold difference as a function of optic flow score for the motion cloud targets was also consistent with the dot-pattern results (color), but the score values did not change substantially between the motion cloud targets. The apparent discrepancy in our overall result from Simoncini et al., 2012 may arise from differences in the precision of the OFR versus pursuit for our respective tasks. In both studies, perceptual sensitivity decreases by approximately a factor of 2 from 0.1 to 0.8 cpd, whereas eye velocity sensitivities increase by a factor of 2 (Simoncini et al., 2012) and a factor of 5 in our data (data not shown). Although the perceptual and behavioral sensitivity curves do not intersect in the Simoncini et al., 2012 results, they do in ours such that the levels of precision are comparable at higher bandwidths.

Pooling data across subjects and target forms, we have replotted the results from Figure 6, A–C, to display pursuit-perception threshold differences as a function of eye acceleration in Figure 6F. The stimuli that generated different levels of precision in perception and behavior induced very low eye accelerations (i.e., poor pursuit); stimuli that produced robust pursuit yielded similar threshold values.

Center of mass motion, aperture translation, had a particularly strong effect on pursuit gain and subsequently on the difference between pursuit and perceptual thresholds. In Figure 6E, we plot the eye speed as a function of time for two, large 10° aperture random dot kinetogram targets that were identical except for their aperture speed. These curves represent the trial averaged eye speeds when one of the two target types was presented throughout the whole experiment. In the “translating” case (black curve), the dots and aperture moved together at 10°/s (flow score of 81°/s) so that the eye had to actually rotate in the orbit to maintain pursuit. In the “stationary” case (gray curve), the dots moved at 10°/s within a stationary aperture with a flow score of 8°/s. Both target types drive pursuit, but the stationary aperture targets yield lower eye speeds, eye acceleration, and pursuit gain compared with targets that translate across the screen even when dot speed is identical in both cases. The difference in pursuit gain might be stimulus driven, arising from biased visual estimates of target speed from the low optic flow targets. If so, eye speed should be attenuated on the first trial with a nontranslating target. In fact, we observed that, on the first trial with the nontranslating target, pursuit gain was high. With subsequent trials, eye speed fell sharply to stabilize at a lower gain from trial 13 onward (data not shown). Because the gain decrease is experience dependent, it seems more likely to arise from downregulation in the motor system. Perhaps the motor system is learning over trials that the eyes do not need to rotate substantially in the orbit because the target is not translating across the screen. When the two target types were randomly interleaved, pursuit velocity gain was intermediate between the gains measured from single target blocks. The relevance to the study at hand is that target conditions that produce low pursuit gain (eye acceleration) may lower the SNR in the eye movements due to weak extraocular muscle contraction or motor system downregulation, reasons that are orthogonal to the connection between sensation and behavior. Although optic flow score is a property of the stimulus, with a demonstrated impact on perceptual thresholds (Fig. 6A,B), the included center of mass term may describe a variable of more pertinence to the motor system than to the visual system per se.

Optic flow score can depend on target speed, as does eye acceleration during pursuit initiation (Lisberger and Westbrook, 1985, Tychsen and Lisberger, 1986). To disentangle the contributions of flow score and target speed to threshold agreement between pursuit and perception, we replotted the data from Figure 6, A and B, explicitly as a function of target speed. In Figure 6D, data symbols correspond to target form and colors to optic flow score (color bar). It is clear that the same threshold differences can occur at multiple target speeds and that, near the same target speed, threshold differences are strongly correlated to optic flow score.

The strong dependence of pursuit-perception threshold differences on optic flow score is highlighted in Figure 6G, which summarizes data across subjects and target forms from Figure 6, A and B. Pursuit gain, measured by open-loop peak eye acceleration, is strongly dependent on optic flow values within the range of target forms that we tested. The quality of pursuit affects eye velocity variation such that pursuit direction thresholds are more strongly dependent on optic flow compared with perceptual thresholds. High flow conditions correspond to high SNR conditions when the eye movement is the best possible proxy for the underlying sensory estimate of target motion and most directly comparable to perception.

We find that thresholds for speed discrimination have the same dependence on optic flow and eye acceleration as direction discrimination data. In Figure 7, A and B, we plot data from two subjects (C.S. and T.M.) performing speed discrimination tasks using some of the same stimuli shown in Figure 6 (symbol type). Symbol colors correspond to optic flow score. High optic flow targets produce high gain pursuit and, under these conditions, pursuit and perception are comparable. Low flow conditions that produce a weak pursuit response also create a disparity in precision between eye speed and speed perception.

Figure 7.

Pursuit and perceptual thresholds for speed discrimination depend on optic flow score. Thresholds are fractions of base speed. A, Data for subject C.S. B, Data for subject T.M. Symbol definitions: (X) coherent motion dot pattern target, 5° stationary aperture, 100 3-pixel dots that had a central speed of 6°/s; (▷) similar to (X) but its aperture also translated across the screen at the same speed as the dot pattern; (□) similar to (X) but with a circular aperture of 10° and 400 3-pixel dots; (○) 0.25° spot target with a base speed of 6°/s; (♢) same as (○), but with a base speed of 15°/s; (★) Gaussian blob (after Rasche and Gegenfurtner, 2009) with an SD of 0.5° and a base speed of 11°/s. Colors correspond to optic flow score (a.u.).

Correlation between perceptual direction estimates and eye movements

No solid experimental paradigm for testing the correlation between open-loop pursuit and perceptual judgments of target motion exists (Spering and Montagnini, 2011). One of the difficulties in analyzing eye movements and perceptual reports on the same trial is that the viewing time for pursuit and perception will not be equal. Because of the substantial latency period for pursuit onset (∼150 ms or longer), the eye movement will be derived from a substantially earlier estimate of target motion. Restricting the target motion duration to very short intervals can also present a problem because repeated presentations of short-duration target motion can drastically lower pursuit gain, complicating an analysis of the visual contribution to smooth eye movement (Kowler and McKee, 1987). With these caveats in mind, we took an approach similar to Stone and Krauzlis (2003) to analyze correlations between perceptual estimates of motion direction and pursuit. After a fixation interval of random duration, subjects pursued a spot target moving at 15°/s in a step-ramp fashion. The target moved for 450 ms before being extinguished. Motion directions ranged from −6° to +6° about rightward/leftward in 1° intervals and stimuli were presented in a randomly interleaved fashion such that the direction differences spanned intervals from 0 to 6°. Subjects pressed a button after every pair of trials to indicate whether the second target direction was CW or CCW with respect to the first. We analyzed eye direction in a time window from 190 to 240 ms after pursuit onset (see Materials and Methods). We translated eye direction measurements to ups (+) and downs (−) to compute correlations with the binary up/down perceptual reports of the direction difference between the second and first target motions. We computed the percentage of trials in which the signs agreed, which we plot as a function of target direction difference (signal) in Figure 8A. When there was an actual difference in target direction between the two motion intervals, there is a sensory signal and both perceptual judgment and change in eye direction can become correlated if each form a correct estimate of target direction. However, when both intervals had the same direction, there was no “correct” answer to the up versus down (CW/CCW) choice. In this absence of actual visual signals, behavior is driven by internal fluctuations and the extent of correlation between noise in pursuit and perception will determine the extent of sign agreement between the eye rotation and the perceptual report. We find agreement between the sign of eye direction and perceptual report on 70–71% of zero-signal trials in three subjects and in 59% in another subject (mean = 68%; Fig. 8A, red symbols). Our results are consistent with Stone and Krauzlis (2003), who used 600 ms of target motion and a contact-lens-mounted induction coil to measure eye movements (67% and 74% in two subjects). What does the percentage of sign agreement indicate about the scale of the underlying correlation between perception and pursuit? We plot the relationship between percentage sign agreement and the Pearson correlation coefficient in Figure 8B. Two uncorrelated binary random processes will have sign agreement 50% of the time, but that fraction grows as a function of the correlation coefficient. The relationship is nonlinear such that the fraction of sign agreement falls off quickly for correlations only modestly less than unity. A 70% sign agreement corresponds to a correlation coefficient of 0.6. The fact that the two behaviors are correlated above chance level without a sensory signal suggests that a source of shared variation is added upstream of the divergence between pursuit and perceptual pathways.

To understand how strongly our pursuit-perception correlation results constrain the contributions of shared versus independent sources of noise in pursuit and perception, we created two simple models (Fig. 8C,D; Materials and Methods). In each model, a homogeneous population of sensory units contributes individual direction estimates that are drawn from a Gaussian distribution with and SD of 15–30° to correspond to the average level of direction discrimination in MT neurons (Osborne et al., 2004). We synthesized stimulus conditional correlations (also called noise correlations) between the model units that limited the output precision of the direction decoder. In one model (Fig. 8C), we used a single decoder that simply averaged all inputs to compute target direction. Because a single decoder would create perfectly correlated perceptual and pursuit responses, we added output noise to both behavioral channels. We simulated pursuit and perceptual outputs across a large number of trials and then computed the percentage sign agreement as a function of two parameters: the level of noise correlations in the sensory population and the scale of the output noise. The results are plotted in Figure 8E. We found that the variance of the added downstream noise, rather than the correlation between neurons, determined the percentage sign agreement between the model outputs. The observed level of correlation between pursuit and perception requires that downstream noise has an SD equivalent to about 70% of threshold. Such a large amount of downstream noise is difficult to reconcile with the other experimental results. For the second model (Fig. 8D), we created two sensory populations each with its own decoder. The populations were homogeneous and identical to each other and the decoders were identical. We simulated different levels of within-population correlation and between-population correlation. The inspiration for this model was the idea that different subpopulations of extrastriate cortex (MT, MST) might project to targets involved in pursuit versus perception, and we wanted to capture the possibilities ranging from identical to completely independent populations. At one extreme, two fully correlated populations act like a single population and, at the other extreme, two uncorrelated populations act like they receive no common input. After the decoding stage, no additional noise was added to the pursuit and perception outputs. In Figure 8F, we show the results of these simulations, plotting percentage sign agreement (color) as a function of the level of within-population correlation and between-population correlation coefficients. We find that a wide range of correlation values can generate the observed 70% sign agreement (cyan colors). An interesting feature of the pattern in Figure 8F is that small changes in the between-population correlation produce large changes in the output correlation between pursuit and perception. Of course, these are not the only possible models of information flow from sensation to behavior (Stone and Krauzlis, 2003; Liston and Stone, 2008; Hohl et al., 2013) or, indeed, of population coding/decoding (Seung and Sompolisnky, 1993; Salinas and Abbott, 1995; Oram et al., 1998; Abbott and Dayan, 1999; also reviewed in Averbeck et al., 2006; Huang and Lisberger, 2009; Graf et al., 2011; Webb et al., 2011), but these conceptual models demonstrate how much or how little parameter tuning is necessary to account for experimental data.

Discussion

Knowing where a target is and how it is moving is critical to planning appropriate behavior. We ask whether a sensory estimate is formed once and then parceled out to different behavioral pathways, or whether each processing stream decodes a private estimate of target motion. Our focus is on short-timescale estimates of motion direction and speed that are formed from extrastriate cortical activity. MT neurons have a demonstrated role in both the perception of visual motion and in smooth pursuit eye movements (Newsome et al., 1985; Newsome and Pare, 1988; Newsome et al., 1988; Newsome et al., 1989; Zohary et al., 1994; Britten et al., 1996; Groh et al., 1997; Lisberger and Movshon, 1999; Born et al., 2000), although other cortical and subcortical areas also carry visual motion information and could contribute to either behavior (Krauzlis, 2004; Ilg and Thier, 2008). Perception and pursuit are therefore two behavioral outcomes of the same motion-processing stream. What remains unclear is whether each behavior is driven by a common sensory input or by independently generated inputs (Milner and Goodale, 2006; Gegenfurtner et al., 2011; Osborne, 2011; Schütz et al., 2011; Spering and Montagnini, 2011; Westwood and Goodale, 2011). As Westwood and Goodale (2011) point out, it would be surprising if vision for perception and vision for action were completely distinct, and weadd that it would be equally surprising if there were no independent downstream processing of visual signals by the perceptual versus motor pathways. We focus here on the narrow context of motion estimation for pursuit or perception on short timescales.

Both pursuit and perception are more precise than individual MT neurons. Behavioral direction discrimination thresholds are ∼10× lower (1.5–3.2°) than neural discrimination thresholds (15–30°) (Osborne et al., 2004). Perceptual speed discrimination thresholds are lower than for individual MT neurons as well (Liu and Newsome, 2005). The improvement in behavioral over neural precision suggests that population decoding diminishes the impact of fluctuations in individual neurons. We have performed experiments designed to test the hypothesis that sensory decoding happens upstream of the divergence between perceptual and oculomotor pathways and contributes the dominant source of variation in both behaviors. In previous work, we compared monkey pursuit with human perception (Osborne et al., 2005, 2007). This study benefits from within-species and within-subject comparison.

Several of our results point to shared variation in pursuit and perception. Threshold values are very similar, both over time and with the addition of “noise” to the visual stimulus. The noisy dots results in particular argue for shared variation because we kept the eye movement the same across conditions such that contributions from motor noise should have remained constant. We find that both pursuit and perceptual thresholds increase together, as did Watamaniuk and Heinen (1999), suggesting a common, sensory source of variation. This is consistent with our previous analyses of monkey pursuit, which suggested that <10% of the variance in pursuit arises from private motor sources (Osborne et al., 2005, 2007).

Some studies have reported larger levels of pursuit variation compared with perception (Watamaniuk and Heinen, 1999; Gegenfurtner et al., 2003; Krukowski and Stone, 2005; Rasche and Gegenfurtner, 2009; Simoncini et al., 2012) although others have not (Kowler and McKee, 1987; Stone and Krauzlis, 2003). This literature was recently reviewed by Spering and Montagnini (2011). We invested some effort to determine why. We approximated some of the targets and reproduced similar threshold differences, if not the actual threshold values. Any discrepancies likely arise from experimental details and are not central to the interpretation. We find that targets that drive weak eye acceleration elicit noisier eye movements. But motor factors alone cannot explain the observed changes in perceptual thresholds, leading us to define an optic flow score to quantify motion energy in space-time. Targets with more illuminated pixels moving at faster speeds have higher optic flow scores. By comparing optic flow across target forms, we provide a common framework for interpreting the relationship between pursuit and perceptual variation.

Recent work by Simoncini et al. (2012) explores the relationship among spatial frequency bandwidth, speed perception, and OFR behavior. They found discrepant levels of precision between eye velocity and speed perception for motion clouds with high spatial frequency bandwidth. Because high-bandwidth motion clouds drive the largest eye accelerations, that result is in seeming conflict with our experiments using similar stimuli, although our studies agree in other respects. The difference appears to arise from a difference in behavioral precision between the two studies, which could be due to several factors such as testing direction rather than speed discrimination or our reconfiguring the motion clouds to translate for pursuit. A more systematic analysis of motion estimation for perception and action as a function of optic flow versus spatial-temporal frequency bandwidth awaits future study.

Because our goal is to “look through” behavioral reports to the underlying sensory estimation process, we focus on high-optic-flow stimuli that drive high gain pursuit. Under these conditions, pursuit and perceptual thresholds for motion discrimination are within error bars, at least after the eyes have been moving for ∼50 ms. The leveling off of threshold values over time is consistent with the time course of information in MT, which improves little after the first 100 ms of neural response (Osborne et al., 2004, 2007). The correlation between eye direction and perceptual judgments within trials is also consistent with a shared source of variation. Our results are quite similar to those reported by Stone and Krauzlis (2003), but not to two studies comparing pursuit with speed perception, which found no correlation (Gegenfurtner et al., 2003; Rasche and Gegenfurtner, 2009).

Taken as a whole, our results are consistent with (at least) two conceptual models of motion decoding. We simulated noise correlations between neurons in a homogeneous population that limited how precisely the decoder(s) could estimate target direction and that in turn created downstream trial-to-trial fluctuations in behavioral output (Shadlen et al., 1996; Liston and Stone, 2008; Webb et al., 2011). Both models could generate the observed level of covariation between eye direction and perceptual judgment. However, the parameter ranges necessary to capture the data were more plausible in one model. The upstream model used a single decoder operating on a homogeneous population with additive noise at each output to break the perfect correlation arising from a common sensory estimate (Fig. 8C). A surprisingly large amount of output noise is needed, ∼70% of threshold, to create the observed level of sign agreement between pursuit and perception. Large additive noise levels are possible, but this possibility requires that pursuit and perception be noisy and yet have nearly balanced levels of noise. Substantial motor noise is not consistent with several physiological studies of oculomotor system variability. One study linked neural variation in the cerebellar floccular complex and variation in eye movements to upstream (sensory) inputs (Medina and Lisberger, 2007). Two others found that extraocular motorneuron variability has a substantial visual component (van Beers, 2007; Joshua and Lisberger, 2014). High motor noise levels also seem to be ruled out by comparisons between different eye movement behaviors. For example, eye velocity variability in vestibulo-ocular reflex movements is substantially smaller than in pursuit (Lisberger, 2010; Osborne, 2011). If most of the noise is added in motor processing, then the levels of variance in vestibular versus visually mediated eye movements should be similar. However, differences in movement precision could be explained by differences between visual and vestibular sensory precision (Guo and Raymond, 2010). Another possibility is that the single-trial data underestimate the correlation between pursuit and perception due to mismatched viewing times, tracker noise, task design, etc. In that case, large amounts of additive noise would not be necessary to make the upstream model work.

A conceptual model that overcomes the need for adding large private noise sources to perception and pursuit is a twin decoder model. Perception and pursuit might each generate a private motion estimate by decoding subpopulations from the same sensory area or two identically informative populations. These neural populations could be composed of differently projecting neurons in MT or from two closely related extrastriate areas such as MT and MST. For any given stimulus, the sensory estimates for pursuit and perception might differ slightly from trial-to-trial neural fluctuations but, overall, each would have the same precision. Some target forms could raise thresholds by increasing cortical variation such that each decoder and behavioral output is affected. One difference between the single-estimate (upstream) and twin-decoder (downstream) models is that the latter does not necessitate adding substantial output noise to recreate the observed levels of pursuit-perception correlation as long as the cortical subpopulations are not perfectly correlated. Pairwise noise correlations in MT range from ∼0 to 0.3 and depend on tuning differences and receptive field proximity (Huang and Lisberger, 2009; Cohen and Kohn, 2011). Both within- and between-population correlations contribute to sign agreement at the behavioral output and a wide range of correlation levels can create the observed 70% sign agreement between pursuit and perception. Interestingly, the output sign agreement is quite sensitive to the between-population correlation. Small value reductions create large changes in sign agreement between the outputs. Given the range of observed pairwise correlations within MT, it is plausible that both populations could arise within that cortical area. The other possibility, that sensory populations from two different cortical areas could encode similar levels of motion information and be highly correlated with each other at that level, awaits experimental support.

Our results place strong constraints on the nature of visual motion representation underlying the initiation of smooth pursuit and the perception of a moving target. The data argue more strongly for highly precise twin decoders of closely related sensory populations. However, we cannot rule out a single decoder combined with balanced levels of private noise added at each output. All of our results are consistent with a common, upstream sensory origin for the dominant source of variation in pursuit initiation and short-timescale motion perception. Although substantial contributions from sensory noise are being identified in other behaviors, eye movements, in which the kinematics are fairly simple and reaction times are short, are likely to be the clearest demonstration of sensory-driven variation (Osborne, 2011).