Abstract
Adaptation to both common and rare sounds has been independently reported in neurophysiological studies using probabilistic stimulus paradigms in small mammals. However, the apparent sensitivity of the mammalian auditory system to the statistics of incoming sound has not yet been generalized to task-related human auditory perception. Here, we show that human listeners selectively adapt to novel sounds within scenes unfolding over minutes. Listeners' performance in an auditory discrimination task remains steady for the most common elements within the scene but, after the first minute, performance improves for distinct and rare (oddball) sound elements, at the expense of rare sounds that are relatively less distinct. Our data provide the first evidence of enhanced coding of oddball sounds in a human auditory discrimination task and suggest the existence of an adaptive mechanism that tracks the long-term statistics of sounds and deploys coding resources accordingly.
Introduction
For many species, survival depends on the ability to encode the current sensory scene with a high degree of accuracy, while remaining alert to novel events in the environment (Bregman, 1990; McDermott, 2009). These two demands appear in conflict in terms of their call on neural resources. Adaptation to “enhance” representation of both common (Dean et al., 2005, 2008; Sadagopan and Wang, 2008; Watkins and Barbour, 2008; Wen et al., 2009; Barbour, 2011; Jaramillo and Zador, 2011; Rabinowitz et al., 2011; Walker and King, 2011) and rare (Ulanovsky et al., 2003, 2004; Nelken, 2004; Peréz-González et al., 2005; Malmierca et al., 2009; Yaron et al., 2012) sounds has been reported in neurophysiological studies, seemingly in the same brain centers and using similar probabilistic stimulus paradigms. How then does sensitivity to the statistical distribution of sounds manifest in sensitivity to both high-probability and low-probability events?
To assess neural sensitivity to the statistics of sounds, Dean et al. (2005, 2008) introduced a probabilistic paradigm in which stimulus intensities were selected according to distributions featuring low-probability regions (LPRs) and high-probability regions (HPRs). We used a similar paradigm in which listeners were presented with three variants of a stimulus, one of which occurred with high probability (80%) and the other two with low probability (10% each). Stimuli consisted of two sounds (noise bursts). One presentation of the stimulus, followed by a response, constituted a trial. After hearing the stimulus, the subject was asked to report “which sound was louder?”, indicating their response by pressing 1 or 2 on a keypad. In the first experiment, the three stimulus variants differed in terms of their overall intensity (35, 55, or 75 dB SPL). In the second experiment, the three variants differed in terms of the intersound interval (ISI; 350, 700, or 1050 ms).
Materials and Methods
The overall method was broken down into a two-stage procedure. The first, or calibration, stage determined the just-noticeable difference (JND) for intensity for pairs of sounds at each possible intensity and ISI generating, in each case, the intensity difference for a fixed a priori probability of success in the discrimination task (∼80%) for each listener. The second, probabilistic, stage presented the listener with three different stimuli, each set to the sound-level JNDs determined in the calibration stage, and stimuli occurring with a priori probability within a given epoch (Fig. 1).
Figure 1.
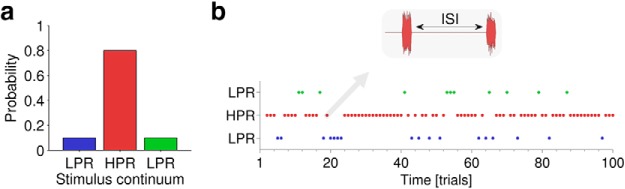
Stimulus probability. a, In each of two experiments, listeners were presented with 1000 calibrated trials. Each trial was selected from three possible stimuli according to a priori distributions that changed before each 100-trial epoch. The three stimuli consisted of changes in different sound features (intensity in Experiment 1, ISI in Experiment 2). Within an epoch, one of the three stimuli was selected with a priori probability of 80% (red, high-probability stimulus) and the other two versions were each selected with 10% probability (blue, green, low-probability stimulus). b, Plot of an example epoch consisting of 100 stimuli selected at random according to the probabilities described in a.
Stimuli and task.
Listeners discriminated intensity of pairs of 50 ms bursts of wideband noise (20 Hz–20 kHz), gated with 5 ms raised-cosine ramped envelopes and separated by a silent ISI. One of the noise bursts was randomly selected to be louder than the other and the task (in each trial) was to indicate on a keypad which sound (of the pair) was louder. Presentation of each new trial followed a subject's registration of the response to the previous trial. Directly after the response was entered, subjects were provided correct/incorrect feedback. Each noise burst was generated randomly before presentation. In the first experiment, the root-mean-squared (rms) SPL was 35, 55, or 75 dB and the ISI was fixed at 350 ms. In the second experiment, the rms SPL was fixed at 55 dB and the ISI was 350, 700, or 1050 ms. Noise bursts were generated digitally at 24-bit resolution. Beyerdynamic DT100 isolating headphones were used to present the stimulus (diotic) to listeners directly from a computer, at a sampling rate of 48,000 Hz.
Experiment 1: calibration procedure.
For each of the three possible stimuli for which intensity JNDs were obtained (35, 55, 75 dB), an adaptive three-down one-up, two-interval forced-choice procedure was used to estimate the point of 79.4% correct identification (Levitt, 1971). At the start of the adaptive sequence, the size of the intensity difference was set to 8 dB. Three consecutive correct responses in trials resulted in a reduction in the size of the intensity difference and one incorrect response resulted in an increase. Following a reversal (an increase in intensity difference following a decrease, or vice versa), the step size (starting value of 4 dB) was divided by two. Minimum step size was limited to 0.1 dB. After 20 reversals, the estimated JND was taken as the arithmetic mean of the last 10 reversals. The three runs, corresponding to the three stimuli, were conducted in a block lasting no longer than 20 min. Within-block run order was random. Each listener completed one block. The slowly converging adaptive procedure was designed to take ∼5 min per run, allowing sufficient time for long-term adaptation to converge before the ultimate estimate of JND being acquired.
Experiment 1: probabilistic procedure.
In the second, probabilistic, stage, listeners were presented with a block of 1000 individually calibrated stimuli (35, 55, 75 dB), where the intensity difference for each stimulus was the estimated JND obtained from the previous calibration procedure. Unbeknownst to the listeners, the 1000 trials were divided into 100-trial epochs. Within an epoch, each trial was selected from the three possible stimuli according to a priori distributions (Fig. 1a), where one stimulus (i.e., a pair of noise bursts) was selected at 80% probability and the other two at 10% probability each (Fig. 1b). Over an epoch, this generated three possible distributions for the three possible stimuli: A, 10:10:80%; B, 10:80:10%; and C, 80:10:10% (Figs. 2a–c, 3a–c). Ten consecutive epochs were presented in a block. For each epoch, one of the three distributions was chosen with equal likelihood. This was performed in the following manner: three of each kind (A–C) were included plus one (of A/B/C) at random, for a total of 10 epochs. The epoch order was randomly shuffled and any permutations in which two sequential distributions of the same kind occurred (e.g., ACCBABACBC, where the second C immediately follows the first C) were rejected and reshuffled. Each listener completed one block (of 10 epochs), taking ∼30 min.
Figure 2.
Intensity discrimination accuracy changed over time for different intensity statistics. a–c, Mean (±SEM) accuracy for each stimulus (35, 55, or 75 dB) in different epochs. The color-coded correlations (r values shown below each respective diagram distribution) capture significant overall trends with time. For each epoch, correlations were also computed between the two respective low-probability (10%) functions and r values are noted (in black) with bracket. Correlation values are only given where significant (p < 0.01). a, Performance in epochs where 35 dB trials occur with 80% probability. b, Performance in epochs where 55 dB trials occur with 80% probability. c, Performance in epochs where 75 dB trials occur with 80% probability. Asterisks denote significant fluctuations in performance (p < 0.01, Friedman rank sum test). Each trial corresponds to ∼2 s (mean trial time across both experiments, 2 s; SD, ±0.3).
Experiment 2.
The calibration and probabilistic procedures of Experiment 1 were replicated for Experiment 2, where the three possible stimuli had ISIs of 350, 700, or 1050 and stimulus level was fixed at 55 dB SPL.
Participants.
Nine normal-hearing listeners participated (Experiment 1: mean ± SD, 29 ± 4 years, one female; Experiment 2: mean ± SD, 30 ± 5 years, two females). Seven of the listeners in Experiment 2 also participated in Experiment 1. Participants were voluntary, unpaid, and gave verbal informed consent before the experiment. The experimental protocol (including consent) was approved by the ethics committee of Queen Mary University of London.
Results
In each experiment, the three possible a priori distributions provide three contexts within which trials of each stimulus can be assessed. For each listener, continuous percentage-correct functions, for each stimulus in each context (3 × 3), were calculated using a 40-trial selective (rectangular) sliding window collapsed across epochs (N = 10). Each function was tested for significant overall fluctuations in performance (Friedman rank sum test), and for fluctuations in the difference in performance between each pair of stimuli within a given context (Friedman rank sum test on the derivative). The latter derivative test identifies fluctuations that indicate selectivity and/or prioritization between stimuli. The Durbin–Watson test statistic across all data of both experiments was close to 2 (mean, 1.93; SD, ±0.39) indicating that correction for serial correlation was not required. Correlations, computed on the grand-average performance functions, are given with 95% confidence intervals (CIs).
Experiment 1
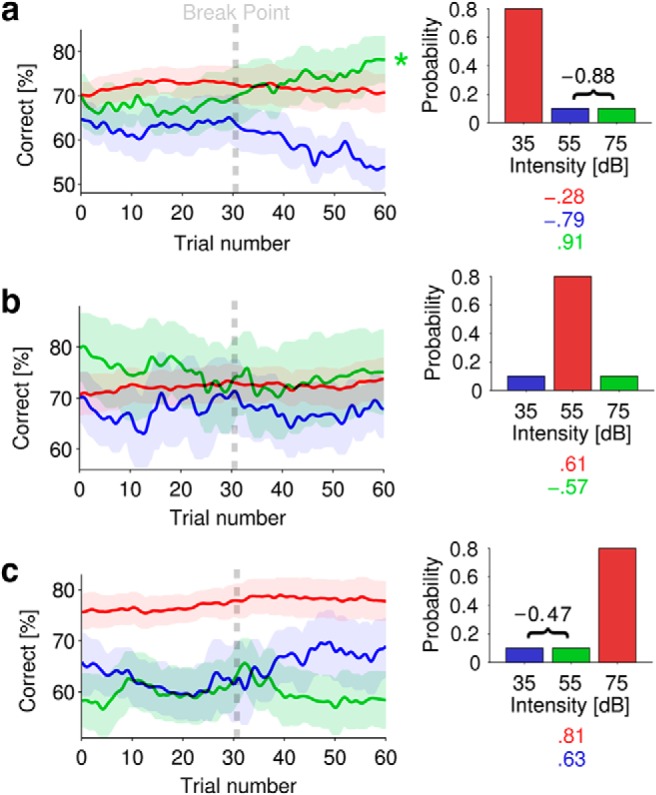
From the calibration procedure, the mean JNDs (±SD) were as follows: 2.4 ± 1.1 dB, 2.5 ± 1.1 dB, and 2.6 ± 1.6 dB for the 35, 55, and 75 dB stimuli respectively. Figure 2 plots mean performance (±SEM) for the three calibrated stimuli (35, 55, 75 dB) within each possible context. Figure 2a plots performance in the three possible stimuli when the 35 dB stimulus is selected at 80% probability. Figure 2b,c plots the same for the three possible stimuli when the 55 and 75 dB stimuli respectively are selected at 80% probability.
For all three high-probability stimuli, performance shows little evidence of significant fluctuation (not significant, Friedman rank sum test), suggesting that adaptation, if it occurs, is rapid for common sounds (Dean et al., 2005, 2008). Indeed, it should be noted that our paradigm (including the low-pass effects of the 40-trial sliding integration window) practically precludes capture of such adaptation. In Figure 2a, performance for low-probability stimuli (55 and 75 dB) is relatively steady (but lower) until approximately half-way through the epochs when performance for the two stimuli starts to diverge, with performance for the 55 dB stimulus declining (not significant, Friedman rank sum test), and for the 75 dB stimulus increasing (χ2(59) = 119.2, p < 0.01, Friedman rank sum test) until it surpasses even that for the 35 dB (HPR) stimulus. Over the whole epoch, performance for low-probability stimuli at 55 and 75 dB is inversely correlated (r = −0.88, p < 0.01, 95% CI [−0.79, −0.92]) and diverges around the “breakpoint” at ∼30 trials: performance deteriorates for the 55 dB stimulus (r = −0.79, p < 0.01, 95% CI [−0.67, −0.87]), while performance for the 75 dB stimulus improves (r = 0.91, p < 0.01, 95% CI [0.85, 0.94]). Further evidence of selectivity/prioritization is seen by examining the derivatives; performance for the 75 dB stimulus changes relative to that for the 55 dB stimulus (χ2(59) = 94.7, p < 0.01, Friedman rank sum test on the derivative between the stimuli) and relative to the 35 dB (HPR) stimulus (χ2(59) = 140.6, p < 0.01, Friedman Rank Sum test on the derivative of performance between the stimuli).
In Figure 2b, when the HPR corresponds to the 55 dB stimulus, performance shows little evidence of significant fluctuation for any stimulus (not significant, Friedman rank sum test). In Figure 2c, when the HPR corresponds to the 75 dB stimulus, performance for the low-probability stimuli is similar to that of Figure 2a; performance for the (low probability) 35 and 55 dB stimuli is inversely correlated (r = −0.47, p = 0.02, 95% CI [−0.24, −0.65]) and splits after the breakpoint; performance for the 55 dB stimulus deteriorates (not significant, Friedman rank sum test), while performance for the 35 dB stimulus improves (not significant, Friedman rank sum test) gradually (r = 0.63, p < 0.01, 95% CI [0.45, 0.76]).
These data are consistent with the existence of an adaptive mechanism that tracks the statistics of the stimulus, refining predictions over timescales of ∼1 min. For the “most odd” stimulus, when the HPR corresponds to the 35 and 75 dB stimuli, performance improves (at the expense of the alternate low-probability stimulus) after ∼1 min, suggesting the slow build-up of oddball selectivity. When the HPR corresponds to the 55 dB stimulus (Fig. 2b), however, neither of the other two stimuli is “more odd” than the other (and the 55 dB stimulus lies at the mean of the whole distribution), and overall performance is similar for all stimuli. This means that statistical evidence for stimulus prioritization is relatively weak.
Experiment 2
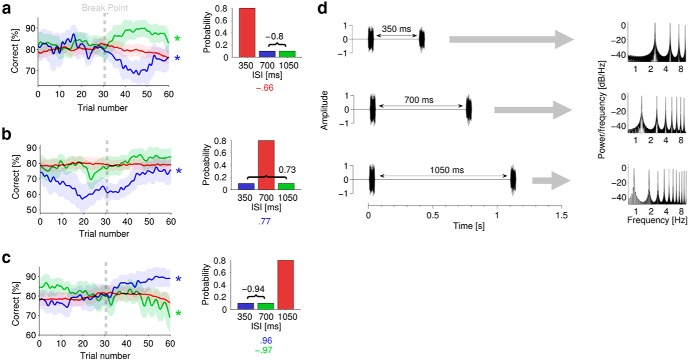
From the calibration procedure, the mean JNDs (±SD) were as follows: 2.4 ± 0.9 dB, 2.3 ± 0.9 dB, and 2.1 ± 0.4 dB, for the 350, 700, and 1050 ms stimuli respectively. Figure 3 plots mean performance (±SEM) for the three calibrated stimuli (350, 700, 1050 ms) within each possible context. Figure 3a plots performance for the three possible stimuli when the 350 ms stimulus is selected at 80% probability. Figure 3b,c plots the same for the three possible stimuli when the 700 and 1050 ms stimuli respectively are selected at 80% probability.
Figure 3.
Accuracy changed over time for different temporal statistics. a–c, Mean (±SEM) accuracy for each stimulus (ISI of 350, 700, or 1050 ms) in different epochs. The color-coded correlations (r values shown below each respective diagram distribution) capture significant overall trends with time. For each epoch, correlations were also computed between the two respective low-probability (10%) functions and r values are noted (in black) with bracket. Correlation values are only given where significant (p < 0.01). a, Performance in epochs where 350 ms trials occur with 80% probability. b, Performance in epochs where 700 ms trials occur with 80% probability. c, Performance in epochs where 1050 ms trials occur with 80% probability. Asterisks denote significant fluctuations in performance (p < 0.01, Friedman rank sum test). d, Example waveforms for pairs of 50 ms noise signals. By varying the interval (ISI) between two sounds, we vary the effective modulation power spectrum. The left side shows the waveforms with different ISIs. The right side of the panel shows the corresponding envelope power spectrum. Each trial corresponds to ∼2 s (mean trial time across both experiments, 2 s; SD, ±0.3).
Again, for all three high-probability stimuli, performance shows little evidence of significant fluctuation (not significant, Friedman rank sum test), suggesting that adaptation, if it occurs, is rapid for common sounds. In Figure 3a, performance for low-probability stimuli (700 and 1050 ms) is relatively steady until approximately half-way through the epoch when the two functions diverge abruptly, with performance for the 700 ms stimulus declining (χ2(59) = 134.6, p < 0.01, Friedman rank sum test), and that for the 1050 ms stimulus increasing (χ2(59) = 84.6, p = 0.02, Friedman rank sum test) until it surpasses that for the 350 ms (HPR) stimulus. Over the whole epoch, mean performance for low-probability stimuli at 700 and 1050 ms is inversely correlated (r = −0.8, p < 0.01, 95% CI [−0.7, −0.88]) and diverges around the “breakpoint” at ∼30 trials. The derivative provides further evidence of this selectivity/prioritization; performance for the 1050 ms stimulus changes with respect to that for the 350 ms stimulus (χ2(59) = 176.5, p < 0.01, Friedman rank sum test on the derivative of performance between the stimuli).
In Figure 3b, when the HPR corresponds to the 700 ms stimulus, performance for the low-probability stimuli (350 and 1050 ms) is positively correlated (r = 0.73, p < 0.01, 95% CI [0.58, 0.83]). Performance deteriorates early and then rises around a similar breakpoint to that observed in the other data. The fluctuations in performance only reach significance for the 350 ms stimulus (χ2(59) = 101.4, p < 0.01, Friedman rank sum test), offering some evidence of oddball effects, but are approximately paralleled for the (correlated) 1050 ms stimulus, indicating little evidence of prioritization/selectivity.
In Figure 3c, when the HPR corresponds to the 1050 ms stimulus, performance for the low-probability stimuli is again inversely correlated (r = −0.94, p < 0.01, 95% CI [−0.9, −0.96]). For the 700 ms stimulus, performance deteriorates (χ2(59) = 102.5, p < 0.01, Friedman rank sum test) gradually (r = −0.97, p < 0.01, 95% CI [−0.94, −0.98]), while performance for the 350 ms stimulus improves (χ2(59) = 82.9, p < 0.01, Friedman Rank Sum test) with a similar gradient (r = 0.96, p < 0.01, 95% CI [0.94, 0.98]) and surpasses performance for the HPR (1050 ms) stimulus. Again, the derivatives provide further evidence of selectivity/prioritization; performance for the 350 ms stimulus changes with respect to that for the 700 ms stimulus (χ2(59) = 135.7, p < 0.01, Friedman rank sum test on the derivative of performance between the stimuli) and with respect to that for the 1050 ms stimulus (χ2(59) = 124, p < 0.01, Friedman rank sum test on the derivative of performance between the stimuli). Also, performance for the 700 ms stimulus changes with respect to that for the 1050 ms stimulus (χ2(59) = 105.8, p < 0.01, Friedman rank sum test on the derivative of performance between the stimuli).
Consistent with the first experiment assessing stimuli of different intensities, the inverse correlation of performance in low-probability stimuli is only evident when the high-probability stimulus is presented with either low (350 ms) or high (1050 ms) ISIs. Additionally, the low-probability stimulus furthest in ISI from the high-probability stimulus ISI is enhanced after the breakpoint at the expense of the competing low-probability stimulus. This further supports the notion that the auditory system prioritizes resource allocation in favor of those low-probability sounds most different to the high-probability sounds. In both experiments, the selective enhancement of low-probability “oddball” sounds emerges around trial 30, which equates to ∼60 s into the epoch (mean trial time, 2 s; SD, ±0.3).
Discussion
We have demonstrated in human listeners a common strategy for processing the statistical distributions of sounds varying in intensity or timing. Sounds with the most-commonly occurring intensities, or presented with the most-commonly occurring intervals, are strongly represented throughout. Selective enhancement of novel events then appears to emerge after some time within the high-probability context. Discrimination performance for low-probability sounds that are most unlike the high-probability sounds is enhanced at the expense of discrimination in low-probability sounds that are most like the sounds heard with high probability. It is also striking that discrimination performance in these “oddball” low-probability sounds can surpass that of high-probability sounds (Fig. 3). Note too, that while previous reports of sensitivity to “oddball” sounds indicate improved detection of these events (Slabu et al., 2012), here we demonstrate improved discrimination for low-probability events.
At a phenomenological level, the adaptation evident in our data is consistent with the concept of perceptual learning (Skoe et al., 2013; de Souza et al., 2013). Perceptual learning is thought to reflect enhancement of perception due to synaptic plasticity (which follows practice) and hence our data may reflect rapid perceptual learning. More generally, the data are consistent with a process wherein listeners construct an internal model of the acoustic input that processes surprising, or “oddball,” stimuli. Although there are several potential neural mechanisms that might underpin such adaptation, it is implied that the neural representation of the stimuli changes over time.
Neural mechanisms
Our data are consistent with experimental recordings from small mammals in which firing rates of auditory neurons adapt to the unfolding distributions of sound intensity (Ulanovsky et al., 2003, 2004; Nelken, 2004; Dean et al., 2005, 2008; Peréz-González et al., 2005; Sadagopan and Wang, 2008; Watkins and Barbour, 2008; Malmierca et al., 2009; Wen et al., 2009; Barbour, 2011; Jaramillo and Zador, 2011; Rabinowitz et al., 2011; Walker and King, 2011; Yaron et al., 2012). This feature of neural coding, which emerges at the level of the primary auditory nerve, improves coding (discrimination) of the most-likely occurring intensities in a distribution of sounds (Dean et al., 2008). As a population, midbrain neurons also show the capacity to accommodate bimodal (with equal probability) distributions of sound intensity (Dean et al., 2005), suggesting the possibility of simultaneous adaptive coding for multiple sounds with different features. At both the midbrain (Dean et al., 2008) and cortical (Ulanovsky et al., 2004; Yaron et al., 2012) levels, neurons demonstrate adaptation time scales on the order of hundreds of milliseconds to tens of seconds. The breakpoint in performance at ∼60 s is relatively close to the time-scale of long-term adaptation reported in these studies. This time scale is also consistent with recent studies of slowly ramped intensity increments (Simpson and Reiss, 2013; Simpson et al., 2013) and brainstem-mediated “rapid learning” (Skoe et al., 2013), suggesting a common role of long-term adaptation in humans. Ulanovsky et al.'s (2004) study in cats also demonstrated that cortical neurons adapt more quickly to high-probability sounds than to low-probability sounds, and that multiple timescales of “stimulus-specific” adaptation occurred concurrently. These multiple timescales appear consistent with the features of our behavioral data.
The adaptation to temporal statistics implicit in our data is less straightforward to explain, but nevertheless is consistent with recent reports implicating auditory cortex neurons in adaptive coding of temporal intervals (Jaramillo and Zador, 2011). In both cases, the timing intervals may be considered in terms of (low) modulation rates. Emerging evidence suggests auditory cortex maintains a bank of independent cortical modulation filters (CMFs), each tuned to different (low) modulation rates (Xiang et al., 2013). CMFs have been implicated in speech processing (Ding and Simon, 2013) and the detection of intensity changes (Simpson and Reiss, 2013; Simpson et al., 2013). Contrast gain adaptation has been demonstrated in cortical neurons, whereby functions describing neuronal firing rate versus sound level show gain adjustments to best match the intensity variance of the stimulus (Rabinowitz et al., 2011). Combining these two cortical processing features, by assuming that contrast and modulation processing occurs by common means, a plausible explanation for adaptation to time intervals lies in the specificity of adaptation to particular CMFs. Our temporal stimuli can be considered in terms of the statistical manipulation of modulation energy (Fig. 3d) with respect to the rate at which energy is modulated. As shown in Figure 3d, the ISIs of 350, 700, and 1050 ms produce energy in the envelope modulations with fundamental frequencies of ∼3, 2, and 1 Hz respectively, and would, therefore, maximally excite different modulation filters. The power spectra in Figure 3d also demonstrate that the almost instantaneous envelopes generate steadily decreasing modulation energy in harmonics of the fundamental. Hence, it may be that rate selectivity of CMFs, as proxy selectors of ISIs, combined with independent CMF (contrast) adaptation, underlies the adaptive coding of temporal intervals.
A phenomenological model of selective adaptation
Selective adaptation to oddball sounds probably involves some form of interaction between adaptive effects (Ulanovsky et al., 2004; Dean et al., 2008; Yaron et al., 2012) and neural tuning widths on sensory continua (O'Connell et al., 2011). However, building a detailed biophysical model of this phenomenon is challenging given the paucity of relevant physiological data and the vast range of possible circuits. To this end, we generated a largely phenomenological model in which neurons' adaptive states are determined by integrating prior input, which we hope will facilitate future consideration of neural mechanisms. We presumed that neural tuning to sound level or ISI lies on a continuum, and that a sound holding a particular stimulus value will influence the adaptation state of neurons tuned to that stimulus value in an excitatory fashion, and that of neurons tuned to adjacent stimulus values in an inhibitory manner (and will have no influence on the adaptation state of neurons tuned to distant stimulus values). A long-term integration of this influence, mediated through a suitable nonlinearity, sets the adaptation state. Although it could also represent other neural properties, most simply this influence could be seen as some measure related to the membrane potential of the neurons in the population. In this case, for sound level, this would require nonmonotonic rate-level functions for the model in its simplest form. Such neurons have been found at many levels of the auditory brain (Sutter and Schreiner, 1995), including in studies of adaptive coding for sound level in the cortex (Watkins and Barbour, 2008).
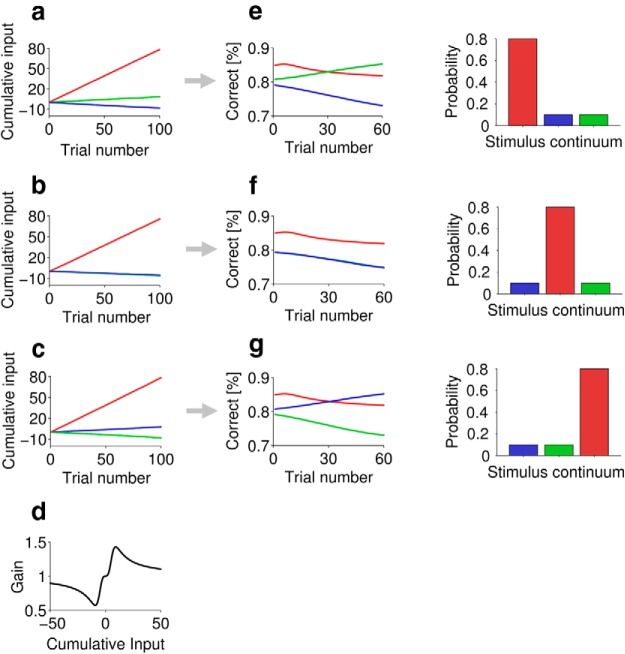
Figure 4a–c illustrates the integrated influence over the time course of a block of 100 stimuli for the three different distributions conditions in the experiment (simulated for 10,000 blocks and averaged). Each block, as in the experiments, consists of 100 trials, and on each trial t the stimulus u(t) = (u1(t), u2(t), u3(t)) is either stimulus 1, (1, 0, 0), stimulus 2, (0, 1, 0), or stimulus 3, (0, 0, 1), where stimuli 1, 2, and 3 lie at points along a sensory continuum. In each trial, the probability of each stimulus is identical to that used in the psychophysical experiments (i.e., 80 or 10%, depending on the distribution). Dividing the neural population into three groups (to simplify the model, at the cost of fully modeling the spread of neural rate-level functions), group 1 neurons are positively influenced by stimulus 1, group 2 by stimulus 2, and group 3 by stimulus 3. Additionally, stimulus 1 negatively influences group 2, stimulus 2, group 1 and group 3, and stimulus 3, group 2. Assuming the time constant of integration is large (on the order of minutes), we can simply consider xi(T), the cumulative sum of influence to a neuronal group i at a given trial number T, to be expressed by the following equation:
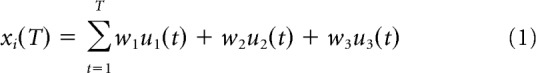 |
where for group 1 the input weights w = (w1, w2, w3) will be (1, −1/5, 0), for group 2 they will be (−1/5, 1, −1/5), and for group 3 they will be (0, −1/5, 1). Observe that in Figure 4a–c, neurons selective for (positively influenced by) the most common stimulus (red) show the fastest rise in cumulative influence, as expected from the stimulus statistics. In Figure 4a, the “green” neural group rises in cumulative influence, but the “blue” neural population drops. This occurs because the blue group is negatively influenced by the very common stimulus 1, whereas the green group is only negatively influenced by the rare stimulus 2. The opposite profile is observed in Figure 4c. In Figure 4b, as the blue and green groups are equally negatively influenced by the common stimulus, the influence on both groups drops.
Figure 4.
A phenomenological model. a–c, Cumulative influence on the three neural groups for the three stimulus distributions. d, Dependence of gain on cumulative input. e–g, Predictions of probability correct for the three stimuli for the three stimulus distributions. For each row of plots, the bar plot shows the probability of stimulus 1, 2, and 3, from left to right. Colors and plot order as in the experimental data. The green line is hidden behind the blue line in b and f.
The adaptation state of a model neural group depends on the cumulative influence it receives. The adaptation state can be construed as a gain on neuronal responses, scaling their tuning functions and increasing their capacity to discriminate sounds (under reasonable assumptions, Fisher information scales with maximum firing rate; Dayan and Abbott, 2001). Although adaptation state could also represent more complex qualities of the neural group, such as the sharpness of tuning functions or the shifting of the slopes of tuning functions over the stimulus range (Dean et al., 2005).
Hypothesizing that a neuronal group's gain increases as cumulative influence increases but at large cumulative input the gain then decreases, and that the opposite effect is seen for cumulative negative influence (gain decreases, then increases), the gain factor, Gi(T), can be described as a function of cumulative influence xi(T) using the following static nonlinearity:
For clarity, the dependence of x and G on T and i is not shown. The free parameters a and b are set to ¾ and respectively. This function is plotted in Figure 4d.
To translate the gain into probability correct (P), we assume that probability correct for a stimulus depends on the gain of the neural group that is positively influenced by that stimulus (we assume this relationship to be sigmoidal).
Assuming stimuli are set such that the sigmoid for a gain of G = 1 generates 80% correct performance (p = 0.8), similar to the psychophysical data, then algebraically c = −log(0.25). For clarity, the dependence of P and G on T and i is not shown.
Estimates of P for the three stimuli for the three stimulus distributions, smoothed over 40 trials, are plotted for the basic model in Figure 4e–g. As in the experimental data, the most distinct oddball rises in probability correct, and the less distinct oddball falls (Fig. 4e,g). Note that this is not the case for the paradigm in which the high-probability stimulus lies in the middle of the overall distribution (Fig. 4f), again consistent with the experimental data. A slightly more complex model (with inhibitory influence −1/3, b = 1/4) was also developed where summation from t = 1 to T in Equation 1 was replaced by a weighted sum that extended back before t = 1 into a preceding stimulus distribution (randomly chosen in accordance with Experiment 1: Probabilistic procedure), with weights exponentially decaying into the past from T (40 trial time constant, weights sum to 100); this model gave similar results to Figure 4e–g.
Attention
Our listeners were instructed to attend each and every trial, and confirmed (after test) that they made every effort to do so. The necessary attention span (∼30 min on average) should not tax an average adult. It might be argued that listeners' attention was captured by, or directed to, the “oddball” stimulus, and that top-down processing (e.g., of salience) could mediate such “oddball” selectivity. However, it is equally plausible that the well established low-level adaptive substrates can explain the data and even provide an explanation of the nature and substrates of attention itself, rendering attention deterministic—an involuntary statistical consequence of adaptive processing. In this scenario, “auditory boredom” would also be a predictable and involuntary consequence of the adaptive processing. Attention has featured prominently in investigations of “cocktail party listening.” Cortical entrainment (synchronization of neuronal duty-cycle with the envelope of the stimulus) has been suggested as one low-level substrate (Ding and Simon, 2013; Lakatos et al., 2013; Zion Golumbic et al., 2013), and even if entrainment is not a substrate, it is associated with, and mediated by, attention. Auditory neurons appear to exist in a state of perpetual oscillation, between excitatory and refractory states, known as the duty cycle (Lakatos et al., 2013). Entrainment of the neuronal duty cycle to a common stimulus modulation occurs when the refractory period is brought forward in time by excitation of the neuron (also referred to as phase-reset). Therefore, low-level adaptive processes described earlier are inherently implicated in the process of entrainment. Extrapolating further, the suggested adaptive-statistical filtering would directly mediate entrainment and hence would mediate the putative substrate of attention.
The sensitivity to “oddball” events demonstrated here might prove useful in exploiting the structural statistics of speech and perhaps even music. Such processing could facilitate the extraction of statistically salient signals from within predictable noise (such as multitalker babble, for example), and may even underpin higher-level statistical percepts (McDermott and Simoncelli, 2011; McDermott et al., 2013). Furthermore, if such adaptive coding is a fundamental, low-level feature of the auditory system, it may be that prosody, melody, and even the very structure of language and music have evolved to exploit such adaptive coding.
Footnotes
This work was supported by a studentship from the Engineering and Physical Sciences Research Council (to A.J.R.S.). N.S.H. was supported by the Wellcome Trust [040044], [WT076508AIA], including a Sir Henry Wellcome Postdoctoral Fellowship, and by the Department of Physiology, Anatomy and Genetics, University of Oxford.
The authors declare no competing financial interests.
References
- Barbour DL. Intensity-invariant coding in the auditory system. Neurosci Biobehav Rev. 2011;35:2064–2072. doi: 10.1016/j.neubiorev.2011.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bregman AS. Auditory scene analysis: the perceptual organization of sound. Cambridge, MA: MIT; 1990. [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. Cambridge, MA: MIT; 2001. [Google Scholar]
- Dean I, Harper NS, McAlpine D. Neural population coding of sound level adapts to stimulus statistics. Nat Neurosci. 2005;8:1684–1689. doi: 10.1038/nn1541. [DOI] [PubMed] [Google Scholar]
- Dean I, Robinson BL, Harper NS, McAlpine D. Rapid neural adaptation to sound level statistics. J Neurosci. 2008;28:6430–6438. doi: 10.1523/JNEUROSCI.0470-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Souza AC, Yehia HC, Sato MA, Callan D. Brain activity underlying auditory perceptual learning during short period training: simultaneous fMRI and EEG recording. BMC Neurosci. 2013;14:8. doi: 10.1186/1471-2202-14-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding N, Simon JZ. Adaptive temporal encoding leads to a background-insensitive cortical representation of speech. J Neurosci. 2013;33:5728–5735. doi: 10.1523/JNEUROSCI.5297-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaramillo S, Zador AM. Auditory cortex mediates the perceptual effects of acoustic temporal expectation. Nat Neurosci. 2011;14:246–251. doi: 10.1038/nn.2688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Musacchia G, O'Connel MN, Falchier AY, Javitt DC, Schroeder CE. The spectrotemporal filter mechanism of auditory selective attention. Neuron. 2013;77:750–761. doi: 10.1016/j.neuron.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49(Suppl 2):467+. [PubMed] [Google Scholar]
- Malmierca MS, Cristaudo S, Pérez-González D, Covey E. Stimulus-specific adaptation in the inferior colliculus of the anesthetized rat. J Neurosci. 2009;29:5483–5493. doi: 10.1523/JNEUROSCI.4153-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH. The cocktail party problem. Curr Biol. 2009;19:R1024–R1027. doi: 10.1016/j.cub.2009.09.005. [DOI] [PubMed] [Google Scholar]
- McDermott JH, Simoncelli EP. Sound texture perception via statistics of the auditory periphery: evidence from sound synthesis. Neuron. 2011;71:926–940. doi: 10.1016/j.neuron.2011.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH, Schemitsch M, Simoncelli EP. Summary statistics in auditory perception. Nat Neurosci. 2013;16:493–498. doi: 10.1038/nn.3347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelken I. Processing of complex stimuli and natural scenes in the auditory cortex. Curr Opin Neurobiol. 2004;14:474–480. doi: 10.1016/j.conb.2004.06.005. [DOI] [PubMed] [Google Scholar]
- O'Connell MN, Falchier A, McGinnis T, Schroeder CE, Lakatos P. Dual mechanism of neuronal ensemble inhibition in primary auditory cortex. Neuron. 2011;69:805–817. doi: 10.1016/j.neuron.2011.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-González D, Malmierca MS, Covey E. Novelty detector neurons in the mammalian auditory midbrain. Eur J Neurosci. 2005;22:2879–2885. doi: 10.1111/j.1460-9568.2005.04472.x. [DOI] [PubMed] [Google Scholar]
- Rabinowitz NC, Willmore BD, Schnupp JW, King AJ. Contrast gain control in auditory cortex. Neuron. 2011;70:1178–1191. doi: 10.1016/j.neuron.2011.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadagopan S, Wang X. Level invariant representation of sounds by populations of neurons in primary auditory cortex. J Neurosci. 2008;28:3415–3426. doi: 10.1523/JNEUROSCI.2743-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson AJ, Reiss JD. The dynamic range paradox: a central auditory model of intensity change detection. PLoS One. 2013;8:e57497. doi: 10.1371/journal.pone.0057497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson AJ, Reiss JD, McAlpine D. Tuning of human modulation filters is carrier-frequency dependent. PLoS One. 2013;8:e73590. doi: 10.1371/journal.pone.0073590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skoe E, Krizman J, Spitzer E, Kraus N. The auditory brainstem is a barometer of rapid auditory learning. Neuroscience. 2013;243:104–114. doi: 10.1016/j.neuroscience.2013.03.009. [DOI] [PubMed] [Google Scholar]
- Slabu L, Grimm S, Escera C. Novelty detection in the human auditory brainstem. J Neurosci. 2012;32:1447–1452. doi: 10.1523/JNEUROSCI.2557-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutter ML, Schreiner CE. Topography of intensity tuning in cat primary auditory cortex: single-neuron versus multiple-neuron recordings. J Neurophysiol. 1995;73:190–204. doi: 10.1152/jn.1995.73.1.190. [DOI] [PubMed] [Google Scholar]
- Ulanovsky N, Las L, Nelken I. Processing of low-probability sounds by cortical neurons. Nat Neurosci. 2003;6:391–398. doi: 10.1038/nn1032. [DOI] [PubMed] [Google Scholar]
- Ulanovsky N, Las L, Farkas D, Nelken I. Multiple time scales of adaptation in auditory cortical neurons. J Neurosci. 2004;24:10440–10453. doi: 10.1523/JNEUROSCI.1905-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker KM, King AJ. Auditory neuroscience: temporal anticipation enhances cortical processing. Curr Biol. 2011;21:R251–R253. doi: 10.1016/j.cub.2011.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins PV, Barbour DL. Specialized neuronal adaptation for preserving input sensitivity. Nat Neurosci. 2008;11:1259–1261. doi: 10.1038/nn.2201. [DOI] [PubMed] [Google Scholar]
- Wen B, Wang GI, Dean I, Delgutte B. Dynamic range adaptation to sound level statistics in the auditory nerve. J Neurosci. 2009;29:13797–13808. doi: 10.1523/JNEUROSCI.5610-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang J, Poeppel D, Simon JZ. Physiological evidence for auditory modulation filterbanks: Cortical responses to concurrent modulations. J Acoust Soc Am. 2013;133:EL7–EL12. doi: 10.1121/1.4769400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaron A, Hershenhoren I, Nelken I. Sensitivity to complex statistical regularities in rat auditory cortex. Neuron. 2012;76:603–615. doi: 10.1016/j.neuron.2012.08.025. [DOI] [PubMed] [Google Scholar]
- Zion Golumbic EM, Ding N, Bickel S, Lakatos P, Schevon CA, McKhann GM, Goodman RR, Emerson R, Mehta AD, Simon JZ, Poeppel D, Schroeder CE. Mechanisms underlying selective neuronal tracking of attended speech at a “cocktail party.”. Neuron. 2013;77:980–991. doi: 10.1016/j.neuron.2012.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]