A planning target volume margin formula for hypofractionated intracranial stereotactic radiotherapy under cone beam CT image guidance with a six-degrees-of-freedom robotic couch and a mouthpiece-assisted mask system: a preliminary study

Abstract

Objective:

A planning target volume (PTV) margin formula for hypofractionated intracranial stereotactic radiotherapy (SRT) has been proposed under cone beam CT (CBCT) image guidance with a six-degrees-of-freedom (6-DOF) robotic couch.

Methods:

CBCT-based registration using a 6-DOF couch reportedly led to negligibly small systematic positioning errors, suggesting that each in-treatment positioning error during the treatment courses for the patients employing this combination was predominantly caused by a random gaussian process. Under this assumption, an anisotropic PTV margin for each axis was formulated based on a gaussian distribution model. 19 patients with intracranial lesions who underwent additional post-treatment CBCT were consecutively selected, to whom stereotactic hypofractionated radiotherapy was delivered by a linear accelerator equipped with a CBCT imager, a 6-DOF couch and a mouthpiece-assisted mask system. Time-averaged patient-positioning errors during treatment were estimated by comparing the post-treatment CBCT with the reference planning CT images.

Results:

It was suggested that each histogram of the in-treatment positioning error in each axis would approach each single gaussian distribution with a mean of zero. The calculated PTV margins in the x, y and z directions were 0.97, 1.30 and 0.88 mm, respectively.

Conclusion:

The empirical isotropic PTV margin of 2 mm used in our facility for intracranial SRT was consistent with the margin calculated by the proposed gaussian model.

Advances in knowledge:

We have proposed a PTV margin formula for hypofractionated intracranial SRT under CBCT image guidance with a 6-DOF robotic couch.

Frameless radiotherapy for treating intracranial lesions has been widely adopted under the guidance of on-board cone beam CT (CBCT) and a mask system with a six-degrees-of-freedom (6-DOF) robotic couch^1–3 or a semi-robotic couch including manual angle adjustments.⁴ Reported maximum registration errors along any Cartesian co-ordinate axis were 0.5 mm for a phantom;¹ and 1.0 or 3.2 mm (mask dependent),² 2.0 ³ and 1.2 mm⁴ for patients. The mean ± standard deviation (SD) along any Cartesian co-ordinate axis was 0.07 ± 0.17 mm for a phantom based on 12 plans and 5 repeated CBCT acquisitions,¹ 0.2 ± 0.4 mm for 10 patients with 6 fractions³ and 0.4 ± 0.3 mm for a phantom and 0.5 ± 0.3 mm for patients including manual couch angle adjustments.⁴ Meyer et al¹ stated that there was no systematic error because they observed a small mean error for their phantom study.

Margins between clinical target volumes (CTVs) and planning target volumes (PTVs) are often calculated using a formula proposed by van Herk et al.^5,6 This formula employed two independent statistical models including a patient-to-patient variation model that gives a mean preparation error in all fractions for each patient, and a random error model during treatment delivery owing to random tumour movement. A patient population coverage probability of 90% in a facility was calculated by the patient-to-patient variation model, and the random error model was used to add further margins by increasing penumbra widths. Our intracranial stereotactic radiotherapy (SRT) utilizes an Elekta Synergy® (Elekta AB, Stockholm, Sweden) linear accelerator (linac) equipped with a CBCT imager, XVI and a 6-DOF robotic couch, HexaPOD™ (Elekta AB), which are identical to the system that Meyer et al¹ described. Consequently, our study can be based on the small mean preparation error reported by Meyer et al, and the above margin model may not be applicable. In addition, the previous margin model assumed that the tumour was spherical, and the margin was defined in the radial direction of the spherical co-ordinate system. For example, Guckenberger et al² calculated the PTV margin in the radial direction using registration results for 47 patients with various treatment sites and fixation means, leading to a PTV margin of 1.7 mm that achieved 90% population coverage. Meanwhile, a more accurate margin formula in the Cartesian co-ordinate system that complies with patient couch movements was proposed, in which the margins were anisotropically defined along the x, y and z directions.⁷

The purpose of this study was to propose a PTV margin formula as per the Cartesian co-ordinate system for hypofractionated intracranial SRT under CBCT image guidance with a 6-DOF robotic couch.

METHODS AND MATERIALS

Patients

19 consecutive patient cases with intracranial lesions who underwent pre-treatment and post-treatment CBCT were consecutively selected for this study. We received informed written consent from all the patients before treatment. Their ages ranged from 44 to 92 years. Of the 19 cases, 11 were male and 8 were female. 11 patients had brain metastasis, 3 patients had acoustic schwannoma and 2 patients had primary brain tumour (malignant lymphoma and malignant meningioma). The prescribed total dose ranged from 20 to 40 Gy in four fractions, except for a case in which eight fractions were applied (only the first four fractions of this case were considered for the analysis).

Image-guided radiotherapy procedure

SRT was performed for intracranial lesions using an Elekta Synergy linac equipped with a CBCT imager, a 6-DOF couch, a HexaPOD and a mouthpiece-assisted mask system, Uni-frame® and Precise Bite™ (CIVCO, Kalona, IA). For intracranial treatment, an add-on dynamic multileaf collimator (Elekta AB) with a leaf width of 3 mm was used.

Bone anatomy matching was performed between a reference planning CT image and a CBCT image acquired immediately before treatment. The patient couch was repositioned according to the positioning errors derived from the bone-matching calculation. Immediately after treatment, another CBCT image was acquired, and a time-averaged patient-positioning error during treatment was estimated by registering the post-treatment CBCT image to the reference planning CT image by bone matching. The duration from the start of the pre-treatment CBCT to the end of the post-treatment CBCT data acquisition was 13.8 ± 4.7 min, wherein each half-arc CBCT required a scanning time of 30 s.

Proposed margin formula

The traditional van Herk formula assumed that the mean interfractional preparation error for each patient statistically deviated among patients, which could be approximated by a gaussian distribution with a SD of Σ. Under this assumption, a PTV margin required for a CTV dose >95% of a prescribed dose for 90% of the patients in a facility was given by 2.5 Σ under a spherically symmetric condition, thereby leading to an isotropic margin perpendicular to a spherical tumour surface (i.e. in the radial direction).⁵ Subsequently, van Herk showed that a treatment execution error should be added to the above PTV margin owing to random tumour movement during treatment. When the random movement was approximated by another gaussian distribution with an SD of σ, the additional margin was given by 1.64 times the SD of total execution errors combined with the penumbra width, minus 1.64 times the SD corresponding to the penumbra width.⁵ The combined formula was further reduced to 2.5 Σ + 0.7 σ with a maximum error of 1 mm, provided that the SD corresponding to the penumbra width is 3.2 mm and the SD of the total execution errors is <5 mm.⁵

When CBCT is used for phantom positioning, the resulting preparation error is expected to be less than a pixel dimension of the reconstructed CBCT (approximately 0.5 mm), which was validated by Meyer et al.¹ When CBCT is used for patient tumour positioning, we can therefore assume that the PTV margin needs to be calculated by random errors, which may be approximated by a gaussian distribution model with a mean of zero and an SD. We also assume that the SD may be calculated by all the treatment execution errors for all the patients in a facility.

In this study, PTV margins that provide a treatment fraction coverage probability of 90% for the entire population are calculated along the x, y and z directions on the basis of the SDs of a three-dimensional (3D) gaussian distribution model for positioning errors,⁷ in which the coverage probability of 90% corresponds to 2.11 times the SDs of the 3D gaussian distribution in the Cartesian co-ordinate system. This is owing to the fact that recent image-guided radiotherapy is performed under Cartesian co-ordinate system with a 3- or 6-DOF couch, and the positioning errors may not be spherically symmetric thereby discouraging use of 2.5 times SD. Because the SD was calculated by all the treatment execution errors in each axis, the coverage probability in this study does not refer to patient population but to treatment fraction.

RESULTS

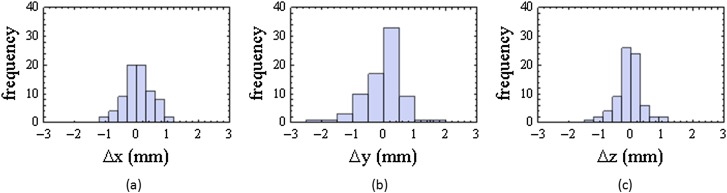
Figure 1a–c illustrate histograms of the skull-positioning errors in the x, y and z directions for the 19 patients, respectively. Although the number of samples was not sufficiently large, it was assumed that each histogram could be approximated by a gaussian distribution with a mean of zero.

Figure 1.

Histograms of the skull-positioning errors in (a) x, (b) y and (c) z directions for the 19 patients. In this study, it was assumed that each histogram could be approximated by a gaussian distribution with a mean of zero.

Table 1 depicts means and SDs of the skull-positioning errors measured immediately after treatment for the 19 patients in each of 4 fractions in x, y, z, R_x, R_y and R_z directions, where the x axis goes from left to right, the y axis goes from caudal to cranial and the z axis goes from posterior to anterior directions. R_x, R_y and R_z are rotation angles around the x, y and z axis, respectively. Mean errors in all fractions are also shown with SDs. Having assumed that the execution errors are approximated by a 3D gaussian distribution as observed by Figure 1a–c, the PTV margins in the x, y and z directions were calculated as 2.11 times each SD marked by ^a in each direction as shown in Table 1,⁷ leading to 0.97, 1.30 and 0.88 mm, respectively.

Table 1.

Means and standard deviations (SDs) of the skull-positioning errors measured immediately after treatment

Direction	Fraction number				All fractions	2.11 SD
	1	2	3	4
x (mm)	−0.05 ± 0.47	−0.12 ± 0.42	0.16 ± 0.44	−0.04 ± 0.49	−0.01 ± 0.46a	0.97
y (mm)	−0.07 ± 0.75	−0.11 ± 0.72	−0.23 ± 0.60	−0.02 ± 0.45	−0.11 ±  0.63a	1.30
z (mm)	−0.16 ± 0.54	−0.06 ± 0.38	−0.06 ± 0.41	−0.23 ± 0.29	−0.13 ± 0.42a	0.88
Rx (deg)	0.10 ± 0.42	0.18 ± 0.36	0.06 ± 0.29	0.15 ± 0.29	0.12 ± 0.34
Ry (deg)	0.15 ± 0.38	−0.08 ± 0.51	−0.08 ± 0.41	−0.1 ± 0.35	−0.03 ± 0.42
Rz (deg)	−0.03 ± 0.44	−0.19 ± 0.68	−0.22 ± 0.60	−0.33 ± 0.56	−0.19 ± 0.57

Each error was calculated by the bone-matching procedure available in the on-board cone beam CT system, and therefore, considered as an average positioning error during beam delivery. Mean errors in all fractions are also shown with SDs.

^aPlanning target volume margins were calculated by 2.11 times the SD in x, y and z directions.

DISCUSSION

The PTV margins required for hypofractionated intracranial SRT under CBCT image guidance with a 6-DOF robotic couch have not been published as a function of bone registration errors. In this study, it was assumed that the treatment execution error distribution after CBCT-based registration with a mouthpiece-assisted mask and the HexaPOD couch could be approximated by a single 3D gaussian distribution with a mean of zero and three anisotropic SDs in the x, y and z directions. Applying the resulting three SDs to a previously proposed anisotropic formula⁷ led to PTV margins in the x, y and z directions that covered 90% of the treatment fractions in our facility. Our empirical PTV margin is isotropically 2 mm towards a direction perpendicular to a CTV contour on each CT axial slice. The calculated SDs resulted in a planar margin of 1.3 mm as a vector length on the xz plane, which is consistent with our clinical margin setting of 2 mm.

A major limitation of this study was that the number of samples was not large enough to firmly confirm the assumption of our model; and therefore, the validity of the proposed mathematical model should be further investigated after accumulation of more cases. Lastly, rotation angle errors were ignored for the margin calculation, which may be allowed for a single small tumour positioned at the linac isocentre.

CONCLUSION

A PTV margin formula was proposed for hypofractionated intracranial SRT based on a 3D gaussian random error model in the Cartesian co-ordinate system. Using clinical data, it was shown that each histogram of the in-treatment positioning error in each axis would approach a single gaussian distribution with a mean of zero. The calculated PTV margins in the x, y and z directions were 0.97, 1.30 and 0.88 mm, respectively. The empirical isotropic PTV margin of 2 mm used in our facility for intracranial SRT was consistent with the margin calculated by the proposed gaussian model.