Evidence Synthesis for Medical Decision Making and the Appropriate Use of Quality Scores

Abstract

Meta-analyses today continue to be run using conventional random-effects models that ignore tangible information from studies such as the quality of the studies involved, despite the expectation that results of better quality studies reflect more valid results. Previous research has suggested that quality scores derived from such quality appraisals are unlikely to be useful in meta-analysis, because they would produce biased estimates of effects that are unlikely to be offset by a variance reduction within the studied models. However, previous discussions took place in the context of such scores viewed in terms of their ability to maximize their association with both the magnitude and direction of bias. In this review, another look is taken at this concept, this time asserting that probabilistic bias quantification is not possible or even required of quality scores when used in meta-analysis for redistribution of weights. The use of such a model is contrasted with the conventional random effects model of meta-analysis to demonstrate why the latter is inadequate in the face of a properly specified quality score weighting method.

A common problem with meta-analyses is that they combine results from studies that may be quite heterogeneous (in terms of the effect estimate) and efforts have been made to account for this heterogeneity in meta-analytic summaries. One common method of dealing with this has been through study “quality appraisals” that usually involve quantifying the number of study deficiencies according to a pre-specified number of components (items) that are reported in or can be inferred from the published paper. The premise is that a poor quality study may lead to systematic bias in the estimate of a treatment’s effectiveness, if it avoids protecting the study from threats to internal validity.¹ In addition, the number of non-faulty quality traits are presumed to predict the extent to which aspects of a study’s design and conduct protect against biases and inferential errors.² Although such quality assessment has sometimes been extended beyond the appraisal of internal validity, in this discussion reference will only be made to the latter—how well the study was designed and executed to prevent systematic errors or bias.³ If the quality items or traits are assigned a number of points based on the a priori judgment of clinical investigators, they can then be summed into a univariate “quality score” that has previously been given the interpretation of capturing the essential features of a “multidimensional quality space”^3,4 and has been used as a weighting factor in averaging across studies.^5–7 or as a covariate for stratifying study results.^8,9

Greenland has raised scientific objections to the creation of this sort of univariate quality score from quality items.^4,10,11 This seems to be supported by empirical findings of deficiencies when stratifying by such scores⁸ or when associating them with variations in treatment effects,^12,13 although there are also reports of beneficial inferences through such scores.^3,14 Greenland suggests that the rationale behind their use as weights in meta-analysis lacks rigorous justifications and may even be in error and proposed instead direct modeling of component item quality.⁴ In agreement with Greenland, there has been the emergence of component item quality modeling schemes,^15,16 but this paper will attempt to show that, in general, correct quality-score weighting methods can produce less variable effect estimates, as has been suggested by some authors who continue to use and even promote such scores.^6,17,18 This justification stands, even when the component quality items do not capture all traits contributing to bias in study-specific estimates. Furthermore, an attempt will be made to demonstrate if the possible decrease in variance with such quality weighting can be a worthwhile trade-off against bias and how it performs against the random effect methods. It will be argued that quality-score weighting methods take precedence over direct modeling of quality dimensions,¹⁵ in part because the impact of a quality dimension on the direction or magnitude of an effect estimate are unknowns. It will also be demonstrated that for quality weights to work well only requires the quality score to be constructed to maximize its correlation with study deficiencies that have an impact on study effects, rather than any requirement for the quality score to be a specific function of quantitatively measured bias.

Bias, Quality and Meta-Analysis Models

The following evaluation starts off, as suggested by Greenland and O’Rourke,⁴ with a response-surface model for meta-analysis where the expected study-specific effect estimate is a function of the true effect in the study, plus bias terms that are influenced by quality items. Exactly the same terminology and notation as used by Greenland and O’Rourke will be used to make it clear to readers where the divergence is; so let i = 1, ..., I index studies, and let X be a row vector of J quality items. For example, X could contain indicators of quality of the design or conduct of a study, such as use of blinding or allocation concealment in meta-analyses of randomized trials, or measures taken to avoid confounding in meta-analyses of observational studies. Similarly, δ_i= expected study-specific effect estimate; θ = the parameter that the meta-analysis aims to estimate (which is the true but unknown effect of study treatment), and χ_i = value of X for study i. The study-specific estimate δ_i, is the effect size actually reported in study i (such as a standardized mean difference). If χ_o is the value of X that is a priori taken to represent the “best quality” with respect to the measured quality items, then the response-surface approach⁴ has been used to model δ_i as a regression function of θ and χ_i, and a simple fixed effects additive model would be:

$${\delta }_i=\theta +b_i$$ (1)

where b_i is the bias resulting in deviation of δ_i from the true value θ, and which has previously been interpreted as being associated with χ_i deviating from the ideal χ_o, with this ideal supposedly implying lack of bias. In reality, this model is constrained by the fact that quality scoring does not specify the value of b_i accurately, in the sense that even when a study has an ideal value χ_o, there would still be a bias component of δ_i that is due either to other unmeasured quality items or that is poorly measured by the quality assessment scale or both (ie, X cannot be expected to capture all bias information). In this situation, and because there are only a few (I) observations δ̂_i, ..., δ̂_i, in most meta-analyses, these data constraints need to be overcome by specifying a more appropriate model. Current methods do so by employing models in which neither b_i nor its component effects are present and, therefore, in order to capture more uncertainty than fixed effect models, resort to constraining the underlying effect of interest to be a random effect drawn from a fictional distribution with unknown mean and variance. These models have been criticized for the fictional assumption that there is a random sample of studies in a meta-analysis¹⁹ or ignoring study traits such as differences in the way in which treatment protocols were designed or conducted.^6,20 So, rather than add a fictional residual random treatment effect to the model, this paper diverges from other authors^4,7 by assuming that while the θ can be treated as fixed, the effects of bias on the uncertainty of estimates can be included by the creation of a synthetic standard error that includes a component of variance for between study bias,^21,22 and thus, model 1 becomes

$${\delta }_i=\theta +b_i=\theta +\beta +{\varepsilon }_i$$ (2)

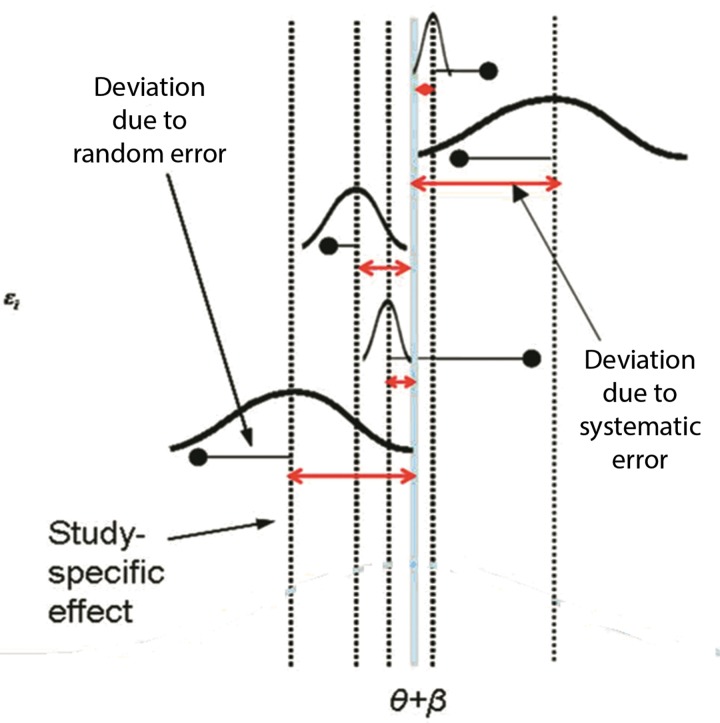
Under model 2, E(δ_i) = θ + β, E(ɛ_i) = 0, var(ɛ_si) = φ_i² with s indexing study subjects, b_{i ~} N (β, φ²) and β (the super-population bias across studies), though expected to be zero, may not cancel across studies if systematic biases were predominantly in one direction. It is unlikely that under model 2, the study specific bias effects, ɛ_i and the sampling error residuals δ̂_i – δ_i are correlated, but even so, χ_i cannot be used to estimate θ from the bias-adjusted estimates δ̂ – b_i, since measurement of b_i cannot be achieved through interpretation of χ_i. Some researchers have suggested that quality reflects the within study variability that is unrelated to internal biases,¹⁶ ie, ν_i /(ν_i + φ_i2), where ν_i = var(δ̂_i | δ_i), but this seems to contradict the type of information available from quality appraisal. Rather, from model 2, χ_i can be expected to reflect the proportion of the total bias variability that is unrelated to internal study biases, ie, φ² /(φ² + φ_i²). There is then the expectation that the model would improve if χ_i can be used to redistribute weights, such that it reduces the variance of the weighted estimator, or in the case of non-zero β, reduces it far enough to counter the increase in bias. This model is depicted in figure 1, and it is of interest to note that bias variances need not be known for this model use of information contained in X.

Figure 1.

Conceptualization of model 2.

Methodology of Quality Weights

As described by Greenland,⁴ to create a univariate score, the vector of quality items X can be replaced with a unidimensional scoring rule s(X), which is usually a weighted sum Xq = ∑_j q_j X_j of the J quality items in X, where q is a column vector of “quality weights” specified a priori and commonly taken to be equal in the absence of specific weighting data. This score can then be re-scaled between 0 and 1 and is interpreted as an intraclass correlation. Since we do not know the value of the bias variances, we divide s_i by the maximum s_i in the list of studies resulting in the same minimum and maximum quality scores Q_i for any a priori specified function. The quality scores, Q_i, are then used for quality weighting by averaging the study-specific estimates, δ̂_i, after multiplying the usual inverse-variance weight by Q_i. For example, even though the unconditional variance of δ̂_i is ν_i + φ_i², the usual inverse variance weight for δ_i would be ŵ_i = 1/ νⁱ (since φ_i² is unknown), and the “quality-adjusted” weight is Q_i w_i.⁶ If the quality score is conceptualized as maintaining a monotonic relationship with the ratio of between to total bias variance, it can then be used to redistribute study weights away from studies of lesser quality and thus greater internal “noise.” The latter weights can be expected to decrease variance of the weighted estimator, because s_i ≡ φ² /(φ²+ φ_i²)²³ and, thus, the proportional contribution of φ_i² to total bias (in the context of the studies within the meta-analysis of interest) declines in a monotonic fashion as s_i increases from zero to 1.

This sort of weighting does not require X to contain all bias-related covariates, and the quality score need not be a function of quantitatively measured bias. Also, Q_i = 1 does not imply the absence of study deficiencies, but rather the relative strength (rank) of the study given the data at hand. To see how this works, the same example given by Greenland⁴ can be taken. Let u_i be any study-specific weight and let a subscript u denote averaging over studies using the u_i as weights then for example:

$${\delta }_u=\sum u_i\hspace{0.17em}{\delta }_i/\sum u_i$$ (3)

Under model 2,x

$${\delta }_u=\theta +b_u=\theta +\beta +{\varepsilon }_u$$ (4)

Thus, δ_u equals the true effect θ plus external bias across studies (if any) plus the u-average internal bias ɛ_u. Therefore, any unbiased estimator of δ_u will certainly be biased for θ in those situations where the super-population bias across studies does not cancel and thus β ≠ 0. The expectation, however, is that even under the latter constraint, such bias will be overshadowed by the expected decrease in overall variance of this weighted estimator such that an optimal bias-variance trade-off can be reached. The coverage properties of the estimators CI has further been augmented by creating a system that redistributes weights from lower scoring studies to other studies proportional to their values on Q_i.¹⁷ All that is required of the quality scores in this model is that they are a monotone function of the safeguards in a study and so rank the studies with respect to safeguards (rather than be any fixed function of bias).⁶ It is important that such identified safeguards have a clear link to systematic error, and so cannot be ethical concerns or attributes linked solely to precision. The use of quality weighting in this way means that the two assumptions outlined by Greenland⁴ are acknowledged: (a) that there is useful information in studies of less-than-maximal quality, and that some degree of bias is tolerable if it comes with a large variance reduction, and (b) that errors due to bias are not considered more costly than errors due to chance, as would be implicitly assumed had we limited our attention to unbiased estimators.

Issues with Quality Scoring

An important issue where care must be taken is to ensure that the quality scoring rule contains items relevant to systematic bias (eg, excludes items related to whether power calculations were reported or ethics was properly sought), as such items will disproportionately reduce the impact of the resulting scores, even if conceptualized as deficiency scores given that these deficiencies must still link to systematic error. Furthermore, inclusion of such items can distort deficiency rankings of the studies as well.

Another issue is that given that the scoring rule s(X) is usually a weighted sum of the J quality items in X, where q is a column vector of “quality weights” there should be special attention given to determining the proper weight q that an item should have. In the absence of such weighting data, q is currently taken to be an equal weight across items. There is thus an urgent need to generate this information from meta-epidemiological studies.

Greenland has alluded to “score validations” as being typically circular,⁴ in that the criteria for validation hinge on score agreement with opinions about which studies are “high quality,” not on actual measurements of bias. This argument is no longer circular if score measurements are viewed in the context of study deficiencies, since actual measurement of bias is no longer being sought through quality scores. Greenland also suggests that perhaps the worst problem with common quality scores is that they fail to account for the direction of bias induced by quality deficiencies.¹⁰ While this failing can nullify the value of a quality score in regression analyses based on the bias modeling outlined by Greenland,⁴ not so in quality weighted meta-analyses (as defined here), as neither magnitude nor direction of bias are being assessed. In this paper, the pragmatic view is being taken that a study with two or more identified deficiencies can be afflicted by more bias variance than one with none regardless of the magnitude or direction of the resulting bias. Thus, bias cancellation phenomena are not relevant when quality scores are conceptualized of as deficiency scores, and there is also no need to reconstruct a quality score as a bias score with signs attached to the contributing items as illustrated by Greenland⁴ or by Thomson et al.¹⁵ Indeed, the amount of bias expected a priori and their directions are unknowns that cannot and should not be imputed when constructing the quality scores. Hence, reconstructing the scores to maximize their correlation with bias^4,15 does not appear to be necessary or essential for the intelligent use of quality scores in properly specified quality effects models such as that described in this paper or reported by others.^17,18

Finally, how the proposed model for quality scores could be used to further clinical decision support through research synthesis is, in general, a bigger question and an area of ongoing controversy. It would be envisaged that in the future, special interest groups could take the lead in quality scoring all the pertinent literature in their field based on their own consensus criteria. Currently, this is being done by the PEDro database owners, and recently they were criticized for this,²⁴ but we were quick to respond to this criticism in their support.²⁵ The availability and acceptance of models described in this paper should help pave the way for more widespread support for such endeavors in the near future.

A Comparison of Quality and Random Effect Models

A simulation can be set up under model 2 by assigning a value θ =0.5, representing a standardized mean difference effect size. Five hypothetical studies can be generated by incorporating N randomly allocated subjects (constrained between 50 and 1000 in steps of 50 by generating a random integer between 1 and 20 and multiplying by 50) in each study and assuming N/2 are in the treatment and control groups respectively for simplicity. Bias, b_i, is generated and added to each study by arbitrarily assigning β = 0 (making the assumption that external biases across studies cancel, thus resulting in an unbiased estimator) and fixing φ² at an arbitrary 0.15, which is about 10-fold higher than the average v_i based on the true effect (0.5) and study size (N) (to make the studies heterogeneous). Since the external bias variance for the meta-analysis has been fixed, and if the probability of credibility or quality (s_i) input for each study is also fixed, this can then be used to simulate the individual study bias variances since φ_i² ≈ (φ² – φ²s_i) /s_i. The values of were fixed at 0.1, 0.2, 0.5, 0.8 and 0.9 for studies 1 to 5 respectively. Even though latter quality input is fixed, because the actual φ² value for each set of studies will differ from the starting value, the actual quality also differs from these values (though rank by quality remains the same). This adds the required “subjectivity” in quality assessment to the analysis.

Thus, with the true underlying parameter of interest fixed at 0.5, then for each study i=1,…,5, δ_i = 0.5 + β + ɛ_i can be generated by sampling ɛ_i from a normal distribution with mean 0.5 (β = 0) and variance φ_i². The final study estimate δ̂_i, is then determined by adding sampling error to δ_i by generating this error from a normal distribution with mean zero and variance $v_{ES=\mathit{0.5}}=\frac{4}{N}+\frac{{0.5}^2}{\mathit{2}N}$. A set of five studies are finally created with effect size δ_i and variance $v_i=\frac{4}{N}+\frac{{\widehat{\delta }}_i^{\mathit{2}}}{\mathit{2}N}$, and this set of studies is then the simulation set. To generate the study estimates for each iteration, a simulation software (Ersatz version 1.3; Epigear International Pty Ltd) was used. Essentially, each simulation underwent 50,000 iterations, and at each iteration first created five studies, then meta-analyzed them and finally computed the input for the performance measures and stored these. Then, the next iteration did the same and so on until 50,000 iterations were completed. The meta-analysis estimates computed under each iteration for both the random and quality effects methods used another plug-in (MetaXL version 1.3, Epigear International Pty Ltd) that includes the analogous quality effects (QE) model of Doi and Thalib^6,26 and the random effects (RE) model of Dersimonian and Laird.²⁷ Performance measures were then computed as detailed by Burton et al.²⁸ This process was then repeated, in run 2 with β = 0 but randomly mis-specified quality input into the quality effects model and then, in run 3 for β = 0.1 (and properly specified quality) to simulate 20% external bias across the latter studies. Model and study parameters are summarized in Table 1 across the three simulation runs.

Table 1.

Summary of simulation parameters.^*

Simulation	Model parameters	Study parameters	Values allocated through simulation
1	θ = 0.5	si fixed at 0.1, 0.2, 0.5, 0.8 and 0.9 for studies 1 to 5 respectively	N was randomly allocated between 50 and 1000 in steps of 50 with N/2 in each group (intervention/control)
	β = 0
	φ2 = 0.15	δi = 0.5 + β + ɛi
		φi2 ≈ (φ2 – φ2si) /si	δi ~ N (0.5, φi2)
		${\text{v}}_i=\frac{4}{N}+\frac{{\widehat{\delta }}_i^{\mathit{2}}}{\mathit{2}N}$	${\delta }_i~N({\delta }_i,\frac{4}{N}+\frac{{0.5}^2}{\mathit{2}N})$
2	Same as simulation (1)	Qi randomly allocated between 0.1 and 0.9. Rest same as simulation (1)	Same as simulation (1)
3	β = 0.1	Same as simulation (1)	δi ~ N (0.6, φi2)
	Rest same as simulation (1)		Rest same as simulation (1)

^*performance measures used are defined in Burton et al ²⁸

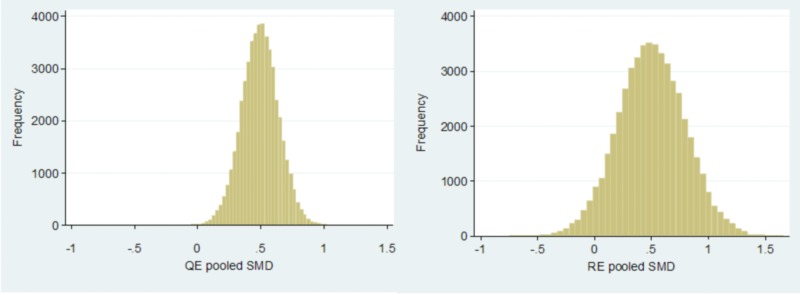
Results were exactly as expected. With β = 0 and properly specified quality, the RE model had a MSE (0.0862) that was four-fold higher than the MSE (0.0212) of the QE model (figure 2). However, there was not much bias that was similar with the QE (−1.1%) compared to the RE model (0.09%). Coverage probability and CI width were better at 97.6% and 0.81 with the QE model compared to 89.7% and 0.99, respectively, with the RE model. In addition, 76% of the pooled estimates were closer to the parameter of interest with the QE as compared to the RE model.

Figure 2.

Comparison of the distribution of pooled estimates by the quality effects (left panel) and random effects (right panel) models when β = 0 and quality is not-mis-specified (simulation 1).

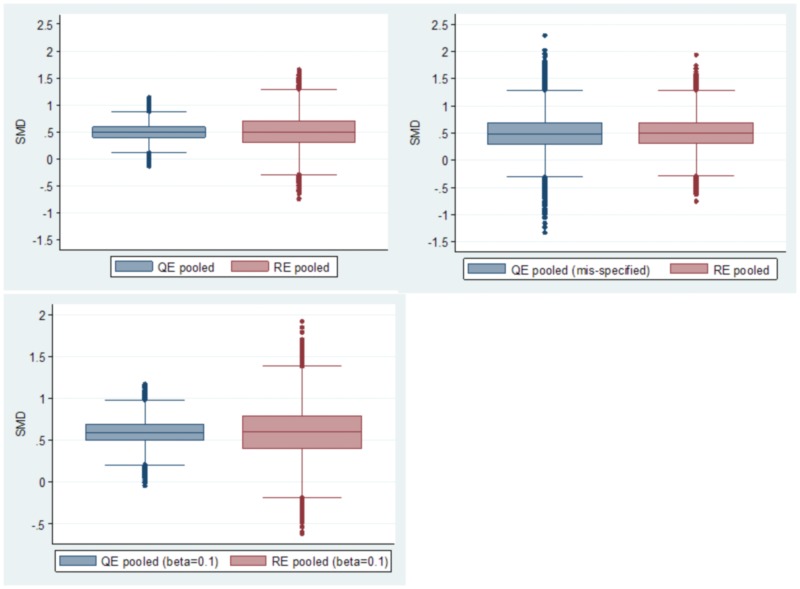
When Q_i was mis-specified at the point of meta-analysis only, (replaced by a random quality between 0.1 and 0.9 by generating a random integer between 1 and 9 and dividing by 10), the QE model results now became identical to that of the RE model (MSE 0.10 vs 0.09; figure 3, top right panel). The latter is because the QE model with random misspecification simply defaults to a RE model. When super-population bias was constrained to a non-zero value (0.1), but with proper specification of quality (figure 3, lower panel), both models were equally biased (18.8% [0.094] QE vs 19.6% [0.098] RE), but the QE model had a much better bias-variance tradeoff (MSE 0.0299 vs 0.0959). Coverage of the CI and CI width were 95% and 0.81 with the QE model compared to 85.5% and 0.99 with the RE model. This is depicted in the lower panel of figure 3. While these simulation results presented here need to be reproduced in wide-spread real world applications, they fit well with the theoretical model, and thus there is every expectation of similar results with real world applications.

Figure 3.

Comparison of the distribution of pooled estimates by the quality effects model when β = 0 (top left panel; simulation 1) and mis-specified quality effects model when β = 0 (top right panel; simulation 2) in comparison to the RE model. The bottom panel (simulation 3) represents the constraint that β = 0.1. Each panel represents a separate simulation run with 50,000 iterations involving 250,000 individual studies.

Conclusion

The random effects model, with the assumption that the true effect θ varies in a simple random manner across studies, has no credibility^4,29 and, therefore, the quality weighted model analogous to the theory outlined above addresses this by allowing bias to vary and redistributing weights through quality based on the expected bias variance differences across studies. In this case, however, the quality score is no longer conceptualized as a bias score, but rather a deficiency score, and this is necessary because the impact of quality dimensions on the direction and magnitude of bias are unknowns. However, Greenland visualized quality information as a means to specifying bias magnitude and direction quantitatively, and was thus forced to conclude that common quality score methods are both biased as well as require special cases of mixed effect meta-regression models.⁴ Currently, there exists one model that implements the bias-variance concept through quality scores, and it is demonstrated here via simulation that under all constraints, it would certainly represent a model with a better bias-variance tradeoff than the random effects model. It is also demonstrated here that the random effects model is simply a quality effects model, where quality is randomly assigned to studies (a mis-specified quality effects model) and nothing more. This then obviates the common argument regarding the subjectivity of quality scoring, since in the worst case scenario (a completely random assignation of the quality score to studies), the performance of both models converge. The latter precludes criticism regarding the subjectivity of the quality scores, because so long as they contain some information value, the quality effects estimator will always outperform the random effects estimator. Improvements to the quality effects model can be expected to occur as quality assessment tools become more objective and validated over time, and more information accrues regarding the appropriate weighting of quality items within a univariate score. It, therefore, seems that the time is right to herald the discontinuation of such “random effect” models in the face of better alternatives and available software. It is hoped that this would herald a new era of more reliable research synthesis results through meta-analysis.