Coupled Positive and Negative Feedbacks Produce Diverse Gene Expression Patterns in Colonies

ABSTRACT

Formation of patterns is a common feature in the development of multicellular organism as well as of microbial communities. To investigate the formation of gene expression patterns in colonies, we build a mathematical model of two-dimensional colony growth, where cells carry a coupled positive-and-negative-feedback circuit. We demonstrate that the model can produce sectored, target (concentric), uniform, and scattered expression patterns of regulators, depending on gene expression dynamics and nutrient diffusion. We reconstructed the same regulatory structure in Escherichia coli cells and found gene expression patterns on the surface of colonies similar to the ones produced by the computer simulations. By comparing computer simulations and experimental results, we observed that very simple rules of gene expression can yield a spectrum of well-defined patterns in a growing colony. Our results suggest that variations of the protein content among cells lead to a high level of heterogeneity in colonies.

Importance Formation of patterns is a common feature in the development of microbial communities. In this work, we show that a simple genetic circuit composed of a positive-feedback loop and a negative-feedback loop can produce diverse expression patterns in colonies. We obtained similar sets of gene expression patterns in the simulations and in the experiments. Because the combination of positive feedback and negative feedback is common in intracellular molecular networks, our results suggest that the protein content of cells is highly diversified in colonies.

IMPORTANCE

Formation of patterns is a common feature in the development of microbial communities. In this work, we show that a simple genetic circuit composed of a positive-feedback loop and a negative-feedback loop can produce diverse expression patterns in colonies. We obtained similar sets of gene expression patterns in the simulations and in the experiments. Because the combination of positive feedback and negative feedback is common in intracellular molecular networks, our results suggest that the protein content of cells is highly diversified in colonies.

INTRODUCTION

In living organisms, variations in gene expression can be observed both within and between populations (1, 2). Heterogeneity in gene expression has a substantial influence on susceptibility to disease, disease prognosis, the efficiency of drug therapy, and development of mental health disorders such as drug dependence (3–5). Bacteria use gene expression variation to evade the host immune system and antimicrobial treatment (6). Patterns in living organisms are formed by cells which have the same genome but execute different gene expression programs, i.e., express a different subset of genes, as seen in biofilms (7) or self-organization of multicellular organisms (8).

Heterogeneity of gene expression in individuals can be attributed to either genotypic or nongenotypic variations. Genotypic variations are heritable changes in DNA sequence that cause expression differences, such as single nucleotide polymorphisms (SNPs) and copy number variations (CNVs) of expression qualitative trait loci (eQTLs) (9). Nongenotypic variations include epigenetic modifications and also gene expression stochasticity at the single-cell level (10, 11).

There are two different reasons for temporal fluctuation of gene expression in a single cell. Gene expression is generally affected by noise, which results from processes of a random nature, e.g., production and degradation of gene products, and interactions that require collision of diffusible molecules. In general, processes carried out by fewer molecules have higher noise (12). The other class of fluctuations is due to the regulatory network architecture and affects only a subset of genes.

Gene regulatory networks contain many positive and negative feedbacks (13), which provide basic functions that cells require to survive. For example, positive feedbacks provide “switches” which allow cells to be in one mode or another (e.g., make a gene silent or active) and maintain the chosen state for several generations by epigenetic memory. Negative feedbacks are widely used to maintain homeostasis; however, with a time delay, they can cause stable oscillations (14). During development of multicellular structures, daughter cells stick together and the epigenetic memory may appear visible as a spatiotemporal expression pattern. Colonies grown from a mixture of genetically different cells show sectored patterns that result from segregation of cells into monoclonal domains (15). Cells inside colonies can communicate by diffusible signals, which may coordinate gene expression and result in pattern formation (16, 17). Also, nutrient diffusion is a primary morphogenetic determinant, but its effect can be overruled by the genetic circuitry regulating expression of a gene (18).

In this work, we utilized a combination of mathematical modeling and experiments to explore pattern formation in colonies of genetically identical cells which can shift between high and low gene expression states. To understand the major determinants of pattern formation, we built a mathematical model of colony growth where cells carry a coupled positive- and negative-feedback loop. We demonstrate that coherent patterns can be formed by the concerted action of the epigenetic memory of the cell state, mechanical interactions between the cells, and implicit cell-cell communication by nutrient consumption. We analyze how formation of target, sectored, and nonsectored patterns depends on gene expression dynamics, which is affected by the stability of the components, the strengths of regulatory interactions, and the properties of the promoters used. We reconstructed the circuit in Escherichia coli cells and found intricate gene expression patterns on the surface of colonies which are qualitatively in agreement with the patterns produced by the computer simulations.

RESULTS

Description of the mathematical model for colony growth and pattern formation.

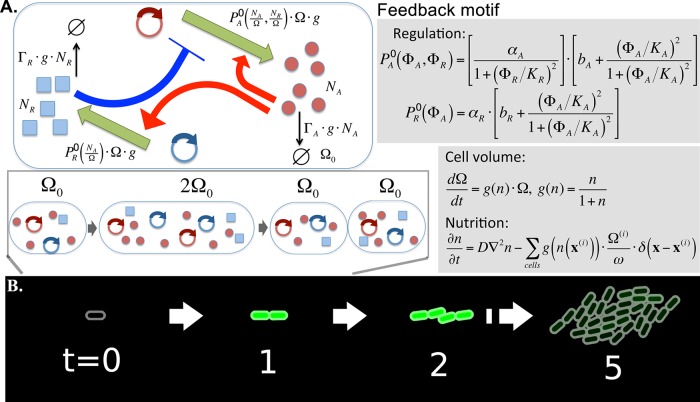
To explore the possible gene expression patterns and the main determinants of their formation in a growing colony of genetically identical cells, we constructed a mathematical model. We consider cells carrying a simple genetic-feedback motif with combined positive and negative feedbacks (Fig. 1A). Despite their simplicity, coupled positive- and negative-feedback loops are core motifs in the regulation of different pathways in both prokaryotes and eukaryotes (19–22). The behavior of this motif has been extensively studied under conditions of constant growth (23). It is known to produce oscillatory gene expression in a wide range of parameters at constant growth rates, as well as monostability and bistability, depending on the parameters (see Fig. S1 and S2 in the supplemental material). In this circuit regulator A activates both its own transcription and the transcription of protein R, which in turn inhibits transcription of A. We simulate the stochastic production and degradation of proteins A and R in each cell. At the same time, each cell experiences exponential growth with a nutrition-dependent growth rate g(n), and when the cell’s volume reaches the threshold value, the cell splits into two cells. Nutrients, which are initially distributed uniformly, are consumed and diffuse in 2-dimensional (2D) space as the cells grow. Cells are modeled as elongated objects in 2 dimensions that mechanically push each other, eventually forming a circular colony (Fig. 1B). We are interested in patterns formed after a relatively long time, when the nutrition becomes limited for cells located in the middle of the colony and their metabolic activities slow down. To include this effect in the simplest way, we assume that the production and degradation of proteins are proportional to the growth rate g(n). In order to see the effect of nutrient depletion in a relatively small colony in the simulations, parameters are set so that the consumption is fast enough to reveal the slowdown of growth within the present simulation scale. At the same time, the diffusion is fast enough not to induce the diffusion-limited instability in colony morphology which would result in a branching colony shape (24, 25). We also assume that gene copy numbers grow in proportion to the cell’s volume, which is a plausible assumption, especially for genes carried by plasmids (26). A detailed description of the simulation procedure is provided in Materials and Methods.

FIG 1 .

Schematic description of the model. (A) Activator A activates its own transcription and transcription of R, while R represses the transcription of A. Numbers of protein A, N_A, and protein R, N_R, were simulated stochastically. The cell volume is denoted by Ω; hence, the densities of proteins A and R are given by $N_A/\Omega$ and $N_R/\Omega$, respectively. The production rates of A and R are assumed to be $P_A^0\left({\Phi }_A,{\Phi }_R\right)\cdot \Omega \cdot g$ and $P_R^0\left({\Phi }_R\right)\cdot \Omega \cdot g$, respectively, where $P_X^0$ includes the effect of the activation and repression with Hill coefficient 2. The proportionality to cell volume Ω is due to the assumption that the gene copy number grows with the cell volume, while the proportionality to cell growth rate g is introduced as the simplest way to include the slowing down of the metabolism with the nutrition availability. Similarly, the active degradation of the protein is assumed to be proportional to g(n). The cell volume grows exponentially with nutrition (n)-dependent growth rate. The time unit is chosen so that the highest growth rate in very rich medium becomes unity. The nutrients diffuse with diffusion rate D and are consumed by the growing cells, with a proportionality constant between the growth rate and consumption rate of ω. A cell division happens when volume Ω reaches the threshold 2Ω₀, and proteins are stochastically separated to the two daughter cells. (B) As cells divide, cells interact mechanically to push each other, and eventually form a nearly circular colony.

Simulation of expression pattern formation in bacterial colonies.

Various patterns of protein A expression were obtained in simulations of colony growth which could be assigned to one of the three qualitative classes: concentric (target), sectored, and nonsectored. We first explored the case without the negative feedback through the repressor by setting the production rate of R (α_R) to zero (Fig. 2). In this positive-feedback motif, the parameters are chosen so that the single-cell dynamics of protein A expression shows bistable behavior. With the parameters used in Fig. 2A, the switching rate from (to) a low-A state to (from) a high-A state in a single cell growing at the maximum rate is 1 per 149 generation times (1 per 1,442 generation times). This long-lasting memory over many cell generations results in sectored patterns of high-A cells and low-A cells. When the parameters are set so that the switching rates are much higher (1 per 16 generation times and 1 per 9 generation times, respectively), the pattern becomes much more noisy, with many more sectors (Fig. 2B). When the single-cell dynamics does not show bistability, the level of A becomes rather uniform over the cells.

FIG 2 .

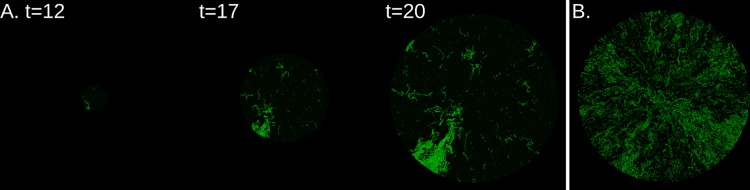
Pattern formation by colony growth model coupled with the positive-feedback motif that shows bistability. The repressor was removed by setting α_R = 0. There are about 80,000 cells in the biggest colonies. The aspect ratio of a cell just after cell division is 2:1, and the diameter of the biggest colony equals about 530 times the length of the shorter axis of the cell. The simulation is started with a cell which does not contain any A protein. (A) Time series of colony and pattern development using parameter values α_A = 240, b_A = 0.03, K_A = 36, and Γ_A = 240, measured in units of time scale (the generation time at maximum growth) and units of concentration (1 molecule per cell volume Ω₀). For the colony snapshots, the brightness is proportional to the density of the A proteins in cells, and the maximum level is tuned so that the cell with the highest concentration in time 20 (${\varphi }_A^{max}\approx 100$) appears as a fully saturated spot. (B) Representative result of simulations performed using a lower production rate of the A protein and more frequent switching between the high and low states (α_A = 60, b_A = 0.03, K_A = 9, and Γ_A = 2). The brightness was normalized by the maximum concentration${\varphi }_A^{max}\approx 35$.

The mixed-feedback motif containing the negative feedback through the repressor produced much richer patterns in the simulations. Figure 3 shows a time series of snapshots for a parameter set that produced oscillatory expression of A in single cells (see Fig. S1A in the supplemental material). When the colony size is small, the level of A oscillates in synchrony in all the cells, which appear as all parts of the colony being bright or dark at almost the same time (t = 11 and 12). As the colony grows, nutrients are depleted in the middle of the colony, slowing down the dynamics and making the oscillations out of phase. Changes in nutrient levels during simulations are shown in Fig. 3. When the colony becomes large enough, cells become metabolically inactive in the middle of the colony due to unavailability of nutrients; that is, in the simulations, we freeze the level of A in these cells. Note that the protein level does not correlate with the nutrition level, since, due to the food depletion, we stop the production, degradation, and dilution of proteins. Freezing the oscillatory expression at different phases leads to the formation of a “target” pattern (t = 20). Cells closer to the edge still grow and show an oscillatory behavior. However, the synchrony is lost due to the noise in the production and degradation of A. The elongated shape of cells and their mechanical interaction introduce a local ordering of cells with some buckling (27), which appears as a wiggly pattern of cells with high concentration of A.

FIG 3 .

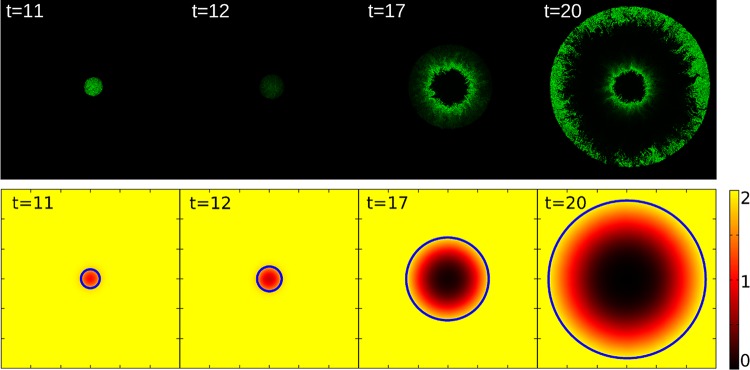
Pattern formation by the colony growth model coupled with the feedback motif. There are about 80,000 cells in the biggest colonies. All simulations are started with a cell that does not contain any A or R proteins. The top panel shows a time series of snapshots in the oscillatory case using parameter values α_A = 600,000, b_A = 0.001, K_A = 4,000, K_R = 200, α_R = 10,000, b_R = 0.001, Γ_A = 2, and Γ_R = 0.05. For the colony snapshots, the brightness is proportional to the density of the A proteins for each cell, and the maximal level is tuned so that the cell with the highest concentration in time 20 (${\varphi }_A^{max}\approx 10,200$) appears as a fully saturated spot. The spatial variations of nutrient levels are shown in the bottom panel. The color code indicates the nutrition level, and the blue circles show the edge of the colony at each time step. The whole simulated space (600 by 600) is shown.

The effect of noise on the target pattern is studied by changing the parameters so that the average protein copy number is 10-fold lower, while the oscillation time scales remain the same (Fig. 4B). The lower protein copy number results in relatively stronger noise. Stronger noise gives larger fluctuations in the oscillation period (28), which leads to faster desynchronization of the phases of oscillations in the daughter cells. This is reflected in the noisier pattern at the edge of the colony. If the relative noise is increased further, the target pattern is lost and high-A cells are scattered randomly in the colony.

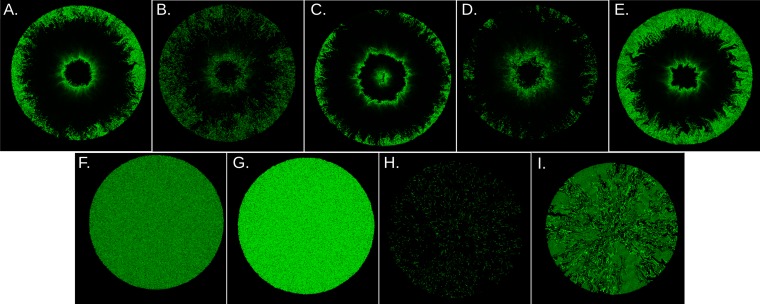
FIG 4 .

Pattern formation under different parameter regimes. (A) The pattern observed at t = 20 in Fig. 3 is shown for comparison. (B to I) The brightness was normalized by maximal concentration ${\varphi }_A^{max}$ in each image. Parameters used are the same as those described for panel A, unless otherwise noted. (B) Noisier oscillatory case with fewer molecules, obtained by α_A = 60,000, K_A = 400, K_R = 20, α_R = 1,000. The maximal concentration is ${\varphi }_A^{max}\approx 1,590$. (C) Oscillatory case with a shorter period, with α_A = 1,200,000, α_R = 20,000, Γ_A = 4, and Γ_R = 1. The maximal concentration is ${\varphi }_A^{max}\approx 9,000$. (D) Pattern obtained using shorter cells. The aspect ratio of a cell just after cell division is 1:1. The maximal concentration is ${\varphi }_A^{max}\approx 9,900$. The colony diameter is about 360. (E) A pattern obtained by elongated cells. The aspect ratio of a cell just after cell division is 3:1. The maximal concentration is ${\varphi }_A^{max}\approx 10,700$. The colony diameter is about 650. (F) A pattern observed with a high R production rate, α_R = 200,000. The maximal concentration is ${\varphi }_A^{max}\approx 2,600$. (G) A pattern observed with a low R production rate, α_R = 1,000. The maximal concentration is ${\varphi }_A^{max}\approx 21,000$. (H) A pattern observed with low basal A production, b_A = 0.0001. The maximum concentration is ${\varphi }_A^{max}\approx 14,200$. (I) A pattern observed with a low b_A (i.e., 0.0001) and α_R (i.e., 500). The maximal concentration is ${\varphi }_A^{max}\approx 168,000$. The corresponding system dynamics for panel A and for panels F to I in single cells are shown in Fig. S1 in the supplemental material.

The pattern is also affected by the oscillation period. When the single-cell oscillation period is shorter, the number of rings in the gene expression pattern increases (Fig. 4C). The brightness of the center of the colony is determined by the phase of the oscillation at the center when the food is depleted; hence, this also depends on the oscillation period.

The aspect ratio of the cell is another factor that affects the pattern obtained in the simulations. Less-elongated cells allow straighter boundaries between the bright and dark regions (Fig. 4D), while more-elongated cells produce patterns that are more wiggly (Fig. 4E).

The parameter region for the oscillatory behavior is limited (see Fig. S2 in the supplemental material), and by changing a few parameter values we can get diverse variations in patterns. To demonstrate this, we varied the production rate of R (α_R) and the level of A production in the absence of A-mediated activation (b_A) from the parameter set for Fig. 3 to study the effect of nonoscillatory A expression on patterns produced by the mixed-feedback motif. When the production rate of R was high (α_R = 100,000), the concentration of A was low for all the cells (Fig. 4F), while weaker R production (α_R = 500) resulted in high A levels in all the cells (Fig. 4G). The corresponding time developments of A level in single cells are shown in Fig. S1B and C in the supplemental material, respectively. Both of these conditions produced an almost uniform concentration of A in the colonies. However, in the case of low A, the relative difference between cells was higher because of the higher relative fluctuation. When the basal (nonactivated) level of A production was set to be low (b_A = 0.0001), only a few cells were observed with high A levels, appearing at rather scattered locations (Fig. 4H). In these cells, the A level was temporarily excited by noise. Once A was excited, it activated both A and R production, resulting in a high but short peak of A, followed by repression of A by R. Single-cell dynamics shows rather periodic noise-induced oscillation in this parameter region (see Fig. S1D in the supplemental material) (29). However, the phases of oscillations in different cells were not well synchronized; thus, the pattern looks scattered. Finally, in the bistable case, when cells were allowed to switch between the low- and high-A states due to noise (see Fig. S1E), sectored patterns of low-A cells and high-A cells were observable (Fig. 4I), in similarity to Fig. 2.

In summary, the model can produce sectored patterns when the feedback circuit provides bistability between high-A and low-A levels (Fig. 2 and 4I), target patterns when the feedback circuit shows temporal oscillation of the A level (Fig. 4A to E), uniform patterns when the system stays in a stable steady state (Fig. 4F and G), and a random scattered pattern when the feedback is excitable by noise (Fig. 4H).

Reconstruction of the circuit in E. coli.

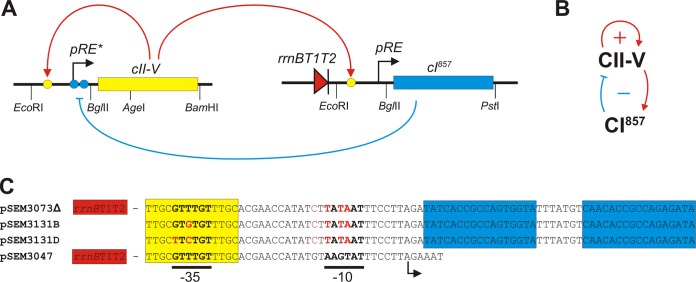
To explore pattern formation in vivo, we reconstructed the regulatory motif used in the in silico simulations in Escherichia coli cells. In this experimental system (Fig. 5), cells contain two different plasmids, each carrying a regulator (corresponding to A and R in the model) and the regulatory elements required for establishing the structure of the motif. The reconstructed circuit is based on regulators and regulatory elements obtained from bacteriophage λ. The λ regulators we utilize are CI (30) (equivalent to R) and CII (31) (equivalent to A). To be able to monitor the level of the activator in live cells in real time, we fused the short-lived CII protein to Venus yellow fluorescent protein (YFP), which has a very fast maturation time, obtaining a small (338-amino-acid) fluorescent activator protein called CII-V. We constructed three different plasmids containing a CII-V activated promoter, the CII-V open reading frame, and a properly placed ribosome binding element. These plasmids differed in the intrinsic (nonregulated) activity of the promoter (corresponding to b_A in the model) and in the copy number of the plasmid (Fig. 5C). The λ pRE promoter, which served as a basis for engineering the CII-V-regulated promoters, is not recognized as a promoter in the absence of CII (32). Therefore, we modified the pRE promoter sequence by replacing the −10 promoter element with the consensus sequence (TATAAT).

FIG 5 .

Elements and interactions of the circuit constructed in E. coli cells. (A) Schematic drawing of the regulatory elements and interactions. Yellow and blue circles represent CII and CI binding sites, respectively. The red triangle represents the rrnB T1T2 terminators which inhibit transcription of the CI gene from other promoters located upstream of pRE. Restriction sites used in the construction of the cassettes are shown on the bottom. Construction of the CII-V and CI expression cassettes is described in Materials and Methods. (B) Simplified structure of the coupled positive- and negative-feedback loops. (C) Sequences of the pRE derivative promoters used in the different plasmids. Red letters indicate changes relative to the wild-type pRE sequence. Yellow and blue boxes represent CII and CI binding sites, respectively. Positions of the −35 and −10 promoter elements and the transcription start site (arrow) are indicated below the sequences. Plasmid pSEM3073Δ has a high copy number but a lower level of unregulated CII-V transcription. Plasmids pSEM3131B and pSEM3131D have lower copy numbers but higher levels of unregulated CII-V expression due to mutations in the −35 region of the pRE derivative promoter. These plasmids also lacked the terminator sequence upstream of the pRE derivative promoter.

The negative feedback (Fig. 5B) was implemented by placing the CI gene in a low-copy-number plasmid under CII-V control (Fig. 5A). Transcription of the CI gene was initiated at the pRE promoter (Fig. 5C), which was placed downstream of two transcriptional terminators (Fig. 5A). In this way, CI expression occurred only in the presence of CII-V. CI is a stable protein (33); therefore, we created a second version of the plasmid which encoded CI fused to the ssrA degradation tag.

Expression patterns in colonies carrying the reconstructed circuit.

To explore pattern formation in colonies grown from single cells carrying the circuits composed of coupled positive- and negative-feedback loops (Fig. 5), the CII-V and CI expression plasmids were introduced into wild-type E. coli host cells. We used wild-type cells (strain K-12 MG1655) and cells in which enhanced CII stability was reported (mutants ΔhflK and ΔhflC) due to the lower activity of the FtsH (HflB) protease (34).

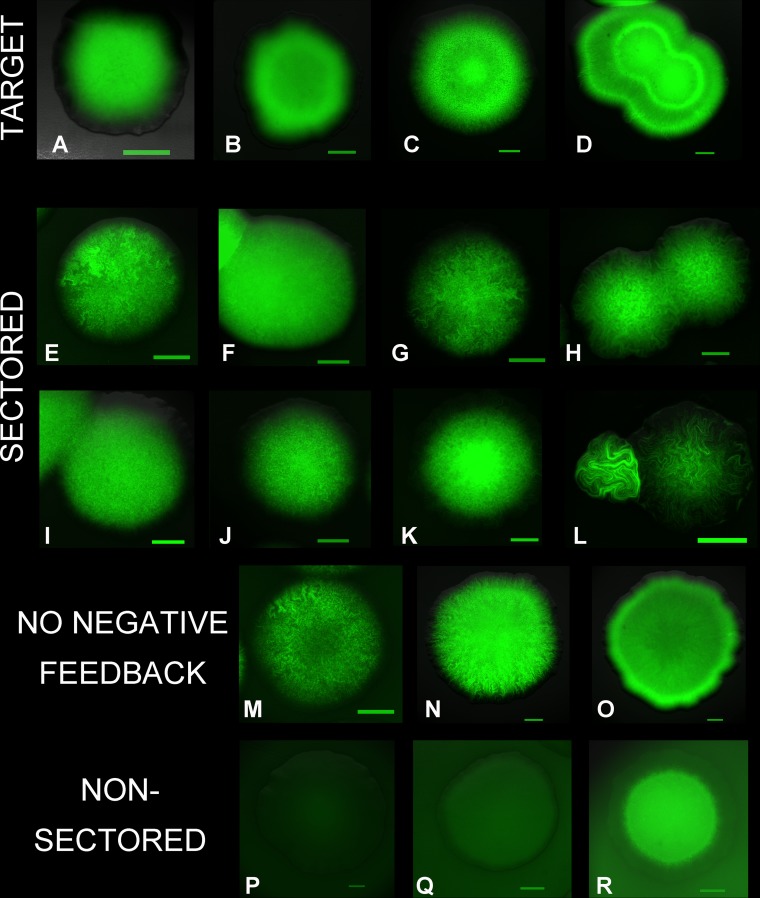
Colonies of cells carrying different combinations of the CI and CII-V expression plasmids were grown on LB plates (containing appropriate antibiotics), starting from single cells. Depending on the combinations of plasmids and cell types, cells of the colonies expressed the CII-V protein at different levels, providing diverse patterns (Fig. 6). From the single cells plated, E. coli colonies developed through a single layer of cells to a 3-dimensional structure which contained an increasing number of layers toward the center (35). Although the development of these multiple layers is not well understood and was not included in the model, the intricate patterns observed on the surface reflected the patterns found in quasi-2-dimensional growth of colonies (see Fig. S3 in the supplemental material) and could be assigned to one of the three categories suggested by the 2-dimensional simulations (target, sectored, and nonsectored patterns). At high basal CII-V expression and increased CI degradation rate levels (high b_A and high Γ_R), we observed development of concentric patterns (target patterns) formed by cells with high and low CII-V levels (Fig. 6A to D), resembling the simulated patterns obtained with parameter sets which produce oscillatory A levels in single cells (Fig. 4A to E). Formation of the target pattern required high basal activity of the CII-V promoter. Colonies containing plasmids pSEM3073Δ and pSEM3131D produced sectored patterns (Fig. 6E and F). The presence of relatively large sectors in Fig. 6E suggests that the rate of switching between the low and high CII-V states is lower with pSEM3073Δ than with pSEM3131D. This is most likely due to the uncontrolled copy number of pSEM3073Δ. Formation of the target pattern also required active degradation of CI. At the normal degradation rate of CI (Γ_R = ~0), CII-V expression in the colonies was uniformly low in wild-type cells (Fig. 6Q) but allowed formation of sectored patterns in hfl mutants (Fig. 6G and I).

FIG 6 .

Expression pattern of the CII-V protein in colonies carrying engineered regulatory circuits. The colonies developed from single cells. The green areas are formed by cells expressing CII-V at high levels. The intensity of the green color is proportional to CII-V expression in each image, but color intensities are not comparable between images. Scale bars, 300 μm. (A to D) Development of target pattern in colonies of wild-type cells carrying the coupled feedback loop. Colonies carried the plasmids encoding a short-lived CI (pSEM3047) and CII-V with a high basal transcription rate (pSEM3131B). Images were taken after 1 (A and B), 2 (C), and 3 (D) days of incubation of plates. (E and F) Sectored patterns formed in colonies carrying the coupled feedback loop. Colonies of wild-type cells carried the plasmids encoding a short-lived CI (pSEM3047) and CII-V with a low basal transcription rate, pSEM3073Δ (E) and pSEM3131D (F). (G to L) Sectored patterns formed in colonies carrying the coupled feedback loop in hflC (G, J, and K) and hflK (H, I, and L) mutants. For panels G and I, the long-lived version of CI (pSEM3061) was used. CII-V with a high basal transcription rate was used for panels I and L, while CII-V had low basal transcription rates in the experiments whose results are shown in panels G, H, and K (pSEM3073Δ) and in panel J (pSEM3131D). (M to O) Examples of CII-V expression patterns in colonies carrying the positive autoregulatory circuit in wild-type cells. Cells contained plasmid pLG338 (no CI) and one of the CII-V expression plasmids (pSEM3073Δ [M] or pSEM3131B [N and O]). Images were taken after 1 (M and N) or 2 (O) days of incubation of plates. (P to R) Nonsectored patterns formed in wild-type colonies (P and Q) and hflK mutant colonies. Cells carried genes encoding constitutively expressed (P) or long-lived (Q and R) CI and CII-V on plasmid pSEM3131B (P and Q) or pSEM3131D (R).

In the Hfl mutants, CII-V levels were generally higher in the middle of the colony (Fig. 6G to L and R). This feature could not be reproduced in the model by simply decreasing the degradation rate of the activator (Γ_A). To allow accumulation of CII-V in the middle of the colony, the degradation rate should decrease faster than the production rate as the growth rate decreases. That is, in the absence of the HflKC complex, HflB is most likely less efficient in degrading CII at lower growth rates or in stationary phase. Also, high CII expression in Hfl mutants resulted in elongated cells, leading to more-wiggly patterns (Fig. 6H, K, and L). Formation of filaments was previously reported in the absence of sufficient HflB activity (36).

Disruption of the negative-feedback loop by CII-V-independent CI expression resulted in strong inhibition of CII-V expression and a lack of pattern formation (Fig. 6P). However, elimination of CI-mediated control did not result in uniformly high expression (Fig. 6M to O). Generally, cells close to the edge of the colonies showed higher expression and exhibited wiggly patterns. These results confirmed that expression of positively autoregulated CII-V can switch between high and low states and maintain the high state for several generations. We can also conclude that CII-V production and/or degradation is generally noisy in this experimental system. The ratio of cells expressing CII-V at high levels was larger with the pSEM3131B plasmid, where the basal CII-V transcription (high b_A) was higher (Fig. 6N), than with pSEM3073Δ, where basal transcription was low (Fig. 6M). High basal expression allows easier establishment of the CII levels required for maintaining the high-expression state.

DISCUSSION

Cellular molecular networks are composed of simple motifs such as feedback and feed-forward loops (13, 37). These motifs can perform well-defined functions such as maintaining homeostasis or cellular memory, accelerating response times (38), or provide fold change detection (39). Biological processes often require more-complex functions and dynamics, which are typically achieved by coupling simple motifs, such as positive- and negative-feedback loops (13, 22, 40–43).

Here we provide both theoretical and experimental results which show that a small circuit composed of coupled positive- and negative-feedback loops can produce intricate gene expression patterns in colonies formed by isogenic cells. The circuit used was not directly connected to cell-cell communication systems. The theoretical modeling showed that formation of gene expression patterns in colonies depends on (i) the physical characteristics of cells (e.g., shape and mechanical interactions), (ii) extracellular signals that affect growth rate (e.g., availability of nutrients), and (iii) the properties of the genetic circuit regulating a given gene. In our simulations and experiments, colonies developed from a single cell placed on a uniform field. In such a case, the external signals affect cells in a coordinated, position-dependent way; that is, they promote a concentric pattern of heterogeneity because cells located at the same distance from the center of the colony are affected in similar ways (44). Uncoordinated heterogeneity of gene expression levels of cells is determined by the stochasticity of intracellular processes. It is strongly affected by the properties of the regulatory circuitry used, which determine the distributions of switching times between the on and off states of gene expression. The average switching times determine the length of memory in the system, which can be observed as the extent of high- and low-expression domains in the colony. In that sense, previous studies with two genetically different cells represented a case where the switching times were infinite (15). Switching between the two states disrupts the growth of uniform domains and can result in patterns of different degrees of regularity. For example, the use of weaker promoters, unregulated plasmid copy numbers, or randomly distributed low-copy-number components broadens the distribution of switching times and contributes to the irregularity of the pattern.

The observed patterns in the E. coli colonies certainly present similarities to the simulated patterns despite the simple modeling. However, the similarities are mostly qualitative because many crucial processes underlying pattern formation, such as the effect of nutrient diffusion and growth-rate-mediated global feedback on gene expression (45), the structure and function of intracellular molecular networks, cell-to-cell signaling in colonies, 3D development of colonies, etc., are poorly understood.

Coupling of positive and negative feedbacks is common in many intracellular regulatory pathways, and it represents only one of the many different genetic circuits that can create heterogeneous gene expression. Our theoretical modeling and experimental results suggest that, in a growing colony, the protein content of cells is highly diversified because expression of each gene shows a specific pattern in the colony.

In summary, we can conclude that simple growth and gene regulatory rules can lead to highly diverse patterns with a high degree of heterogeneity in biological systems. This observation shows a strong analogy with previous findings in complex system research, where extremely complex patterns were produced using simple algorithms such as diffusion-limited aggregation (DLA) (46). DLA-based models could reproduce the branching and fractal shape of bacterial colonies observed when the diffusion of nutrients is limited (24, 25). The main advantage of our theoretical model is that it includes gene regulation as well. Therefore, it is suitable for simulation of colony shape and gene expression heterogeneity at the same time.

MATERIALS AND METHODS

The cell growth and interaction model.

The model is 2-dimensional, and each cell is modeled as an object consisting of two circles of radius r attached at opposite sides of a rectangular shape, to mimic the elongated shape of E. coli (47). The position and the shape of cell i are fully described by the position of the center of the two circles, $x_1^{\left(i\right)}$ and $x_2^{\left(i\right)}$. Each circle feels the force described by a potential $V^{\left(i\right)}=V_{int}^{\left(i\right)}+V_{cc}^{\left(i\right)}$, where the first term describes the internal force to keep the cell’s shape and the second term describes the cell-cell interaction. The circles move according to the overdamped equation of motion $\frac{d{x}_j^{\left(i\right)}}{dt}=-\frac{1}{\eta }{\nabla }_j{V}^{\left(i\right)}$, where η denotes the viscosity from media and the agar on which the cell is growing. Inertia is not included because it is negligibly low at the bacterial-cell scale.

The internal force is modeled by the linear repulsive potential $V_{int}^{\left(i\right)}=\frac{1}{2}{k}_{int}\left(l^{\left(i\right)}\left(t\right)-\left|x_1^{\left(i\right)}-x_2^{\left(i\right)}\right|\right)$, with a spring constant k_int and a time-dependent natural length l⁽ⁱ⁾(t) [where “(i)” represents a cell identifier] that keeps the elongated shape of the cell. The total length of the cell is given by$L^{\left(i\right)}\left(t\right)=l^{\left(i\right)}\left(t\right)+2r$, which grows over time when nutrients are available. We assume that the length grows exponentially with local nutrient density as$\frac{d{L}^{\left(i\right)}}{dt}=g\left(n\right)\cdot L^{\left(i\right)}$.

The nutrient level is measured at the center of the cell as $x_c^{\left(i\right)}=\frac{1}{2}\left[x_1^{\left(i\right)}+x_2^{\left(i\right)}\right]$. We assume a low Monod’s growth value $g\left(n\right)=g_0\frac{n}{n+K_n}$, where g₀ is the maximum growth rate in nutrient-rich medium (48).

When L⁽ⁱ⁾ reaches the threshold length L_th, the cell splits in half, giving rise to two daughter cells. To introduce slight randomness into the cell division timing and cell alignment, we follow Cho et al. (47). The two new daughter cells, i₁ and i₂, share the position of one of the poles with the mother cell as $x_j^{\left(i_j\right)}=x_j^{\left(i\right)}$, with j = 1,2. The natural length at the division is given by $l^{\left(i_1\right)}=\left(\frac{1}{2}{L}_{th}-r\right)\cdot \left(1+p_{div}\right)-r$ and $l^{\left(i_2\right)}=\left(\frac{1}{2}{L}_{th}-r\right)\cdot \left(1-p_{div}\right)-r$, where p_div is a uniformly distributed random number in the expression$\left(-p^0{}_{div},p^0{}_{div}\right)$. The position of the new pole is given by $x_2^{\left(i_1\right)}=x_1^{\left(i\right)}+l^{\left(i_1\right)}\cdot \frac{x_2^{\left(i\right)}-x_1^{\left(i\right)}}{\left|x_2^{\left(i\right)}-x_1^{\left(i\right)}\right|}$ and $x_1^{\left(i_2\right)}=x_2^{\left(i\right)}+l^{\left(i_2\right)}\cdot \left[\frac{x_1^{\left(i\right)}-x_2^{\left(i\right)}}{\left|x_1^{\left(i\right)}-x_2^{\left(i\right)}\right|}+a\right]$ with $a=\left(x_{div},x_{div}\right)$, where $x_{div}$ is a uniformly distributed random number in $\left(-x^0{}_{div},x^0{}_{div}\right)$.

The cell-cell interaction is described by a two-body repulsive potential. We adopt a simple linear form, $V_{cc}^{\left(i\right)}=\frac{1}{2}{k}_{cc}\sum _{j\in H_{ij>0}}{H}_{ij}\left[x_1^{\left(i\right)},x_2^{\left(i\right)},x_1^{\left(j\right)},x_2^{\left(j\right)}\right]$, where $H_{ij}\left[x_1^{\left(i\right)},x_2^{\left(i\right)},x_1^{\left(j\right)},x_2^{\left(j\right)}\right]$ is the linear overlap between particles i and j, defined as H_ij = 2r − r_ij, where r_ij is the shortest distance between the lines connecting $[x_1^{\left(i\right)},x_2^{\left(i\right)}]$ and $[x_1^{\left(j\right)},x_2^{\left(j\right)}]$. The sum over j runs for all the particles in contact with particle i, namely, the particles that satisfy H_ij = ≥0.

The nutrient field model.

The nutrient field n(x,t) obeys the diffusion equation with the consumption by the cellular growth $\frac{\partial n}{\partial t}=D{\nabla }^{2}n-{\sum _{\text{all }i}cg\left(n\right)\cdot L}^{\left(i\right)}\cdot \delta \left[x-x_c^{\left(i\right)}\right]$, with a proportionality constant c.

Conversion of cell length to cell volume.

We need to convert the cell length L⁽ⁱ⁾ to the cell volume Ω⁽ⁱ⁾ when we calculate the concentration of proteins from the number of proteins per cell. We assume that Ω⁽ⁱ⁾ is proportional to L⁽ⁱ⁾ as Ω⁽ⁱ⁾ = ω⁽ⁱ⁾ with a proportionality constant ω. This allows us to express the cell growth model and the nutrition field model in the form shown in Fig. 1. (Equations in Fig. 1 use g₀ = 1 and c = 1 as assumed values in the parameters in Table S1 in the supplemental material. The cell division threshed volume is given by 2Ω₀ = ωL_th.)

The feedback motif model.

Each cell carries the genetic circuit outlined in Fig. 1, which is controlled by transcriptional activator proteins (A) and repressor proteins (R). Because the transcriptional regulatory proteins in E. coli are typically dimers, we assume cooperativity in DNA binding (with Hill coefficient = 2). This provides a minimal nonlinearity that allows bistability and oscillations in a wide range of parameters. Protein A activates its own production as well as the production of protein R, while protein R represses the production of protein A. We denote the number of protein A and protein R in cell i as $N_A{}^{\left(i\right)}$ and $N^{\left(i\right)}{}_R$ respectively. The concentration of protein A and protein R at a given moment is then given by ${\Phi }_A{}^{\left(i\right)}=N_A{}^{\left(i\right)}/{\Omega }^{\left(i\right)}$ and ${\Phi }_R{}^{\left(i\right)}=N_R{}^{\left(i\right)}/{\Omega }^{\left(i\right)}$, respectively. The production rates (P) of protein A and R are given, respectively, as follows:

$P^{\left(i\right)}{}_A=P_A^0[{\Phi }^{\left(i\right)}{}_A,{\Phi }^{\left(i\right)}{}_R]\cdot {\Omega }^{\left(i\right)}\cdot g\left\{n\right[x_c^{\left(i\right)}\left]\right\}$, with $P_A^0\left({\Phi }^{}{}_A,{\Phi }^{}{}_R\right)=\left[\frac{{\alpha }_A^{}}{1+{\left({\Phi }^{}{}_R/K_R\right)}^2}\right]\cdot \left[b_A+\frac{{\left({\Phi }^{}{}_A/K_A\right)}^2}{1+{\left({\Phi }^{}{}_A/K_A\right)}^2}\right]$

and

$P^{\left(i\right)}{}_R=P_R^0\left[{\Phi }^{\left(i\right)}{}_A\right]\cdot {\Omega }^{\left(i\right)}\cdot g\left\{n\left[x_c^{\left(i\right)}\right]\right\}$, with $P_R^0\left({\Phi }^{}{}_A\right)={\alpha }_R^{}\cdot \left[b_R+\frac{{\left({\Phi }^{}{}_A/K_A\right)}^2}{1+{\left({\Phi }^{}{}_A/K_A\right)}^2}\right]$

The active degradation rates (Г) of protein A and R are given, respectively, by ${\Gamma }^{\left(i\right)}{}_A={\Gamma }_A^{}\cdot N^{\left(i\right)}{}_A\cdot g\left\{n\left[x_c^{\left(i\right)}\right]\right\}$ and ${\Gamma }^{\left(i\right)}{}_R={\Gamma }_R^{}\cdot N^{\left(i\right)}{}_R\cdot g\left\{n\left[x_c^{\left(i\right)}\right]\right\}$. Here, α_A(b_A + 1) and α_R(b_R + 1) denote the maximum production rates of protein A and protein R per unit volume per growth time, respectively. The parameters K_A and K_R are dimensionless and characterize the intrinsic promoter activity in the absence of regulatory proteins. The parameters K_A and K_R characterize the dissociation constants for the complexes formed between proteins A and R and the promoters, respectively. The degradation rates of proteins A and R per molecule per growth time are given by Γ_A and Γ_R. Using these rates, $N_A{}^{\left(i\right)}$ and $N^{\left(i\right)}{}_R$ are updated accordingly following the procedure given below. At cell division, the proteins are allocated to the two daughter cells following the binomial distribution with equal probabilities.

Numerical integration method, initial condition, and boundary condition.

The considered space is a 2-dimensional square with linear size L. Initially, one cell is located in the middle of the square, and the protein numbers in the cell are set to be zero for both proteins A and R. Initially, the nutrients are distributed uniformly over the system as $n\left(x,0\right)=n_0$. The boundary condition is set to be $n\left[\right(L,y),t]=n\left[\right(x,L),t]=n_0$ all through the simulations.

The equation of motion for each cell is integrated by the Euler method with a constant time step dt. The diffusion equation for the nutrition field is solved in parallel by finite-difference method, with central difference in space on a square lattice with a constant lattice size dx and forward difference in time with a time step dt.

The protein production is simulated in parallel stochastically for each cell as follows. For a given time step, if $r^{\left(i\right)}{}_{\text{sum}}=P_{{}_A}^{\left(i\right)}+P_R^{\left(i\right)}+{\Gamma }_{{}_A}^{\left(i\right)}+{\Gamma }_R^{\left(i\right)}$ satisfies $r^{\left(i\right)}{}_{\text{sum}}\cdot dt<1$, then one of the reaction is chosen with the probability$k^{\left(i\right)}{}_X\cdot dt$, where k is either P or Γ and X is either A or R, and the corresponding protein number is increased or decreased by 1; nothing happens with the probability $1-r^{\left(i\right)}{}_{\text{sum}}\cdot dt.$

When the number of proteins is very high, $r^{\left(i\right)}{}_{sum}\cdot dt$ may exceed 1 (dt is chosen with a value that is low enough so that this occurs only rarely). In this case, we approximate the reaction in the following way. If $P^{\left(i\right)}{}_X\cdot dt>1$ [${\Gamma }^{\left(i\right)}{}_X\cdot dt>1$], increase (decrease) the corresponding number of protein X by $\Vert P^{\left(i\right)}{}_X\cdot dt\Vert$ [$\Vert {\Gamma }^{\left(i\right)}{}_X\cdot dt\Vert$], where $\Vert Y\Vert$ is the nearest integer function of a real number Y; otherwise, increase (decrease) the number of protein X by 1 with probability $P^{\left(i\right)}{}_X\cdot dt$ [${\Gamma }^{\left(i\right)}{}_X\cdot dt>1$]. Perform this for all four reactions in one time step.

Parameters.

The parameters used for cell growth and nutrient level simulation are listed in Table S1 in the supplemental material.

The diameter of a cell is taken to be the unit length, and the time unit is taken to be the inverse of the maximum growth rate. For E. coli, the unit length corresponds to about 1 µm and the unit time corresponds to about 30 min. The simulation time and space steps are taken to be dt = 5 × 10⁻⁶ and dx = 1. For the parameters for motifs, the time unit is also taken as the generation time at the maximum growth rate. We take volume ${\Omega }_0$ (the volume just after cell division) as a unit volume and use 1 molecule per unit volume as a concentration unit. If we consider an E. coli cell volume (about 1 µm³), the unit concentration is close to 1 nM. The parameter values given in the Fig. 2 caption are expressed in this concentration unit. When implementing this in the simulation, we set the proportionality constant between the cell length and the volume as ω = 2/L_th so that Ω₀ = 1 and Ω⁽ⁱ⁾ is measured in this unit volume.

Bacterial strains and plasmid construction.

Plasmids used in this study are listed in Table S2 in the supplemental material. The oligonucleotides used for plasmid construction are listed in Table S3. Plasmid pSEM3073, carrying the positively autoregulated CII-V protein, was constructed by inserting the CII-V expression cassette between the EcoRI and BamHI sites of plasmid pSEM2027 (49). The zeocin resistance marker of the plasmid was removed by deletion of the XhoI-SalI fragment (pSEM3073Δ). The expression cassette (Fig. 5) was synthesized in vitro by PCR. The promoter and cis regulatory region, which is a modified version of the pRE promoter of bacteriophage λ, were amplified using primers PREUP and PREDN/O and purified λ DNA as a template (pRE*). The DNA fragment encoding the CII protein of bacteriophage λ was amplified using primers CIIUP2 and CIIDN. The 5′ region of the CII-encoding sequence, which overlaps with the pRE promoter, was mutagenized to eliminate the homology with pRE but to keep the encoded protein unchanged. The DNA sequence encoding the Venus variant of yellow fluorescent protein (YFP) was amplified with primers VENYUP and VENYDN using plasmid pBES2 as a template. Plasmids pSEM3131B and pSEM3131D were selected from a pool of plasmids created by amplifying the CII-V expression cassette using primers PREUPRND and VENYDN and pSEM3073 as a template and inserting it between the EcoRI and BamHI sites of plasmid pBR322 (50). The sequence corresponding to the −35 promoter element of the pRE promoter was randomized in primer PREUPRND. The sequences of the promoter regions in the expression cassettes are shown in Fig. 5.

To create plasmid pSEM3047, the sequence of the λ pRE promoter was PCR amplified using primers pREUP and pREDNBG and was inserted between the EcoRI and PstI sites of plasmid pSEM2027 (pSEM2027pRE). The sequence encoding the temperature-sensitive variant of the λ CI repressor (CI⁸⁵⁷) fused to a C-terminal ssrA tag (26) was PCR amplified using primers CIUP and CIDNSSR and purified λ DNA (Fermentas) as a template and was inserted between the EcoRI and BglII sites of plasmid pSEM2027pRE. The resulting plasmid was digested by SalI and BamHI, and the fragment containing the zeocin resistance gene, the rrnB T1T2 terminators, the pRE promoter, and the CI gene was inserted between the SalI and BamHI sites of plasmid pLG338 (GenBank accession no. KM604642) (51). Plasmid pSEM3049 was created by replacing the EcoRI-BglII fragment (carrying pRE) with the EcoRI-BamHI fragment of pBR322, which carries the promoter of the tetracycline resistance gene. Plasmid pSEM3061 was created similarly to pSEM3047 except that it carries the CI gene without the ssrA tag. The sequences of the cloned fragments and their flanking regions were verified in all constructed plasmids (Eurofins MWG Operon).

E. coli strains MG1655, BW25113ΔhflK (52), and BW25113ΔhflC (52) were transformed by electroporation with the appropriate plasmids before imaging was performed.

Imaging of CII-V expression in bacterial colonies.

Cells were transformed with the CII-V gene-containing plasmid by electroporation and plated on LB plates containing the appropriate antibiotics (ampicillin at 100 mg/ml, kanamycin at 30 mg/ml, and zeocin at 80 mg/ml). Plates were incubated at 32°C to allow development of colonies (1 to 3 days). Images were captured with a Nikon Eclipse Ti fluorescence microscope (×4 magnification) using NIS Elements image analysis software (Nikon). Contrast stretching was applied using the “Auto scale” function of NIS Elements.

SUPPLEMENTAL MATERIAL

Figure S1 

Simulated single-cell behavior. For stochastic simulation (dotted lines), single-cell behavior is followed with keeping the growth rate g = 1. Deterministic simulations are obtained by solving the ordinary differential equations $\frac{d{\varphi }_A}{dt}=\left[\frac{{\alpha }_A}{1+{\left({\varphi }_R/K_R\right)}^2}\right]\cdot \left[b_A+\frac{{\left({\varphi }_A/K_A\right)}^2}{1+{\left({\varphi }_A/K_A\right)}^2}\right]\cdot g-{\Gamma }_A\cdot g\cdot {\varphi }_A-g\cdot {\varphi }_A$ and $\frac{d{\varphi }_R}{dt}={\alpha }_R\cdot \left[b_R+\frac{{\left({\varphi }_A/K_A\right)}^2}{1+{\left({\varphi }_A/K_A\right)}^2}\right]\cdot g-{\Gamma }_R\cdot g\cdot {\varphi }_R-g\cdot {\varphi }_R$ for A (${\varphi }_A$) and R (${\varphi }_R$) concentrations, respectively, where the third terms on the right-hand side represent dilution by cell growth. Solid lines in panels A to E represent the results with initial conditions ${\varphi }_A=0$ and ${\varphi }_R=0$, while the dashed line in panel E represents the result with initial conditions ${\varphi }_A=2,000$ and ${\varphi }_R=0$. (A) Oscillation obtained with ${\alpha }_A=300,000$, $b_A=0.001$, $K_A=4,000$, $K_R=200$, ${\alpha }_R=10,000$, $b_R=0.001$, ${\Gamma }_A=2$, and ${\Gamma }_R=0.5$. (B) Low-A state obtained when R production is strong, ${\alpha }_R=200,000$. (C) High-A state obtained when R production is weak, ${\alpha }_R=1,000$. (D) Excitable behavior obtained with low leak for A, $b_A=0.0001$. (E) Bistable behavior obtained when a weak R and a low leak for A are combined, with $b_A=0.0001$ and ${\alpha }_R=500$. Download

Figure S2 

Parameter regions for monostable, bistable, and oscillatory behaviors when $b_A$ and ${\alpha }_R$ are varied. The rest of the parameters are fixed to ${\alpha }_A=300,000$, $K_A=4,000$, $K_R=200$, ${\alpha }_R=10,000$, $b_R=0.001$, ${\Gamma }_A=2$, and ${\Gamma }_R=0.5$. Download

Figure S3 

Comparison of patterns observed in quasi-2-dimensional colonies (top left) and 3-dimensional colonies (top right) of wild-type cells carrying plasmids pSEM3131B (CII-V with high basal transcription rate) and pSEM3047 (short-lived CI). The colony on the left was grown from a single cell between a glass plate and a layer of LB agar and was about 700 μm in width. Assuming that E. coli cells are 0.5 μm in width and 2 μm in length and that cells do not overlap, the colony is estimated to contain ~385,000 cells. An image obtained by simulation is shown at the bottom left and is composed of ~380,000 cells. The levels of average brightness of the cross-section through the middle of the experimentally observed and simulated 2D colonies are presented at the bottom right. After the maximum brightness and the colony width were normalized to a value of 1, the relative positions of the peaks were similar. Parameters used in the simulation were α_A = 600,000, b_A = 0.001, K_A = 4,000, K_R = 200, α_R = 10,000, b_R = 0.001, Г_A = 0, and Г_R = 0. A higher initial nutrition level (n₀ = 4) and a larger diffusion constant for the food (D = 1,000) with system size L of 1,200 were used to obtain a wider ring than was seen with the default parameter values. To simulate a large number of cells, k_int/η = k_cc/η = 10³ was used, which allows a time step 100 times bigger for simulation. The default values are used for the rest of the parameters. The softer cell results in a significant overlap of the cells in the middle of the colony, giving a width of the shown colony of ~580 in the unit of cell width. Download

Table S1 

Default parameter values used in the simulations. The numbers shown are relative to the chosen unit time, length, and concentration scales as indicated in the description. The mechanical interaction parameters are chosen in such a way that the maximum cell-cell overlap or deformation at the end of the simulation is about 20%. The nutrition parameters are chosen so that the consumption is fast enough to see the slowdown of the growth within the present simulation scale, and at the same time the diffusion is enough not to induce diffusion-limited instability in colony morphology (24). The simulation shown in Fig. 4D was performed using L_th = 2, while L = 900 and L_th = 6 were used in the simulation shown in Fig. 4E

Table S2 

Plasmids used in this study.

Table S3 

Oligonucleotides used in this study.