Abstract
Single particle reconstruction methods based on the maximum-likelihood principle and the expectation-maximization (E–M) algorithm are popular because of their ability to produce high resolution structures. However, these algorithms are computationally very expensive, requiring a network of computational servers. To overcome this computational bottleneck, we propose a new mathematical framework for accelerating maximum-likelihood reconstructions. The speedup is by orders of magnitude and the proposed algorithm produces similar quality reconstructions compared to the standard maximum-likelihood formulation. Our approach uses subspace approximations of the cryo-electron microscopy (cryo-EM) data and projection images, greatly reducing the number of image transformations and comparisons that are computed. Experiments using simulated and actual cryo-EM data show that speedup in overall execution time compared to traditional maximum-likelihood reconstruction reaches factors of over 300.
Keywords: Cryo-electron microscopy, Single particle reconstruction, Maximum-likelihood, Maximum-a-posteriori, Expectation-maximization algorithm, Fast image processing
1. Introduction
Single particle reconstruction from cryo-electron microscopy (cryo-EM) is an iterative process that infers the 3D structure of a macromolecule or a “particle” from many noisy 2D projections of the particles lying at random orientations. Currently popular approaches to single particle reconstruction are based on the maximum-likelihood principle or the related maximum-a-posteriori principle. All these methods are optimized using the expectation-maximization (E–M) algorithm (Dempster et al., 1977), which iterates between the expectation step (E-step) and the maximization step (M-step). The E-step calculates latent probabilities for every possible alignment between particle image and structure projection. The M-step then uses these latent probabilities to give weights for alignments in calculating the reconstruction. E–M algorithms have gained popularity because they perform more favorably compared to other approaches for data with low signal-to-noise ratio (SNR).
The maximum-likelihood principle and related methods have been applied to many cryo-EM reconstruction problems. The first application of the maximum-likelihood principle in cryo-EM was for aligning particle images to a single 2D reference (Sigworth, 1998). Since then, several extensions have been proposed. The maximum-likelihood framework has been applied to 2D multireference image refinement (Scheres et al., 2005b), single particle reconstruction (Doerschuk and Johnson, 2000; Yin et al., 2001, 2003), and reconstruction of structurally heterogeneous data (Scheres et al., 2007). Another extension incorporates prior probability functions (priors) which encourage smoothness of the 3D structure, thereby limiting the amount of noise that propagates through to the reconstruction (Scheres, 2012a,b). More recent priors include enforcing a sparse representation by using an adaptive, non-Fourier basis, which improves the SNR and hence the resolution of the reconstruction (Kucukelbir et al., 2012). Maximum-likelihood with priors is referred to as the Bayesian or maximum-a-posteriori approach.
While reconstruction methods based on maximum-likelihood and the E–M algorithm have several desirable properties, from a computational point of view, the E–M algorithm is very slow (Cheng and Walz, 2009; Sigworth et al., 2010). The computational bottleneck of the E–M algorithm is the calculation of the latent probabilities in the E-step. In its naive form, the computational complexity of the E-step is the number of particle images × the number of projection directions × the number of image rotations and translations; this much computation is prohibitive. For example, Scheres (2012b) reports that a straightforward E–M reconstruction of 5053 GroEL particles required almost 25 days, even while using 56 CPUs in parallel. As data sets are larger by an order of magnitude or more, such execution times are clearly unacceptable.
Several heuristics have been proposed to accelerate E–M reconstruction algorithms (Sigworth et al., 2010). All of these heuristics depend on the observation that latent probabilities tend to be peaky; that is, the latent probabilities are high for relatively few alignments and very low for the rest. If the high probability alignments can be found quickly, then the rest can be ignored, speeding up the calculations. An early strategy used this idea by calculating latent probabilities only for those alignments whose probabilities in the previous iteration exceed some threshold (Scheres et al., 2005a). A more sophisticated strategy utilizes ideas from adaptive integration, in which the probabilities are calculated on a coarse sampling and then refined only where most of the probability mass is concentrated (Tagare et al., 2008, 2010). This adaptive E–M algorithm can be combined with GPU implementation (Tagare et al., 2010) and local orientation searches (Scheres, 2012b) for further speedup.
Another strategy is to exploit known symmetries of the particle. For example, Lee et al. (2007) exploits icosahedral symmetry of viruses to accelerate E–M reconstructions. The approach utilizes a fixed basis of spherical harmonics to efficiently sample rotations (Doerschuk and Johnson, 2000). Furthermore, a linear transformation of the data is applied to speed up E–M calculations.
This paper proposes a completely novel heuristic for speeding up the E–M algorithm. The idea is to represent the particle images and structure projections in two different, relatively low-dimensional subspaces that are adapted to the data. This representation is accurate, so the projections can be rotated, translated, and compared with the particle images simply by performing the corresponding operations on the subspace bases. Because the number of basis elements is much smaller than the number of images and projections, substantial speedup is possible. The approximation using the subspaces is integrated into the maximum-a-posteriori framework. We refer to the proposed algorithm as SubspaceEM.
The SubspaceEM algorithm is developed below in the spatial domain. However, as will become clear in the Discussion section, the SubspaceEM algorithm applies without change to the Fourier domain, where equally significant speedups can be expected. This is important because some E–M algorithms are implemented in the spatial domain (e.g., ML3D in Xmipp (Sorzano et al., 2004)) while others are interpreted in the Fourier domain (e.g., RELION (Scheres, 2012b)). The subspace idea applies to both.
In the following, we begin by describing the mathematical derivations and implementation of the proposed SubspaceEM algorithm. After the discussion of the algorithm, experiments are presented comparing SubspaceEM with the classic E–M algorithm in reconstructing both simulated and real cryo-EM data. The computational cost of the SubspaceEM algorithm is compared with a straightforward implementation of the E–M algorithm. The purpose of these experiments is to examine the potential of the SubspaceEM algorithm to reduce computational costs by orders of magnitude without loss in the quality of 3D reconstruction.
2. Mathematical Methods
2.1. The Maximum-likelihood and Maximum-a-posteriori Formulations
We first briefly review the maximum-likelihood and maximum-a-posteriori formulations for single particle reconstruction. An extensive overview of the theory of maximum-likelihood methods for cryo-EM analysis is available in Sigworth et al. (2010).
Suppose that S is a particle structure, mathematically represented as a set of density values on a grid in a three-dimensional cube. The structure is projected along D directions and a set of F contrast transfer functions (CTFs), belonging to F defocus classes, are applied to each projection. This results in M = D × F “filtered projected” structures, each with a specific defocus class. Let denote the M = D × F projection operators composed with CTF operators. Then, each filtered projected structure is given by (S). Reconstruction algorithms, including the E–M algorithm, compare particle images with these M = D×F filtered projected structures, but the comparison of any particle image is only with the filtered projected structures that have the same defocus class as the image. To express this in the following mathematics, we tag each filtered projected structure (S) with its defocus class, denoted by Cj. The value of Cj is an integer from 1, …, F. We emphasize that Cj is not the CTF function, but an integer which indexes the defocus class. In the following, to simplify the terminology, we will call the projection operator and (S) a structure projection whose defocus class is Cj.
Next, let xi, i = 1, …, N, be the cryo-EM particle images. Similar to the structure projections, each particle image xi is tagged with its defocus class, denoted by . The defocus class is also an integer from 1, …, F and is assigned according to the CTF measured from the micrograph. The cryo-EM image formation model is that xi is a projected structure of the same defocus class, rotated and translated, and further corrupted by zero mean additive noise. The identity of the projection direction is lost in the image formation process. Letting zi denote the index of the unknown projection operator relating the structure S to the image xi, the image formation process is
| (1) |
In the above equation, is the 2D transformation operator which rotates and shifts the image according to the transformation parameter τi = {φi, tix, tiy}, which specifies the in-plane rotation angle φi and the translations tix and tiy along the x and y image axes. Further, ni is the additive white Gaussian noise with zero mean and standard deviation σ. Finally, states that the image xi can only arise due to the action of a projection operator whose defocus class Czi is identical to the image defocus class .
Under the image formation model in Eq. (1), the conditional probability density that image xi comes from structure S is
| (2) |
where ( ( (S)), σ2) is the probability density function of a Gaussian random variable with mean ( (S)) and variance σ2
The variables zi and τi are nuisance or latent variables because their values are unknown and are not of particular interest. These variables are eliminated by marginalization, that is, by integrating them out. Let α = {α1, …, αM }, where αj is the probability that zi = j, let Ωτi be the domain of possible values for the transformation parameter τi, and let p(τi) be the probability of τi. Then, marginalization results in
| (3) |
where the sum over j marginalizes zi and the integral marginalizes τi. Simplifying the notation by setting Θ = {S, σ, α} gives p (xi|S, σ, α) = p(xi|Θ). In statistical estimation terminology, Θ are the parameters of the problem.
The single particle reconstruction problem is to recover Θ, with particular interest in the structure S, from the particle images xi, i = 1, …, N. Under the maximum-likelihood principle, the estimate of the parameters Θ is
| (4) |
Related to the maximum-likelihood estimate is the maximum-a-posteriori estimate. Given a prior density p(Θ) of Θ, the maximum-a-posteriori estimate of Θ is
| (5) |
Often, useful prior knowledge is available only for some parameters, and it is common to set the prior of the remaining parameters to a uniform or noninformative density (Bishop, 2006) so that these parameters can be dropped from the maximization altogether.
The maxima in Eqs. (4)-(5) are numerically found using the E–M algorithm (Dempster et al., 1977). This optimization algorithm iteratively alternates between the E-step and the M-step. The E-step computes the probability of the latent variables zi and τi given the data xi and the current parameter estimates. The M-step updates the parameters Θ given the latent probabilities.
For single particle reconstruction, the E-step requires calculating the sum of squared differences (SSDs) between each image xi and each projection (S) with the same defocus class for every transformation value τi, ||xi − ( (S))||2. The SSD calculations involve a very large number of image transformations (M structure projections) and image comparisons (N particle images × D structure projections). This is what makes the E-step the computational bottleneck in the E–M algorithm.
2.2. The Idea Behind the SubspaceEM Algorithm
We now turn to discussing our proposed method for speeding up the E–M algorithm. The method is based on the key observation that the latent probabilities are insensitive to high frequencies in the images; that is, accurate latent probabilities can be calculated using only the low frequencies in the images. This property has already been experimentally verified; results from simulated images confirm that discarding high frequency information in the data or applying an appropriate low-pass filter to the intermediate structures does not affect matching accuracy (Scheres and Chen, 2012). Even for conventional (not E–M) single particle reconstruction methods, low-pass filtering the images is known to improve alignment (Henderson et al., 2011; Grigorieff, 2007).
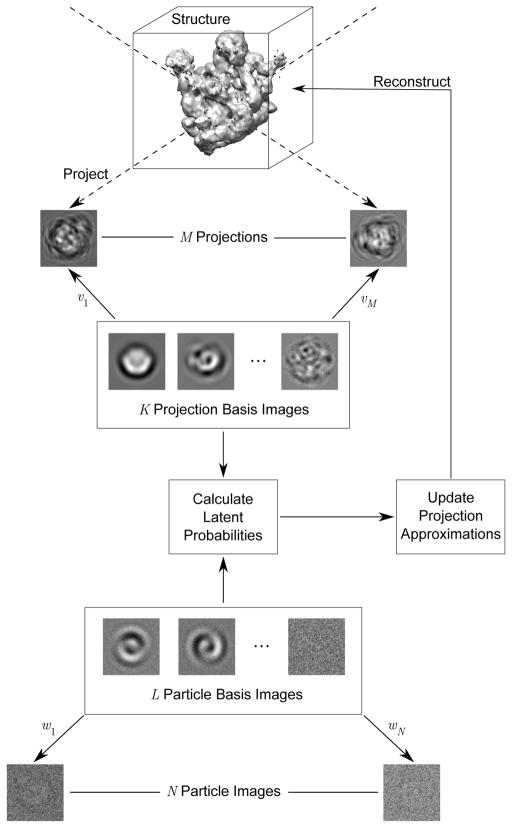
Low-pass filtering is especially useful when the bandwidth of the filter adapts to the images. One natural technique to “adaptively low-pass filter” the images is to project them onto a low-dimensional subspace, which is chosen to give accurate representations of the images. Our use of this idea is illustrated in Fig. 1, which shows two subspaces. The first subspace approximates the M structure projections. This subspace is restricted to have dimension K, with K much smaller than M, but large enough to capture most of the information in the projections. Every structure projection is approximated as some linear combination of K basis images of this subspace, in which the coefficients of the basis elements are v (Fig. 2A). In a similar fashion, the N particle images are approximated by the second subspace of dimension L, with L much smaller than N. Each particle image is approximated by a linear combination of the L basis images of the subspace with coefficients w (Fig. 2B).
Fig. 1.
Schematic for the fast E–M framework. We approximate the M projections from the current structure in some subspace that can be described by K basis images, where K < M. Each projection is approximated in the subspace using corresponding coefficients v. Similarly, we approximate the N particle images in some subspace represented by L basis images, with L < N. Each image approximation can be written using corresponding coefficients w. The proposed algorithm greatly reduces computational cost because it only rotates and compares the basis images to calculate the latent probabilities.
Fig. 2.
Structure projection and particle image models using subspace approximations. (A) Structure projection model. (B) Particle image model.
Incorporating the subspace approximations into the E–M algorithm, the SSDs between structure projections and particle images can be calculated simply by comparing the K × L subspace bases and applying the coefficients of their approximations (details are given below). Further, the approximated images and projections can be rotated and translated by performing these operations on their bases. This reduces the computation considerably.
The approximated images and structure projections give fast and accurate estimates of the probabilities of latent variables. However, because these approximations do not have high frequency content, the reconstructed structure from the approximations does not have as high a resolution as it could. But this is easily fixed - after the E–M algorithm terminates, an additional step which uses the calculated latent probabilities with the original particle images gives a structure that preserves the high frequency content. This is the SubspaceEM algorithm.
2.3. Statistical Models
To proceed with a mathematical description of the algorithm, we adopt the following convention: every particle image and structure projection is represented by a column vector of pixel values. The standard inner product of any two vectors u and v is < u, v >= uTv, and the norm of any vector u is ||u||, so ||u||2 =< u, u >. A subspace is represented by a matrix, called the basis matrix, whose columns are the basis vectors of the subspace.
Let B be the basis matrix with L columns for the particle image subspace and wi be the coefficients for representing particle image xi in basis B. Then,
| (6) |
where Bwi is the approximation of xi in the subspace spanned by basis B, and n0i is the error in approximating the particle image in the subspace.
Similarly, let A be the basis matrix with K columns for the structure projection subspace and let vj be the coefficients for representing the jth projection in the basis A. Then,
| (7) |
where Avj is the approximation of the projection (S) in the subspace spanned by basis A, and n2j is the error in approximating the projection in the subspace. For simplicity, this error is modeled as white Gaussian noise with standard deviation σ2.
Finally, a particle image approximation is related to a projection approximation by image rotation and translation. As above, let zi be the unknown index relating the approximate particle image Bwi to the corresponding approximate structure projection Avzi. Then,
| (8) |
where n1i is the error in representing the approximated particle image by the aligned approximated projection. This error is modeled as white Gaussian noise with standard deviation σ1.
Eqs. (6)–(8) define the new image formation model. Note that Eq. (8) is very similar to the classical model in Eq. (1), in which the subspace approximations Bwi and Avzi replace the image xi and the projection (S). Furthermore, the error ni in Eq. (1) is now distributed over three error terms: n0i, n1i, and n2j.
For the new model to be useful, it is essential that the image approximation be good. Because the particle images do not change as the structure is estimated, we fix the subspace and therefore approximate the images before running the reconstruction algorithm. We choose the image subspace basis B using principal component analysis (PCA) (Jolliffe, 2002) of the particle images. For a given subspace dimension, PCA finds a basis for the subspace that minimizes the mean-squared error between the data and the projection of the data onto that subspace. The choice of the dimension of the principal component subspace is discussed below. Once the subspace is determined, the particle images are projected onto it and the approximated images Bwi are taken to be data. In contrast to this, both the subspace basis A and the coefficients vj for approximating the structure projections are taken to be unknown, since the structure and the projections themselves are unknown, and are estimated along with the structure. The set of parameters to estimate is then Θ = {S, σ1, σ2, α, A, v}, where v = {v1, …, vM } is the set of coefficient vectors for approximating the structure projections.
2.4. Maximum-a-posteriori Estimation with the E–M Algorithm
Using the new model, the single particle reconstruction problem is to recover the parameters Θ from the particle images xi and the approximated images Bwi for i = 1, …, N. Under the maximum-a-posteriori estimation framework, the estimate for the parameters is
| (9) |
The maximization in Eq. (9) is similar to the classical maximum-a-posteriori problem in Eq. (5), with the approximated particle images replacing the original data.
The first term of the objective function in Eq. (9) contains the log of the conditional probability of an approximated image given the parameters. Similar to the traditional maximum-likelihood formulation, zi and τi are latent variables. Marginalizing with respect to zi and τi, the conditional probability is
| (10) |
For simplicity, we set p(τi) to a uniform density. Further, using the model in Eq. (8),
| (11) |
The second term of the objective function in Eq. (9) is the log of the prior p(Θ). Using the dependencies in Eq. (7) and assuming S, σ1, σ2, and α are independent, p (Θ) = p (S, σ1, σ2, α, A, v) = p (A, v|S, σ2) p (S) p (σ2) p (σ1) p (α). The density for p (A, v|S, σ2) is derived from Eq. (7):
| (12) |
where ). The priors for α, σ1, σ2, and S are assumed to be uniform and thus are dropped altogether from the maximization.
Eqs. (9)–(12) define the maximum-a-posteriori reconstruction problem. It is straightforward to derive an E–M algorithm for the problem. Details of the derivation are given in Appendix A. The iterative updates of the algorithm are given below in Eqs. (13)–(19) and are executed in sequence. Each update is calculated using the most recent estimate for the parameters thus far. Note that to denote this, the parameters on the right-hand side of Eqs. (13)–(19) should have iteration superscripts, but we have omitted these superscripts for clarity.
In iteration n, the E-step involves calculating the probability of zi and τi given the data Bwi and the estimate for the parameters Θ[n−1] from the previous iteration. We denote these latent probabilities as W[n] (j, τi) = p (zi = j, τi | Bwi, Θ[n−1]) and they are computed as
| (13) |
Note that the SSDs ||Bwi − (Avj)||2 are calculated between the approximated particle image and approximated projection, while in StandardEM the SSDs compare the particle image and projection.
The M-step updates all the parameters Θ[n] using the latent probabilities W[n] (j, τi) from the E-step:
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
In Eqs. (15) and (16), P is the number of pixels in a particle image, and in Eqs. (17) and (18), is the 2D transformation operator which performs the inverse transformation of . Because the objective function on the right-hand side of Eq. (19) is quadratic in S, its minimum is found efficiently by the conjugate gradient method.
The update expressions for α, σ1, and S are similar to those in the standard maximum-likelihood framework, while the remaining update equations are unique to the subspace formulation. To gain some intuition about the new update expressions, note in Eq. (17) that the update for the basis A depends on a weighted combination of the data and the prior model, that is, the basis depends on the aligned approximated particle images (Bwi) and the current projections of the estimated structure (S). The weighting between these two terms depends on the variance of the error in aligning the approximated particle images and projections and the variance of the error in approximating the projections . If the alignment of the approximated particle images to the approximated projections is poor compared to the approximation of the structure projections, will be larger than , and the prior term will drive the subspace estimate. On the other hand, if the error between the aligned images and the projections is small compared to the error in approximating the projections, will be larger than , and the data term will have a greater influence in estimating the new basis. The image resulting from the combination of the data and prior is compared against the current approximation coefficients vj and normalized (by the expression in the brackets with the inverse) to give the update for basis A.
A similar weighting between the data and current structure is seen in the coefficient update in Eq. (18). For each projection, the weighted compromise between the particle images and current projection is multiplied by the basis matrix AT to get a representation of the combined image in the subspace. This representation is then normalized by (ATA)−1 and the sum of the weights in the denominator of Eq. (18) to give the updated coefficients vj. In this way, the estimate of the subspace and coefficients for the projection approximations adapts to both the particle data and the evolving structure estimate.
2.5. Fast Computation of Latent Probabilities
The latent probabilities in Eq. (13) require calculating the SSDs between each approximated particle image and projection. These SSDs can be written as
| (20) |
where the last equality makes use of the fact that the inner product of two vectors is invariant under rotations. We write it as above because the number of basis elements K needed to represent the projections is smaller than the number of elements L needed to represent the particle images, and thus fewer transformation operations are executed. This inner product can be further simplified by utilizing the subspace representations. Writing out the matrix multiplication Avj in terms of the columns of A, the approximated projection can be written as , where ak is the basis image from the kth column of A and is the kth component of the vector vj. Similarly, let , where bl is the lth column of B and is the lth component of wi. Then,
| (21) |
Eqs. (20) and (21) are at the heart of the computational speedup of SubspaceEM. First, note that the term || (Bwi)||2 in Eq. (20) is the squared norm of the approximated image, which stays the same with each E–M iteration. Thus, these values need be computed just once at the initialization of the algorithm. The second term in Eq. (20) is the squared norm of the approximated projection, which is computed once at the start of each E–M iteration. For a fixed image size, its complexity is order K. The last term in Eq. (20), calculated by way of Eq. (21), dominates the cost of computing the SSDs. In each iteration, every basis image ak is transformed for every value of rotation and translation. For a fixed number of rotations and translations, these image transformations also have complexity of order K. Finally, the inner product between the subspace bases in Eq. (21) has complexity of order K × L. Thus, overall the computation cost of calculating the SSDs in each iteration is order K × L.
A similar analysis can be performed for the cost of calculating the SSDs in the classical E–M formulation. In each iteration, every projection must be transformed for every rotation and translation, giving complexity of order M. For each transformation value and defocus class, D projections must be compared against particle images belonging to the same defocus class. Thus, the overall complexity for calculating the SSDs in each iteration is order D × N.
Comparing the complexity of the classical E–M algorithm with SubspaceEM shows that the speedup of the proposed method depends on how small the dimensions of the subspaces are compared to the number of particle images and projections. As demonstrated by the experiments in the Results section, the subspace dimensions needed for accurate latent probability calculations are generally an order of magnitude or more smaller than the number of particle images and projections. Therefore, the SubspaceEM algorithm results in substantial computational speedup.
2.6. Choosing the Subspace Dimensions
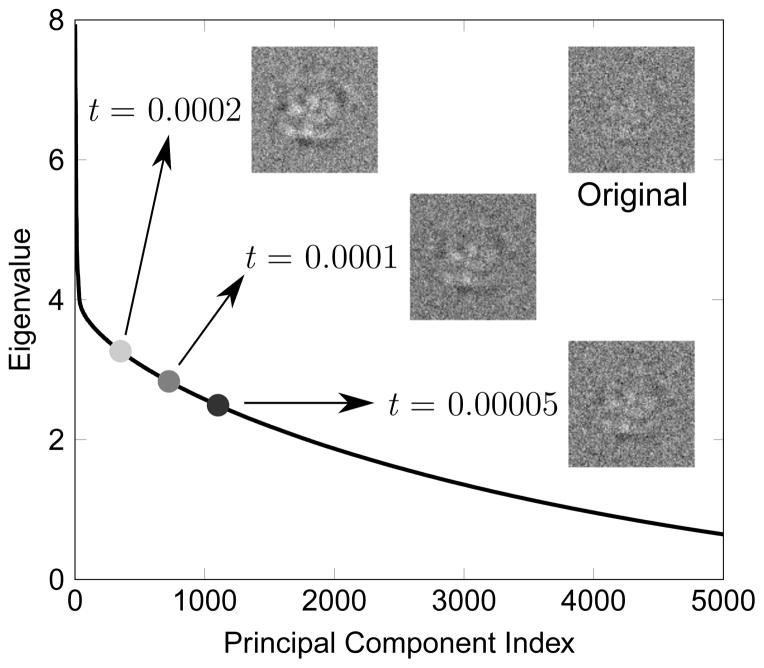
The SubspaceEM algorithm requires selecting the dimensions of the approximating subspaces. Recall that PCA is used to find a basis that is adapted to the particle images. In addition, we use PCA to initialize the basis for the projections. Many rules have been proposed in the literature for choosing the number of principal components such that little information is lost (Jolliffe, 2002; Peres-Neto et al., 2005). We apply the popular Cattell’s scree test (Cattell, 1966). In PCA, each principal component is associated with a principal value, which is an eigenvalue. Cattell’s scree test plots the eigenvalues, ordered from largest to smallest, against the index of the corresponding principal component. The principal component index at which the eigenvalue plot starts to level off in a straight, not necessarily horizontal line is chosen as the cutoff for the number of components, determining the dimension of the approximating subspace. A numerical way to determine this point is to calculate the second difference between adjacent eigenvalues and keep components up to the point where the absolute second difference is less than some threshold t.
An example of an eigenvalue plot is shown in Fig. 3. The cutoff point that satisfies the absolute second difference threshold is highlighted for various values of t. The approximations of the particle images corresponding to the different cutoff points are also displayed. Experiments reported below show that the reconstructions are insensitive to the range of choices for t in Fig. 3. Nominally, we use t = 0.0001.
Fig. 3.
Plot of eigenvalues from PCA of simulated cryo-EM data. The number of components for various values of the threshold t are noted along with corresponding approximated images for the sample particle image in the upper right. The particle image intensities are first normalized to have mean of zero and standard deviation of one before performing PCA.
2.7. Final Algorithm and Implementation
The proposed SubspaceEM method is outlined in Fig. 4. Given as input a set of particle images x, an initial volume S[0], and a threshold t for determining the subspace dimensions, the algorithm outputs a final reconstruction Ŝ.
Fig. 4.
The SubspaceEM algorithm.
Steps 1–4 are initialization steps for the algorithm. Step 2 performs PCA of the particle images, fixes the dimension L of the particle image subspace according to the threshold t, and sets the subspace approximations of the images. Step 3 performs PCA of the initial structure projections, fixes the dimension K of the projection subspace according to the threshold t, and initializes the projection subspace basis and coefficients for each projection. Step 4 initializes the remaining parameters. The vector α is initialized by setting all of its components to 1/M. The standard deviation of the pixel noise in the approximated images σ1 is initialized to the standard deviation of the noise in the original particle images. The standard deviation for the pixel noise in the projections σ2 is initialized to be a hundred times larger than the noise in the approximated images, so that the data drives the parameter estimates in the initial E–M iterations.
After the initializations, the E–M algorithm using the subspace approximation framework is executed in Step 6. As discussed above, the latent probabilities are well estimated at convergence, but the structure S[n] is missing some high frequency information from the original images due to the subspace approximations. To correct for this, Steps 7–8 use the estimated latent probabilities and the original particle images to compute the final reconstruction Ŝ.
Finally, we run the algorithm twice. The final structure Ŝ from the first run (SubspaceEM-1x) is used as the initial structure S[0] in a second run (SubspaceEM-2x). The entire algorithm in Fig. 4 (except for Step 2, which depends only on the particle images) is then executed again. In particular, this means that the dimension of the approximating subspace for the structure projections is recalculated. This improves the result, likely because the approximating subspace is a better fit, which allows the algorithm to escape from a local minimum of the first run. In practice, additional iterations of the algorithm do not appear to improve results any further, and we only execute two iterations.
3. Experimental Methods
3.1. Reconstruction Experiments
We carried out experiments to investigate the quality of the reconstructions and the potential computational savings of the SubspaceEM algorithm compared to the traditional maximum-likelihood formulation. A straightforward implementation of the maximum-likelihood approach in Eq. (4) with the classical image model in Eq. (1) was used, which we refer to as StandardEM. Experiments were carried out using both simulated and real cryo-EM data, described below. For each of these cryo-EM datasets, we estimated reconstructions using the StandardEM algorithm and the proposed SubspaceEM algorithm.
In addition, we tested the sensitivity of the SubspaceEM algorithm to the choice of parameter threshold t, which determines the cutoff for the number of basis components to represent the projection and the particle images. We tested the robustness of the algorithm to our chosen value of t = 0.0001 by changing the parameter to the values t = 0.0002 and t = 0.00005. These values for t resulted in approximately 50 – 100 projection basis elements for the first SubspaceEM run and 100–300 projection basis elements in the second SubspaceEM run. The number of basis elements for the particle image subspace had greater variation, from a few hundred to over one thousand elements. The exact number of components used for each data set are given in Table 1.
Table 1.
Values tested for the threshold t and the corresponding number of components for each dataset and basis.
| K, SubspaceEM-1x | K, SubspaceEM-2x | L | |
|---|---|---|---|
| 0.05 SNR Simulated Data | |||
| t = 0.0002 | 52 | 118 | 302 |
| t = 0.0001 | 73 | 225 | 641 |
| t = 0.0005 | 77 | 280 | 1062 |
| 0.02 SNR Simulated Data | |||
| t = 0.0002 | 50 | 135 | 351 |
| t = 0.0001 | 51 | 163 | 724 |
| t = 0.00005 | 52 | 197 | 1103 |
| 25K Real Images, 5° Sampling | |||
| t = 0.0002 | 82 | 206 | 359 |
| t = 0.0001 | 100 | 176 | 431 |
| t = 0.00005 | 101 | 219 | 529 |
3.2. Simulated Data
We created a low noise (SNR = 0.05) and high noise (SNR = 0.02) synthetic dataset of 10000 cryo-EM images. These images were simulated from the 50S ribosomal subunit structure published by Voss et al. (2010), available online at the National Research for Automated Molecular Microscopy (NRAMM) website. The NRAMM volume is 100 × 100 × 100 voxels with a voxel size of 3.09 Å. To create a synthetic cryo-EM image, we projected the structure along some direction randomly chosen from a 2° sampling on the sphere. We then applied one of three CTFs, based on imaging with 120 keV electrons and defocus values of −1.0, −1.8, or −2.6 μm. Finally, we randomly rotated and translated the projection and added white Gaussian noise to achieve an SNR of 0.05 for the low noise dataset and 0.02 for the higher noise case.
For each dataset, we ran reconstructions using a 5° angular stepsize for both the projection direction around the sphere and in-plane image rotation. The 5° stepsize and three CTF classes resulted in 4998 projections. Translational search was performed in the range of ±4 pixels. We used the NRAMM volume low-pass filtered to 60 Å as the initial structure.
3.3. Real Data
For experiments with real data, we used a 25000 (25K) image subset of the 1.3 million particles of the 70S ribosome published by Brilot et al. (2013). The original particle images collected by Brilot et al. (2013) are 320 × 320 with a pixel size of 1.04 Å. We grouped the images into five CTF classes with defoci at −2.63, −3.16, −3.63, −4.10, and −4.76 μm at 300 kV. To run the StandardEM algorithm in a reasonable amount of time on a single multi-core desktop computer, we downsampled the cryo-EM images by a factor of four. Prior to running the structure estimation algorithms, the particle images were phase-flipped, pre-whitened, and normalized to have intensities with mean of zero and standard deviation of one.
The experiments involved 25000 particle images with an angular search stepsize of 5° around the sphere (8330 projections) and 2° for in-plane rotation. A translational search of ±4 pixels was used. The algorithms were initialized with the published volume from 1.3 million particles low-pass filtered to 60 Å.
3.4. Algorithm Implementation and Evaluation Criteria
The SubspaceEM and StandardEM algorithms were implemented using MATLAB software (MATLAB, 2013). The code is available for download from the MATLAB Central File Exchange at http://www.mathworks.com/matlabcentral/fileexchange/50091. Rotation operations were performed on the GPU using built-in MATLAB functions with the default (bilinear) interpolation setting. The algorithms were considered converged when the squared norm of each projection reference used in calculating the SSDs differed by no more than 1% from the previous iteration. Specifically, the norms of the approximated projections were compared in SubspaceEM, while the norms of the structure projections were compared in StandardEM.
We evaluated the goodness of the reconstructions using the Fourier shell correlation (FSC). Prior to computing the FSCs, structures were aligned to one another using UCSF Chimera (Pettersen et al., 2004), and a soft, spherical mask with a Gaussian fall-off at the edge was applied to each volume. The FSC between each reconstruction and published structure was calculated to determine how closely the reconstruction agrees with the existing structure. The resolution of the reconstruction based on these comparisons was estimated using the frequency which coincides with FSC = 0.5. Furthermore, for the real dataset, two independent reconstructions were obtained from the data randomly split in half, and the gold standard FSC (Scheres and Chen, 2012) was calculated to assess the consistency of the estimated reconstructions. Because calculation of a gold standard FSC requires half-dataset reconstructions, the threshold of FSC = 0.143 was used to report the resolution (Rosenthal and Henderson, 2003). Finally, the FSCs between SubspaceEM and StandardEM reconstructions were calculated to directly compare the results produced by the two algorithms. Since reconstructions from the same whole dataset were compared, the structures were considered similar up to the more conservative FSC = 0.5 threshold.
In addition to measuring reconstruction quality, we evaluated algorithm efficiency by measuring total CPU times1 for different parts of the algorithms. We measured the average CPU time to compute the exponential function of the SSDs in Eq. (13) in the E-step (denoted as “Average SSD Time” in the tables), the average CPU time for one E–M iteration, and the total CPU time to run the entire algorithm. For the SubspaceEM method, we reported the calculation times for each run of the algorithm (SubspaceEM-1x and SubspaceEM-2x) as well as overall statistics after finishing the two runs (SubspaceEM-Overall). The speedup in CPU time was calculated as the StandardEM time divided by the SubspaceEM-Overall time. All reconstructions for each dataset were performed on the same machine for fair comparison of run times.
4. Results
4.1. Simulated Data Experiments
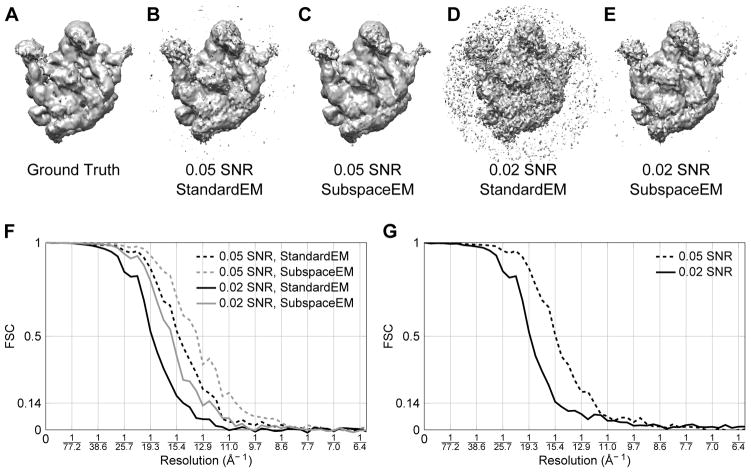
The original NRAMM reconstruction, used as the ground truth in the simulations, is shown in Fig. 5A. The reconstructions for the 0.05 SNR simulated data are in Figs. 5B and 5C, and the reconstructions for the 0.02 SNR data are in Figs. 5D and 5E. The 0.02 SNR reconstructions appear noisier and lower resolution than the 0.05 SNR reconstructions, as expected. However, for each dataset, the SubspaceEM algorithm structure appears less noisy compared to the StandardEM result. The StandardEM algorithm was run with no additional low-pass filtering of the images or structure, which may have partly contributed to the noisier result.
Fig. 5.
Reconstruction results from simulated data experiments. Reconstructions were obtained from 10000 simulated particle images with a pixel size of 3.09 Å, using 5° projection direction sampling. (A) Ground truth structure of the 50S ribosomal subunit obtained from Voss et al. (2010). (B) StandardEM reconstruction from 0.05 SNR simulated data. (C) SubspaceEM reconstruction from 0.05 SNR simulated data. (D) StandardEM reconstruction from 0.02 SNR simulated data. (E) SubspaceEM reconstruction from 0.02 SNR simulated data. (F) FSCs between true and estimated structures. (G) FSCs between StandardEM and SubspaceEM reconstructions.
FSCs between the ground truth structure and the estimated reconstructions are plotted in Fig. 5F. The FSCs confirm that the SubspaceEM reconstructions contain more detail than the StandardEM results; the StandardEM and SubspaceEM algorithms produced structures with resolutions of 15.2 Å and 13.4 Å for the 0.05 SNR dataset and 19.0 Å and 16.0 Å for the 0.02 SNR dataset, respectively. Furthermore, the FSCs comparing the StandardEM and SubspaceEM results suggest that the methods produced structures that are similar up to about the resolution of the StandardEM structure (Fig. 5G).
Table 2 displays computing times for StandardEM and SubspaceEM. The time to compute the SSDs in one iteration using StandardEM was on the order of a few days, while SubspaceEM took only a few minutes. Although the SubspaceEM algorithm was run twice and required more E–M iterations than StandardEM to converge, the total CPU time for SubspaceEM was less than two hours, while StandardEM needed up to four weeks to finish processing.
Table 2.
CPU time and speedup for simulated data experiments. Times are reported as the sum of execution time across all processes.
| Average SSDa Time (min) | Average Iteration Time (min) | # EM Iterations | Total CPU Time (hrs) | |
|---|---|---|---|---|
| Simulated 0.05 SNR | ||||
| StandardEM | 4004 | 4022 | 10 | 670 |
| SubspaceEM-1x | 2.8 | 6.1 | 6 | 0.8 |
| SubspaceEM-2x | 4.3 | 7.2 | 6 | 0.9 |
| SubspaceEM-Overall | 3.5 | 6.7 | 12 | 1.7 |
| Simulated 0.02 SNR | ||||
| StandardEM | 3914 | 3924 | 7 | 458 |
| SubspaceEM-1x | 2.6 | 7.1 | 5 | 0.8 |
| SubspaceEM-2x | 3.7 | 6.8 | 6 | 0.9 |
| SubspaceEM-Overall | 3.2 | 7.0 | 11 | 1.6 |
| Speedupb | ||||
| Simulated 0.05 SNR | 1144 | 600 | - | 394 |
| Simulated 0.02 SNR | 1223 | 561 | - | 280 |
SSD = Sum of squared differences. In StandardEM, the differences are calculated between images and projections. In SubspaceEM, the differences are between approximated images and approximated projections.
Speedup is calculated as (StandardEM time)/(SubspaceEM-Overall time).
The computational speedup of SubspaceEM over StandardEM is shown at the bottom of Table 2. On average, the SSD calculation is over 1000 times faster, while the computation for an entire E–M iteration is over 500 times faster for SubspaceEM. Note that the time to update the structure dominates the M-step in both algorithms; since the reconstruction time is a much smaller fraction of the time to complete a StandardEM iteration compared to a SubspaceEM iteration, the speedup factor is reduced. The overall computational speedup is further reduced to about a factor of 300 due to the SubspaceEM algorithm requiring more iterations to converge than StandardEM.
4.2. Real Data Experiments
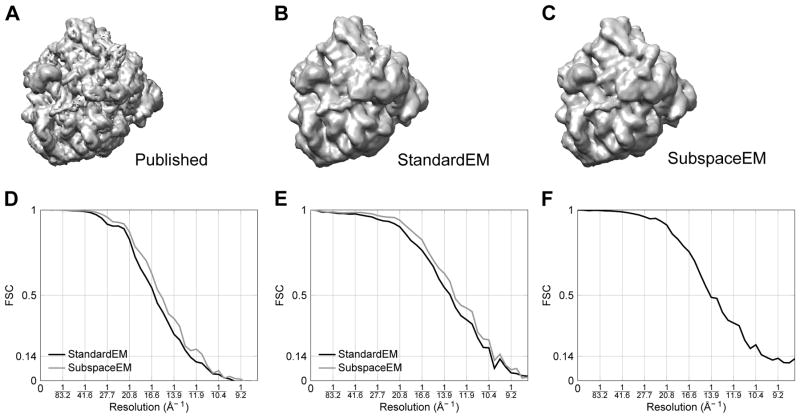
Fig. 6 summarizes the reconstruction results using the real data. The StandardEM and SubspaceEM reconstructions appear very similar (Figs. 6B and 6C). Gold standard FSCs suggest a resolution of 12.4 Å using StandardEM and 11.3 Å using SubspaceEM (Fig. 6D). The FSCs comparing the StandardEM and SubspaceEM volumes with the structure from Brilot et al. (2013) show agreement with the published volume up to 13.3 Å and 12.9 Å, respectively (Fig. 6E). The FSC between the StandardEM and SubspaceEM reconstructions suggest structural agreement is limited by the slightly lower resolution of the StandardEM result (Fig. 6F).
Fig. 6.
Reconstruction results from real data experiments. Reconstructions were obtained from 25000 particles images with a pixel size of 4.16 Å, using 5° projection direction sampling. (A) Structure of the 70S ribosome from Brilot et al. (2013). (B) StandardEM reconstruction. (C) SubspaceEM reconstruction. (D) Gold standard FSCs. (E) FSCs between structure from Brilot et al. (2013) and estimated structures. (F) FSC between StandardEM and SubspaceEM reconstructions.
Computation times are listed in Table 3. StandardEM required weeks of CPU time to complete one iteration, while an iteration of SubspaceEM ran in less than half an hour. Overall, the total CPU time was about six hours for SubspaceEM compared to almost three months for StandardEM.
Table 3.
CPU time and speedup for real data experiments. Times are reported as the sum of execution time across all processes.
| Average SSDa Time (min) | Average Iteration Time (min) | # EM Iterations | Total CPU Time (hrs) | |
|---|---|---|---|---|
| 25K Images, 5° Sampling | ||||
| StandardEM | 23950 | 23956 | 5 | 1996 |
| SubspaceEM-1x | 15.9 | 18.8 | 8 | 2.6 |
| SubspaceEM-2x | 19.2 | 21.8 | 7 | 2.7 |
| SubspaceEM-Overall | 17.5 | 20.2 | 15 | 5.3 |
| Speedupb | 1369 | 1186 | - | 377 |
SSD = Sum of squared differences. In StandardEM, the differences are calculated between images and projections. In SubspaceEM, the differences are between approximated images and approximated projections.
Speedup is calculated as (StandardEM time)/(SubspaceEM-Overall time).
Speedup factors for the real data experiments are shown at the bottom of Table 3. Both the SSD calculation time and iteration time for SubspaceEM were about 1000 times faster than for StandardEM. The increased speedup of the E–M iterations in this experiment compared to the simulated experiments is due to the greater number of particles, resulting in longer SSD calculations. As in the simulated experiments, SubspaceEM required more iterations to converge compared to StandardEM, and thus the speedup for overall runtime is smaller compared to the average speedup per E–M iteration. Still, SubspaceEM ran over 300 times faster than StandardEM.
4.3. Parameter Sensitivity
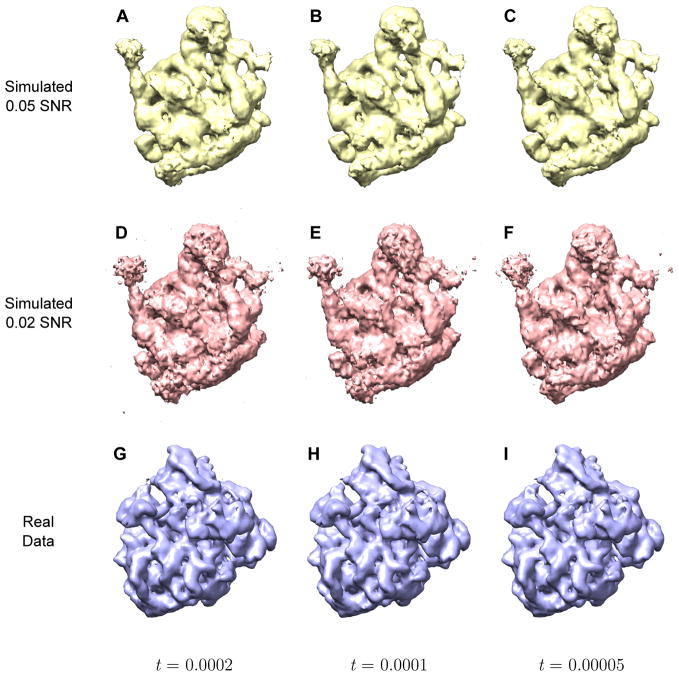
The SubspaceEM reconstructions from varying the number of basis components are shown in Fig. 7. Each row shows the reconstructions using the same dataset. With t decreasing from left to right, each column corresponds to the same value for t. For each dataset, the reconstructions agree in a similar way to the published structure, as evidenced by the overlap in the FSC curves comparing the estimated and baseline structures (Fig. 8). Note that SubspaceEM produced very similar reconstructions even though the number of basis elements used varied by up to an order of magnitude (Table 1), demonstrating the robustness of the algorithm to the choice of threshold t.
Fig. 7.
SubspaceEM reconstructions using different values for the threshold t. Each row corresponds to reconstructions using the same dataset, with number of basis components used increasing from left to right. (A) Simulated 0.05 SNR, t = 0.0002. (B) Simulated 0.05 SNR, t = 0.0001. (C) Simulated 0.05 SNR, t = 0.00005. (D) Simulated 0.02 SNR, t = 0.0002. (E) Simulated 0.02 SNR, t = 0.0001. (F) Simulated 0.02 SNR, t = 0.00005. (G) Real data, t = 0.0002. (H) Real data, t = 0.0001. (I) Real data, t = 0.00005.
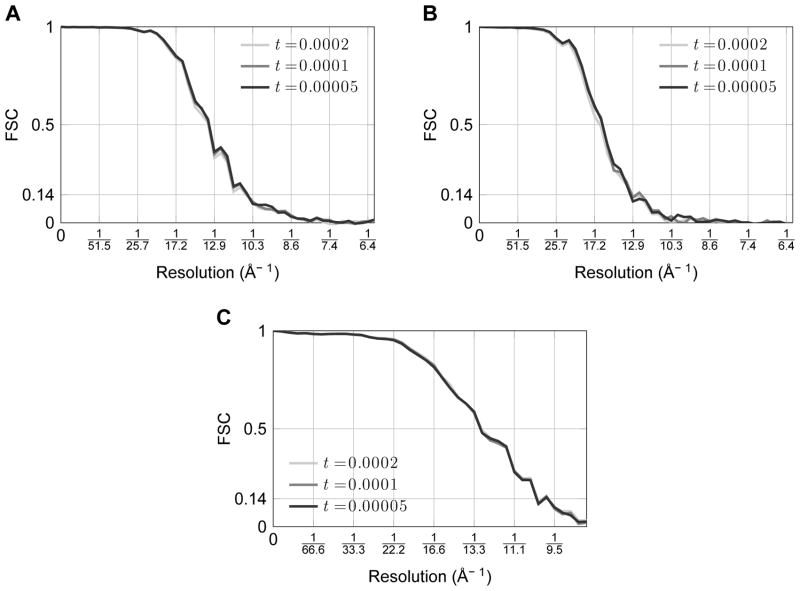
Fig. 8.
FSCs evaluating SubspaceEM reconstructions using different values for the threshold t. (A) True vs. estimated structures for 0.05 SNR data. (B) True vs. estimated structures for 0.02 SNR data. (C) Brilot et al. (2013) structure vs. estimated structures for real data.
5. Discussion
5.1. SubspaceEM Algorithm Discussion
The SubspaceEM algorithm is a new method for performing fast cryo-EM single particle reconstruction. The approach finds two image subspaces, one for approximating the particle images and one for approximating the projections of the current structure estimate. The particle image subspace is estimated from the particle data, while the structure projection subspace is iteratively estimated within the E–M framework from the weighted aligned particle images and current structure. Using these two subspaces, the match between each transformed projection and particle image can be quickly calculated by performing the appropriate operations on the subspace bases and applying the image coefficients. This gives the SubspaceEM algorithm significant speedup compared to the conventional E–M algorithm for maximum-likelihood reconstruction because the numbers of image comparisons and transformations are greatly reduced.
An alternative to using two subspaces is to approximate both the particle images and structure projections with a single subspace, for which there are two options. One option is to just use the PCA subspace of the data by itself. A second option is to iteratively estimate one subspace within the E–M algorithm. It turns out that both of these alternatives have significantly worse computational performance as well as worse representational accuracy.
To understand the effect on computational performance, recall that if the dimension of the projection approximation subspace is K and the dimension of the image approximation subspace is L, then the computational complexity of the each E–M iteration is K × L. The dimension L is typically one or two orders of magnitude larger than the dimension K. If a single subspace is used for approximating both, then K = L, and the computational complexity increases by an order of magnitude or two. Keeping the subspaces separate reduces K and gives a faster algorithm.
In considering the accuracy, the key factor is that the number of particle images is one or two orders of magnitude more than the number of structure projections. Hence, if a single subspace is used to approximate the particle images as well as projections, then the subspace is determined solely or mostly by the particle images. There is no guarantee that the projections will be approximated well, since the data are unaligned and noisy. This implies that the latent probabilities may not be approximated well, and the accuracy of the reconstruction may suffer. Instead, using two subspaces approximates the data as well as the projections independent of their relative sizes, giving accurate approximations for both. Further, the accuracies of both can be independently controlled by choosing a separate dimension for each.
The dimension of each approximating subspace is constant during a single run of the SubspaceEM algorithm (e.g., as indicated in Table 1). This is simply what is dictated by the mathematics of the E–M algorithm. Of course, changing the dimension of the approximating subspaces will further improve the accuracy, and our approach to this is to run the SubspaceEM algorithm twice. After the SubspaceEM algorithm is run for the first time, its final structure is used as the new initial input for a second run. Specifically, the projections from the first reconstruction are used with the scree test to increase the dimension of the structure projection subspace, and SubspaceEM is run the second time with this new dimension. Our experience with the SubspaceEM algorithm is that it is not necessary to repeat this further; running SubspaceEM twice gives reconstructions that are as good as with multiple repeats.
5.2. SubspaceEM Reconstruction Quality
The proposed SubspaceEM algorithm consistently produced reconstructions with resolutions that were comparable to or better than results from the classic E–M reconstruction algorithm. Restricting the data and projections to a lower dimensional subspace undeniably results in some loss of high frequency information. While the structure estimated by the E–M algorithm using the subspace approximations (after Step 6 in Fig. 4) is of lower resolution, the latent probabilities are very well approximated, i.e., the cryo-EM data are well-aligned to the projections. Thus, we are able to get back an accurate, higher resolution structure using the original data and the final latent probabilities. A similar strategy is often used in traditional reconstruction methods: low-pass filtering the images to calculate the best match between the projections and data, and then including higher frequency information to calculate the reconstructions.
The SubspaceEM reconstruction is driven by the likelihood function, which has multiple local maxima. The E–M algorithm, as well as other popular reconstruction methods, only guarantee convergence to a local maximum. Since the SubspaceEM algorithm follows an E–M derivation, it too will converge to a local maximum. Standard techniques for avoiding bad local maxima can be used with SubspaceEM. For example, the algorithm could be run many times with different initial structures, and the result with the highest likelihood would be chosen as the final reconstruction. The computational speed of the SubspaceEM algorithm makes this an attractive strategy for handling suboptimum reconstructions.
One additional consideration for SubspaceEM compared to StandardEM is the choice of subspace dimensions, governed by the threshold parameter t. If t is chosen to be too large, the subspace dimensions may be too small to retain enough image information for accurate particle alignment. On the other hand, the smaller the value of t, the larger the dimensions of the subspaces, and the closer the approximations get to exactly representing the particle images and projections. The experiments show robustness of the SubspaceEM algorithm to a wide range of subspace dimensions (Fig. 8).
While SubspaceEM produced good results for the tested datasets regardless of the choice of subspace dimensions, there may be cases where the alignment information is in such high frequencies that the subspace approximations may not give accurate alignment. For example, successful determination of the structure of apoferritin by cryo-EM required frequencies beyond 10 Å (Russo and Passmore, 2014). Recall that our algorithm uses Cattell’s scree test to determine the subspace dimensions (Section 2.6). If it is imperative that certain frequencies be preserved, the scree test could be replaced by another test that adjusts the subspace dimensions to keep as many basis elements as needed to cover the desired frequency range. Compared to the scree test, a test to keep very high frequencies would likely give higher dimensions for the subspaces and reduce the computational speedup of SubspaceEM. However, note that even if all the basis elements are kept, the computational complexity would be no more than in the traditional E–M reconstruction algorithm.
5.3. Reduction in Computational Costs
The primary advantage in applying our SubspaceEM approach is the very large computational savings. The sizes of the datasets and projections tested were ~104 and ~103, respectively, while the image and projection bases each consisted of ~102 elements. Thus, we expect the SSD computations for the latent probabilities to be accelerated by a factor of ~ 103. The experimental results matched our theoretical expectations, with the speedup in calculating the SSDs reaching over a factor of 1000. While we ran the SubspaceEM algorithm two times for each dataset to handle the local minimum problem, using the reconstruction from the first run to initialize the second, the overall CPU time using SubspaceEM was still over hundreds of times faster than using StandardEM.
The greatly reduced computational time for the proposed SubspaceEM algorithm has implications for single particle reconstruction with modern direct detector methods. As image acquisition techniques improve and the size of cryo-EM datasets grow, the image analysis is often limited by the availability of computational power. The significant speedup of our approach allows a much larger number of images to be processed in a reasonable amount of time, using fewer computational resources. In addition, unlike other acceleration methods which reduce the parameter search space, the SubspaceEM algorithm performs a truly exhaustive search for the optimal alignment parameters. The implementation of the SubspaceEM algorithm can be further optimized and combined with other acceleration techniques such as hardware parallelization to further minimize the wall-clock time.
5.4. Extensions of the SubspaceEM Algorithm
While presented above in the spatial domain, the SubspaceEM algorithm applies without change to the Fourier domain. These two domains provide representations of images in two different orthonormal bases. In the spatial domain, an image is represented in terms of a delta function basis, while in the Fourier domain, an image is represented in a (co-)sinusoidal basis. Note that in the SubspaceEM algorithm, the two subspace bases (the columns of the B and A matrix) are defined solely in terms of particle images and structure projections. All of the calculations of the algorithm can be carried out in any coordinate system in which the images and the projections are represented. Furthermore, since the calculations in the SubspaceEM algorithm give identical results in any orthonormal basis, the algorithm and all its results, including the expected speedup, apply identically to both the spatial and Fourier domains.
An additional consideration in a Fourier domain implementation is the practice of low-pass filtering to limit the resolution of the particle images based on the resolution of the current structure. This helps to reduce overfitting of the data. We show below that the application of the SubspaceEM algorithm to limited resolution images in the Fourier domain would provide computational gains comparable to those seen in the spatial domain implementation.
To illustrate the effect of a Fourier implementation on the speedup potential of the SubspaceEM algorithm, we ran the following numerical analysis. Using three sets of images from the real data experiment, the subspace dimensions were determined using Cattell’s scree test and a threshold of t = 0.0001 as described in Section 2.6. The structure projection subspace dimension was calculated for two sets of projections: the projections of the structure used to initialize the reconstruction, and the projections from the last iteration of the second run of the algorithm (SubspaceEM-2x). The particle image subspace dimension was calculated from the 25K particle images. For each of the three sets of images, the subspace dimensions were computed from the images represented in both the spatial and Fourier domains. In addition, the subspace dimensions were calculated for each set of images in Fourier space restricted to a resolution of 12 Å, the approximate resolution of the final reconstruction, and also to 20 Å, representing greater low-pass filtering in earlier reconstruction iterations.
The results of the scree tests for each set of images are shown in Fig. 9. The subspace dimensions from the scree test are denoted on the eigenvalue plots by the filled circles. We make three observations about the plots. First, as expected, the plots for each image set in the spatial and Fourier domain are identical, and thus the subspace dimensions are the same regardless of the image representation. Therefore, for the same set of images, the speedup of the spatial implementation of SubspaceEM would apply equally to a Fourier implementation. Second, limiting the resolution of the images has only a small effect on the scree plot. The plots are actually identical for the initial structure projections, since the initial structure was already low-pass filtered at 60 Å (Fig. 9A). The greatest difference is seen in the plots for the particle images, because these images are much noisier than the structure projections (Fig. 9C). The last observation is that the subspace dimension, as calculated by the scree test, changes by only a small amount for the images with limited resolution compared to the original images. The small change occurs because limiting the resolution effectively reduces the noise in the images, resulting in more image details being represented in more of the principal components. Since the change in dimension is small, the speedup for a Fourier domain implementation would be similar to the results reported for the spatial domain.
Fig. 9.
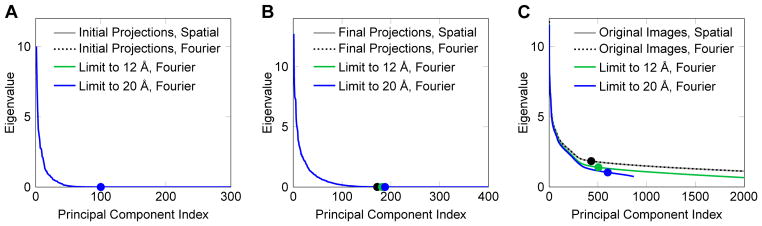
Scree tests for different sets of images from the real data experiment. For each image set, PCA was performed on the original images represented in the spatial and Fourier domains. In addition, PCA was performed on the images limited to 12 Å and 20 Å resolution, represented in Fourier space. The filled circles on the eigenvalue plots denote the calculated subspace dimensions using t = 0.0001. The plots for the spatial and Fourier versions of each image set are identical, while the plots for the limited resolution images compared to the original images show a small change. (A) Scree tests for projections of the initial structure. Because the initial structure is low-pass filtered at 60 Å, the plots and calculated dimensions are identical for each case. (B) Scree tests for projections from the last iteration of SubspaceEM-2x. (C) Scree tests for the particle images.
Finally, the ideas used in the SubspaceEM algorithm may be applied to other cryo-EM reconstruction problems. One direction is to adapt the subspace approximation approach to the classical best-match formulation for single particle reconstruction. Like in the E–M formulation, the computational bottleneck in the best-match strategy is in calculating the goodness of the alignment between each particle and projection image. Thus, application of the subspace method to the best-match approach should result in a speedup factor similar to the experiments presented here. In addition, a straightforward extension of the SubspaceEM algorithm to 3D multireference refinement would greatly accelerate structurally heterogeneous data analysis. We would propose using one subspace in which to represent all the projections from the different structures, which should result in even greater speedup than in the single particle case.
Acknowledgments
This work was supported by NIH grants R01 LM010142 (to H.D.T) and R21 NS085776 (F.J.S) and by the Yale School of Medicine Brown-Coxe Fellowship (N.C.D.). We thank Nikolaus Grigorieff for generously providing the data for the real data experiments.
Appendix A. M-Step Objective Function and Updates
The M-step of the E–M algorithm corresponds to maximizing a function Q with respect to the parameters Θ. For our problem, the Q function simplifies to
| (A.1) |
Maximizing the Q function of Eq. (A.1) with respect to each of the parameters gives the updates in Eqs. (14)–(19). Update expressions for αj, , and S are similar to those in the traditional E–M algorithm for reconstruction, and we omit their derivation here. The updates for the projection basis A and the projection coefficients vj are derived below.
Let Aij be the entry in the ith row and jth column of matrix A. Then the derivative is defined as the matrix whose entry in the ith row and jth column is . Thus, the derivative of Eq. (A.1) with respect to A yields
| (A.2) |
Setting Eq. (A.2) equal to zero and rearranging so terms involving A are all on one side, we get
| (A.3) |
Multiplying both sides by and and then multiplying both sides on the right by the inverse of the expression in the brackets gives the update expression in Eq. (17).
Taking the derivative of Eq. (A.1) with respect to vj,
| (A.4) |
Setting Eq. (A.4) equal to zero and moving all terms with vj to one side gives
| (A.5) |
Finally, multiplying both sides of Eq. (A.5) on the left by (ATA)−1 and dividing through by the quantity in the brackets on the left hand side gives the update in Eq. (18).
Footnotes
The MATLAB implementation for the StandardEM algorithm makes use of the parfor function to allow the code to run across several MATLAB processes at the same time. We use the term “CPU time” to mean the sum of execution time across all processes.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bishop C. Pattern Recognition and Machine Learning. Springer; 2006. [Google Scholar]
- Brilot AF, Korostelev AA, Ermolenko DN, Grigorieff N. Structure of the ribosome with elongation factor g trapped in the pretranslocation state. Proc Natl Acad Sci USA. 2013;110:20994–20999. doi: 10.1073/pnas.1311423110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cattell RB. The scree test for the number of factors. Multivar Behav Res. 1966;1(2):245–276. doi: 10.1207/s15327906mbr0102_10. [DOI] [PubMed] [Google Scholar]
- Cheng Y, Walz T. The advent of near-atomic resolution in single-particle electron microscopy. Annu Rev Biochem. 2009;78:723–742. doi: 10.1146/annurev.biochem.78.070507.140543. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the em algorithm. J Roy Statist Soc Ser B. 1977;39(1):1–38. [Google Scholar]
- Doerschuk PC, Johnson JE. Ab initio reconstruction and experimental design for cryo electron microscopy. IEEE Trans Inf Theory. 2000;46(5):1714–1729. [Google Scholar]
- Grigorieff N. Frealign: High-resolution refinement of single particle structures. J Struct Biol. 2007;157(1):117–125. doi: 10.1016/j.jsb.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Henderson R, Chen S, Chen JZ, Grigorieff N, Passmore LA, Ciccarelli L, Rubinstein JL, Crowther RA, Stewart PL, Rosenthal PB. Tilt-pair analysis of images from a range of different specimens in single-particle electron cryomicroscopy. J Mol Biol. 2011;413(5):1028–1046. doi: 10.1016/j.jmb.2011.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolliffe IT. Principal Component Analysis. Springer; 2002. [Google Scholar]
- Kucukelbir A, Sigworth FJ, Tagare HD. A bayesian adaptive basis algorithm for single particle reconstruction. J Struct Biol. 2012;179(1):56–67. doi: 10.1016/j.jsb.2012.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Doerschuk PC, Johnson JE. Exact reduced-complexity maximum likelihood reconstruction of multiple 3-d objects from unlabeled unoriented 2-d projections and electron microscopy of viruses. IEEE Trans Image Process. 2007;16:2865–2878. doi: 10.1109/tip.2007.908298. [DOI] [PubMed] [Google Scholar]
- MATLAB. R2013a (Version 8.1) The MathWorks, Inc; Natick, MA, USA: 2013. [Google Scholar]
- Peres-Neto PR, Jackson DA, Somers KM. How many principal components? stopping rules for determining the number of non-trivial axes revisited. Comput Stat Data An. 2005;49(4):974–997. [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. Ucsf chimera–a visualization system for exploratory research and analysis. J Comput Chem. 2004;25(13):1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Rosenthal PB, Henderson R. Optimal determination of particle orientation, absolute hand, and contrast loss in single-particle electron cryomicroscopy. J Mol Biol. 2003;333(4):721–745. doi: 10.1016/j.jmb.2003.07.013. [DOI] [PubMed] [Google Scholar]
- Russo CJ, Passmore LA. Ultrastable gold substrates for electron cryomicroscopy. Science. 2014;346(6215):1377–1380. doi: 10.1126/science.1259530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW. A bayesian view on cryo-em structure determination. J Mol Biol. 2012a;415:406–418. doi: 10.1016/j.jmb.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW. Relion: Implementation of a bayesian approach to cryo-em structure determination. J Struct Biol. 2012b;180:519–530. doi: 10.1016/j.jsb.2012.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW, Chen S. Prevention of overfitting in cryo-em structure determination. Nat Methods. 2012;9:853–854. doi: 10.1038/nmeth.2115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheres SHW, Gao H, Valle M, Herman GT, Eggermont PP, Frank J, Carazo JM. Disentangling conformational states of macromolecules in 3d-em through likelihood optimization. Nat Methods. 2007;4:27–29. doi: 10.1038/nmeth992. [DOI] [PubMed] [Google Scholar]
- Scheres SHW, Valle M, Carazo JM. Fast maximum-likelihood refinement of electron microscopy images. Bioinformatics. 2005a;21:ii243–ii244. doi: 10.1093/bioinformatics/bti1140. [DOI] [PubMed] [Google Scholar]
- Scheres SHW, Valle M, Nuez R, Sorzano CO, Marabini R, Herman GT, Carazo JM. Maximum-likelihood multi-reference refinement for electron microscopy images. J Mol Biol. 2005b;348(1):139–149. doi: 10.1016/j.jmb.2005.02.031. [DOI] [PubMed] [Google Scholar]
- Sigworth FJ. A maximum-likelihood approach to single-particle image refinement. J Struct Biol. 1998;122:328–339. doi: 10.1006/jsbi.1998.4014. [DOI] [PubMed] [Google Scholar]
- Sigworth FJ, Doerschuk PC, Carazo JM, Scheres SHW. Chapter ten - an introduction to maximum-likelihood methods in cryo-em. Methods Enzymol. 2010;482:263–294. doi: 10.1016/S0076-6879(10)82011-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorzano COS, Marabini R, Velazquez-Muriel J, Bilbao-Castro JR, Scheres SHW, Carazo JM, Pascual-Montano A. Xmipp: a new generation of an open-source image processing package for electron microscopy. J Struct Biol. 2004;148(2):194–204. doi: 10.1016/j.jsb.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Tagare HD, Barthel A, Sigworth FJ. An adaptive expectation-maximization algorithm with gpu implementation for electron cryomicroscopy. J Struct Biol. 2010;171:256–265. doi: 10.1016/j.jsb.2010.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagare HD, Sigworth F, Barthel A. Fast, adaptive expectation-maximization alignment for cryo-em. In Med Image Comput Comput Assist Interv. 2008;11:855–862. doi: 10.1007/978-3-540-85990-1_103. [DOI] [PubMed] [Google Scholar]
- Voss NR, Lyumkis D, Cheng A, Lau PW, Mulder A, Lander GC, Brignole EJ, Fellmann D, Irving C, Jacovetty EL, Leung A, Pulokas J, Quispe JD, Winkler H, Yoshioka C, Carragher B, Potter CS. A toolbox for ab initio 3-d reconstructions in single-particle electron microscopy. J Struct Biol. 2010 Mar;169(3):389–398. doi: 10.1016/j.jsb.2009.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin Z, Zheng Y, Doerschuk PC. An ab initio algorithm for low-resolution 3-d reconstructions from cryoelectron microscopy images. J Struct Biol. 2001;133:132–142. doi: 10.1006/jsbi.2001.4356. [DOI] [PubMed] [Google Scholar]
- Yin Z, Zheng Y, Doerschuk PC, Natarajan P, Johnson JE. A statistical approach to computer processing of cryo-electron microscope images: virion classification and 3-d reconstruction. J Struct Biol. 2003;144:24–50. doi: 10.1016/j.jsb.2003.09.023. [DOI] [PubMed] [Google Scholar]