Abstract
Monitoring depth of anesthesia (DOA) via vital signs is a major ongoing challenge for anesthetists. A number of electroencephalogram (EEG)-based monitors such as the Bispectral (BIS) index have been proposed. However, anesthesia is related to central and autonomic nervous system functions whereas the EEG signal originates only from the central nervous system. This paper proposes an automated DOA detection system which consists of three steps. Initially, we introduce multiscale modified permutation entropy index which is robust in the characterization of the burst suppression pattern and combine multiscale information. This index quantifies the amount of complexity in EEG data and is computationally efficient, conceptually simple and artifact resistant. Then, autonomic nervous system activity is quantified with heart rate and mean arterial pressure which are easily acquired using routine monitoring machine. Finally, the extracted features are used as input to a linear discriminate analyzer (LDA). The method is validated with data obtained from 25 patients during the cardiac surgery requiring cardiopulmonary bypass. The experimental results indicate that an overall accuracy of 89.4 % can be obtained using combination of EEG measure and hemodynamic variables, together with LDA to classify the vital sign into awake, light, surgical and deep anesthetised states. The results demonstrate that the proposed method can estimate DOA more effectively than the commercial BIS index with a stronger artifact-resistance.
Keywords: Depth of anesthesia, Electroencephalogram (EEG), Permutation entropy, Hemodynamic parameters
Introduction
Estimating the depth of anesthesia (DOA) is a challenge in anesthesia research. One of the most reported cases in many studies is intraoperative awareness during anesthesia which may cause psychological impacts on patients (Sebel et al. 2004). Researchers have focused on finding reliable noninvasive ways to monitor DOA in clinical applications. Investigators pay a great attention to the analysis of brain activity through the electroencephalogram (EEG) because the central nervous system is the target of anesthetic drugs (Hutt and Longtin 2010). Analysis of the EEG signal during surgery is helpful for monitoring DOA (Al-Kadi et al. 2013) because of reducing anesthetic drug consumption and resulting in faster wake-up and recovery from anesthesia.
During the past two decades, one of the most popular EEG-based commercial monitor systems in hospitals is the Bispectral index (BIS; Aspect Medical Systems, Newton, MA, USA) (Rampil 1998). The range of the recorded BIS is between 0 (suppression state of EEG) to 100 (awake). Decreasing values indicate deepening levels of hypnosis. The BIS index present significant advantages such as comprehensive clinical validation (Myles et al. 2004; Luginbühl et al. 2003). The BIS index is based on the power distribution of the Fourier transform of the EEG signal, and quantifies the phase coupling between different EEG frequencies (Rampil 1998). However, this frequency based method is more suitable for the analysis of stationary signals. Also, the BIS index has received some criticism, such as being sensitive to artifact (Shalbaf et al. 2012a), causing paradoxical results during burst suppression pattern (Muncaster et al. 2003), not being responsive to some anesthetic agents (Johansen and Sebel 2000), not regaining its baseline value after emergence (Sleigh and Donovan 1999) and inducing large time delays (Pilge et al. 2006). In addition, it has been reported that dose–response models based on the BIS are only moderately accurate (Lehmann et al. 2002).
Nonlinearity can be seen in many dynamical systems found in nature, including the heart (Shalbaf et al. 2013a) and brain (Fell et al. 2000). Since population neural activity exhibits nonlinear behaviors, it is reasonable to apply methods from the theory of nonlinear dynamics and information theory, such as complexity measures and fractal (Ahmadi and Amirfattahi 2010; Ferents et al. 2006, Hosseini et al. 2010; Shalbaf et al. 2013c), recurrence quantification analysis (Talebi et al. 2012), bayesian analysis (Nguyen-Ky et al. 2013), sample entropy (Shalbaf et al. 2012b) and manifold learning with isomap algorithm (Kortelainen et al. 2011a, b) to the EEG signals for DOA estimation and brain dynamic assessing. Recently, a new method, called permutation entropy (PE) has been developed to explore the order pattern structure of a dynamical time series (Bandt and Pompe 2002; Olofsen et al. 2008). PE is an emerging complexity measure for analyzing non-stationary data. Although PE is computationally efficient, conceptually simple and artifact resistant, it doesn’t work at deep anesthetised state, mainly due to high-frequency waves during the suppression period (Shalbaf et al. 2013b; Li et al. 2008). In this paper, we introduce modified permutation entropy (MPE) index which is robust in the characterization of the burst suppression pattern at high doses of anesthetics. To achieve this goal, the part of the EEG signal that contains EEG suppressions are calculated separately by another nonlinear algorithm and then the calculation theory of PE is modified.
Recently multiscale entropy has been suggested to evaluate the complexity of EEG series (Costa et al. 2003). Brain activity is regulated by complicated self-regulating systems which process inputs from interacting mechanisms that operate across multiple temporal scales. The EEG is an integrated appearance of this brain function and shows complicated fluctuations which contain knowledge about the underlying dynamics (Ouyang et al. 2009). Thus, multiscale entropy can be valuable for discovering the dynamical characteristics intrinsic in brain functions on multiple temporal scales instead of a single scale. In this research, multiscale entropy was applied to EEG recordings, and MPE values were combined at multiple scales to develop a new index named multiscale modified permutation entropy (MMPE) to estimate DOA.
We cannot reliably detect all the levels of anesthesia in clinical application with just EEG indices (Shalbaf et al. 2013b; Nguyen-Ky et al. 2013). EEG signals originate from the central nervous system but, anesthesia is related to central and autonomic nervous system functions (Huang et al. 2008). Also, anesthetic agents make a continuum of neurophysiologic and hemodynamic changes. This challenge opens new possibilities for future researches. Autonomic nervous system activity should thus be evaluated to improve DOA monitoring reliability. The most common way of determining the activity of the autonomic nervous system is to quantify the changes in heart rate (HR), which measures from the electrocardiogram (ECG) signal and mean arterial pressure (MAP), which measures from the invasive blood pressure (IBP) signal. Hemodynamic parameters have the potential for real time applications without expensive instruments. The relation of HR and MAP with anesthesia has been extensively studied during the past two decades (Sleigh and Donovan 1999; Nakatsuka et al. 2002; Shafqat et al. 2011). Hemodynamic parameters are correlated to the regulation of autonomic nervous system, which is highly affected by surgical anesthesia and sleep (Baharav et al. 1995; Mahfouf et al. 2003; Shieh et al. 2005). Thus theoretically, MAP and HR have been commonly accepted as a potential indicator of anesthetic depth.
In this research, a novel automated method for assessing the anesthesia depth level using vital sign is proposed. We hypothesized that a combination of EEG measure (MMPE index) and hemodynamic variables (HR and MAP index) in combination with linear discriminate analyzer (LDA) classifier may distinguish between the four anesthetised states more reliably than EEG indices do on their own. The capabilities of this method to classify the vital sign into awake, light anesthetised, surgical anesthetised and deep anesthetised states are investigated in comparison with the BIS index during cardiac surgery requiring cardiopulmonary bypass (CPB). The performance of the proposed scheme is evaluated using sensitivity and classification accuracy.
Methods
Subjects and data acquisition
We studied 25 patients (age 22–75 year) undergoing cardiac surgery requiring CPB. All of the patients gave written informed consent and the protocols used in this study were approved by the institutional review board and ethics committee, Department of Anesthesiology, Faculty of Medicine, Shahid Beheshti University of Medicine, Tehran, Iran. Each Patient was premedicated by intramuscular morphine 0.1 mg/kg and promethazine 0.5 mg/kg.
After arrival in operative room, ECG, pulse oxymetry and invasive arterial blood pressure monitoring (Alborz B9 monitor, Saadat Co., Tehran, Iran) were established and raw heart rate parameter (sampled at 0.1/s) and mean arterial pressure (MAP) index (sampled at 0.1/s) were recorded via an RS232 interface onto a personal computer for later analysis. MAP is defined as the average pressure in a patient’s arteries during one cardiac cycle. It is considered a better indicator of perfusion to vital organs than systolic blood pressure. MAP is determined by invasive monitoring using Swan-Ganz catheter, MEDEX disposable pressure transducer and complex algorithm implemented in Alborz monitor.
BIS-QUATRO Sensor™ (Aspect Medical Systems, Newton, MA, USA) composed of a self-adhering flexible band holding four electrodes was used to record EEG signal between the forehead and temple simultaneously with hemodynamic recording. The used EEG montage was Fpz-At1, and the ground electrode was placed at Fp1. Sensor was connected to a BIS-XP Monitor (Aspect Medical Systems) and raw EEG signal (sampled at 200/s) and BIS index (sampled at 0.1/s) were recorded via an RS232 interface onto a personal computer using a Bi-spectrum analyzer developed with C++ Builder (Hagihira et al. 2001). EEG segments with maximum amplitude greater than 200 µV were rejected as nonlinear distortions of the amplitude in EEG signal. Also, a band pass filter with low and high cut-off frequency were set at 0.5 and 47 Hz respectively and the notch filter was set at 50 Hz. Sampling frequency of EEG signal is finally transformed to 100/s.
All the patients were induced in the same manner by intravenous thiopental sodium (5 mg/kg), pancuronium Bromide (0.1 mg/kg), fentanyl (5 µg/kg), and lidocarine (1.5 mg/kg). Anesthesia continued by administration of isoflurane (1 MAC), morphine (0.2 mg/kg) and O2 (100 %). During coronary artery bypass grafting under CPB, patients were maintained with propofol (50–150 µg/kg/min) by means of an infusion pump and undergone mild hypothermia (31–33 °C) for organ protection. After patients rewarming and obtaining standard CPB separation criteria, anesthesia continued by isoflurane (1 MAC) and O2 (100 %) administration. After tracheal extubation, patients were taken to the post-anesthesia care unit.
Based on drug delivery protocol, loss of consciousness (LOC) time, response to stimulation and anesthesiologist’s assessment, the patient was considered to be in one of the four different levels of anesthesia, namely, awake, light anesthesia, surgical anesthesia and deep anesthesia; then the corresponding vital signals including EEG data and hemodynamic variables are selected. LOC time was assessed based on the loss of the response to a verbal command from the anesthesiologist. The vital signals before beginning drug delivery were considered the awake state. In this state, the EEG signal exhibits blink artifacts superimposed with high-frequency waves (Campagna et al. 2002). The time span between 10 s before LOC time and 30 s after LOC time was considered the light anesthetised state. In this state, some ‘spindle-like’ waves appear in EEG signal whose frequency is often related to the anesthesia drug concentration in the blood. Surgical anesthetised state referred to the EEG signal during the equilibrium phase of anesthesia and was determined based on response to stimulation and anesthesiologist’s assessment. In this state, spindle-like’ waves with low frequency about 8 Hz is seen in EEG signal. Deep anesthetised state was concluded on the foundation of the anesthesiologist’s assessment. In this state, large amplitude delta and sub-delta waves may be seen in EEG signal (Campagna et al. 2002). Also, in some subjects, the EEG waveform changes into a burst suppression pattern with increasing anesthetic drug concentration (Sarkela et al. 2002). Burst suppression is a pattern of high amplitude EEG activity, commonly called the bursts, intervened by relatively low amplitude activity, called the suppressions, typically under 10 uv peak-to-peak. A total of 1,000 s of EEG data and hemodynamic variables was obtained for each state. The EEG recordings and hemodynamic variables were divided into patterns of 10 s duration. Thus, 100 test patterns of each state were obtained for the purpose of experimental analysis. It should be noted that while patients went through CPB, their heart was stopped and heart rate could not be measured; therefore in this period vital signs were not extracted.
Permutation entropy
Permutation Entropy (PE) is a statistical parameter that quantifies the amount of regularity in EEG data (Bandt and Pompe 2002). It is found that PE index properly tracks the dynamics of brain activity (Shalbaf et al. 2013b, c; Olofsen et al. 2008). This feature converts a given EEG series into a series of ordinal patterns, implying that a nonstationary series is transformed to an almost stationary ordinal series.
Given a time series XN = [x1, x2, …, xN] with N points, vectors are constructed with the embedding dimension, m, and the time lag τ. Then, Xi can be arranged in an increasing order. There will be J = m! possible order patterns, which are also called permutations. The vectors Xi can be represented by a symbol sequence in which each permutation is considered as a symbol. For the time series XN, the probabilities of the diverse symbols are determined as P1, … Pj; the normalized PE of this time series is defined by:
| 1 |
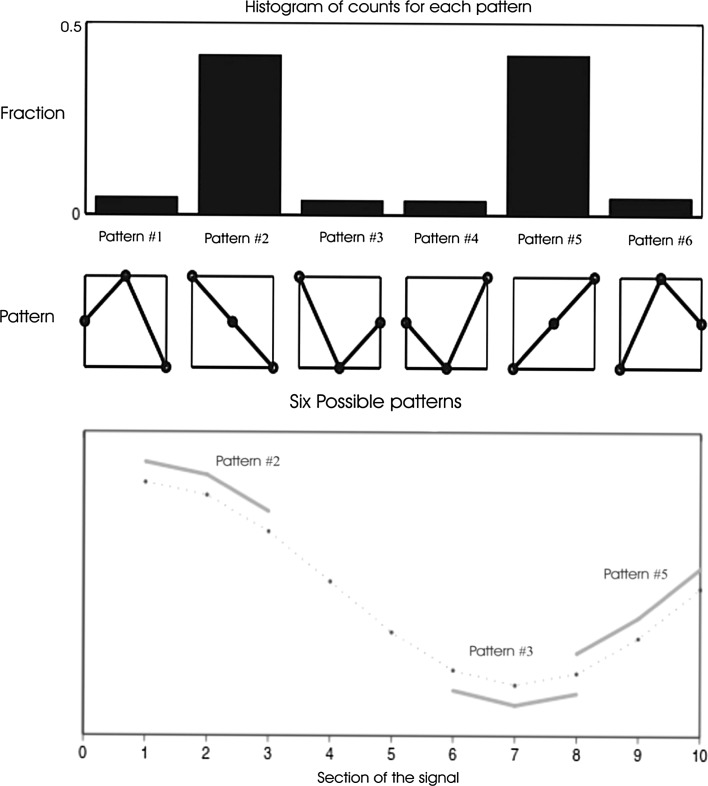
The smallest and the largest values of PE are zero and one, reflecting a highly regular time series and equal probability of all permutations, respectively. Extraction of ordinal patterns from the EEG signal and histogram of the relative numbers of each pattern are shown in Fig. 1. The calculation of PE depends on the selection of time interval (N), embedding dimension (m) and time lag (τ). Based on the suggestions by other studies, the value N is set optimally to 1,000 points (data length of 10-s in this study) (Shalbaf et al. 2013b, c; Olofsen et al. 2008). For the time lag, it is adequate to use a value of τ = 1 to extract most of the information in the EEG (Bandt and Pompe 2002; Li et al. 2008). The appropriate value for m is determined six according to other studies (Shalbaf et al. 2013b; Li et al. 2008) and sampling frequency of EEG signal.
Fig. 1.
Extraction of ordinal patterns from the EEG signal. While the algorithm moves consecutively through the EEG signal, the sections including of three data points are classified as one of the six possible patterns, demonstrated in the second row. On the top row of the diagram, a histogram of the relative numbers of each pattern in the EEG signal is shown
Modified permutation entropy
PE does not work at deeply anesthetised state, mainly due to high-frequency waves during the suppression period (Li et al. 2008; Shalbaf et al. 2013b, c; Olofsen et al. 2008). In this paper, we introduce modified permutation entropy (MPE) index which is robust in the characterization of the burst suppression pattern at high doses of anesthetics. To achieve this goal, the part of the EEG signal that contains EEG suppressions is determined separately by another nonlinear algorithm as described below; all suppressions sample is treated as a same symbol and probability of the this new symbol is determined as Pj+1 whereas the probabilities of the other diverse symbols (P1, … Pj) associated with the bursts are computed as described previously in Sect. “Permutation entropy”. Therefore, MPE index is defined by:
| 2 |
Suppression is detected by applying a technique based on nonlinear algorithm (Sarkela et al. 2002). Given a time series XN = [x1, x2, …, xN] with N points, a non-linear energy operator (nleo) is derived for each 0.05-s epoch (5 sample) as follow:
| 3 |
then, NLEO is applied to estimate the signal power from overlapping 1-s frames offset by 0.05-s as follow:
| 4 |
during suppression periods, ECG artifacts may corrupt classification and therefore their interference is eliminated in the burst suppression band. This is performed by replacing the current nelo(m) by the average nleo from the frame of 1-s (NLEO(m)), if the following rules are fulfilled:
1. The squared difference between the current nleo from the 0.05 s epoch (nelo(m)) and the average nleo for the 1-s frame (NLEO(m)) is over three times bigger than the ECG threshold (THECG):
| 5 |
This threshold is calculated by mean of all the squared differences in the frame of 1-s as follow:
| 6 |
2. The 1-s frame includes at most four epochs that fulfill condition 1.
suppression is detected if NLEO is below a fixed another threshold for at least 0.5 s.
Multiscale modified permutation entropy
Several measures based on nonlinear dynamics such as PE, have been proposed to evaluate complex EEG series during anesthesia. But, these measures are still single-scale based and may not totally explain the dynamical characteristics of EEG series. Recently multiscale entropy has been suggested to evaluate the complexity of EEG series (Costa et al. 2003). The basic idea of Multiscale entropy analysis is to account for the correlations of a time series over multiple temporal scales instead of a single scale (Ouyang et al. 2009). Given a time series XN = [x1, x2, …, xN], first a ‘coarse-graining’ procedure is implemented by averaging the data points in non-overlapping windows of length s, constructing a consecutive coarse-grained time series (ys). Each element, y(s)j, of the coarse-grained time series, is calculated according to the below equation:
| 7 |
where s represents the scale factor and 1 ≤ j ≤ N/s. Schematic illustration of the coarse-graining procedure for scale 2 and 3 are shown in Fig. 2. The length of each coarse-grained time series is equal to the length of the original time series N divided by s. Next the modified permutation entropy measure was calculated for each coarse-grained time series. Then, we derive a single index from combining three multiscale analysis (s = 1, 2, 3), called MMPE (multiscale modified permutation entropy), to estimate DOA.
| 8 |
Fig. 2.
Schematic explanation of the coarse-graining procedure for scale 2 and 3
Classification
The aim of linear discriminant analysis (LDA) is to use hyperplanes to separate the data representing the different classes and also to minimize the intra- group variance and maximize the inter-group variance (Fukunaga 1990). LDA is supervised classification and should be trained with some observations first, then tested with other observations to calculate the accuracy. In this technique, models of the probability density functions for data generated from each class are created. Then, a new data point is classified by determining the probability density function whose value is larger than the others. The resulting LDA decision boundaries between classes of data are linear. This technique is simple to use and has a very low computational requirement. Consequently, this classifier has been used successfully in a great number of pattern recognition problems and EEG processing researches such as motor imagery based Brain–Computer Interface (Pfurtscheller 2000) and P300 speller (Bostanov 2004). The LDA classifier is implemented by using MATLAB software version 7.9.
Leave-one-out cross-validation
Leave-one-out cross-validation is an approach for assessing how the results of a statistical analysis will generalize to an independent data set. This technique involves using all observations from one patient as the test data, and the remaining observations from other patients as the training data. This is repeated such that observations from all patients are used once as the test data. The benefit of this technique is that patient observations division is not considered. Also, when all observations from one patient are left out from the training observations of other patients, a real monitoring situation is simulated in which the all observations of the monitored patient are not available when the training is done.
Statistical analysis
The evaluation of the proposed method was determined by computing the sensitivity and classification accuracy. The definitions of these parameters are as follows:
Sensitivity (SEN): Number of correctly detected patterns as a fraction of total number of actual patterns. A pattern indicates one of four different levels of anesthesia
Classification accuracy: Number of correctly detected anesthetic levels as a fraction of total number of applied anesthetic levels
In addition, Mean Absolute Error (MAE) was used as a measure of association between MMPE and BIS index. MAE measures the average magnitude of differences between two indices, without considering their direction. Also, the relative coefficient of variation (CV) (the ratio of the standard deviation to the mean) was calculated to show the effect of artifact to MMPE and BIS before anesthetic delivery. Furthermore, the Mann–Whitney test was used to compare the difference between the performance of MMPE and BIS index.
Implementation
This section explains how the methods were actually applied to the signals. All indices including BIS, MMPE, PE, HR and MAP are computed over a window of 10 s with no overlap to consistently track the transient changes in the vital sign recording. The features extracted from each 10 s EEG and hemodynamic measures are fed into an LDA structure to differentiate between the awake, light, surgical and deep anesthetised states. The classification was carried out using a leave-one-out cross-validation approach. The test performance of the proposed method is determined by computing two statistical parameters described in Sect. “Statistical analysis”.
Results
Figure 3 demonstrates an example of EEG measure and hemodynamic parameters changes occurred during increasing anesthetic drug effect. The changes in HR and MAP parameters in the transition state from awake to anesthetized is shown for six patients. The circle symbols are used to show the time of LOC. HR and MAP are related to autonomic regulation which is affected by surgical anesthesia. Thus theoretically, hemodynamic parameters are a potential indicator of anesthetic depth. BIS index derived from EEG signal is also illustrated together with hemodynamic parameters. As demonstrated, BIS index shows rather same changes for all six patients (Fig. 3a). On the contrary, HR parameter in the transition state from awake to anesthetized is increased for three patients, is decreased for one patient and does not change for two of them (Fig. 3b). Besides, the changes in MAP parameter are not comparable for all six patients (Fig. 3c). The MAP in the transition state for some patients is decreased and for some is remained unchanged. This figure demonstrates that hemodynamic parameters are not an adequate index by itself.
Fig. 3.
An example of the EEG measure and hemodynamic parameters changes that occur during increasing anesthetic drug effect for six patients. The circle symbols are used to show the time of loss of consciousness
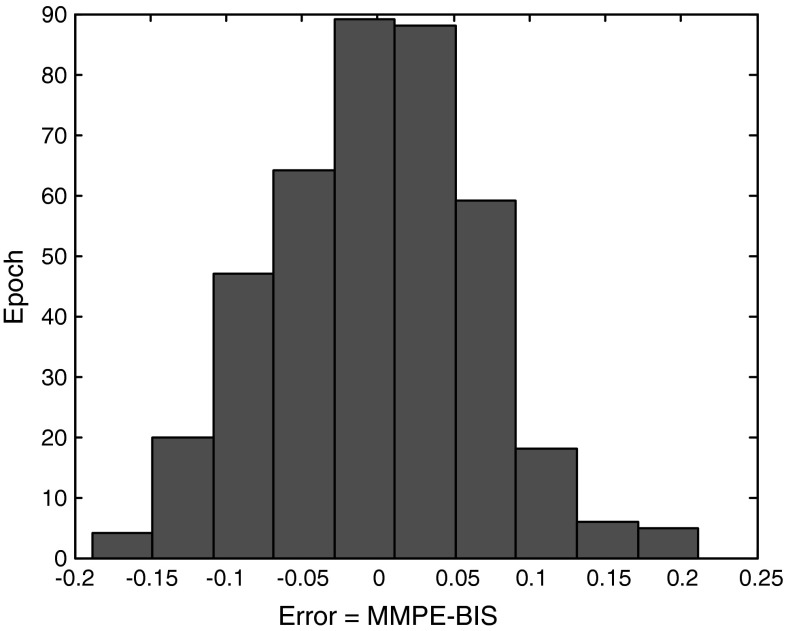
Table 1 shows the values of Mean Absolute Error (MAE) between MMPE and BIS index in different states for all patients (n = 25). The range of the recorded BIS index is between 0 and 100, but is transformed to 0-1 (divided to 100) to make the comparison with MMPE index possible. Low MAE value in all state reveals the comparison of these two indices for tracking gross changes in EEG with increasing and decreasing anesthetic drug effect. Figure 4 shows the histogram of error distribution for all epochs. An epoch error is positive when the value of MMPE is greater than BIS. An epoch error is negative when the value of BIS is greater than MMPE. Epoch errors are in the range of [−0.1, 0.1], indicating very good agreement between MMPE and BIS index.
Table 1.
Values of mean absolute error (MAE) between MMPE and BIS/100 index in different states for all patients (n = 25)
| Awake | Light anesthetic | Surgical anesthetic | Deep anesthetic | Total | |
|---|---|---|---|---|---|
| MAE | 0.04 | 0.07 | 0.03 | 0.06 | 0.05 |
Fig. 4.
Histogram of error distribution for all epochs between MMPE and BIS/100 index for all patients (n = 25)
The baseline variability of MMPE and BIS is estimated by calculating CV before anesthetic delivery in order to compare the performance of MMPE and BIS index regarding artifact resistance. CV for MMPE is 0.012 ± 0.004 [mean ± standard deviation (SD)], compared with 0.017 ± 0.006 for BIS. This difference is statistically significant (P < 0.001). Clearly, this small CV value for MMPE indicates that our EEG measure is better in tolerating artifacts than BIS index during the awake state.
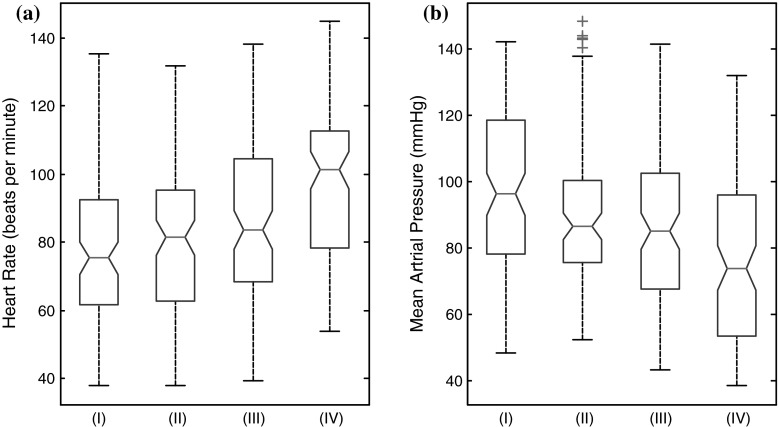
It is worthwhile to investigate hemodynamic based anesthetic depth indicator because ECG and IBP monitoring is easy and cheap. HR parameter is easily derived from ECG data and MAP parameter is also derived from IBP signal. The hemodynamic features extracted from each 10 s segment are fed into an LDA structure. Table 2 shows the classification accuracy and sensitivity values using the MAP and HR parameters along with the LDA classifier for all patients (n = 25). Also, MAP and HR parameters values over 10 s epochs at the four states are analyzed for each patient and a box plot is constructed (Fig. 5). It is found from the experimental results shown in Table 2 that HR parameter yields an overall classification accuracy of 33.4 % with a standard deviation of 7.6 % among the subjects in detecting all four anesthetised states. Also, overall classification accuracy of 35.6 % with a standard deviation of 7.8 % in detecting all anesthetised states is achieved with MAP parameter. Low overall classification accuracy proves that these hemodynamic features alone do not track the four anesthetised state accurately.
Table 2.
Classification accuracy and sensitivity values using EEG measures and hemodynamic parameters during cardiac surgery for all patients (n = 25)
| Method | SEN (%) (awake) | SEN (%) (Light anesthetic) | SEN (%) (surgical anesthetic) | SEN (%) (deep anesthetic) | Classification accuracy (%) |
|---|---|---|---|---|---|
| HR parameter | 45.2 | 27.3 | 12.2 | 48.4 | 33.4 ± 7.6 |
| MAP parameter | 53.2 | 29.3 | 11.4 | 48.3 | 35.6 ± 7.8 |
| HR and MAP parameters | 61.2 | 40.4 | 26.3 | 85.4 | 53.5 ± 6.5 |
| PE index | 85.5 | 74.2 | 82.5 | 25.4 | 66.9 ± 5.4 |
| MMPE index | 87.5 | 81.2 | 88.5 | 83.4 | 85.1 ± 3.5 |
| BIS index | 93.5 | 65.6 | 87.8 | 75.6 | 80.6 ± 4.1 |
| BIS index, HR and MAP | 91.8 | 76.4 | 88.3 | 82.6 | 84.7 ± 3.6 |
| MMPE index, HR and MAP | 92.5 | 86.5 | 90.2 | 88.3 | 89.4 ± 3.2 |
Fig. 5.
Box plots of a Heart Rate (beats per minute) and b Mean Arterial Pressure (mmHg) values at the awake (I), Light anesthetised (II), surgical anesthetised (III) and deep anesthetised (IV) states for all patients (n = 25). The upper and lower lines of the ‘box’ refer to the 75th and 25th percentiles of the sample; the line in the middle of the box is the sample median, and the distance between the top and the bottom of the box is the interquartile range. Plus signs are cases with values that are 1.5 times greater than the interquartile range. The notches in the box are 95 % confidence intervals around the median of a sample
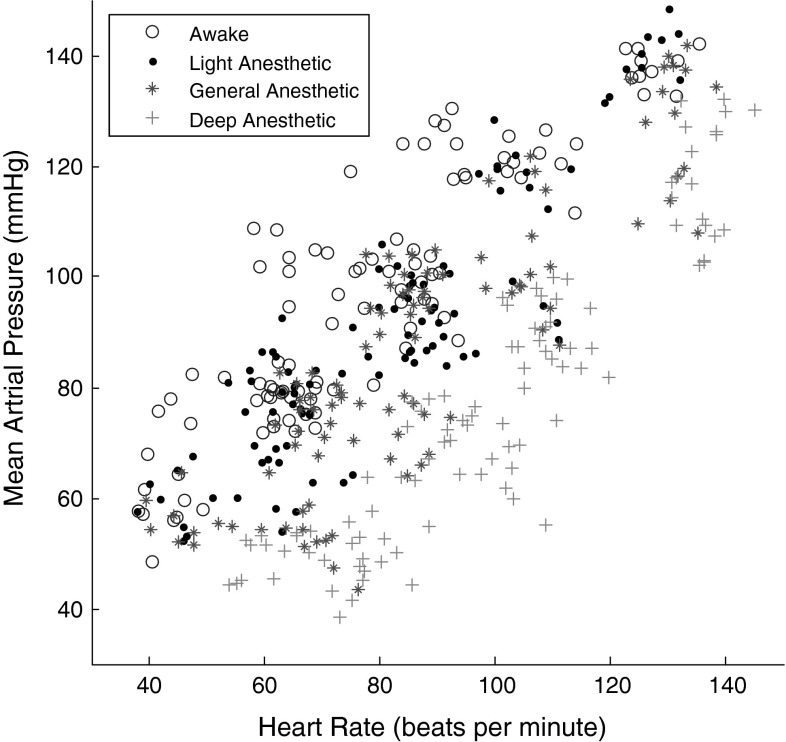
It is demonstrated that the classification based on a single hemodynamic feature yields unsatisfactory results. In this study, two hemodynamic parameters, namely, MAP and HR are used as the inputs for the LDA classifier in order to characterize the patient state. Figure 6 shows two feature values for the four states of anesthesia for all patients (n = 25). It can be observed that the extracted features of the four states are rather different from each other. Table 2 shows the values of classification accuracy and sensitivity using combination of two features for all patients (n = 25). This method achieves 53.5 % overall classification accuracy across the subjects with a standard deviation of 6.5 % in detecting all four anesthetised states. Median overall accuracy demonstrates that using just hemodynamic parameters is not sufficient enough to monitor the DOA in all anesthetised states.
Fig. 6.
Scatter plot of Mean Arterial Pressure (mmHg) and Heart Rate (beats per minute) values of four states of anesthesia for all patients (n = 25)
The EEG signal is the recording of brain electrical activity and it contains valuable information related to the different physiological states of the brain. Table 2 shows the classification accuracy and sensitivity values using the PE and MMPE features extracted from 10 s EEG signal along with the LDA classifier for all patients (n = 25). The average classification accuracy of 66.9 % across the subjects with a standard deviation of 5.4 % in detecting the anesthesia depth levels is obtained with PE feature. Low sensitivity of 25.4 % in detecting the deep anesthetised state shows that this state cannot be differentiated well with PE feature. MMPE feature achieves 85.1 % overall classification accuracy with a standard deviation of 3.5 % among the subjects in detecting all four anesthetised states. It is found from the experimental results shown in Table 2 that MMPE yields an overall sensitivity of 87.5 % in detecting the awake level. High sensitivity obtained for detecting the awake state proves that this method is robust to artifact (eye movement and baseline drift). Also, high sensitivity of 83.4 % in detecting the deep anesthetised state verifies that this proposed index (MMPE) tracks burst suppression pattern more accurately than PE index.
The anesthetic agents make a continuum of neurophysiologic and hemodynamic changes. Thus, a comprehensive set of vital sign is required to adequately describe the transition from awake to deep anesthesia. Table 2 shows the values of classification accuracy and sensitivity using a combination of MMPE parameter extracted from EEG signal and HR and MAP parameters extracted from hemodynamic signals for all patients (n = 25). All parameters were subjected to the LDA. It is found from the experimental results that proposed method yields an overall sensitivity of 92.5 % in detecting the awake level which show that this method is robust to artifact. High sensitivity of 88.3 % in detecting the deep anesthetised level proves that this method tracks the clinical state at high doses of anesthetics with burst suppression pattern. Also, this method achieves an overall classification accuracy of 89.4 % with a standard deviation of 3.2 % in detecting the four anesthetised states which is the best among the all methods. High overall accuracy reveals that the proposed method monitors the DOA in all anaesthesia states correctly.
The comparative analysis with the BIS Index on the same data further substantiates the efficiency of the proposed EEG measure. The range of the recorded BIS is between 0 (suppression state of EEG) to 100 (awake). Decreasing values indicate deepening levels of hypnosis. We have presented the results when the boundaries are set optimally for the classification purposes. Table 2 shows the values of classification accuracy and sensitivity using BIS feature along with the LDA classifier for all patients (n = 25). It is found that BIS index fails to characterize the light anesthetised state (65.6 %) at low concentrations of anesthetic drug. This procedure also achieves a classification accuracy of 80.6 ± 4.1 % compared with 85.1 ± 3.5 % for MMPE index in detecting the four anesthetised states. This difference is statistically significant (P < 0.001) and suggests that MMPE index has a stronger capacity to track the brain state during anesthesia. Furthermore, a combined approach in which BIS measure is supplemented with hemodynamic parameters including HR and MAP parameters together with the LDA classifier is presented in Table 2 for all patients (n = 25). This approach yields 84.7 ± 3.6 % classification accuracy compared with 89.4 ± 3.2 % for our proposed method (MMPE, HR and MAP index) in detecting all four anesthetised states. This difference is statistically significant (P < 0.001). This result also confirms that the proposed EEG measure performs better than BIS index in the same approach.
Discussion
In this work, we demonstrated that the combination of MMPE and hemodynamic parameters had better accuracy to classify four anesthetised states than the method of BIS based on EEG only. The proposed method is evaluated during cardiac surgery requiring CPB in 25 patients. The proposed method shows little overlap between four anesthetised states.
Comparing our method with BIS Index, we found that the computation of BIS value is very complex and requires more computation time than our method (Hagihira et al. 2001). The BIS incorporates three different analysis algorithms, each of them giving a number of quantitative EEG measures predominant within a limited therapeutic window (Rampil 1998). These measures are combined into the final BIS value through a nonlinear weighting function. While this plan is appropriate for classification purposes, calculation requirement of this method can be particularly high. Rather, our proposed EEG measure needs just basic computation like sorting, comparative and adding which can be calculated quickly. Also, the rejection of artifacts (low frequency blinks, eye movement, baseline drift and nonlinear distortion of the amplitude) in BIS is very laborious and time consuming. Artifact analysis is based on statistical (variance and template matching) methods that require some 2 s retrospective EEG signal epochs to identify and remove the artifacts. This requirement is also the main reason for the time delay in BIS response to EEG changes (Shalbaf et al. 2012a). Our proposed method (MMPE index) demonstrates better results to BIS index regarding sensitivity to artifacts, as revealed from the CV value, but without complicated artifact removal step. In MMPE index, we convert a given EEG series into symbolic sequences. These symbol sequences are invariant concerning the types of artifacts.
Entropy is becoming a valuable tool for analysis of EEG activity and has received much attention in recent years (Shalbaf et al. 2012b; Li et al. 2008; Al-Kadi et al. 2013). It has been consistently shown that anesthetised patients have significantly lower entropy values than awake subjects (Olofsen et al. 2008; Viertio-Oja et al. 2004; Sleigh et al. 2004). Since entropy indicates the degree of disorder in a system, lowering of entropy values during anesthesia shows a reduction in intra-cortical information flow. Thus, in agreement with other studies, we infer that the brain under the influence of anesthetic drug demonstrates a more regular and less complex EEG in the frontal region than that of awake subjects (Ferents et al. 2006; Shalbaf et al. 2013b, c).
In this paper, we introduce multiscale modified permutation entropy (MMPE) index based on nonlinear dynamics to analyze EEG series during anesthesia. This index consider both overall signal variability characteristics, naturally related to spectral content, and the signal’s complexity. This proposed index is robust in the characterization of the burst suppression pattern at high doses of anesthetics. To achieve this goal, the part of EEG signal that contains EEG suppressions be calculated separately by another nonlinear algorithm and is treated as a same symbol, whereas the permutation entropy associated with the bursts is computed as described previously. Also, our index is proposed to discover the complexity of EEG signal at multiple scales, because EEG signal naturally shows complicated fluctuations which originate from complex self-regulating systems operating across multiple temporal scales.
Estimation of DOA with a single parameter such as EEG measure does not work well all the time. Autonomic nervous system activity should be evaluated to improve DOA monitoring reliability. The most common way of determining the activity of the autonomic nervous system is to quantify the changes in heart rate and mean arterial pressure, which are measured based on ECG signal and IBP respectively (Huang et al. 2008; Sleigh and Donovan 1999). ECG and IBP signals can be easily acquired using routine monitoring machine and regular electrode leads and catheter. The energy level of these signals is much higher than EEG and is more resistant to artifact. Also, hemodynamic parameters have been correlated to the regulation of autonomic nervous system, which is highly affected by surgical anesthesia; HR is increased and MAP is decreased during surgical anesthesia. In this paper, the identification of anesthesia stages is conducted using a proper set of features including hemodynamic variables and EEG measure. We have proved that a combination of vital sign variables will distinguish between the awake, light, surgical and deep anesthetised states more reliably than EEG indices do in patients undergoing cardiac surgery requiring CPB. Our research strongly suggests that hemodynamic measures can play more roles in the monitoring of anesthetic depth than it currently does. The following three points should be mentioned as areas to be further explored.
First, clinical indices such as blood pressure and heart rate have been used to assess DOA and changed significantly from awake to unconscious state. However, these traditional methods may vary from patient to patient depending on the type of surgery. Also, the use of other drugs like muscle relaxants and vasodilators make the analysis of those clinical signs unreliable and difficult.
Second, a combination of anesthetics and opioids are commonly used during operation. All of these drugs affect EEG (Liley et al. 2010; Kortelainen et al. 2011a) and also hemodynamic variables. Studying the applicability of the proposed approach in this kind of multidrug anesthesia could be mentioned as a possible future work.
Third, it is essentially too optimistic to presume this proposed method can be used as an acceptable anesthetic depth predictor. EEG and hemodynamic measures are only an indirect indicator of anesthesia and are relatively nonspecific (Huang et al. 2008). There are many clinical factors that may affect the autonomic and central nervous system, decreasing the predictive power of related measures. The effects of various factors on our proposed method require supplementary analysis to clarify. However, before the true mechanism of surgical anesthesia can be clearly explored and direct observation can be performed, we can only rely on the indirect measurements to monitor DOA. Finally, there still is no single perfect predictor so that there have been trials to combine several modes of observations to increase the predictability of DOA.
In conclusion, a new method for depth of anesthesia measurement is proposed. The method is based on simultaneous utilization of EEG and hemodynamic parameters (heart rate and mean arterial pressure). A novel EEG measure combining multiscale permutation entropy information, called MMPE, was proposed which is robust in the characterization of the burst suppression pattern at high doses of anesthetics. MMPE and hemodynamic features are then combined using LDA for a measure of depth of anesthesia. The method is validated with data recorded from 25 patients during the cardiac surgery requiring CPB and compared in performance to BIS index. We have shown that our method yields 89.4 % overall accuracy for classifying the vital sign into awake, light, surgical and deep anesthetised states. The high accuracy highlights the potential of the proposed method. Considering the low calculation requirement of this method, a real time system can be developed that assists the anesthesiologist to estimate DOA quickly and accurately.
Acknowledgments
This work was supported by the Saadat Co. (Tehran, Iran).
References
- Ahmadi B, Amirfattahi R. Comparison of Correlation Dimension and Fractal Dimension in Estimating BIS index. Wirel Sens Net. 2010;2:67–73. [Google Scholar]
- Al-Kadi MI, Ibne Reaz MB, Mohd Ali MA. Evolution of electroencephalogram signal analysis techniques during anesthesia. Sensors. 2013;13(5):6605–6635. doi: 10.3390/s130506605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baharav A, Kotagal S, Gibbons V, Rubin BK, Pratt G, Karin J, Akselrod S. Fluctuation in autonomic nervous activity during sleep displayed by power spectrum analysis of heart rate variability. Neurology. 1995;45(6):1183–1187. doi: 10.1212/WNL.45.6.1183. [DOI] [PubMed] [Google Scholar]
- Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series. Phys Rev Lett. 2002;88:174102. doi: 10.1103/PhysRevLett.88.174102. [DOI] [PubMed] [Google Scholar]
- Bostanov V. BCI competition 2003—data sets ib and iib: feature extraction from event-related brain potentials with the continuous wavelet transform and the t-value scalogram. IEEE Trans Biomed Eng. 2004;51:57–61. doi: 10.1109/TBME.2004.826702. [DOI] [PubMed] [Google Scholar]
- Campagna JA, Miller KW, Forman SA. Mechanisms of actions of inhaled anesthetics. J Neural Eng. 2002;348:2110–2124. doi: 10.1056/NEJMra021261. [DOI] [PubMed] [Google Scholar]
- Costa M, Goldberger AL, Peng CK. Multiscale entropy analysis of physiologic time series. Phys Rev Lett. 2003;89:062102. doi: 10.1103/PhysRevLett.89.068102. [DOI] [PubMed] [Google Scholar]
- Fell J, Kaplan A, Darkhovsky B, Röschke J. EEG analysis with nonlinear deterministic and stochastic methods: a combined strategy. Acta Neurobiol Exp. 2000;60:87–108. doi: 10.55782/ane-2000-1328. [DOI] [PubMed] [Google Scholar]
- Ferents R, Lipping T, Anier A, Jntti V, Melto S, Hovilehto S. Comparison of entropy and complexity measures for the assessment of depth of sedation. IEEE Trans Biomed Eng. 2006;53:1067–1077. doi: 10.1109/TBME.2006.873543. [DOI] [PubMed] [Google Scholar]
- Fukunaga K. Statistical pattern recognition. 2. New York: Academic Press; 1990. [Google Scholar]
- Hagihira S, Takashina M, Mori T, Mashimo T, Yoshiya I. Practical issues in bispectral analysis of electroencephalographic signals. Anesth Analg. 2001;93:966–970. doi: 10.1097/00000539-200110000-00032. [DOI] [PubMed] [Google Scholar]
- Hosseini PT, Shalbaf R, Nasrabadi AM. Extracting a seizure intensity index from one-channel EEG signal using bispectral and detrended fluctuation analysis. J Biomed Sci Eng. 2010;3:253–261. doi: 10.4236/jbise.2010.33034. [DOI] [Google Scholar]
- Huang HH, Lee YH, Chan HL, Wang YP, Huang CH. Using a short-term parameter of heart rate variability to distinguish awake from isoflurane anesthetic states. Med Biol Eng Comput. 2008;46:977–984. doi: 10.1007/s11517-008-0342-y. [DOI] [PubMed] [Google Scholar]
- Hutt A, Longtin A. Effects of the anesthetic agent propofol on neural populations. Cogn Neurodyn. 2010;4:37–59. doi: 10.1007/s11571-009-9092-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansen JW, Sebel PS. Development and clinical application of electroencephalographic bispectrum monitoring. Anesthesiology. 2000;93:1336–1344. doi: 10.1097/00000542-200011000-00029. [DOI] [PubMed] [Google Scholar]
- Kortelainen J, Väyrynen E, Seppänen T. Isomap approach to EEG-based assessment of neurophysiological changes during anesthesia. IEEE Trans Neural Syst Rehabil Eng. 2011;19:113–120. doi: 10.1109/TNSRE.2010.2098420. [DOI] [PubMed] [Google Scholar]
- Kortelainen J, Väyrynen E, Seppänen T. Depth of anesthesia during multidrug infusion: separating the effects of propofol and remifentanil using the spectral features of EEG. IEEE Trans Biomed Eng. 2011;58:1216–1223. doi: 10.1109/TBME.2010.2103560. [DOI] [PubMed] [Google Scholar]
- Lehmann A, Boldt J, Thaler E, Piper S, Weisse U. Bispectral index in patients with target-controlled or manually-controlled infusion of propofol. Anesth Analg. 2002;95:639–644. doi: 10.1097/00000539-200209000-00027. [DOI] [PubMed] [Google Scholar]
- Li XL, Cui SY, Voss LJ. Using permutation entropy to measure the electroencephalographic effects of sevoflurane. Anesthsiology. 2008;109:448–456. doi: 10.1097/ALN.0b013e318182a91b. [DOI] [PubMed] [Google Scholar]
- Liley DT, Sinclair NC, Lipping T, Heyse B, Vereecke HE, Struys MM. Propofol and remifentanil differentially modulate frontal electroencephalographic activity. Anesthsiology. 2010;113:292–304. doi: 10.1097/ALN.0b013e3181e3d8a6. [DOI] [PubMed] [Google Scholar]
- Luginbühl M, Wüthrich S, Petersen-Felix S, Zbinden A, Schnider T. Different benefit of bispectral index (BIS) in desflurane and propofol anesthesia. Acta Anaesthesiol Scand. 2003;47:165–173. doi: 10.1034/j.1399-6576.2003.00041.x. [DOI] [PubMed] [Google Scholar]
- Mahfouf M, Asbury AJ, Linkens DA. Unconstrained and constrained generalized predictive control of depth of anesthesia during surgery. Control Eng Pract. 2003;11:1501–1515. doi: 10.1016/S0967-0661(03)00075-3. [DOI] [Google Scholar]
- Muncaster A, Sleigh J, Williams M. Changes in consciousness, conceptual memory, and quantitative electroencephalographical measures during recovery from sevoflurane- and remifentanil-based anesthesia. Anesth Analg. 2003;96:720–725. doi: 10.1213/01.ANE.0000040143.95962.36. [DOI] [PubMed] [Google Scholar]
- Myles P, Leslie K, McNeil J, Forbes A, Chan M. Bispectral index monitoring to prevent awareness during anaesthesia: the B-AWARE randomized controlled trial. Lancet. 2004;363:1757–1763. doi: 10.1016/S0140-6736(04)16300-9. [DOI] [PubMed] [Google Scholar]
- Nakatsuka I, Ochiai R, Takeda J. Changes in heart rate variability in sevoflurane and nitrous oxide anesthesia: effects of respiration and depth of anesthesia. J Clin Anesth. 2002;14:196–200. doi: 10.1016/S0952-8180(01)00384-1. [DOI] [PubMed] [Google Scholar]
- Nguyen-Ky T, Wen P, Li Y. Consciousness and depth of anesthesia assessment based on bayesian analysis of EEG signals. Eng: IEEE Trans Biomed; 2013. [DOI] [PubMed] [Google Scholar]
- Olofsen E, Sleigh JW, Dahan A. Permutation entropy of the electroencephalogram: a measure of anesthetic drug effect. Br J Anaesth. 2008;101:810–821. doi: 10.1093/bja/aen290. [DOI] [PubMed] [Google Scholar]
- Ouyang GX, Dang C, Li XL. Multiscale entropy analysis of EEG recordings in epileptic rats. Biomed Eng Appl Basis Commun. 2009;21:169–176. doi: 10.4015/S1016237209001222. [DOI] [Google Scholar]
- Pilge S, Zanner R, Schneider G, Blum J, Kreuzer M, Kochs EF. Time delay of index calculation: analysis of cerebral state, bispectral, and narcotrend indices. Anesthesiology. 2006;104:488–494. doi: 10.1097/00000542-200603000-00016. [DOI] [PubMed] [Google Scholar]
- Rampil IJ. A primer for EEG signal processing in anesthesia. Anesthesiology. 1998;89:980–1002. doi: 10.1097/00000542-199810000-00023. [DOI] [PubMed] [Google Scholar]
- Sarkela M, Mustola S, Seppanen T, Koskinen M, Lepola P, Suominen K. Automatic analysis and monitoring of burst suppression in anesthesia. J Clin Monit Comput. 2002;17:125–134. doi: 10.1023/A:1016393904439. [DOI] [PubMed] [Google Scholar]
- Sebel PS, Bowdle TA, Ghoneim MM, Rampil IJ, Padilla RE, Gan TJ, Domino KB. The incidence of awareness during anesthesia: a multicenter United States study. Anesth Analg. 2004;99:833–839. doi: 10.1213/01.ANE.0000130261.90896.6C. [DOI] [PubMed] [Google Scholar]
- Shafqat K, Pal SK, Kumari S, Kyriacou PA. Empirical mode decomposition analysis of HRV data from patients undergoing local anaesthesia (brachial plexus block) Physiol Meas. 2011;32:483–497. doi: 10.1088/0967-3334/32/4/008. [DOI] [PubMed] [Google Scholar]
- Shalbaf R, Behnam H, Sleigh JW, Voss LJ. Using the Hilbert-Huang transform to measure the electroencephalographic effect of propofol. Physiol Meas. 2012;33:271–285. doi: 10.1088/0967-3334/33/2/271. [DOI] [PubMed] [Google Scholar]
- Shalbaf R, Behnam H, Sleigh J, Voss L. Measuring the effects of sevoflurane on electroencephalogram using sample entropy. Acta Anaesthesiol Scand. 2012;56:880–889. doi: 10.1111/j.1399-6576.2012.02676.x. [DOI] [PubMed] [Google Scholar]
- Shalbaf A, Behnam H, Alizade-Sani Z, Shojaifard M. Automatic assessment of regional and global wall motion abnormalities in echocardiography images by nonlinear dimensionality reduction. Med Phys. 2013;40:052904. doi: 10.1118/1.4799840. [DOI] [PubMed] [Google Scholar]
- Shalbaf R, Behnam H, Sleigh J, Voss LA, Steyn-Ross A. Monitoring the depth of anesthesia using entropy features and an artificial neural network. J Neurosci Methods. 2013;218:17–24. doi: 10.1016/j.jneumeth.2013.03.008. [DOI] [PubMed] [Google Scholar]
- Shalbaf R, Behnam H, Moghadam JH (2013c) The brain function index as a depth of anesthesia indicator using complexity measures, In Proceedings of IEEE International Conference on Systems, Process and Control. ICSPC, Kuala Lumpur
- Shieh JS, Linkens DA, Asbury AJ. A hierarchical system of on-line advisory for monitoring and controlling the depth of anaesthesia using self-organizing fuzzy logic. Eng Appl Artif Intell. 2005;18:307–316. doi: 10.1016/j.engappai.2004.09.009. [DOI] [Google Scholar]
- Sleigh JW, Donovan J. Comparison of the bispectral index, 95 % spectral edge frequency and approximate entropy of the EEG, with changes in heart rate variability during induction and recovery from general anaesthesia. Br J Anesth. 1999;82:666–671. doi: 10.1093/bja/82.5.666. [DOI] [PubMed] [Google Scholar]
- Sleigh JW, Steyn-Ross DA, Steyn-Ross ML, Grant C, Ludbrook G. Cortical entropy changes with general anaesthesia: theory and experiment. Physiol Meas. 2004;25:921–934. doi: 10.1088/0967-3334/25/4/011. [DOI] [PubMed] [Google Scholar]
- Talebi N, Nasrabadi AM, Curran T. Investigation of changes in EEG complexity during memory retrieval: the effect of midazolam. Cogn Neurodyn. 2012;6:537–546. doi: 10.1007/s11571-012-9214-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viertio-Oja H, Maja V, Sarkela M, Talja P. Description of the entropy algorithm as applied in the Datex-Ohmeda S/5 Entropy module. Acta Anesthesiol Scand. 2004;48:154–164. doi: 10.1111/j.0001-5172.2004.00322.x. [DOI] [PubMed] [Google Scholar]