SUMMARY
Virtual reality (VR) enables precise control of an animal’s environment and otherwise impossible experimental manipulations. Neural activity in navigating rodents has been studied on virtual linear tracks. However, the spatial navigation system’s engagement in complete two-dimensional environments has not been shown. We describe a VR setup for rats, including control software and a large-scale electrophysiology system, which supports 2D navigation by allowing animals to rotate and walk in any direction. The entorhinal-hippocampal circuit, including place cells, grid cells, head direction cells and border cells, showed 2D activity patterns in VR similar to those in the real world. Hippocampal neurons exhibited various remapping responses to changes in the appearance or the shape of the virtual environment, including a novel form in which a VR-induced cue conflict caused remapping to lock to geometry rather than salient cues. These results suggest a general-purpose tool for novel types of experimental manipulations in navigating rats.
INTRODUCTION
Virtual reality (VR) is a powerful method in neuroscience and has been used for a wide range of species, from insects to humans (Ekstrom et al., 2003; Fry et al., 2008; Ahrens et al., 2013). In recent studies, VR systems designed for rodent navigation have emerged as a particularly useful experimental technique (Holscher et al., 2005; Harvey et al., 2009; Dombeck et al., 2010; Chen et al., 2013; Ravassard et al., 2013). Most of these studies combine VR with body fixation or head fixation as methods for restraining the animal’s movements during behavior. The purpose of such restraint is either to eliminate vestibular feedback (Ravassard et al., 2013) or to enable the use of techniques that require minimal brain motion, like two-photon imaging (Dombeck et al., 2010; Harvey et al., 2012) and intracellular recordings (Harvey et al., 2009; Domnisoru et al., 2013; Schmidt-Hieber and Hausser, 2013).
Another powerful, yet underexplored, application of VR is the precise, real-time experimental control of the animal’s sensory environment (Chen et al., 2013). In particular, VR enables experimental manipulations that have inspired interest in various fields, but are either difficult or impossible to perform in real-world environments. Examples include introducing, removing, or teleporting objects (Gothard et al., 1996; Deshmukh and Knierim, 2011), modifying sensory cues (Muller and Kubie, 1987; Anderson and Jeffery, 2003; Leutgeb et al., 2004), rotating the animal’s frames of reference (Shapiro et al., 1997; Kelemen and Fenton, 2010), morphing the shape of an environment (Leutgeb et al., 2005; Wills et al., 2005) and switching between different environments (Muller and Kubie, 1987; Wills et al., 2005; Jezek et al., 2011). Some manipulations might even include changing the rules of physics (Chen et al., 2013) and creating physically impossible environments (Knierim et al., 2000; Aflalo and Graziano, 2008).
Many studies that would benefit from these types of manipulations require the animal to navigate in two dimensions. For instance, 2D environments can be better suited for testing the animal’s spatial memory (e.g., in the Morris water maze task (Morris, 1984; Ravassard et al., 2013)) and the planning of future trajectories (Pfeiffer and Foster, 2013). Two-dimensional navigation is also required for some manipulations that rotate different frames of reference (Kelemen and Fenton, 2010) or change the shape of the environment (Muller and Kubie, 1987; Leutgeb et al., 2005; Wills et al., 2005). In addition, several cell types exhibit patterns of activity that are inherently two-dimensional. For example, grid cells fire at vertices of a hexagonal lattice that spans a 2D environment (Hafting et al., 2005), border cells are active along walls of a 2D enclosure (Solstad et al., 2008), and head direction cells are tuned to the animal’s bearing angle (Taube et al., 1990; Sargolini et al., 2006).
Rats have been shown to successfully navigate in open 2D arenas in VR (Holscher et al., 2005; Cushman et al., 2013). Yet, in spite of the interest in 2D patterns of neural activity, such patterns have not been reported in rodent VR systems. The requirements for a VR system – in which cells would exhibit 2D spatial patterns of activity similar to those in real-world environments – are therefore unknown. In fact, some differences between VR and real-world navigation raise concerns about the feasibility of obtaining such activity patterns. For example, head-fixed or body-fixed systems can conceivably create a conflict between virtual cues and the animal’s sense of direction; such a conflict might destabilize spatial activity patterns (Knierim et al., 1995; Shapiro et al., 1997; Czurko et al., 1999). Furthermore, differences in self-motion and vestibular information available to the animal can disrupt signals that are necessary in some proposed models of grid cells and head direction cells (McNaughton et al., 2006; Clark and Taube, 2012). Finally, the animal’s interactions with the boundaries of a 2D environment might not be sufficiently realistic in VR. Yet, boundaries are critical for the activity of border cells (Solstad et al., 2008), and are hypothesized to be an important contribution to the firing place cells and grid cells (Barry et al., 2006; Solstad et al., 2008).
We built a novel VR system, specifically designed for unconstrained 2D navigation in rats. The system includes hardware, software and electrophysiology components for the study of large neuronal populations in navigating rats during VR manipulations. We found activity patterns throughout the entorhinal-hippocampal system that are similar to the activity patterns observed during 2D navigation in real-world environments. These results illustrate that the spatial memory and navigation system can be engaged in at least one type of a 2D VR apparatus, and suggest a general-purpose tool for studying this system in rats during novel kinds of experimental manipulations.
RESULTS
Apparatus and software
We designed and implemented a fully integrated VR system specialized for 2D navigation in rats. In previous rodent VR systems used for neural recordings, animals were constrained in a single direction on a treadmill, either by head or by body fixation (Harvey et al., 2009; Ravassard et al., 2013). To enable unconstrained 2D navigation, we instead wanted a system that allowed rats to turn and interact with a 360° view of a virtual environment. We therefore designed a spherical treadmill and harness system more similar to the one used in (Holscher et al., 2005), which allowed animals to rotate around the vertical axis (see Experimental Procedures; Figure 1A–D, Figure S1).
Figure 1. Virtual reality (VR) setup for 2D navigation in rats.
(A) Schematic of the setup. For clarity, the screen is rendered partially transparent, and the transparent ceiling is tinted. Inset: yaw blocker in contact with the treadmill, preventing treadmill rotations around the vertical axis. (B) Side view of the setup, showing the light path of the VR projection in red. (C) Photograph of the attachment to the commutator, illustrating components that rotate with the rat. (D) Photograph of a rat in the harness, attached to the commutator via a hinged arm. (E) Schematic illustrating coverage of the animal’s field of view by the VR projection. Rats can fully rotate their bodies to view a 360° screen and walk in any direction on the treadmill. (F) Rendering of a virtual square arena by the VR software. The image is pre-warped by the software for projection onto the conical screen. Inset: schematic of the animal’s position in the square arena. (G) Simulated partial view of the environment from the rat’s location.
In a 360° system, like the one described in (Holscher et al., 2005), the immersive nature of the apparatus makes it challenging to include an electrophysiological recording system that neither obstructs the animal’s view of the virtual environment nor provides unwanted non-VR directional cues. We therefore designed a novel projection system using a truncated cone-shaped screen, as well as a transparent ceiling through which images of virtual environments were projected onto the screen (Figure 1A–B). A commutator and an attachment system for the animal were mounted on the transparent ceiling, entirely avoiding both the light path of the projection system and the rat’s field of view (Figure 1B). We also designed and implemented a 128-channel electrophysiology system that was miniaturized using multiplexing technology to satisfy the constraints of the projection (see Experimental Procedures; Figure 1C, Figure S2). The commutator allowed animals to rotate and walk in any direction of the spherical treadmill. A fluid reward system was also attached to the commutator and rotated with the animal (Figure 1C–D). In addition to covering the full azimuth range of the animal, the projection system covered a wide range of elevation view angles (−30° to +45°, Figure 1E).
We also wrote an open-source Matlab-based software package for designing virtual environments and rendering them on the screen (see Experimental Procedures; Figure S3). The software monitored signals from two optical mice that were positioned on the treadmill’s equator to record rotations of the treadmill around any horizontal axis. These velocity signals were integrated in time to update the animal’s location in a virtual environment, and the environment was then rendered and displayed at the new location. An example of a virtual environment designed and rendered with this software is illustrated in Figure 1F–G. The software pre-warped the image of the environment, such that its projection onto the conical screen was correct from the rat’s viewpoint.
2D navigation
A key requirement for characterizing spatial patterns of activity in the brain is the complete coverage of a 2D environment by the animal’s trajectory. We designed a 2D virtual square arena (1×1 m or 2×2 m) and asked whether rats could be trained to produce sufficient coverage of this arena. In real-world environments, coverage is typically achieved by distributing rewards (such as food pellets) randomly throughout the environment. VR offers the added advantage of allowing precise computer control of successive reward locations, which can be used to randomize the animal’s trajectory or even bias it toward least-visited locations. Using these principles, we implemented two tasks designed to maximize 2D coverage: the “random foraging” task (n=10 rats) and the “target pursuit” task (n=4 rats).
In the random foraging task (see Experimental Procedures), the arena was divided into 9–25 zones, and one of the zones was randomly chosen as the reward zone. Zone boundaries and the reward location were invisible to the animal. On the contrary, in the target pursuit task, the center of the reward zone was indicated by a visual beacon (a small cylinder, visible in Figure 1G). In both tasks, whenever the animal entered the reward zone, a drop of water was delivered, and the reward zone was instantly moved to a new random location. In the target pursuit task, the reward location was randomly drawn from a non-uniform distribution, which was chosen to bias the animal toward or away from the walls of the arena, depending on coverage in prior sessions.
In the random foraging task, rats learned to walk in meandering trajectories that quickly covered a large fraction of the environment (Figure 2A). To quantify coverage, we divided the environment into a 40×40 grid of bins, as is typical for the analysis of spatial patterns of neural activity, and asked what fraction of the total number of bins were visited by the rat. On average, a large fraction of the bins (>90%) were visited within a relatively short time (20–30 min) in a 2×2 m environment (Figure 2B).
Figure 2. Two behavioral tasks for achieving full coverage of 2D environments in VR.
(A) Contiguous trajectories of a rat performing the random foraging task. In each case, a reward is located in one of the unmarked zones, and the rat walks around the environment in search of the rewarded zone (blue). After each success, the target is relocated to another randomly chosen zone. (B) Percent of the environment visited by animals in the random foraging task, as a function of duration of the recording session. Data were averaged across all sessions in 2×2 m environments of a single rat, then averaged across rats. Error bars: standard errors. (C) Contiguous trajectories of a rat performing the target pursuit task. In each case, the center of a rewarded zone is marked by a visible beacon (small cylinder). A circular zone around the beacon was rewarded. (D) Environment coverage in the target pursuit task.
In the target pursuit task, all rats learned to approach visible targets along roughly straight-line trajectories (Figure 2C). The median path length between successive reward sites was 1.91±0.05 times longer than the optimal straight-line path (mean ± standard error, n=4 rats). This ratio is significantly smaller than the ratio observed in the random foraging task (3.53±0.25, n=10 rats, p<0.001, t-test), indicating that the rats’ behavior was indeed guided by the visible targets. Indeed, rats typically demonstrated proficient goal-oriented control of the spherical treadmill: they followed each reward by an abrupt decrease in speed, a change in bearing angle (sometimes by up to 180°), and then acceleration toward the next target (Figure S4). Paths produced by rats in this behavior also covered a large fraction of the environment (>90% of bins) within 20–30 min (Figure 2D).
Thus, rats successfully navigated in 2D virtual arenas, and both the random foraging and the target pursuit tasks appeared to be suitable for producing complete coverage of 2D environments. For analyses in this paper, no significant differences in the firing patterns of cells were observed across the two tasks (see below); data from both tasks were therefore pooled together.
Hippocampal activity in 2D VR
We next asked whether and how the 2D spatial structure of virtual environments is represented in the hippocampus. In 7 rats we recorded 2408 CA1 units (Figure S5A), which were classified as 2093 putative pyramidal cells and 315 putative interneurons based on the firing rate and spike duration (see Experimental Procedures). Of the putative pyramidal cells, 1107 (52.9%) exhibited significant spatially-modulated firing and were classified as place cells (Figure 3A). In two rats, we also recorded CA1 sharp-wave ripple events during sleep to better estimate the total number of units; 45 of the 90 cells in these sessions (50%) were place cells in VR. Pyramidal cells that were not classified as place cells were typically silent (peak firing rate: 0.70±0.04Hz for non-place cells, 4.0±0.12Hz for place cells; median ± bootstrap standard deviation across cells). Similar firing patterns were observed in CA3 (Figure 3B).
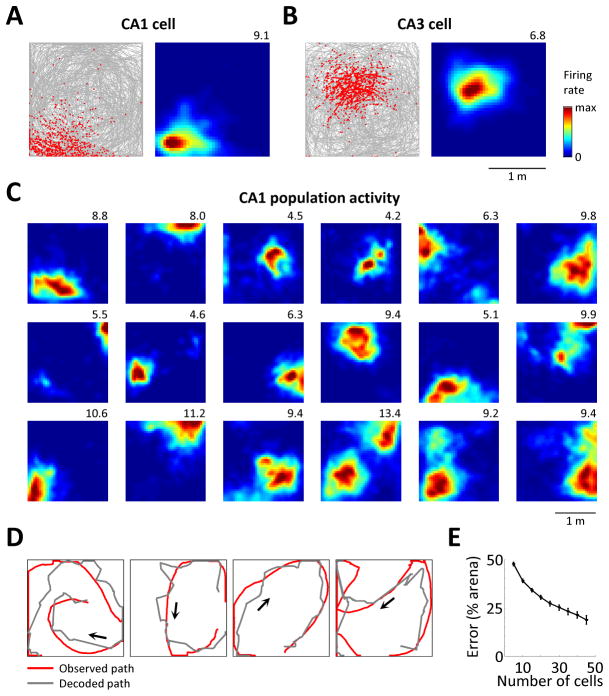
Figure 3. Hippocampal neurons exhibit 2D place fields in VR.
(A) Example of a place cells in CA1. Left: animal’s path during a 30 min session (gray) and locations of spikes (red). Right: rate map of the cell. Number indicates maximum firing rates in Hz. (B) Example of a place cell in CA3. (C) Rate maps of 18 simultaneously recorded place cells in CA1. Every cell with a maximum firing rate of >4 Hz is shown. (D) Typical segments of an animal’s trajectory, showing the performance of an algorithm that uses population activity in CA1 to decode the animal’s virtual location. (E) Performance of the decoding algorithm, as a function of the number of cells used in the analysis. Values are mean ± standard errors across all sessions in all rats.
Place cells in the 2D virtual arena exhibited spatially sparse firing patterns. Most cells fired in a single place field (1.32±0.02 fields on average, ±standard error; similar to real-world recordings (Henriksen et al., 2010)). Each field occupied a small region of the environment; this region was bigger in larger environments but accounted for a similar fraction of the total area (11.4±0.55% in the 1×1 m arena and 14.4±0.35% in the 2×2 m arena; median ± bootstrap standard deviation across n=1831 and 2698 fields, respectively; also similar to the real-world recordings (Fenton et al., 2008; Henriksen et al., 2010)).
Across large populations of simultaneously recorded place cells (Figure 3C), fields appeared to tile most of the environment, suggesting that information about virtual 2D location was contained in the activity of hippocampal populations. To test this directly, we implemented an algorithm similar to the one used for real-world 2D environments ((Wilson and McNaughton, 1993); see Experimental Procedures) that attempted to decode the animal’s position from the population vector of firing rates (smoothed over a 2 s window). The algorithm appeared to accurately recover the animal’s trajectory from the activity of CA1 cells (Figure 3D). We tested the algorithm on all sessions across all animals and quantified its performance for various subsets of recorded neurons (5–45 pyramidal cells, Figure 3E). Performance improved with the increasing number of cells, and for 45 cells the median distance from decoded location to true location (decoding error) was <20% of the width of the environment (similar to (Wilson and McNaughton, 1993)).
Entorhinal cortical activity in 2D VR
The spatial memory system includes the medial entorhinal cortex (MEC), where cells exhibit a diversity of 2D spatial activity patterns. In particular, MEC grid cells, head direction cells, and border cells have been studied in detail (Hafting et al., 2005; Sargolini et al., 2006; Solstad et al., 2008). To identify and characterize these cell types in VR, we recorded 1214 cells in 11 rats during the 2D navigation tasks described above (see Experimental Procedures). Head direction-related signals were also analyzed in 1580 additional cells in 8 rats that were sampling bearing angles by walking in a circle around a virtual environment. To analyze cells belonging to each class, we implemented statistical methods that have been previously used for data in real environments (see Experimental Procedures).
Of all cells, 110 in 3 rats were active non-interneurons recorded in the 2×2 m environment and located in the dorsal 1 mm of the MEC (Figure S5B), where most grid cells with small grid spacing have been previously observed (Stensola et al., 2012). Many of these cells indeed exhibited grid cell firing patterns: they fired in multiple fields arranged at vertices of a hexagonal lattice, and their spatial autocorrelation functions were periodic with 60° symmetry (Figure 4A). Thirty-six cells (33%) had gridness scores that exceeded the value expected by chance in randomly reshuffled datasets (p<0.05, Figure 4B). These cells exhibited a wide range of grid scales (over a factor of 2), consistent with the wide range and possibly with the modularity observed in real-world environments ((Stensola et al., 2012); Figure 4C). However, the scales were larger than those reported in the same region of MEC in real-world environments by roughly a factor of 2.5 (smallest scale of ~100 cm, compared to ~40 cm). Likely because of this grid expansion, none of the cells recorded in the smaller 1×1 m environment could be unambiguously classified as grid cells (n=252 cells), even though we observed some cells with two or three distinct firing fields in this environment. Similarly, none of the cells recorded at the more ventral locations in MEC (n=520 cells) were classified as grid cells – possibly because of the expected increasing dorso-ventral gradient of grid scales (Brun et al., 2008; Stensola et al., 2012) – though we did observe spatially-modulated cells at those locations.
Figure 4. Neurons in the median entorhinal cortex (MEC) exhibit 2D activity patterns.
(A) Examples of grid cells. Top: animal’s path (gray) and locations of spikes (red). Middle: rate maps of the grid cells. Numbers indicate maximum firing rates in Hz. Bottom: autocorrelations of the rate maps. Colors range from dark blue (−1 correlation) to dark red (+1 correlation). (B) Distribution of observed gridness scores across all cells (top plot) and gridness scores in randomly reshuffled datasets (bottom plot). Red line: 95th percentile of the reshuffled distribution, used as a threshold to define grid cells. (C) Distribution of grid spacing across all grid cells. Examples from (A) are marked. (C) Polar plots of example head direction cells, showing firing rate as a function of head direction. Numbers indicate the maximum firing rates in Hz. (E) Directional stability scores across all cells, plotted as in (B) and showing the 99th percentile of the reshuffled distribution. (F) Mean vector lengths for all cells that passed the directional stability threshold. Red line: 99th percentile used to define head direction cells. (G) Rate maps of example border cells. Numbers indicate maximum firing rates in Hz. (H) Border scores across all cells, plotted as in (B) and showing the 95th percentile of the reshuffled distribution. (I) Spatial information rates for all cells that passed the border score threshold. Red line: 99th percentile used to define border cells.
Many cells in MEC exhibited firing rates that were strongly modulated by the animal’s head direction in VR (Figure 4D). To characterize this activity pattern, we analyzed active non-interneurons recorded on sessions that had sufficient sampling of all head directions. Of the 1717 cells recorded, 762 had a relationship between firing rate and head direction that was more stable than expected by chance in randomly reshuffled datasets (p<0.01, Figure 4E). Of these cells, 557 (32% of the total) had a mean vector length larger than expected by chance (p<0.01, Figure 4F) and were therefore not only directionally stable, but also significantly tuned to a single head direction. These directionally-tuned cells were called “head direction cells” and were used for subsequent analyses.
In addition to grid cells and head direction cells, we observed border cells in VR (Figure 4G). These cells exhibited firing fields that were in contact with and stretched along a wall of the environment. Of the 882 active non-interneurons recorded, 50 (5.7%) had a significantly large border score compared to reshuffled datasets (p<0.05, Figure 4H) and also exhibited a significantly large spatial information rate (p<0.05, Figure 4I). In the reshuffled datasets (200 per cell), only 0.024% of the simulated cells passed this dual criterion indicating that, like in real environments (Solstad et al., 2008), border cells in VR likely represented a small, but significant subpopulation of MEC neurons.
Locking of spatial firing patterns to virtual cues
Unlike in head-fixed or body-fixed VR systems, animals in our system changed bearing angle by physically rotating their bodies around the vertical axis. It is therefore conceivable that not only virtual cues, but certain real-world cues provided directional information that could influence the firing patterns of hippocampal and MEC neurons. Such directional cues might include undesirable asymmetries in the projection system or the treadmill, odor and auditory cues in the recording environment, etc. We asked to what extent real-world cues, compared to VR cues, contributed to the firing patterns we observed.
In all recording sessions, the image of the virtual environment was slowly rotated relative to the real environment (by 0.2°/s, 30 min per full rotation, Figure 5A). Therefore, two sets of uncoupled reference frames were defined: one in which the axes were always aligned to particular walls of the virtual environment, and one in which the axes were aligned to the true cardinal directions of the real world (laboratory). We first asked which of these reference frames was better represented by CA1 activity. Figure 5B–C shows the activity of one typical CA1 cell. In the VR reference frame, this cell’s spikes formed a small, spatially localized place field (Figure 5B). However, the same spikes analyzed in the real-world reference frame had a highly dispersed pattern (Figure 5C). This cell therefore appeared to be more informative of the VR, rather than the real-world, reference frame. To perform this comparison for the population of recorded place cells, we measured the spatial information rates of each cell in the two reference frames and compared the two rates. Of the 1296 cells classified as place cells in at least one of the reference frames, most (1023, 79%) had a significantly higher information rate in the VR reference frame (Figure 5D), whereas only 4 (0.31%) had a significantly higher information rate in the real-world reference frame.
Figure 5. Spatial activity patterns in VR follow virtual cues.
(A) Schematic of the experiment, in which the image of the virtual environment was rotated relative to the real-world (laboratory) environment. Two mutually rotating reference frames were defined: the real-world (black) and the VR (green). (B) Activity of a CA1 neuron plotted in the VR reference frame. Left: Animal’s path (gray) and locations of spikes (red). Right: Rate map of the cell. Number indicates the maximum firing rate in Hz. (C) Activity of the same neuron as in (B), plotted the same way but in the real-world reference frame. (D) Difference between spatial information rates in the VR and the real-world reference frames across all cells that had spatially modulated activity in either reference frame. Numbers above 0 indicate cells that preferred the VR reference frame. (E) Activity of an MEC neuron plotted in the VR reference frame. Left: Animal’s head direction as a function of time (gray) and spikes fired by the neuron (red). Right: polar plot of the neuron’s firing rate as a function of head direction. Number indicates the maximum firing rate in Hz. (F) Activity of the same neuron as in (E), plotted the same way but in the real-world reference frame. (G) Difference between mean vector lengths in the VR and the real-world reference frames across all cells whose activity was modulated by head direction in either reference frame. Numbers above 0 indicate cells that preferred the VR reference frame.
We similarly analyzed the activity of head direction cells by measuring the tuning of MEC neurons either to the head direction in VR or to the head direction in the real world. Figure 5E–F shows the activity of a typical MEC neuron. This cell fired at a consistent preferred head direction in the virtual environment. However, in the real-world environment its preferred direction was constantly changing due to the relative rotation of the two reference frames. Therefore, this cell was also more informative of the direction in VR than in the real-world reference frame. For every MEC neuron, we performed this comparison by calculating the mean vector lengths in the two reference frames (to quantify the strength of directional tuning) and by comparing the two lengths. Of the 497 cells selective to head direction in at least one of the reference frames (and with sufficient sampling of directions in both), most had stronger tuning in VR (383, 77%), whereas only a minority of cells (25, 5%) had significantly stronger directional tuning in the real world (Figure 5G). Similar preference for the VR reference frame was observed in grid cells and border cells (Figure S6).
Determination of the initial spatial patterns in VR
We have shown that spatial patterns of activity in the brain preferentially track VR when virtual and real-world cues are moved relative to one another. But what sets the initial patterns of activity, at the very beginning of a recording session? One possibility is that these spatial patterns are entirely determined by the memory of the virtual environment from previous recording sessions. Another possibility is that these patterns are set by the real-world environment (where the animal is located prior to the experiment), but when the VR projection is switched on, they begin to shift in response to the movement of the virtual cues. To distinguish these possibilities, we recorded place cells on two consecutive sessions in the same environment. The initial orientation of the VR environment relative to the real world was different in the two sessions by a randomly chosen rotation angle (Figure 6A). If the initial orientation of place cell maps was determined entirely by the memory of the VR cues, one would expect place cells to fire in the same parts of the virtual environment in the two sessions. On the contrary, if the initial orientation of place cell maps was set by the real-world cues, one would expect place fields to keep their initial orientation relative to the laboratory, but change location in the virtual environment.
Figure 6. Place field locations at the beginning of a session are partially influenced by the real world.
(A) Schematic of the experiment. The orientation of the virtual environment relative to the real-world (laboratory) was discretely changed between two sessions. (B) Rate maps of three place cells recorded on two sessions; the virtual environment was rotated by 77° between sessions. All place fields reappeared in the same positions relative to the VR. (C) Bottom: All ten recorded place cells, including those in (B). Each row is the cross-correlation of rate maps from the two sessions, with the rate map from session 2 rotated by Δ angle. Colors for each cell are scaled from lowest correlation (white) to highest (black). Top: Average cross-correlation across all ten cells. Peak at 0° indicates that rate maps did not rotate relative to VR. (D–E) Another example, plotted the same way as (B–C). In this example, place fields rotated by 90° relative to the VR. (F–G) Another example, plotted the same way as (B–C). In this example, place fields rotated by 180° relative to the VR. (H) For all pairs of sessions, the angle by which the VR was rotated relative to the real world between sessions (“environment rotation”) and the angle by which place fields rotated relative to the virtual environment (“place field rotation”). In most cases, place fields locked better to the virtual environment (points at 0); in other cases, fields locked better to the real world (points closer to the diagonal). In the latter case, rotations relative to the virtual environment appeared to be constrained to multiples of 90°.
Figure 6B illustrates the activity of three typical place cells recorded in this experiment. Although the virtual environment was rotated by 77° between the two sessions, all place fields remained locked to the virtual environment. (E.g. the field of Cell 1 was adjacent to the same virtual wall on both sessions.) Indeed, across the recorded population, the best match between firing rate maps recorded on the two sessions occurred at a 0° rotation relative to virtual coordinates (Figure 6C). Thus, in this example the orientation of the spatial maps appeared to be set by the VR, rather than the real-world cues.
Examples shown in Figure 6D–G illustrate a different behavior, observed on two other example sessions where the virtual environment was rotated by 72° and 155°. In both cases, place cells initially appeared to lock better to the real-world reference frame, rather than to the virtual environment. For example, Cell 3 in Figure 6D fired roughly in the true “north” of the environment on both sessions, even though the true north on the two sessions corresponded to different virtual walls. Interestingly, the rotation of place fields relative to the virtual environment in these examples was not 72° and 155°, as expected from being purely determined by the real-world cues. Rather, place fields rotated by 90° and 180°, which are the closest multiples of 90° to the angles of 72° and 155° (Figure 6E,G). This indicates that, although the location of place fields in these examples was influenced by the real-world cues, these fields were constrained by the square geometry of the virtual environment. For example, cells that fired in a corner on one session continued to fire in a corner (albeit a different one) on the second session, whereas cells that fired along a wall continued to fire along a different wall (e.g., Cell 1 in Figure 6D and Cell 3 in Figure 6F).
Note that in all of the examples in Figure 6, the virtual environment was slowly rotated throughout the session, and place cells followed the virtual environment (as previously shown, Figure 5). Thus, even in the latter two examples (Figure 6D–G), place cell maps were not fully determined by the real-world cues. Rather, real-world cues set the initial orientation of these maps relative to the virtual environment at the beginning of the session. Then, following the animal’s transition into VR, place fields were entirely determined by virtual cues and remained at the initially set virtual location.
Figure 6H shows a summary of the observation across all pairs of sessions where an accurate estimate of place map rotation could be obtained. In 15 pairs of recording sessions, the virtual environment was rotated by an absolute amount of less than 45°; in 14 of these pairs of sessions, place fields did not rotate relative to the virtual environment by an amount significantly different from 0°. In 36 additional pairs of sessions, the virtual environment was rotated by an absolute amount that exceeded 45°. In 22 of these pairs of sessions (61%), place fields locked better to the virtual cues than to the real-world reference frame. In the remaining cases, place fields initially aligned better to the real-world reference frame, and tended to rotate either by ±90° or by 180° relative to the virtual environment. The rotation angle in these cases deviated from the nearest multiple of 90° by an average of only 4.5±0.9°, which was significantly less than if the rotation purely aligned place fields to real-world cues with no regard for the 90° symmetry (24.8±1.8°, p<0.001, paired t-test).
Hippocampal remapping in VR
In real-world experiments, hippocampal neurons respond to changes of environment by exhibiting various types of “remapping” (Muller and Kubie, 1987; Leutgeb et al., 2004; Wills et al., 2005; Colgin et al., 2008). We wanted to see whether these types of hippocampal remapping could be observed across different virtual environments, but in the same real-world context (recording room, VR apparatus, etc.). We designed three distinct virtual environments (Figure 7A). Environments A and B were geometrically similar: both were square arenas of the same size (1×1 or 2×2 m in different rats) and had four objects placed at the corners. However, the shapes of these objects, as well as the visual patterns on the walls and the floors of the arenas were distinct. Environment C was geometrically distinct from both A and B: it was a circular arena (1.4 or 2.8 m diameter) and was surrounded by three objects separated by roughly 120°.
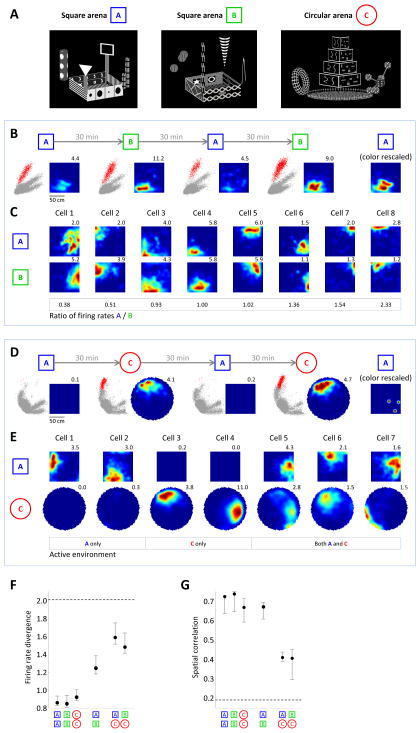
Figure 7. Place cells exhibit different types of remapping in VR.
(A) Images of virtual environments used for inducing hippocampal remapping. (B) Example of a CA1 neuron recorded across four alternating sessions in geometrically similar (square) environments. Sessions were 30 min long, separated by 30 min. For each session, Left plots: all recorded spikes, with the spikes of the shown neuron in red. Spikes are plotted in a projection of a 4-dimensional space defined by the amplitudes of the waveforms on the four wires of the tetrode. Right plots: Rate maps of the neuron. All four rate maps are color-scaled to the same maximum firing rate. Numbers indicate maximum firing rates for each session. Rightmost plot: rate map from the first session scaled to its own maximum firing rate. (C) Rate maps of simultaneously recorded place cells on sessions in the two square environments. Colors of all rate maps are independently scaled. Boxed numbers: ratios of peak firing rates; cells are sorted from those more active in square arena B to those more active in square arena A. (D) Example of a CA1 neuron recorded across four alternating sessions in geometrically different (square and circle) environments, plotted the same way as the cell in (B). The cell fired very few spikes on the sessions in the square environment. (E) Rate maps of simultaneously recorded place cells on sessions in the square and circular environments. For each cell, colors are scaled to the maximum firing rate across the two rate maps. (F) Firing rate divergence for all pairs of environments. Higher numbers indicate rate remapping. Values are medians across cells ± bootstrap standard deviations of the median. Dashed line: average divergence across reshuffled datasets, in which cell identities were scrambled. (G) Spatial cross-correlation values for all pairs of environments. Lower numbers indicate global remapping. Values are medians across pairs of sessions ± bootstrap standard deviations of the median. Dashed line: average cross-correlation across reshuffled datasets.
We recorded 402 place cells in 4 rats on alternating sessions in geometrically similar environments (A and B). Figure 7B–C shows typical examples of simultaneously recorded CA1 place cells in this experiment. Although the two environments were visually distinct, cells tended to fire in the same locations relative to one another in both square arenas. However, some changes in firing rate were observed. For example, the cell in Figure 7B exhibited a higher firing rate in square arena B and showed consistent increases and decreases in firing rate across multiple switches between the two environments. Examples in Figure 7C illustrate that such changes in firing rate were non-homogenous across the population: while some cells were more active in square arena A, others had a similarly strong preference for square arena B. These changes were similar to the “rate remapping” reported in geometrically similar real-world environments (Muller and Kubie, 1987; Leutgeb et al., 2004).
In real-world navigation experiments, stronger remapping is often observed when differently-shaped environments are used (Muller and Kubie, 1987; Wills et al., 2005). Therefore, we recorded 419 neurons in 4 rats on alternating sessions in geometrically distinct virtual environments (A and C or B and C). We indeed observed stronger changes in firing patterns across these environments. For example, the cell shown in Figure 7D had a place field in the circular arena, but was virtually silent in the square arena. Across the population, many cells were similarly active in only the square or the circular environment (Figure 7E). Other cells had place fields in both environments; however, while some of these fields were located at similar positions relative to one another, the locations of other fields changed across environments (e.g. rightmost cell in Figure 7E). These types of changes were similar to the “global remapping” reported in differently-shaped real environments (Muller and Kubie, 1987; Wills et al., 2005).
We quantified changes in both the firing rate and the spatial patterns across all cells. Changes in firing rate were measured using firing rate divergence (Lever et al., 2002), which quantified the change in peak firing rates across environments compared to the observed changes across sessions in the same environment. Across every pair different environments, the firing rate divergence exceeded values expected from repetitions of any individual environment (p<0.001 for all comparisons, paired t-test, Figure 7F). To quantify changes in spatial patterns, we measured the correlation of rate maps across different environments and across sessions in the same environment. Since rates were normalized to compute correlation, this measure was not sensitive to overall changes in firing rate, but only reflected changes in spatial pattern. Across repetitions of the same environment, median correlation values were high (0.67–0.74, Figure 7G). For recordings in geometrically similar environments (A and B), the correlation was not significantly different (0.67, p>0.3 for all comparisons, Wilcoxon rank sum test). However, in geometrically distinct environments (A and C or B and C), the correlation was significantly lower (0.41 in both cases, p<0.001).
DISCUSSION
In this study, we designed and tested a new VR apparatus that can potentially be exploited for a variety of rodent experiments. In most previous studies, VR has been used as a tool to restrict the animal’s movements during behavior, either to enable recording techniques that require brain stability (Harvey et al., 2009; Dombeck et al., 2010), or to eliminate vestibular information available to the animal (Ravassard et al., 2013). Yet a different, currently underexplored VR application is the precise, real-time experimental control of changes to environments (Chen et al., 2013). Many experiments that can benefit from such VR manipulations are performed during open-range navigation in 2D environments (Gothard et al., 1996; Leutgeb et al., 2005; Wills et al., 2005; Kelemen and Fenton, 2010). Additionally, many cell types studied during navigation (such as hippocampal and entorhinal cells) have noteworthy firing patterns in 2D (O’Keefe and Dostrovsky, 1971; Hafting et al., 2005; Sargolini et al., 2006; Solstad et al., 2008). Therefore, the main purpose of the technique we developed is to permit maximally unconstrained 2D navigation, while also enabling both large-scale neural recordings and a full control of the visual environment.
Several features of our system specifically addressed these goals. First, like the systems described in (Holscher et al., 2005; Ravassard et al., 2013), our VR system was designed for rats, rather than mice. It can therefore be combined with the large-scale multi-region recording techniques, and also use the rich behavioral repertoire developed in this species. Second, unlike the systems that constrain the animal’s direction on the treadmill (Harvey et al., 2009; Ravassard et al., 2013), our system included a commutator setup to permit full-body rotation and unconstrained navigation in 2 dimensions. For this purpose, we used a novel projection system that created a 360° view of the virtual environment. This projection setup combined an immersive environment with a built-in recording system that neither interfered with the animal’s view nor provided undesirable non-VR directional cues. Finally, the large-scale multi-electrode recording system developed for our setup was miniaturized using multiplexing technology to satisfy the constraints of the VR projection.
In addition to the hardware components, the system we designed included a novel software package for rendering images of virtual environments and controlling VR experiments in real time. Many commercial software systems for 3D graphics are available, but these programs are usually designed for advanced 3D gaming or animation. Consequently, they are difficult to modify, both to attain the basic structure of a rodent VR experiment and to eliminate unwanted features, such as complex frame-by-frame movement control, intended for human use. These software systems often require substantial customization to implement any new type of an experiment (Harvey et al., 2009). On the contrary, our software package has been specifically designed for rodent navigation experiments and streamlined some critical functions, such as pre-warping environment images for projections onto curved screens, monitoring and processing the animal’s velocity, delivering rewards, synchronizing behavioral data with electrophysiology, and implementing arbitrary experimental logic. In addition, the software included functions for object-oriented access to the environment, which were optimized for real-time environment manipulations.
A critical proof of principle for a VR apparatus is the presence of firing patterns that are expected during similar behavioral tasks in real-world experiments. We recorded cells in two hippocampal areas (CA1 and CA3), and observed firing within localized place fields that were small, covered the entire 2D environment and, across the population, faithfully represented the animal’s virtual location. Furthermore, in MEC we observed three major classes of cells that have been previously studied in detail: grid cells, head direction cells, and border cells (Hafting et al., 2005; Sargolini et al., 2006; Solstad et al., 2008). All cell types appeared to have qualitatively similar firing patterns to their counterparts in real environments and occurred in similar proportions within the population. These familiar firing patterns across multiple cell types and brain areas suggest that the entire entorhinal-hippocampal network might be engaged in 2D VR in a similar way to its engagement during real-world navigation.
Several aspects of VR are different from real-world navigation in 2D, including self-motion and vestibular information available to the rat, as well as the nature of interactions with borders of the environment. Our results indicate that, at least in the VR system we designed, these differences do not preclude the functioning of many circuit mechanisms involved in real-world navigation. Firing patterns in 2D have not yet been reported in other rodent VR systems, and we therefore do not know whether any features specific to our apparatus (e.g., full-body rotation of the rat) are required to engage these circuit mechanisms. Future comparisons across systems should elucidate the minimal requirements of a VR system for the study of 2D navigation.
One notable quantitative difference with real-world environments we found was the expansion of spacing between grid cell firing fields in VR. The smallest grid spacing we observed was ~1 m, which is roughly 2.5x larger than the smallest spacing observed at the same recording locations (dorsal-most region of MEC) during real-world navigation (Stensola et al., 2012). Previously, grid cells in VR have only been recorded on 1D linear tracks, but the grid spacing on these tracks was similar to our observations (smallest spacing of 1.1 m in (Domnisoru et al., 2013)). Furthermore, expansion of grid spacing has been observed in some real-world conditions, such as in novel environments (Barry et al., 2007).
One possible mechanism of grid expansion in VR could be related to the frequency of theta oscillations. As in other VR systems (Domnisoru et al., 2013; Ravassard et al., 2013), the theta frequency we observed was lower than the typical frequencies in real-world environments (Figure S7A–C); this frequency reduction has been proposed to result from differences in vestibular inputs (Russell et al., 2006; Ravassard et al., 2013). Although the causal relationship between theta frequency and grid spacing is unknown, a correlation between the two has been observed (Giocomo et al., 2007). Another possible reason for grid expansion could be the fact that rodents in VR systems typically run, rather than walk. In fact, the average speed in our system (~40 cm/s) was much greater than the speeds in random foraging experiments ((Lu and Bilkey, 2010); Figure S7D–E). It is conceivable that the grid cell spacing is rescaled by the typical speed that an animal previously used to navigate in a given environment – for instance, via a normalization of the velocity-related inputs into MEC. Finally, a third possible mechanism is that the velocity-related signals might be different between VR and the real world due to differences in the optic flow or the proprioceptive feedback. If the grid cell network acts as an integrator of velocity-related inputs (McNaughton et al., 2006), a rescaling of these inputs would result in a corresponding rescaling of the grid periodicity. One piece of evidence that the velocity-related signals might be different in VR is that the slope of the firing rate-velocity relationship in CA1 neurons was flatter in our system than in real-world environments ((Lu and Bilkey, 2010); Figure S7F). Further studies are required to distinguish between the possible causes of grid expansion, both in VR and in real-world situations; such studies may be generally informative about the mechanisms of grid formation.
One goal of VR is to provide computer control of the animal’s sensory experience during navigation, and it is therefore important to uncouple relevant sensory cues from undesirable real-world cues that may be available in a laboratory. We rotated virtual environments relative to the real world and found that all firing patterns in the hippocampus and MEC predominantly followed virtual cues during this manipulation. Previous studies showed that, when two mutually rotating reference frames are available, hippocampal activity can follow both in an alternating fashion (Kelemen and Fenton, 2010). It is possible that in our system, only the VR reference frame engaged activity because the real-world cues were, by design, less salient. This may reflect the importance of designing a sufficiently immersive VR apparatus and a projection system that deprives the animal of real-world directional cues. Alternatively, the VR reference frame could be preferred by the entorhinal-hippocampal circuit because it is more behaviorally relevant to the animal during the navigation tasks they performed in this study.
We found one situation in which place fields could be partially influenced by real-world cues: at the very beginning of a training session, when the animal was transitioned into the VR apparatus. If, at this moment, the VR and the real-world cues had a relative orientation different from the one previously experienced by the rat, place fields in almost half of the cases coherently realigned to better match their prior position in the real-world reference frame. Previous studies found that conflicts between cues can cause realignment of place fields relative to an environment (Knierim et al., 1995; Shapiro et al., 1997; Czurko et al., 1999). However, our results are surprising because, following this initial realignment, place fields proceeded to track the VR reference frame. Thus, our results may constitute a form of hippocampal remapping in which the place fields align to the same set of visual cues, but at different orientations on different sessions. Because, by design, only visual cues could contribute to place cell formation in VR, these results demonstrate that the hippocampus may form an internally consistent spatial map that is not driven by the sensory environment.
Interestingly, when place fields aligned better to the real world, their resulting rotation relative to the virtual environment was restricted to multiples 90°. This shows that even when influenced by non-VR cues, the place map was still constrained to the square shape of the virtual environment. These results are consistent with models that emphasize the importance of geometry, and in particular environment borders, in the formation of 2D patterns of spatial activity (Barry et al., 2006; Solstad et al., 2008). More generally, our results indicate that the shape of a virtual 2D enclosure is reflected by hippocampal activity, in spite of the artificial nature of virtual walls that define this shape. In MEC, this conclusion is further supported by the presence of border cells.
One particularly promising application of VR is the ability to modify or switch spatial environments using computer control. We recorded hippocampal activity in different environments and found that place cells exhibited both rate remapping and global remapping in VR. Rate remapping occurred across environments that were geometrically similar, whereas global remapping occurred across environments that had different shapes and arrangements of virtual objects. These results appear to be analogous to real-world experiments, where changing visual features is more likely to trigger rate remapping, whereas changing enclosure shape is more likely to trigger global remapping (Muller and Kubie, 1987; Colgin et al., 2008). However, there are some differences: For instance, the two square environments we used were more distinct than those in typical rate remapping experiments, where a single cue or enclosure color is usually changed (Muller and Kubie, 1987; Leutgeb et al., 2004). Also, environments we used for global remapping were different not only in shape, but in other features like the number and shape of objects. Although our experiments demonstrate the feasibility of studying remapping in VR, the exact conditions under which different types of remapping occur, and how different these conditions are from those in real-world experiments, remain to be elucidated.
In summary, we demonstrated that many commonly studied neural phenomena in the rat spatial memory system are engaged during 2D navigation in VR. The method we presented fully integrates hardware, software, electrophysiological recording, and behavioral training components. We therefore expect it to be useful for a wide range of navigation experiments that can benefit from virtual reality.
EXPERIMENTAL PROCEDURES
Virtual reality apparatus
As in previously described systems (Holscher et al., 2005; Ravassard et al., 2013), rats in our VR setup navigated by walking on a spherical treadmill. The treadmill was a hollow Styrofoam ball (46 cm diameter, 420 g weight; Universal Foam Products), whose surface was roughened with a file to provide better grip for rats during walking. Irregular markings were drawn on the surface to facilitate optical tracking of treadmill rotation. An antistatic agent (Lysol) was applied to the treadmill daily to reduce low-frequency, saturating noise in electrical recordings.
The treadmill was placed in a custom-designed plastic holder that was manufactured using selective laser sintering (American Precision Prototyping). The bottom of the holder contained a 5 cm opening, through which pressurized air (25–30 psi) was delivered to float the treadmill. Three laminar flow nozzles (Lechler Whisperblast 1/4″) in an air supply manifold between the pressure source and the treadmill were used to reduce air turbulence and its associated noise. Floating allowed the treadmill to rotate around any horizontal axis with minimal friction. Unlike in head-fixed and body-fixed setups, where animals provide a signal to change the view angle in VR via rotation of the treadmill around the vertical axis (yaw), animals in our system could physically turn their bodies over the full 360° azimuth range. Yaw was therefore undesirable and was prevented using a method similar to one previously described (Holscher et al., 2005): the holder was tilted by 5°, and the treadmill at its equator was pressed against a small vertical wheel (25 mm diameter, scroll wheel of an optical mouse). Rotations of the treadmill were monitored by two optical mice (Logitech MX-518), separated by 90° along the equator of the treadmill. Mouse inputs were converted by a LabView routine to two analog signals, which were proportional to components of the treadmill velocity along two orthogonal horizontal axes.
Rendering of virtual environments was displayed to the rat on a custom-made projection screen (white spandex for front projection screens, Rose Fabrics) that had the shape of an inverted truncated cone stretched between two stainless steel rings (112 cm and 58 cm diameter top and bottom rings, respectively, 104 cm height). The screen covered a wide angle of the animal’s field of view (360° of azimuth, −30° to +45° of elevation), providing a full-surround image, while also permitting efficient access to the animal (via lifting of the bottom ring). The top ring of the screen was mounted on a horizontal sheet of transparent Plexiglas-like acrylic (122×122×1.2 cm). Images of a virtual environment were projected onto the screen through the acrylic sheet by an LCD projector (InFocus 5102) using a short-throw lens (InFocus LENS-037). With a 1024×768 pixel projection image, a resolution of >1 cycle per degree was achieved everywhere on the screen. This value is roughly at the limit of rat visual acuity (Birch and Jacobs, 1979).
The rat was constrained on the apex of the treadmill by a harness, consisting of a jacket for the front legs (Harvard Apparatus), a cotton belt supporting the abdomen (12×5 cm) and a neoprene backbone (10×4.5 cm, 70A hardness). A neodymium magnet (50×25×3 mm, K&J Magnetics) on the backbone was used to fasten the animal to an aluminum arm containing three hinges, which permitted a small amount of up-and-down body movement during walking. The arm was attached to the bottom of a 25-channel slip-ring commutator (Dragonfly Commutators), which allowed the rat to turn and walk in any horizontal direction on the treadmill. A 25 ml fluid reservoir, a solenoid valve and a lick tube were attached to the same arm that held the animal; thus they rotated with the animal and were used to deliver water rewards.
Virtual reality control software
The software for VR control was written in Matlab and called ViRMEn (Virtual Reality Matlab Engine). It consisted of three components: 1) A graphical user interface (GUI) for designing virtual environments, 2) An object-oriented toolbox for representing and programmatically modifying environments and 3) A 3D graphics engine for rendering images of virtual environments and interacting with the animal’s behavior in real time.
Some screenshots of the user interface are shown in Figure S3A–B; the interface contained modules for designing environments, organizing multiple environments, and editing textures of objects. Figure S3C shows the hierarchical Matlab class structure that defined the object-oriented toolbox. This hierarchical structure allowed programmatically creating and modifying virtual objects and entire virtual environments. The workflow of the graphics engine is illustrated in Figure S3D. The engine could apply an arbitrary transformation to a virtual environment to display it on a screen of any shape (e.g., conical or toroidal). It could also read an input device (such as an optical mouse) to obtain the animal’s velocity information. When processing velocity information, the engine performed continuous-time collision detection to manage the animal’s contact with boundaries of the virtual environment. Finally, the engine executed user-written code customized for each experiment, which could implement experiment logic, reward delivery, data logging, real-time environment manipulations in response to the animal’s behavior, etc.
For fast graphics, ViRMEn accessed low-level OpenGL commands using the OpenTK library (opentk.com). Environments used in this study (Figure 7A) contained 25000–40000 triangles and were typically displayed with 30 Hz refresh rate on a computer with a NVIDIA Quadro 4000 graphics card. The object-oriented toolbox provided the experimenter with access to individual components of the environment and therefore allowed real-time modifications to environments, movements or removal of individual objects, and even switching between different environments.
Full description of ViRMEn is provided in the software documentation. The software is freely available from virmen.princeton.edu.
Subjects
All animal procedures were approved by the Princeton University Institutional Animal Care and Use Committee and carried out in accordance with the National Institutes of Health standards. Subjects were adult male Long-Evans rats (Taconic). Training started at an age of ~10 weeks. Animals were placed on a water schedule in which supplemental water was provided after behavioral sessions, such that the total daily water intake was 5% of body weight.
Behavioral training
On the first 1–2 days of training, rats were habituated to handling and to being constrained by the harness in their home cages. On the following 1–2 days, they were placed without the harness on a non-floating treadmill and trained to drink water from the reward lick tube. After these habituation sessions (typically on day 3 or 4 of training), rats were subjected to the full experimental procedure that included the harness constraint, the floating of the treadmill using pressurized air, and the rendering of a virtual environment on the screen.
Initially, animals were trained in 10–30 min sessions (1 session/day) in a virtual environment consisting of an infinitely-long linear track (23 cm wide) with patterned cylinders placed periodically along the walls at 152 cm intervals. Whenever the rat reached a distance of <25 cm from one of the cylinders, that cylinder was removed, and a reward (25 μL of water) was delivered. The cylinder was reintroduced only when the next reward was received at another cylinder; thus two consecutive rewards could not be received at the same cylinder. Initially, VR was implemented with a gain of 3 along the direction of the linear track – i.e., walking 1 cm in that direction on the surface of the treadmill propelled the animal 3 cm along the virtual track. After rats learned to walk continuously and receive hundreds of rewards within a single session (typically after 3–4 days), task difficulty was increased gradually by reducing the gain by 0.5% after every reward. After another 2–3 days, the gain was set to 1.
Surgery to implant microdrive assemblies was performed after about 1 week of training on the linear track. After a recovery period of about 1 week, rats we re-trained on the linear track until they reached the approximate pre-surgery rate of rewards during performance. They were then introduced to a 2D virtual environment and trained to fully cover this environment during walking (see below). Over the following 1–3 months, rats were recorded either in a single square environment (one or two 60 min sessions/day), two different square environments (4 interleaved 30 min sessions/day), or a square and a circular environment (also 4 interleaved 30 min sessions/day). Square environments were either 1×1 or 2×2 m (for different rats) and contained different distal objects in the four corners, as well as different patterns and shapes on the walls. Circular environments were 1.4 or 2.8 m in diameter and consisted of a uniformly-patterned wall and three distal objects separated by roughly 120°. All patterns and object shapes were distinct in different environments.
To train animals to cover a large fraction of locations in 2D virtual environments, we implemented either a “target pursuit” task or a “random foraging” task. In the random foraging task, the environment was divided into zones whose boundaries were invisible to the animal, and one of the zones was chosen as the reward location. In the target pursuit task, a small cylinder (12.5 cm diameter, 7.5 cm height) indicated the location of a reward. The rat was required to reach a distance of 18–100 cm from the center of the cylinder (depending on the stage of training), at which point a 25 μL water reward was delivered, and the cylinder was moved to a new reward location. In some rats, a variable reward schedule was implemented, where the probability of reward was 40–80%. The probability was chosen based on performance on prior sessions and reduced if the rat obtained too many rewards in a brief period of time. In these animals, a sound (short beep) was played to indicate successive hitting of the target, regardless of whether a reward was subsequently delivered.
For the random foraging task, the zones in the square environments were arranged in an NxN grid, with each zone occupying 1/N2 of the environment. Circular environments were subdivided into equal-area zones according to the following scheme. For a total of 7 zones, zone 1 was a disk of radius 0.38R concentric with the environment, where R was the environment radius, zones 2 and 3 were 180° sectors of an annulus with radii 0.38R and 0.65R, and zones 4–7 were 90° sectors of an annulus with radii 0.65R and R. For a total of 15 zones, zone 1 was a disk of radius 0.26R, zones 2–3 were 180° sectors of a annulus with radii 0.26R and 0.45R, zones 4–7 were 90° sectors of an annulus with radii 0.45R and 0.68R, and zones 8–15 were 45° sectors of an annulus with radii 0.68R and R. Initially, square environments were divided into 9 zones and circular environments into 7 zones. During training the number of zones was increased to at most 25 and 15 zones for square and circular environments, respectively.
In the target pursuit task, the random reward location was drawn not from a uniform distribution, but from a 2D distribution where the distance r of the reward from the center was proportional to rp. The exponent p was <2 in order to bias locations toward the center of the environment or >2 in order to bias locations toward the walls. The exponent was chosen at the beginning of each session based on environment coverage in the previous session.
For recordings of head direction cells in some rats, a variant of the target pursuit task was implemented, in which the animal walked in a circular trajectory around the environment. Target positions were defined in polar coordinates, with the center of the environment designated as the origin. For each (n+1)th target, the angle in polar coordinates was offset from the angle of the nth target by a random value, typically between 60° and 90°. The radius of the (n+1)th target in polar coordinates was offset from the radius of the nth target by a random value, typically between −50 and +50 cm (not allowing values less than 0 or greater the environment radius). The targets were offset in a consistently clockwise or counterclockwise direction; the direction was switched every 10–20 min.
At the beginning of each session, the animal’s virtual position was in the center of either the square or the circular environment. The environment was oriented at a randomly-chosen angle relative to the real-world laboratory environment. During the session, the environment was rotated at 0.2°/s, thus making 1 full revolution every 30 min. Because sessions were either 30 or 60 min, the initial orientation of the environment was the same as the final orientation. Whenever a new environment was introduced, the animal was first trained for 5 days (typically 20 sessions). Only data obtained after the 5th day were used for analysis.
Electrophysiological recording system
Circuits for a custom 128-channel recording system (Figure S2A–B) compatible with the VR projection setup were custom-designed with the PADS software, printed (Sunstone Circuits), and assembled at the Princeton Physics Department electronics facility. The system contained small headstages (28×15×1.8 mm, 1.2 g), each of which filtered, amplified, and time-division multiplexed 32 input channels onto a single output wire using a miniature multiplexing amplifier array (Intan Technologies, RHA2132). The filtering was set to a band-pass of 5Hz-7.5kHz. A lightweight 9-wire cable (Omnetics) connected each headstage to an interface board attached to the commutator above the animal. We used a 1 MHz crystal oscillator on the interface board to provide a clock signal to each multiplexer; divided by 32 channels, this clock provided a sampling rate of 31.25 kHz for each channel. The interface board also provided further amplification and multiplexing of signals from up to 4 headstages.
Multiplexed signals were digitized by a National Instruments PCI-6133 data acquisition card and recorded with custom-written software in Matlab. Pulses from the 1 MHz oscillator were delayed by 820 ns and used as external clock signals to synchronize the data acquisition card with the multiplexer; the delay provided enough time for the multiplexer output to relax between channels. The software implemented real-time demultiplexing and appropriate filtering to display spike or LFP bands of all channels. Across the 128 channels, the measured input-referred noise of the system was 2.05–2.73 μV RMS (average 2.34 μV RMS, Figure S2C).
Tetrode recording devices
Tetrodes were constructed from twisted wires that were either PtIr (18 μm, California Fine Wire) or NiCr (25 μm, Sandvik). Tetrode tips were gold-plated to reduce impedances to 150–250 kΩ at 1 kHz.
Microdrive assembly devices contained either 8 or 16 independently-movable tetrodes. Each tetrode could be manually advanced using the screw/shuttle system adapted from (Kloosterman et al., 2009). Devices were custom-designed and manufactured using 3D stereolithography and were compatible with the Neuralynx EIB-36N or EIB-36N-16TT electrode interface boards. Devices with 8 tetrodes directed all tetrodes into a single brain area (hippocampus or MEC) using a single cannula, whereas those with 16 tetrodes directed 8 tetrodes into the hippocampus and 8 into MEC using two cannulas. In both cases, a single cannula consisted of 8 stainless steel tubes (0.014″ O.D.) soldered together; for the 16-tetrode device, the two cannulas were spaced 4.5 mm apart. For each recorded brain area, a reference electrode (0.004″ coated PtIr, 0.002″ uncoated 300 μm-long tip) was inserted next to the cannula to a fixed depth of about 1 mm dorsal to the targeted recording location.
Surgery
Animals were anesthetized with 1–2% isofluorane in oxygen and placed in a stereotaxic apparatus. The cranium was exposed and cleaned, small holes were drilled at 6–7 locations, and bone anchor screws (#0–80 x 3/32″) were screwed into each hole. A ground wire (5 mil silver) was inserted between the bone and the dura through another drilled hole. An antibiotic solution (baytril, 3.8 mg/ml in saline) was applied to the surface of the cranium. Craniotomies and duratomies were made either above the hippocampus or above the MEC, or both. A microdrive assembly (described below) was lowered to the surface of the brain and anchored to the bone screws with light-curing acrylic (Flow-It ALC flowable composite). Animals received injections of dexamethasone and buprenorphine after the surgery.
Recording procedures
For CA1 and CA3, the center of the electrode-guiding cannula was at 3.5 mm posterior to Bregma, 2.5 mm lateral to the midline. For MEC, the cannula was implanted at a 10° tilt with electrode tips pointed in the anterior direction (Hafting et al., 2005). The center of the cannula was 4.5 mm lateral to the midline, and the posterior edge of the cannula was ~0.1 mm anterior to the transverse sinus. On the day of the surgery, tetrodes were advanced to a depth of 1 mm. On the following days, hippocampal tetrodes were advanced in steps 60 μm/day and recorded while animals were resting or walking in their home cages. When sharp-wave ripples were observed, the tetrodes were retracted by 120 μm and not moved for at least 3 days, then advanced by 15 μm/day until the CA1 pyramidal cell layer was reached. Some of the tetrodes were advanced by ~1 mm past the CA1 location is steps of 15–125 μm/day until the CA3 pyramidal cell layer was reached. Entorhinal tetrodes were advanced in steps of 60 μm/day until theta-modulated units were observed; then tetrodes were either left in place or advanced by no more than 30 μm/day.
Histology
In some animals, small lesions to mark tetrode tip locations were made by passing anodal current (15 μA, 1 s) through one wire of each tetrode. Animals received an overdose of ketamine and xylazine and were perfused transcardially with saline followed by 4% formaldehyde. Brains were extracted, and sagittal sections (80 μm thick) were cut and stained with the NeuroTrace blue fluorescent Nissl stain. Locations of all tetrodes were identified by comparing relative locations of tracks in the brain with the locations of individual tetrode guide tubes within the cannula of the microdrive assembly.
Data analysis
Spike sorting
Electrode signals were filtered using a Parks-McClennan optimal equiripple FIR filter (passband above 1kHz, stopband below 750Hz, 344-point window), and the sum of the four signals from each tetrode was calculated. Thresholds of −3 and +3 standard deviations were computed for each tetrode during each recording session. Waveforms that exceeded at least one of these two thresholds were extracted and sorted using custom-written software in Matlab. Clustering was performed manually in two-dimensional projections of a four-dimensional space, whose dimensions were defined by the peak-to-peak amplitudes of the waveforms on the four wires of each tetrode. For remapping experiments, cluster boundaries were defined at roughly the same locations for data recorded in the two environments in order to identify units recorded across sessions.
For each identified cluster, spike duration was measured as the time from the trough of the average waveform to the following peak. Units that had thin spikes (<500 μs) and high average firing rates (>5Hz in the hippocampus, >10Hz in MEC) were identified as interneurons and were not used in any analyses. Units that fired less than 100 spikes were also excluded from all analyses, except the estimation of the fraction of active cells in CA1.
In the hippocampus, electrodes were generally kept at the same location for long periods of time and therefore often recorded the same units on multiple days. To detect these instances, we measured the dissimilarity of pairs of clusters, defined as the average of the Mahallanobis distances from points in the first cluster to the second cluster and points in the second cluster to the first cluster. For pairs of clusters recorded on different tetrodes, this pairwise distance almost always exceeded 20. However, for many pairs recorded on subsequent days on the same tetrode, the pairwise distance was less than 20. We therefore defined clusters whose pairwise distance was less than 20 as belonging to same unit.
Rate maps and reshuffling analysis
To calculate firing rate maps, only data with instantaneous running speeds exceeding 5 cm/s were used. Position values were sorted into a 40×40 grid of bins. The number of spikes and the total occupancy duration in each bin were calculated, and both the spikes and the occupancy duration were smoothed with a 7×7-point Hamming filter. The firing rate in each bin was calculated as the ratio of the number of smoothed number of spikes to the smoothed occupancy duration. Firing fields were defined as contiguous regions of the environment that occupied at least 32 bins and where the firing rate exceeded 20% of the maximum firing rate.
For each cell, we also calculated the spatial information rate in bits per spike (Skaggs et al., 1993) as
where λi is the mean firing rate in the ith spatial bin, λ is the overall mean firing rate, and pi is the fraction of time the animal spent in the ith bin.
For the analysis of various cell types described below, we generated 200 reshuffled samples for each cell, in which the spike times during a recording session were shifted forward in time by a random amount between 20 s and the duration of the recording session minus 20 s. Spikes with resulting times exceeding the end of the session were wrapped to the beginning of the session. The rate map and all statistics described below were then recomputed for each reshuffled sample.
Analysis of place cells
Place cells were defined as cells whose information rate exceeded 99% of the values for the reshuffled samples. To decode the animal’s location from the activity of hippocampal populations, we used a procedure adapted from (Wilson and McNaughton, 1993). In each spatial bin, the average population vector of firing rates was computed for all pyramidal cells recorded in a given session. Firing rates as a function of time were then measured using a 2 s rolling square window, and the instantaneous population vector was computed from the firing rates at each point in time. The decoded location was defined as the location of the bin whose average population vector had the smallest Euclidean distance to the instantaneous population vector. The decoding error was defined as the median distance between the decoded location and the animal’s actual location across the entire recording sessions.
Analysis of grid cells
To detect grid cells, we measured the gridness score (Langston et al., 2010) of each MEC unit, as follows. First, the unbiased autocorrelation of the cell’s rate map (Hafting et al., 2005) was calculated. For grid cells, the autocorrelation map contained a central peak surrounded by 6 peaks that were separated by about 60°. Autocorrelation as a function of distance from the center was computed, and the radius of the central peak was defined as the distance closest to the center at which autocorrelation was either negative or exhibited a local minimum. We then considered a set of annulus-shaped samples of the autocorrelation map, where the inner radius of each annulus was the radius of the central peak, and the outer radius was varied in steps of 1 bin from a minimum of 4 bins more than the radius of the central peak to 4 bins less than the width of the environment. The Pearson correlation of each annulus with its rotation was calculated for rotation angles of 60° and 120° (group 1) and then for 30°, 90°, and 150° (group 2). The difference between the minimum of the group-1 correlation values and the maximum of the group-2 correlation values was computed, and the gridness score was defined as the maximum difference across all annulus samples. Cells whose gridness score exceeded 95% of the reshuffled samples (see above) were defined as grid cells.
Analysis of border cells
To detect border cells, we measured the border score (Solstad et al., 2008) of each MEC unit, as follows. For each firing field, we defined a contact length as the maximal fraction of a wall in contact with that field. We also defined d as the average distance from the wall to all spatial bins covered by the field, weighted by the firing rate within each bin. The value of (c − d)/(c + d) was measured for each field, and the border score of the cell was defined as the maximum of these values across all fields. The value could hypothetically range from −1 (for fields not touching walls) to +1 (for fields that exclusively covered bins adjacent to a wall). Border cells were defined as cells that satisfied two criteria (Bjerknes et al., 2014): a border score exceeding 95% of the reshuffled values (see above) and a spatial information rate that also exceeded 95% of the reshuffled values.
Analysis of head direction cells
For head direction cells, we measured bearing angle as the direction of the treadmill rotation for times when the instantaneous speed exceeded 5 cm/s. Because the animal’s mouth was almost always in contact with the lick tube, the bearing angle was strongly correlated with the head direction and used as the head direction estimate. Data were sorted into 3° bins, and for each bin the number of spikes and the total amount of time spent heading in that direction (occupancy) were computed for each MEC cell. The number of spikes and the occupancy were smoothed with a 5-point (15°) square window, and the firing rate in each bin was calculated as the ratio of the smoothed spike count and the smoothed occupancy. Only cells whose smoothed occupancy in every bin exceeded 10 s were included in analysis.
We first computed a directional stability index (Sargolini et al., 2006; Giocomo et al., 2014), as follows. The entire recorded session was divided into 10 min intervals, and the firing rate as a function of head direction was computed for all odd-numbered intervals (0–10 min, 20–30 min, etc.) and for all even-numbered intervals (10–20 min, 30–40 min, etc.). Directional stability was defined as the correlation of the two tuning curves. Cells whose stability exceeded 99% of the reshuffled values (see above) were considered to be directionally stable.
For further analysis, we applied a second (“directional selectivity”) criterion to the directionally stable cells, as follows (Giocomo et al., 2014). Firing rate was normalized by the average firing rate across all head direction bins. For each bin, we then defined a vector whose length was the normalized firing rate in that bin, and whose direction was the midpoint of the bin. We then measured the vector average of the vectors from all bins and measured the length of this mean vector (mean vector length, MVL) and the preferred head direction as the angle of the mean vector. The value of MVL could hypothetically range from 0 (for cells with 180° symmetry of the head direction tuning curve) to 1 (for cells that fired in only one head direction bin). Head direction cells were defined as cells whose directional stability and MVL values both exceed 99% of the corresponding reshuffled values (see above).
Analysis of environment rotation experiments
For recording sessions in which the virtual environment was rotated relative to the real world, we defined two reference frames in polar coordinates: the real-world reference frame and the VR reference frame. In the real-world reference frame the 0° direction pointed orthogonally into the northern wall of the laboratory. In the VR reference frame, the 0° direction pointed orthogonally into a designated wall of the virtual environment. The origin (0,0) in both reference frames was defined to be the center of the environment, and radius r was therefore defined as the distance from the center. For analysis purposes, square environments were warped onto a circular disk by dividing the radius r by 1/cos((θVR − π/4)mod π/2 − π/4), which ranged from 1 at midpoints of walls to at corners of the environment. Note that this warping procedure tended to increase the number of cells that were classified as place cells.
We asked whether place cells and head direction cells aligned better to the real-world or to the VR reference frame. For place cell analysis, the animal’s position was measured in two sets of polar coordinates: (r,θVR) and (r,θR) where θVR is the angle in the VR reference frame and θR is the angle in the real-world reference frame. The spatial information rates HVR and HR were measured using these two sets of position data, and the difference ΔH = HVR − HR was measured between them. A cell was considered to prefer the VR reference frame if both HVR and ΔH were higher than 99% of the corresponding reshuffled values (see above). Conversely, it was considered to prefer the real-world reference frame if HR was higher than 99% of the reshuffled values and ΔH was lower than 99% of the reshuffled values.
For the analysis of head direction cells, we measured the mean vector lengths MVLVR and MVLR using the animal’s head direction defined either in the VR or the real-world reference frame, respectively. The difference ΔMVL = MVLVR − MVLR was computed between these values. A cell was considered to prefer the VR reference frame if it passed the significance criteria for directional selectivity in the VR reference frame, and ΔMVL was higher than 99% of the reshuffled values. Conversely, it was considered to prefer the real-world reference frame if it passed these significance criteria in the real-world reference frame, and ΔMVL was lower than 99% of the reshuffled values.
For experiments in which place cells were recorded during two consecutive sessions in the same virtual environment, we wanted to measure the angle by which the place cell map for the entire recorded population rotated between the two sessions. As described above, we first warped square rate maps onto a circular disk. We then rotated the rate maps from one of the sessions in 1° increments, and for each angle measured the Pearson correlation between the maps from the two sessions. For each place cell, we therefore obtained a curve of correlation as a function of rotation angle. The mean correlation was then calculated across all simultaneously recorded place cells, and the “place field rotation” angle was defined as the angle at which maximum correlation was observed. To calculate the error in this angle estimate, we performed a bootstrap analysis in which place cells were resampled 1000 times with replacement from the recorded population, and the place field rotation angle was recalculated for each resampled dataset. Only pairs of sessions where more than 2 place cells were recorded and for which the 95th percentile bootstrap confidence interval of the rotation angle was narrower than 90° were included in analysis.
Analysis of remapping
To quantify changes in firing rate across different environments (e.g. A and B), we analyzed cells recorded on three consecutive sessions (1, 2 and 3), where sessions 1 and 3 were from the same environment (e.g. A) and session 2 was from a different environment (e.g. B). The firing rate divergence (Lever et al., 2002) for a place cell i in these two environments was defined as
where and are the peak firing rates of cell during these three sessions. The divergence of environments A and B for the entire population of recorded place cells was defined as the median of all values of and across all cells i and j. To calculate the firing rate divergence value for a single environment (e.g. ), we used cases where the same cell was recorded on three consecutive sessions in the same environment. In these cases, values of divergence could be smaller than 1 if the firing rates on sessions closer in time (1 and 2) tended to be more similar than the rate on sessions farther apart in time (1 and 3).
To quantify changes in spatial patterns of activity across different environments, we calculated a spatial cross correlation index on all pairs of sessions with at least 5 recorded place cells. Rate maps from the square environment were warped onto a circular disk using the procedure described above. Rate maps of all cells in one environment were then rotated in 1° increments, and at each angle the Pearson cross correlation between maps from different environments was computed. At each angle, we calculated the average cross correlation across all simultaneously recorded place cells. The spatial correlation index for the pair of sessions was then defined as the maximum average correlation across all rotation angles.
Supplementary Material
HIGHLIGHTS.
Virtual reality (VR) system for unconstrained 2D navigation in rats
Flexible control software and integration with large-scale electrophysiology
2D activity of place cells, grid cells, head direction cells and border cells in VR
Conventional and novel forms of hippocampal remapping in VR
Acknowledgments
We thank members of the Tank and Brody labs, as well as G. Buzsaki and M. Long for comments, R. Harrison, S. Chidzik and B. Harrop for help with electronic circuit design and fabrication, and S. Lowe for assistance with machining. This work was supported by NIH grants 5R01MH083686, 5R37NS081242 and 5RC1NS068148, and a postdoctoral fellowship from the Helen Hay Whitney Foundation (DA).
References
- Aflalo TN, Graziano MS. Four-dimensional spatial reasoning in humans. Journal of experimental psychology Human perception and performance. 2008;34:1066–1077. doi: 10.1037/0096-1523.34.5.1066. [DOI] [PubMed] [Google Scholar]
- Ahrens MB, Huang KH, Narayan S, Mensh BD, Engert F. Two-photon calcium imaging during fictive navigation in virtual environments. Frontiers in neural circuits. 2013;7:104. doi: 10.3389/fncir.2013.00104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson MI, Jeffery KJ. Heterogeneous modulation of place cell firing by changes in context. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2003;23:8827–8835. doi: 10.1523/JNEUROSCI.23-26-08827.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barry C, Hayman R, Burgess N, Jeffery KJ. Experience-dependent rescaling of entorhinal grids. Nature neuroscience. 2007;10:682–684. doi: 10.1038/nn1905. [DOI] [PubMed] [Google Scholar]
- Barry C, Lever C, Hayman R, Hartley T, Burton S, O’Keefe J, Jeffery K, Burgess N. The boundary vector cell model of place cell firing and spatial memory. Reviews in the neurosciences. 2006;17:71–97. doi: 10.1515/revneuro.2006.17.1-2.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birch D, Jacobs GH. Spatial contrast sensitivity in albino and pigmented rats. Vision research. 1979;19:933–937. doi: 10.1016/0042-6989(79)90029-4. [DOI] [PubMed] [Google Scholar]
- Bjerknes TL, Moser EI, Moser MB. Representation of geometric borders in the developing rat. Neuron. 2014;82:71–78. doi: 10.1016/j.neuron.2014.02.014. [DOI] [PubMed] [Google Scholar]
- Brun VH, Solstad T, Kjelstrup KB, Fyhn M, Witter MP, Moser EI, Moser MB. Progressive increase in grid scale from dorsal to ventral medial entorhinal cortex. Hippocampus. 2008;18:1200–1212. doi: 10.1002/hipo.20504. [DOI] [PubMed] [Google Scholar]
- Chen G, King JA, Burgess N, O’Keefe J. How vision and movement combine in the hippocampal place code. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:378–383. doi: 10.1073/pnas.1215834110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark BJ, Taube JS. Vestibular and attractor network basis of the head direction cell signal in subcortical circuits. Frontiers in neural circuits. 2012;6:7. doi: 10.3389/fncir.2012.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colgin LL, Moser EI, Moser MB. Understanding memory through hippocampal remapping. Trends in neurosciences. 2008;31:469–477. doi: 10.1016/j.tins.2008.06.008. [DOI] [PubMed] [Google Scholar]
- Cushman JD, Aharoni DB, Willers B, Ravassard P, Kees A, Vuong C, Popeney B, Arisaka K, Mehta MR. Multisensory control of multimodal behavior: do the legs know what the tongue is doing? PloS one. 2013;8:e80465. doi: 10.1371/journal.pone.0080465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czurko A, Hirase H, Csicsvari J, Buzsaki G. Sustained activation of hippocampal pyramidal cells by ‘space clamping’ in a running wheel. The European journal of neuroscience. 1999;11:344–352. doi: 10.1046/j.1460-9568.1999.00446.x. [DOI] [PubMed] [Google Scholar]
- Deshmukh SS, Knierim JJ. Representation of non-spatial and spatial information in the lateral entorhinal cortex. Frontiers in behavioral neuroscience. 2011;5:69. doi: 10.3389/fnbeh.2011.00069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dombeck DA, Harvey CD, Tian L, Looger LL, Tank DW. Functional imaging of hippocampal place cells at cellular resolution during virtual navigation. Nature neuroscience. 2010;13:1433–1440. doi: 10.1038/nn.2648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domnisoru C, Kinkhabwala AA, Tank DW. Membrane potential dynamics of grid cells. Nature. 2013;495:199–204. doi: 10.1038/nature11973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ekstrom AD, Kahana MJ, Caplan JB, Fields TA, Isham EA, Newman EL, Fried I. Cellular networks underlying human spatial navigation. Nature. 2003;425:184–188. doi: 10.1038/nature01964. [DOI] [PubMed] [Google Scholar]
- Fenton AA, Kao HY, Neymotin SA, Olypher A, Vayntrub Y, Lytton WW, Ludvig N. Unmasking the CA1 ensemble place code by exposures to small and large environments: more place cells and multiple, irregularly arranged, and expanded place fields in the larger space. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2008;28:11250–11262. doi: 10.1523/JNEUROSCI.2862-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry SN, Rohrseitz N, Straw AD, Dickinson MH. TrackFly: virtual reality for a behavioral system analysis in free-flying fruit flies. Journal of neuroscience methods. 2008;171:110–117. doi: 10.1016/j.jneumeth.2008.02.016. [DOI] [PubMed] [Google Scholar]
- Giocomo LM, Zilli EA, Fransen E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giocomo LM, Stensola T, Bonnevie T, Van Cauter T, Moser MB, Moser EI. Topography of head direction cells in medial entorhinal cortex. Current biology : CB. 2014;24:252–262. doi: 10.1016/j.cub.2013.12.002. [DOI] [PubMed] [Google Scholar]
- Gothard KM, Skaggs WE, Moore KM, McNaughton BL. Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1996;16:823–835. doi: 10.1523/JNEUROSCI.16-02-00823.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hafting T, Fyhn M, Molden S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- Harvey CD, Coen P, Tank DW. Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature. 2012;484:62–68. doi: 10.1038/nature10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, Tank DW. Intracellular dynamics of hippocampal place cells during virtual navigation. Nature. 2009;461:941–946. doi: 10.1038/nature08499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henriksen EJ, Colgin LL, Barnes CA, Witter MP, Moser MB, Moser EI. Spatial representation along the proximodistal axis of CA1. Neuron. 2010;68:127–137. doi: 10.1016/j.neuron.2010.08.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holscher C, Schnee A, Dahmen H, Setia L, Mallot HA. Rats are able to navigate in virtual environments. The Journal of experimental biology. 2005;208:561–569. doi: 10.1242/jeb.01371. [DOI] [PubMed] [Google Scholar]
- Jezek K, Henriksen EJ, Treves A, Moser EI, Moser MB. Theta-paced flickering between place-cell maps in the hippocampus. Nature. 2011;478:246–249. doi: 10.1038/nature10439. [DOI] [PubMed] [Google Scholar]
- Kelemen E, Fenton AA. Dynamic grouping of hippocampal neural activity during cognitive control of two spatial frames. PLoS biology. 2010;8:e1000403. doi: 10.1371/journal.pbio.1000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloosterman F, Davidson TJ, Gomperts SN, Layton SP, Hale G, Nguyen DP, Wilson MA. Micro-drive array for chronic in vivo recording: drive fabrication. Journal of visualized experiments : JoVE. 2009 doi: 10.3791/1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knierim JJ, Kudrimoti HS, McNaughton BL. Place cells, head direction cells, and the learning of landmark stability. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1995;15:1648–1659. doi: 10.1523/JNEUROSCI.15-03-01648.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knierim JJ, McNaughton BL, Poe GR. Three-dimensional spatial selectivity of hippocampal neurons during space flight. Nature neuroscience. 2000;3:209–210. doi: 10.1038/72910. [DOI] [PubMed] [Google Scholar]
- Langston RF, Ainge JA, Couey JJ, Canto CB, Bjerknes TL, Witter MP, Moser EI, Moser MB. Development of the spatial representation system in the rat. Science. 2010;328:1576–1580. doi: 10.1126/science.1188210. [DOI] [PubMed] [Google Scholar]
- Leutgeb JK, Leutgeb S, Treves A, Meyer R, Barnes CA, McNaughton BL, Moser MB, Moser EI. Progressive transformation of hippocampal neuronal representations in “morphed” environments. Neuron. 2005;48:345–358. doi: 10.1016/j.neuron.2005.09.007. [DOI] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Treves A, Moser MB, Moser EI. Distinct ensemble codes in hippocampal areas CA3 and CA1. Science. 2004;305:1295–1298. doi: 10.1126/science.1100265. [DOI] [PubMed] [Google Scholar]
- Lever C, Wills T, Cacucci F, Burgess N, O’Keefe J. Long-term plasticity in hippocampal place-cell representation of environmental geometry. Nature. 2002;416:90–94. doi: 10.1038/416090a. [DOI] [PubMed] [Google Scholar]
- Lu X, Bilkey DK. The velocity-related firing property of hippocampal place cells is dependent on self-movement. Hippocampus. 2010;20:573–583. doi: 10.1002/hipo.20666. [DOI] [PubMed] [Google Scholar]
- McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the ‘cognitive map’. Nature reviews Neuroscience. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
- Morris R. Developments of a water-maze procedure for studying spatial learning in the rat. Journal of neuroscience methods. 1984;11:47–60. doi: 10.1016/0165-0270(84)90007-4. [DOI] [PubMed] [Google Scholar]
- Muller RU, Kubie JL. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1987;7:1951–1968. doi: 10.1523/JNEUROSCI.07-07-01951.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J, Dostrovsky J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain research. 1971;34:171–175. doi: 10.1016/0006-8993(71)90358-1. [DOI] [PubMed] [Google Scholar]
- Pfeiffer BE, Foster DJ. Hippocampal place-cell sequences depict future paths to remembered goals. Nature. 2013;497:74–79. doi: 10.1038/nature12112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ravassard P, Kees A, Willers B, Ho D, Aharoni D, Cushman J, Aghajan ZM, Mehta MR. Multisensory control of hippocampal spatiotemporal selectivity. Science. 2013;340:1342–1346. doi: 10.1126/science.1232655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell NA, Horii A, Smith PF, Darlington CL, Bilkey DK. Lesions of the vestibular system disrupt hippocampal theta rhythm in the rat. Journal of neurophysiology. 2006;96:4–14. doi: 10.1152/jn.00953.2005. [DOI] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Schmidt-Hieber C, Hausser M. Cellular mechanisms of spatial navigation in the medial entorhinal cortex. Nature neuroscience. 2013;16:325–331. doi: 10.1038/nn.3340. [DOI] [PubMed] [Google Scholar]
- Shapiro ML, Tanila H, Eichenbaum H. Cues that hippocampal place cells encode: dynamic and hierarchical representation of local and distal stimuli. Hippocampus. 1997;7:624–642. doi: 10.1002/(SICI)1098-1063(1997)7:6<624::AID-HIPO5>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, Gothard KM, Markus EJ. An information theoretic approach to deciphering the hippocampal code. In: Hanson SJ, Cowan JD, Giles CL, editors. Advances in neural information processing. San Mateo, CA: Morgan Kaufmann; 1993. pp. 1030–1037. [Google Scholar]
- Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Froland K, Moser MB, Moser EI. The entorhinal grid map is discretized. Nature. 2012;492:72–78. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- Taube JS, Muller RU, Ranck JB., Jr Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1990;10:420–435. doi: 10.1523/JNEUROSCI.10-02-00420.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wills TJ, Lever C, Cacucci F, Burgess N, O’Keefe J. Attractor dynamics in the hippocampal representation of the local environment. Science. 2005;308:873–876. doi: 10.1126/science.1108905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. Dynamics of the hippocampal ensemble code for space. Science. 1993;261:1055–1058. doi: 10.1126/science.8351520. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.