Contributions of Dynamic Systems Theory to Cognitive Development

Abstract

This paper examines the contributions of dynamic systems theory to the field of cognitive development, focusing on modeling using dynamic neural fields. A brief overview highlights the contributions of dynamic systems theory and the central concepts of dynamic field theory (DFT). We then probe empirical predictions and findings generated by DFT around two examples—the DFT of infant perseverative reaching that explains the Piagetian A-not-B error, and the DFT of spatial memory that explain changes in spatial cognition in early development. A systematic review of the literature around these examples reveals that computational modeling is having an impact on empirical research in cognitive development; however, this impact does not extend to neural and clinical research. Moreover, there is a tendency for researchers to interpret models narrowly, anchoring them to specific tasks. We conclude on an optimistic note, encouraging both theoreticians and experimentalists to work toward a more theory-driven future.

Mathematical modeling of human behavior has a long history in Psychology dating back to the early 19^th century (see, e.g., Fechner, 1860; Weber, 1842-1853). The history of formal modeling in developmental science is, by contrast, much shorter. Thus, this special issue offers a welcome opportunity to evaluate the contributions of computational modeling to developmental science in its infancy, when prospects for the future are just beginning to come into focus.

Our paper emphasizes a particular type of computational modeling using dynamic neural fields (DNFs) that has emerged from the broader framework of Dynamic Systems Theory (DST). We begin with a brief overview of DST, highlighting the contributions of this theoretical framework to the field of cognitive development. We then focus on Dynamic Field Theory (DFT) for the remainder of the paper. The goal is to highlight how DFT has been useful in understanding cognitive development and generating new empirical predictions and findings. We emphasize two primary examples—the DFT of infant perseverative reaching (e.g., Thelen et al., 2001) proposed to explain the classic Piagetian A-not-B error, and the DFT of spatial memory used to explain changes in spatial cognition in early development (e.g., Spencer et al, 2007). These examples are ideal in the context of the special issue, because in each case there are alternative formal theories. This allows us to discuss the impact of DFT in particular as well as the impact of formal modeling more generally. We evaluate impact using a systemic analysis of the literature in each domain. These analyses reveal that computational modeling is making in-roads into mainstream cognitive development; however, there is much to be done to fully integrate formal approaches into mainstream cognitive development. This will require effort from both theoreticians and experimentalists. We conclude by trying to convince both groups that the effort is worth it.

1. Dynamic Systems Theory: Overview and Contributions

Dynamic systems theory (DST) emerged within developmental science within the last 20 years. This theory is based on advances in physics, mathematics, biology, and chemistry that have changed our understanding of non-linear, complex systems (see Prigogine & Stengers, 1984 for review). The developmental concepts that underlie DST are based on pioneering work by Thelen and Smith (1994) as well as early work from other theoreticians such as Fischer (e.g., Fischer & Rose, 1996), van Geert (e.g., 1997; 1998), and Molenaar (e.g., van der Maas & Molenaar, 1992; Molenaar & Newell, 2010). In this section, we briefly highlight several contributions of DST. This foreshadows our more in-depth discussion of dynamic field theory. For a more detailed treatment of the contributions of DST to development, see the 2011 special issue of Child Development Perspectives.

DST has made major contributions to developmental science by formalizing multiple concepts central to a developmental systems perspective (for discussion of developmental systems theory, see Lerner, 2006). The first concept is that systems are self-organizing. Complex systems like a developing child consist of many interacting elements that span multiple levels from the genetic to the neural to the behavioral to the social. Interactions among elements within and across levels are nonlinear and time-dependent. Critically, such interactions have an intrinsic tendency to create pattern (e.g., Prigogine & Nicolis, 1971). Thus, there is no need to build pattern into the system ahead of time—developing systems are inherently creative, organizing themselves around special habitual states called “attractors”.

The notion that human behavior is organized around habits dates back at least to William James (1897). But DST helps formalize the more specific notion of an attractor, providing tools to characterize these special states (see van der Maas & Molenaar, 1992; van der Maas, 1993 for discussion). For instance, one typical way to characterize a habit is to simply measure how often the habitual state is visited. Importantly, DST has encouraged researchers to also measure how variable performance is around that state, and whether the system stays in that state when actively perturbed. This is particularly revealing over learning and development because habits often become more stable—more resistant to perturbations—over time.

Within this context, DST also helps clarify the relationship between two related concepts central to developmental science—qualitative and quantitative change (see Spencer & Perone, 2008; van Geert, 1998). According to DST, qualitative change occurs when there is a change in the number or type of attractors, for instance, going from one attractor state in a system to two. Critically, such special changes—called bifurcations—can arise from gradual, quantitative changes in one aspect of the system. A simple example is the shift from walking to running. As speed quantitatively increases across this transition in behavior, there is a sudden and major reorganization of gait that has a qualitatively new arrangement of elements (Diedrich & Warren, 1995).

Gait changes are one of the classic examples first studied by researchers interested in applying the concepts of DST to human behavior. This early work led naturally to the use of dynamic systems concepts to explain transitions in motor skill both in real time and over learning and development (e.g., Adolph & Avolio, 2000; Fogel & Thelen, 1987; Thelen, 1995; Thelen, Corbetta & Spencer, 1996; Whitall & Getchell, 1995). One conclusion from these studies is that the brain is not the “controller” of behavior. Rather, it is necessary to understand how the brain capitalizes on the dynamics of the body and how the body informs the brain in the construction of behavior (Thelen & Smith, 1994). This has led to an emphasis on embodied cognitive dynamics (see Schöner, 2009; Spencer, Perone, & Johnson, 2009), that is, to a view of cognition in which brain and body are in continual dialogue from second to second. We will return to this theme below in our discussion of dynamic field theory which offers a formal mathematical treatment of embodied cognition.

Another DST concept that has been particularly salient in developmental science is the notion of “soft assembly.” According to this concept, behavior is always assembled from multiple interacting components that can be freely combined from moment to moment on the basis of the context, task, and developmental history of the organism. Esther Thelen talked about this as a form of improvisation in which components freely interact and assemble themselves in new, inventive ways like musicians playing jazz. This gives behavior an intrinsic sense of exploration and flexibility (see Spencer et al., 2006).

A final contribution of DST are the host of formal modeling tools that can capture and quantify the emergence and construction of behavior over development (such as growth models, oscillator models, dynamic neural field models), and statistical tools that can describe the patterns of behavior observed over development (Lewis, Lamey, & Douglas, 1999; Molenaar, Boomsma, & Dolan, 1993; van der Maas et al., 2006; Molenaar & Newell, 2010). These tools have enabled researchers to move beyond the characterization of what changes over development toward a deeper understanding of how these changes occur.

2.1 Dynamic Field Theory: Cognition and Real-time Neural Dynamics

DST is very good at explaining the details of action, for instance, how infants transition from crawling to walking. Consequently, DST has had a major impact in motor development. DST also provides a good fit with aspects of perception. For instance, there are elegant dynamic systems models of how the visual array changes as animals move through the environment that explain, for instance, when a gannet will pull in its wings when diving for a fish (Schöner, 1994).

But what about cognition—can DST explain something as complex as working memory, executive function, and language? This was a central challenge to the theory in the 1990s, following innovative studies applying DST to motor development. Several initial models in this direction captured cognition at a relatively abstract level of analysis. For instance, van der Maas and Molenaar (1992) proposed a model that captured transitions in children's conservation behavior using a specific variant of DST called catastrophe theory. The model provided a quantitative analysis of stage-like transitions in thinking defined over abstract dimensions of cognitive level, perceptual salience, and cognitive capacity. Similarly, van Geert (1998) proposed a dynamic systems model defined over the abstract dimension “developmental level” to reinterpret several classical concepts from Piaget's theory and Vygotsky's theory. Both approaches showed the promise of DST for offering new insights into classic questions—such as the nature of quantitative versus qualitative developmental change (see Spencer & Perone, 2008)—and also highlighted the potential for integrating quantitative models and rich behavioral data sets.

A second group of dynamic systems models also moved into the foreground in cognitive development during the 1990s—connectionist models of development (see Spencer, Thomas, McClelland, 2009 for a discussion of the link between DST and connectionism). These models attempted to explain cognition at a less abstract level and interface with known properties of the brain. Connectionist models have made substantive contributions to the field of cognitive development, a topic which is discussed in other contributions to this special issue. Thus, we will not discuss connectionism in detail.

A third dynamic systems approach to cognition also emerged in the late 1990s—Dynamic Field Theory (DFT). DFT represented an explicit effort to create an embodied approach to cognition that would build from and connect to the dynamic systems concepts emerging in the fields of perceptual and motor development. Thus, DFT retains transparent ties to central dynamic systems concepts such as attractor states, bifurcations, and soft assembly. But it also offers a mechanistic-level understanding of how brains work with a well-specified perspective on how the brain and body work together to enable cognition and action in the world (e.g., Sandamirskaya & Schöner, 2010; Lipinski, Sandamirskaya, & Schöner, 2009; Engels & Schöner, 1995).

Figure 1 shows an overview of the neural concepts that underlie the basic computational unit in DFT—a dynamic neural field (DNF). Figure 1A shows an arrangement of excitatory neurons on a cortical surface in, for instance, parietal cortex. Each excitatory neuron has a receptive field that is, in this case, tuned to spatial information such as the direction of a stimulus relative to the head. As an example, the third neuron on the cortical sheet will fire maximally when a leftward stimulus is presented—this is the neuron's “preferred” direction indicated by the vector. The neuron will also fire when a less preferred stimulus direction is presented (e.g., slightly down and leftward), but it will fire at baseline levels when a rightward stimulus direction is presented. These tuning properties are captured by the tuning curve shown for neuron 3. The curve shows the average activation level interpolated across 360° of stimulus space (e.g., Georgopoulos et al, 1989). Figure 1A also shows “lateral” excitatory connections among the excitatory neurons in the cortical sheet (see green lines). For instance, neuron 3 excites neuron 5. This makes sense because both neurons prefer leftward stimulus directions.

Figure 1.

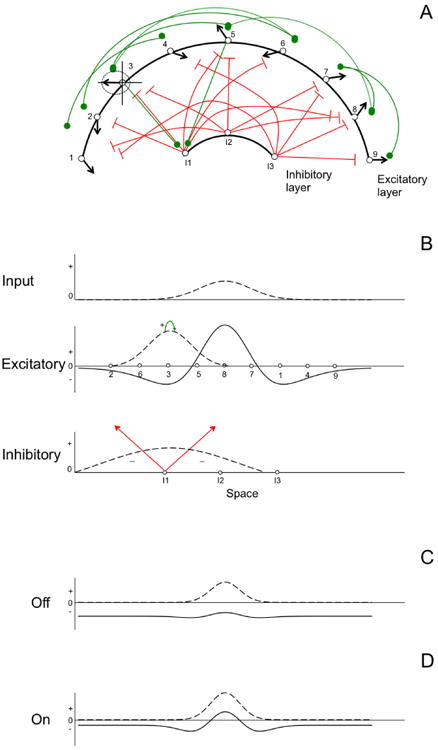
Overview of concepts underlying dynamic neural fields (DNFs). (A) A layer of excitatory neurons coupled to a layer of inhibitory interneurons. Each excitatory neuron is tuned to a particular spatial direction, indicated by black arrows showing its preferred stimulus direction. Green connections are excitatory; red connections are inhibitory. (B) The system of cortical connections in (A) rearranged as a layered DNF architecture. Neurons are rearranged according to functional topography, such that neurons' preferred direction runs systematically left to right. The dashed line in the top panel of 1B shows input given to the model that forms a “peak” of activation in the excitatory layer. Dashed line in the excitatory layer shows the tuning curve of activation for neurons surrounding neuron 3. Dashed line in the bottom panel shows the broad projection of inhibition back into the excitatory layer. (C) The “off” state of the field with weak input. (D) The “on” state of the field. Here, slightly stronger input engages neural interactions forming a peak.

The second layer in Figure 1A shows a collection of inhibitory interneurons. These neurons are stimulated by neurons in the excitatory layer and inhibit other neurons in that layer. For instance, inhibitory neuron 1 is stimulated by neurons 3 and 5 in the excitatory layer (see excitatory synaptic connections in Figure 1A; for simplicity, we omitted all remaining connections from the excitatory to the inhibitory layer). When inhibitory neuron 1 becomes active, it inhibits the firing of neurons 2, 6, 3, 5, and 8 in the excitatory layer. This keeps excitation from spreading uncontrollably in the excitatory layer. This is needed because stimulation of neuron 3 excites neuron 5, which excites neuron 8, which excites neuron 7, and so on.

Figure 1B takes this cortical picture and reorganizes it to form a DNF. Rather than showing the neurons organized as they are on the cortical surface (Figure 1A), Figure 1B shows them organized by their functional connection properties (called a functional topographic map). Thus, neurons in the excitatory layer have preferred directions that run systematically from left to right. The interneurons are organized similarly. Next, each neuron's tuning curve is standardized to create the pattern of local excitation shown around neuron 3 (see dashed curve). This Gaussian distribution shows the strength of excitation passed between neuron 3 and its neighbors (e.g., neuron 5) once neuron 3 exceeds its firing threshold (i.e., its activation goes above 0). This occurs when, for instance, a leftward stimulus direction is presented. Neuron 3 also stimulates the first interneuron (see green arrow). Activation of inhibitory neuron 1 causes inhibition to be broadly spread to the excitatory layer (see red arrows) based on the tuning properties of this interneuron (see dashed curve).

What is the result of these volleys of locally excitatory and broadly inhibitory neural interactions? The result is a “bump” (e.g., Edin et al, 2007; Wang, 2001) or “peak” of activation—the basic unit of cognition in DFT. The top panel of Figure 1B shows the input pattern (dotted line) generated when a stimulus is presented directly in front of the simulated neural system. This input stimulates neuron 5 a little, neuron 8 a lot, and neuron 7 a little. These neurons, in turn, excite one another and pass activation to the inhibitory layer. The inhibitory layer passes inhibition back. As these interactions play out over time, a peak forms (solid line in excitatory layer) that actively “represents” the stimulus direction at the level of the neural population. That is, the population of neurons “knows” at some moment in time that the stimulus is directly ahead.

Note that although this is an abstraction away from real neurons in the brain, all the steps discussed above can be reconstructed with real neural data. For instance, Bastian and colleagues (2003) used multi-unit recordings in motor cortex to construct a dynamic neural field from neurophysiological data. Results were then used to quantitatively test predictions of a DFT of motor preparation (Erlhagen & Schöner, 2002). Thus, when asked whether we think the brain actually works like a dynamic neural field model, the answer is ‘yes’—at least at the level of neural populations.

Figure 1 follows from a population dynamics approach to neuroscience (see Amari, 1977; Amari & Arbib, 1977; Wilson & Cowan, 1972); it also carries forward some of the key concepts of DST discussed earlier. For instance, in the lower panels of Figure 1, we show the state of the excitatory layer following two inputs that differed very slightly in strength. In Figure 1C, the input was sufficiently weak such that strong local excitatory interactions were never engaged. We call this the “off” state because the activation pattern will relax back to the neuronal resting state given sufficient time. Figure 1D shows what happens when the input is increased slightly—now a robust peak turns “on” and remains stable as long as the input remains present. Figures 1C and 1D are qualitatively different—they are formally different attractor states—yet they arise from a small quantitative difference in the strength of neural input. This is one example of how DFT sheds light on the quantitative versus qualitative distinction in development: small differences in the situation—a slightly more salient input—can lead to a non-linear or qualitative shift in responding—actively encoding the stimulus versus missing it altogether.

Interestingly, we can take this example one step further by noting that there are multiple types of “on” states (i.e., different attractor states) within DFT. For instance, Figure 2 shows two qualitatively different types of peak states that have played a central role in the examples we discuss below. The first example was generated by the same model shown in Figure 1. The only difference here is that we show the model in action through time. In Figure 2A, an input is presented 100 ms into the simulation. This builds a robust peak of activation in the excitatory layer. Critically, the peak becomes unstable once the input is removed and the field returns to its resting state (see red line in Figure 2B). We refer to this state as the self-stabilized state—the peak is only maintained when stabilized by an input; it mimics the properties of “encoding”.

Figure 2.

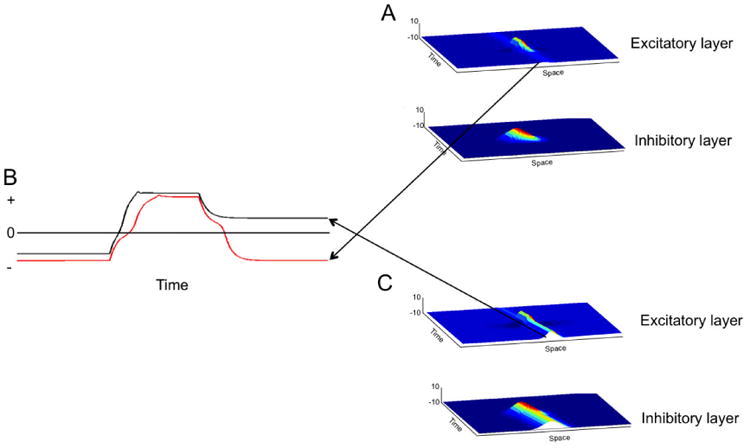
Two qualitatively different states of dynamic neural fields: self-stabilized (A) and self-sustained (C) representations. The red line in (B) shows how activation at the center field site in (A) returns to baseline after the removal of the stimulus. The black line in (B) shows how activation at the center field site in (C) is sustained throughout the simulation.

Figure 2C shows a similar run of the model. Now, however, we have boosted the strength of locally excitatory interactions. As can be seen in the figure, this small change in excitation leads to a big difference in performance—the peak is maintained throughout the simulation, even though the input was removed as in Figure 2A (see black line in Figure 2B). We refer to this state as the self-sustaining state—the peak sustains itself in the absence of input; this mimics the properties of “working” or “active” memory. In the next section, we discuss where the boost in local excitation might come from.

Before concluding this section, let us return to a key issue raised previously—in what sense is DFT “embodied?” That is, how can dynamic neural fields be integrated with perceptual and motor systems? Schöner and colleagues (e.g., Sandamirskaya & Schöner, 2010) have done extensive work on this topic and have developed a formal approach to embodiment that specifies the link between DNFs and motor control. For instance, Bicho and Schöner (1997; 1998) have shown how DNFs can interface continuously with a motor system to enable an autonomous robot to navigate in real-world contexts. Although a formal treatment of this work is beyond the scope of this paper (for a review, see Schöner, 2009), it highlights that DFT offers a rigorous approach to cognitive dynamics that is grounded in neurophysiology on one hand and more classic approaches to motor control and development on the other.

2.2 Dynamic Field Theory: Learning and Development

Before moving to some examples, we need to go one step farther in our survey of DFT and ask how this theory addresses learning and development. Figure 3A shows a variant of the DNF model from Figure 1 with one layer added. We call this a Hebbian layer (HL) because it implements a form of Hebbian learning. As is shown in the figure, neurons in the excitatory layer are connected one-to-one with neurons in the HL. Consequently, when there is robust activation in the excitatory layer (i.e., neuron 8 > 0), activation begins to build at the associated site in the HL. This, in turn, projects activation back onto the excitatory layer (see green arrows from HL to the excitatory layer). Critically, activation in HL grows quite slowly, that is, over a learning timescale rather than over the timescale of, say, encoding or working memory maintenance. Moreover, when activation grows at some sites in HL, it decays at all other un-stimulated sites. Thus, this form of Hebbian learning is competitive. Note that sites in the HL operate more like synapses than neurons, that is, they grow or shrink in activation continuously over a slow timescale rather than actively firing in real-time. In this sense, the HL is like a weight matrix in a connectionist network (for discussion, see Faubel & Schöner, 2008; Spencer, Dineva & Schöner, 2009).

Figure 3.

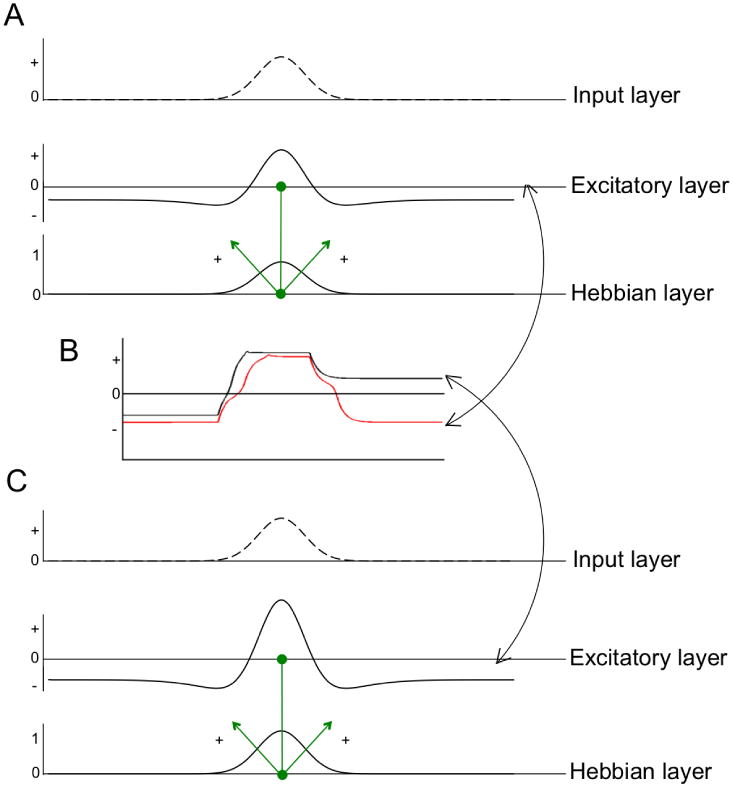
Variation of the three-layer DNF architecture showing input to the model, a layer of excitatory neurons, and a Hebbian layer. Neurons in the excitatory layer are connected one-to-one to neurons in the Hebbian layer (see green connections); these sites project activation back to the excitatory layer. When the excitatory layer is given a relatively weak input, activation from the Hebbian layer can help create a self-stabilized peak (see A and red line in B). With slightly more Hebbian activation, the weak input can create a self-sustaining peak in the excitatory layer (see C and black line in B).

What is the effect of activation in the HL? As in a connectionist network, stronger weights lead to stronger excitatory interactions among a local group of connected neurons. For instance, the pattern shown in Figure 3A enhances processing of the input, leading to a robust peak. Indeed, in this example, we used the weak input from Figure 1C. Recall that this weaker input failed to build a robust peak and the DNF stayed in the “off” state. Now, after a bit of learning, the DNF model can build a robust peak even when the input is less salient (see red line in Figure 3B).

Interestingly, Figure 3C takes this learning one step further. Recall that the DNF model from Figure 1 operated in the self-stabilized or “encoding” state. Consequently, when the input was removed, the peak returned to the resting level. After some learning, however, this same DNF model enters the self-sustaining state: with the extra excitation provided by a strong memory trace in the HL, the field is able to form a working memory for the stimulus and maintain this memory after the stimulus is removed (see black line in Figure 3B). Thus, learning can qualitatively alter the type of peak present in a neural field (see Spencer & Perone, 2008 for discussion).

To date, we have focused most of our efforts on learning understanding the properties of the DNF model shown in Figure 3 (e.g., Lipinski, Spencer, & Samuelson, 2010; Lipinski, Simmering, Johnson, & Spencer, 2010). But what about development—can DFT capture patterns of change that happen over weeks, months, and years? There are two avenues we have explored on this front. The first avenue involves developing the feed-forward mapping from the input layer into the neural field. This type of slow learning—akin to perceptual learning—has been important in several projects where we have modeled infants' and young children's performance in quantitative detail (Schutte & Spencer, 2009; Perone & Spencer, in press). In these cases, we have implemented this form of developmental change by changing the precision (i.e., the width) and strength of the input pattern.

A second avenue for slow change over development involves changing the connection pattern within and across layers. For instance, in several papers, we have implemented a particular developmental hypothesis called the spatial precision hypothesis (SPH). This posits that locally excitatory and laterally inhibitory interactions become stronger over development. For instance, in several projects, we have captured developmental change by increasing the strength of neural interactions in excitatory and inhibitory layers (Schutte & Spencer, 2009; Perone & Spencer, in press). This has effectively captured both quantitative and qualitative changes over development as we discuss in greater detail below.

3.1 Applications of Dynamic Field Theory: The Piagetian A-not-B Error

One goal of the special issue is to communicate the central concepts behind formal models. We did this above by highlighting the link between, for instance, the psychological construct of “encoding” and self-stabilized peaks. Here we carry this idea forward in the context of a specific example—the Piagetian A-not-B error. We also pursue a second goal—highlighting how DFT has been useful in understanding cognitive development and generating new empirical predictions and findings.

In his book, The Construction of Reality in the Child (1954), Piaget described a hiding and finding game he played with his infant children that has become a signature task in the study of infant cognition: the A-not-B task. In this task, the experimenter hides a toy repeatedly at a non-descript “A” location. After some initial training, an 8- to 10-month-old infant will reliably retrieve the toy from A when presented with two possible hiding locations following a brief delay (e.g., 3 seconds). After several successful hiding and finding events at A, the experimenter hides the toy at a nearby “B” location. Young infants (e.g., 8 months) will reach back to A after a short delay—they reach to A and not B. Older infants (e.g., 12 months), by contrast, successfully search at the B location.

The A-not-B task has a long history, with over a hundred different experimental variants. This provides fertile ground for theory development because the landscape is so empirically rich. Thus, in their 1994 book, Thelen and Smith proposed a re-conceptualization of this literature, focusing on why infants show this funny habit of reaching to A instead of B. This account was based on the dynamic systems concept of an attractor and a consideration of changes in infants' reaching skill during the first year. In 1999, Smith, Thelen and colleagues tested several implications of this dynamic systems account. Most radically, they predicted that infants would make the A-not-B error even when no toys were hidden at A or B. This prediction ran counter to the dominant explanations of this error at the time that centered on object permanence and infants' understanding of the object concept. Results showed that, as predicted, infants continued to make the A-not-B error when reaching for the lids that covered the hiding locations, even though all objects were in plain sight.

After these successful empirical tests of the dynamic systems account, Thelen, Schöner, Scheier, and Smith (2001) formalized this perspective in the DFT of infant perseverative reaching. This model consisted of the basic architecture shown in Figure 3—an input layer, a dynamic neural field, and a Hebbian layer. The 8- to 10-month-old model had weak neural interactions such that peaks in the field—that is, decisions to reach to an “A” to the left or to a “B” location to the right—were self-stabilized: they relaxed back to the neural resting level when input was removed. The older infant model, by contrast, had stronger neural interactions such that peaks were more likely to enter the self-sustaining state and be actively maintained during the delay. Interestingly, the model required only a small quantitative change to capture the dramatic shift in infants' perseverative tendencies over development (much like the small quantitative change required in Figure 2 to shift from the “encoding” mode to the “working memory” mode).

The DFT of preservative reaching successfully captured many effects from the literature including manipulations to the stable perceptual cues in the task (e.g., the appearance of the lids and hiding box), the salience of the cuing event (e.g., whether the experimenter drew attention to one side of the box or the other), and the influence of long-term memory built-up from trial to trial. In addition, the model generated several novel predictions. For instance, Clearfield and colleagues (2009) predicted a set of interactions between delay and the salience of the cuing event in the A-not-B task. Most notably, the DNF model predicted that infants would show perseveration after no delay with a weak cue. This contrasts with previous explanations where the delay is critical because the error is centrally about the representation of the toy or hiding location. As predicted by the DFT, however, infants did perseverate in a no delay condition, but only with a weak cue—with a stronger cue and no delay, infants were accurate as reported in previous studies (e.g., Wellman et al., 1986; Diamond, 1985). Thus, in this case, the DFT predicted a suite of effects in quantitative detail, and this prediction involved the interaction of two factors. Such predictions provide a strong test of the theory.

3.2 Formal Models of A-not-B: What Do They Contribute?

The previous section highlights one way to evaluate the usefulness of a theory. One can ask, for instance, whether the theory explains a broad range of findings. In the case of the DFT of perseverative reaching, the answer is certainly ‘yes’. One can also ask whether the theory leads to novel predictions. Again, in the case of the DFT, the answer is ‘yes’. Although these evaluative questions help establish the usefulness of a theory, they are also somewhat narrowly focused: all of the papers discussed above were from one large group of researchers. This raises the question: what has the DFT contributed beyond this group? Has the theory been useful to a more general audience? And beyond the DFT, can we say that formal theories of the A-not-B error are having an impact in cognitive development?

To examine the impact of formal theories of the A-not-B error, we conducted a systematic review of the A-not-B literature during a two-decade span from 1990-2011 (for a list of the studies we included, see the supplemental materials). In particular, we searched the PsycINFO and Web of Science databases, identifying all papers with the terms “A-not-B”, “A-not-B Task”, “A-not-B Error”, “AB Task”, “AB Error”, “Piagetian Stage IV Error”, or “Stage IV Error” in any field. All identified papers were then examined to ensure that they were developmental studies (empirical or theoretical) that did more than tangentially mention one of the key phrases. Finally, we added 4-5 papers that we knew of that were missed by this analysis. The final sample included 82 papers.

Next, we classified these papers into five categories: modeling, neurophysiological / biological, clinical, empirical-only, and empirical tests of formal theories. The results are shown in Figure 4. We classified papers as “modeling” if they included a formal mathematical model as part of the research or if the paper was from one of the modeling groups and was testing a key aspect of the proposed theoretical account. The modeling category included papers examining Munakata's (1998) Parallel Distributed Processing model, as well as a connectionist model by Mareschal, Plunkett, and Harris (1999). Next, we included Thelen et al's (2001) DFT of preservative reaching and associated papers from this group that tested different aspects of the theoretical account. We also included several papers by Zelazo, Marcovitch, and colleagues that were related to a hierarchical competing systems model, as well as two developmental robotics papers. Note that one model by Dehaene and Changeux (1989) was excluded from our analysis because it fell outside of the temporal window we examined.

Figure 4.

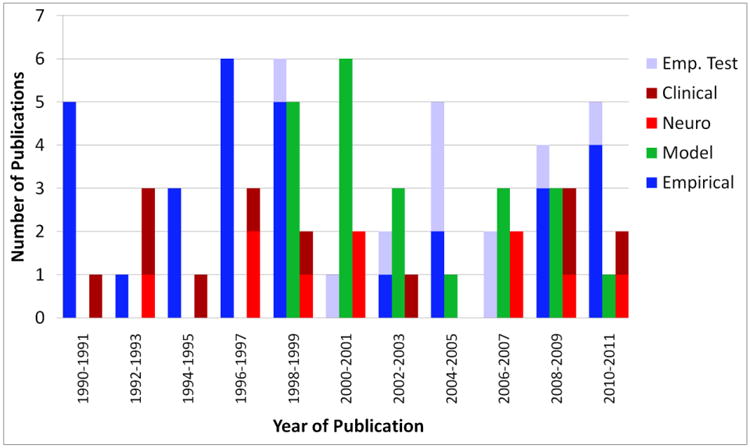
Results of the systematic analysis of the A-not-B literature from 1990 to 2011.

As shown in Figure 4, publication of research employing formal models ramped up in 1998 with the publication of Munakata's PDP model. The rate of modeling publications has been steady since then and rivals or exceeds that of empirical research in some years. The critical question is whether these formal models have had an impact beyond the researchers who employ them. This can be examined by looking at the other categories in Figure 4.

The neurophysiological/biological category comprised mostly electrophysiological research (e.g. Bell & Fox, 1992; 1997; Bell, 2001) as well as comparative (e.g. Diamond, 1990a; 1990b) and biological studies (Dettmer, et al., 2009). Of these papers, none used formal models to significantly inform or generate hypotheses. Indeed, none of the papers in this category after 1998 even cited a formal model. The clinical category consisted of research comprising atypically developing populations. From this category, only a single paper (Mauerberg-deCastro, et al., 2009) significantly employed a formal model in the research. Across the neurophysiological and clinical categories, then, formal models have had little impact.

The lack of contact between modeling work and these specialized areas of research is unfortunate because models may be particularly useful in these areas. For instance, there is clearly an opportunity to tie neural and biological studies of behavior to neurally-ground models of behavior such as the DFT (see, Bastian & Schöner, 2003; McDowell, Jeka, Schöner & Hatfield, 2002); however, this has not occurred in the A-not-B literature. The clinical literature also represents a missed opportunity, as formal models can be useful tools to help evaluate the mechanisms thought to underlie psychopathology (Harm & Seidenburg, 1999; Joanisse & Seidenberg, 2003; Lewis & Elman, 2008; McMurray, Samelson, Lee, & Tomblin, 2010; Plaut, McClelland, Seidenburg, & Patterson 1996; Thomas & Karmiloff-Smith, 2003).

The next category of research we considered included all other empirical contributions, that is, research without neural/biological measures that assessed the performance of non-clinical populations with authors who were not directly associated with a modeling group. Because we were primarily interested in evaluating the impact of modeling on this literature, we categorized the empirical papers by whether they used formal models to significantly inform or generate hypotheses (“empirical tests”) versus cases where they did not (“empirical”). For example, Berger (2004) was in the “empirical tests” category. This study investigated the effect of cognitive load on infant perseveration in a locomotor A-not-B task, while controlling for motor habit which is central to the DFT. Similarly, Ruffman, Slade, Sandino, and Fletcher (2004) designed a series of experiments to differentiate between hypotheses generated from formal theories versus infants' beliefs about object location.

Because there were few formal computational models in the developmental A-not-B literature prior to 1998 (but see Dehaene & Changeux, 1989), we focused on research published from 2000 to 2011 (to give the modeling papers some time to impact the empirical literature). Within this period, there were 19 total paper classified in an empirical category. Of these, 9 were “empirical tests”. Thus, roughly half (47%) of the empirical papers in the last 12 years have used formal models to significantly inform or generate hypotheses. These data are quite encouraging—models are clearly having an impact.

4.1 Application of Dynamic Field Theory 2.0: The Development of Spatial Cognition

One of the limitations of the A-not-B example above is that it is a relatively narrow topic. Thus, in this section, we focus on how we have moved from the dynamic field model of A-not-B to a more general theory of the development of spatial cognition (see Simmering et al, 2008; Schutte & Spencer, 2009; Spencer et al., 2007). Note that this work has also been extended into the field of visual cognition, including perceptual discrimination and working memory for features (Simmering & Spencer, 2008; Johnson, Spencer, Luck & Schöner, 2009; Johnson, Spencer, & Schöner, 2009; see the chapter by Simmering in this issue).

Achieving something as simple as remembering the location of a favorite toy can require a remarkable degree of sophistication. First, you need to perceive the location of the toy the first time you play with it. You can easily do this retinally, but that is not very useful because our eyes move around so much. Thus, children and adults commonly encode locations relative to a body-centered or world-centered frame of reference (e.g., a few inches to the right of the table's edge). Achieving this is a real trick because everything needs to be actively coordinated. For instance, to establish a neural representation in world-centered coordinates requires that you update the relationship between your body and the world every time you move (e.g., Pouget, Deneve, Duhamel, 2002; Schneegans & Schöner, 2012). But we cannot stop there: once you encode the location in a world-centered frame, you need to remember the location during, for instance, a 20 s delay when the toy is occluded by your brother who has come over to interfere with your play time. This requires some form of active or working memory, and this memory has to be updatable as you move around the world and as objects move. Next, you need to take that working memory and turn it into an action that will, for instance, get your hand to the toy after pushing your brother out of the way. Finally, you need to use your encoding and memory abilities to do something longer-term—to remember where the toy is located days and weeks later.

In the sections that follow, we provide an overview of a DFT of spatial cognition that can overcome many of these challenges. Interested readers are referred to Spencer et al (2007), Schutte and Spencer (2009), and Lipinski et al. (2011) for more detailed discussions.

4.1.1 Real-time cognitive dynamics

As a first step in understanding how people remember the locations of objects, we used a simple laboratory task developed by Huttenlocher and colleagues (1994). The task involves having children remember the location of a toy buried in a long, narrow sandbox. The task is simple enough for 18-month-olds to complete, yet it is also empirically rich. For instance, when people remember a location in a sandbox, they anchor their memory to the available reference frame—the edges and symmetry axes of the box. In real time, this anchoring results in biases away from the reference axes and toward the center of, for instance, left and right spatial categories (e.g., Huttenlocher et al., 1991; Spencer & Hund, 2002). Interestingly, when the location is aligned with a reference axis, errors are small and the variance across trials is small as well (Schutte & Spencer, 2002; Spencer & Hund, 2002).

The DFT of spatial cognition presents a detailed, mechanistic explanation of how people encode a location in a frame of reference, actively remember the location in working memory, and keep themselves in register with the perceptual surrounds such that they can reach for the hidden object a short time later (see Lipinski et al., 2011; Spencer et al, 2007). For simplicity, we focus on the perceptual and working demands in the sandbox task in this section using the three-layer architecture shown in Figure 5. This DNF model consists of an excitatory perceptual field (PF; first layer of Figure 5) which codes perceptual structure in the task space; an excitatory spatial working memory field (SWM; third layer of Figure 5) which receives excitatory input from the perceptual field (see green arrows) and maintains the memory of the target location; and an inhibitory field (Inhib; second layer of Figure 5) which receives input from both the perceptual and SWM fields (see green arrows) and sends inhibition back to both fields (see red arrows). For each layer, location is represented along the x-axis, activation along the y-axis, and time along the z-axis.

Figure 5.

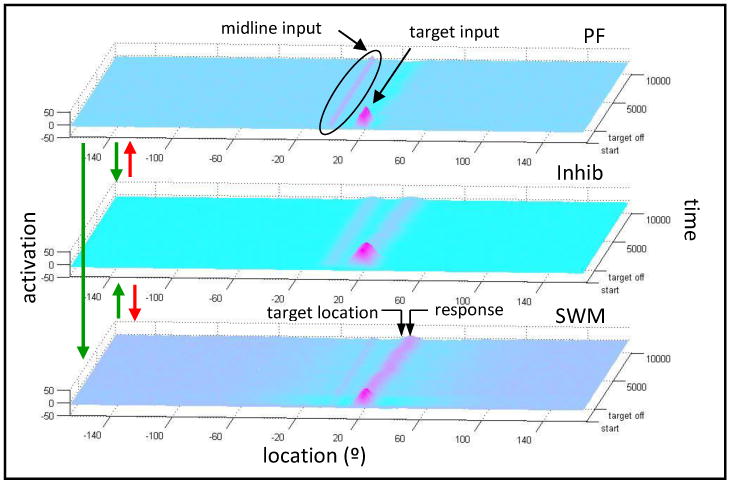
Simulation of the 3-layer DNF model. Panels represent: perceptual field [PF]; inhibitory field [Inhib]; working memory field [SWM]. Arrows show connections between fields. Green arrows represent excitatory connections and red arrows represent inhibitory connections. In each field, location is represented along the x-axis (with midline at location 0), activation along the y-axis, and time along the z-axis. The trial begins at the front of the figure and moves toward the back. See text for additional details.

Figure 5 shows the model's performance in a single trial with a target 20° from the midline (0°) of the task space. When the target appears (see “target input” in Figure 5), peaks build in the excitatory fields at the target location. During the memory delay, the target peak in the perceptual field dies out; however, the peak in the SWM field self-sustains due to the stronger neural interactions in this layer. Note that a second peak is maintained in the perceptual field during the delay at the location of the nearest reference axis—the symmetry axis aligned with the center of the sandbox (see “midline input”). This peak helps the model maintain neural activation in a world-centered reference frame (for discussion, see Spencer et al., 2007). Spatial memory biases in the sandbox task emerge from the interaction of the midline peak in the perceptual field and the target peak in SWM during the delay. In particular, inhibition associated with the reference frame pushes or “repels” the WM peak away from the midline axis (see arrows in the lower panel of Figure 5 that mark the target location and the response location).

The DNF model predicts that there should be a time-dependent “drift” of spatial memory during the delay, that is, memory should be more and more strongly repelled from midline as the delay increases. Spencer and Hund confirmed this prediction with both children (2003) and adults (2002). In addition, the model predicts that response variability should increase over the memory delay. This has also been empirically confirmed (Spencer & Hund, 2002; 2003). Finally, the model explains why there is no memory drift and low response variability when the target is aligned with the reference frame: in this case, excitatory input from the midline peak in the perceptual field attracts the WM peak, keeping it accurately positioned during the delay. Note that the empirical observation of low response variability when a target is aligned with a perceived reference frame is theoretically important because a second account of spatial memory—the Category Adjustment Model (CAM) from Huttenlocher and colleagues (1991; 1994)—does not capture this finding.

4.1.2 Spatial memory and learning

The model in Figure 5 captures the real-time neural dynamics that underlie memory for a single location in a world-centered reference frame. But how do you learn, for instance, where your favorite toy typically is? For this, we need to add learning and long-term memory formation to the model in the form of a Hebbian layer, creating a “3-layer+” model. This brings the 3-layer model into register with the type of perseverative phenomena studied in the A-not-B task. For instance, Simmering and colleagues (2008) showed that the 3-layer+ model will make the A-not-B error, and Schutte and Spencer (2009) showed that the 3-layer+ model captures A-not-B-type biases in the sandbox task (see Spencer, Smith, & Thelen, 2001).

To probe whether this addition to the DNF model effectively captures longer-term spatial learning, we have conducted several studies with adults in, once again, a task pioneered by Huttenlocher and colleagues (1991). In this task, adults remember the location of a dot inside a circle on a computer screen. After a brief delay, they are asked to reproduce the location. Interestingly, an initial probe of spatial learning in this task revealed null results. In particular, Huttenlocher and colleagues (2004) gave two groups of participants different dot distributions over trials. In one distribution—the “+” distribution—the dots were clustered near the horizontal and vertical symmetry axes. In a second distribution—the “X” distribution—the dots were clustered near the diagonals. If participants build-up a long-term memory of the target distribution, one might expect opposite spatial memory biases in these conditions—toward the vertical and horizontal axes with the + distribution and toward the diagonal axes with the X distribution. Huttenlocher et al. (2004) found no systematic differences across conditions. They concluded that—consistent with the CAM—participants did not remember the target distributions in detail; rather, they used a summary prototype representation at the center of each quadrant.

One of the challenges with studying long-term memory, however, is that effects often build-up slowly over learning. Critically, participants in the study by Huttenlocher et al. (2004) only responded once to each target. To probe whether this might explain the absence of learning effects, Lipinski and colleagues (2010) replicated key aspects of this study, but had participants respond multiple times to each target. Results showed a systematic bias toward a long-term memory of each target distribution, that is, memory biases were pulled in opposite directions across conditions. These data were captured in quantitative detail by the 3-layer+ model. Note that because the CAM has no memory beyond a summary prototypical representation for each category, it fails to capture these empirical results.

4.1.3 The development of spatial memory

Thus far, we have described how the DFT captures the integration of perception and working memory in real-time as well as over learning. But what about development? Much of our developmental work has focused on a transition in spatial category biases in early development first documented by Huttenlocher and colleagues (1994) in the sandbox task. They found that young children's memory responses were biased toward the midline of the sandbox, rather than away from midline as discussed above.

To explain this developmental change, Spencer, Schutte, and colleagues (Schutte, Spencer & Schöner, 2003; Schutte & Spencer, 2009; Simmering et al., 2008; Spencer et al., 2007) proposed the spatial precision hypothesis. According to this hypothesis, the neural interactions that underlie spatial cognition become stronger over development, that is, locally excitatory interactions and laterally inhibitory interactions strengthen. When this hypothesis is implemented in the 3-layer model, the model captures a suite of developmental changes in spatial memory biases between 3 and 5 years (e.g., Simmering et al., 2006). For instance, one consequence of stronger neural interactions is that peaks can become more precise. This predicts that there should be systematic changes in the precision of children's ability to perceive and remember locations relative to a reference frame. Consistent with this, recent data show that children's perception of symmetry axes becomes more precise in early development during the same developmental period when there is a shift in spatial memory biases (Ortmann & Schutte, 2010).

Most surprisingly, simulations of the DFT that implemented the spatial precision hypothesis predicted that the developmental shift in spatial memory—from biases toward midline to biases away from midline—would not happen in an all-or-none fashion (Schutte & Spencer, 2009). Rather, the model predicted a complex pattern of change between 3 and 5 years from gradual narrowing of the bias toward midline, to a period of intermediate responding where targets very close and very far from midline would be accurate but targets in an intermediate spatial zone will show bias away from midline, to finally an expansion of the repulsion effect across a broad spatial range. Empirical data with children confirmed this pattern. Schutte and Spencer (2002) found that 3-year-olds showed a bias toward midline across a broad range of targets. At 3 years 8 months of age, children's responses were biased toward midline only at the hiding location closest to midline; other locations were accurate (Schutte & Spencer, 2009). At 4 years 4 months, children's responses were biased away from midline only at an intermediate location and the other locations were accurate. Finally, by 5 years 4 months, responses were biased away from midline across a broad range, that became broader still at 6 years (see Spencer & Hund, 2002). In a set of follow-up simulation, Schutte and Spencer (2009) showed that the 3-layer model can quantitatively simulate this complex pattern. Note that, at present, no other model explains this suite of developmental effects.

Given that the DFT simulated this complex pattern, Schutte and Spencer (2010) went a step further and tested an additional prediction of the model that making the midline symmetry axis more salient would shift the transition in spatial memory biases to an earlier point in development. To test this empirically, they added two lines to the midline axis of their task space. As predicted, the added perceptual structure switched the memory responses of children 3 years 8 months of age from being biased toward midline to being biased away from midline. This influence of perceptual structure on the developmental transition in memory bias provides further support for the specific type of integration of perception and working memory captured by the DFT.

4.2 Formal Models of Spatial Memory: What Do They Contribute?

As with our survey of the A-not-B literature, we can ask what the DFT has contributed to the field of spatial cognition. First, it explains a broad range of findings and integrates the A-not-B error (Simmering et al., 2008), changes in position discrimination in early development (Simmering, et al., 2006), and a suite of changes in spatial memory biases all within a single framework. Second, the DFT has led to novel predictions that have been tested empirically. This includes observations that are difficult to explain otherwise, such as the complex pattern of change in spatial memory biases between 3 and 5 years. Finally, the model effectively integrates perceptual, working memory, and long-term memory processes in a way that is predictive in real-time (e.g., Spencer & Hund, 2003), over learning (e.g., Lipinski, Spencer, & Samuelson, 2010), and over development (e.g., Schutte & Spencer, 2009). This was our initial goal as we seek to develop a broad, integrative theory of spatial cognitive development.

But what about outside the group of researchers who employ formal models? Has this work had an impact in the field more generally? To examine the impact of formal theories of spatial cognition, we conducted a second systematic review of the literature. This review examined a three-decade span from 1980-2011 (for details, see supplemental materials). We chose to include a wider temporal window because some of the early work on the CAM was published in the 1980s. In particular, we searched the PsycINFO and Web of Science databases, identifying all papers with the terms “spatial categorization”, “spatial working memory”, “spatial organization”, “spatial memory”, and “spatial perception”. As before, all papers were checked to ensure that they were developmental studies (empirical or theoretical) and that they did more than simply mention one of the key search terms. Finally, we added by a handful (4-5) of papers by hand that we noticed were missed by this analysis. The final sample included 168 papers.

Next, the papers were classified into the same five categories used previously: modeling, neurophysiological/biological, clinical, empirical only, and empirical tests of formal theories. We classified papers as “modeling” if they included a formal mathematical model as part of the research or if the paper was from one of the modeling groups and was probing issues related to the theoretical account. The modeling category included papers related to the CAM, as well as papers related to DFT. There was also one modeling paper by Rotzer et al. (2009) that used a neural network model of spatial working memory. As shown in Figure 6, publication of research employing formal models began with the first application of the Category Adjustment Model to the study of development (Huttenlocher, et al., 1994). Modeling work remained relatively dormant for several years until the early 2000s with the publication of the DFT account spatial memory. Since then, the rate of modeling publications rivals that of empirical research and in some years exceeds it.

Figure 6.

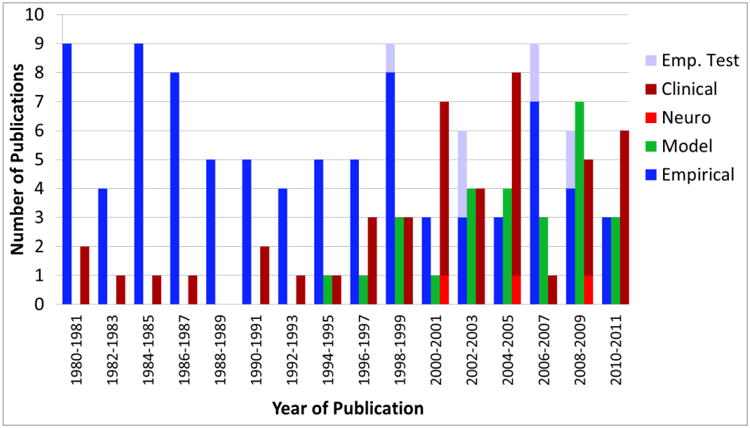
Results of the systematic review of the spatial categorization/spatial memory literature from 1980-2011.

What about the non-modeling categories? For neural research, models have once again had relatively little impact. The neurophysiological/biological category comprised mostly fMRI studies (e.g. Schweinsberg, Nagel, & Tapert, 2005; Vuontela, et al., 2009). Of these developmental papers, none used formal models of spatial memory to significantly inform or generate hypotheses. The clinical category consisted of research using atypically developing and other specialized populations (including some cross-cultural work). Once again, no papers made significant contact with formal models. Although it is significant that the clinical literature made no contact with formal theories, it is worth noting that many of these papers used tasks that are not obviously addressed by either the CAM or DFT (e.g., the Corsi block task).

The final category we considered was the empirical category which we divided into papers that used formal models to significantly inform or generate hypotheses (“empirical tests”) and papers that did not (“empirical”). For example, Hund and Plumert (2003) investigated the role of object categorization on spatial learning and categorization, drawing inspiration from the DFT. In another example, Nardini and colleagues (2009) tested the effects of different frames of reference in an experiment that built on the CAM model from Huttenlocher and colleagues (1991; 1994).

As with our analysis of the A-not-B literature, we investigated the effects of models on the empirical literature by focusing on the 12-year period from 2000-2011. Of the 30 total empirical papers published during this period, 7 were classified as “empirical tests” (23%). Thus, clearly models are having less of an impact on spatial cognitive development than in the A-not-B literature. That said, it is important to place this result in the context of several observations. First, Figure 6 shows a slight increase in papers in the modeling category toward the end of the 12-year period. Given that most of these papers directly test formal models with empirical data, the decline in “empirical tests” is somewhat misleading. Second, many of the “empirical” papers in the 12-year period focused on the topic of spatial reorientation (e.g., Learmonth, Newcombe, Sheridan, & Jones, 2008). This literature examines spatial memory in the context of navigation, inspired, in part, by research examining the role of hippocampus in navigation (e.g., Burgess, Maguire & O'Keefe, 2002). It is not transparent how models of spatial memory developed to explain location memory in a small scale space can be extended to capture findings in navigation and reorientation (although recent DNF models of navigation take a step in this direction; see, e.g., Bicho & Schöner, 1997). This observation resonates with our evaluation of the clinical literature in that clinical studies often use tasks that have not been directly captured by formal models (e.g., the Corsi block task; Pagulayan, et al., 2006). Thus, results from Figure 6 appear to reflect a compartmentalization of the spatial memory literature into modeling papers, empirical probes of spatial memory in the context of navigation, and clinical studies using standardized assessment tasks.

5. Conclusions: What Role Will Formal Theories Play in the Future?

The goal of the present paper was to highlight how DFT has been useful in understanding cognitive development using two literatures to provide concrete examples. These examples showed how DFT has been an effective framework for doing what theories are supposed to do—integrate empirical findings, explain links among diverse results, and generate novel predictions. We also noted cases where DNF models went above and beyond what can be accomplished with verbal concepts alone, generating predictions that were hard to explain otherwise.

The two empirical literatures we examined were also useful in that there are multiple formal models of the phenomena in question. This allowed us to conduct two systematic analyses of the literature to evaluate the contributions of formal models more generally. These analyses revealed a steady rate of modeling publications in the last decade. More critically, the analyses also revealed several epochs during which empiricists have engaged formal models in a significant way. These data directly show that models are having an impact in cognitive development beyond the group of researchers using these tools directly. From our vantage point, this is an exciting result.

But these analyses also revealed an important missed opportunity in that neurophysiological and clinical studies rarely interface with formal models. It is unfortunate that neural studies do not engage formal models like DFT that have an established tie to neurophysiology, because models offer a way to test and generate neural hypotheses and link them to the behavior of the organism. Similarly, models can help organize and explain data from complex networks in the brain. Clinical studies should also be a target for further integration with formal models because models can help probe hypotheses about the mechanisms that underlie atypical behaviors. For instance, models have played an instrumental role in several studies examining the processes that underlie dyslexia (Harm & Seidenburg, 1999; Plaut, McClelland, Seidenburg, & Patterson, 1996) and specific language impairment (McMurray, Samuelson, Lee, & Tomblin, 2010; Joanisse & Seidenberg, 2003).

What does the future hold? In a recent paper, Simmering and colleagues (2011) argued that we need more communication back and forth between experimentalists and theoreticians and, critically, that both need to be valued. Our analysis shows positive trends in this regard, but we must all strive to do better in the future. How? One idea is to train graduate students to at least be familiar with different classes of models. Consistent with this, there are a growing number of summer courses on different modeling approaches (see, e.g., the DFT summer school; http://www.uiowa.edu/delta-center/research/dft/school.html), and some conferences (e.g., the Annual Meeting of the Cognitive Science Society) regularly have pre-conference meetings to give students exposure to modeling techniques. Graduate students should be encouraged to attend such offerings. Another key idea is to engage in more formal discussions—in papers and at conferences—where we try to bring experimentalists and modelers together around specific topics. Too often, detailed discussion happens in separate “camps” and there is little resolution or substantive movement forward.

Regardless of the mechanisms that move us forward as a field, our view is that complex theories and formal models are here to stay. Why? Because development is the most complex of topics—more complex than major topics in biology, chemistry and physics. (To quote our colleague, Ed Wasserman, “This isn't rocket science. Rocket science is child's play next to the study of learning and development.”) Moreover, we have to do the job of neuroscientists and cognitive psychologists and understand how the cognitive and behavioral system changes through time. We cannot just think our way out of this degree of complexity using verbal concepts alone. Models are a part of the future. The sooner we embrace this view and more fully integrate empirical and theoretical work, the faster we will become a mature, cumulative, and groundbreaking science.