Accuracy of Volumetric Bone Mineral Density Measurement in High Resolution Peripheral Quantitative Computed Tomography

Abstract

Accurate bone mineral density (BMD) quantification is critical in clinical assessment of fracture risk and in the research of age-, disease-, treatment-related musculoskeletal changes. The development of high-resolution peripheral quantitative computed tomography (HR-pQCT) imaging has made possible in vivo assessment of compartmental volumetric BMD (vBMD) and bone microarchitecture in the distal radius and tibia. HR-pQCT imaging relies on a polychromatic X-ray source and therefore is subject to beam hardening as well as scatter artifacts. In light of these limitations, we hypothesize that the accuracy of HR-pQCT vBMD measurement in the trabecular compartment (vBMD_trab) is not independent of bone density and geometry, but rather influenced by variations in trabecular bone volume fraction and cortical thickness. The goal of this study, therefore, was to evaluate the accuracy of HR-pQCT vBMD_trab measurement in the radius and tibia, and to determine the dependence of this measurement on geometric and densitometric parameters. Our approach was to use a series of idealized hydroxyapatite (HA) phantoms with varying densities and geometries to quantify the accuracy of HR-pQCT analysis. Two sets of custom-made HA phantoms designed to mimic the distal tibia and distal radius were manufactured. Geometric and densitometric specifications were based on a dataset of healthy volunteers and osteopenic patients. Multiple beam hardening correction (BHC) algorithms were implemented and evaluated in their ability to reduce measurement error. Substantial errors in measured vBMD_trab were found. Overestimation of vBMD_trab increased proportional to cortical shell thickness and decreased proportional to insert density. The most pronounced vBMD_trab overestimation therefore occurred in the phantoms with the lowest insert densities and highest shell thickness, where error was as high as 20 mgHA/cm³ (33%) in the radius phantom and 25 mgHA/cm³ (41%) in the tibia phantom. Error in vBMD_trab propagates to the calculation of micro-architectural measures; 41% error in vBMD_trab will produce 41% error in volume fraction (BV/TV) and trabecular thickness (Tb.Th), and 5% error in trabecular separation (Tb.Sp). BHC algorithms supplied by the manufacturer failed to eliminate these errors. Our results confirm that geometric and densitometric variations influence the accuracy of HR-pQCT vBMD_trab measurements, and must be considered when interpreting data across populations or time-points.

Introduction

Osteoporosis is a skeletal disease characterized by reduced bone mass and disruption of microarchitecture, leading to increased bone fragility and fracture risk. This disease is increasing in prevalence as the world’s population ages, necessitating advancements in fracture prediction, prevention, and treatment. Areal bone mineral density (aBMD), as measured by dual energy X-ray absorptiometry (DXA), has been the primary clinical measure used to characterize the disease. Though low aBMD is strongly associated with fracture risk, a number of clinical studies have highlighted the limitations of DXA measurements to completely characterize bone strength and response to therapy [1–4]. A 2D imaging modality, DXA cannot differentiate between cortical and trabecular compartments nor can it image micro-architecture, an important component of bone quality [5–8]. A high-resolution in vivo volumetric imaging technique may be essential to improved fracture prediction and prevention.

The recent development of high-resolution peripheral quantitative computed tomography (HR-pQCT) imaging has made possible in vivo assessment of compartmental volumetric BMD (vBMD) and bone microarchitecture in the distal radius and tibia [9, 10]. In standard HR-pQCT trabecular structure analysis, a number of structural parameters are derived from the density of the trabecular compartment (vBMD_trab) rather than directly measured from the trabecular structure. Trabecular bone volume fraction (BV/TV) is calculated from vBMD_trab using an assumed tissue density value of 1200 mg hydroxyapatite (HA)/cm³. Micro-architectural parameters trabecular thickness (Tb.Th) and trabecular separation (Tb.Sp) are derived from BV/TV using plate model assumptions [11]. Therefore, in this modality, accurate measurement of linear attenuation is critical not only for vBMD_trab assessment but for trabecular structure analysis as well.

HR-pQCT imaging relies on a polychromatic X-ray source and therefore is subject to beam hardening artifacts. Beam hardening results from the preferential attenuation of low energy radiation, which alters (‘hardens’) the energy spectrum of the beam as it passes through an object, shifting the energy spectrum toward higher energy photons. This effect compounds as the beam traverses greater amounts of material.

Beam hardening artifacts manifest in a ‘cupping’ profile with linear attenuation depressed towards the center of the imaged object [12] and produce inaccuracies in attenuation measurements. In many CT systems filters are used to precondition the beam by removing low-energy photons. Beam hardening correction (BHC) algorithms are employed to further mitigate beam hardening artifacts; however, there is evidence that artifacts are not completely eliminated by these algorithms [13–16].

Scatter is another potentially important source of error in computed tomography measurements [17]. In reconstructed data scatter effects will be visually similar to beam hardening artifacts, producing cupping and banding artifacts, and may be dominant if the detector is uncollimated [17–19].

Specimen geometry, volume fraction, and composition have been shown to influence tissue mineral density measurement in ex vivo µCT imaging even in the presence of a beam filter and BHC [14–16], suggesting that patient geometry and BMD may influence clinical evaluation of trabecular bone density and structure via HR-pQCT. The cortical shell of the tibia and radius may exacerbate imaging artifacts and errors in HR-pQCT measurement of vBMD_trab. These errors would propagate to structural measures, possibly masking or exaggerating the effects of aging, disease, or therapy in clinical HR-pQCT studies.

We hypothesize that the accuracy of HR-pQCT vBMD_trab measurement is influenced by variations in trabecular and cortical bone density and geometry. The goal of this study, therefore, was to evaluate the accuracy of HR-pQCT measurement of vBMD in the trabecular compartment of the radius and tibia, and to determine the dependence of this measurement on geometric and densitometric variables. Our approach was to use a series of idealized hydroxyapatite phantoms of the distal radius and tibia with varying densities and geometries to quantify the accuracy of HR-pQCT analysis. Specifically, our objectives were to: (1) quantify error in HR-pQCT vBMD_trab measurements using idealized hydroxyapatite phantoms; (2) analyze spatial dependence of image artifacts and measurement bias due to cortical thickness and trabecular density; and (3) evaluate multiple BHC algorithms in their ability to reduce measurement error.

Materials and Methods

Phantoms

Two sets of custom-made HA phantoms were purchased from QRM (Mohrendorf, Germany). These idealized phantoms were designed to mimic the distal tibia and distal radius regions scanned in the standard HR-pQCT protocol. Geometric specifications were based on the range of cortical thicknesses and diameters drawn from a dataset of 80 normal volunteers and 52 osteopenic patients [10, 20].

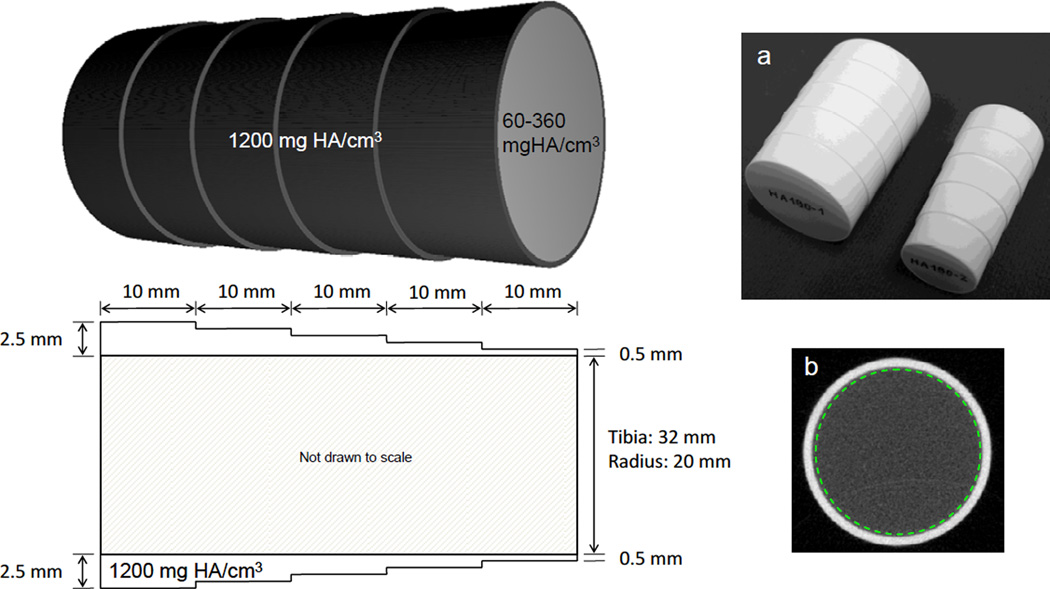
Each phantom set consists of an outer shell representing the cortical compartment and 6 removable inserts representing the trabecular region (Fig. 1). Each piece is 5 cm in length. The outer shells were manufactured of hydroxyapatite with a density of 1200 mgHA/cm³, which approximates the average density of human cortical bone [21–23]. The inner diameter of the shell is 20 mm in the radius phantom and 32 mm in the tibia phantom. The outer diameter of each shell is graduated such that thickness varies from 0.5 mm to 2.5 mm in 0.5 mm increments, each 1 cm in length. The 6 removable inserts representing the trabecular region were manufactured with densities of 60, 120, 180, 240 and 360 mgHA/cm³. These densities are equivalent to 5–30% volume fraction based on an assumed tissue density of 1200 mgHA/cm³. Manufacturing tolerances for hydroxyapatite concentration were set to +/− 0.5%, based on % concentration by weight of each component (epoxy and HA). A previous evaluation of hydroxyapatite distribution in a density phantom created using the identical manufacturing process found that while local inhomogeneities exist within a single image slice (readily apparent at µCT resolutions), when sampled over multiple slices these inhomogeneities are averaged such that the mean attenuation of the imaged region is accurate and consistent with respect to the overall mean of the entire phantom length, with RMS error of 0.11% to 0.15% [24].

Figure 1.

Idealized hydroxyapatite (HA) phantoms representative of the distal radius and tibia. Cortical thicknesses and diameters were based on measurements drawn from a dataset of healthy volunteers and osteoporotic patients. Outer shells representing cortical tissue have a density of 1200 mg HA/cm³ and thickness varying from 0.5 to 2.5 mm. Six removable inserts representing the trabecular compartment vary in density from 60 to 360 mg HA/cm³. (a) Photograph of the two phantoms (outer shells with 180 mg HA/cm³ inserts in place). (b) Single slice of the image data from the radius phantom (1.0 mm shell thickness, 60 mg HA/cm³ insert density) showing region of interest definition (dashed line).

HR-pQCT Imaging

The phantoms were imaged on an HR-pQCT scanner (XtremeCT, Scanco Medical AG, Brüttisellen, Switzerland) using the standard in vivo protocol. In this protocol, scans are performed using a 60 kVp X-ray source potential and 900 µA X-ray tube current. Plates of Cu (0.3 mm) and Al (1 mm) filter soft x-rays in order to reduce patient dose and precondition the energy spectrum to minimize beam hardening. A 3072 × 256 element CCD detector acquires 750 projections at 100 ms integration time per rotation. Within each scanned zone, a single image stack composed of 110 slices is acquired at an isotropic voxel size of 82 µm, producing a 9.02 mm axial scan length. To mimic the presence of soft-tissue surrounding bone, phantoms were imaged while submerged in water inside acrylic cylinders (diameter = 25.4 mm radius, 76.2 mm tibia). For comparison, phantoms were also scanned in air using custom-made acrylic stands. Care was taken during each scan to ensure that the phantom was motionless and aligned with the axis of the scanning bed.

HR-pQCT Analysis

To minimize the influence of object geometry on reconstructed linear attenuation values, a voltage- and scanner-specific BHC created by the manufacturer is implemented automatically in all standard clinical analyses on the HR-pQCT system. To create the BHC function, a step wedge phantom composed of 200 mgHA/cm³ was imaged at the appropriate source voltage (60 kVp) in air. This concentration was originally chosen by the manufacturer as a reasonable approximation of apparent level mineral density in bone. The X-ray intensity measured by the detector for each width of the wedge (I) and the unobstructed reference intensity (I_o) were measured. A polynomial was then fit to the ln(I_o/I) versus thickness data. The deviation of this polynomial from linearity indicates the degree of beam hardening and was used to derive a correction function. This correction is applied to the projection data – adjusting each pixel intensity prior to reconstruction. A more in-depth description of the beam hardening correction procedure can be found in our previous publication [24].

To investigate the influence of the correction function on the calculated vBMD_trab, a second BHC based on a 1200 mgHA/cm³ wedge phantom was applied by our group and compared to the standard manufacturer-provided correction. The 1200 mgHA/cm³ BHC was implemented by obtaining the correction function (based on a 1200 mgHA/cm³ wedge phantom scanned on an identical system) from the manufacturer and applying it to raw projection data using the same software routines used by the standard clinical analysis protocol.

Calibration of attenuation values to HA density was performed by creating a linear conversion based on a density phantom provided by the manufacturer. This density phantom contains rods of HA-resin mixtures (0, 100, 200, 400, and 800 mgHA/cm³). Density phantom scans were corrected using the appropriate BHC prior to creation of the linear conversion.

Regions of interest were identified immediately inside the high density shell for each slice of the image data (Fig. 1b), creating a volume of interest (VOI) encompassing the entire trabecular region. Two voxels were peeled from the circumference of the original VOI to exclude partial-volume effects, providing the baseline measurement of HA density for the trabecular region (vBMD_trab). Following this, 10–100 voxels were successively peeled in the radius, and 10–180 voxels were peeled in the tibia, to investigate variation in vBMD_trab with distance from the insert/shell interface.

The density value measured for each insert in each configuration was compared to the known density of the manufactured phantom. Plots were created to investigate the dependence of vBMD_trab on shell thickness and on depth from the insert/shell interface. These investigations were repeated with image data reconstructed with the 1200 mgHA/cm³ BHC to explore the effects of BHC algorithm.

Reproducibility

To determine vBMD_trab measurement precision, the radius and tibia phantoms were scanned three times each with sample repositioning between each scan. Coefficient of variation (CV%) was calculated at each shell thickness.

Results

Substantial errors in measured vBMD_trab were found within the geometric and densitometric ranges covered by the phantoms (Table 1Fig. 2). In general, with the exception of the two highest density inserts, density was overestimated. Measurement error was most pronounced at the lowest insert densities where overestimation was as high as 20 mgHA/cm³ (33%) in the radius phantom and 25 mgHA/cm³ (41%) in the tibia phantom. The CV% of the vBMD_trab measurement was <0.5% in the radius phantom and <1.0% in the tibia phantom.

Table 1.

Effect of shell thickness (Ct.Th) and insert density on vBMD_trab measurement. Data shown are for phantoms scanned in water and images reconstructed using the 200 mg HA/cm³ beam hardening correction. Data in units of mg/cm³.

Tibia phantom scan in water							Radius phantom scan in water
	Insert density (mg/cm3)							Insert density (mg/cm3)
Ct.Th (mm)	60	120	180	240	300	360	Ct.Th (mm)	60	120	180	240	300	360
0.5	64.02	117.90	177.50	234.15	292.53	349.36	0.5	59.17	119.46	177.67	237.79	293.40	350.92
1.0	68.70	125.00	182.17	242.46	296.34	353.34	1.0	65.58	125.00	184.25	243.50	297.73	356.81
1.5	72.33	128.99	186.50	247.31	296.69	354.21	1.5	69.91	129.16	185.98	246.97	299.81	357.33
2.0	79.26	135.05	194.47	249.91	299.98	357.85	2.0	74.59	131.59	189.28	251.30	304.31	361.83
2.5	84.81	139.38	197.42	249.91	303.45	358.54	2.5	79.96	135.57	194.47	253.20	304.14	359.06
Tibia phantom scan in air							Radius phantom scan in air
	Insert density (mg/cm3)							Insert density (mg/cm3)
Ct.Th (mm)	60	120	180	240	300	360	Ct.Th (mm)	60	120	180	240	300	360
0.5	56.89	116.71	176.22	237.62	295.13	353.40	0.5	59.16	125.04	185.57	244.43	304.97	366.32
1.0	62.02	121.72	182.76	241.45	298.90	355.76	1.0	68.59	130.09	190.54	252.04	309.33	369.95
1.5	67.64	127.01	184.99	243.34	299.11	356.91	1.5	73.06	135.44	194.03	253.31	312.34	370.54
2.0	71.78	128.20	187.42	244.33	300.42	357.48	2.0	77.79	139.71	197.43	256.89	315.18	372.92
2.5	73.62	128.05	185.53	243.11	297.96	353.45	2.5	82.26	141.05	198.83	257.33	307.46	368.74

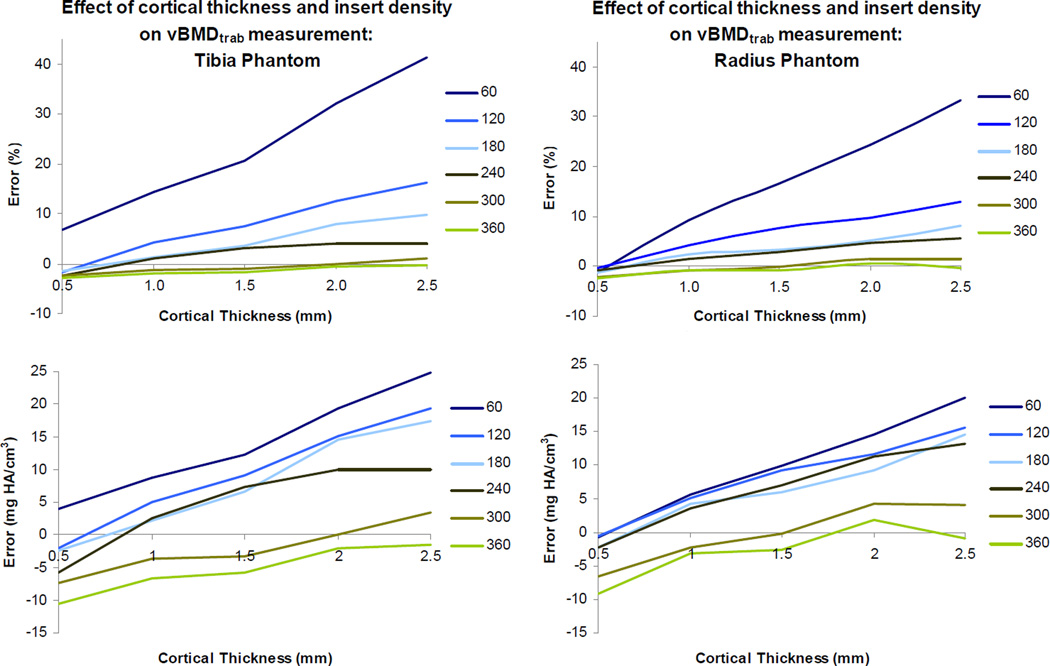
Figure 2.

Quantification of vBMD_trab measurement error. Percent error (top) and absolute error (bottom) are plotted against cortical thickness for each insert density (60 mg HA/cm³ through 360 mg HA/cm³). Phantoms were scanned in water and data was reconstructed using the 200 mg HA/cm³ beam hardening correction.

Measured vBMD_trab increased with cortical shell thickness in both the radius and tibia phantoms (Fig. 2). This was consistent for all densities and scanning media, and for both the 200 and 1200 mgHA/cm³ BHC algorithms. Overestimation of vBMD_trab decreased with increasing insert density. For the smallest shell thickness (0.5mm), this effect resulted in a transition from overestimation of density at 60 mgHA/cm³ to underestimation at 360 mgHA/cm³. For the greatest shell thickness (2.5mm), this effect resulted in a transition from overestimation at 60 mgHA/cm³ to negligible error at 360 mgHA/cm³. The highest overestimation of vBMD_trab (in terms of both absolute error and percent error) was consistently found in the 60 mgHA/cm³ insert density.

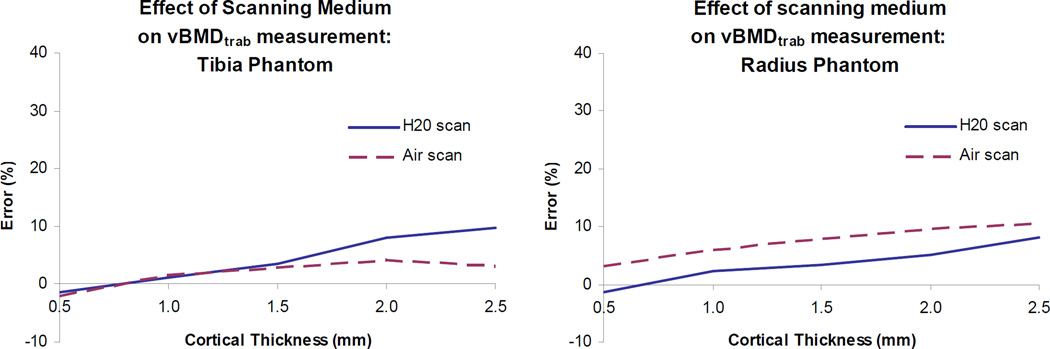
Performing the scans in air – rather than the more physiological scenario of scanning in water – increased error in the radius phantom but decreased error in the tibia phantom (Fig. 3). All insert densities followed the trends seen in Fig. 3, with the largest discrepancy between air and water scans (23% and 41% error, respectively) in the 60 mg HA/cm³ insert density tibia scan. In water, the percent error in vBMD_trab calculated for the radius insert was consistently lower than that found for the tibia. This trend was reversed when the phantoms were scanned in air.

Figure 3.

Effect of scanning medium on vBMD_trab measurement. Results are shown for the 180 mg HA/cm³ inserts with the 200 mg HA/cm³ beam hardening correction. Results for inserts of other densities follow the same trends (data not shown).

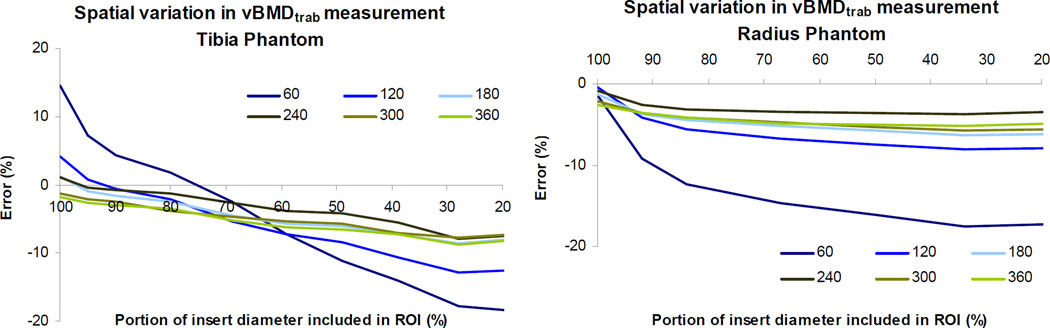
Error in vBMD_trab measurement varied spatially across the image cross-section (Fig. 4). Overestimation of vBMD_trab was highest at the periphery and decreased towards the center of the cross-section, with the most precipitous drop in measured vBMD_trab near the periphery of the insert for both radius and tibia phantoms.

Figure 4.

Spatial variation in vBMD_trab measurement for phantoms scanned in water with the 200 mg HA/cm³ correction. Percent error is plotted against percent of full diameter included in the analyzed region of interest (ROI). Measured vBMD_trab is highest at the periphery of the insert, decreasing towards the center of the cross-section. Results are shown for shell thicknesses of 1.0 mm (tibia) and 0.5 mm (radius) and for all insert densities (60 mg HA/cm³ through 360 mg HA/cm³). Results for all shell thicknesses follow the same trends (data not shown).

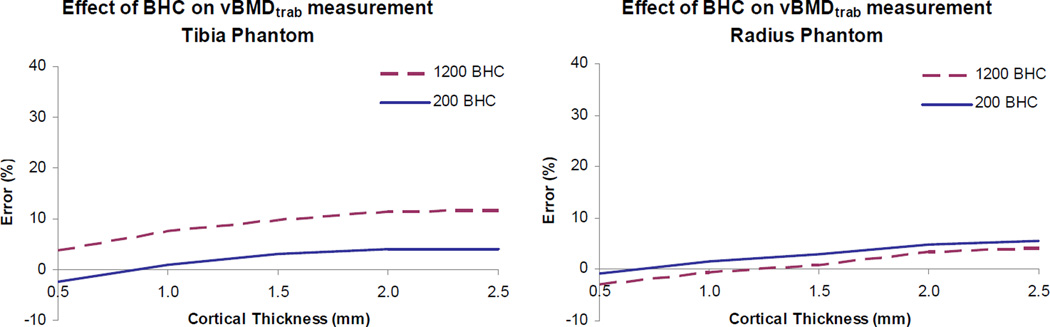
The application of a BHC algorithm based on a 1200 mgHA/cm³ wedge phantom resulted in increased vBMD_trab (increased overestimation for all but the two highest density inserts) in the tibia phantom as compared to results based on the 200 mgHA/cm³ BHC (Figure 5). For all but the highest densities, vBMD_trab error increased by approximately 7% when the 1200 mgHA/cm³ BHC was applied to the tibia phantom. In the radius phantom, application of the 1200 mgHA/cm³ BHC reduced vBMD_trab minimally (< 2%).

Figure 5.

Effect of beam hardening correction (BHC) on vBMD_trab measurement in tibia and radius phantoms scanned in water. Percent error is plotted for each thickness of the phantom ‘cortical’ shell. These results are for the 240 mg HA/cm³ inserts. Results for inserts of other densities follow the same trends (data not shown).

Discussion

This study was conducted to determine the accuracy of HR-pQCT vBMD measurement in the trabecular compartment of the radius and tibia, as well as the dependence of vBMD accuracy on object geometry and density. Using idealized hydroxyapatite phantoms approximating the geometry and density of the human radius and tibia, substantial errors in measured vBMD_trab were detected. Density was overestimated by up to 41%, with the greatest errors occurring in phantoms with high cortical thickness and low density within the trabecular compartment. The vBMD_trab measurement is critical to the calculation of micro-architectural measures in HR-pQCT imaging; 41% error in vBMD_trab will propagate to produce 41% error in BV/TV and Tb.Th and 5% error in Tb.Sp. Beam hardening correction algorithms supplied by the manufacturer failed to completely eliminate errors in densitometric measurements. Our results confirm that geometric and densitometric variations influence the accuracy of HR-pQCT vBMD_trab measurements, and must be considered when interpreting data across populations or timepoints.

This study benefitted from the use of idealized phantoms, which allowed controlled variation of geometric and densitometric parameters. Data gathered from normal volunteers and osteopenic patients were employed in designing the phantoms to ensure physiologically appropriate ranges of geometry and density. By varying shell thickness and insert density, as well as scanning medium and BHC algorithm, the effects of each variable on measured vBMD_trab were evaluated independently.

The use of idealized phantoms to quantify error in an in vivo modality does pose a few limitations. Phantoms were constructed with circular rather than physiologically accurate cross-sections, which may affect the magnitude and spatial distribution of error in the vBMD_trab measurement. Perhaps more importantly, interactions of the beam with trabecular architecture, marrow, and adjacent bones were not considered. The use of water to simulate soft tissue surrounding the bone is also a simplification, as soft tissue is not symmetrically distributed around the bone as is the water in our phantom holder. Finally, motion artifacts common in HR-pQCT scanning are not present in the scanning of phantoms. It is unclear exactly what effect motion would have on vBMD_trab measurement errors. Previous in vivo studies have reported vBMD_trab CV% values of 0.3 to 1.2% [10, 25], which are comparable to those measured in this study.

Beam hardening correction algorithms are utilized in the reconstruction of HR-pQCT data in an effort to minimize beam hardening error. The BHC applied in standard HR-pQCT reconstruction is based on a density step wedge phantom of 200 mgHA/cm³. This density was chosen as an approximation of vBMD in human trabecular bone. The average Ct.Th for osteopenic women is approximately 0.6 mm in the radius and 1.0 mm in the tibia [10]. At these Ct.Th values in the inserts nearest the assumed trabecular density (180 and 240 HA) the vBMD_trab measurement performs well, with 1% underestimation in the radius and 1% overestimation in the tibia. However, according to our database of normal control subjects, the combination of high Ct.Th (greater than 1.5 mm) and low vBMD_trab (less than 200 mg HA/cc) is not uncommon in healthy individuals. Our data show that for this combination of geometry and density, large errors are present despite the implementation of the BHC. These results suggest that it may not be appropriate to use a single BHC for all objects when performing HR-pQCT studies. Instead, it may be necessary to group subjects or specimens by geometry and density, customizing the BHC algorithm for each group.

An alternative BHC based on a 1200 mg/cm³ step wedge phantom was applied in this study to determine whether accuracy would be improved. This was not the case; in fact, the 1200 mg/cm³ BHC increased error (increased overestimation) in the tibia phantom, indicative of an overcorrection (Fig. 5). Our previous studies have shown that the 1200 mg/cm³ BHC produces superior results relative to the 200 mg/cm³ BHC in µCT imaging [15]. The discrepancy between the µCT results and the results of this HR-pQCT study may be related to the homogeneity of the phantom inserts and the relatively lower resolution of HR-pQCT. In µCT imaging of trabecular structure, individual voxels within trabeculae detect tissue densities near 1200 mg/cm³. A 1200 mg/cm³ BHC is more appropriate in the µCT imaging scenario regardless of the fact that the volume-averaged or apparent density of the trabecular sample may be close to 200 mg/cm³. In HR-pQCT imaging of the homogeneous phantom inserts, apparent and voxel-level density values are identical, both much lower than 1200 mg/cm³. Partial volume effects due to the relatively large voxel size in HR-pQCT may cause this to be true even when trabecular structure exists. However, errors due to photon scatter may differ in structured vs homogenous phantoms. Further work – experimental and computational – will have to be undertaken to investigate this.

Presence of scatter can be observed by varying the distance between the object and the detector – this alteration will not affect beam hardening but will change the relative scatter contribution. Object positioning has been found to influence µCT densitometric measurements, presumably due to scatter artifacts [26]. In our HR-pQCT system, adjusting the phantom position along the beam path between the two extremes permitted by scanner geometry altered the vBMD_trab measurement by an average of 3.6% and 5.5% in the radius and tibia phantoms, respectively (data not shown). Magnitude of the relative scatter contribution is influenced by object density and geometry, in addition to object position relative to the detector [19, 27]. Preliminary results of Monte Carlo simulations performed in cooperation with the manufacturer (data not shown) confirm that scatter will drive the magnitude of vBMD_trab towards overestimation with a magnitude proportional to shell thickness.

The tibia and radius phantom scans exhibited opposite effects in response to the change in scanning medium. These differences in effect size and direction may be due to the interplay between beam hardening and scatter, and the relative effect of the scanning media on both of these phenomena. Though our study did not investigate these effects independently, we do believe this is an important area of future research. The design of the wedge phantom used to determine the beam hardening correction algorithm becomes another area of concern in the context of scatter artifacts. The geometry and scan position of the wedge phantom may cause scatter artifact differing from that occurring in radius and tibia measurements. Consequently, the BHC derived from the wedge phantom scan may introduce error or bias when applied to subject scan data. A cylindrical BHC phantom may be more appropriate in terms of modeling scatter in this application.

A bowtie attenuator may aid in shaping the beam to minimize scatter in cylindrical objects [19]. For more complex subjects, precise post-subject collimation or scatter correction must be employed to eliminate scatter artifacts [17]. Collimation may be difficult to achieve in combination with the high-resolution detectors utilized in HR-pQCT systems. The implementation of an empirical scatter correction factor is complicated since scatter patterns depend in a complex way on object composition as well as object and scanner geometry [17]. Corrections based on Monte Carlo simulation would be more flexible and accurate [28–31], and should be investigated.

Fracture risk in osteoporosis is currently assessed using a T-score calculated from areal BMD measured by DXA. There is a trend toward the use of volumetric rather than areal BMD for its ability to distinguish trabecular and cortical compartments. However, before HR-pQCT can be utilized as a clinical standard, its accuracy over the geometric and densitometric ranges found in the population must be determined and compared to that of DXA. In this context, the findings of this study have important clinical consequences.

Our results indicate considerable error exists in HR-pQCT vBMD measurement. Errors in vBMD will propagate to micro-architectural parameters in HR-pQCT analysis. The greatest overestimation of vBMD_trab was found in low density phantoms; this will manifest as an overestimation of trabecular vBMD in subjects with low bone density, possibly leading to underestimation of fracture risk in this vulnerable population. Longitudinal decreases in vBMD will be underestimated according to our results, again putting a vulnerable population at risk. In this system changes in vBMD and Ct.Th cannot be isolated. Longitudinal cortical thinning will artificially reduce the vBMD_trab measurement, possibly obscuring or overestimating the true response of the trabecular compartment. Cortical thickness within the 9 mm HR-pQCT scan zone varies substantially, particularly in the distal radius [10, 32]. This has implications for measurements of vBMD_trab and architecture distribution within a subject, as our results show, as well as for finite element methods that incorporate HR-pQCT BMD measures in density-scaled models [33]. Beam hardening correction algorithms designed to eliminate the dependence of densitometric measures on geometric variations do not completely eliminate this interaction. More robust BHC algorithms and scatter artifact correction may improve the accuracy of HR-pQCT densitometric and structural measures and facilitate the use of HR-pQCT as a clinical gold standard.