“Glucose-at-a-Glance”

Abstract

The standard continuous glucose monitoring (CGM) output provides multiple graphical and numerical summaries. A useful adjunct would be a visualization tool that facilitates immediate assessment of both long- and short-term variability. We developed an algorithm based on the mathematical method of delay maps to display CGM signals in which the glucose value at time t_i is plotted against its value at time t_i+1. The data points are then color-coded based on their frequency of occurrence (density). Examples of this new visualization tool, along with the accompanying time series, are presented for selected patients with type 2 diabetes and non-diabetic controls over the age of 70 years. The method reveals differences in the structure of the glucose variability between subjects with a similar range of glucose values. We also observe that patients with comparable hemoglobin A1c (HbA1c) values may have very different delay maps, consistent with marked differences in the dynamics of glucose control. These differences are not accounted by the amplitude of the fluctuations. Furthermore, the delay maps allow for rapid recognition of hypo- and hyperglycemic periods over the full duration of monitoring or any subinterval. The glucose-at-a-glance visualization tool, based on colorized delay maps, provides a way to quickly assess the complex data acquired by CGM systems. This method yields dynamical information not contained in single summary statistics, such as HbA1c values, and may also serve as the basis for developing novel metrics of glycemic control.

Continuous glucose monitoring (CGM), used in the management of patients with diabetes mellitus, provides serial measures of glucose levels. The standard CGM report includes multiple graphical and numerical summaries. We introduce a new method, termed glucose-at-a-glance, to visualize and analyze CGM outputs, which may facilitate the clinical assessment of short- and long-term glucose variability.

The new method is based on density delay maps, which display the value of a variable at time t_i versus its value at time t_i+1. Up to the present, the primary biomedical application of traditional delay maps has been in the research analysis of heart rate time series,^1-4 where these graphs are referred to as Poincaré plots. In addition, 2 parameters of delay maps, quantifying the local and global time series’ standard deviations (abbreviated SD1 and SD2), have been proposed for the analysis of CGM data.^5,6 Here, we adapt and expand the delay map approach in new directions to allow for visualization of CGM data by adding a color scheme that represents different levels of density of the data points. To our knowledge, such colorized delay maps have not been previously used to help display and summarize CGM data.

Complementary to hemoglobin A1c (HbA1c) measurements, the gold standard in assessing recent glycemic control, and to currently used CGM statistical summaries, the density delay maps provide rapidly accessible information about actual glucose dynamics. This information relates both to the temporal “structure” of serum glucose variability and the duration of periods of hypo/hyperglycemia.

Methods

Clinical Data

To illustrate the visualization method, we used previously acquired CGM data from elderly subjects over the age of 70 years without diabetes (unpublished data) and with type 2 diabetes, who had been enrolled in clinical studies by the Joslin Geriatric Diabetes Research Group. The glycemic status of the diabetic subjects varied widely, as reflected in their HbA1c values. The CGM data were obtained using the iPro™ system version 1 or 2 (Medtronic, Inc., Minneapolis, MN) set at a sample rate of 1 measurement every 5 minutes. The studies had been approved by the Institutional Review Board at the Joslin Diabetes Center.^7,8

Colorized Delay Map

The algorithm for constructing the “glucose-at-a-glance” plots comprises 2 basic sequential steps: (1) constructing a delay map and (2) color coding this map.

Delay Map Construction

The CGM data used here consist of glucose measurements sequentially acquired at 5-minute intervals. The delay map is simply a plot of the i^th glucose value versus its (i+1)^th value.

Delay Map Colorization

Each data point in the delay map (representing 2 consecutive CGM measurements) is assigned a color according to its density, calculated using a standard nonparametric technique.^9,10

In the implementation used here, the color spectrum (given by the vertical bar on the right side of the graphs) ranges from a dark red-brown to a dark blue, where the former represents the most frequently occurring pairs of glucose values (G_i, G_i+1) and the latter the least frequently occurring ones. Additional technical details are provided in the appendix, including an explanation of how these maps can be used to calculate the percentage of time that consecutive glucose values are within a given range (subregion) of the delay map.

The delay map also provides insight into the structure of the variability of the CGM measurements. For example, uncorrelated outputs, such as white noise, yield delay maps with the appearance of circularly, symmetric scatter plots. In contrast, the delay maps of correlated output variables representing processes with feedback control show more complex patterns, as described below.

Results

To illustrate the basic principles of this methodology, we present original CGM time series and their respective colorized delay maps. For demonstration purposes, we show examples of data obtained from the following individuals: 2 non-diabetic subjects (Figure 1), 3 patients with diabetes with HbA1c values of 9.4% (Figure 2), and 3 patients with diabetes with HbA1c values of 7.1% (Figure 3).

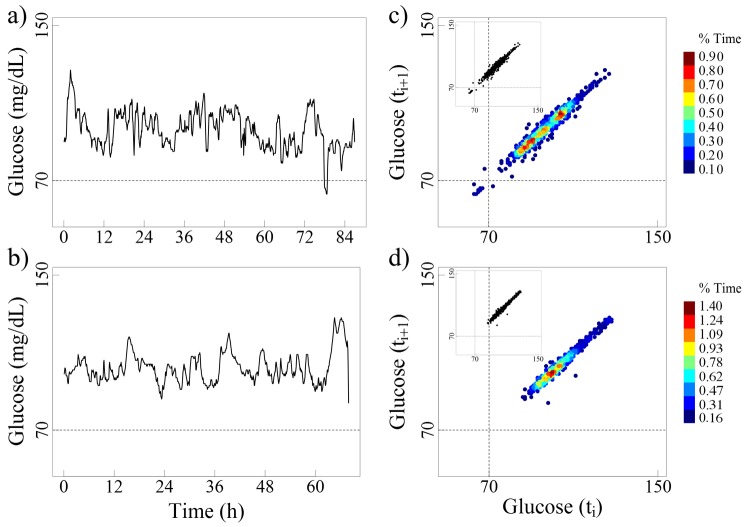
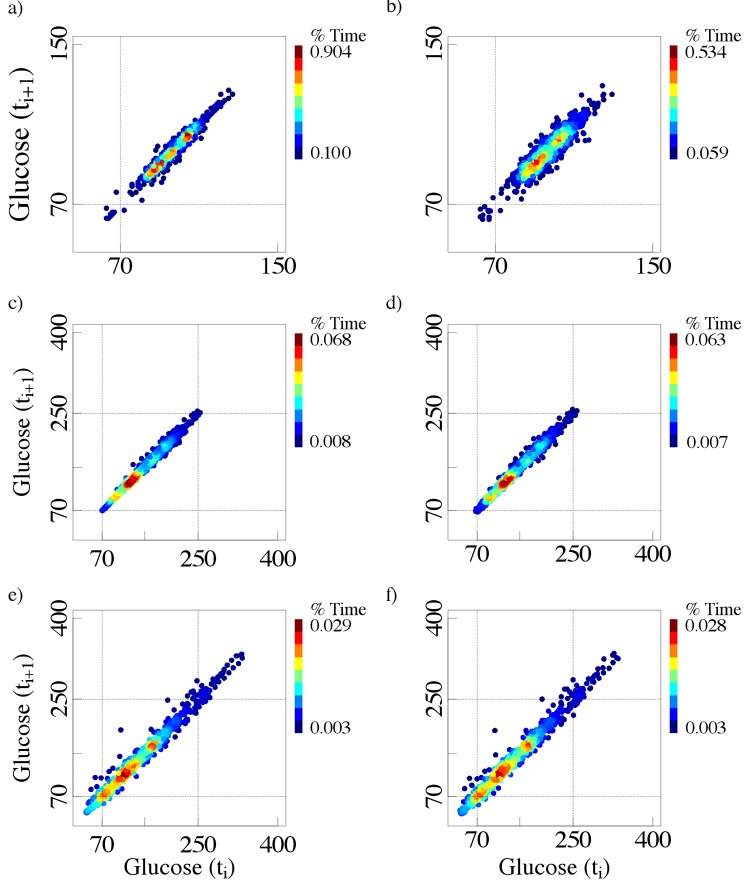
Figure 1.

The left panels (a and b) present the glucose time series for 2 non-diabetic elderly subjects (82 and 76 years, respectively). The right panels (c and d) present their respective colorized delay maps, where the brown color indicates the most frequent pairs of glucose values and the blue color the least frequent ones. The insets display the traditional monochromatic delay maps.

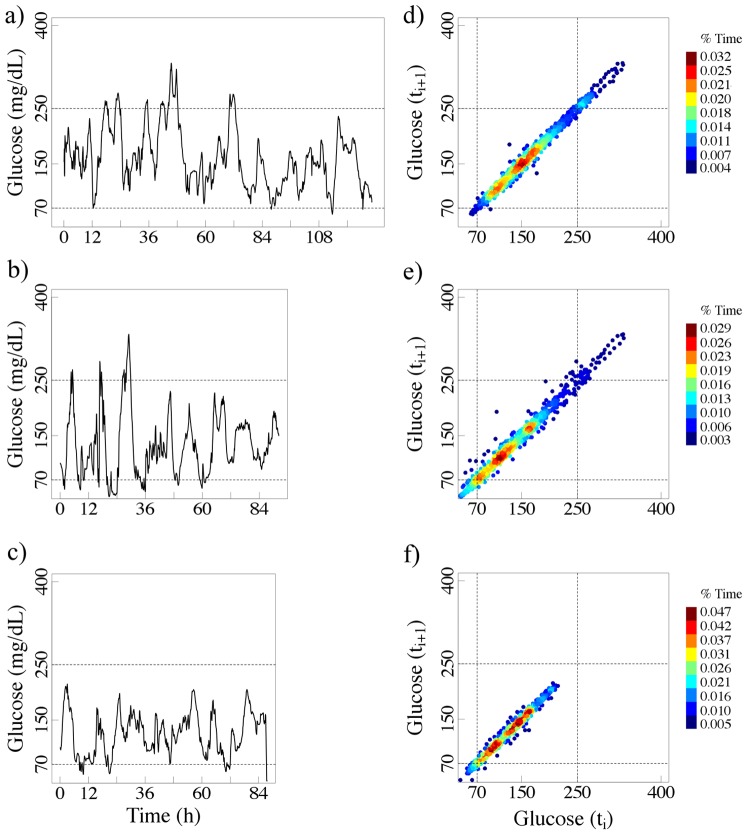
Figure 2.

The left panels (a, b, and c) show the glucose time series for 3 patients (76, 72, and 72 years, respectively) with 9.4% HbA1c values. The right panels (d, e, and f) show their colorized delay maps.

Figure 3.

The left panels (a, b, and c) present the glucose time series for 3 patients (73, 77, and 73 years), all with 7.1% HbA1c values. The right panels (d, e, and f) present their colorized delay maps.

The maps from both the non-diabetic subjects and the patients with diabetes have a stretched elliptical shape, a finding indicating that a given glucose value is followed (or preceded) by one of similar magnitude. The width of the ellipse measured perpendicularly to the diagonal line reflects the amplitude of the short-term (5 min in these cases) glucose fluctuations. Delay maps for measures 10 min far apart would have a slightly larger width. In fact, the width will increase as the time delay between consecutive glucose values expands.

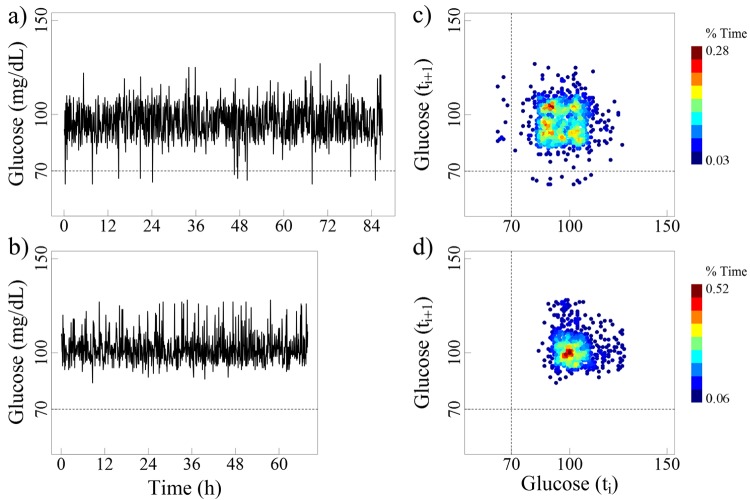
To illustrate what the typical shape of the delay map is for a random sequence, we randomized the time series from non-diabetic subjects by shuffling the order of the glucose values. The time series for the randomized signals and their respective colorized density maps are presented in Figure 4. Note the dramatic change in the shape of the delay map that becomes much more circular. This change is consistent with the fact that a given value is likely followed or preceded by another of (unrelated) magnitude.

Figure 4.

The left panels (a and b) show the randomized glucose time series values for the 2 non-diabetic subjects, shown in Figure 1. The right panels (c and d) show their colorized delay maps.

In the “real-world” examples shown here, as expected, the glucose values of non-diabetic subjects fluctuate within a relatively narrow range (50-150 mg/dL). The delay maps for these healthy subjects show small, well-circumscribed zones of increased density, representing “preferred” glucose values (Figure 1). The glucose time series for the patients with type 2 diabetes present larger elliptical patterns, covering higher ranges of values compared to their non-diabetic counterparts. Selected examples of the effect of noise on these delay maps are also presented in the appendix.

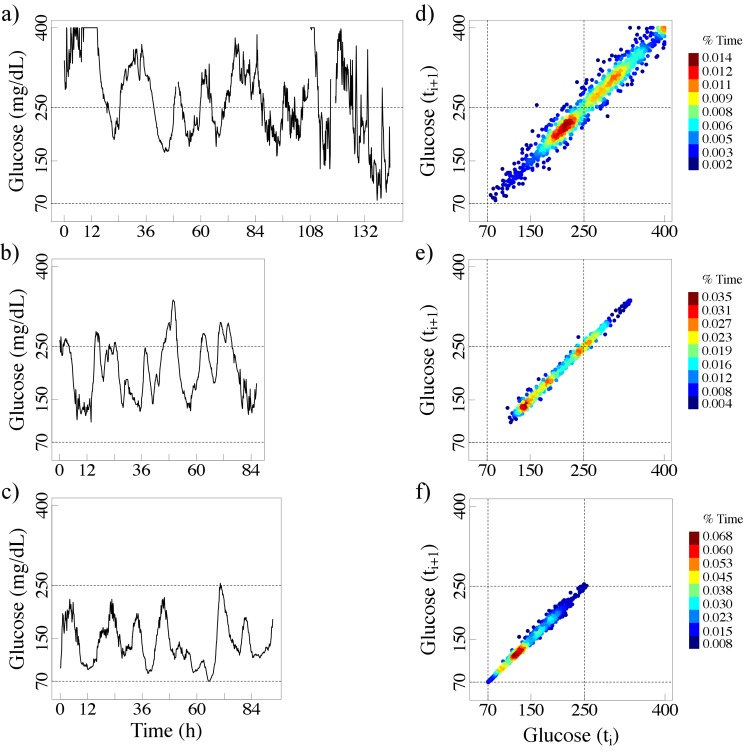
Furthermore, patients with comparable HbA1c values can exhibit very different glucose fluctuation patterns. Note that in Figures 2 and 3, the axes of the colorized delay maps cover a wider range of values than those required for non-diabetic subjects (Figure 1). By way of comparison we present (Figure 5) the delay maps for the same 2 non-diabetic subjects using the wider axis range (50 - 400 mg/dL).

Figure 5.

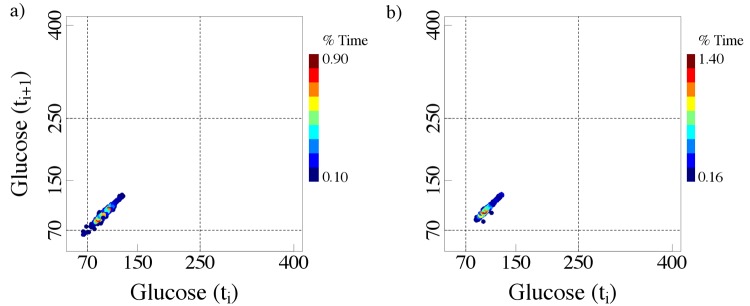
Colorized delay maps of time series of 2 non-diabetic nondiabetic subjects. Note that the difference between these panels and those presented in Figure 1 is the use of expanded axis ranges (50-400 mg/dL).

An apparent limitation of the density delay map method, as described here, is the fact that it does not give information about the time of occurrence of any given point (representing a consecutive pair of values). To add such information, a “point-and-click” adjunct can be incorporated that localizes any point of interest in the delay map onto the original time series (Figure 6).

Figure 6.

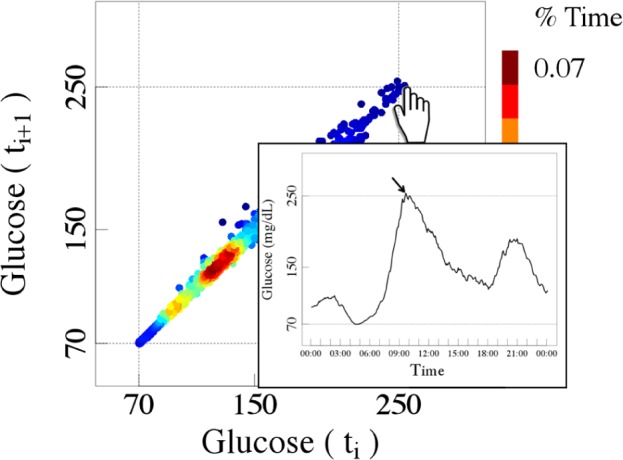
Example of a dynamic view of one of the colorized delay maps (Figure 3f) showing how the point-and-click option can be used to link any point on the delay map to its location on the original CGM time series.

Discussion

The “glucose-at-a-glance” visualization tool is a new way to display the complex, frequently sampled data acquired by CGM systems. The motivation is to enhance and facilitate assessment of glucose dynamics. Of note, the colorization based on the frequency of occurrence of sequential glucose values is of key importance in enriching the information provided by monochromatic delay maps (insets, Figure 1). As described above, the latter have been widely used by investigators probing heartbeat dynamics^2-4 and suggested for exploring CGM data.^5,6 To our knowledge, however, the colorized density maps along with the point-and-click adjunct connecting these maps with the glucose time series (Figure 6) have not been previously introduced.

The analysis presented here, based on the density delay map method, shows that the differences in the glucose dynamics of non-diabetic subjects and patients with diabetes are encoded both in the amplitude of the analyte fluctuations and their temporal structures. In particular, the colorized delay maps of non-diabetic subjects show relatively small brown-yellow zones corresponding to sustained periods of stable glucose levels. In contrast, the patients with diabetes often show a single or multiple enlarged “smeared out” brown-yellow zone indicating the absence of a stable baseline or the presence of multimodal instabilities, such that the glucose values appear to oscillate between different “attractors.”

Finally, this new visualization tool provides information complementary to the HbA1c values. As discussed above, the range and the structure of glucose variability may be very different for patients with comparable HbA1c values. The clinical implications of this graphically depicted instability remain to be determined.

Future Directions

The translational utility of the colorized delay map (“glucose-at-a-glance”) method as a general visualization tool in both types 1 and 2 diabetes mellitus will require clinical testing. The method may also inform more basic work on models of glucose control in health and disease, since the output of such models should replicate the graphical representations shown here. We note that for this presentation, we used the shortest delay provided by a commercial system, corresponding to a sampling rate of 5/min. One can use longer delays depending on clinician preferences. For this demonstration, we also used the entire time series. However, the method can be applied to any segment of interest (e.g., daytime glucose values) provided that a reasonable number of points (of the order of 50 or more) is available. We did not have access to longitudinal studies. However, we anticipate that the colorized density delay map will change over time, depending on therapeutic interventions, diet, and so forth. Finally, the use of this class of density delay maps to develop and test new quantitative metrics of variability also requires prospective evaluation.

Conclusions

The “glucose-at-a-glance” visualization tool, which is based on colorized delay (Poincaré) maps, provides a way to facilitate the assessment of complex data acquired by CGM systems. This method yields dynamical information not contained in single summary statistics, such as HbA1c values, and may serve as the basis for developing novel metrics and models of glycemic control.

Appendix

Color-coding Algorithms

In this implementation, we arbitrarily divided the interval of the density values into 9 equally spaced bins, each of which is assigned a different color according to a preselected chromatic scheme. In each figure the values next to the color bar legend represent the upper density value for each bin.

The delay maps presented in this article were created in R¹¹ using the functions smoothScatterCalcDensity and densCols from the open source software package grDevices. The number of bins used was 250, and the bandwidth was calculated using the smoothScatterCalcDensity default formula.

Delay Map: Subregion Analysis

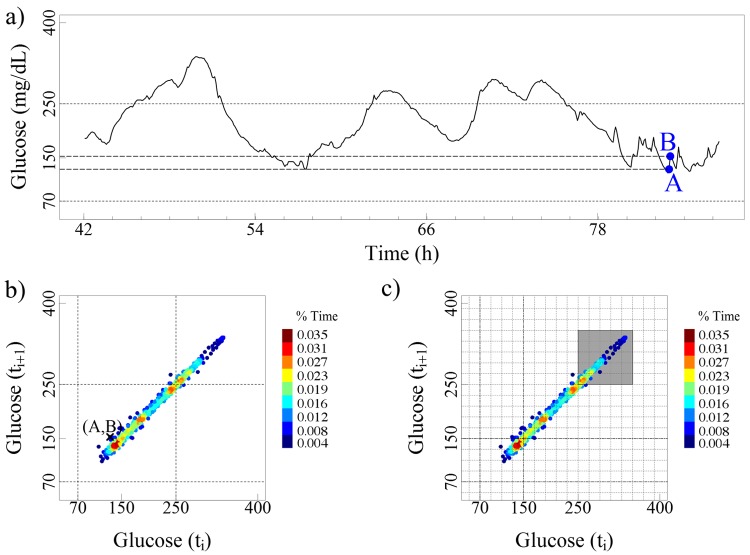
One can also quantify properties of selected subregions of the delay maps. As an example, consider two consecutive glucose values, 129 and 153 mg/dL, corresponding to points A and B in Figure A1a. The value 129 occurs 7 times and the value 153 occurs 9 times. Given that the original recording comprised 1000 data points, the relative-frequency of these values is 0.007 and 0.009, respectively. However, these values occur sequentially (Figure A1b) only 1 time, resulting in a relative-frequency of 0.001 (dark blue) for pair (A, B). To calculate the amount of time that pairs of consecutive measurements occur in a given region, we simply add the frequency of occurrence of each of the points that lie in that preselected region of interest. For example, the percentage of time that the glucose values of the subject depicted in Figure A1c is in the highlighted region (>250 mg/dL) is 22. As a more general example, consider that there were a region X in Figure A1c with 10 red-brown data points, 5 green, and 2 yellow. Taking into consideration the color bar legend with the percentage time for individual points, the estimated percentage time in that region X would be (10 × 0.035) + (5 × 0.019) +(2 × 0.023) = 0.491.

Figure A1.

Panel (a) shows a section of the glucose time series from a patient with diabetes (same as the one selected for Figure 2b). Panels (b) and (c) show the delay map derived from the entire glucose time series. Our technology allows one to visualize where any two consecutive glucose values, e.g., A and B, from the time series graph in (a) lie in the delay map (b). In addition, this tool has the capability of calculating the percentage of time that 2 consecutive glucose measurements are within a given selected range, e.g., gray area in (c).

Effect of Noise on Delay Maps

To help analyze the effect of noise of any source on the output of the delay map method, we show examples of delay plots for 1 non-diabetic subject and for 2 patients with diabetes, before and after adding Gaussian white noise (mean = 0 and variance = 5 mg/dL) to the original data (Figure A2). This degree of noise had only a minimal effect on the plots.

Figure A2.

The panels on the left show the delay maps for the original CMG data and those on the right display the delay maps for the CMG data with white noise (mean = 0 and variance = 5 mg/dL). Each row represents a different subject. The plots in the first row were constructed using data from one of the non-diabetic subjects (presented in Figure 1a). The plots in the 2 other rows were constructed using data from patients with diabetes (same as those shown in Figures 3c and 4b). The added noise does not have a prominent effect on the graphs for these recordings.