Does grassroots democracy reduce income inequality in China?

Abstract

Using village and household survey data collected from 48 villages of eight Chinese provinces for the period 1986–2002, this paper studies how the introduction of village elections affects income distribution at the village level. We estimate both a static fixed-effect panel model and a dynamic panel model for the within-village Gini coefficient and take care of the endogeneity of the introduction of elections. The dynamic panel model shows that having elections reduces the Gini coefficient by 0.04, or 14.3% of the sample average. We also find that elections tend to increase the income shares of poorer portions of the population. Further econometric analysis based on dynamic panel models shows that elections increase per-capita public expenditures by 271 Yuan, but do not increase the level or progressiveness of net or total income transfer in a village. Therefore, elections’ positive role in reducing income inequality is not played through more income redistribution, but through more pro-poor public investment.

There is a growing interest in studying the role of local political institutions in promoting economic growth and equality. This paper adds to the literature by accomplishing two objectives. One is to test whether democratization of Chinese villages centered at the village election has resulted in more equal income distribution within the village in the last twenty years. Besides its possible consequences on social justice, a topic frequently tackled at the national level, income inequality may result in more adverse effects in a local community in terms of public goods provision (Bardhan and Mookherjee, 2005), health outcomes, and for that matter, local economic growth (see Angus Deaton, 2003 for a critical survey). Our other objective is to find out the channel(s) by which village elections have improved income distribution if any improvements have happened at all. Democracy could reduce income inequality by two ways. One is to lead the government to cater to the interests of the median voter who in general prefers the redistribution of income (Alesina and Rodrik, 1994; Benabou, 1996). The other is to press the government to spend more on public projects that enhance the income capability of the poorer. The second channel is preferred over the first under normal circumstances because the first is more likely to lead to unproductive redistribution, but the second enhances productivity in the society.

Existing evidence suggests that grassroots democracy does raise the responsiveness of the local government and leads to pro-poor policies at the local level. Raghabendra Chattopadhyay and Esther Duflo (2004) found that the election of a woman village head in Indian villages had led to the introduction of pro-woman policies. Andrew Foster and Mark Rosenzwig (2001) found that village elections in India had increased local governments’ investment in road building and reduced their investment in irrigation facilities. They interpreted this finding as evidence for a pro-poor policy because irrigation benefited landlords and building roads provided jobs to the landless. Xiaobo Zhang, Shenggen Fan, Linxiu Zhang, and Jikun Huang (2004) found that village elections increased the share of public investment in village expenditures using a sample from Jiangsu province, China. Shuna Wang and Yang Yao (2007) found similar results using a larger sample covering eight Chinese provinces. Li Gan, Lixin Xu, and Yang Yao (2005, 2006) further found that village elections helped to reduce the negative impacts of health shocks on farmers’ income and strengthen farmers’ consumption smoothing capabilities. All these findings suggest that grassroots democracy could function to reduce income inequality at the local level. Nevertheless, they do not provide direct evidence for the strength of that relationship, nor do they tell us the channel by which democracy improves income equality. On the other hand, however, decentralization associated with grassroots democracy could also make elite capture easier at the local level when the local society is socially or economically divided (Bardhan and Mookherjee, 2005). Therefore, it is theoretically unclear whether income distribution would be unequivocally improved by grassroots democracy.

Existing studies using country-level data have not provided conclusive results for the impacts of democracy on equality.¹ One problem with cross-country studies is that the function of democracy depends on a country’s social settings and other institutional arrangements, but cross-sectional regressions tend to ignore those factors. Since village elections operate in the same institutional framework and roughly the same set of social settings, a micro-level study has an advantage over cross-country studies.

Our study makes use of a unique panel dataset with a sample of 48 villages from 8 Chinese provinces for the period 1986–2002. China began to experiment village elections in 1987 and enacted The Organizational Law of Village Committees (OLVC) to formalize them in 1998. Since then, almost all Chinese villages have held at least one election. In the meantime, income inequality rose from 0.29 in 1987 to 0.35 in 2000 in rural China (Riskin et al., 2002). Our data thus cover a critical period of both the election and income distribution. It is also noteworthy that the election operates in what Daron Acemoglu calls “a weakly institutionalized polity” (Acemoglu, 2005) because no direct elections are found beyond the village in China. That is, village elections in China face extra constraints imposed by the authoritarian nature of the Chinese state, so it remains a question as to whether the elections could bring real power to the villagers in the first place. In this regard, our study contributes to the understanding of decentralized governance in a weakly institutionalized polity.

To avoid the complexities arising from political cycles, we focus on the effects of the introduction of the first election. We estimate both a static fixed-effect panel model and a dynamic panel model on the within-village Gini coefficient to pin down them. We also deal with the endogeneity of the introduction of elections with the instrumental variables (IV) method. In addition to the Gini coefficient, we also study how elections affect the income shares of the lower income percentiles of population. Moreover, we explore the channels, i.e., by more income redistribution or by more public investment, for elections to reduce income inequality.

The rest of the paper is organized as the follows. Section 1 provides a brief introduction to village elections in China. Section 2 introduces the data and some key descriptive results. Section 3 presents the main results concerning the impacts of elections on income distribution. Section 4 is comprised of two parts. The first part studies the effects of elections on income redistribution, and the second part studies the effect of elections on public investment. Section 5 concludes.

1. A brief introduction to village elections in rural China

The Chinese commune system was dissolved in the early 1980s. The commune as an administrative unit was replaced by the township, and the production brigade under the commune was replaced by the village committee (VC). The 1982 Constitution defines the village committee as a self-governing body of the villagers (Clause 111). However, committee members had been appointed rather than elected except in a few localities. In 1987, under the leadership of Vice Chairman Peng Zhen, the National People’s Congress (NPC), the Chinese legislative body, passed a tentative version of the OLVC that required the village committee be elected. This law triggered elections in Chinese villages. By 1994, half of the Chinese villages had begun elections. By 1997, 25 of the 31 mainland provinces had adopted a local version of the law, and 80% of the villages had begun elections (Ministry of Civil Affairs, 1998). In 1998, the formal version of the OLVC was passed by the NPC and the election has since spread quickly to virtually all the villages.

The VC is comprised of three to seven members depending on the size of the village. The core members are the chairman, vice chairman, and accountant. Before 1998, candidates for the chairman were usually appointed by the township government although popular nomination, a mixture of government appointment and popular nomination, and nomination by villager representatives also existed. The formal version of the OLVC requires that candidates be nominated by villagers, and the minimum number of villagers to propose a candidate is ten. A primary election, then, is held to reduce the number of candidates to two, and the formal contest is run between these two frontrunners. This version of election is popularly called hai-xuan. Since 1998 hai-xuan has become more popular. The term of the committee is three years but no term limit is required.

Village elections in China operate in a weak institutional environment. In a typical village, the elected VC faces two major challenges that may hinder its ability to serve the wills of the villagers. The first is its relationship with the communist party committee in the village. Despite the fact that the party committee is not popularly elected, the OLVC stipulates that the VC work under the leadership of the party committee, reflecting the nature of China’s one-party system. Since he/she is appointed by the higher authority, the party secretary often pursues a different agenda than the VC’s. Backed by popular votes, however, the chairman of the VC often defies the direction of the party secretary, but the result of the contest is not always in his favor (Oi and Rozelle, 2000; Guo and Bernstein, 2004). To reconcile the conflicts between the VC and the party secretary, the central government has begun to encourage the latter to run for the VC chairman in elections. While this will ease the tension inside the village (Guo and Bernstein, 2004), the VC still needs to face a second challenge that comes from above. Since village elections operate in an authoritarian institutional environment, where the upper-level governments, the township and county governments in particular, are not elected and often intrude in village elections and other village affairs, their effectiveness to serve the wills of the villagers has been called in doubt. Evidence does show that informed local people tend not to trust the election. For example, in a survey conducted in Fujian province, Yang Zhong and Jie Chen (2002) found that it was the villagers who had low levels of internal efficacy and democratic values that were more likely to participate in elections, and those with higher levels of internal efficacy and democratic orientation stayed away from elections due to their awareness of the institutional constraints placed on them.

The above two challenges raise the question as to whether elections would enhance the VC’s accountability to the local population. This question is compounded by the possibility of elite capture inside the village. Rising business elites have been frequently found to dominate village elections (Liu et al., 2001). Although there are not a priori reasons to believe that business elites would necessarily steer the VC to adopt pro-rich policies, this belief lingers within the Chinese academia and policy circles.

2. Data and descriptive evidence

2.1. Data

Our data come from two sources. One is the National Fixed-point Survey (NFS) maintained by the Research Center of Rural Economy (RCRE), the Ministry of Agriculture, and the other is a retrospective survey conducted by ourselves in the spring of 2003. The NFS was started in 1986 and has maintained a longitudinal survey frame of about 350 villages and 24,000 households in all Chinese continental provinces. It adopted a mixture of typical and random sampling methods when it was first started. The 29 provinces (Chongqing and Hainan were later separated from Sichuan and Guangdong, respectively) were divided into three regions, east, central, and west. While the number of sample households was proportional to the population in most provinces, some typical provinces in each region – eastern, central, and western – were given a larger sample size. A “typical” province is one whose characteristics (mainly income and cropping patterns) are about the average levels of the region it belongs to. For example, Henan was regarded as a typical province in the central region. In each province, three strata were identified. The first one, based on geographic topology, divided a province into three regions: plain, hilly, and mountainous. The second stratus consisted of counties that were divided into three groups by per-capita income: low, middle, and high. Several representative counties, i.e., counties with average characteristics (cropping pattern, population, and non-farm activities) of their income group, were chosen for the sample. The last stratus was village. Within each county, one representative village was chosen for sampling. Within this chosen village, households were randomly sampled. There are about 2600 counties in China; the NFS sample covers about 14% of them. The number of households surveyed in each village ranged from 50 to more than 100. These numbers would add up to reflect the population share of each geographic region in a province.

The NFS was intended to survey the same households all the time (that is also what “fixed-point” means). After 20 years in place, however, about one third of the original households dropped out of the sample. One reason for the attrition is that the sample household migrated to the city. The other, and more important, reason is that the whole village dropped out because it was annexed into a city. There have been roughly one fifth of the original villages that have dropped out. In contrast, only two counties have dropped out. When drop-outs happened, replacements were made with survey units with similar characteristics of the drop-outs. However, the numbering of the replacements has not been properly handled. There are a considerable number of replacements that were assigned the same identification number of the survey units that they had replaced.

The NSF uses household bookkeeping to record household data. It collects detailed information on household production, consumption, asset accumulation, employment, and income. It also collects detailed village data covering a wide range of information on land, income, employment, and government revenue and spending. A nice feature of it is that it surveys at least 50 households in a village so the calculation of the Gini coefficient can be carried out with reasonable accuracy.

The 2003 retrospective survey was conducted on 1354 households in 48 villages of 8 provinces. From south to north, they are Guangdong, Hunan, Zhejiang, Henan, Sichuan, Gansu, Shanxi, and Jilin. They were deliberately selected to cover a wide range of geographic, economic, and social diversities. In particular, Guangdong and Zhejiang are located at China’s coast and more advanced than the other provinces; Hunan, Henan, Sichuan, and Jilin represent the average province in the country; and Gansu and Shanxi are two of the poorest provinces. One major task of the retrospective survey was to establish a panel structure for the NFS data. Miss-numbering made it impossible to retrieve the panel structure directly from the NFS data. We then used three household characteristics to match households through time: the building area of the house, the amount of land, and the number of land parcels. The building area of the house was used to identify households that had been split. It is usually the case that rural households build new houses or expand old houses for their sons’ marriages, which often leads to splits. NFS continues to survey one of the split households. However, the split households may not be regarded as the same as the old household because their characteristics change dramatically. The amount of land and the number of land parcels are also important criteria because the change of landholding should be small between two consecutive years although it could happen due to reallocation of land within the village.² Using these three criteria, we calculated the Euclidean distance, i.e., the square-root of the sum of the squared differences, between two observations of consecutive years with the same household identification number. Those with a distance larger than the median were dropped from the sample. The remaining observations were checked manually by the names of their household heads and other family characteristics. Household-year observations were kept in the sample if they shared the same household head or experienced minor changes in household characteristics. Other households were dropped. Villages with few matched households were also dropped. This process required intensive manual reading and subjective judgments by the authors. The matched households were checked again in the survey to make sure that they had stayed in the survey for the entire sample period. Notice that the households that we surveyed were a subset of the NFS sample households in a village. We will use the NFS sample to calculate the Gini coefficient because it has more households. For household-level panel analysis, we will use our smaller sample.

All the household-level data used in this study come from the NFS survey. So do most village-level data except those on elections which come from the retrospective survey. The village questionnaire of the survey was administered on the village committee asking information about village elections, healthcare plans, and other kinds of public interventions. Later, phone interviews also retrieved information on village lineages and other information.

We have village-level data for the period of 1986–2002 and household-level data for the period of 1987–2002. Most of our regressions are thus for the period of 1987–2002. The NFS did not conduct surveys in 1990, 1992, and 1994, so data for those three years are missing. We use the average of the nearby two years to make up the missing data in our analysis.

2.2. Village elections

Except a few cases of interruptions, our sample villages had held elections every three years as long as they had started them. So the introduction of the first election is the key. Fig. 1 presents the number of villages having started elections and their accumulative percentage in each year. The year 1987 was the start of village elections in China. Twelve villages in our sample had their first election in that year. Except Hunan and Guangdong, all the other six provinces had some villages holding elections in that year.

Fig. 1.

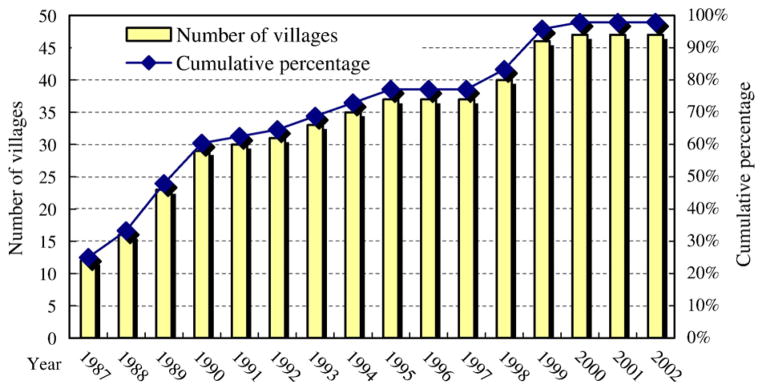
Introduction of village election in the sample villages.

The introduction of elections had a clear regional pattern. After the central government put the OLVC in experiment in 1988, provinces began to enact local laws to specify the details of the implementation of the law.³ However, the adoption of the election in villages of the same province was not uniform. Some began elections before the province adopted the OLVC, and some after. Table 1 presents the year for each sample province to adopt the OLVC and the median and standard deviation of the year of the first election in its villages. Except Guangdong, a rich province in the sample, all the other provinces adopted the OLVC in the period 1988–1992.⁴ The median year of the first election was close to the year when a province adopted the OLVC, and the standard deviation was small in most provinces although Henan, Gansu, and Shanxi had large ones.⁵ In Gansu, the poorest province in the sample, villages started elections much later than the province adopted the OLVC. By 2003, there was still one village in the province that had not started elections. This shows that at least in some provinces local initiatives played a role in starting elections in a village, which raises the possibility that the introduction of elections was endogenous. To address this issue, we will find instruments for the first election and perform two-stage estimations for it. The nice feature of our data is that high-income and low-income villages were mixed in terms of the timing of the first election. The introduction of the election is an irreversible process, so if the timing of the first election were closely associated with the income level, it would be hard to distinguish between the true effects of elections and the effects of income. The mixed nature of our data helps us get around this problem.

Table 1.

Adoption of the OLVC in sample provinces

	Guangdong	Hunan	Zhejiang	Henan	Sichuan	Gansu	Shanxi	Jilin
Year adopting OLVC	1998	1989	1988	1992	1991	1989	1991	1991
Median year of first election	1999	1988	1989	1991	1989	1995	1993	1989
St. dev. of year of election	0.5	1.7	3.9	4.6	1.7	6.8	4.6	2.7

Source: survey data.

2.3. Trends of income distribution

We use the Gini coefficient to describe income distribution in a village. Income is per-capita household net income provided by the NFS household survey. Household net income is defined as household income (earned income and net transfer from the government) net of operational costs. We have converted it into 2002 Yuan using the rural CPI published in China Statistical Yearbook. We calculate the Gini coefficient for each village in each year using the original NFS sample. The calculation is based on individuals, so people from the same household have the same income (i.e., the household per-capita income). Fig. 2 plots the average Gini coefficients of the 48 villages during 1987–2002. We have patched up the figures for 1990, 1992, and 1994 with the averages of the nearest two years. There is apparently an increasing trend of income inequality in the study period. The Gini coefficient rose from 0.26 in 1987 to 0.28 in 1992, and then to 0.32 in 2001, and 0.31 in 2002. This trend matches the national trend. The Gini coefficient in rural China increased from 0.29 in 1987 to 0.35 in 2000 (Riskin et al., 2002). It is understandable that our estimates of the Gini coefficient are smaller than the estimates for the whole country. However, the growth of the Gini coefficient in our sample was quite close to that at the national level: it grew by 0.05 in 15 years in our sample and grew by 0.06 in 13 years at the national level.

Fig. 2.

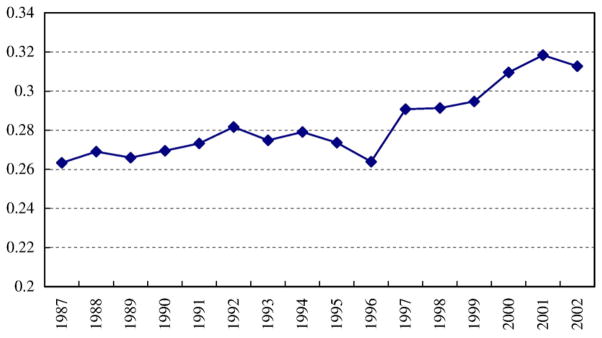
Trend of the Gini coefficient in the sample villages: 1987–2002.

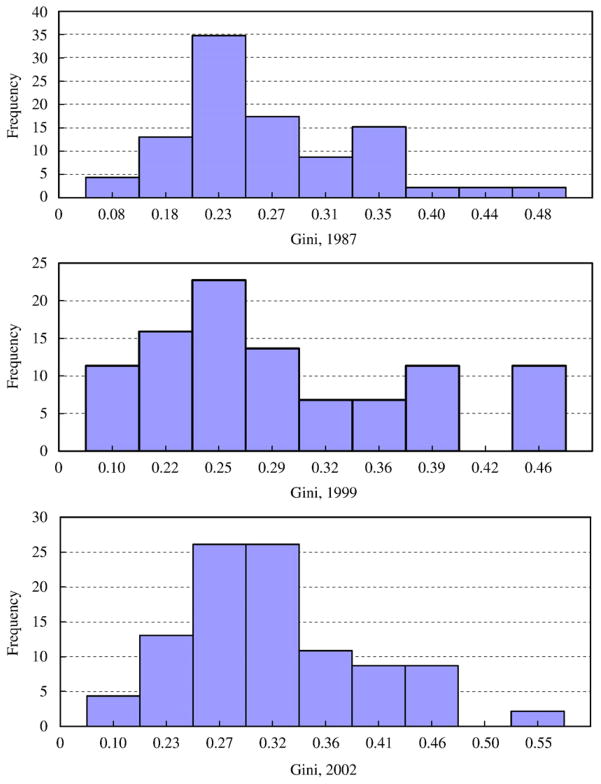
Using data of nine provinces from the NFS survey (seven overlap with our provinces), Dwayne Benjamin, Loren Brandt, and John Giles (2005) have carefully documented the evolution of income inequality in rural China. In addition to using the rural CPI to deflate income, they also provided spatially deflated estimates. Fig. 3 provides the histograms of our estimates of the Gini coefficients in 1987, 1999, and 2002. They largely agree with the histograms provided by Benjamin, Brandt, and Giles (2005) except minor differences,⁶ and show that income distribution was becoming more unequal.

Fig. 3.

Histograms of the Gini in 1987, 1999, and 2002.

Notes: The number for each bar in the figures is the average of the Ginis represented by the bar.

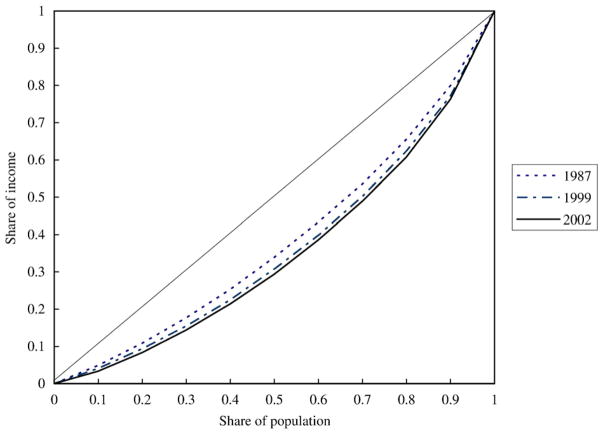
To provide a fuller picture of the within-village income distribution, Fig. 4 presents the Lorenz curves for 1987, 1999, and 2002. The curves are drawn using the average income shares for each year. There are no crossings between any two of the three curves, so income distribution was unambiguously becoming more unequal. In particular, the shares of income of the lower ten and twenty percent of population decreased from 4.91% to 3.38% and from 10.9% to 8.37%, respectively. The introduction of elections is an irreversible event, so it is important to avoid capturing the time trend in estimating its effects on income inequality. Since income distribution has become unambiguously more unequal, our estimates for the effects cannot be caused by the time trend if we find that they are to significantly reduce income inequality.

Fig. 4.

Lorenz curves for 1987, 1999, and 2002.

3. Impacts of elections on income inequality

3.1. Econometric models

The baseline model that we are going to estimate for the impact of elections on income inequality is a panel model with village and year specific effects for the ith village:

$$G_{it}=\alpha E_{it}+x_{it}{\beta }_1+w{\beta }_2+{\alpha }_i+e_{it},t=1,2,\dots ,T,$$ (1)

where T is the number of years covered by our data, which is 16; G_it is the Gini coefficient of village i in year t; E_it is a dummy variable indicating the introduction of the first election (that is, it equals 0 for years before the first election was introduced in a village, and equals 1 for the year of the first election and all the subsequent years); x_it is a set of explanatory variables that may or may not be subject to the influence of village elections, w is a T×1 row vector standing for a set of year dummies; α_i is the time-invariant and village-specific effect for village i; e_it is an i.i.d. error term; and α, β₁ and β₂ are parameters to be estimated in addition to α_i.

The fixed-effect estimator for model (1) allows us to control for the endogeneity of the first election caused by its correlation with the village and year fixed effects, but it does not control for the endogeneity stemming from the correlation of the election with unobserved time-variant village characteristics in e_it. For example, the timing of the first election may be affected by the level of contests within a village that is linked with income distribution. To account for such possibilities, we will find instruments and use the two-stage panel method to estimate Eq. (1) again.

The Gini coefficient may exhibit persistence over time as it is unlikely to change radically over a short period of time. We therefore also estimate a dynamic panel model with unobserved village specific effects,

$$G_{it}=\gamma G_{it-1}+\alpha E_{it}+x_{it}{\beta }_1+w{\beta }_2+{\alpha }_i+e_{it}t=2,3,\dots ,T,$$ (2)

where G_{it – 1} is the lagged Gini, and w now is a (T – 1)×1 row vector. This model can also be augmented by instrumenting E_it. We use the GMM proposed by Manuel Arellano and Stephen Bond (1991) and Stephen Bond (2002) to estimate model (2).

The validity of the GMM estimator rests on three assumptions: the dependent variable is stationary; the error term is serially uncorrelated;⁷ and the moment conditions for the validity of the instruments are met. The first assumption is automatically met because the Gini coefficient is bounded in the interval [0,1]. For the second assumption, we use the m₁ and m₂ test statistics proposed by Bond (2002) to conduct the test. For the moment conditions, we use the standard GMM test of over-identifying restrictions, or the Sargan test. Under the null that the moment conditions are valid, the Sargan statistic has an asymptotic chi-square distribution. Because the number of total instruments is different in difference estimations, in this paper we provide the p-value of each of the Sargan statistics.

3.2. Control variables

We have included in x_it per-capita income, its square, village population (in logarithm), share of emigrant workers, unemployment rate, and the coefficients of variation of household size, average schooling years of adult household members, household per-capita landholding, and number of wage earners in a household. Per-capita income and its square are included to capture the Kuznets curve. Village population is included to control for the possibility that the Gini coefficient is linked to village size (for example, households in a larger village tended to be more heterogeneous so income inequality could be higher). An emigrant worker is a person who works more than six months outside his own county. Share of emigrant workers is included because it is found in the literature that it is the more educated people that are more likely to migrate to the city (Zhao, 1999), which may have different impacts on within-village income distribution depending on the nature of emigration. If people emigrate by families, then a village with a larger share of emigrants will have a more equal income distribution. But if emigration is seasonal or the amount of remittance is large, then a village with more emigrants will have a more unequal income distribution because emigrants’ education usually has a larger return in their destinations than in their home villages. The NFS counts 300 days of unemployment as one unemployed person and the unemployment rate is defined as the share of unemployed persons in the total number of laborers in a village. It is natural to expect that a village with a higher unemployment rate would have a more unequal income distribution because it is the poorer portion of the population that are more likely to be unemployed. The four coefficients of variation (CVs) are included to control village variations along multiple dimensions of income sources. Supposedly, the Gini coefficient would become larger as the households become more dispersed along these dimensions. Descriptive statistics of the variables as well as the Gini coefficient and the election dummy are provided in Table 2.

Table 2.

Summary statistics for variables

Variable	Mean	Std. Dev.	Min	Max
Village variables (48 villages for the period 1987–2002)
Gini coefficient	0.28	0.08	0.09	0.69
Lower 10% income share (%)	4.29	1.78	0.00	12.27
Lower 20% income share (%)	9.69	2.99	0.00	17.85
Lower 30% income share (%)	16.10	4.10	2.02	26.70
Lower 40% income share (%)	23.43	5.20	3.10	36.78
Election dummy	0.7	0.46	0	1
Per-capita net income (1000 Yuan)	6.42	12.39	0.37	119.78
Village population (logarithm)	7.06	0.71	5.46	8.57
Share of emigrant workers (%)	14.51	13.42	0.00	65.91
Unemployment rate (%)	0.18	0.69	0.00	17.09
CV of household size	0.34	0.08	0.12	0.79
CV of household adults’ average schooling years	0.35	0.11	0.04	1.00
CV of per-capita household landholding	0.58	0.72	0.04	5.57
CV of number of household wage earners	2.05	1.45	0.00	5.57
Per-capita public expenditures (1000 Yuan)	0.39	2.98	0.00	82.07
Household variables (1,111 households for the period of 1987–2002)
Per-capita net transfer income	64.3	286.70	−349.9	2439.77
Per-capita total transfer income	97.04	283.2	0	2519.29
Per-capita net earned income (1000 Yuan)	2.32	2.47	−12.10	113.32
Per-capita landholding (mu)	1.36	1.89	0.00	24.00
Average age	31.70	9.56	8.20	82.50
Male ratio	0.55	0.21	0.00	1.00
Average schooling years of adults	5.20	1.87	0.00	12.00

Notes: All financial data are measured in 2002 Yuan using the rural CPI published by China Statistical Yearbook as the deflator. Net income is household income net of operational cost, taxes, and fees, plus transfer income. Taxes are income handed over to higher-level governments above the village. Fees are collected to finance the operation of the village government and village public good provision. The exchange rate between Yuan and US dollar is 7.11 Yuan to 1 dollar as of March 2008. One mu is one fifteenth of a hectare. Per-capita public expenditures are for 1986–2002.

Some further discussions about the control variables are warranted for their relationships with the estimation of the effect of elections. Supposedly, elections can reduce income inequality in two broad ways. One is the direct way in which the elected village committee either increases income transfers to the poor or invests more in pro-poor public projects. The other way is indirect and may be specific to the Chinese reality. After the rural reform began at the end of the 1970s, the Chinese land tenure has become a two-tier system in which land is legally owned by the village but farmed by individual farmers. The village has the right to redistribute land periodically in response to demographic changes so land distribution can be maintained at a relatively egalitarian manner (Dong, 1996). Therefore, one source of elections’ positive effects in reducing income inequality could be that the elected village committee redistributes village land to the advantage of the poor. Another source could be that the elected village committee raises the education of the poor, and a third source could be for the committee to spend more resources to generate jobs for the poor. By including the CVs of landholding, adult education, and the number of wage earners, our econometric models provide an estimate for the direct (marginal) effect of elections. In addition to this direct effect, we will also estimate our model by taking out all the control variables. This will give us the estimate for the gross effect of elections, that is, the sum of its direct and indirect effects.

3.3. Instruments

For the IV estimation of both the static and dynamic models, we find three instruments for the election dummy: a dummy indicating whether a province has adopted the OLVC and two variables describing lineages in a village: the number of surnames and the percentage of population of the largest surname in a village. While the use of the first variable is self-evident, some explanations are needed for the last two variables. Since parties other than the communist party are not allowed, villagers have to find other vehicles for political mobilization. Although the role of lineages has diminished considerably in village life after the harsh suppression happening between 1949 and 1978, it seems that organizing along the line of lineages is a natural choice of the candidates when it comes to competing for votes in elections. Many studies found that lineages played a significant role in the village political life (Huang, 1998; Dong, 2002; Liu et al., 2001). There can be two kinds of story for the roles of the two lineage variables to play in elections. One is based on the premise that families with the same surname share common interests because they belong to the same lineage. When the number of surname is large, contests of interests could become more intensified so the demand for elections becomes higher. On the other hand, the dominance of a single surname would defuse the need for elections as people in the village tend to share the same interests from the beginning. The other kind of story recognizes the problem of coordination. When a village has many surnames and is not dominated by a large surname, it could be difficult for it to even organize an election. Both stories, however, indicate that lineages are important factors affecting the timing of the first election. Zhang et al. (2004) also used our two variables of surnames as instruments for the introduction of elections. We improve upon their work by adding a province’s adoption of the OLVC as another instrument. Since the distribution of surnames does not change in a meaningful way over time, we interact the two variables of surnames with the provincial adoption dummy and use them together with the latter in the first-stage regressions. This gives us the advantage to do the first-stage regressions also using the two-way fixed-effect model.

There is a possibility that lineages also have a direct impact on income distribution because risk and income sharing may happen within a surname. However, Huang (1998) found that income sharing was weak among kinship groups; instead, “[t]he connection and interaction between kin members nowadays is becoming more based on individual interests than merely on reciprocity and the obligation to aid one another.” (Huang, 1998; pp. 188) Even if income sharing happens among the same surname, the scope of reciprocity is likely to be confined within a small number of closely knitted families.⁸ In this case, income inequality within the entire village may not be reduced by income sharing, just like club convergence does not necessarily lead to σ-convergence of income in the world. Therefore, we contend that the two lineage variables are reasonable instruments for the introduction of village elections.

Variations in these two variables are large. The smallest number of surnames was 1, but the largest was 147, with the average being 18.4. The smallest population share of the largest surname was 7% while the largest was 100%, with the average being 43.2%. When we run a regression of the election dummy on the three instruments and the village and year dummies using the linear probability model, we yield an R² of 0.68 and an F-statistic of 21.0. All the three instruments are highly significant. The adoption of the OLVC by a province increases the chances of its villages to start elections by 26%. Conditional on the adoption of the OLVC at the provincial level, the chances of having elections increase by 0.2% for one percent increase of the population share of the largest surname, but decrease by 0.4% for one more surname in the village. So it seems that the coordination story makes more sense. On the other hand, we have also found that none of the three instrumental variables are significantly correlated with the village Gini coefficient. Therefore, they are reasonable instruments.

3.4. Results for the Gini coefficient

The results of the static models are presented in Table 3. The number of observations is 707 after observations with missing data are dropped. We run four regressions. Regressions (1) and (2) treat the introduction of elections as exogenous and estimate its total and direct effects, respectively, and regressions (3) and (4) estimate the two effects again, but treat elections as endogenous. Regression (1) shows that elections reduce the Gini coefficient by 0.015, and the effect is significant at the 5% significance level. However, regression (2) finds that the effect of elections is highly insignificant. This shows that there are significant correlations between elections and the control variables. These correlations are either a result of the interaction between elections and the control variables or a result of their correlations with some other common uncontrolled factors. It seems that the second possibility is more plausible because by using IVs for elections, regressions (3) and (4) show that the total and direct effects of elections are both significant at the 1% significance level. Regression (3) shows that the gross effect is −0.087, and regression (4) shows that the direct effect is −0.074. To choose between these models, we rely on Hausman statistic to test the endogeneity of the election dummy. As it is often of interest to just compare the estimates of the parameters of interest rather than comparing the estimates of a linear combination of the parameters (Wooldridge, 2002), we test the endogeneity of elections by just comparing the estimates on the election dummy. In this case, the Hausman statistic is just the t statistic with the numerator to be the difference between the IV estimate and the fixed-effect estimate, and the denominator is the square root of the difference between the squared standard error between these two estimates. Table 3 indicates that the endogeneity tests get a t statistic of −3.91 for the gross effect model and −3.41 for the direct effect model. Both statistics strongly reject the null of the exogeneity of the election dummy. Later we perform the same set of tests for the dynamic model by comparing the estimates from the IV regression treating just the lagged dependent variable as endogenous, and that treating both the lagged dependent variable and elections as endogenous. The resulted t statistic for the gross effect dynamic model is −2.39, and that for the direct effect dynamic model is −1.86. As both test statistics indicate that we cannot treat elections as exogenous, we will only report results when elections are treated endogenous in later estimations that only involve village-level data.

Table 3.

Elections’ impacts on the Gini coefficient: static models

	Elections exogenous		Elections endogenous
	(1)	(2)	(3)	(4)
Election dummy	−0.015** (0.006)	−0.004 (0.006)	−0.087*** (0.019)	−0.074*** (0.021)
Per-capita net income (1000 Yuan)		0.001** (0.000)		0.001** (0.000)
Per-capita net income squared		−0.000** (0.000)		−0.000** (0.000)
Log village population		0.043** (0.020)		0.044** (0.022)
Share of emigrant workers		0.000 (0.000)		−0.000 (0.000)
Unemployment rate		−0.001 (0.003)		−0.002 (0.003)
CV of household size		0.119*** (0.031)		0.091** (0.036)
CV of average schooling years of household adults		−0.008 (0.034)		−0.045 (0.039)
CV of per-capita household landholding		0.000 (0.005)		0.003 (0.005)
CV of number of household wage earners		0.014*** (0.002)		0.009*** (0.003)
Constant	0.263*** (0.006)	−0.101 (0.138)	0.280*** (0.008)	−0.068 (0.153)
Year Dummies	Y	Y	Y	Y
Adjusted R2	0.704	0.729	0.637	0.668
Hausman t statistic for endogeneity of elections		−3.91***		−3.41***

Notes: The dependent variable is the Gini coefficient. The number of observations is 707 for 48 villages in the period of 1987–2002. Villages 3304, 3307, 4312, 4314 miss data between 1992 and 1999, and village 6211 misses data before 2000. To keep the maximum number of villages, non-missing observations between 1987 and 1991 are kept for villages 3304, 3307, 4312, 4314, and village 6211 is kept with data after 2000. Regressions (1) and (2) treat elections exogenous and are estimated by the standard two-way fixed-effect panel method. Regressions (3) and (4) treat elections endogenous and are estimated by the two-stage-least-squares fixed-effect panel method. The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames and the percentage of population of the largest surname in a village are used as instruments for village elections. The linear probability model is assumed for the first-stage estimation. Figures in parentheses are standard errors.

^{* , **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

Regressions (2) and (4) produce qualitatively similar results for the control variables. Income and its square are significant and their signs are consistent with the Kuznets curve. Village population and the CVs of household size and number of wage earners are significant and increase the Gini, but other variables are not significant.

The estimation results of the dynamic models are presented in Table 4. Regression (1) estimates the gross effect and regression (2) estimates the direct effect. Since the m₁ and m₂ statistics indicate that the first-order differenced error term has significant first-order serial correlation but there is no significant second serial correlation, the null of no serial correlations for the level error terms is not rejected. In addition, the Sargan statistic gives a p-value of 1 for all the four specifications, indicating that the over-identifying restrictions are not rejected. Therefore there is no evidence against the appropriateness of the current specification.

Table 4.

Elections’ impacts on the Gini coefficient: dynamic models

	(1)	(2)
Lagged Gini	0.352*** (0.097)	0.295* (0.152)
Election dummy	−0.026* (0.015)	−0.040** (0.016)
Per-capita net income (1000 Yuan)		0.002** (0.001)
Per-capita net income squared		−0.908e–6 (0.839e–6)
Log village population		−0.007 (0.037)
Share of emigrant workers (%)		0.001 (0.002)
Unemployment rate (%)		0.001 (0.001)
CV of household size		0.194 (0.182)
CV of average schooling years of household adults		−0.016 (0.055)
CV of per-capita household landholding		0.016 (0.019)
CV of household wage earners		0.003 (0.002)
Constant	0.004*** (0.001)	0.003** (0.001)
Year Dummies	Y	Y
m1	−3.36	−2.55
m2	0.66	0.49
Sargan p-value	1.000	1.000

Notes: The dependent variable is the Gini coefficient. The sample is the one used by the regressions reported in Table 3. All results are estimated using the two-step GMM method proposed by Arellano and Bond (1991), and Bond (2002). Year dummies are included in all models. Both regressions treat elections endogenous. The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames and the percentage of population of the largest surname in a village are used as instruments for village elections. The linear probability model is assumed for the first-stage estimation. Figures in parentheses are robust standard errors.

^{*, **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

As for the estimation results, lagged Gini has a significant coefficient, indicating that there exists path-dependence in the series of Gini. The election dummy is shown to significantly reduce the Gini coefficient. Unlike in the static models, the gross effect is smaller than the direct effect, which means that some of the indirect effects cancel each other when path-dependence of the Gini coefficient is controlled for. Both effects are economically significant. The gross effect is to reduce the Gini coefficient by 0.026, which is 9.3% of the sample average of 0.28. The direct effect is estimated at 0.040, or 14.3% of the sample average. The average Gini increased by 0.05 in our sample period of 15 years. The estimate of the direct effect means that having elections will wipe out 80 percent of this increase. The steady-state values of the gross and direct effects are 0.040 and 0.058, respectively. These are large effects even compared with the highest value that the Gini coefficient had reached in our sample. However, their magnitudes should be weighed against the steady-state value of the Gini. Income inequality is still rising in rural China and is unlikely to stabilize in a short period of time. So it is premature to judge the relative magnitudes of elections’ long-term effects based on the income inequality currently observed. For now, we are more confident in elections’ short-term effects.

The above results of elections may suffer from the problem that the introduction of elections might have been concurrent with the implementation of some government policies that reduce income inequality in the countryside.⁹ This problem may have a bite because by 1999 all but two villages had introduced elections so our panel estimates for elections’ impacts lose counterfactuals. Here we adopt a simple approach to tackle this problem, which is to rerun our regressions on a sub-sample of 1987–1998. By 1998 there were 8 villages in the sample that had not introduced elections so our panel estimation has a relatively large set of counterfactuals. The results of the dynamic model regressions are presented in Table 5. The m₁ and m₂ statistics show no evidence of first-order serial correlations for the level error terms and the Sargan statistic indicates that the over-identifying restrictions are not rejected. The results largely agree with those shown in Tables 3 and 4 although there are more significant results among them than among those in Table 4. In particular, both the gross and direct effects of elections remain significant. The sizes of estimates are smaller than what are found with the full sample, but are still substantial. The gross effect is to reduce the Gini coefficient by 0.015, which is 5.6% of the sample mean of 0.27 for the period of 1987–1998, and 50% of the growth of the Gini coefficient in the same period. In addition, the statistical significance of the gross effect has been raised from 10% in the full sample to 1% in the current sub-sample. Therefore, our estimates for elections’ effects on income distribution cannot be attributed to the concurrent introduction of pro-poor government policies and village elections.

Table 5.

Dynamic models: 1987–1998 sub-sample

	(1)	(2)
Lagged Gini	0.575*** (0.049)	0.476*** (0.103)
Election dummy	−0.015*** (0.005)	−0.021* (0.011)
Per-capita net income (1000 Yuan)		0.001 (0.001)
Per-capita net income squared		−7.35e–06 (8.44e–06)
Log village population		0.049 (0.070)
Share of emigrant workers (%)		0.0001 (0.0002)
Unemployment rate (%)		0.002* (0.001)
CV of household size		0.026 (0.026)
CV of average schooling years of household adults		−0.150 (0.107)
CV of per-capita household landholding		−0.023* (0.012)
CV of household wage earners		0.006*** (0.002)
Constant	0.002*** (0.000)	0.002* (0.001)
Year Dummies	Y	Y
m1	−4.01	−3.44
m2	−1.67	−1.50
Sargan p-value	1.000	1.000

Notes: The dependent variable is the Gini coefficient. The data range is from 1987 to 1998. After first differencing and taking lags 442 observations for 47 villages are used in the estimations. All results are estimated using the two-step GMM method proposed by Arellano and Bond (1991), and Bond (2002). Year dummies are included in all models. Both regressions treat elections endogenous. The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames and the percentage of population of the largest surname in a village are used as instruments for village elections. The linear probability model is assumed for the first-stage estimation. Figures in parentheses are robust standard errors.

^{*, **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

3.5. Results for the poorer population

The Gini coefficient is a measure of the overall inequality and improvements on it may not be a direct result of improvements made to the income shares of the poorest portions of the population. To show that elections improve income distribution through genuinely pro-poor policies, we need to prove that they increase the income shares of the lower percentiles of population. For that, we study elections’ impacts on the income shares of the lower 10%, 20%, 30%, and 40% of population and present selected results in Table 6 (the basic statistics of the dependent variables can be found in Table 2). For each income group, we estimate both the static and dynamic models, and within each model we study both the gross and direct effect of elections. The specifications of the regressions are the same as those used for the Gini coefficient except now the dependent variables are changed to the shares of income. The static models show that elections have significantly positive gross and direct effects on the income shares of all the four income groups. The gross effects for the lower 10%, 20%, 30%, and 40% of population are, respectively, 37.3%, 25.8%, 26.1%, and 22.2% of their respective sample means. These are very large effects. The direct effects are only slightly smaller, and in the case of the lower 10% of population, the direct effect is even slightly larger than the gross effect. It is also interesting to find that the effect is significantly larger for the lower 10% of population than for the other three groups of population, and it is the smallest for the lower 40% of population. The results from the dynamic models are much weaker, though. Although all the estimates are still positive, but we find significant results only for the gross effects on the lower 10% and 30% of population and for the direct effect on the lower 20% of population. However, even with those weaker results, the same pattern established by the static models still holds, i.e., elections tend to have more pronounced impacts on poorer groups than on richer groups of the population. In other words, elections improve income distribution more likely by leading to pro-poor policies.

Table 6.

Elections’ impacts on income shares of the lower 40% of population

	Lagged dependent variable	Election dummy
Lower 10%
Static model: gross effect		0.016*** (0.004)
Static model: direct effect		0.017*** (0.005)
Dynamic model: gross effect	0.382*** (0.091)	0.006*** (0.002)
Dynamic model: direct effect	0.141 (0.156)	0.003 (0.004)
Lower 20%
Static model: gross effect		0.025*** (0.007)
Static model: direct effect		0.022*** (0.008)
Dynamic model: gross effect	0.329*** (0.113)	0.006 (0.005)
Dynamic model: direct effect	0.008 (0.182)	0.011** (0.006)
Lower 30%
Static model: gross effect		0.042*** (0.010)
Static model: direct effect		0.038*** (0.011)
Dynamic model: gross effect	0.511*** (0.117)	0.015*** (0.007)
Dynamic model: direct effect	0.375 (0.260)	0.020 (0.014)
Lower 40%
Static model: gross effect		0.052*** (0.012)
Static model: direct effect		0.046*** (0.014)
Dynamic model: gross effect	0.339*** (0.116)	0.010 (0.010)
Dynamic model: direct effect	0.311 (0.192)	0.003 (0.019)

Notes: The dependent variables are shares of income in decimal terms. The regressions are based on data for 45 villages in the period of 1987–2002 with various data lengths. Both village and year fixed effects are included in each regression. All models are estimated treating the election dummy endogenous. Instruments and estimation methods are the same as used in previous tables. Dynamic models pass all the tests. Results of other variables are not shown. Figures in parentheses are robust standard errors.

^{*, **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

4. Sources of elections’ positive effects on income equality

We found in the last section that elections’ positive effects on income equality remained after a set of variables of a reasonable range were controlled for. That is to say, elections have a significant direct effect on income distribution. As we discussed before, the direct effect could come from two possible sources. One is for the village to engage in more pro-poor income transfers, and the other is to increase public investment that benefits the poor more. The first kind of actions is detrimental to economic growth (Alesina and Rodrik, 1994), but the second kind may help growth. In particular, if it is not financed by more taxes but by reallocation within government budget from consumption to investment, public investment has a much larger chance to help growth. However, the NFS does not provide information on public investment. Instead, it provides information on village public expenditures. Public expenditures include three items: transfer income to households, spending on local public services such as schools and village clinics, and investment in productive projects such as roads and irrigation. The first item is income redistribution, and the other two items are public investment. NFS does not provide village-level information on these specific items. However, its household survey provides information on the amount of fees that a household pays to the village and the amount of income that a household receives from the village.¹⁰ Fees are collected by the village to finance village affairs, including the operational costs of the village committee and public expenditures.

Using the available village and household-level information, we form a strategy to test whether elections have improved income distribution by more redistribution of income or by more public investment. We will first study how village elections change the amount of net transfer income that a household gets from the village. Net transfer income is defined as the amount of transfer income minus the amount of fees. If elections do not affect its level and progressiveness, we know that the improvement of income equality is not caused by more income redistribution. Next we will study village elections’ impact on public investment. This amounts to studying elections’ impacts on public expenditures and total transfer income. If elections increase the former but do not affect the level of the latter, then we know that public investment must have increased because transfer income and public investment are the only two components of public expenditures.

We obtain the figures for fees and transfer income for the period 1987–2002 from the accompanying household survey of the NFS. After households with missing data are dropped, 1,111 households remain in the sample. The longest time span is 16 years and the shortest is 5 years. The figures for public expenditures are obtained from the village survey of the NFS. There are 47 villages in the sample providing 695 observations with valid data for the period of 1986 to 2002. We have converted all the financial data into 2002 Yuan and use their per-capita figures in regressions. The basic statistics of the three dependent variables can be found in Table 2.

4.1. Net transfer income

For net transfer income, we are interested in both the average effect of elections and their effect on households with different levels of income. The latter is concerned with the relative income of a household in its village. For that purpose, we define the variable of relative income by dividing household per-capita net earned income (i.e., net income before taxation and transfer income) by the village mean earned income. If income redistribution is progressive, a higher relative income will result in a smaller amount of net transfer income. The equation that we will estimate is the following dynamic panel model:

$$W_{\mathit{ijt}}=\lambda W_{\mathit{ijt}-1}+{\alpha }_1{E}_{jt}+{\alpha }_2{Y}_{\mathit{ijt}}+{\beta }_1{E}_{jt}+Y_{\mathit{ijt}}+Z_{\mathit{ijt}}{\beta }_2+{\alpha }_{ij}+w{\beta }_3+e_{\mathit{ijt}},t=2,\dots ,T,$$ (3)

where W_ijt is per-capita net transfer income (Yuan) of the ith household in village j in year t, Y_ijt is its relative income, Z_ijt is a set of family characteristics that may affect its payment of fees and transfer income, α_ij is the fixed-effect for this household, w is the set of year dummies, and e_ijt is an i.i.d. error term. Z_ijt includes per-capita landholding (mu), average age, male ratio, and average schooling years of adults. All these variables are meant to control family attributes that may affect the amount of fees paid by a household and the amount of transfer income received by it. Their basic statistics can be found in Table 2. The parameter α₁ captures elections’ impact on the level of net transfer income, and the parameter β₁ captures their impact on the progressiveness of income transfer in terms of earned income.

Before we run the regressions we need to test the stationarity of the dependent variable. As discussed by Richard Blundell, Stephen Bond, and Frank Windmeijer (2000) and Michael Binder, Cheng Hsiao, and M. Hashem Pesaran (2005), the first-difference GMM estimator breaks down in the case of a unit root dependent variable. To see whether the series of net transfer income is stationary, we perform the Levin–Lin–Chu (LLC) panel unit root test as proposed in Andrew Levin, Chien-Fu Lin, and Chia-shang Chu (2002). One can view this test as a pooled Augmented Dickey–Fuller (ADF) test when lags are included, with the null hypothesis of nonstationarity (I(1) behavior). This test is suitable for the current dataset, as it is designed for panel data of moderate sample size like ours, and allows for individual effects, time effects and possibly a time trend. Serial correlation in the error term is also allowed. In addition, the LLC test has the nice feature that the proposed t-star statistic is distributed standard normal under the null hypothesis of nonstationarity so that it is very convenient to make inference. Table 7 provides the Levin–Lin–Chu panel data unit root test statistics for net transfer income. The LLC panel data unit root test rejects the null of nonstationarity at the 1% significance level.

Table 7.

Panel data unit-root tests for net transfer income

Chosen deterministics	Lag	Coefficient	t-value	t-star	P>t
(1)	(2)	(3)	(4)	(5)	(6)
Constant	1	−0.71	−141.75	−126.15	0.000
Constant	2	−0.36	−54.05	−4.85	0.000
Constant and trend	1	−0.94	−229.13	−198.04	0.000
Constant and trend	2	−0.69	−66.77	−17.50	0.000

Notes: Column (1) allows different specifications of the deterministic terms, column (2) allows different lag orders used in the LLC test, column (3) gives the estimated coefficients, column (4) gives the usual t-values, and columns (5) and (6) provide the t-star statistics for inference and their p-values.

While elections appear to be an endogenous explanatory variable for the village-level data, it is not necessarily so for the household-level data because the households covered in our panel study are only a small sample from each village. We have performed the Hausman t test for the endogeneity of elections following the suggestion of Wooldridge (2002). The t statistic indicates that the null of the exogeneity of elections survives with a large margin. Table 8 therefore provides the results for net transfer income treating elections as exogenous.

Table 8.

Effects of elections on net transfer income

	(1)	(2)
Lagged net transfer income	0.809*** (0.008)	0.808*** (0.008)
Election dummy	−2.234 (3.541)	−7.191 (5.082)
Relative per-capita net earned income	−9.076*** (2.326)	−15.424*** (5.220)
Election dummy×Relative Per-capita net earned income		7.900 (5.809)
Per-capita land (mu)	−2.512*** (0.796)	−2.560*** (0.797)
Average age	0.336** (0.168)	0.326* (0.168)
Male ratio	8.026 (7.005)	7.943 (7.005)
Average schooling years of adults	−0.408 (0.811)	−0.400 (0.811)
Constant	4.055 (11.248)	8.467 (11.706)
Year dummies	Yes	Yes
Hausman t statistic for endogeneity of elections	1.46	1.29

Notes: The dependent variable is per-capita net transfer income. Elections are treated as exogenous. The number of observations is 13,131 for 1,111 households in the period of 1988–2002. GMM is used to estimate each model. The Hausman t statistic is calculated based on Wooldridge (2002). The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames in a village and the percentage of population of the largest surnames are used as the instruments for elections. The linear probability model is assumed for the first-stage estimation.

^{*, **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

Both regressions show that net transfer income is progressive in terms of relative earned income and per-capita landholding. By the short-run estimates provided in regression (1), a family would receive about 9.08 Yuan less of net transfer income if its earned income increased by an amount of the village average income, and having one mu more of land would lead to a reduction of 2.51 Yuan. Neither is large effect. Although equality by household size is emphasized in land allocation (Liu et al., 1998), land distribution deviates from equality because of demographic changes. The progressiveness of income redistribution with respect to landholding is a kind of compensation to this deviation. The most important result is that elections are shown to have no significant impact on either the level or the progressiveness of net transfer income. This concludes our first step to prove that elections improve income distribution not by engaging in more income redistribution or making it more progressive.

4.2. Public investment

The regression that we will run for public expenditures are the dynamic panel models presented in Eq. (2) where the Gini coefficient is replaced by per-capita public expenditures in the village. The control variables are the same as before. We only study the direct effect of elections so all the control variables are put in the regressions. We do this because we want to know channels of elections’ direct effect on income distribution. Table 9 presents the results. Now elections are treated as endogenous as we did for other village-level regressions. Again, the LLC panel data unit root test rejects the null of nonstationarity at the 1% significance level. In addition, the m₁ and m₂ statistics show no evidence of first-order serial correlations for the level error terms and the Sargan statistic indicates that the over-identifying restrictions are not rejected.

Table 9.

Effects of elections on village per-capita public expenditures

Variables	Estimated Coefficients
Lagged public expenditures	0.205*** (0.040)
Election dummy	0.271* (0.142)
Per-capita net income (1000 Yuan)	0.046*** (0.008)
Per-capita net income squared	−0.000*** (0.000)
Log village population	1.735*** (0.323)
Share of emigrant workers (%)	0.003* (0.002)
Unemployment rate (%)	−0.008 (0.011)
CV of household size	−0.033 (0.556)
CV of average edu. of household adults	−0.477 (0.824)
CV of per-capita household landholding	0.008 (0.214)
CV of number of household wage earners	0.045* (0.027)
Constant	−0.025** (0.011)
Year dummies	Yes
m1	−1.38
m2	0.20
Sargan p-value	1.00

Notes: The dependent variable is per-capita public expenditures (1000 Yuan) in 2002 Yuan. After differencing and taking lags, 695 observations for 47 villages in the period of 1987–2002 are in the sample. The model is estimated using the two-step GMM method proposed by Arellano and Bond (1991), and Bond (2002). The election dummy is treated endogenous. The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames and the percentage of population of the largest surname in a village are used as instruments for village elections. The linear probability model is assumed for the first-stage estimation. Figures in parentheses are robust standard errors.

^{*, **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

Elections are shown to significantly increase public expenditures. The magnitude of the effect is 237 Yuan, which is substantial because the sample average is 390 Yuan. The statistically significant control variables are village per-capita income, its square, village population, and the CV of the number of household wage earners. The effect of per-capita income shows an inverse U curve. The other two significant variables increase public expenditures. It seems that there is a scale effect that enables a larger village to afford more public expenditures. On the other hand, a more diverse village in terms of industrial employment may be correlated with a more vibrant local industry that provides a village more financial resources for public expenditures.

To show elections’ effects on public investment, our remaining task is to study how per-capita total transfer income changes as a village begins to hold elections. To that end, we repeat the two regressions for net transfer income by replacing the dependent variable with per-capita total transfer income. The Hausman t statistics again indicate that the null of the exogeneity of election to household is not rejected. The results are presented in Table 10 treating elections as exogenous.

Table 10.

Effects of elections on per-capita total transfer income

	(1)	(2)
Lagged total transfer Income	0.810*** (0.008)	0.810*** (0.008)
Election dummy	4.973 (3.511)	1.877 (5.047)
Election dummy×relative Per-capita net earned income		4.952 (5.801)
Relative per-capita net Earned income	−9.650*** (2.307)	−13.642*** (5.218)
Per-capita land (mu)	−0.314 (0.787)	−0.341 (0.788)
Average age	0.332** (0.167)	0.325* (0.167)
Male ratio	5.303 (6.962)	5.240 (6.962)
Average schooling years of adults	0.235 (0.806)	0.242 (0.806)
Constant	−2.803 (11.195)	11.100 (11.593)
Year dummies	Yes	Yes
Hausman t statistic for Endogeneity of elections	1.60	1.38

Notes: The dependent variable is per-capita total transfer income received by a household in 2002 Yuan. There are 13,131 observations for 1111 households for the period of 1988–2002. GMM is used to estimate each model. The Hausman t statistic is calculated based on Wooldridge (2002). The timing of a province’s adoption of the OLVC and its interactive terms with the number of surnames and the percentage of population of the largest surname in a village are used as instruments for village elections. The linear probability model is assumed for the first-stage estimation. Robust standard errors are in parentheses.

^{* , **, and ***}indicate the 10%, 5%, and 1% significance level, respectively.

Total transfer income is shown to be progressive with respect to relative earned income, but not with respect to landholding. As in the case of net transfer income, elections are not significant in affecting either the level or the progressiveness of total transfer income. This concludes our second step of proof with a positive result that elections improve income distribution by increasing public investment.

5. Conclusions

In this paper we use a unique panel data set to study the effects of grassroots democracy on income distribution. Using the dynamic panel model and accounting for the endogeneity of the election, we have found that the direct effect of elections is to reduce the Gini coefficient by 14.3% and its gross effect is to do so by 9.3%. We have also found that elections tend to increase the income shares of the poorer portions than of the richer portions of population, so their positive effect in reducing the Gini coefficient is more likely to be brought by pro-poor policies. Further econometric analysis has shown that elections have not significantly changed the level and progressiveness of net and total transfer income. In addition, elections are found to significantly increase per-capita public expenditures. Therefore, the reduction of the Gini coefficient is not a result of pro-poor income redistribution, but instead a result of increased public investment. Since the level of public goods provision is generally low in rural China, it is reasonable to believe that poor households would benefit more from increased public investment because the rich can rely more on their own investment to generate income.¹¹

Our work contributes to the analysis of decentralized governance in weakly institutionalized polities that by far the academia lacks sufficient understanding on (Acemoglu, 2005). We show that grassroots democracy works to enhance local governance even in the highly centralized political system in China. The period covered by our study was one when income inequality in rural China rose up quickly, so our finding of the positive role of village elections in reducing income inequality by way of more public investment is especially significant. Inside China, village elections have been frequently criticized as an expensive yet ineffective device to strengthen the accountability of the village government. Our results provide strong evidence to disqualify such criticisms.