Role of intraglomerular circuits in shaping temporally structured responses to naturalistic inhalation-driven sensory input to the olfactory bulb

Abstract

Olfaction in mammals is a dynamic process driven by the inhalation of air through the nasal cavity. Inhalation determines the temporal structure of sensory neuron responses and shapes the neural dynamics underlying central olfactory processing. Inhalation-linked bursts of activity among olfactory bulb (OB) output neurons [mitral/tufted cells (MCs)] are temporally transformed relative to those of sensory neurons. We investigated how OB circuits shape inhalation-driven dynamics in MCs using a modeling approach that was highly constrained by experimental results. First, we constructed models of canonical OB circuits that included mono- and disynaptic feedforward excitation, recurrent inhibition and feedforward inhibition of the MC. We then used experimental data to drive inputs to the models and to tune parameters; inputs were derived from sensory neuron responses during natural odorant sampling (sniffing) in awake rats, and model output was compared with recordings of MC responses to odorants sampled with the same sniff waveforms. This approach allowed us to identify OB circuit features underlying the temporal transformation of sensory inputs into inhalation-linked patterns of MC spike output. We found that realistic input-output transformations can be achieved independently by multiple circuits, including feedforward inhibition with slow onset and decay kinetics and parallel feedforward MC excitation mediated by external tufted cells. We also found that recurrent and feedforward inhibition had differential impacts on MC firing rates and on inhalation-linked response dynamics. These results highlight the importance of investigating neural circuits in a naturalistic context and provide a framework for further explorations of signal processing by OB networks.

in the mammalian olfactory system, neural representations of olfactory information are organized into temporally discrete “packets” that are tightly coupled to the respiratory cycle (Schaefer and Margrie 2007; Wachowiak 2011). Respiration-coupled activity is prominent at all levels of olfactory processing, including sensory neurons [olfactory receptor neurons (ORNs)], neurons of the olfactory bulb (OB) and olfactory cortical areas, and typically occurs as transient (100–200 ms) bursts of excitation and inhibition linked to particular latencies or phases of the respiratory cycle. This stereotyped dynamic structure may play a critical role in odor information processing by creating a temporal window within which odor information is encoded among neurons of the OB and integrated by downstream neurons in olfactory cortical networks (Bathellier et al. 2008; Cury and Uchida 2010; Miura et al. 2012; Schaefer and Margrie 2007; Shusterman et al. 2011). There is also substantial behavioral evidence that the precise dynamics of activity within this respiration-linked window shapes odor perception (Abraham et al. 2010; Smear et al. 2011; Wesson et al. 2008). Thus understanding how respiratory patterning of olfactory activity arises is critical to understanding the neural mechanisms underlying odor coding.

Respiration-linked packets of activity first arise among ORNs, where inhalation drives a transient burst of excitation in a subset of odorant-responsive ORNs that converge to specific OB glomeruli (Carey et al. 2009; Chaput and Chalansonnet 1997; Spors et al. 2006; Wesson et al. 2008). Output from the OB via mitral/tufted cells (MCs) is also transient and linked to inhalation but is distinct from the simple excitatory bursts of ORN input, with MCs showing odorant- and cell-specific sequences of excitation and inhibition (Carey and Wachowiak 2011; Cury and Uchida 2010; Shusterman et al. 2011). At the population level, odorant-evoked excitatory responses of MCs show a shorter duration and shorter rise time than do those of ORNs (Carey and Wachowiak 2011). This “temporal sharpening” of respiration-linked excitation is a key feature of the input-output transformation performed by the OB network. However, which circuit elements mediate this transformation remains unclear.

The network of connections localized to the glomerular layer, which we refer to as the glomerular network, has been ascribed a major role in shaping MC response dynamics. The glomerular network includes connections between ORNs, MCs, several classes of GABAergic inhibitory interneurons and at least one type of excitatory interneuron (external tufted, or ET, cells) (Gire et al. 2012; Gire and Schoppa 2009; Hayar et al. 2004a; Shao et al. 2009; Wachowiak and Shipley 2006). Glomerular circuits hypothesized to be important in shaping respiration-coupled MC response dynamics include feedforward excitation mediated by ET cells, feedforward intraglomerular inhibition mediated by periglomerular (PG) neurons, recurrent inhibition (RI) mediated by reciprocal connections between PG, ET and MCs, as well as interglomerular inhibitory connections formed by short-axon cells (Gire and Schoppa 2009; Liu et al. 2013; Shao et al. 2012, 2013; Wachowiak and Shipley 2006). The intrinsic properties of these neuron types may also play an important role in shaping temporally-structured activity in the OB. For example, the intrinsic bursting of ET cells generates patterned excitation in the frequency range of natural sniffing behavior (Hayar et al. 2004b), and the intrinsic properties of MCs appear to facilitate temporally precise and well-structured output in response to phasic inputs, such as those driven by inhalation (Balu et al. 2004; Desmaisons et al. 1999; Heyward et al. 2001; Margrie and Schaefer 2003; Rubin and Cleland 2006). With a few exceptions, however (Cang and Isaacson 2003; Fukunaga et al. 2012; Phillips et al. 2012; Schaefer et al. 2006), these phenomena have been largely described in OB slice experiments, and thus the contribution of synaptic and intrinsic properties of glomerular neurons to the temporal sharpening of inhalation-driven ORN inputs in vivo, and in particular during natural odor sampling, remains unclear.

Here, we used a small-network modeling approach to explore how several well-described OB circuits might contribute to the temporal shaping of sensory inputs driven by inhalation. Using biophysically-based models of major OB circuit elements, we asked what are the minimal circuits necessary to transform inhalation-driven packets of sensory input into temporally-sharpened bursts of MC output. Model simulation and evaluation were highly integrated with experimental data: we used dynamic input patterns derived from recordings of ORN population responses during naturalistic odorant sampling (i.e., sniffing), then used single-unit recordings from MC responses evoked by the same naturalistic odorant sniffs to evaluate the accuracy of model output (Carey and Wachowiak 2011). This approach identified several features of glomerular circuits that shape MC spiking responses with realistic inhalation-coupled temporal structure, including slow-onset and slowly-decaying inhibition and parallel feedforward excitation via ORNs and ET cells. Overall these results establish a computational framework for further investigation of input-output transformations by OB networks in the context of active olfactory sensation.

MATERIALS AND METHODS

Model design.

The MC model (and simulated RI) was taken from Bathellier et al. (2006); the PG cell model was modified from the Hodgkin-Huxley implementation of Moehlis (2006) to include a fast-inactivating transient potassium current (Puopolo and Belluzzi 1998). The ET cell model was generated from a minimal single-compartment Hodgkin-Huxley-style model which includes only those active currents necessary for bursting in the absence of sensory input (Sherwood et al. 2010). Each of these single cell models includes several ionic currents; the current balance equations for the membrane voltage of the respective cells are as follows.

1) MC:

$$\text{d}V/\text{d}t\text{=}-\left(I_{\text{Na}}\text{+}{I}_{\text{NaP}}\text{+}{I}_{\text{Ka}}\text{+}{I}_{\text{Kfast}}\text{+}{I}_{\text{Ks}}\text{+}{I}_{\text{L}}\right)/C$$

2) ET:

$$\text{d}V/\text{d}t\text{=}-\left(I_{\text{Na}}\text{+}{I}_{\text{NaP}}\text{+}{I}_{\text{Kfast}}\text{+}{I}_{\text{CaT}}\text{+}{I}_{\text{H}}\text{+}{I}_{\text{L}}\right)/C$$

3) PG:

$$\text{d}V/\text{d}t\text{=}-\left(I_{\text{Na}}\text{+}{I}_{Ka}\text{+}{I}_{\text{Kfast}}\text{+}{I}_{\text{L}}\right)/C$$

where C is capacitance. Here the ionic current symbols are as follows: I_Na, fast transient sodium; I_NaP, persistent sodium; I_Kfast, delayed rectifier potassium; I_Ka, fast-inactivating transient potassium; I_Ks, slow-inactivating transient potassium; I_H, hyperpolarization-activated cation; and I_CaT, T-type calcium current. As usual, I_L = g_L (V − V_L), where I_L is leak current, g_L is leak conductance, V is membrane voltage, and V_L is leak reversal potential. The kinetic equations and parameter values for each current were derived from the references above and may differ among cell types.

The implementation of RI between MCs and PG or granule cells (GC) was modified from Bathellier et al. (2006), with each MC spike triggering a slowly-decaying inhibitory synaptic conductance (g_syn) [difference of exponentials: latency time (t_latency) = 1 ms, rise time (τ_rise) = 1 ms, decay time (τ_decay) = 500 ms, synaptic reversal potential (V_rev) = −70 mV]. Shorter RI decay values matching those of Bathellier et al. (τ_decay = 150 ms) yielded similar results. The excitatory synaptic connection between the ET and MC models simulates fast, nonadapting excitation using a model adapted from a two-state α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid/kainite receptor-mediated synaptic transmission model (Destexhe et al. 1994). This synaptic current takes the form I_syn = g_[ET-MC] s(V_ET)(V_MC − V_rev), where g_[ET-MC] is maximum conductance for ET-MC synapse, V_ET is membrane voltage of the ET cell model, and V_MC is membrane voltage of the MC model. Here s(V_ET) represents the level of transmitter release and obeys the differential equation ds/dt = α/{1.0 + exp[−(V_ET − V_1/2)/k]}(1 − s) − β × s, where α = 2.16 and β = 0.216, V_1/2 is membrane voltage at half-maximal release, and k determines the steepness of the voltage-dependent logistic function. The “fast” feedforward inhibitory PG-MC synapse uses the same form. The “slow” feedforward inhibition (FFI) synapse is also nonadapting and is based on a model for second-messenger-activated synaptic transmission (Destexhe et al. 1994), with kinetic parameters adjusted using a parameter search and exponential curve fitting to match the desired rise and decay times (τ_rise of 14 ms and τ_decay of 140 ms, 170 ms, or 200 ms; see results).

Models were implemented in Matlab, and simulations were performed using the “ode15s” differential equation solver. For efficiency of simulation, capacitance and conductance constants were rescaled, and in most cases combined. As a result, conductance values (e.g., g_[ET-MC] and g_L) provided have arbitrary units and depend on the postsynaptic neuron type; we do not attempt to provide biologically-relevant units or to make conductance values comparable across neuron types. Detailed descriptions of the cellular and synaptic model components can be found in the references cited above, while parameter values and source code implementing the intraglomerular network models described below can be found in the ModelDB database (Hines et al. 2004) (http://senselab.med.yale.edu/modeldb/default.asp; Model no. 152111).

Modeling experimentally derived synaptic inputs.

Dynamic sensory inputs to all model circuits were derived from ORN responses recorded from anesthetized rats using published data taken from calcium imaging from ORN presynaptic terminals (Carey and Wachowiak 2011), in which odorants were naturalistically sampled using a “sniff playback” approach to reproduce intranasal pressure transients generated (and previously recorded from) awake, head-fixed rats (Cheung et al. 2009). A total of 25 ORN input traces were used, with each trace representing the presynaptic calcium signal imaged from a distinct glomerulus. The 25 traces encompassed a range of different odorants and odorant concentrations, as follows: [0.2% saturated vapor ethyl butyrate (n = 4 glomeruli), 0.5% ethyl butyrate (1), 1% ethyl butyrate (6), 2% ethyl butyrate (2), 2% menthone (3); 0.5% propyl acetate (2), 1.5% propyl acetate (1), 0.5% heptanal (6)]. Data were compiled from 4 rats.

To convert presynaptic calcium signals into synaptic inputs for the model, raw imaging traces from individual glomeruli were preprocessed to remove photobleaching effects and low-pass filtered. Traces were then temporally deconvolved (Verhagen et al. 2007; Yaksi and Friedrich 2006) to generate an estimate of the change in action potential firing rate across the imaged ORN population. Next, to simulate a population of ORNs converging onto their postsynaptic target, the deconvolved population firing rate trace was scaled to a peak rate of 50 Hz (Duchamp-Viret et al. 2000) and used as the rate function for 500 independent inhomogeneous Poisson processes, representing 500 convergent ORN spike trains. Because short-term plasticity in the form of presynaptic inhibition and synaptic depression is well-established at the ORN synapse (Aroniadou-Anderjaska et al. 2000; Murphy et al. 2004; Wachowiak et al. 2005), we next implemented a depression function that attenuated the amount of spike-driven transmitter release based on the interval from the previous spike, following the paired-pulse depression model from Murphy et al. (2004), with a time constant of recovery of 675 ms and maximal attenuation of 82%. Each scaled spike train was then convolved with a simulated excitatory postsynaptic current (difference of two exponentials with τ_rise = 1 ms and τ_decay = 2 ms) to generate an ORN input trace, all of which were then averaged to generate the synaptic input current from the ORN population, I_ORN(t). This input current was multiplied by an input gain factor G with arbitrary units (analogous to an effective g_syn for the ORN synapse) and then injected into the model. Thus, in each model studied, the current from the ORN to each postsynaptic target N takes the functional form I_syn = G_[ORN-N] I_ORN(t), where I_ORN(t) is independent of the state of the postsynaptic neuron.

Analysis of model MC and ET output.

Sniff-triggered spike time histograms [peristimulus time histograms (PSTHs), bin size, 20 ms] were generated for each model MC, and temporal response parameters (peak firing rate, response duration, response latency) were measured from a double-sigmoid curve fit to each PSTH, as described previously for experimental data (Carey and Wachowiak 2011). For visual comparison of model and experimental MC response dynamics, for each unit instantaneous firing rate was calculated from each interspike interval and interpolated between spike times to generate a continuous firing rate trace (Carey and Wachowiak 2011). These traces were then averaged across all model or experimental units.

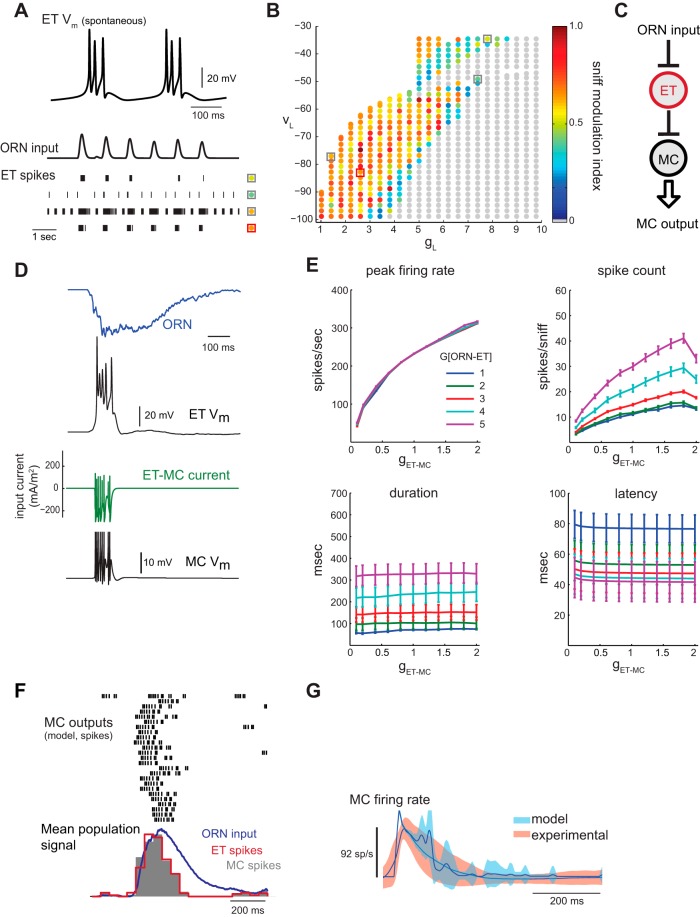
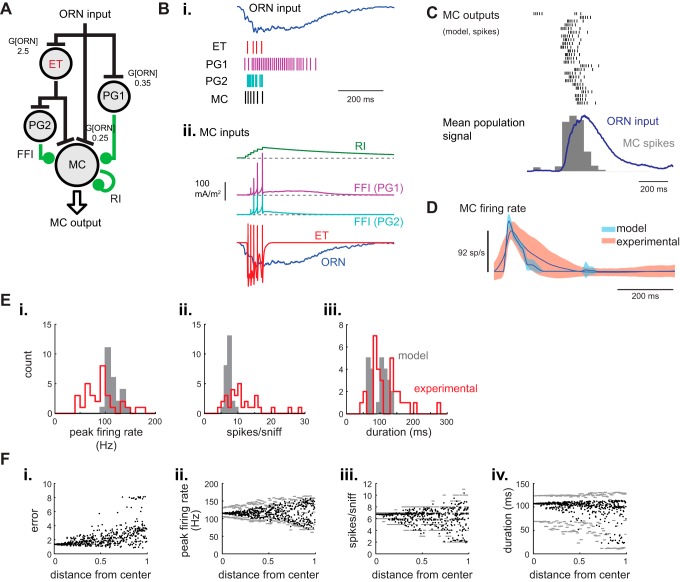
For ET cell calibration, a sniff modulation index (“SMI”, see Fig. 4) was calculated for inhalations at 1 Hz by generating a PSTH using only “burst spikes” (spikes that were within 50 ms of another spike), ignoring isolated spikes, then defining SMI as (PSTH_max − PSTH_min)/“nonsniffspikes”, where “nonsniffspikes” was the total number of spikes evoked outside the sniff responses. This factor penalized tonic firing, as well as bursting between sniffs. Modulation indexes were calculated for ET cell responses to ORN input gains of 2.4 and 4.8, and these two indexes were summed to generate the final SMI plotted in Fig. 4.

Fig. 4.

Generating patterned MC output via feedforward excitation mediated by external tufted (ET) cells. A: spontaneous (top) and ORN-driven responses during inhalation in a model ET cell. See text for details of ET cell model. Top trace shows spontaneous bursting of ET cell in the absence of synaptic input. Bottom traces show rasters of ET cell spikes evoked by a sequence of inhalation-driven ORN input bursts. Each row of spikes represents a different set of ET cell leak parameters (V_L, g_L), indicated by square and colored circle corresponding to a location in the (V_L, g_L) plane shown in C. Depending on leak parameters, the ET cell may spike, burst, or fire tonically in response to inhalation-linked ORN input. B: exploration of model ET cell leak parameters to optimize inhalation-linked modulation of spiking. Pseudocolor points indicate the degree of modulation of spike rate by inhalation, quantified as sniff modulation index (SMI, see materials and methods) for each (V_L, g_L) pair in response to the ORN input trace shown in A. The ET responses at the boxed (V_L, g_L) points are shown in the spike rasters in B to illustrate ET behavior in several regions of the parameter space. The center of the region where the highest SMI values were observed is located near g_L = 2.6, V_L = −85 mV (red box, orange point). In this region, the ET model is generally silent in the absence of ORN input and generates a brief spike burst in response to each inhalation (e.g., bottom spike raster in A). These leak parameters were used for all subsequent ET cell simulations. C: schematic of ORN-ET-MC circuit model. D: example traces of ORN input, ET cell response (V_m), ET cell-driven current to the MC, and MC response (V_m). ET spiking output shows bursting linked to the onset of sniff-driven ORN input. The MC, coupled to the ET model through an excitatory synapse, follows the ET cell bursting pattern. G_[ORN-ET] = 4, g_[ET-MC] = 0.3. E: effect of ET-MC synaptic strength (g_[ET-MC]) on response dynamics in the ORN-ET-MC model for five ORN-ET input gains (G_[ORN-ET]). Peak firing rates increase dramatically with ET-MC synaptic strength, while spike counts increase more modestly. MC response duration and latency are unaffected by changes in ET-MC synaptic strength, suggesting that these parameters are determined by the shape, but not the magnitude, of the ET synaptic input. In contrast, peak firing rate is completely unaffected by the ORN-ET input gain. F: response of ORN-ET-MC model to the 25 different sniff-driven ORN input waveforms, showing spike rasters and population histogram (gray) for each model MC response, as in previous figures. The populations spike histogram of each ET cell response is also shown (red trace). Parameters are set as in D. G: dynamics of experimental and model MC firing rate responses relative to time of inhalation for the ORN-ET-MC model. The main discrepancies from the experimental dataset with this model are in the slightly faster onset and slightly elevated firing rates during the decay phase of the response.

In the parallel excitation model (notation: ORN-[ET]-MC; see Fig. 5A), we provided excitatory input to the MC through both the ORN-MC and ORN-ET-MC pathways. The ORN-MC pathway is a current with gain G_[ORN-MC], while the ET-MC pathway is a conductance with maximal synaptic conductance g_[ET-MC]; these gain and maximal conductance values are not directly comparable. Thus, for each input pathway, we quantified its effective strength by computing the charge per presynaptic action potential passed to the MC, averaged over our set of test stimuli. More formally, the mean charge per presynaptic action potential transferred via the ET-MC synapse, Q_ET-MC, was computed for each test stimulus (sniff) by integrating the ET-MC synaptic current over time and dividing by the number of ET spikes. The mean charge transfer for the ORN-MC synapse, Q_ORN-MC, for each input trace, was computed similarly by computing the integral of current I_ORN(t) divided by the time interval equal to the average duration of an ET spike. The ratio of Q_ET-MC to Q_ORN-MC was then averaged over the whole set of test inputs. We found that <Q_ORN-MC/Q_ET-MC> = 3.9 ± 1.7 (SD); i.e., the effective strength of the ORN-MC pathway is 3.9 ± 1.7 times that of the ORN-ET-MC pathway. This correction factor was used to normalize the gain and conductance parameters into effective “input strength” values via each pathway, having arbitrary units (see axes of Fig. 5, B and E). With this normalization, equal input strengths (points along the diagonal) correspond to 50/50 mean charge contribution of each pathway. In reality these axes represent g_[ET-MC] (on the horizontal axis) and G_[ORN-MC]/3.9 (on the vertical axis). This correction factor was further used to determine the synaptic strength between the ET and PG cell in the integrated model; because ORN inputs are 3.9 times “stronger” than ET inputs, g_[ET-PG] (ET-PG conductance) was set as 3.9 × G_[ORN-PG] (ORN-PG input gain).

Fig. 5.

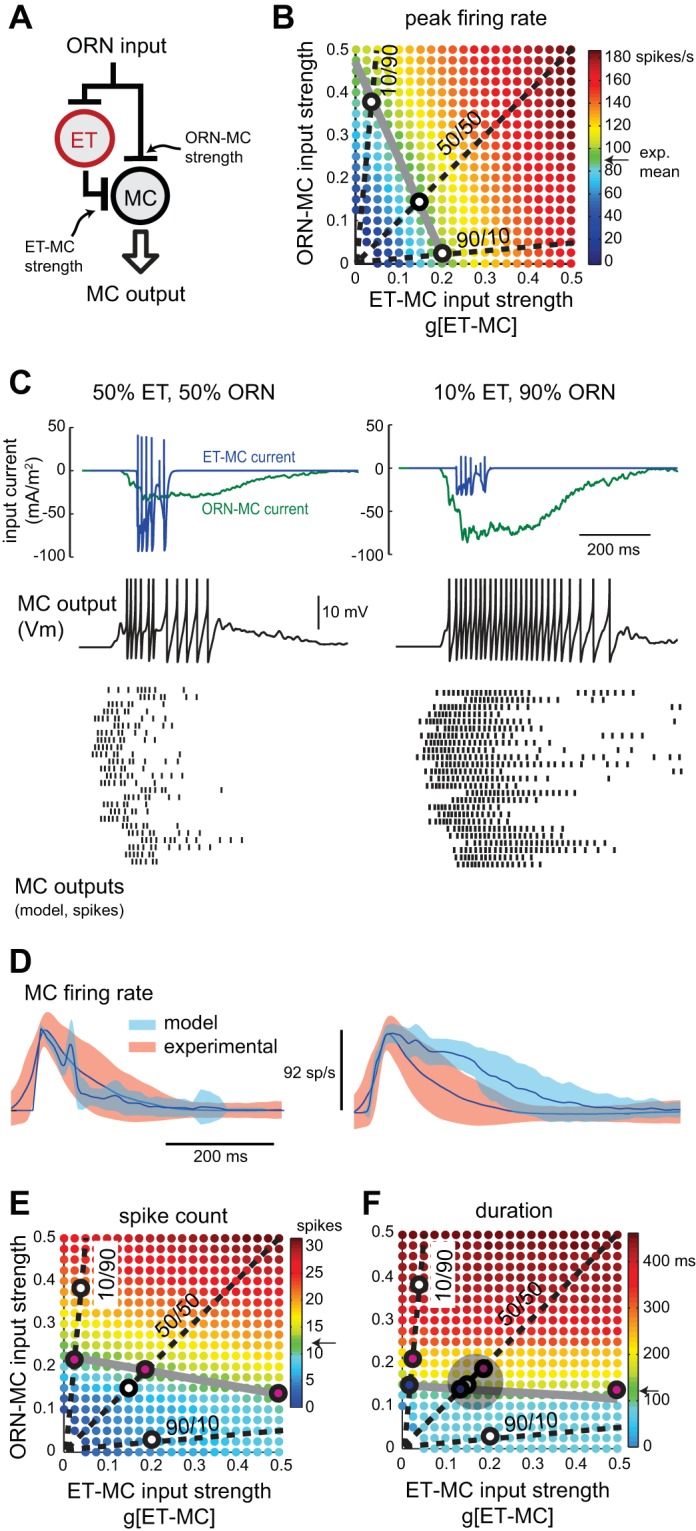
Exploring parallel excitatory input pathways in the glomerular circuit. A: schematic of ORN-[ET]-MC parallel excitation model. MC and ET cell receive direct ORN input, and the MC also receives excitatory input from the ET cell. B: peak firing rate as relative strengths of feedforward ET-MC excitation (horizontal axis) and direct ORN-MC excitation (vertical axis) are varied. Units for ORN-MC input strength are scaled so that equivalent values represent equivalent charge transfer to the MC compared with ET-MC inputs; see materials and methods for calculation. Dashed lines indicate parameter pairs where ET-MC/ORN-MC input strength ratio is 10/90, 50/50 and 90/10. Gray line indicates parameter pairs where ORN-[ET]-MC model peak firing rate approximates the experimental mean rate of 92 spikes/s. The intersections (white circles) of the dashed lines and gray line occur at parameter pairs that produce peak firing rates matching the experimental mean for each input strength ratio. C: sniff-driven MC output from the ORN-[ET]-MC model at the “optimal” parameter values (indicated by white circles in B) at ET-MC/ORN-MC input strength ratios of 50/50 (left), and 10/90 (right). Top traces show input currents to the MC originating from ORNs (green) and ET cells (blue) for a representative ORN input waveform. Middle trace shows the MC V_m response. At bottom are MC spike rasters for all 25 ORN input waveforms at the two input strength ratios. G_[ORN-ET] is fixed at 1.5. D: comparison of ORN-[ET]-MC model and experimental relative firing rates for the 50/50 (left) and 50/50 (right) input strength ratios. Parameter values are set as in C. Model MC firing dynamics closely match those of the experimental dataset for the 50/50 input ratio, while the 10/90 ratio results in longer MC spike bursts more similar to the ORN-MC model output. E: effect of relative strengths of ET-MC and ORN-MC inputs on sniff-driven spike count. Dashed lines indicate parameter pairs where ET-MC/ORN-MC input strength ratio is 10/90, 50/50 and 90/10, as in B. Gray line indicates parameter pairs where spike count matches the experimental mean of 12 spikes/sniff. The intersections (magenta circles) of the dashed and gray lines occur at parameter pairs that produce experiment-matched spike counts for the respective input strength ratios. White circles indicate parameter pairs that produce experiment-matched peak firing rates, from B. F: effect of relative strengths of ET-MC and ORN-MC excitation on sniff-driven MC burst duration, with dashed lines and symbols representing input ratios and matches to the experimental mean, as in E. Blue filled circles at the intersection of the dashed and gray lines indicate parameter pairs that produce experimentally matched burst durations for each input strength ratio. White and magenta circles are transferred from B and E and represent experimentally matched parameter pairs for peak rate and spike count, respectively. The white, magenta and blue circles on the 50/50 line cluster closest to one another (within the light gray circle), indicating that model output can approximate the experimental dataset across peak firing rate, spike count, and duration measures simultaneously when the ET-MC/ORN-MC input strength ratio is ∼50/50. For the 90/10 ratio, duration and spike count are simultaneously optimal, but peak firing rate is too high (∼160 spikes/s). For the 10/90 ratio, no output measures may be optimized simultaneously.

RESULTS

Overview of approach.

Our goal was to explore the contribution of several known OB circuits to the temporal sharpening of sensory inputs that is a hallmark of OB input-output transformations in vivo. Rather than explore all potential known circuits, our approach was to identify one or more minimal circuit configurations that transformed inhalation-driven input patterns into bursts of MC output that matched those recorded in vivo. To this end, we implemented a series of models of roughly increasing circuit complexity and attempted to optimize model performance at each iteration. Each cellular element in the model was implemented as a single-compartment, Hodgkin-Huxley model neuron using parameters taken from previously described models or from experimentally measured intrinsic properties (see materials and methods and text below for details). Each cell type was represented by a single point-source element meant to represent the population of all such neuron types within a glomerular module. Different relative numbers of each cell type were encapsulated in the relative synaptic strength parameters specified in the text. We did not include tonic activity in any model elements, although tonic levels of excitatory and inhibitory synaptic transmission are present in vivo and in OB slices (Hayar et al. 2004b; Pírez and Wachowiak 2008; Shao et al. 2009). Additional simplifying assumptions specific to each circuit model are given in their respective sections below.

We implemented the following OB circuits: 1) a MC receiving direct ORN input and no inhibition (ORN-MC); 2) the ORN-MC circuit with RI mediated by PG and/or GC (ORN-MC_RI); 3) the ORN-MC circuit with PG cell-mediated FFI (ORN-PG-MC); 4) a feedforward excitatory circuit mediated by ET cells (ORN-ET-MC); 5) a feedforward excitatory circuit consisting of the ORN-MC and ORN-ET-MC circuits in parallel (ORN-[ET]-MC); and 6) an “integrated” model consisting of the parallel feedforward excitatory circuit (5) with the addition of one ORN-PG and one ORN-ET-PG feedforward inhibitory circuit. Naturalistic “sensory” inputs to the models consisted of dynamic synaptic inputs that were derived from odorant-evoked ORN presynaptic calcium signals during natural sampling (i.e., “sniffing”) of odorants (Carey et al. 2009; Carey and Wachowiak 2011). Finally, model output (in the form of MC spiking patterns) was tuned by varying synaptic strength parameters (see materials and methods) and evaluated by comparison to an experimental dataset consisting of extracellular recordings from presumptive MCs responding to odorants sampled at 1 Hz with the same naturalistic waveforms used to activate ORN inputs (Carey and Wachowiak 2011). Thus model construction and evaluation were both constrained by experimental data. We limited our evaluation to data from 1-Hz inhalations only to avoid confounds from frequency-dependent changes in circuit dynamics in this initial characterization.

It was neither computationally feasible nor desirable to explore all conceivable parameter combinations for each model. As our goal was to compare the input-output characteristics of different OB circuits, we held most parameters controlling the intrinsic properties of the cellular components fixed across circuit models. The only parameters varied were those with obvious importance for synaptic transmission and input integration: in particular, synaptic input gain, synaptic kinetics and cell excitability (g_L and V_L) (see materials and methods). For each model circuit, we explored a large, biologically plausible region of the hyperplane defined by these free parameters by incrementally varying each parameter and measuring model output in terms of the dynamics and magnitude of inhalation-driven MC spiking (additional details below). We then identified the parameter values leading to model output that most closely matched that of experimental measurements of response strength and dynamics. For each iteration of increasing circuit complexity, the parameters of the prior circuit were typically held fixed at their optimal values, and a new set of free parameters corresponding to the added circuit connections were explored and optimized using the same experimental benchmarks.

ORN-MC circuit.

We first tested how a monosynaptic connection between ORNs and MCs transformed dynamic, sniff-driven ORN inputs. The model MC was modified slightly from a previous, single-compartment biophysical model of the MC (Bathellier et al. 2006) which includes Hodgkin-Huxley channel kinetics that are well-constrained by published intrinsic parameters (see materials and methods). This model approximates the spike clustering that MCs exhibit in response to DC current injection in vitro (Fig. 1A) (Balu et al. 2004; Chen and Shepherd 1997; Desmaisons et al. 1999). A synaptic current waveform representing the “sniff-triggered” input from a population of homotypic ORNs converging onto a MC was derived from experimental measurements of odorant-evoked ORN activity and delivered to the model MC, as described in the materials and methods and below.

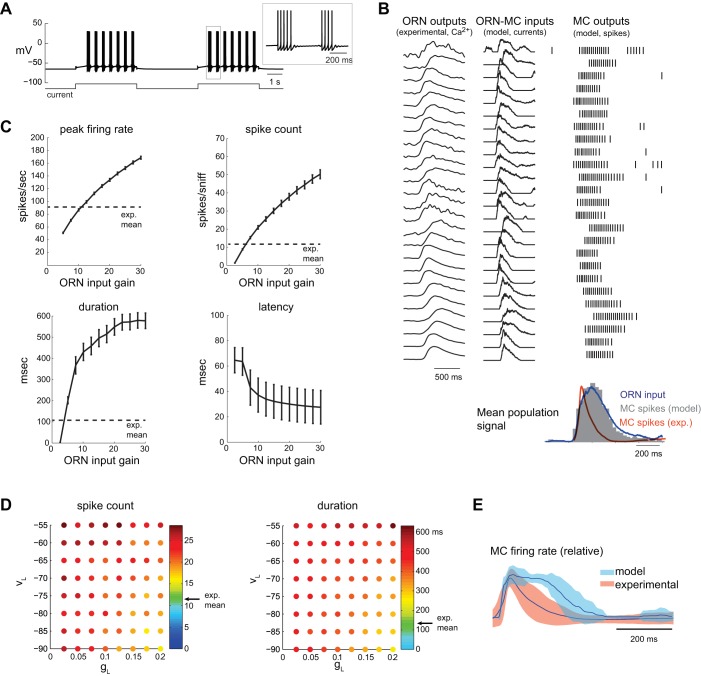
Fig. 1.

Response of model mitral/tufted cells (MC) to naturalistic sensory inputs. A: response of model MC to current step. MC responds with clusters of spikes, as seen in the simulated membrane voltage (V_m). Between spike clusters, the model exhibits subthreshold oscillations, which are visible in the inset. B: model MC responses to the experimentally obtained olfactory receptor neuron (ORN) input set {ORN-MC gain (G_[ORN-MC]) = 7.5}. Left: raw presynaptic calcium signals (gray) for the 25 different glomeruli used for the input dataset (see materials and methods). Center: ORN-MC synaptic input current waveforms for each MC. Right: spike rasters of MC firing responses to each of the sniff-driven inputs. Input currents are reversed in polarity to facilitate comparison to ORN calcium signals. Bottom: histogram of model MC spiking output (time bin = 20 ms, averaged across all inputs, dark gray), showing a close match to the ORN input population firing rate envelope (averaged across all inputs, blue). Orange trace shows average MC response firing rates from the experimental dataset, which consists of much shorter sniff-triggered bursts. Histogram and traces are scaled to the same peak value. C: effects of varying ORN input gain (G_[ORN-MC]) on different parameters of the sniff-driven model MC spike burst. Values for leak parameters were fixed in these examples at g_L (leak conductance) = 0.1 and V_L (leak reversal potential) = −65 mV. The peak firing rate, evoked spike count per sniff, and response duration all increase with ORN input gain, while latency decreases. Error bars show means ± SE of the MC response averaged across the population of 25 ORN inputs shown in B. D: effects of varying MC leak parameters on sniff-driven response dynamics. Each grid shows g_L vs. V_L. For each (g_L, V_L) point, ORN input gain is varied to achieve a mean MC peak firing rate (averaged across all 25 ORN inputs) matching that of the experimental dataset (92 spikes/s). Pseudocolor values at each point indicate the spike count (left) or burst duration (right) for that excitability value. Arrow (“exp. mean”, green pseudocolor) indicates the mean value of the experimental MC dataset. Both spike count and duration remain larger than the experimental mean values at all tested g_L and V_L values. E: dynamics of experimental and model MC firing rate responses relative to time of inhalation, averaged across all recorded (orange) or model (blue) units. g_L = 0.1, V_L = −65 mV, G_[ORN-MC] = 7.5. Before averaging, instantaneous firing rate was calculated from each interspike interval, and a continuous trace interpolated between spike times. Shading indicates variance (SD) around mean. The model MC population responds with a longer duration and broader peak firing profile. The experimental dataset represents the sniff-triggered response to the same sniff waveform recorded from 37 MCs (Carey and Wachowiak 2011).

In vivo, sniff-triggered ORN inputs to different glomeruli vary in the latency, rise-time and duration of their activation (Carey et al. 2009; Spors et al. 2006). To explore model MC responses across this range of dynamics, we used sniff-triggered presynaptic calcium signals imaged from ORN inputs to 25 different glomeruli in the awake rat. Figure 1B shows raw presynaptic calcium signals and derived synaptic input current waveforms (I_ORN-MC; see materials and methods) for each of the 25 ORN inputs, along with spike rasters of each model MCs response for a gain of 7.5 (tested range: 0–30). Note that these presynaptic signals already reflect the modulation of input strength by presynaptic inhibition mediated by glomerular circuits. In general, one sniff-triggered bout of ORN input elicited a discrete burst of action potentials in the model MC. Across the population, MC spiking dynamics approximated that of the presynaptic ORN inputs, as reflected in comparisons of individual I_ORN traces as well as in the comparison between “sniff-triggered” population averages of ORN and MC spiking patterns (Fig. 1B, bottom). However, model MC responses differed from the experimental dataset of presumptive MC responses to inhalation of odorant (n = 37 units), with experimentally recorded MC responses showing substantially shorter sniff-triggered spike bursts (Fig. 1B).

We attempted to maximize the correspondence between the model ORN-MC circuit output and experimental data by varying three parameters that influence MC excitability and are not well-constrained by prior data: the ORN input gain (G_[ORN-MC]) and the V_L and g_L of the model MC. To explore this parameter space, we used several measures of sniff-evoked firing patterns as benchmarks to compare model output with experimental data: peak firing rate, total number of sniff-evoked spikes and burst duration (Fig. 1C). Across the population of 25 ORN inputs, for fixed leak parameters in the MC (g_L = 0.1, V_L = −65 mV), increasing the ORN input gain increased peak firing rate, number of spikes and duration of the MC spike burst; increasing input gain also decreased the latency of the response relative to inhalation time, to a minimum of ∼30 ms (Fig. 1C).

To explore effects of MC excitability on response dynamics, we varied V_L and g_L systematically and, at each value, adjusted ORN input gain to achieve a mean peak firing rate across the MC population that most closely matched that of the experimental dataset. Figure 1D plots the spike count (left) and burst duration (right) values at the optimal gain level at each (V_L, g_L) combination. Mean values from the experimental dataset for each parameter are indicated by the color green in each subplot (∼12 spikes/sniff and a duration of ∼120 ms). For the range of leak parameters tested (which covers a biophysically realistic range of intrinsic excitability values), when input gain was adjusted to match peak firing rate, both spike count and duration were significantly higher than the mean values from the experimental dataset. As a result, even after optimizing model MC parameters, the population of model MC responses remained longer than that of experimentally recorded responses (Fig. 1E).

These results suggest that, while MC intrinsic properties can generate some degree of temporal patterning in response to unpatterned synaptic inputs (Balu et al. 2004; Rubin and Cleland 2006), the ORN-MC circuit by itself does not generate MC spiking patterns with a temporal structure matching those measured in vivo in response to natural odorant sampling. Rather, MC spiking responses roughly follow that of ORN synaptic input. Thus additional synaptic connections must be important to generate realistic respiration-patterned activity in MCs.

Next we added RI to the ORN-MC circuit model. In the context of our model, RI encompasses a variety of potential circuits, including inhibitory feedback from PG or GCs coupled through reciprocal dendrodendritic synapses (Fig. 2A) (Chen et al. 2000; Isaacson and Strowbridge 1998; Murphy et al. 2005; Schoppa and Urban 2003), as well as intraglomerular inhibition between different MCs innervating the same glomerulus. Rather than implementing an additional cell type (i.e., GCs) mediating RI, RI was modeled as a rapid-onset, slowly-decaying chloride conductance (τ_decay = 500 ms, V_rev = −70 mV; see materials and methods for details) triggered by each MC spike. The slow decay of RI was chosen based on evidence that RI between MCs and GCs, as well as inhibitory signaling from PG cells, involves long-lasting, asynchronous GABA release (Chen et al. 2000; Isaacson and Strowbridge 1998; Murphy et al. 2005; Schoppa et al. 1998; Smith and Jahr 2002). The time course of RI evoked by a single sniff, with the ORN input trace and the corresponding response in the model MC, is shown in Fig. 2B. The maximal conductance of the sniff-evoked RI input, g_RI, was varied to simulate different strengths of RI. The addition of RI strongly decreased peak firing rates and spike counts across the MC population, although this effect saturated as RI strength increased (Fig. 2C). Notably, however, response durations and latencies, and thus the overall shape of the sniff-triggered MC response, remained essentially unchanged (Fig. 2C). Optimizing RI strength to generate the best match across response descriptors of the experimental dataset, as was done for the intrinsic leak parameters of MC, led to peak spike rates and total spike counts that were smaller than experimental values (g_RI = 0.25, G_[ORN-MC] = 10; Fig. 2, D and E). Using a faster τ_decay of 150 ms as originally implemented by Bathellier et al. (2006) yielded similar results (not shown).

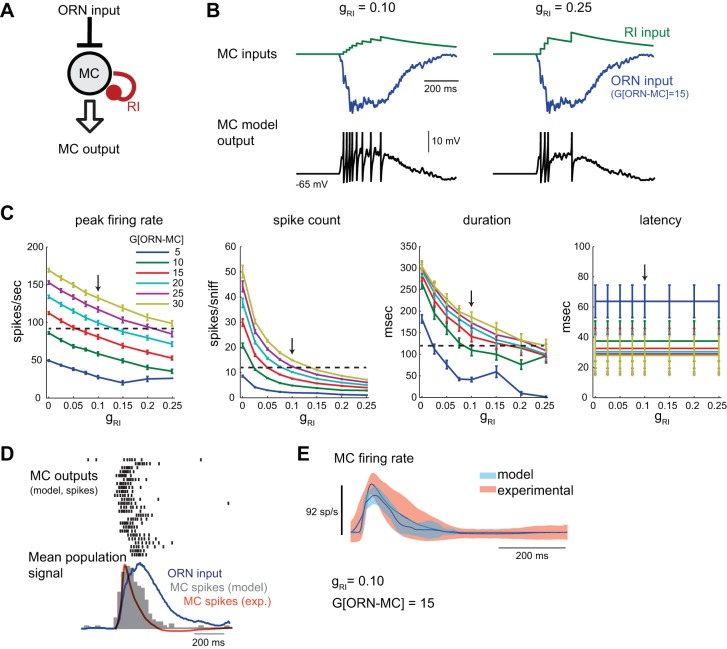
Fig. 2.

Effect of recurrent inhibition (RI) on model MC output. A: schematic of ORN-MC_RI model with RI simulating inhibitory feedback from periglomerular (PG) or granule cell (GC) neurons onto the MC after each MC spike. See text for details. B: input currents (RI, green; ORN, blue) to the model MC and MC V_m in response to one inhalation of odorant. As the strength of RI [RI conductance (g_RI)] is increased, MC spiking is reduced. Spikes are clipped. C: summary of effects of RI strength (g_RI) on response dynamics to sniff-driven ORN inputs at several ORN input gains (range tested: 0–30), averaged across all ORN inputs as in Fig 1 (mean ± SE). Increasing RI reduces peak MC firing rates, spike counts, and response durations, but has little effect on latencies. Horizontal dashed line indicates mean experimental value, as in Fig. 1; arrow indicates optimal value for RI strength (g_RI = 0.10) for best match across peak firing rate, spike count and duration for the model MC population. Latency values are also shown. D: response of ORN-MC_RI model to the 25 different sniff-driven ORN input waveforms. Spike rasters (top) and histogram (gray, bottom) of the model MC population show reduced firing rates compared with the ORN-MC model and moderate temporal sharpening relative to the dynamics of the ORN input, but the model MC population response remains longer than that of the experimental dataset (orange trace). g_RI = 0.10, G_[ORN-MC] = 15. E: mean and variance of experimental and model MC firing rate responses relative to time of inhalation, averaged across all recorded (orange) or model (blue) units as described above.

ORN-PG-MC circuit.

We next tested the effect of PG cell-mediated FFI on MC responses. In vitro experiments have implicated FFI in shaping both the excitability and temporal structure of MC responses to ORN input (Gire and Schoppa 2009; Shao et al. 2012, 2013). We implemented a model PG cell modified from a standard spiking Hodgkin-Huxley neuron (Moehlis 2006; Puopolo and Belluzzi 1998) which received excitatory ORN input and provided inhibitory input to the MC (Fig. 3A; see also materials and methods). The PG-MC synapse was first modeled using rapid kinetics consistent with “fast” GABA_A-mediated inhibition, in which each PG spike evoked a brief (τ_rise of 7 ms and τ_decay of 14 ms) conductance transient in the MC. Implementing the ORN-PG-MC circuit with this synapse tended to disrupt inhalation-linked patterning, primarily because FFI strongly suppressed MC spiking before coherent spike bursts could develop (Fig. 3B, right). At lower FFI strengths, MC spike bursts simply followed ORN input dynamics as in the ORN-MC circuit (Fig. 3B, left). Adjusting ORN input gain to both the PG and MC also failed to produce discrete MC spike bursts with each inhalation (not shown) due to the rapid onset time of FFI. Thus “fast” FFI was not able to produce a temporal sharpening of MC responses relative to ORN input bursts without also disrupting inhalation-linked patterning.

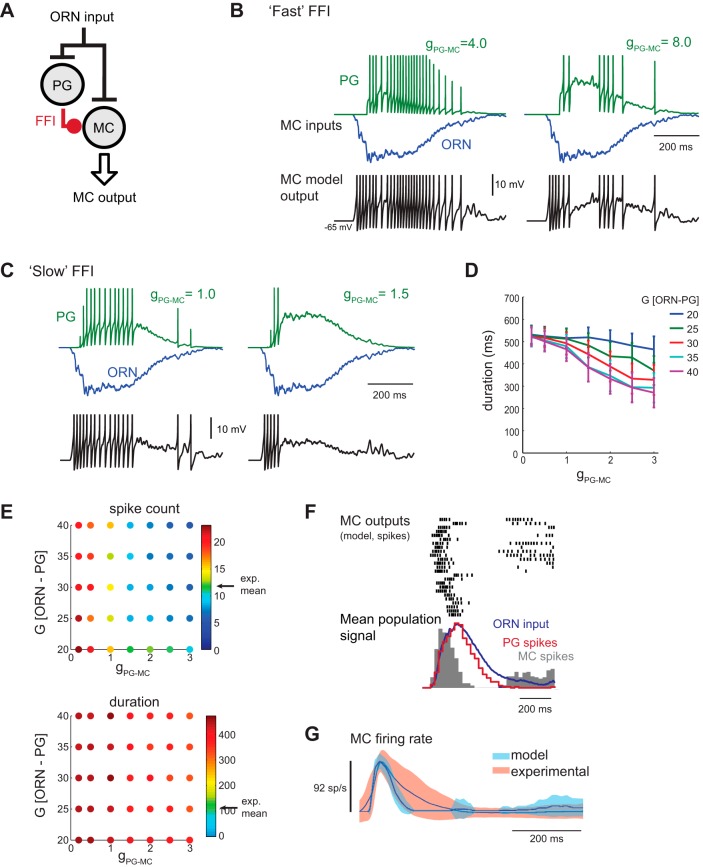
Fig. 3.

Effect of feedforward inhibition (FFI) on model MC output. A: schematic of glomerular circuit incorporating FFI. ORN input is injected simultaneously to the MC model and a single-compartment PG cell model. The PG cell provides inhibitory synaptic input to the MC. See text for details. B: example response of a model PG and MC to inhalation of odorant using the “fast” FFI synapse at two different FFI strengths (g_PG-MC = 4.0 and 8.0). Top traces show synaptic input currents to the model MC from the PG cell (PG, green trace) and from a sample ORN population (ORN, blue). Bottom trace shows model MC V_m. At low FFI strengths (left), MC spiking remains prolonged and roughly follows ORN input dynamics. At higher FFI strengths (right), MC spiking does not occur in a single burst and thus does not permit inhalation-linked spike patterning. ORN input gain (G_[ORN-PG] and G_[ORN-MC]) = 18. Spike-evoked synaptic input transients are clipped. C: input currents (FFI, green; ORN, blue) to the model MC and MC V_m in response to inhalation of odorant using the “slow” FFI synapse model at two different FFI strengths. The slower FFI current lags the ORN input current and accumulates over the course of the sniff, allowing the inhalation-linked MC spike burst to develop but shortening burst duration. ORN input gain values are different for PG and MC inputs: G_[ORN-PG] = 35; G_[ORN-MC] = 18. D: increasing the strength of slow FFI (g_PG-MC) reduces the duration of the model MC spike burst. Plots show mean ± SE of the burst duration averaged across all 25 ORN input traces for different gains of ORN input to the PG cell (G_[ORN-PG]). ORN input gain to the MC was held fixed (at 18). Due to its slow onset, response latency is unaffected by FFI (not shown). E: effects of varying FFI conductance (g_PG-MC) and input gain to the PG cell (G_[ORN-PG]) on spike count (top) and duration (bottom) of the sniff-driven MC spike burst. ORN input gain to the MC (G_[ORN-MC]) is calibrated at each tested point to generate a peak firing rate of ∼92 spikes/s. With the ORN-PG-MC model, spike counts matching the experimental dataset (arrow, “exp. mean”) can be achieved within a limited range of FFI strengths and ORN-PG input gains (indicated by green dots). Response durations remain longer than experimentally recorded values at all parameter combinations, primarily as a result of firing bursts late in the sniff phase. F: response of the ORN-PG-MC model to the 25 ORN input waveforms, showing spike rasters and population histogram (gray) for each model MC response as in Fig. 2D. The population spike histogram of each PG cell response is also shown (red trace). FFI conductance (g_PG-MC = 1.5) and gain (G_[ORN-PG] = 35; G_[ORN-MC] = 18) parameters were chosen to produce 92 spike/s peak MC firing rate. PG cell spiking roughly follows ORN input dynamics, while the MC spike burst is shortened and reaches a peak earlier relative to ORN inputs. Note the emergence of late-phase spiking in some MC units with this circuit. G: population mean and variance of experimental and model MC firing rate responses relative to time of inhalation for the ORN-PG-MC model. In contrast to the ORN-MC models in Figs. 1 and 2, the ORN-PG-MC population shows slightly shorter bursts than the experimental dataset.

In vitro, GABAergic FFI onto MCs can exhibit slow kinetics that may be mediated by prolonged, asynchronous release of transmitter from PG cells (Murphy et al. 2005; Smith and Jahr 2002) or by other intrinsic or network mechanisms (Cadetti and Belluzzi 2001; Liu et al. 2013; Shao et al. 2009). In a feedforward circuit, such kinetics could integrate ORN inputs and produce a delayed inhibition that could substantially alter the dynamics of the MC response. Thus we modified the kinetics of the PG-MC synapse to produce a slower rise and decay (τ_rise of 14 ms and τ_decay of 170 ms; see materials and methods for details). Figure 3C shows the excitatory (ORN) and FFI input currents to the model MC over the course of one inhalation. FFI accumulates more slowly over the course of the ORN input burst. Consequently, slow FFI, unlike RI or fast FFI, modulates the duration of the MC spike burst, with an inverted sigmoid relationship between the strength of the PG-MC synapse (g_[PG-MC]) and MC burst duration (Fig. 3D).

We tuned the ORN-PG-MC model to match experimental MC response dynamics using the same approach as for the ORN-MC circuit: G_[ORN-PG] and FFI strength (g_[PG-MC]) were varied (G_[ORN-PG] range: 20–40; g_[PG-MC] range: 0–3.0), and, at each of these parameter values, ORN-MC input gain was varied to match the mean experimental peak firing rate (∼92 Hz), after which total spike count and burst duration of the model MC were compared with the experimental data (Fig. 3E). Model optimization led to closer matches to experimental data than for the ORN-MC circuit, and the ORN-PG-MC model with slow FFI exhibited substantial temporal sharpening of the sniff-triggered MC spike burst relative to the dynamics of ORN input (Fig. 3, F and G). Qualitatively similar results were obtained with τ_decay values of 140 and 200 ms (not shown). Thus the gradual development of FFI over the course of a single inhalation significantly transformed ORN input dynamics into MC spike bursts that matched more closely those recorded from the intact OB in vivo.

ORN-ET-MC circuit.

We next investigated the role of ET cells in shaping MC spiking dynamics. ET cells provide significant feedforward excitatory input to MCs (De Saint Jan et al. 2009; Gire et al. 2012; Hayar et al. 2004a; Najac et al. 2011; Shao et al. 2012). ET cells intrinsically burst at frequencies in the range of inhalation frequencies in behaving rodents, can be entrained to phasic ORN input, and have been hypothesized to play a critical role in maintaining MC patterning by providing direct excitation to MC, driving FFI of PG cells, or both (Gire et al. 2012; Wachowiak and Shipley 2006). To our knowledge, however, bursting ET cells have not yet been incorporated into a network model of olfactory processing.

We generated an intrinsically bursting ET cell model (Fig. 4A) using a subset of active conductances known to be necessary for generating bursting in vitro (Hayar et al. 2004b; Liu and Shipley 2008b) (see materials and methods for conductances used). The parameters of the active conductances were optimized to match bursting behavior in the absence of synaptic input with experimental data reported from OB slices (Liu and Shipley 2008b; Sherwood et al. 2010). Additional currents important in modulating intrinsic or sensory-evoked bursting (Liu and Shipley 2008a, 2008b) were not included in this model. Excitability of the ET cell in the presence of sniff-driven sensory inputs was then tuned by adjusting the leak parameters V_L and g_L to achieve maximal entrainment to repeated sniffs (at 1-Hz sniff frequency). Entrainment was defined using a SMI (see materials and methods) that was highest when ET cell bursts occurred reliably to each sniff and did not occur between sniffs. Many V_L and g_L combinations resulted in a lack of ET cell responsiveness to ORN input, even at different input gains, while other combinations yielded poor entrainment due to weak responsiveness or near-continuous spiking (Fig. 4, A and B). We used the leak parameters V_L = −85 mV and g_L = 2.6 for all subsequent ET cell simulations, as they were centrally located within a large region with high SMIs. We note that this region was characterized by a lack of bursting in the absence of sensory input, although rhythmic, spontaneous bursting is a defining feature of ET cells. Slight increases in V_L and g_L did produce endogenous ET cell bursting. We nonetheless chose this region of the (V_L, g_L) parameter plane because ET cell behavior was more robust to changes in the strength of ORN input. We did not attempt to tune the ET cell SMI, or analyze ET cell spiking, at sniff frequencies above 1 Hz.

We incorporated the model ET cell into a simple feedforward excitatory circuit (ORN-ET-MC, Fig. 4C). In this circuit, the MC receives only feedforward excitation through a fast, nonadapting synapse with a reversal potential of 0 mV (Destexhe et al. 1994). Under these conditions, the ET cell responds to each sniff with a spike burst, and the MC also responds with bursts of similar latency and duration (Fig. 4D). The strength of the ET-MC connection (g_[ET-MC]) affected peak firing rate and total spike count of the MC response but had little effect on MC response duration or latency (Fig. 4E). Increasing the gain of ORN input to the ET cell led to increases in ET (and thus MC) burst duration and spike count and modest decreases in onset latency but had no effect on peak firing rate (Fig. 4E).

To optimize MC output dynamics of the ORN-ET-MC circuit, the g_[ET-MC] was adjusted to match mean peak MC firing rate to the experimental dataset in response to sniff-driven ORN inputs, after which the ORN input gain G_[ORN-ET] was adjusted to match the mean response durations from the experimental dataset (as G_[ORN-MC] had been for the ORN-MC model). After this optimization, the population dynamics of the ORN-ET-MC model roughly matched that of the experimental dataset, with spike bursts that were more transient than the simple ORN-MC model (Fig. 4, F and G). This model differed from the ORN-PG-MC circuit, however, in that MC response dynamics in the ORN-ET-MC circuit were largely determined by the dynamics of the ET cell's response (Fig. 4F). Thus MC spiking occurred in a temporal window demarcated by the ET cell's burst envelope, the start and end points of which were determined by the gain of the ORN-ET connection (tested range: 1–5) and the intrinsic bursting properties of the ET cell. As a result, MC response dynamics (latency and duration) could not be effectively modulated other than by changing ORN input strength (Fig. 4E).

Parallel feedforward inputs to MCs.

ORNs provide excitatory input to both MC and ET cells, although the degree to which MC excitation is mediated by ORN vs. ET cell input remains unclear (Gire et al. 2012; Najac et al. 2011; Shao et al. 2012). Thus we next implemented a feedforward excitatory circuit, including the ORN-MC and ORN-ET-MC pathways connected in parallel (notation: ORN-[ET]-MC; Fig. 5A) and explored the impact of different relative strengths of each pathway in shaping MC output dynamics. Relative strength was defined as the ratio of the charge per presynaptic action potential passed to the MC from ORNs directly vs. from the ET cell (see materials and methods for details).

We first explored how varying the strength of each pathway affected peak MC firing rates (Fig. 5B). Increasing the strength of either pathway led to increases in firing rate; however, the ET-MC synapse was ∼1.5 times as efficient in evoking changes in peak firing rate (e.g., increasing ET-MC or ORN-MC input strength from 0 to 0.4 led to firing rate increases to ∼140 and ∼90 Hz, respectively; Fig. 5B). A target MC peak firing rate (e.g., the experimental mean of ∼92 spikes/s) could be generated by a wide range of ORN-to-ET-input ratios (gray line, Fig. 5B). However, different ratios produced different temporal patterns of MC output. Examples of synaptic input currents to and spike output from a model MC, as well as spike output across the model population for two different ratios (all producing approximately the same peak firing rate), are shown in Fig. 5C. As the MC input ratio is shifted from 50% ORN vs. ET inputs (Fig. 5C, left) to being dominated by ORN inputs (e.g., 90% ORN-MC, Fig. 5C, right), MC spiking dynamics shift from following the shorter ET cell burst to following the slower time course of the ORN input. In general, MC spiking more closely approximated the experimental dataset at ratios in which the MC received similar or stronger ET cell input than ORN input (Fig. 5D).

We next tested the effect of varying input ratio on total spike count and response duration (Fig. 5, E and F). Each of these parameters was most strongly affected by changes in the strength of the ORN-MC pathway. For each, a range of input ratios could generate MC responses with spike counts or durations matching the mean of the experimental dataset (Fig. 5, E and F). However, a ratio of ∼50% ET-MC to 50% ORN-MC (1:1 ET/ORN input strength) generated MC responses in which all three metrics (peak spike rate, total spike count and response duration) simultaneously approximated their experimental means at a particular input gain (Fig. 5F). While a 1:1 ratio was optimal for this dataset, we note that even higher ET-MC ratios (e.g., 90% ET-MC strength) also closely approximated experimental MC output dynamics (not shown, but see Fig. 4G). These results predict that a parallel excitatory network in which feedforward, ET cell-mediated input to the MC matches or dominates the direct ORN input would generate MC output dynamics that approximate those recorded in vivo. Furthermore, the results suggest that each pathway makes a distinct contribution to shaping MC spiking dynamics. In the ORN-ET-MC pathway, intrinsic ET cell bursting properties predominantly determine the threshold and temporal window for MC activation, while the direct ORN-MC pathway mainly contributes to peak spike rate and to modulating the duration of the sniff-evoked spike burst.

Integrated glomerular circuit model.

Finally, having generated several glomerular circuits that could mediate realistic temporal sharpening of sniff-driven ORN inputs, we incorporated these circuits into an “integrated” network model and evaluated its performance in shaping MC response patterns (Fig. 6A). This model combined the ORN-[ET]-MC model using a 1:1 ET/ORN input strength ratio, with three pathways of MC inhibition: RI, “slow” FFI via a PG cell receiving direct ORN input (ONd-PG), and FFI via a PG cell receiving excitatory input from the ET cell (ETd-PG) (Shao et al. 2009). ET cell-driven FFI was included because approximately two-thirds of PG cells are directly driven by ET cells and not by ORNs (Shao et al. 2009). Parameter values for circuit connection strengths were conserved from the small circuit models, with the following exceptions (Table 1). To accommodate inhibition, the strengths of the excitatory connections onto the MC were doubled from the values determined in the ORN-[ET]-MC model. ORN input gain (G_[ORN-X]) was adjusted proportionally across the different input connections. The strengths of the two new inhibitory synaptic connections onto the MC (e.g., ONd-PG-MC, ETd-PG-MC) were then adjusted to approximate mean peak firing rate, spike count and response duration with the experimental dataset across all ORN input traces.

Fig. 6.

Generating naturalistic MC response dynamics with an integrated glomerular circuit model. A: schematic of the integrated glomerular circuit model. The model incorporates direct ORN-MC excitation in parallel with feedforward excitation through an ET cell. Two PG cell pathways, one receiving direct ORN input (ONd-PG) and the other receiving excitatory input from the ET cell (ETd-PG), provide FFI to the MC. The MC also receives RI, simulating interactions between MC and GCs and/or PGs. Values at each synapse indicate the ORN input gains (G_[ORN-X] used; inhibitory inputs in this figure were as follows: g_[ONd-PG-MC] = g_[ETd-PG-MC] = 0.5; g_[RI] = 0.1). B: responses of the model circuit elements to one inhalation of odorant. i: ORN input current and spike rasters showing output from the ET, ONd-PG, ETd-PG and MC components of the integrated model in response to a representative sniff-driven ORN input (same input trace as previous figures). ii: Synaptic input currents to the model MC originating from different sources. Traces are offset from each other to facilitate comparison. C: response of the integrated model to the 25 different sniff-driven ORN input waveforms, showing spike rasters and population histogram for each model MC response, as in previous figures, along with the population ORN input dynamics (blue). Input gains and synaptic conductances are set at parameters given in A. Note the temporal sharpening relative to ORN input dynamics. D: dynamics of experimental and model MC firing rate responses relative to time of inhalation for the integrated model. The dynamics of the model output closely match those of the experimental dataset. E: histograms comparing distributions of response parameters for the model MC driven by each of the 25 ORN input traces (gray bars) and for each of 37 MT units recorded in the experimental dataset (red). The distribution of model MC outputs is narrower than that of the recorded units for each parameter, but the distributions have similar means and modes. The distribution of MC response durations is bimodal for both the model and experimental datasets. Bin sizes are 10 Hz (peak firing rate; i), 1 spike (spikes per sniff; ii), and 10 msec (duration; iii). F: exploration of parameter space of circuit connection strengths in the integrated model. The five synaptic input strengths to the model MC were varied systematically by up to 50% in either direction, with “distance from center” expressed as the Euclidean distance of a parameter set from the initially optimized parameter values (see text for details). Plots show, from left to right: “error”, the sum squared error of the means of the model MC population response metrics (peak firing rate, spike count, and response duration) relative to their respective means in the experimental dataset (i), and mean peak firing rate (ii), mean spike count (iii), and median response duration (iv) of model MC outputs. Solid circles show mean (or median) values for the population of 25 modeled MC outputs; gray bars indicate the range, defined by the 80th and 20th percentiles of values within each bin of distance-from-center values (bin size, 0.01). Note that error increases gradually with distance from center (i), and that each response parameter is relatively robust to modest changes in connection strengths (ii–iv).

Table 1.

Values for synaptic connection strengths after model optimization for the minimal circuit models tested and for the integrated glomerular network model (see text for details)

Circuit Model	G[ORN-MC]	gRI	G[ORN-PGON]	gPGON-MC	G[ORN-ET]	gET-MC	gET-PGET	gPGET-MC
ORN-MC	7.5
ORN-MC-RI	15	0.1
ORN-PG-MC (slow)	18		35	1.5
ORN-ET-MC					4	0.3
ORN-ET-MC parallel	3.8				1.5	0.15
Integrated model	7.7	0.1	35	0.25	2.5	0.3	1.37	0.25

ORN, olfactory receptor neuron; MC, mitral/tufted cell; RI, recurrent inhibition; PG, periglomerular cell; ET, external tufted cell; G_[ORN-MC], ORN input gain to MC; g_RI, maximum conductance for RI; G_[ORN-PGON], ORN input gain to PG_ON; g_PGON-MC, maximum conductance for PG_ON-MC synapse; g_ET-MC, maximum conductance for ET-MC synapse; g_ET-PGET, maximum conductance for ET-PG_ET synapse; g_PGET-MC, maximum conductance for PG_ET-MC synapse.

In Fig. 5, “ORN-MC input strength” is a rescaled version of G_[ORN-MC]. The value of 3.8 here is equivalent to an ORN-MC input strength of 0.15 (see materials and methods).

Sniff-driven spiking dynamics were distinct for each cellular element in the model, resulting in distinct temporal profiles of excitatory and inhibitory synaptic inputs to the MC (Fig. 6B). The optimized model produced MC responses that were, across the population, slightly more transient than the experimental dataset (Fig. 6, C and D), with slightly higher peak firing rates and slightly lower total spike counts (Fig. 6E). However, in general, the integrated glomerular circuit model successfully recapitulated the temporal sharpening of ORN input dynamics that was a hallmark of the MC unit recordings (Fig. 6, C and D). Notably, the integrated model also produced MC responses with a bimodal distribution of spike burst durations (Fig. 6E), recapitulating the distribution of response durations in the experimental dataset and implying that this bimodal distribution may arise from variation in the dynamics of ORN inputs to different glomeruli.

In general, however, the distribution of model MC output response parameters was more narrow than that recorded experimentally (Fig. 6E), suggesting that diverse MC response patterns cannot be captured solely by a fixed set of network connection strengths, even with the normal variation in ORN input dynamics. One possibility is that MC response diversity arises from modest variations in the strength of circuit connections within the glomerular network. An alternate possibility is that our approach of optimizing model output using isolated subcircuits generated an integrated network model that was only locally optimized to the MC population mean. To test this and to further validate the choice of parameters for the integrated network model, we varied the strengths of the five synaptic connections onto the MC. For each simulation in this parameter exploration, a value for each of the five connection strength parameters was chosen uniformly within a range from 50% to 150% of the values given in Table 1. For each set of five parameters, we calculated its distance (Euclidean distance in normalized, five-dimensional space) from the original parameter set and measured peak spike rates, spike counts and response durations as a function of this distance (Fig. 6F). Parameter sets closest to those originally derived from the isolated circuit models (i.e., as specified above) provided MC outputs that most closely approximated our mean target metrics. Error (i.e., summed variance from experimental means across each MC response parameter) grew slowly as the parameter sets diverged from these original optimized values (Fig. 6F), suggesting that the minimal circuit optimization strategy yielded a parameter set that is near optimal for the integrated network model, and that model responses are robust to modest parameter changes.

Varying the strength of connections within the glomerular network by up to 50% also yielded variation in MC response parameters that approximated the range of those measured experimentally, for example, with mean MC peak firing rates varying from ∼60 to 150 Hz. Inhalation-driven spike counts and spike burst durations did not reach values as high as those in the experimental dataset, but nonetheless covered much of the range observed experimentally (Fig. 6F). This result implies that changes in the relative strength of connections within this simplified glomerular network can account for much of the measured diversity in inhalation-driven MC response dynamics.

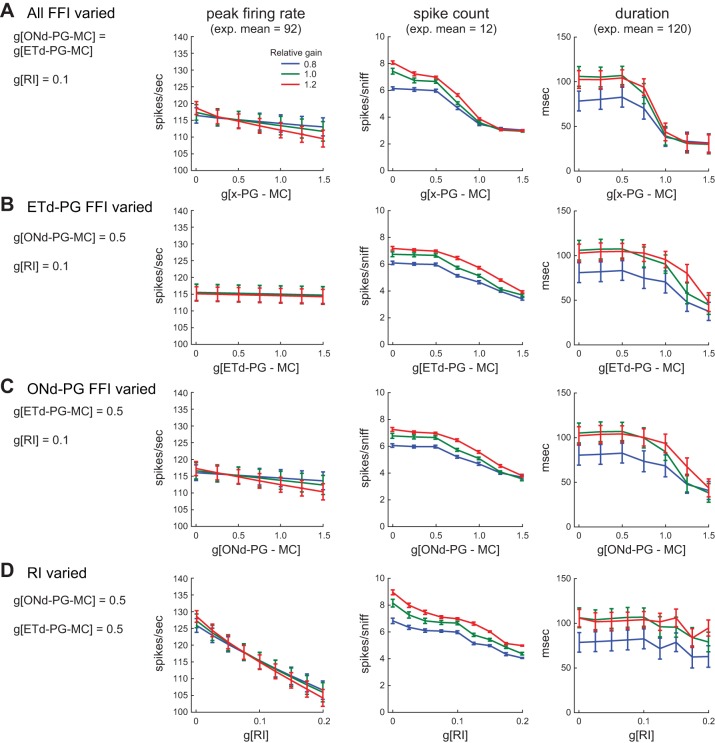
We next used the model to explore the contributions of particular inhibitory circuits to shaping MC response dynamics. For example, GABAergic inhibition across glomerular circuits shapes both the magnitude and temporal structure of sensory-evoked MC responses in OB slices (Shao et al. 2012, 2013); these experiments could not distinguish between RI or FFI mediated by particular glomerular circuits. We explored this in the model by varying the strength of FFI mediated by ONd-PGs and ETd-PGs, either independently or simultaneously (Fig. 7, A–C). We also varied the strength of RI, representing dendrodendritic inhibition between MCs and PGs or GCs, while leaving FFI parameters fixed (Fig. 7D).

Fig. 7.

Contributions of inhibitory glomerular circuits to MC response patterns. A: effects of varying FFI strength (changing ONd-PG-MC and ETd-PG-MC connection strengths simultaneously) on MC response parameters. RI strength is fixed. Results for three ORN input gains are shown. Input gain was varied proportionally across all ORN input channels, and legend shows gain relative to values in Fig. 6A. Increasing FFI via both inhibitory pathways only slightly lowers peak firing rate (left). Spike count (center) decreases substantially due to a stepwise decrease in burst duration (right). B: effects of varying ETd-PG-mediated FFI (ORN-ET-PG-MC pathway), leaving ONd-PG-MC and RI strengths fixed. There is little impact on peak firing rate and more modest impact on spike count and duration. C: effects of varying ONd-PG-mediated FFI (ORN-PG-MC pathway), leaving ETd-PG-MC and RI strengths fixed. Effects of varying ONd-PG FFI are similar to those of varying ETd-PG-FFI, with no impact on peak firing rate and modest impacts on spike count and duration. D: effects of varying RI, leaving FFI strengths fixed. Peak firing rate (left) and spike count (center) decrease substantially with increasing RI, while MC burst duration (right) is only slightly affected by RI strength.

Several interesting relationships emerged from these manipulations. For example, the strength of FFI had relatively little impact on peak MC firing rates but could substantially impact MC burst duration. Peak firing rate showed, at most, a 5% decrease as g_[ONd-PG-MC] and g_[ETd-PG-MC], either alone or in tandem, were increased from zero to the maximal tested value of 1.5 (Fig. 7, A–C). However, the direct (ONd-PG) and indirect (ETd-PG) FFI pathways each showed modest effects on response duration when the strength of each pathway was varied individually (Fig. 7, B and C) and showed larger effects when both pathways were varied together (Fig. 7A). This effect was nonlinear for both FFI pathways (ONd-PG and ETd-PG, respectively), with FFI strength shortening burst duration substantially only at higher values (Fig. 7, B and C). In contrast, RI more strongly affected peak firing rates but had little impact on burst duration: MC peak rates decreased by ∼25% as RI strength was increased over the tested range (with a concomitant decrease in total spike count), but varying RI strength only shortened MC burst duration by, at most, 25% at the highest values tested (Fig. 7D). Finally, ORN input gain had little effect on peak MC firing rates, but a substantial effect on burst duration and, consequently, total spike count (Fig. 7). These simulations thus suggest that this “minimal” integrated OB circuit model acts robustly to temporally sharpen ORN inputs across a wide range of network synaptic strengths, and also suggest that different inhibitory pathways within the OB circuit make distinct contributions to the transformation of inhalation-driven bursts into patterned MC responses.

DISCUSSION

We explored how certain previously identified OB circuits shape inhalation-linked patterns of MC output in the context of naturalistic odor sampling (i.e., sniffing). We used a small-network modeling approach to reproduce key circuits in the OB network, focusing on well-described elements of the OB glomerular network, and asked how these elements, in isolation and integrated into multielement circuits, transform sniff-driven packets of sensory input into MC spiking responses. Recent experimental and theoretical studies have highlighted the importance of the glomerular circuitry in the larger OB network (De Saint Jan et al. 2009; Gire et al. 2012; Gire and Schoppa 2009; Hayar et al. 2004a; Linster and Cleland 2009; Shao et al. 2009, 2012; Wachowiak and Shipley 2006), but the exact roles that individual glomerular circuits of this network might play in shaping OB output in vivo remain unclear. The current study incorporates glomerular circuitry into a dynamic, biologically constrained network model and evaluates how the circuitry transforms sensory inputs in the temporal domain relative to sniffing.

Strategies for modeling OB network function.

The network model was constrained by experimental data: in addition to incorporating biophysically realistic circuit elements, sensory input to the model OB network was derived from recordings of ORN inputs to the OB of intact rats, and an experimental dataset of presumptive MC recordings, evoked by the same naturalistic sniffing patterns used to drive the ORN responses, was used as a benchmark for evaluating model output. The use of input waveforms with naturalistic dynamics differs from the constant, pulsatile or sinusoidal inputs used in most earlier network models of olfactory processing (Arruda et al. 2013; Bathellier et al. 2006; Brody and Hopfield 2003; Davison et al. 2003; Kunsting and Spors 2009; Linster and Cleland 2009; Margrie and Schaefer 2003; Rubin and Cleland 2006). Using experimentally derived inputs was important for several insights into OB network organization. For example, we found that slow FFI from PG cells to MCs was necessary to allow MC spike bursts to develop during the course of an inhalation-driven burst of sensory input. We also found that RI did little to alter the inhalation-linked dynamics of MC firing, while FFI and feedforward excitation mediated by ET cells played an important role in shaping these dynamics. These results are discussed in more detail below.

A common approach to modeling neural circuit function is to construct a single, “maximal” model incorporating as much knowledge as possible about the network; in our case such an approach would require exploring a prohibitively large parameter space. Instead we employed a strategy of incrementally increasing network complexity, tuning parameters and comparing model output to experimental data at each step. The benefit of this approach was that it allowed us to explore a broader range of parameter space, to test whether particular circuits are necessary or sufficient to generate a realistic temporal transformation of sniff-driven sensory inputs, and to generate hypotheses regarding the roles of particular circuits and, and circuit features, in generating these patterns. The set of minimal circuits tested is necessarily incomplete, but represents canonical subcircuits hypothesized in earlier studies as playing important roles in shaping inhalation-driven MC response patterns (Fukunaga et al. 2014; Gire and Schoppa 2009; Shao et al. 2012; Wachowiak and Shipley 2006).

Our strategy to evaluate model performance was to assess how accurately the OB network generated output parameters, in particular, spiking dynamics, matching those recorded experimentally given biologically realistic inputs. This strategy differs from other models which have sought to identify circuit mechanisms capable of mediating particular neural computations, such as concentration-invariant odor discrimination (Brody and Hopfield 2003; Cleland et al. 2007, 2012; Margrie and Schaefer 2003), contrast enhancement and pattern decorrelation (Cleland and Linster 2012; Cleland and Sethupathy 2006; Imam et al. 2012; Luo et al. 2010; Wiechert et al. 2010), and representation sparsening (Assisi et al. 2007; Finelli et al. 2008), among others. Our approach does not presume that any particular computation might be performed by a specific circuit component (nor does it investigate OB computations), but rather seeks to identify how specific network components influence experimentally measured output features, in this case, inhalation-driven MC spiking patterns.

Role of OB circuits in shaping inhalation-driven response dynamics.

This approach led to several insights about critical circuits involved in the transformation of inhalation-driven sensory inputs into dynamic output patterns. First, our results suggest that multiple, relatively simple circuit configurations are capable of approximating the temporal sharpening of sensory inputs that has been observed experimentally (Carey and Wachowiak 2011; Shao et al. 2012). For example, in addition to the “integrated” circuit model, the ORN-PG-MC circuit with slow FFI, the ORN-ET-MC circuit and the ORN-[ET]-MC circuit with parallel ET and ORN-mediated excitation of MCs were each capable of generating MC output patterns that approximated experimental data in terms of peak firing rates, spike counts and burst durations. Thus the glomerular network may include multiple circuits that conjointly sharpen sensory input. Analogous arrangements have been reported among motor pattern generating networks, where disparate combinations of intrinsic currents, synaptic mechanisms, and network connectivities can produce functionally identical rhythmic output (Prinz et al. 2004; Roffman et al. 2012). The ability of multiple subnetworks to generate functionally appropriate output dynamics may enable modulation of finer-scale features of the MC response, such as synchrony of spike timing or input-output dynamic range, without disrupting the basic inhalation-driven “packets” of activity that are the basis for transmitting odor information to downstream processing centers.

Second, the models suggested that that the kinetics of inhibition are critical in shaping MC responses. The rapid onset dynamics associated with classical, GABA_A-mediated transmission acted to suppress MC and ET cell responses in a blanket fashion, preventing the generation of discrete inhalation-triggered bursts. Slower-onset and longer-lasting FFI was instead necessary to mediate temporal sharpening of inhalation-triggered MC spikes while still permitting the development of a unitary spike burst following each inhalation. This slow, long-lasting inhibition may be due to one or a combination of several factors, including asynchronous GABA release from juxtaglomerular neurons (Murphy et al. 2005; Smith and Jahr 2002), N-methyl-D-aspartate receptor-dependent GABA release from GC (Isaacson and Strowbridge 1998; Schoppa and Urban 2003; Shao et al. 2012), polysynaptic activation of GABA release from PG or short-axon cells (Liu et al. 2013; Shao et al. 2009), intrinsic properties of PG cells such as hyperpolarization-activated cation currents (Cadetti and Belluzzi 2001) or even inhibition driven by cortical feedback (Boyd et al. 2012). Regardless of mechanism, our OB network model suggests a functional role for this “slow” inhibition in the context of natural odor sampling, namely, to allow for synaptic integration over the course of an inhalation-evoked burst of sensory input, the duration of which roughly matches the decay time constant of the inhibition. Notably, GABAergic glomerular circuits also mediate presynaptic inhibition of ORN inputs with similarly slow onset and decay kinetics (McGann et al. 2005; Wachowiak et al. 2005), modulating the strength of sensory inputs without altering the temporal dynamics of each inhalation-driven burst (Pírez and Wachowiak 2008). Given the possibility that multiple inhibitory pathways with distinct kinetics may be present within glomerular circuits (Shao et al. 2012), it may be interesting to explore how onset and decay kinetics separately contribute to shaping MC temporal response patterns. These parameters could be explored not only for the different FFI circuits, but also for RI circuits which may vary in kinetics, depending on whether RI is mediated by PG cells or GC.

Third, we found that, in the integrated glomerular network model, RI and FFI played distinct roles in shaping MC responses. FFI could substantially impact MC burst duration but appeared to do so nonlinearly, with burst duration remaining robust to FFI strength at lower values but shortening significantly at higher values. These results are consistent with experimental evidence that FFI from PG to MCs shapes the temporal structure of sensory-evoked responses on a time scale matching that of respiratory patterning (Shao et al. 2012). This result is also interesting given that we had earlier found a bimodal distribution of inhalation-driven MC spike burst durations (Carey et al. 2009) roughly corresponding to the range of durations generated by varying FFI strength in the network model. In contrast, RI strength affected peak firing rates in a graded manner, but had little impact on MC burst duration. This result is consistent with hypotheses that RI between MC and GC affects MC response gain and fine-scale temporal dynamics, such as synchrony of spike timing in the gamma frequency range (Bathellier et al. 2006; David et al. 2009; Fukunaga et al. 2014; Schoppa 2006), but not respiratory patterning.

Our modeling results support experimental evidence that the ET cell plays a central role in conducting olfactory signals through the glomerulus and also suggest that ET cell-mediated excitation of MCs, in addition to FFI, plays an important role in shaping the dynamics of OB output (Carlson et al. 2000; De Saint Gire et al. 2012; Jan et al. 2009; Shao et al. 2012). A key determinant of these dynamics is the bursting behavior of ET cells (Hayar et al. 2004b; Liu and Shipley 2008a, 2008b). In addition, the fact that MC response amplitudes (in terms of peak spike rate) were more dependent on the strength of the ET-MC connection than on the ORN-MC connection suggests that the ET cell may serve as an effective target for centrifugal systems that modulate OB output strength (Liu et al. 2012).

Control of MC excitation by ET cell bursting may facilitate odor coding in several ways. First, the all-or-none burst response of the ET cell to ORN inputs of sufficient amplitude may enhance the reliability of sensory signal transmission and filter out small transient fluctuations in the input (Gire and Schoppa 2009; Liu and Shipley 2008b); this effect was evident in our glomerular model. Second, the ET cell burst may regularize the strength and duration of the signal received by the MC. Somewhat surprisingly, in our model ET cell-mediated MC excitation led to temporally sharper MC responses than ORN-driven excitation, due to the fact that inhalation-driven ORN inputs decay relatively slowly. Temporally sharper responses are important in enabling faithful transmission of inhalation-linked response patterns across the biological range of sniff frequencies (Carey et al. 2009). In general, bursting neurons can more reliably transmit temporal information than simple spiking neurons, since burst timing and the timing of spikes within a burst are typically more precise than the timing of individual spikes emitted by nonbursting neurons, particularly in the presence of a noisy background (Izhikevich 2002; Kepecs and Lisman 2003).

Finally, while we identified circuit configurations and connection strengths that best approximate the mean dynamics of inhalation-driven activity across a population of MT cells, it is important to note that the responses of individual MT cells are temporally diverse and can vary substantially around this mean (Carey and Wachowiak 2011; Cury and Uchida 2010; Smear et al. 2011). This diversity could reflect different strengths of circuit connections within different glomeruli or even different individual MT cell subtypes, for example, mitral vs. tufted cells (Fukunaga et al. 2012). Indeed, we could generate MC response dynamics that varied across the range of response durations in our experimental dataset by varying the strength of particular circuit connections, such as FFI or ORN input gain. It would be interesting to further explore how diversity in glomerular circuit connectivities can account for diversity in MC response patterns using this model framework, ideally compared with intracellular recordings of inhalation-driven MC changes in membrane potential (Fukunaga et al. 2014).

Further explorations of OB network function using a small-network model.

The small-network model developed here identifies glomerular circuit elements important for generating realistic temporal patterns of output across a MC population given realistic input patterns, but it does not (nor is it meant to) reproduce all known circuits within the OB network, or even all known properties of individual cell types. For example, our minimal ET cell model lacks a calcium-activated potassium current and a high-voltage-activated calcium current, both of which regulate ET cell burst duration and interspike interval (Liu and Shipley 2008b). Inclusion of these currents could allow for finer tuning of sensory-driven ET cell burst properties and, consequently, MC response dynamics. Neither does the model incorporate the known diversity in intrinsic bursting frequencies across the ET cell population, which is thought to allow for entrainment of ET cell bursting to sensory inputs driven by a range of sniff frequencies and to tonically inhibit MCs (Hayar et al. 2004b; Wachowiak and Shipley 2006). The impact of these additional circuit properties could be explored by expanding the glomerular network to include multiple ET cells with varying current densities and bursting behavior.

At the circuit level, the network model could also be expanded to include an emerging diversity of inhibitory circuits in the glomerular and infraglomerular layers, such as FFI mediated by short-axon cells (Liu et al. 2013; Whitesell et al. 2013), PG cell-mediated FFI of ET cells (Gire and Schoppa 2009; Shao et al. 2012), GABAergic input to MCs from recently described parvalbumin-expressing external plexiform interneurons (Huang et al. 2013; Kato et al. 2013; Miyamichi et al. 2013) and RI between PG and MCs (Murphy et al. 2005). Each of these circuits has the potential to contribute further to inhalation-linked temporal patterning. Distinct kinetics and connection strengths across different inhibitory circuits may enable a greater diversity of MC response patterns than captured in our initial model. A similar framework could be used to address the importance of interglomerular interactions via short-axon cells in the glomerular layer or between MC/GCs.

We focused here on temporal shaping of ORN inputs by the OB network, since this transformation was highly constrained by experimental data, but an expanded glomerular network model may also be used to explore how the OB transforms representations of odorant identity or concentration in the context of natural sampling behavior. For example, FFI via the ON-PG-MC circuit has been hypothesized to sharpen MC response spectra by amplifying PG cell responses to weak sensory inputs (Cleland and Linster 2012; Gire and Schoppa 2009). This hypothesis could be further developed by providing experimentally obtained input waveforms representing the response of the same population of ORNs to a range of different odorants or odorant concentrations. The same framework should also be useful for generating predictions of how the OB network transforms sensory inputs as a function of changes in odor sampling behavior, such as the bursts of high-frequency sniffing that are a hallmark of exploratory behavior (Macrides 1975; Verhagen et al. 2007; Welker 1964).

GRANTS

This work was supported by the National Institute on Deafness and Other Communications Disorders (Collaborative Research in Computational Neuroscience Grants DC011423 and F31 DC010312) and the National Science Foundation (Grants DMS-1022945 and DMS-1148230).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: R.M.C., W.E.S., A.B., and M.W. conception and design of research; R.M.C. and W.E.S. performed experiments; R.M.C. and W.E.S. analyzed data; R.M.C., W.E.S., M.T.S., A.B., and M.W. interpreted results of experiments; R.M.C. and M.W. prepared figures; R.M.C., W.E.S., and M.W. drafted manuscript; R.M.C., W.E.S., M.T.S., A.B., and M.W. edited and revised manuscript; R.M.C., W.E.S., M.T.S., A.B., and M.W. approved final version of manuscript.