Bias in estimating the causal hazard ratio when using two-stage instrumental variable methods

Abstract

Two stage instrumental variable methods are commonly used to estimate the causal effects of treatments on survival in the presence of measured and unmeasured confounding. Two stage residual inclusion (2SRI) has been the method of choice over two stage predictor substitution (2SPS) in clinical studies. We directly compare the bias in the causal hazard ratio estimated by these two methods. Under a principal stratification framework, we derive a closed form solution for asymptotic bias of the causal hazard ratio among compliers for both the 2SPS and 2SRI methods when survival time follows the Weibull distribution with random censoring. When there is no unmeasured confounding and no always takers, our analytic results show that 2SRI is generally asymptotically unbiased but 2SPS is not. However, when there is substantial unmeasured confounding, 2SPS performs better than 2SRI with respect to bias under certain scenarios. We use extensive simulation studies to confirm the analytic results from our closed-form solutions. We apply these two methods to prostate cancer treatment data from SEER-Medicare and compare these 2SRI and 2SPS estimates to results from two published randomized trials

1. Introduction

Evaluating the effectiveness of treatment and identifying the causal relationship between exposure and disease are critical objectives for clinical and health services researchers. Confounding is often a concern when analyzing nonrandomized observational studies and even randomized studies with non-compliance [1]. Instrumental variable (IV) methods are increasingly being used in clinical comparative effectiveness studies to potentially control for both measured and unmeasured confounding. Angrist et al.[2] defined the IV for causal effects of treatment on outcome to be a variable satisfying the following five assumptions: i) The potential outcomes on one subject are unrelated with the particular assignment of treatment to the other subjects; ii) IV is randomly (or ignorably) assigned; iii) Any effect of IV on the outcome must be mediated by treatment received (the exclusion restriction);iv) IV has nonzero effect on treatment received; v) There are no defiers. (for details see section 2)

In a recent clinical study, we were interested in comparing the effectiveness of two treatments for prostate cancer in elderly men using SEER-Medicare, a large national observational database. Specifically, we planned to use IV methods to estimate the effect of the addition of external beam radiation therapy (EBRT) to androgen suppression therapy (ADT) in improving overall survival in men with locally advanced prostate cancer. We considered a commonly used IV in health services research: local area treatment patterns defined by the percentage of active treatment in hospital referral regions (HRR). This IV has been shown to capture regionally distinct structural variation in care [3]. Such variation is not fully explained by patient characteristics. Further, this IV varies across HRRs and is strongly associated with treatment assignment. Finally, it is balanced across important observed prognostic factors. Although there is an extensive literature on the importance of choosing an appropriate instrument, less attention has been paid to using the appropriate modeling approach once an IV is selected.

Recently, there has been rapid uptake and widespread use of two IV based analytic approaches called two-stage residual inclusion (2SRI) and two-stage predictor substitution (2SPS)[4, 5]. These methods have been used to correct for bias due to endogeneity in non-linear models for both binary and time-to-event outcomes. Among these two IV approaches, 2SRI was shown to consistently estimate a conditional causal parameter under certain assumptions [4] and has been adopted as the method of choice in clinical research studies involving survival outcomes[6, 7, 8]. The conditional causal parameter that Terza et al.[4] consider is only identified by making homogeneity assumptions that go beyond the five assumptions for a valid IV defined in the first paragraph. Angrist et al. [2] showed that under these five assumptions for a valid IV, the only treatment effect that is identified is the average treatment effect for the compliers, where the the compliers are the subjects who would take the treatment if encouraged to do so by the IV but would not take the treatment if not encouraged by the IV; this is called the local average treatment effect (LATE). In the context of a binary outcome, Cai et al.[5] demonstrated that both the 2SRI and 2SPS methods generated biased estimates of LATE among compliers for binary outcome. In this paper, we focus on the properties of 2SPS and 2SRI as estimators of the LATE for time-to-event data.

Despite the fact that there is growing interest in applying two stage IV methods to time-to-event data, little is known about the potential bias of using such methods to estimate LATE among compliers. We derive closed form expressions of the bias and conduct extensive simulations to quantify this bias. We then apply both of the two-stage IV methods to our prostate cancer treatment data and compare them to the results from two published randomized clinical trials [9, 10]

2. Notation, Assumptions, Compliance Categories, and Model

2.1. Notation

Following the notation of Cai et al.[5] and Nie et al.[11], an N-dimensional vector of binary IV is represented by Ṟ. An IV value of 1 represents encouragement to receive the active treatment and 0 represents no encouragement to receive the active treatment. In a RCT setting, where the IV is the randomized assignment, then an IV value of 1 represents random assignment to treatment and 0 represents random assignment to control; in the prostate cancer observational study described in the introduction, an IV value of 1 represents a high local area rate (above median) of adding EBRT to ADT and 0 represents a low local area rate (below the median) of adding EBRT to ADT. The ith element R_i = 1 implies that subject i is encouraged to receive the active treatment, whereas R_i = 0 indicates that subject i is not encouraged to receive the active treatment. Let Ẕ^Ṟ be an N-dimensional vector of potential treatment received given Ṟ, and ith element $Z_i^{\underset{¯}{R}}=1$ indicates that subject i receives the active treatment and $Z_i^{\underset{¯}{R}}=0$ means that subject i receives the control under Ṟ.

Similarly, we define Ṯ^Ṟ,Ẕ to be an N-dimensional vector of potential survival time under Ṟ and Ẕ, and ith element $T_i^{\underset{¯}{R},\underset{¯}{Z}}$ is the potential survival time for subject i under Ṟ and Ẕ. Let Ḻ^{Ṟ, Ẕ} to be an N-dimensional vector of potential censoring time under Ṟ and Ẕ, and ith element $L_i^{\underset{¯}{R},\underset{¯}{Z}}$ is the potential censoring time for subject i under Ṟ and Ẕ.

We define Y̱^{Ṟ, Ẕ}=min{Ṯ^Ṟ,Ẕ, Ḻ^Ṟ,Ẕ}, the elementwise minimum of potential censoring and survival times, to be an N-dimensional vector of potential observed follow up time under Ṟ and Ẕ, and ith element $Y_i^{\underset{¯}{R},\underset{¯}{Z}}$ represents the potential follow up time for subject i under Ṟ and Ẕ. Let ${\delta }_i^{\underset{¯}{R},\underset{¯}{Z}}=I\left\{T_i^{\underset{¯}{R},\underset{¯}{Z}}\le C_i^{\underset{¯}{R},\underset{¯}{Z}}\right\}$ indicates whether subject i is observed to terminate by failure ( ${\delta }_i^{\underset{¯}{R},\underset{¯}{Z}}=1$) or by censoring ( ${\delta }_i^{\underset{¯}{R},\underset{¯}{Z}}=0$) given Ṟ and Ẕ. The vector X̱_i represents measured confounding variables for subject i.

2.2. Assumptions

The main assumptions we will make for causal modeling are the five assumptions made by Angrist et al. [2], and a random censoring assumption for the survival setting.

1. Stable Unit Treatment Value Assumption (SUTVA)[12, 13]

   1. if $R_i=R_i^{\prime }$, then $Z_i^{\underset{¯}{R}}=Z_i^{\underset{¯}{R}\prime }$

   2. if $R_i=R_i^{\prime }$ and $Z_i=Z_i^{\prime }$, then $Y_i^{\underset{¯}{R},\underset{¯}{Z}}=Y_i^{{\underset{¯}{R}}^{\prime },{\underset{¯}{Z}}^{\prime }}$

      The SUTVA assumption says that the potential outcomes for subject i are not related with the treatment status of other subjects such that we can write $Z_i^{\underset{¯}{R}}$, $Y_i^{\underset{¯}{R},\underset{¯}{Z}}$, $T_i^{\underset{¯}{R},\underset{¯}{Z}}$, $L_i^{\underset{¯}{R},\underset{¯}{Z}}$, ${\delta }_i^{\underset{¯}{R},\underset{¯}{Z}}$ as $Z_i^{R_i}$, $Y_i^{R_i,Z_i}$, $T_i^{R_i,Z_i}$, $L_i^{R_i,Z_i}$, ${\delta }_i^{R_i,Z_i}$ respectively. The SUTVA assumption also implies the assumption of consistency, such that the value of the potential outcome given a treatment remains unchanged no matter what the treatment assignment mechanism is [12]

2. Independence of the instrument Ṟ [14]:

   Conditional on a vector of confounders X̱, the random vector (Y̱^Ṟ,Ẕ, Ṯ^Ṟ,Ẕ,Ḻ^Ṟ,Ẕ,Ẕ^Ṟ) is independent of Ṟ. In a randomized trial where R is the IV, the independence assumption holds without conditioning on X̱.

3. Exclusion Restriction

   ∀Ẕ,Ṟ, and Ṟ′, we have:

   Ṯ^Ṟ,Ẕ=Ṯ^Ṟ′,Ẕ,Ḻ^Ṟ,Ẕ = Ḻ^Ṟ′,Ẕ, Y̱^Ṟ′,Ẕ = Y̱^Ṟ′,Ẕ, This assumption implies that any effect of IV on potential outcomes must be through its effect on treatment actually received. Thus, we can write $T_i^{\underset{¯}{R},\underset{¯}{Z}}$, $L_i^{\underset{¯}{R},\underset{¯}{Z}}$, $Y_i^{\underset{¯}{R},\underset{¯}{Z}}$ as $T_i^{Z_i}$, $L_i^{Z_i}$, $Y_i^{Z_i}$ by combining the exclusion restriction and SUTVA assumptions.

4. Non-zero Average Causal Effect of Ṟ on Ẕ

   $$E\left[Z_i^1-Z_i^0\right]\ne 0$$

   This assumption means the IV is correlated with treatment received.

5. Monotonicity [15]

   $$Z_i^1\ge Z_i^0,\forall i\in N$$

   This assumption rules out the existence of defiers. No subject always does the opposite of the treatment assigned.

6. Independent censoring

   The distribution of potential survival time Ṯ^Ṟ,Ẕ is independent of the distribution of potential censoring time Ḻ^Ṟ,Ẕ.

2.3. Compliance Categories

Under the framework of principal stratification and potential outcomes [2, 16], subjects in a two-arm randomized trial can be categorized into 4 principal strata: Always takers (AT) are subjects who always take the treatment regardless of assignments (Z¹ = 1, Z⁰ = 1); Compliers (C) are subjects who comply with their assignments (Z¹ = 1, Z⁰ = 0); Never takers (NT) are the subjects who never take the treatment no matter which group they are assigned to (Z¹ = 0, Z⁰ = 0); Defiers (D) are the subjects who take the treatment opposite of their assignments (Z¹ = 0, Z⁰ = 1).

2.4. Model

We first define the probability of receiving the treatment Pr(R = 1) = r, the probability of being a always taker Pr(AT) = ρ_a, and the probability of being a complier Pr(C) = ρ_c. We also define the probability of being a defier Pr(D) = ρ_d, but under the monotonicity assumption, there are no defiers so that ρ_d = 0. Hence, the probability of being a never taker Pr(NT) is equal to 1 − ρ_a − ρ_c.

We assume both potential censoring time and potential survival time follow the Weibull distribution with the same shape parameter α. The potential censoring time for the subjects in each principal strata follows Weibull(α, λ), and we define the parameters of the probability distribution of potential survival time for each principal strata as follows:

$$\begin{array}{c}{T}^1\mid \mathit{AT}~\mathit{Weibull}(\alpha ,{\theta }_{\mathit{at}}^1),T^0\mid \mathit{AT}~\mathit{Weibull}(\alpha ,{\theta }_{\mathit{at}}^0)\\ T^1\mid C~\mathit{Weibull}(\alpha ,{\theta }_c^1),T^0\mid C~\mathit{Weibull}(\alpha ,{\theta }_c^0)\\ T^1\mid \mathit{NT}~\mathit{Weibull}(\alpha ,{\theta }_{\mathit{nt}}^1),T^0\mid \mathit{NT}~\mathit{Weibull}(\alpha ,{\theta }_{\mathit{nt}}^0)\end{array}$$

We also examined scenarios in which different shape parameters α’s are assumed for the potential censoring time and the potential survival time. These details are given in Appendix E. The density of Weibull distribution is f(t) = (α/K)(t/K)^K−1exp(−(t/K)^α) and the hazard rate is h(t) = αK^−αt^α−1. In the case of Weibull regression with covariates X, K^−α can be reparameterized as exp(βX). The hazard rate for the compliers if treated is $h(T^1=t\mid C)=\alpha t^{\alpha -1}{\left({\theta }_c^1\right)}^{-\alpha }$. The hazard rate for the compliers if not treated is $h(T^0=t\mid C)=\alpha t^{\alpha -1}{\left({\theta }_c^0\right)}^{-\alpha }$. Hence, the log causal hazard ratio ϕ for the compliers is the difference between two log hazard rates:

$$\begin{array}{lll}\varphi & =& \mathit{log}\left[h(T^1=t\mid C)\right]-\mathit{log}\left[h(T^0=t\mid C)\right]\\ & =& -\alpha (\mathit{log}\left({\theta }_c^1\right)-\mathit{log}\left({\theta }_c^0\right))\end{array}$$

3. Two Stage Predictor Substitution (2SPS) Method

The 2SPS method is frequently used and simple to implement [4]. In the first stage, the treatment received Z is regressed on the IV-treatment assignment R, and let P = E (Z∣R). In the second stage, a log linear model including P, defined as:

$$\mathit{log}\left[h(Y\mid P)\right]=\eta +\mathit{\xi P}+\mathit{log}\left(h_0\left(y\right)\right),h_0\left(Y\right)=\alpha y^{\alpha -1}$$

is fitted to estimate the coefficient ξ. This is 2SPS estimator of the log causal hazard ratio. We first derive a closed form expression to the probability limit of the maximal likelihood estimator (M.L.E) of ξ, then take the difference between this probability limit and true log causal parameter ϕ for the expression of the asymptotic bias of the 2SPS estimator as an estimator of the log causal hazard ratio for compliers.

3.1. Probability limit of M.L.E of causal parameter

Let P̂ denote the predicted value from the estimated binary regression model. i.e., P̂ = Ê(Z∣R). When P̂ is substituted for P, the second stage Weibull model becomes:

$$\mathit{log}\left[\lambda (Y\mid \widehat{P})\right]={\eta }^{\ast }+{\xi }^{\ast }\widehat{P}+\mathit{log}\left(h_0^{\ast }\left(y\right)\right)$$

Let ξ̂* and ξ̂ denote the estimators (M.L.E) of ξ* and ξ respectively. As sample size n → ∞, P̂ → P, ${\widehat{\xi }}^{\ast }\stackrel{p}{\to }\widehat{\xi }$, and $\widehat{\xi }\stackrel{p}{\to }\xi$. Therefore, ${\widehat{\xi }}^{\ast }\stackrel{p}{\to }\xi$. To derive closed form expression for the asymptotic bias, we need to re-express ξ in terms of parameters specified in Section 2 under the principal stratification framework.

Only always takers receive the treatment when assigned to control (R = 0). Both always takers and compliers take the treatment when assigned to treatment (R = 1). Thus, it can be shown that [5]:

$$p_0=E(Z\mid R=0)={\rho }_a,p_1=E(Z\mid R=1)={\rho }_a+{\rho }_c$$

Since P = {p₀, p₁} is an one-to-one transformation of R = {0, 1}, we have the following for the second stage Weibull regression:

$$\begin{array}{lll}\mathit{log}\left(h(Y\mid R=0)\right)& =& \mathit{log}\left(h(Y\mid P=p_0)\right)\\ & =& \eta +\xi p_0+\mathit{log}\left(h_0\left(y\right)\right)\end{array}$$ (1)

and,

$$\begin{array}{lll}\mathit{log}\left(h(Y\mid R=1)\right)& =& \mathit{log}\left(h(Y\mid P=p_1)\right)\\ & =& \eta +\xi p_1+\mathit{log}\left(h_0\left(y\right)\right)\end{array}$$ (2)

Instead of working with a second stage model involving P, we can work with a model involving R instead. Solving (1) and (2), we have:

$$\xi =\frac{\mathit{log}\left(h(Y\mid R=1)\right)-\mathit{log}\left(h(Y\mid R=0)\right)}{p_1-p_0}$$ (3)

The log linear model including R assumes two underlying Weibull distributions of the same shape parameter α*, Weibull(α*, K₀) and Weibull(α*, K₁), for subjects assigned to control (R = 0) and treatment (R = 1) respectively. Thus, (3) can be expressed as:

$$\xi =\frac{\mathit{log}\left(K_1^{-{\alpha }^{\ast }}\right)-\mathit{log}\left(K_0^{-{\alpha }^{\ast }}\right)}{{\rho }_c},K_1^{-{\alpha }^{\ast }}=e^{\eta +{\xi }_{p_1}},K_0^{-{\alpha }^{\ast }}=e^{\eta +{\xi }_{p_0}}$$ (4)

It is worth noting that both follow up times of subjects assigned to control, denoted as Y∣R = 0, and follow up times of subjects assigned to treatment, denoted as Y∣R = 1, actually follow mixture distributions consisting of three different Weibull distributions. Details are given in Appendix A. However, the second stage Weibull model of 2SPS method imposes the two Weibull distributions, with the same shape parameter α* but different scale parameters K₀, K₁, upon subjects assigned to treatment (R = 1) or assigned to control (R = 0) respectively. Thus, the M.L.E of α*, K₀, K₁ are derived by maximizing the likelihood function L_n (α*, K₀, K₁) that consists of products of two Weibull densities: Weibull(α*, K₀) and Weibull(α*, K₁).

Let α̂* denote the M.L.E of α* and We set $\mathrm{E}\left(\frac{\partial \log \left(L_n\right({\alpha }^{\ast },{\widehat{K}}_0\left({\alpha }^{\ast }\right),{\widehat{K}}_1\left({\alpha }^{\ast }\right))}{\partial {\alpha }^{\ast }}\right)$, the expectation of score equation derived from profile likelihood of α*, equal to 0 and let $\stackrel{\sim }{a^{\ast }}$ be the solution. Under the assumptions stated in Section 2 and consistency of M.L.E, the probability limit of the estimator α̂* is $\stackrel{\sim }{a^{\ast }}$. Details are given in Appendix C. Once the parameters of the principal strata are defined, $\stackrel{\sim }{a^{\ast }}$ can be solved numerically using a root-finding algorithm such as the “bisection” method. Let K̂₀, K̂₁ be the M.L.Es of the two scale parameters K₀, K₁ respectively. After the value of $\stackrel{\sim }{a^{\ast }}$ is determined, the probability limits of the estimators K̂₀, K̂₁ can be derived as follows:

$$\begin{array}{ll}\stackrel{\sim }{K_0}& =[\frac{1}{P(\delta =1\mid R=0)}\times \\ & {\{{\rho }_a\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_n\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\}]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$ (5)

and,

$$\begin{array}{ll}\stackrel{\sim }{K_1}& =[\frac{1}{P(\delta =1\mid R=1)}\times \\ & {\{{\rho }_a\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_n\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\}]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$ (6)

The detailed steps of the derivation of (5) and (6) are given in Appendix C. By substituting (5) and (6) into (4), we derive the expression of log causal hazard ratio ξ as the following:

$$\begin{array}{l}\xi =\left\{\mathit{log}\right([\frac{1}{P(\delta =1\mid R=1)}\times \\ {\{{\rho }_a\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{\alpha \ast }/\alpha }+{\rho }_n\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{\alpha \ast }/\alpha }\}])}^{-1}\\ -\mathit{log}\left(\right[\frac{1}{P(\delta =1\mid R=0)}\times \\ {\{{\rho }_a\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}]}^{-\stackrel{\sim }{\alpha \ast }/\alpha }+{\rho }_n\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+{\rho }_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{\alpha \ast }/\alpha }\left\}\right])}^{-1}\}\\ \times \frac{1}{{\rho }_c}\end{array}$$ (7)

Thus, (7) is the closed-form expression of the probability limit of the log causal hazard ratio estimator ξ̂* from the 2SPS Weibull model.

3.2. Bias analysis

The asymptotic bias of the causal parameter ξ of the 2SPS Weibull regression model is simply the difference between the true log causal hazard ratio ϕ and the derived closed form expression of ξ, such that

$$B_{2\mathit{sps}}=\xi +\alpha (\mathit{log}\left({\theta }_c^1\right)-\mathit{log}\left({\theta }_c^0\right))$$ (8)

We can re-paramterize ${\theta }_{\mathit{nt}}^0$ in (8) with one additional parameter $\mathrm{\Delta }=-\alpha (\mathit{log}\left({\theta }_{\mathit{nt}}^0\right)-\mathit{log}\left({\theta }_c^0\right))$ as the following:

$$\mathit{log}\left({\theta }_{\mathit{nt}}^0\right)=\mathit{log}\left({\theta }_c^0\right)+\frac{\mathrm{\Delta }}{\alpha }$$ (9)

Δ in (9) is the log hazard ratio between never takers and compliers given no treatment. It can be interpreted as the magnitude of the unmeasured confounding because the differences between principal strata are attributable to the unmeasured confounding [5]. When Δ = 0 or ${\theta }_{\mathit{nt}}^0={\theta }_c^0$, there is no unmeasured confounding.

We make the following observations about the bias of 2SPS method from (3.11): 1) When α = 1 and we treat α* as a known parameter and fix it at 1, that is the scenario when the survival outcomes of all principal strata follow exponential distributions and we also fit an exponential model in the second stage instead of estimating the shape parameter for a more general form of Weibull distribution; 2) When ρ_c = 1, every subject is a complier and (8) can be simplified as $\frac{1}{{\alpha }^{\ast }}-\frac{\gamma }{\alpha }-\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)\frac{1}{\alpha }=0$. Then we have $\stackrel{\sim }{{\alpha }^{\ast }}=\alpha$. Setting ρ_c = 1, ρ_a = 0, and ρ_n = 0, (8) becomes 0 so that bias B_2sps = 0 when a randomized controlled trial has perfect compliance; 3) When there is no causal effect ( ${\theta }_c^1={\theta }_c^0$), all terms in (8) cancel out and we have B_2sps = 0; 4) When ρ_a = 0 and ${\theta }_c^0={\theta }_n^0$, there is no confounding because there are no always takers and never takers can’t get treatment so that the confounding can only be attributable to the difference between never takers and compliers given no treatment[5]. However, (8) can not be reduced to 0 under this setting so that the bias of 2SPS method B_2sps is generally not 0 even when there is no confounding. 5) λ, the scale parameter of the censoring distribution is involved in bias equation (9), which coincides with the results in Struthers and Kalbfleisch[17].

We can analyze how parameters influence the relationship between the magnitude of confounding and bias using derived closed form expression (9). For the purpose of demonstration only, here we create four scenarios in which there are no always takers. The results are revealed in Figure 1 (a)-(d).

Figure 1.

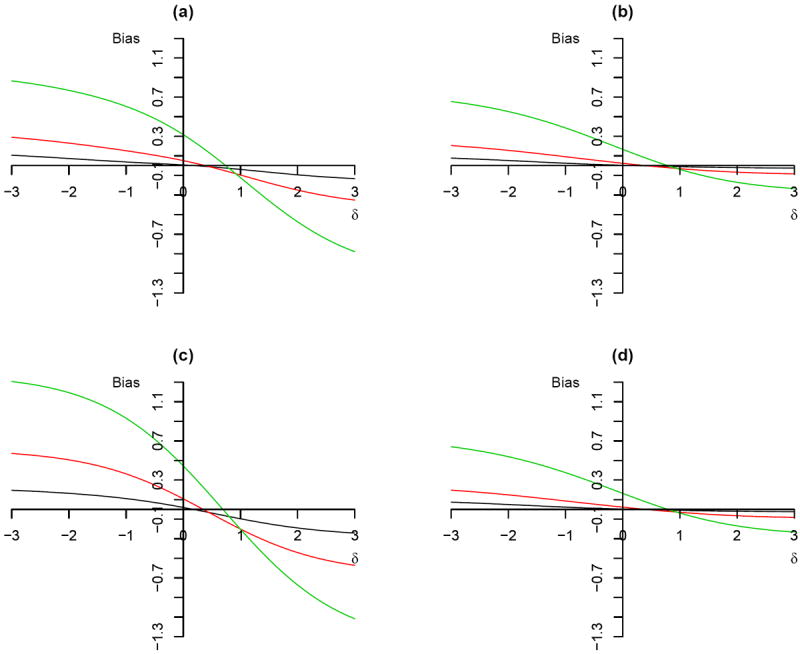
Plot of bias against magnitude of unmeasured confounding Δ using 2SPS method:(a) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.5, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$. (b) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.8, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$. (c) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.5, ${\theta }_c^1=33.3$, ${\theta }_c^0=16.7$. (d) P (R = 1) = 0.5, ρ_a = 0, ρ_c = 0.8, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$. The different colour of solid line corresponds to different shape parameter: black (α = 0.5), red (α = 1), and green (α = 2).

In Figure 1, we can clearly see that the bias of the 2SPS method is not 0 when there is no confounding. The bias increases with the larger shape parameter α of the survival function (within each principal stratum). The bias is the smallest when we have an decreasing hazard rate (α < 1) and the highest when we have an increasing hazard rate (α > 1). By comparing Figure 1 (a) and (b), we also observe that the bias decreases as the compliance rate increases from 0.5 to 0.8. When the scale parameter (θ_c) is smaller, the bias is also smaller (Figure 1 (a) vs. (c)). Although the probability of being randomly assigned to the treatment group is involved in computing the shape parameter of the second stage Weibull regression model, its effects on the bias are very small (compare Figure 1 (b) to (d)).

4. Two Stage Residual Inclusion (2SRI) Method

Similar to the 2SPS method, the 2SRI method involves two stage modeling [4]. In the first stage, we regress the treatment received Z on the IV-treatment assignment R and calculate the residual term E = Z − E (Z∣R). In the second stage, we fit a log linear model on both treatment received variable Z and residual E as,

$$\mathit{log}\left(h(Y\mid Z,E)\right))={\lambda }_0+{\lambda }_{1}Z+{\lambda }_{2}E+\mathit{log}(h_0\left(y\right)),h_0\left(Y\right)=\alpha y^{\alpha -1}$$ (10)

, to estimate the regression coefficient λ₁. This is 2SRI estimaor of the log causal hazard ratio. We derive the probability limit of the M.L.E of λ₁ first and then calculate the asymptotic bias by taking the difference between this probability limit of the estimator and true log causal hazard ratio among compliers.

4.1. Probability limit of M.L.E of causal parameter

As discussed in a previous study[5], (10) is not the true model for the hazard function h(Y∣Z, E). In fact the true model includes the interaction term between Z and E. However, deriving the closed-form expression for the probability limit of the estimator from (10) is very difficult when (10) is not the true model. With one additional assumption that there are no always takers, (10) becomes the true model. We derive a closed-form expression of the probability limit of the estimator of causal parameter λ₁ assuming that there are no always takers and thus (10) is the true model. Let Ê denote the residuals from the estimated binary regression model in the first stage. i.e., Ê = Z − Ê(Z∣R). When Ê is substituted for E, (10) becomes:

$$\mathit{log}\left[h(Y\mid Z,\widehat{E})\right]={\lambda }_0^{\ast }+{\lambda }_1^{\ast }Z+{\lambda }_2^{\ast }\widehat{E}+\mathit{log}\left(h_0^{\ast }\left(y\right)\right)$$

Let ${\widehat{\lambda }}_1^{\ast }$ and λ̂₁ be the estimators (M.L.E) of ${\lambda }_1^{\ast }$ and λ₁. As sample size n → ∞, Ê → E, ${\widehat{\lambda }}_1^{\ast }\stackrel{p}{\to }{\widehat{\lambda }}_1$, and ${\widehat{\lambda }}_1\stackrel{p}{\to }{\widehat{\lambda }}_1$. Thus, ${\widehat{\lambda }}_1^{\ast }\stackrel{p}{\to }{\lambda }_1$. To derive a closed form expression for the asymptotic bias, we need to first re-express λ₁ in terms of the parameters specified in section 2.3 under the principal stratification framework.

As shown in a previous study[5], under the no always taker assumption, the first stage binary regression is E(Z∣R) = ρ_a + ρ_cR and residual term E = Z − E (Z∣R), thus the residual term can be re-expressed as E = Z − ρ_a − ρ_cR. Since {Z, E} has an one to one relationship with {Z, R}, we can establish the following equivalence between the model involving {Z, E} and the model involving {Z, R} for the second stage Weibull model:

$$\begin{array}{lll}\mathit{log}\left(h(Y\mid Z,E)\right)& =& {\lambda }_0+{\lambda }_{1}Z+{\lambda }_{2}E+\mathit{log}\left(h_0\left(y\right)\right)\\ & =& {\lambda }_0+{\lambda }_{1}Z+{\lambda }_2(Z-{\rho }_a-{\rho }_{c}R)+\mathit{log}\left(h_0\left(y\right)\right)\\ & =& \mathit{log}\left(h(Y\mid Z,R)\right)\end{array}$$ (11)

Under the no always taker assumption, the second stage Weibull regression model defined by (10) assumes the three underlying Weibull distributions with the same shape parameter but different scale parameters for subjects in the three different subgroups: 1) ~ Weibull(α*, K₀) for those who are assigned to treatment and receive the treatment actually (Z = 1, R = 1). Only compliers are in this group; 2) ~ Weibull(α*, K₁) for those who are assigned to treatment but do not receive the treatment actually (Z = 0, R = 1), This group has only never takers; 3) ~ Weibull(α*, K₂) for those who are assigned to control and do not receive the treatment (Z = 0, R = 0), both never takers and compliers are in this group. There are no subjects that are assigned to control but still take the active treatment (Z = 1, R = 0) under the assumption of no always takers. Thus, the M.L.E of α*, K₀, K₁, K₂ are derived by maximizing the likelihood function L_n(α*, K₀, K₁, K₂) that consists of products of three Weibull densities: Weibull(α*, K₀), Weibull(α*, K₁), and Weibull(α*, K₂).

Let α̂* denote the M.L.E of α* and set $\mathrm{E}\left(\frac{\partial \log \left(L_n\right({\alpha }^{\ast },{\widehat{K}}_0\left({\alpha }^{\ast }\right),{\widehat{K}}_1\left({\alpha }^{\ast }\right),{\widehat{K}}_2\left(\alpha \right))}{\partial {\alpha }^{\ast }}\right)$, the expectation of score equation derived from profile likelihood of α*, to 0 and let $\stackrel{\sim }{{\alpha }^{\ast }}$ be the solution. Under the assumptions stated in section 2 and consistency of the M.L.E, the probability limit of the estimator α̂* is $\stackrel{\sim }{{\alpha }^{\ast }}$. Details are given in Appendix D. With the parameters of principal strata defined, $\stackrel{\sim }{{\alpha }^{\ast }}$ can be solved numerically using a root-finding algorithm. Let K̂₀, K̂₁, K̂₂ be the M.L.Es of two scale parameters K₀, K₁, K₂. Once the value of $\stackrel{\sim }{{\alpha }^{\ast }}$ is determined, we compute the probability limits of the estimators K̂₀, K̂₁, K̂₂ as follows:

$$\stackrel{\sim }{K_0}={\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_c^1}{\lambda }\right)}^{\alpha }}}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}$$ (12)

and

$$\stackrel{\sim }{K_1}={\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}$$ (13)

and

$$\stackrel{\sim }{K_2}={\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_{\mathit{nt}}+\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_c}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}{\rho }_{\mathit{nt}}+\frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}{\rho }_c}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}$$ (14)

The derivation of (12),(13) and (14) is detailed in Appendix D. Based on (11), we can establish the following three equations with all possible combination of values of Z and R excluding the always takers scenario (Z=1, R=0).

1. When Z=1 and R=1, there are only compliers in this subgroup.

   $$\begin{array}{lll}\hfill \mathit{log}\left(h(Y\mid Z=1,R=1)\right)& =& \mathit{log}\left(h\right(Y^{\left(1\right)}\mid Z=1,R=1\left)\right)\\ \hfill \to {\lambda }_0+{\lambda }_1+{\lambda }_2(1-{\rho }_C)& =& \mathit{log}\left({\stackrel{\sim }{K_0}}^{-\stackrel{\sim }{\alpha \ast }}\right)\\ & =& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_c^1}{\lambda }\right)}^{\alpha }}}\right]}^{-1}\right)\end{array}$$ (15)
2. When Z=0 and R=1, there are only never takers in this subgroup.

   $$\begin{array}{lll}\hfill \mathit{log}\left(h(Y\mid Z=0,R=1)\right)& =& \mathit{log}\left(h\right(Y^{\left(0\right)}\mid Z=0,R=1\left)\right)\\ \hfill \to {\lambda }_0+{\lambda }_2(-{\rho }_C)& =& \mathit{log}\left({\stackrel{\sim }{K_1}}^{\stackrel{\sim }{-{\alpha }^{\ast }}}\right)\\ & =& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}\right]}^{-1}\right)\end{array}$$ (16)
3. When Z=0 and R=0, there are mixture of both never takers and compliers in this subgroup.

   $$\begin{array}{lll}\mathit{log}\left(h(Y\mid Z=0,R=0)\right)& =& \mathit{log}\left(h\right(Y^{\left(0\right)}\mid Z=0,R=0\left)\right)\\ \hfill \to {\lambda }_0& =& \mathit{log}\left({\stackrel{\sim }{K_2}}^{-\stackrel{\sim }{{\alpha }^{\ast }}}\right)\\ & =& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_{\mathit{nt}}+\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_c}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}{\rho }_{\mathit{nt}}+\frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}{\rho }_c}\right]}^{-1}\right)\end{array}$$ (17)

We then derive the closed form expression for the causal parameter λ₁ by solving (15),(16), and (17) for λ₁ as follows:

$$\begin{array}{lll}{\lambda }_1& =& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_c^1}{\lambda }\right)}^{\alpha }}}\right]}^{-1}\right)\\ & -& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_{\mathit{nt}}+\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_c}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}{\rho }_{\mathit{nt}}+\frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}{\rho }_c}\right]}^{-1}\right)\\ & -& \frac{1-{\rho }_C}{{\rho }_C}\left(\mathit{log}\right({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_{\mathit{nt}}+\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }{\rho }_c}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}{\rho }_{\mathit{nt}}+\frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}{\rho }_c}\right]}^{-1}\left)\right)\\ & -& \mathit{log}\left({\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}}\right]}^{-1}\right)\end{array}$$

4.2. Bias analysis

To compute asymptotic bias of the 2SRI method, we subtract the true log hazard ratio ϕ from the closed-form expression of λ₁.

$$B_{2\mathit{SRI}}={\lambda }_1+\alpha (\mathit{log}\left({\theta }_c^1\right)-\mathit{log}\left({\theta }_c^0\right))$$ (18)

We can re-parameterize ${\theta }_{\mathit{nt}}^0$ in (18) in the way as in Section 3 and let ${\theta }_{\mathit{nt}}^0={\theta }_c^0{e}^{\frac{\mathrm{\Delta }}{\alpha }}$. From the derived expression of asymptotic bias of 2SRI estimator, we can make the following observations: 1) When α = 1, the survival outcome within a principal stratum follows an exponential distribution. If we treat α* as known and set α* = 1, it means we fit an exponential regression model in the second stage; 2) When there is perfect compliance (ρ_c = 1), we have B_2SRI = 0. In this scenario, $\stackrel{\sim }{{\alpha }^{\ast }}=\alpha$. By plugging ρ_c = 1 into (18), we can easily verify the results; 3) When there is no confounding ( ${\theta }_c^0={\theta }_n^0$), B2_SRI = 0; 4) When there is no causal effect ( ${\theta }_c^1={\theta }_c^0$), B_{2 SRI} is not 0; 5) λ, the scale parameter of the censoring distribution is involved in bias equation (18), similar to the findings for 2SPS method.

We can analyze how parameters influence the relationship between the magnitude of confounding and bias from the 2SRI method using (18). Similar to the previous section, four scenarios were created assuming there are no always takers. The results are shown in Figure 2 (a)-(d). In Figure 2, it is apparent that the bias of the 2SRI method is 0 when there is no confounding. Intuitively, under the condition of no confounding, substituting the term of the estimated residuals in the second stage survival model has no effect on the estimate of the causal parameter. By comparing Figure 2 (a) and (b), we also observe that the bias decreases as the compliance rate increases from 0.5 to 0.8. When the scale parameter (θ_c) is smaller, the bias tends to be smaller (Figure 2 (a) vs. (c)). The probability of being randomly assigned to the treatment group has very small impact on the bias (compare Figure 2 (b) to (d)).

Figure 2.

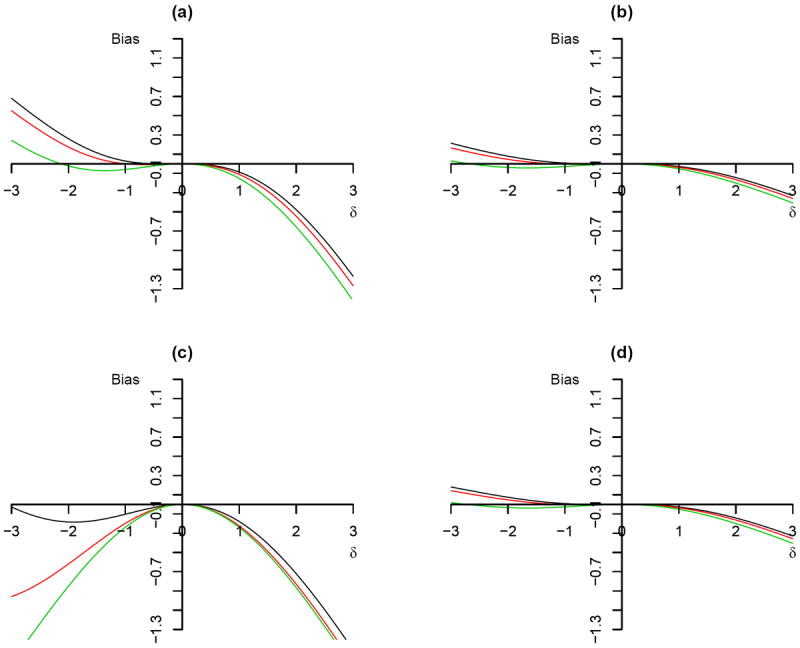
Plot of bias against magnitude of unmeasured confounding Δ using 2SRI method: (a) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.5, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$. (b) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.8, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$.(c) P (R = 1) = 0.8, ρ_a = 0, ρ_c = 0.5, ${\theta }_c^1=33.3$, ${\theta }_c^0=16.7$. (d) P (R = 1) = 0.5, ρ_a = 0, ρ_c = 0.8, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$. The different colour of solid line corresponds to different shape parameter: black (α = 0.5), red (α = 1), and green (α = 2).

5. Simulation

5.1. Simulation algorithm

We follow the five step algorithm used by Cai et al.[5] to generate data for a simulation study. In the first step, a data set of N subjects is generated. Always takers, compliers, and never takers among these subjects are generated from a multinomial distribution with probabilities {ρ_a, ρ_c, ρ_n}. At the second step, treatment assignment status R is generated for each subject with probability P(R = 1) = ρ_r. Because outcome in the present study is time to event, we modified step 3 to generate potential survival time {T⁰, T¹} and censoring time {L⁰, L¹} for each principal stratum based on the parameters ${\theta }_{\mathit{at}}^0$, ${\theta }_c^0$, ${\theta }_{\mathit{nt}}^0$, ${\theta }_{\mathit{at}}^1$, ${\theta }_c^1$, ${\theta }_{\mathit{nt}}^1$, λ. For instance, if a subject is a complier, the potential time to death under control $T_c^0$ is generated from weibull (α, ${\theta }_c^0$) and the potential time to death under treatment $T_c^1$ is generated from weibull (α, ${\theta }_c^1$). The potential censoring time { $L_c^0$, $L_c^1$} are generated from weibull(α, λ). At step 4, we use compliance status (always taker, complier, or never taker) and treatment assignment status R to determine the treatment received status Z. For instance, if a subject is a complier and assigned to treatment group (R = 1), then Z = 1. If a subject is an always taker but assigned to the control group, then Z = 0. At step 5, the observed survival time and censoring time are generated as follows:

$$T=T^{1}Z+T^0(1-Z),\mathrm{and}L=L^{1}Z+L^0(1-Z)$$

and finally observed follow up time and censoring indicator are given as:

$$Y=\mathit{min}(T,L),\mathrm{and}\delta =I(L\ge T)$$

5.2. Simulation results

To demonstrate the consistency between the derived closed form expressions and the asymptotic biases from the 2SPS and 2SRI approaches under the assumption of no always takers (ρ_a = 0), we ran the simulation 2000 times, with the sample size n=10000, according to the same parameter settings presented in Figure 1 d) and Figure 2 d). Table 1 shows simulation results from 4 scenarios (α = 0.5, 1, 1.5, 2). As shown in this table, the biases from simulated results are consistent with the values computed with the derived analytic formula for both the 2SPS and 2SRI Weibull models. We also considered 2SPS and 2SRI Cox models (the second stage regression is a Cox model instead of a Weibull model). The pattern of the biases from 2SPS and 2SRI Cox models remains the same as for the 2SPS and 2SRI Weibull models respectively. With decreasing hazard (α = 0.5), the bias from using the 2SPS approach is smaller than the bias from the 2SRI approach. When the hazard is constant or increasing (α ≥ 1), the results are mixed. With stronger negative confounding, the 2SPS method produces smaller bias than the 2SRI method. However, with no confounding or stronger positive confounding, the 2SPS method produces larger bias than the 2SRI method.

Table 1.

Bias in estimating log causal hazard ratio parameter (ρ_a = 0, ρ_c = 0.5, ρ_r = 0.8, ${\theta }_c^1=3.33$, ${\theta }_c^0=1.67$)

α	δ	${\mathrm{Bias}}_{2\mathrm{sps}}^{\mathrm{analytic}}$	${\mathrm{Bias}}_{2\mathrm{sps}}^{\mathrm{AFT}}$	${\mathrm{Bias}}_{2\mathrm{sps}}^{\mathrm{Cox}}$	${\mathrm{Bias}}_{2\mathrm{sri}}^{\mathrm{analytic}}$	${\mathrm{Bias}}_{2\mathrm{sri}}^{\mathrm{AFT}}$	${\mathrm{Bias}}_{2\mathrm{sri}}^{\mathrm{Cox}}$
0.5	2	-0.094	-0.093	-0.091	-0.477	-0.476	-0.476
	1.5	-0.067	-0.068	-0.064	-0.238	-0.239	-0.235
	1	-0.039	-0.040	-0.039	-0.086	-0.087	-0.086
	0.5	-0.013	-0.016	-0.012	-0.015	-0.018	-0.014
	0	0.007	0.009	0.007	0.000	0.002	0.000
	-0.5	0.023	0.020	0.026	0.000	-0.003	-0.001
	-1	0.038	0.037	0.051	0.029	0.028	0.029
	-1.5	0.055	0.053	0.075	0.114	0.112	0.108
	-2	0.073	0.074	0.101	0.261	0.263	0.236
1	2	-0.250	-0.253	-0.247	-0.545	-0.550	-0.544
	1.5	-0.177	-0.175	-0.177	-0.285	-0.284	-0.284
	1	-0.096	-0.093	-0.097	-0.110	-0.107	-0.112
	0.5	-0.017	-0.020	-0.018	-0.022	-0.025	-0.023
	0	0.051	0.053	0.055	0.000	0.002	0.000
	-0.5	0.107	0.106	0.116	-0.007	-0.008	-0.009
	-1	0.152	0.153	0.177	0.000	0.000	0.002
	-1.5	0.193	0.191	0.232	0.057	0.053	0.055
	-2	0.230	0.232	0.280	0.175	0.176	0.157
1.5	2	-0.422	-0.423	-0.418	-0.605	-0.607	-0.602
	1.5	-0.285	-0.285	-0.284	-0.326	-0.325	-0.326
	1	-0.132	-0.133	-0.134	-0.133	-0.134	-0.134
	0.5	0.019	0.023	0.021	-0.028	-0.027	-0.029
	0	0.153	0.152	0.159	0.000	-0.004	0.000
	-0.5	0.261	0.266	0.274	-0.015	-0.012	-0.015
	-1	0.345	0.342	0.376	-0.030	-0.033	-0.027
	-1.5	0.412	0.412	0.461	-0.005	-0.008	-0.002
	-2	0.467	0.468	0.531	0.078	0.075	0.068
2	2	-0.574	-0.578	-0.571	-0.656	-0.656	-0.653
	1.5	-0.359	-0.360	-0.357	-0.362	-0.361	-0.359
	1	-0.122	-0.124	-0.122	-0.152	-0.153	-0.152
	0.5	0.111	0.115	0.112	-0.034	-0.032	-0.036
	0	0.317	0.320	0.324	0.000	0.003	0.002
	-0.5	0.481	0.479	0.494	-0.022	-0.026	-0.026
	-1	0.605	0.605	0.636	0.059	-0.059	-0.056
	-1.5	0.698	0.701	0.747	-0.069	-0.069	-0.063
	-2	0.769	0.770	0.833	-0.023	-0.024	-0.026

${\mathit{Bias}}_{2\mathit{sps}}^{\mathit{analytic}}$ - bias computed using analytic formula derived for 2SPS method; ${\mathit{Bias}}_{2\mathit{sps}}^{\mathit{AFT}}$ - bias computed via simulation for 2SPS Weibull accelerated failure time model; ${\mathit{Bias}}_{2\mathit{sps}}^{\mathit{Cox}}$ -bias computed via simulation for 2SPS Cox model; ${\mathit{Bias}}_{2\mathit{sri}}^{\mathit{analytic}}$ - bias computed using analytic formula derived for 2SRI method; ${\mathit{Bias}}_{2\mathit{sri}}^{\mathit{AFT}}$ -bias computed via simulation for 2SRI Weibull accelerated failure time model; ${\mathit{Bias}}_{2\mathit{sri}}^{\mathit{Cox}}$ -bias computed via simulation for 2SRI Cox model;

To evaluate the performance of both 2SPS and 2SRI methods in the setting where there are always takers, we simulated the data with various combination of parameters based on the following settings: i) Shape parameter α varies among {0.5, 1, 2}, which represent decreasing, constant, and increasing hazard scenarios; ii) Probabilities of being always takers ρ_a and compliers ρ_c were set to 3 combinations: {0.2, 0.7}, {0.7, 0.2}, and {0, 0.5}. In this way, low, medium, and high levels of compliance were represented; iii) probability of being assigned to treatment ρ_r were set to {0.1, 0.5} to reflect both new and relatively established treatments; iv) Scale parameter of censoring distribution were set to {0.5, 1, 2}; v) Each of the parameters ${\theta }_{\mathit{at}}^0$, ${\theta }_c^0$, ${\theta }_c^1$ was set to {0.5, 1, 3} separately. Thus, 1458 possible combinations were created. For each setting, we generated 10,000 observations and fit the 2SPS and 2SRI models to the data. This process was repeated 2000 times.

The results are presented in Figure 3. The magnitude of bias increases with increasing magnitudes of unmeasured confounding. As the value of shape parameter α increases, the magnitude of bias increases. In the scenarios with decreasing hazard, the 2SPS method outperforms the 2SRI method. The 2SRI method tends to have larger asymptotic bias when the magnitude of unmeasured confounding is large. In the scenarios with constant hazard, the 2SPS method slightly outperforms the 2SRI method when the magnitude of unmeasured confounding is large. In the scenarios with increasing hazard, both approaches produce larger biases. The 2SRI method performs better when the magnitude of unmeasured confounding is small. When there are always takers, the 2SRI method could be biased even when there is no measured confounding. We also compared the two methods using mean square error and the conclusions remain the same (4).

Figure 3.

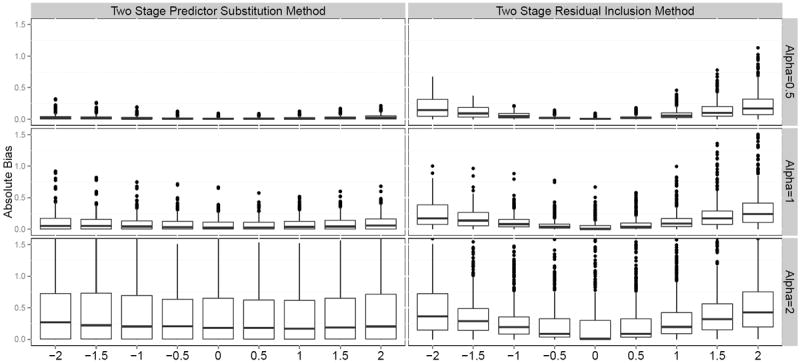
Absolute bias in estimating log causal hazard ratio using two stage IV methods (X-axis is the magnitude of confounding Δ, Y-axis is the absolute bias). For 2SRI method or 2SPS method, the biases computed for each of 1458 possible scenarios were grouped by the magnitude of shape parameter α (decreasing hazard for α = 0.5, constant hazard for α = 1, and increasing hazard for α = 2) and the magnitude of confounding Δ (larger values represent lager confounding effects and 0 represents no confounding).

6. Seer-Medicare Prostate Cancer Study

Prostate cancer is the highest prevalence non-skin malignancy among American men (In 2011, there were an estimated 2,707,821 men living with prostate cancer in the United States. The number of deaths was 23.0 per 100,000 men per year). Unlike prostate cancers that are diagnosed at an early stage, locally advanced prostate cancer is associated with substantial morbidity and mortality. Radiation therapy is a common treatment for locally advanced prostate cancer. Two randomized trials recently demonstrated that radiation therapy reduces mortality for men with locally advanced tumors who also receive systemic androgen deprivation[9, 10]. However, both trials excluded elderly patients and those with early stage, PSA-screen detected cancer and therefore had less generalizability, a common criticism of randomized evidence. Therefore, we applied two-stage IV methods to evaluate survival outcomes in locally advanced prostate cancer, assessing survival outcomes of androgen deprivation therapy with or without radiation therapy in comparison to the randomized trials.

We analyzed data from the Surveillance, Epidemiology and End Results (SEER)-Medicare database. The SEER-Medicare database links patient demographic and tumor-specific data collected by SEER cancer registries to Medicare claims for inpatient and outpatient care. We considered patients with prostate cancer diagnosed between January 1, 1995 and December 31, 2007 in SEER with follow up through December 31, 2010 in Medicare. The following patients were excluded: 1) older than age 85; 2) with unknown urban category; 3) in hospital referral regions (HRR) with less than 50 patients; 4) with unknown distance to the closest radiation facility; 5) patients who died within the first 9 months of the study. A total of 31,541 patients were selected and categorized as receiving androgen deprivation with or without radiation therapy.

The cohort was divided into the following three groups: 1) patients with American Joint Commission on Cancer (AJCC) Tumor stage (T-stage) of T2 or T3 and aged 65-75 (called the RCT Cohort). The patients in the “RCT Cohort” are most comparable to the patients from the two randomized studies of androgen deprivation with or without radiation therapy[9, 10]; 2) elderly patients under-represented or excluded from the published randomized trials with T-stage T2 or T3, aged 76-85 (called the “Elderly Cohort”); and 3) patients with early stage, PSA-screen detected cancer with T-stage T1 disease who were excluded from the published randomized trials (called the “Screen-Detected Cohort”).

The study by Widmark et al.[9] included men from 47 centers in Europe diagnosed between February, 1996 and December, 2002. 875 patients with locally advanced prostate cancer (T3; 78%; prostate-specific antigen (PSA) ≤ 70 ng/mL; N0; M0) were enrolled. 439 patients were randomly assigned to androgen deprivation alone and the other 436 patients received androgen deprivation with radiation therapy. The study by Warde et. al. enrolled 1,205 patients with locally advanced (T3 or T4) prostate cancer, organ-confined disease (T2) with either PSA >40 ng/mL or PSA >20 ng/mL and a Gleason score of 8 or higher between 1995 and 2005. 1205 patients were randomly assigned to receive the androgen deprivation alone (n=602) or androgen deprivation with radiation therapy (n=603). The hazard ratios for overall mortality reported previously [9] and [10] were 0.68 (95% CI 0.52–0.89) and 0.77 (95% CI 0.61–0.98). For ease of comparison, we combined the results of the randomized trials using weighted-average meta-analysis. The meta-analytic HR was 0.73 (0.61–0.87).

To assess the effectiveness of androgen deprivation with or without radiation therapy in reducing overall mortality (death from any cause), we performed two-stage IV Weibull regression analysis (2SPS and 2SRI) using a local area treatment rate instrument and controlling for the propensity score. The local area treatment rate instrument was defined as the proportion of patients who received definitive treatment (surgery or radiation therapy) among all patients with prostate cancer in the hospital referral region (HRR) and we categorized this instrument into a binary variable according to its median. This IV measures the aggressiveness of local area treatment and captures regionally distinct structural care variation not fully explained by patient characteristics. The IV was strongly associated with treatment assignment and balanced important prognostic factors [3]. The propensity score model included potential confounding variables including age, race, ethnicity, clinical T stage, N stage, and World Health Organization tumor grade, 17 categories of co-morbid disease, urban residence, and census track median income.

As shown in Table 2, there is variability in the estimated HRs obtained from the 2SPS and 2SRI methods. We estimated the shape parameter α ≈ 1.6 from the data. Using Figure 3, we can see that the bias for both the 2SPS and 2SRI methods is the largest when we have an increasing hazard (α > 1), even when the magnitude of unmeasured confounding is relatively small. When the hazard function is a decreasing one (α < 1), the 2SPS method produces more stable and less biased estimates than the 2SRI method. In this case, 2SPS may be a more appropriate approach to use. In the RCT Cohort, the estimated HRs (HR=0.96) from both IV methods are much larger than the meta-analytic HR from the two randomized studies. Note that the confidence intervals are also much larger in both IV analyses than in the original RCTs. In the published RCTs, the authors concluded that there was a statistically significant treatment effect (combined therapy is better) whereas from our IV analysis, we can’t draw this conclusion. In the total study sample and separately in the RCT Cohort and the Screen-Detected Cohort, the two IV estimates are quite similar. However, for the Elderly Cohort, the estimate from the 2SPS method is different from the estimate from the 2SRI method.

Table 2.

Bias in estimating causal hazard ratio parameter for prostate cancer study

Outcome	Group	IV2sri	IV2sps
All cause mortality	Total (n=31541)	0.57(0.17-1.06)	0.59(0.19-1.09)
	RCT Cohort (n=12924)	0.96(0.18-5.81)	0.97(0.18-5.94)
	Elderly Cohort (n=14340)	0.74(0.20-1.83)	0.96(0.26-2.35)
	Screen-Detected Cohort (n=4277)	0.34(0.02-2.99)	0.35(0.03-3.22)

7. Discussion

Many clinical and health services studies are using health care databases to compare the treatment effectiveness for drug and surgical therapies, but are prone to unmeasured confounding. Two stage IV methods have been gaining popularity among clinical researchers because these methods provide a relatively simple approach to analyzing survival outcome studies in the presence of unmeasured confounding. However, current knowledge about potential bias in estimating the log causal hazard ratio is limited. As demonstrated in our prostate cancer study, the large treatment effects estimated from two stage IV methods could be attributable to potential bias. We have derived closed-form expressions for the asymptotic bias of the 2SRI and 2SPS approaches assuming the survival times follow a Weibull distribution with shape parameter α and scale parameter K. We have demonstrated that these analytic results are consistent with our simulation results.

For binary outcomes, two previous studies[5, 18] demonstrated that the bias in the treatment effect estimated using the 2SRI approach increases as the magnitude of confounding increases. In this current work, we have shown analytically and by simulation that the 2SRI and 2SPS approaches are both biased in estimating the causal hazard ratio among compliers. In some situations when the hazard is decreasing (e.g among patients who have recently received a kidney transplantation), the 2SPS method is less biased than the 2SRI method and could be a more appropriate method to use. When the hazard is an increasing function, both IV methods may produce very large bias even under a moderate amount of unmeasured confounding. In this case, we recommend exercising caution when interpreting results from two-stage IV survival models.

We have shown that even when all IV assumptions are met, both the 2SRI and the 2SPS methods could fail to consistently estimate the causal hazard ratio among compliers. Our analytic results for bias may help to guide researchers in deciding when the bias is likely to be reasonably small so that two stage IV methods may be reasonably applied. Furthermore, in a sensitivity analysis approach, one may estimate the shape parameter and the censoring proportion among patients assigned to treatment or control from the data. With the shape parameter and censoring proportions fixed based on our known data the level of the unmeasured confounding could be varied to examine how the estimates would change, as shown in Figures 1 and 2. Alternative methods include partial likelihood estimation [19].

Figure 4.

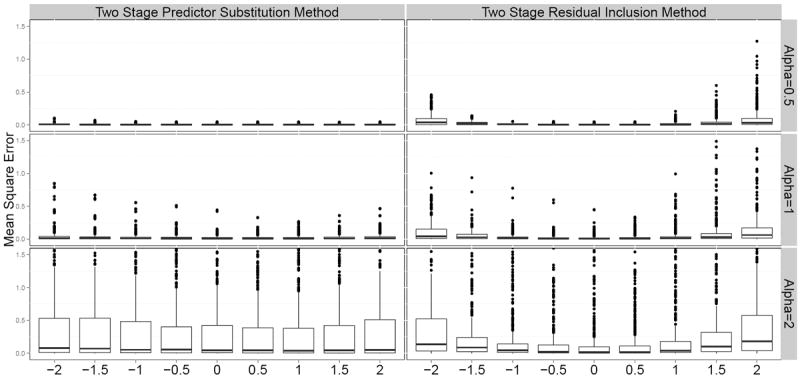
Mean square error in estimating log causal hazard ratio using two stage IV methods (X-axis is the magnitude of confounding Δ, Y-axis is the Mean Square Error). For 2SRI method or 2SPS method, the mean square error computed for each of 1458 possible scenarios were grouped by the magnitude of shape parameter α (decreasing hazard for α = 0.5, constant hazard for α = 1, and increasing hazard for α = 2) and the magnitude of confounding Δ (larger values represent lager confounding effects and 0 represents no confounding).

Appendix

Appendix A: Mixture of Weibull Distributions

Prove the distribution function of observed survival time T conditional on random assignment R can be expressed as the following equations:

$$F(T\mid R=0)=1-(e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }}{\rho }_A+e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }}{\rho }_N+e^{-{\left(\frac{t}{{\theta }_C^0}\right)}^{\alpha }}{\rho }_C)$$ (A.1)

and,

$$F(T\mid R=1)=1-(e^{-{\left(\frac{t}{{\theta }_C^1}\right)}^{\alpha }}{\rho }_C+e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }}{\rho }_N+e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }}{\rho }_A)$$ (A.2)

In the above equations, AT represents always takers, C represents compliers, and NT represents never takers. Other definitions of parameters and distributions that are used in the proof are given below:

$$\begin{array}{lll}\hfill R& =& 1\mathrm{if\; assigned\; to\; treatment};0\mathrm{if\; assigned\; to\; control}\\ \hfill Z& =& 1\mathrm{if\; receives\; treatment};0\mathrm{if\; receives\; control}\\ \hfill {\rho }_r& =& P(R=1)\\ \hfill {\rho }_A& =& P\left(\mathit{AT}\right)\\ \hfill {\rho }_C& =& P\left(C\right)\\ \hfill {\rho }_N& =& 1-{\rho }_A-{\rho }_C\end{array}$$

$$\begin{array}{lll}\hfill T^1& =& \mathrm{potential\; outcome\; for\; a\; patient\; under\; treatment}\\ \hfill T^0& =& \mathrm{potential\; outcome\; for\; a\; patient\; under\; control}\\ T^1\mid \mathit{AT}& ~& \mathit{weibull}(\alpha ,{\theta }_{\mathit{AT}}^1)\\ \hfill T^1\mid C& ~& \mathit{weibull}(\alpha ,{\theta }_C^1)\\ \hfill T^1\mid \mathit{NT}& ~& \mathit{weibull}(\alpha ,{\theta }_{\mathit{NT}}^1)\\ \hfill T^0\mid \mathit{AT}& ~& \mathit{weibull}(\alpha ,{\theta }_{\mathit{AT}}^0)\\ \hfill T^0\mid C& ~& \mathit{weibull}(\alpha ,{\theta }_C^0)\\ \hfill T^0\mid \mathit{NT}& ~& \mathit{weibull}(\alpha ,{\theta }_{\mathit{NT}}^0)\end{array}$$

no defiers under monotonicity assumption

Proof

$$\begin{array}{lll}F(T^{\left(1\right)}\mid Z=1,R=1)& =P(T^{\left(1\right)}\le t\mid Z=1,R=1)& \\ & =\frac{P(T^{\left(1\right)}\le t,Z=1,R=1)}{P(Z=1,R=1)}& \\ & =\frac{P(T^{\left(1\right)}\le t,\mathit{AT},R=1)+P(T^{\left(1\right)}\le t,C,R=1)}{P(\mathit{AT},R=1)+P(C,R=1)}& \\ & =\frac{P(T^{\left(1\right)}\le t,\mathit{AT})P(R=1)+P(T^{\left(1\right)}\le t,C)P(R=1)}{(P\left(\mathit{AT}\right)+P\left(C\right))P(R=1)}& \because R\perp (T^{\left(1\right)},T^{\left(0\right)}),\\ & R\perp \mathrm{principal\; strata}& \\ & =\frac{P(T^{\left(1\right)}\le t\mid \mathit{AT})P\left(\mathit{AT}\right)+P(T^{\left(1\right)}\le t\mid C)P\left(C\right)}{P\left(\mathit{AT}\right)+P\left(C\right)}& \\ & =(1-e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }})\frac{P\left(\mathit{AT}\right)}{P\left(\mathit{AT}\right)+P\left(C\right)}& \\ & +(1-e^{-{\left(\frac{t}{{\theta }_C^1}\right)}^{\alpha }})\frac{P\left(C\right)}{P\left(\mathit{AT}\right)+P\left(C\right)}& \end{array}$$

$$\begin{array}{llll}F(T^{\left(0\right)}\mid Z=0,R=1)& =& P(T^{\left(0\right)}\le t\mid Z=0,R=1)& \\ & =& \frac{P(T^{\left(0\right)}\le t,Z=0,R=1)}{P(Z=0,R=1)}& \\ & =& \frac{P(T^{\left(0\right)}\le t,\mathit{NT},R=1)}{P\left(\mathit{NT}\right)P(R=1)}& \\ & =& P(T^{\left(0\right)}\le t\mid \mathit{NT})& \because R\perp (T^{\left(1\right)},T^{\left(0\right)}),R\perp \mathrm{principal\; strata}\\ & =& (1-e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }})& \end{array}$$

F(T∣R = 1) can be expressed as:

$$\begin{array}{lll}F(T\mid R=1)& =& P(T\le t,Z=1\mid R=1)+P(T\le t,Z=0\mid R=1)\\ & =& P(T\le t\mid Z=1,R=1)P(Z=1\mid R=1)\\ & +& P(T\le t\mid Z=0,R=0)P(Z=0\mid R=1)\\ & =& P(T^{\left(1\right)}\le t\mid Z=1,R=1)P(Z=1\mid R=1)\\ & +& P(T^{\left(0\right)}\le t\mid Z=0,R=1)P(Z=0\mid R=1)\\ & =& \left(\right(1-e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }})\frac{P\left(\mathit{AT}\right)}{P\left(\mathit{AT}\right)+P\left(C\right)}+(1-e^{-{\left(\frac{t}{{\theta }_C^1}\right)}^{\alpha }}\left)\frac{P\left(C\right)}{P\left(\mathit{AT}\right)+P\left(C\right)}\right)(P\left(\mathit{AT}\right)+P\left(C\right))\\ & +& (1-e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }})\left(P\left(\mathit{NT}\right)\right)\\ & =& 1-(e^{-{\left(\frac{t}{{\theta }_C^1}\right)}^{\alpha }}{\rho }_C+e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }}{\rho }_N+e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }}{\rho }_A)\end{array}$$

$$\begin{array}{ll}F(T^{\left(1\right)}\mid Z=1,R=0)& =P(T^{\left(1\right)}\le t\mid Z=1,R=0)\\ & =\frac{P(T^{\left(1\right)}\le t,Z=1,R=0)}{P(Z=1,R=0)}\\ & =\frac{P(T^{\left(1\right)}\le t,\mathit{AT},R=0)}{P(\mathit{AT},R=0)}\\ & =\frac{P(T^{\left(1\right)}\le t\mid \mathit{AT})P\left(\mathit{AT}\right)P(R=0)}{P\left(\mathit{AT}\right)P(R=0)}\\ & =P(T^{\left(1\right)}\le t\mid \mathit{AT})\\ & =1-e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }}\end{array}$$

$$\begin{array}{ll}F(T^{\left(0\right)}\mid Z=0,R=0)& =P(T^{\left(0\right)}\le t\mid Z=0,R=0)\\ & =\frac{P(T^{\left(0\right)}\le t,Z=0,R=0)}{P(Z=0,R=0)}\\ & =\frac{P(T^{\left(0\right)}\le t,\mathit{NT},R=0)+P(T^{\left(0\right)}\le t,C,R=0)}{P(\mathit{NT},R=0)+P(C,R=0)}\\ & =\frac{P(T^{\left(0\right)}\le t\mid \mathit{NT})P\left(\mathit{NT}\right)+P(T^{\left(0\right)}\le t\mid C)P\left(C\right)}{P\left(\mathit{NT}\right)+P\left(C\right)}\\ & =(1-e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }})\frac{P\left(\mathit{NT}\right)}{P\left(\mathit{NT}\right)+P\left(C\right)}\\ & +(1-e^{-{\left(\frac{t}{{\theta }_C^0}\right)}^{\alpha }})\frac{P\left(C\right)}{P\left(\mathit{NT}\right)+P\left(C\right)}\end{array}$$

F(T∣R = 0) can be expressed as:

$$\begin{array}{lll}F(T\mid R=0)& =& P(T\le t,Z=1\mid R=0)+P(T\le t,Z=0\mid R=0)\\ & =& P(T\le t\mid Z=1,R=0)P(Z=1\mid R=0)\\ & +& P(T\le t\mid Z=0,R=0)P(Z=0\mid R=0)\\ & =& P(T^{\left(1\right)}\le t\mid Z=1,R=0)P(Z=1\mid R=0)\\ & +& P(T^{\left(0\right)}\le t\mid Z=0,R=0)P(Z=0\mid R=0)\\ & =& \left(\right(1-e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }})P\left(\mathit{AT}\right)\\ & +& \left[\right(1-e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right)}^{\alpha }})\frac{P\left(\mathit{NT}\right)}{P\left(\mathit{NT}\right)+P\left(C\right)}+(1-e^{-{\left(\frac{t}{{\theta }_C^0}\right)}^{\alpha }}\left)\frac{P\left(C\right)}{P\left(\mathit{NT}\right)+P\left(C\right)}\right](P\left(C\right)+P\left(\mathit{NT}\right)\\ & =& 1-(e^{-{\left(\frac{t}{{\theta }_{\mathit{AT}}^1}\right)}^{\alpha }}{\rho }_A+e^{-{\left(\frac{t}{{\theta }_{\mathit{NT}}^0}\right))}^{\alpha }}{\rho }_N+e^{-{\left(\frac{t}{{\theta }_C^0}\right)}^{\alpha }}{\rho }_C)\end{array}$$

Appendix B: Proofs related with Derivation of Closed Form Solution

1. Assume survival time T ~ Weibull(α, K) and censoring time L ~ Weibull(α, λ). Let Y = min(T, L) and δ = I(T ≤ L). Show that

   $$Y~\mathit{Weibull}(\alpha ,{(\frac{1}{{\lambda }^{\alpha }}+\frac{1}{K^{\alpha }})}^{-1/\alpha })$$

   and,

   $$P(\delta =1)=\frac{1}{1+\frac{K^{\alpha }}{{\lambda }^a}}$$ (B.1)
   Proof:

   $$\begin{array}{lll}P(Y\ge y)& =& P(\mathit{min}(T,L)\ge y)\\ & =& P(T\ge y,L\ge y)\\ & =& {\mathit{\int }}_y^{+\infty }\alpha \frac{t^{\alpha -1}}{K^{\alpha }}\mathit{exp}(-{\left(\frac{t}{K}\right)}^{\alpha })\mathit{dt}{\mathit{\int }}_y^{+\infty }\alpha \frac{l^{\alpha -1}}{{\lambda }^{\alpha }}\mathit{exp}(-{\left(\frac{l}{\lambda }\right)}^{\alpha })\mathit{dl}\\ & =& \mathit{exp}(-{\left(\frac{y}{K}\right)}^{\alpha })\mathit{exp}(-{\left(\frac{y}{\lambda }\right)}^{\alpha })\\ & =& \mathit{exp}(-{\left(\frac{y}{{(\frac{1}{{\lambda }^{\alpha }}+\frac{1}{K^{\alpha }})}^{-1/\alpha }}\right)}^{\alpha })\end{array}$$
   Thus, $Y~\mathit{Weibull}(\alpha ,{\left(\frac{1}{{\lambda }^{\alpha }}+\frac{1}{K^{\alpha }}\right)}^{-1/\alpha )}$

   $$\begin{array}{lll}P(\delta =1)& =& P(0\le T\le L,0\le L\le \infty )\\ & =& {\mathit{\int }}_0^{+\infty }\alpha \frac{l^{\alpha -1}}{{\lambda }^{\alpha }}\mathit{exp}(-{\left(\frac{l}{\lambda }\right)}^{\alpha }){\mathit{\int }}_0^l\alpha \frac{t^{\alpha -1}}{K^{\alpha }}\mathit{exp}(-{\left(\frac{t}{K}\right)}^{\alpha })\mathit{dtdl}\\ & =& {\mathit{\int }}_y^{+\infty }\alpha \frac{l^{\alpha -1}}{{\lambda }^{\alpha }}\mathit{exp}(-{\left(\frac{l}{\lambda }\right)}^{\alpha })[1-\mathit{exp}(-{\left(\frac{l}{K}\right)}^{\alpha }\left)\right]\mathit{dl}\\ & =& 1-{\mathit{\int }}_y^{+\infty }\alpha \frac{l^{\alpha -1}}{{\lambda }^{\alpha }}\mathit{exp}(-{\left(\frac{l}{\lambda }\right)}^{\alpha })\mathit{exp}(-{\left(\frac{l}{K}\right)}^{\alpha })\mathit{dl}\\ & =& 1-\frac{1}{1+{(\lambda /K)}^{\alpha }}\\ & =& \frac{1}{1+{\left(\frac{K}{\lambda }\right)}^{\alpha }}\end{array}$$
2. Assume survival time T is a mixture of three Weibull distributions with Density $f\left(t\right)={\sum }_{i=1}^3{p}_{i}f\left(t_i\right)$. T₁ ~ Weibull(α, K₁), T₂ ~ Weibull(α, K₂), and T₃ ~ Weibull(α, K₃). The weights are p₁, p₂, p₃ and ${\sum }_{i=1}^3{p}_i=1$. The censoring time L ~ Weibull(α, λ). Let Y = min(T, L) and δ = I(T ≤ L). Show that

   $$P(\delta =1)=p_1\frac{1}{1+\frac{K_1^{\alpha }}{{\lambda }^a}}+p_2\frac{1}{1+\frac{K_2^{\alpha }}{{\lambda }^a}}+p_3\frac{1}{1+\frac{K_3^{\alpha }}{{\lambda }^a}}$$ (B.2)
   Proof:

   $$\begin{array}{lll}P(\delta =1)& =& P(\delta =1,G=1)+P(\delta =1,G=2)+P(\delta =1,G=3)\\ & =& P(\delta =1\mid G=1)P(G=1)+P(\delta =1\mid G=2)P(G=2)+P(\delta =1\mid G=3)P(G=3)\\ & =& p_1\frac{1}{1+\frac{K_1^{\alpha }}{{\lambda }^a}}+p_2\frac{1}{1+\frac{K_2^{\alpha }}{{\lambda }^a}}+p_3\frac{1}{1+\frac{K_3^{\alpha }}{{\lambda }^a}}\end{array}$$
3. Given X follows a Weibull distribution (α*, K). Show that

   $$E\left(X^{\alpha }\right)=\mathrm{\Gamma }(\frac{\alpha }{{\alpha }^{\ast }}+1)K^{\alpha }$$ (B.3)
   Proof:

   $$\begin{array}{lll}E\left(X^{\alpha }\right)& =\mathit{\int }{X}^{\alpha }\frac{{\alpha }^{\ast }}{K^{{\alpha }^{\ast }}}{X}^{{\alpha }^{\ast }-1}{e}^{-\left(\frac{X}{K}\right){\alpha }^{\ast }}\mathit{dx}& \\ & =\mathit{\int }{y}^{\frac{\alpha }{{\alpha }^{\ast }}}\frac{1}{K^{{\alpha }^{\ast }}}{e}^{-\frac{y}{K^{{\alpha }^{\ast }}}}\mathit{dy}& \mathrm{Let}y=x^{{\alpha }^{\ast }}\\ & =\frac{1}{K^{{\alpha }^{\ast }}}\mathit{\int }{y}^{\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)-1}{e}^{-\frac{y}{K^{{\alpha }^{\ast }}}}\mathit{dy}& \\ & =\frac{1}{K^{{\alpha }^{\ast }}}{\left(K^{{\alpha }^{\ast }}\right)}^{\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)}\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)\mathit{\int }\frac{1}{{\left(K^{{\alpha }^{\ast }}\right)}^{\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)}\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)}{y}^{\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)-1}{e}^{-\frac{y}{K^{{\alpha }^{\ast }}}}\mathit{dy}& \\ & =\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)K^{\alpha }& \end{array}$$
4. Given X follows a Weibull distribution (α*, K). Show that

   $$E\left(\mathit{log}\left(X\right)\right)=\frac{-\gamma }{{\alpha }^{\ast }}+\mathit{log}\left(K\right)$$ (B.4)
   Proof:

   $$\begin{array}{lll}E\left(\mathit{log}\left(X\right)\right)& ={\mathit{\int }}_0^{\infty }\mathit{log}\left(X\right)\frac{{\alpha }^{\ast }}{K^{{\alpha }^{\ast }}}{X}^{{\alpha }^{\ast }-1}{e}^{-{\left(\frac{X}{K}\right)}^{{\alpha }^{\ast }}}\mathit{dx}& \\ & =\mathit{\int }\frac{1}{{\alpha }^{\ast }}\mathit{log}\left(y\right)\frac{1}{K^{{\alpha }^{\ast }}}{e}^{-\frac{y}{K^{{\alpha }^{\ast }}}}\mathit{dy}& \mathrm{Let}y=x^{{\alpha }^{\ast }}\\ & =\mathit{\int }\frac{1}{{\alpha }^{\ast }}(\mathit{log}\left(u\right)+{\alpha }^{\ast }\mathit{log}\left(K\right))e^{-u}\mathit{du}& \mathrm{Let}y=u{K}^{{\alpha }^{\ast }}\\ & =\frac{1}{{\alpha }^{\ast }}\underset{-\gamma }{\underbrace{\mathit{\int }\mathit{log}\left(u\right)e^{-u}\mathit{du}}}+\mathit{log}\left(K\right)\mathit{\int }{e}^{-u}\mathit{du}& \mathrm{Let}y=u{K}^{{\alpha }^{\ast }}\\ & =\frac{-\gamma }{{\alpha }^{\ast }}+\mathit{log}\left(K\right)& \end{array}$$
5. Given X follows a Weibull distribution (α*, K). Show that

   $$E\left(X^{\alpha }\mathit{log}\left(X\right)\right)\frac{1}{{\alpha }^{\ast }}\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)\left(K^{\alpha }\right)(\psi (\frac{\alpha }{{\alpha }^{\ast }}+1)+{\alpha }^{\ast }\mathit{log}\left(K\right))$$ (B.5)
   Proof:

   $$\begin{array}{lll}E\left(X^{\alpha }\mathit{log}\left(X\right)\right)& ={\mathit{\int }}_0^{\infty }{X}^{\alpha }\mathit{log}\left(X\right)\frac{{\alpha }^{\ast }}{K^{{\alpha }^{\ast }}}{X}^{{\alpha }^{\ast }-1}{e}^{-{\left(\frac{X}{K}\right)}^{{\alpha }^{\ast }}}\mathit{dx}& \\ & =\mathit{\int }{y}^{\frac{\alpha }{{\alpha }^{\ast }}}\frac{1}{{\alpha }^{\ast }}\mathit{log}\left(y\right)\frac{1}{K^{{\alpha }^{\ast }}}{e}^{-\frac{y}{K^{{\alpha }^{\ast }}}}\mathit{dy}& \mathrm{Let}y=x^{{\alpha }^{\ast }}\\ & =\frac{1}{{\alpha }^{\ast }}\frac{1}{K^{{\alpha }^{\ast }}}\mathrm{\Gamma }(\frac{\alpha }{{\alpha }^{\ast }}+1){\left(K^{{\alpha }^{\ast }}\right)}^{\frac{\alpha }{{\alpha }^{\ast }}+1}& \\ & \underset{E\left(\mathit{log}\left(y\right)\right)}{\underbrace{\mathit{\int }\mathit{log}\left(y\right)\frac{1}{\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right){\left(K^{{\alpha }^{\ast }}\right)}^{\frac{\alpha }{{\alpha }^{\ast }}+1}}{y}^{(\frac{\alpha }{{\alpha }^{\ast }}+1)-1}{e}^{-\frac{y}{K{\alpha }^{\ast }}}\mathit{dy}}}& y~\mathit{gamma}\left(\frac{\alpha }{{\alpha }^{\ast }}+1,K^{{\alpha }^{\ast }}\right)\\ & =\frac{1}{{\alpha }^{\ast }}\frac{1}{K^{{\alpha }^{\ast }}}\mathrm{\Gamma }(\frac{\alpha }{{\alpha }^{\ast }}+1){\left(K^{{\alpha }^{\ast }}\right)}^{\frac{\alpha }{{\alpha }^{\ast }}+1}(\psi (\frac{\alpha }{{\alpha }^{\ast }}+1)+{\alpha }^{\ast }\mathit{log}\left(K\right))& \psi \left(\right)\mathrm{is\; digamma\; function}\\ & =\frac{1}{{\alpha }^{\ast }}\mathrm{\Gamma }\left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)\left(K^{\alpha }\right)(\psi \left(\frac{\alpha }{{\alpha }^{\ast }}+1\right)+{\alpha }^{\ast }\mathit{log}\left(K\right))& \end{array}$$
6. Let T_i denote the survival time and C_i denote the censoring time for subject i. T_i and C_i are independent. T_i ~ weibull(α, K), and C_i ~ weibull(α, λ). Let Y_i = min(T_i, C_i) denote observed follow-up time and δ_i be the indicator variable δ_i = (T_i ≤ C_i). Show that:

   $$E\left(Y_i{\delta }_i\right)=E\left(Y_i\right)E\left({\delta }_i\right)$$ (B.6)
   Proof:

   $$\begin{array}{ll}E\left(Y_i{\delta }_i\right)& =E\left(Y_i{\delta }_i\right(I({\delta }_i=1)+I({\delta }_i=0))\\ & =E\left(Y_i{\delta }_{i}I({\delta }_i=1)\right)+E\left(Y_i{\delta }_{i}I({\delta }_i=0)\right)\\ & =E\left(T_{i}I({\delta }_i=1)\right)\\ & ={\mathit{\int }}_0^{\infty }{\mathit{\int }}_0^{\infty }\mathit{tI}({\delta }_i=1)f(t,c)\mathit{dtdc}\\ & ={\mathit{\int }}_0^{\infty }{\mathit{\int }}_0^{\infty }\mathit{tI}(t\le c)f_t\left(t\right)f_c\left(c\right)\mathit{dtdc}\\ & ={\mathit{\int }}_0^{\infty }\{{\mathit{\int }}_0^{\infty }I(t\le c)f_c\left(c\right)\mathit{dc}\}t{f}_t\left(t\right)\mathit{dt}\\ & ={\mathit{\int }}_0^{\infty }{S}_c\left(t\right)t{f}_t\left(t\right)\mathit{dt}\\ & ={\mathit{\int }}_0^{\infty }t\exp \left(-\frac{t^{\alpha }}{{\lambda }^{\alpha }}\right)\frac{\alpha }{K^{\alpha }}{t}^{a-1}\exp \left(-\frac{t^{\alpha }}{K^{\alpha }}\right)\mathrm{d}t\end{array}$$

Let $K^{\ast }={(\frac{1}{{\lambda }^{\alpha }}+\frac{1}{K^{\alpha }})}^{-1/\alpha }$ and use (B.1)

$$\begin{array}{ll}E\left(Y_i\right)E\left({\delta }_i\right)& =\left(\frac{1}{1+\frac{K^{\alpha }}{{\lambda }^{\alpha }}}\right){\mathit{\int }}_0^{\infty }y\frac{\alpha }{K^{\ast \alpha }}{y}^{\alpha -1}\exp \left(-\frac{y^{\alpha }}{K^{\ast \alpha }}\right)\mathit{dy}\\ & ={\mathit{\int }}_0^{\infty }\frac{\alpha }{K^{\alpha }}{y}^{\alpha -1}\exp \left(-\frac{y^{\alpha }}{K^{\alpha }}\right)y\exp \left(-\frac{y^{\alpha }}{{\lambda }^{\alpha }}\right)\mathit{dy}\end{array}$$

Both E(Y_i δ_i) and E(Y_i) E (δ_i) have the same integral functions. Thus,

$$E\left(Y_i{\delta }_i\right)=E\left(Y_i\right)E\left({\delta }_i\right)$$

Similarly, we can establish the following:

$$E\left(g\left(Y_i\right){\delta }_i\right)=E\left(g\left(Y_i\right)\right)E\left({\delta }_i\right)$$

Appendix C: Derivation of probability limits of M.L.E of α, K₀, K₁ for 2SPS

Let Y = min(T, C) be observed follow-up time and δ = I(T ≤ C) be the censoring time. The subjects are assigned to either treatment group (R = 1) or control group (R = 0). The distribution of each subgroup has different scale parameter K but the same shape parameter α*. Thus, likelihood function of observed follow up time Y can be written as:

$$\begin{array}{l}L\left(y\right)=\prod _{i\in \{R=1\}}^{n_{R1}}{\left[({\alpha }^{\ast }/K_1){(y_i/K_1)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{(y_i/K_1)}^{{\alpha }^{\ast }}\left)\right]\\ \times \prod _{i\in \{R=0\}}^{n_{R0}}{\left[({\alpha }^{\ast }/K_0){(y_i/K_0)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{(y_i/K_0)}^{{\alpha }^{\ast }}\left)\right]\end{array}$$

For treatment assignment group and control assignment group, subjects are from compliers (c), never takers (nt), and always takers (at). Let n_R1, n_R0 denote number of subjects assigned to treatment (R = 1) and control (R = 0). Let n_{R1, at}, n_{R1, nt}, n_{R1, c} denote number of always takers, never takers, and compliers that are assigned to treatment group. n_{R1, at} + n_{R1, nt} + n_{R1, c} = n_R1. Let n_{R0, at}, n_{R0, nt}, n_{R0, c} denote number of always takers, never takers, and compliers, who are assigned to control group.n_R0,at + n_{R0, nt} + n_{R0, c} = n_R0. Therefore, the likelihood can be rewritten as:

$$\begin{array}{lll}L\left(y\right)& =& \prod _{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{\left[({\alpha }^{\ast }/K_1){\left(y_i/K_1\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\left(-{\left(y_i/K_1\right)}^{{\alpha }^{\ast }}\right)\right]\\ & \times & \prod _{i\in \{R=1,c\}}^{n_{R_1,c}}{\left[\left({\alpha }^{\ast }/K_1\right){\left(y_i/K_1\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}(-{\left(y_i/K_1\right)}^{{\alpha }^{\ast }})\right]\\ & \times & \prod _{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{\left[({\alpha }^{\ast }/K_1){\left(y_i/K_1\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}(-{\left(y_i/K_1\right)}^{{\alpha }^{\ast }})\right]\\ & \times & \prod _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{\left[({\alpha }^{\ast }/K_0){\left(y_i/K_0\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}(-{\left(y_i/K_0\right)}^{{\alpha }^{\ast }})\right]\\ & \times & \prod _{i\in \{R=0,c\}}^{n_{R_0,c}}{\left[({\alpha }^{\ast }/K_0){\left(y_i/K_0\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}(-{\left(y_i/K_0\right)}^{{\alpha }^{\ast }}\right)]\\ & \times & \prod _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{\left[({\alpha }^{\ast }/K_0){\left(y_i/K_0\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}(-{\left(y_i/K_0\right)}^{{\alpha }^{\ast }})\right]\end{array}$$

Next, the log likelihood function is:

$$\begin{array}{lll}l\left(y\right)& =& \sum _{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_1\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_1\right))\}\\ & +& \sum _{i\in \{R=1,c\}}^{n_{R_1,c}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_1\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_1\right))\}\\ & +& \sum _{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_1\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_1\right))\}\\ & +& \sum _{i\in \{R=1\}}^{n_{R_1}}-{\left(y_i/K_1\right)}^{{\alpha }^{\ast }}\\ & +& \sum _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_0\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_0\right))\}\\ & +& \sum _{i\in \{R=0,c\}}^{n_{R_0,c}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_0\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_0\right))\}\\ & +& \sum _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_0\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_0\right))\}\\ & +& \sum _{i\in \{R=0\}}^{n_{R_0}}-{\left(y_i/K_0\right)}^{{\alpha }^{\ast }}\end{array}$$

To derive the M.L.E of K₀, K₁, take the first derivative of l(y) with respect to K₀, K₁ and set score equation to 0, we have

$${\widehat{K}}_0={\left[\frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{y}_i^{{\alpha }^{\ast }}}{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i}\right]}^{1/\alpha \ast }$$ (C.1)

and,

$${\widehat{K}}_1={\left[\frac{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{y}_i^{{\alpha }^{\ast }}}{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{\delta }_i}\right]}^{1/{\alpha }^{\ast }}$$ (C.2)

To derive the M.L.E of α*, take the first derivative of l(y) with respect to α* and set score equation to 0 and replace K₁, K₀ with the expressions (C.1) and (C.2), we have

$$\begin{array}{lll}0& =& \frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i}{{\alpha }^{\ast }}+\sum _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,c\}}^{n_{R_0,c}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\\ & -& \{\sum _{i\in \{R=0\}}^{n_{R_0}}{\delta }_i\}\frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{y}_i^{{\alpha }^{\ast }}}\\ & +& \frac{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{\delta }_i}{{\alpha }^{\ast }}+\sum _{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,c\}}^{n_{R_1,c}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\\ & -& \{\sum _{i\in \{R=1\}}^{n_{R_1}}{\delta }_i\}\frac{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{y}_i^{{\alpha }^{\ast }}}\\ & =& \frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i}{{\alpha }^{\ast }}+\sum _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,c\}}^{n_{R_0,c}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\\ & -& \left\{\sum _{i\in \{R=0\}}^{n_{R_0}}{\delta }_i\right\}\frac{{\sum }_{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=0,c\}}^{n_{R_0,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=0,c\}}^{n_{R_0,c}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}}\\ & +& \frac{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{\delta }_i}{{\alpha }^{\ast }}+\sum _{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,c\}}^{n_{R_1,c}}\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}\mathit{log}\left(y_i\right)\\ & -& \left\{\sum _{i\in \{R=1\}}^{n_{R_1}}{\delta }_i\right\}\frac{{\sum }_{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=1,c\}}^{n_{R_1,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=1,c\}}^{n_{R_1,c}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}}\end{array}$$

M.L.E α̂* is the solution to the above equation. Next, divide both sides by total number of subject n, we have

$$\begin{array}{lll}0& =& \frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i/n_{R_0}}{{\alpha }^{\ast }}\frac{n_{R_0}}{n}+\left\{\sum _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,c\}}^{n_{R_0,c}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\right\}/n_{R_0}\frac{n_{R_0}}{n}\\ & -& \frac{n_{R_0}}{n}\left\{\sum _{i\in \{R=0\}}^{n_{R_0}}{\delta }_i/n_{R_0}\right\}\frac{\{{\sum }_{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=0,c\}}^{n_{R_0,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)\}/n_{R_0}}{\{{\sum }_{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=0,c\}}^{n_{R_0,c}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\}/n_{R_0}}\\ & +& \frac{{\sum }_{i\in \{R=1\}}^{n_{R_1}}{\delta }_i/n_{R_1}}{{\alpha }^{\ast }}\frac{n_{R_1}}{n}+\left\{\sum _{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,c\}}^{n_{R_1,c}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\right\}/n_{R_1}\frac{n_{R_1}}{n}\\ & -& \frac{n_{R_1}}{n}\left\{\sum _{i\in \{R=1\}}^{n_{R_1}}{\delta }_i/n_{R_1}\right\}\frac{\{{\sum }_{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=1,c\}}^{n_{R_1,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)\}/n_{R_1}}{\{{\sum }_{i\in \{R=1,\mathit{at}\}}^{n_{R_1,\mathit{at}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=1,c\}}^{n_{R_1,c}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{R=1,\mathit{nt}\}}^{n_{R_1,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\}/n_{R_1}}\end{array}$$

As n_R1, n_R0, n_{R1, at}, n_{R1, nt}, n_{R1, c}, n_{R0, at}, n_{R0, nt}, n_{R0, c} → ∞, the score equation converges to the following:

$$\begin{array}{lll}0& =& P(\delta =1\mid R=0)P(R=0)/{\alpha }^{\ast }\\ & +& P(R=0)\left\{P\left(\mathit{AT}\right)E\right(\mathit{\delta log}\left(Y\right)\mid \mathit{at},R=0)+P\left(C\right)E(\mathit{\delta log}\left(Y\right)\mid c,R=0)+P\left(\mathit{NT}\right)E(\mathit{\delta log}\left(Y\right)\mid \mathit{nt},R=0\left)\right\}\\ & -& P(\delta =1\mid R=0)P(R=0)\\ & \times & \frac{\left\{P\left(\mathit{AT}\right)E\right(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{at},R=0)+P\left(C\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid c,R=0)+P\left(\mathit{NT}\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{nt},R=0\left)\right\}}{\{P\left(\mathit{AT}\right)E(Y^{{\alpha }^{\ast }}\mid \mathit{at},R=0)+P\left(C\right)E(Y^{{\alpha }^{\ast }}\mid c,R=0))+P\left(\mathit{NT}\right)E(Y^{{\alpha }^{\ast }}\mid \mathit{nt},R=0)\}}\\ & +& P(\delta =1\mid R=1)P(R=1)/{\alpha }^{\ast }\\ & +& P(R=1)\left\{P\left(\mathit{AT}\right)E\right(\mathit{\delta log}\left(Y\right)\mid \mathit{at},R=1)+P\left(C\right)E(\mathit{\delta log}\left(Y\right)\mid c,R=1)+P\left(\mathit{NT}\right)E(\mathit{\delta log}\left(Y\right)\mid \mathit{nt},R=1\left)\right\}\\ & -& P(\delta =1\mid R=1)P(R=1)\\ & \times & \frac{\left\{P\left(\mathit{AT}\right)E\right(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{at},R=1)+P\left(C\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid c,R=1)+P\left(\mathit{NT}\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{nt},R=1\left)\right\}}{\{P\left(\mathit{AT}\right)E(Y^{{\alpha }^{\ast }}\mid \mathit{at},R=1)+P\left(C\right)E(Y^{{\alpha }^{\ast }}\mid c,R=1))+P\left(\mathit{NT}\right)E(Y^{{\alpha }^{\ast }}\mid \mathit{nt},R=1)\}}\end{array}$$ (C.3)

Use the results from Appendix B, we can derive the following:

$$\begin{array}{lll}\hfill E(\mathit{\delta log}\left(Y\right)\mid \mathit{at},R=0)& =& P(\delta =1\mid \mathit{at},R=0)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ & =& \frac{1}{1+\frac{{{\theta }_{\mathit{at}}^1}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha })\\ \hfill E(\mathit{\delta log}\left(Y\right)\mid \mathit{nt},R=0)& =& P(\delta =1\mid \mathit{nt},R=0)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ & =& \frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(\delta \mathit{log}\left(Y\right)\mid c,R=0)& =& P(\delta =1\mid c,R=0)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ & =& \frac{1}{1+\frac{{{\theta }_c^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{at},R=0)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{nt},R=0)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid c,R=0)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid \mathit{at},R=0)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill E(Y^{{\alpha }^{\ast }}\mid \mathit{nt},R=0)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill E(Y^{{\alpha }^{\ast }}\mid c,R=0)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill P(\delta =1\mid R=0)& =& P_{\mathit{at}}\frac{1}{1+\frac{{{\theta }_{\mathit{at}}^1}^{\alpha }}{{\lambda }^a}}+P_{\mathit{nt}}\frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}+P_c\frac{1}{1+\frac{{{\theta }_c^0}^{\alpha }}{{\lambda }^{\alpha }}}\end{array}$$

and,

$$\begin{array}{lll}\hfill E(\mathit{\delta log}\left(Y\right)\mid \mathit{at},R=1)& =& P(\delta =1\mid \mathit{at},R=1)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ & =& \frac{1}{1+\frac{{{\theta }_{\mathit{at}}^1}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(\delta \mathit{log}\left(Y\right)\mid \mathit{nt},R=1)& =& P(\delta =1\mid \mathit{nt},R=1)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right))\\ & =& \frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(\delta \mathit{log}\left(Y\right)\mid c,R=1)& =& P(\delta =1\mid c,R=1)(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ & =& \frac{1}{1+\frac{{{\theta }_c^1}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{at},R=1)\hfill & =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid \mathit{nt},R=1)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid c,R=1)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid \mathit{at},R=1)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill E(Y^{{\alpha }^{\ast }}\mid \mathit{nt},R=1)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill E(Y^{{\alpha }^{\ast }}\mid c,R=1)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill P(\delta =1\mid R=1)& =& P_{\mathit{at}}\frac{1}{1+\frac{{{\theta }_{\mathit{at}}^1}^{\alpha }}{{\lambda }^{\alpha }}}+P_{\mathit{nt}}\frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}+P_c\frac{1}{1+\frac{{{\theta }_c^1}^{\alpha }}{{\lambda }^{\alpha }}}\end{array}$$

Let $\stackrel{\sim }{{\alpha }^{\ast }}$ be the solution to the equation (C.3). By the consistency of M.L.E, Thus, we have ${\widehat{\alpha }}^{\ast }\stackrel{P}{\to }\stackrel{\sim }{{\alpha }^{\ast }}$ Next, substitute α̂* into equation (C.1)

$$\begin{array}{lll}{\widehat{K}}_0& =& {\left[\frac{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{y}_i^{{\widehat{\alpha }}^{\ast }}}{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i}\right]}^{1/{\widehat{\alpha }}^{\ast }}\\ & =& {\left[\frac{n_{R_0}}{{\sum }_{i\in \{R=0\}}^{n_{R_0}}{\delta }_i}\left\{\sum _{i\in \{R=0,\mathit{at}\}}^{n_{R_0,\mathit{at}}}{y}_i^{{\widehat{a}}^{\ast }}+\sum _{i\in \{R=0,\mathit{nt}\}}^{n_{R_0,\mathit{nt}}}{y}_i^{{\widehat{\alpha }}^{\ast }}+\sum _{i\in \{R=0,c\}}^{n_{R_0,c}}{y}_i^{{\stackrel{⌢}{\alpha }}^{\ast }}\right\}/n_{R_0}\right]}^{1/{\widehat{\alpha }}^{\ast }}\end{array}$$

Asymptotically, it converges to

$$\begin{array}{ll}{\widehat{K}}_0& \to {\left[\frac{1}{P(\delta =1\mid R=0)}\{P_{\mathit{at}}E\left(Y_{\mathit{at},0}^{\stackrel{\sim }{{\alpha }^{\ast }}}\right)+P_{\mathit{nt}}E\left(Y_{\mathit{nt},0}^{\stackrel{\sim }{{\alpha }^{\ast }}}\right)+P_{c}E\left(Y_{c,0}^{\stackrel{\sim }{{\alpha }^{\ast }}}\right)\}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\\ & =[\frac{1}{P(\delta =1\mid R=0)}\times \\ & {\{P_{\mathit{at}}\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+P_{\mathit{nt}}\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+P_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\}]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$

Similarly, K̂₁ converges to

$$\begin{array}{ll}{\widehat{K}}_1& \to [\frac{1}{P(\delta =1\mid R=1)}\times \\ & {\{P_{\mathit{at}}\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{at}}^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+P_{\mathit{nt}}\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }+P_c\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[{\frac{1}{{\theta }_c^1}}^{\alpha }+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\}]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$

Appendix D: Derivation of probability limits of M.L.E of α, K₀, K₁, K₂ for 2SRI

Under the no AT assumption, we can find an expression for λ₁ as follows. The first stage regression can be re-expressed as following:

$$\begin{array}{lll}\hfill E(Z\mid R)& =& {\rho }_{\mathit{AT}}+{\rho }_{C}R\\ \hfill E& =& Z-E(Z\mid R)\\ & =& Z-{\rho }_A-{\rho }_{C}R\end{array}$$

Note that Z, E and Z, R are one-to-one correspondence. Knowing Z, E will let us know Z, R and vice versa. Under no always taker assumption, we observe three subgroups 1) Z = 1, R = 1. Only compliers in this group; 2) Z = 0, R = 1, Only never takers in this group; 3) Z = 0, R = 0, both never takers and compliers in this group. There are no patients that are assigned to control but still takes on active treatment (Z = 1, R = 0). For the 3 subgroups, essentially we are fitting 3 Weibull distributions with the same shape parameter α* and 3 different shape parameter K₀, K₁, K₂ with Weibull regression model: logh(t) = λ₀ + λ₁ Z + λ₂ E

The likelihood function is:

$$\begin{array}{ccc}L\left(y\right)& =& \prod _{i\in \{Z=1,R=1,c\}}^{n_{Z_1,R_1,c}}{\left[({\alpha }^{\ast }/K_0){\left(y_i/K_0\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{\left(y_i/K_0\right)}^{\alpha \ast }\left)\right]\\ & \times & \prod _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z_0,R_1,\mathit{nt}}}{\left[({\alpha }^{\ast }/K_1){\left(y_i/K_1\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{\left(y_i/K_1\right)}^{\alpha \ast }\left)\right]\\ & \times & \prod _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z_0,R_0,\mathit{nt}}}{\left[({\alpha }^{\ast }/K_2){\left(y_i/K_2\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{\left(y_i/K_2\right)}^{\alpha \ast }\left)\right]\\ & \times & \prod _{i\in \{Z=0,R=0,c\}}^{n_{Z_0,R_0,c}}{\left[({\alpha }^{\ast }/K_2){\left(y_i/K_2\right)}^{{\alpha }^{\ast }-1}\right]}^{{\delta }_i}\left[\mathit{exp}\right(-{\left(y_i/K_2\right)}^{\alpha \ast }\left)\right]\end{array}$$

The log likelihood is:

$$\begin{array}{lll}l\left(y\right)& =& \sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_0\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_0\right))\}+\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}-{\left(y_i/K_0\right)}^{{\alpha }^{\ast }}\\ & +& \sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_1\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_1\right))\}+\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}-{\left(y_i/K_1\right)}^{{\alpha }^{\ast }}\\ & +& \sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_2\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_2\right))\}+\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}-{\left(y_i/K_2\right)}^{{\alpha }^{\ast }}\\ & +& \sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\{\mathit{log}\left({\alpha }^{\ast }\right)-\mathit{log}\left(K_2\right))+({\alpha }^{\ast }-1)(\mathit{log}\left(y_i\right)-\mathit{log}\left(K_2\right))\}+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}-{\left(y_i/K_2\right)}^{{\alpha }^{\ast }}\end{array}$$

Take the first derivative of l(y) with respective to K₀, K₁, K₂ respectively and set score equation to 0, then we have

$${\widehat{K}}_0={\left[\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{y}_i^{{\alpha }^{\ast }}}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i}\right]}^{1/{\alpha }^{\ast }}$$ (D.1)

$${\widehat{K}}_1={\left[\frac{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}}{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i}\right]}^{1/{\alpha }^{\ast }}$$ (D.2)

$${\widehat{K}}_2={\left[\frac{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}}{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i}\right]}^{1/{\alpha }^{\ast }}$$ (D.3)

Take the first derivative of l(y) with respective to α* and replace K₀, K₁, K₂ with expression (D.1),(D.2),(D.3), then we have:

$$\begin{array}{lll}\frac{\mathit{dlog}\left(L\left(y\right)\right)}{\mathit{d\alpha }}& =& \sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\{\frac{1}{{\alpha }^{\ast }}+\mathit{log}\left(y_i\right)\}-\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}}\\ & +& \sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\{\frac{1}{{\alpha }^{\ast }}+\mathit{log}\left(y_i\right)\}-\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\frac{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\left(y_i\right)}^{{\alpha }^{\ast }}}\\ & +& \sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\{\frac{1}{{\alpha }^{\ast }}+\mathit{log}\left(y_i\right)\}+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\{\frac{1}{{\alpha }^{\ast }}+\mathit{log}\left(y_i\right)\}\\ & -& (\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i)\frac{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}}\\ & =& \sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\mathit{log}\left(y_i\right)-\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}}\\ & +& \sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)-\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\frac{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\left(y_i\right)}^{{\alpha }^{\ast }}}\\ & +& \sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\mathit{log}\left(y_i\right)\\ & -& (\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i)\frac{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_1^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)}{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}}\\ & =& 0\end{array}$$

M.L.E α̂* is the solution to the above score equation. Next, divide the equation by total sample size n,

$$\begin{array}{lll}0& =& \sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\frac{1}{{\alpha }^{\ast }}/n_{Z1,R1,c}\times \frac{n_{Z1,R1,c}}{n}+\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i\mathit{log}\left(y_i\right)/n_{Z1,R1,c}\times \frac{n_{Z1,R1,c}}{n}\\ & -& (\sum _{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i/n_{Z1,R1,c}\times \frac{n_{Z1,R1,c}}{n})\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)/n_{Z1,R1,c}}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\left(y_i\right)}^{{\alpha }^{\ast }}/n_{Z1,R1,c}}\\ & +& \sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\frac{1}{{\alpha }^{\ast }}/n_{Z0,R1,\mathit{nt}}\times \frac{n_{Z0,R1,\mathit{nt}}}{n}+\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)/n_{Z0,R1,\mathit{nt}}\times \frac{n_{Z0,R1,\mathit{nt}}}{n}\\ & -& (\sum _{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i/n_{Z0,R1,\mathit{nt}}\times \frac{n_{Z0,R1,\mathit{nt}}}{n})\frac{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\left(y_i\right)}^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)/n_{Z0,R1,\mathit{nt}}}{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,nt}}{\left(y_i\right)}^{{\alpha }^{\ast }}/n_{Z0,R1,\mathit{nt}}}\\ & +& \{\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i\mathit{log}\left(y_i\right)\}/n_{Z0,R0,\mathit{nt}}\times \frac{n_{Z0,R0,\mathit{nt}}}{n}\\ & +& \{\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\frac{1}{{\alpha }^{\ast }}+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i\mathit{log}\left(y_i\right)\}/n_{Z0,R0,c}\times \frac{n_{Z0,R0,c}}{n}\\ & -& (\sum _{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i+\sum _{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i)/n_{Z0,R0}\times \frac{n_{Z0,R0}}{n}\\ & \times & \frac{\{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}\mathit{log}\left(y_i\right)\}/n_{Z0,R0}}{\{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\alpha }^{\ast }}+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\alpha }^{\ast }}\}/n_{Z0,R0}}\end{array}$$

As sample sizes in each principal strata → ∞, the score equation will converge to:

$$\begin{array}{lll}0& =& \frac{1}{{\alpha }^{\ast }}P(\delta =1\mid Z=1,R=1)P(Z=1,R=1)+E(\mathit{\delta log}\left(y\right)\mid Z=1,R=1)P(Z=1,R=1)\\ & -& P(\delta =1\mid Z=1,R=1)P(Z=1,R=1)\frac{E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=1,R=1))}{E(Y^{{\alpha }^{\ast }}\mid Z=1,R=1)}\\ & +& \frac{1}{{\alpha }^{\ast }}P(\delta =1\mid Z=0,R=1)P(Z=0,R=1)+E(\mathit{\delta log}\left(y\right)\mid Z=0,R=1)P(Z=0,R=1)\\ & -& P(\delta =1\mid Z=0,R=1)P(Z=0,R=1)\frac{E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=1))}{E(Y^{{\alpha }^{\ast }}\mid Z=0,R=1)}\\ & +& \frac{1}{{\alpha }^{\ast }}P(\delta =1\mid Z=0,R=0,\mathit{nt})P(Z=0,R=0,\mathit{nt})+E(\mathit{\delta log}\left(y\right)\mid Z=0,R=0,\mathit{nt})P(Z=0,R=0,\mathit{nt})\\ & +& \frac{1}{{\alpha }^{\ast }}P(\delta =1\mid Z=0,R=0,c)P(Z=0,R=0,c)+E(\mathit{\delta log}\left(y\right)\mid Z=0,R=0,c)P(Z=0,R=0,c)\\ & -& (\frac{P_{\mathit{nt}}}{P_{\mathit{nt}}+P_c}P(\delta =1\mid Z=0,R=0,\mathit{nt})+\frac{P_c}{P_{\mathit{nt}}+P_c}P(\delta =1\mid Z=0,R=0,c))\\ & \times & (P(Z=0,R=0,\mathit{nt})+P(Z=0,R=0,c))\\ & \times & \frac{P\left(\mathit{nt}\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=0,\mathit{nt})+P\left(c\right)E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=0,c)}{P\left(\mathit{nt}\right)E(Y^{{\alpha }^{\ast }}\mid Z=0,R=0,\mathit{nt})+P\left(c\right)E(Y^{{\alpha }^{\ast }}\mid Z=0,R=0,c)}\end{array}$$ (D.4)

where,

$$\begin{array}{lll}\hfill P(\delta =1\mid Z=1,R=1)& =& \frac{1}{1+{\left(\frac{{\theta }_c^1}{\lambda }\right)}^{\alpha }}\\ \hfill P(Z=1,R=1)& =& P(C,R=1)\\ & =& P_{c}P(R=1)\\ \hfill E(\mathit{\delta log}\left(y\right)\mid Z=1,R=1)& =& \frac{1}{1+\frac{{{\theta }_c^1}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=1,R=1)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid Z=1,R=1)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill P(\delta =1\mid Z=0,R=1)& =& \frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}\\ \hfill P(Z=0,R=1)& =& P(\mathit{nt},R=1)\\ & =& P_{\mathit{nt}}P(R=1)\\ \hfill E(\delta \mathit{log}\left(y\right)\mid Z=0,R=1)& =& \frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\end{array}$$

$$\begin{array}{lll}\hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=1)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid Z=0,R=1)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill P(\delta =1\mid Z=0,R=0,\mathit{nt})& =& \frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}\\ \hfill P(Z=0,R=0,\mathit{nt})& =& P(\mathit{nt},R=0)\\ & =& P_{\mathit{nt}}P(R=0)\\ \hfill E(\delta \mathit{log}\left(y\right)\mid Z=0,R=0,\mathit{nt})& =& \frac{1}{1+\frac{{{\theta }_{\mathit{nt}}^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=0,\mathit{nt})& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid Z=0,R=0,\mathit{nt})& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\\ \hfill P(\delta =1\mid Z=0,R=0,c)& =& \frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}\\ \hfill P(Z=0,R=0,c)& =& P(c,R=0)\\ & =& P_{c}P(R=0)\\ \hfill E(\mathit{\delta log}\left(y\right)\mid Z=0,R=0,c)& =& \frac{1}{1+\frac{{{\theta }_c^0}^{\alpha }}{{\lambda }^{\alpha }}}(\frac{-\gamma }{\alpha }+\mathit{log}({\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\\ \hfill E(Y^{{\alpha }^{\ast }}\mathit{log}\left(Y\right)\mid Z=0,R=0,c)& =& (\psi (\frac{{\alpha }^{\ast }}{\alpha }+1)+\mathit{\alpha log}({\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-1/\alpha }\left)\right)\mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha \frac{1}{\alpha }}\\ \hfill E(Y^{{\alpha }^{\ast }}\mid Z=0,R=0,c)& =& \mathrm{\Gamma }(\frac{{\alpha }^{\ast }}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-{\alpha }^{\ast }/\alpha }\end{array}$$

$\stackrel{\sim }{{\alpha }^{\ast }}$ is the solution to the equation (D.4). Thus, ${\widehat{\alpha }}^{\ast }\to \stackrel{\sim }{{\alpha }^{\ast }}$. Probability limits of M.L.E of K₀ can be derived as following:

$$\begin{array}{lll}{\widehat{K}}_0& =& {\left[\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{y}_i^{{\widehat{\alpha }}^{\ast }}}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i}\right]}^{1/{\widehat{\alpha }}^{\ast }}\\ & =& {\left[\frac{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{y}_i^{{\widehat{\alpha }}^{\ast }}/n_{Z1,R1,c}}{{\sum }_{i\in \{Z=1,R=1,c\}}^{n_{Z1,R1,c}}{\delta }_i/n_{Z1,R1,c}}\right]}^{1/{\widehat{\alpha }}^{\ast }}\\ & \to & {\left[\frac{E(y_i^{\stackrel{\sim }{{\alpha }^{\ast }}}\mid Z=1,R=1,c)}{P(\delta =1\mid Z=1,R=1,c)}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\\ & =& {\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^1}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_c^1}{\lambda }\right)}^{\alpha }}}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$

Similarly, for K₁, K₂,

$$\begin{array}{lll}{\widehat{K}}_1& =& {\left[\frac{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{y}_i^{{\widehat{\alpha }}^{\ast }}}{{\sum }_{i\in \{Z=0,R=1,\mathit{nt}\}}^{n_{Z0,R1,\mathit{nt}}}{\delta }_i}\right]}^{1/{\widehat{\alpha }}^{\ast }}\\ & \to & {\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$

$$\begin{array}{lll}{\widehat{K}}_2& =& {\left[\frac{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{y}_i^{{\widehat{\alpha }}^{\ast }}+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{y}_i^{{\widehat{\alpha }}^{\ast }}}{{\sum }_{i\in \{Z=0,R=0,\mathit{nt}\}}^{n_{Z0,R0,\mathit{nt}}}{\delta }_i+{\sum }_{i\in \{Z=0,R=0,c\}}^{n_{Z0,R0,c}}{\delta }_i}\right]}^{1/{\widehat{\alpha }}^{\ast }}\\ & \to & {\left[\frac{\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_{\mathit{nt}}^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\frac{P_{\mathit{nt}}}{P_{\mathit{nt}}+P_c}+\mathrm{\Gamma }(\frac{\stackrel{\sim }{{\alpha }^{\ast }}}{\alpha }+1){\left[\frac{1}{{{\theta }_c^0}^{\alpha }}+\frac{1}{{\lambda }^{\alpha }}\right]}^{-\stackrel{\sim }{{\alpha }^{\ast }}/\alpha }\frac{P_c}{P_{\mathit{nt}}+P_c}}{\frac{1}{1+{\left(\frac{{\theta }_{\mathit{nt}}^0}{\lambda }\right)}^{\alpha }}\frac{P_{\mathit{nt}}}{P_{\mathit{nt}}+P_c}+\frac{1}{1+{\left(\frac{{\theta }_c^0}{\lambda }\right)}^{\alpha }}\frac{P_c}{P_{\mathit{nt}}+P_c}}\right]}^{1/\stackrel{\sim }{{\alpha }^{\ast }}}\end{array}$$

Appendix E: Assumption of the same shape parameter for survival and censoring distributions

In section 2 of the manuscript, we made the assumption that both time to event and censoring time have the same shape parameter so that close form solution could be derived. To evaluate the potential impact on the bias when the time to event and censoring time have two different shape parameters and the assumption is violated, we re-evaluated the scenario in the table 1 with the shape parameter α = 0.5. We set the shape parameter of censoring distribution to be 1.2 and compared the differences. We found that the differences in bias of 2SPS between two scenarios ranges from 0.01 to 0.018 (δ varies from -2 to 2). For 2SRI approach, the differences ranges from 0.001 to 0.13. These differences are attributable to the different censoring proportions between two scenarios. The shape of relationship between bias and δ remains approximately unchanged (data not shown). It should be noted that under the assumption of having the same shape parameters for both survival time and censoring time, the maximum likelihood estimator based on the survival likelihood that does not incorporate the assumption of the shape parameters being the same is not fully efficient.