Generalized adaptive intelligent binning of multiway data

Abstract

NMR metabolic fingerprinting methods almost exclusively rely upon the use of one-dimensional (1D) ¹H NMR data to gain insights into chemical differences between two or more experimental classes. While 1D ¹H NMR spectroscopy is a powerful, highly informative technique that can rapidly and nondestructively report details of complex metabolite mixtures, it suffers from significant signal overlap that hinders interpretation and quantification of individual analytes. Two-dimensional (2D) NMR methods that report heteronuclear connectivities can reduce spectral overlap, but their use in metabolic fingerprinting studies is limited. We describe a generalization of Adaptive Intelligent binning that enables its use on multidimensional datasets, allowing the direct use of nD NMR spectroscopic data in bilinear factorizations such as principal component analysis (PCA) and partial least squares (PLS).

1. INTRODUCTION

By and large, the phrase “NMR metabolic fingerprinting” implies the use of one-dimensional (1D) ¹H NMR spectroscopic methods, due in no small part to the ease and speed of 1D data collection and the large natural abundance of NMR-active protons found in metabolomics samples [1, 2]. Before processed spectra are submitted to multivariate statistical algorithms like principal component analysis (PCA) or partial least squares (PLS) for modeling, they are often subdivided into bins to simplify multivariate analyses [2]. Spectral binning reduces the dimensionality of the data matrix and masks chemical shift variability between samples at the expense of decreased model interpretability: any given bin in a 1D ¹H NMR spectrum may contain several overlapped signals from multiple distinct metabolites [3]. Thus, without utilizing computationally intensive methods of deconvolution to tease apart signal contributions of individual metabolites [4, 5], the resulting metabolic fingerprint from a binned 1D dataset is usually limited to high-level inference about metabolic trends.

By leveraging the connectivities between ¹H and ¹³C nuclei in metabolites, two-dimensional (2D) heteronuclear NMR methods reduce spectral overlap by spreading ¹H information over a second (¹³C) chemical shift dimension [6]. Heteronuclear single quantum coherence (HSQC) experiments are commonly performed in NMR metabolic profiling studies, and provide an NMR singlet or multiplet for each directly bonded ¹H-¹³C pair in the sample. Developments in NMR hardware and acquisition techniques have brought natural abundance ¹H-¹³C HSQC experiment times down to values compatible with high-throughput metabolic fingerprinting studies [7, 8]. However, multivariate analysis of 2D NMR datasets is still a nontrivial undertaking that requires either vectorization [9], which breaks the inherent structure of the data, or the use of multilinear factorizations [10], which are more computationally intensive and difficult to cross-validate.

Spectral binning is another potential means of preparing 2D NMR datasets for multivariate analysis that holds several advantages over binning 1D spectra. First, multiple integration of bins maps each spectrum to an observation vector regardless of its original dimensionality, allowing bilinear PCA and PLS algorithms to be used without concern for loss of the inherent structure of the data. Second, binning of 2D spectral data yields more well-conditioned data matrices than simple vectorization. Finally, because signals are better resolved in 2D spectra, each bin contains substantially fewer signals from distinct metabolites. Multiple different algorithms have been developed to bin 1D NMR data [11-15], and the use of uniform binning on 2D NMR data has also been reported [16]. However, to our knowledge, no methods exist to intelligently bin multidimensional data for use in multivariate analysis. Therefore, we propose a generalization of Adaptive Intelligent (AI) binning [14] to spectral data of any dimensionality, called Generalized Adaptive Intelligent (GAI) binning (Figure 1).

Figure 1.

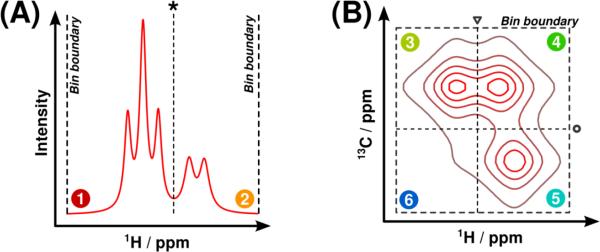
Illustration of the GAI-binning bin subdivision procedure for one-dimensional and two-dimensional spectral fragments. (A) In the one-dimensional case, the bin containing regions 1 and 2 is optimally subdivided (asterisk) when the sum of the objective values in regions 1 and 2 is greater than the original bin's objective value. (B) In the D-dimensional case, there are now D possible dimensions along which an optimal subdivision may exist. The optimal subdivision along the ¹H dimension (triangle) occurs when the sum of the objective values in regions 3+6 and 4+5 exceeds that of the original bin. Similarly, the optimal subdivision along the ¹³C dimension (circle) occurs when the sum of the objective values in regions 3+4 and 5+6 exceeds the original value. A comparison between all possible optimal subdivisions along all dimensions yields the best possible subdivision (circle).

2. CALCULATION

2.1 AI-binning

Generalized AI-binning (GAI-binning) is a logical extension of AI-binning to two or more dimensions. In the AI algorithm (Figure 1A), bins are recursively subdivided until a stopping criterion or minimum bin width is reached [14]. For a 1D dataset containing N spectra, the following objective function is used to assess the quality of each bin:

$$V_b=\frac{1}{N}{\sum }_{n=1}^N{\left[(ma{x}_{n,b}-I_{n,b,1})(ma{x}_{n,b}-I_{n,b,\mathrm{end}})\right]}^{\frac{R}{2}}$$ (1)

where max_n,b is the maximum intensity inside the bin b in spectrum n, and I_n,b,1 and I_n,b,end are the bin edge intensities. The exponent R in the AI objective function is referred to as a ‘resolution parameter’, which offers a means of tuning the binning result based on signal-to-noise and peak resolution of a dataset. By replacing R with R/2 in the exponent of equation 1, we have chosen a slightly modified interpretation of the resolution parameter as a relaxed form of a geometric mean of the differences between the bin edge intensities and the maximum bin intensity. At each subdivision step, new bin edges are chosen to maximize the combined (summed) objective values of the two resulting bins over the objective value of the original bin. If no bin subdivision exists with a combined objective function greater than that of the original bin, recursive subdivision within that bin is terminated, and the AI algorithm terminates once all bins may no longer be subdivided.

2.2 GAI-binning

In two or more dimensions, the set of bin boundary points expands to include all points that lie on the edges (or faces, hyperfaces, etc.) of the bin. By denoting the set of all edge points in bin b as E_b, a new objective function may be constructed:

$$V_b=\frac{1}{N}{\sum }_{n=1}^N{\left[{\prod }_{e\in E_b}(ma{x}_{n,b}-I_e)\right]}^{\frac{R}{\Vert E_b\Vert }}$$ (2)

Thus, the GAI algorithm computes the ‘relaxed’ geometric mean of the differences between the bin maximum and all points on the boundary. In the case of one-dimensional data, it is apparent that equation 2 reduces to equation 1, and GAI-binning operates identically to AI-binning. As dimensionality increases, the risk of floating-point overflow or underflow increases due to the larger bin edge set E_b. To avoid this, the following ‘log-objective’ may be used in lieu of equation 2:

$$V_{b,ln}=\frac{R}{N\Vert E_b\Vert }{\sum }_{n=1}^N{\sum }_{e\in E_b}\ln (ma{x}_{n,b}-I_e)$$ (3)

Like AI-binning, GAI-binning initializes a bin around the entire dataset and proceeds to recursively subdivide each bin until a minimum bin size is reached or no bin may be divided to yield an increase in the objective value. Because the number of ways to subdivide each bin increases with dimensionality, all possible dimensions are tested, and the new bin boundary that maximizes the objective over all possible subdivision dimensions is selected (Figure 1B). Therefore, the GAI algorithm may be considered a form of binary space partitioning (BSP) which limits its partition hyperplanes to lying orthogonally to the basis vectors of the coordinate system [17].

2.3 Noise bin elimination

It is important that noise bins be removed from the data matrix prior to multivariate analysis, as their presence is known to negatively impact the interpretability and reliability of multivariate models [18, 19]. Because the integration of a noisy space of increasing dimensionality (i.e. double or triple integration) results in a random variable having a similarly increasing variance, the importance of noise removal is compounded in multidimensional binning. Therefore, a noise bin removal step based on spectral intensity was added to the GAI algorithm. A running mean and variance calculation was performed to estimate the noise floor of each spectrum. The initial mean μ_n and standard deviation σ_n of the noise were computed using the first 32 points on one edge of the spectrum, which were assumed to contain only baseline noise. Every other data point was then classified as signal or noise based on whether its intensity exceeded the current running noise floor, μ_n + 3σ_n. Upon inclusion of a new noise data point, the mean and standard deviation of the noise were appropriately updated. Once the estimated noise floor was determined for each spectrum in the dataset, a threshold for bin removal was computed as the median noise floor of all the spectra:

$$I_{th}={\mathrm{med}}_n({\mu }_n+k{\sigma }_n)$$ (4)

where k is a user-selectable parameter to adjust the noise threshold. Only bins whose maximum intensity fell above the threshold were retained in the final data matrix.

3. METHODS

3.1 Human liver dataset

Two independently collected ¹H-¹³C HSQC NMR datasets from ongoing metabolomics studies were used as test cases for the GAI-binning algorithm. For the first dataset, twenty-four 1.0 mL samples of SK-Hep1 human liver cells were provided for metabolic fingerprinting, half of which were treated with 50 μM tetrathiomolybdate (TTM). The cells were extracted into 80:20 methanol:water to collect the water-soluble metabolites, spun in a rotary evaporator for two hours, lyophilized at -50°C and 0.02 mBar for 24 hours, and finally redissolved in 600 μL of 50.0 mM phosphate buffer in 99.8% D₂O (Isotec, St. Louis, MO) adjusted to pH 7.4. The redissolved, pH-adjusted samples were then collected into NMR tubes.

Experiments were collected on a Bruker Avance III HD 700 MHz spectrometer equipped with a 5 mm inverse quadruple-resonance (¹H, ¹³C, ¹⁵N, ³¹P) cryoprobe with cooled ¹H and ¹³C channels and a z-axis gradient. A Bruker SampleJet and ICON-NMR were used to automate NMR data collection. A 2D gradient-enhanced ¹H-¹³C HSQC with improved sensitivity [20, 21] (hsqcetgpsi) was collected for each sample. Spectra were collected with 4 scans and 16 dummy scans over a uniform grid of 512 and 64 complex points along the ¹H and ¹³C dimensions, respectively. Spectral windows were set to 3,285 ± 4,545 Hz along ¹H and 12,677 ± 14,620 Hz along ¹³C. All spectra were collected at a sample temperature of 298.0 K.

3.2 Mouse embryonic fibroblast dataset

A second set of samples from kinase suppressor of Ras 1 (KSR1) knockout mouse embryonic fibroblast (MEF) cells was also provided to generate a test ¹H-¹³C HSQC dataset for GAI-binning. For this second dataset, ten cell samples from ksr1^−/− MEFs and ten samples from KSR1-rescued ksr1^−/− MEFs were used to produce metabolite extracts. The cells were washed, extracted into 80:20 methanol:water, spun in a rotary evaporator, lyophilized and redissolved according to the procedures used to extract metabolites from the liver cell samples.

Experiments were collected on a Bruker Avance DRX 500 MHz spectrometer equipped with a 5 mm inverse triple-resonance (¹H, ¹³C, ¹⁵N) cryoprobe with a z-axis gradient. A Bruker BACS-120 sample changer and ICON-NMR software were used to automate data collection. A 2D gradient-enhanced ¹H-¹³C HSQC (hsqcetgp) was collected for each sample. Spectra were collected with 128 scans and 16 dummy scans over a uniform grid of 1024 and 32 complex points along the ¹H and ¹³C dimensions, respectively. Spectral windows were set to 2,359 ± 2,367 Hz along ¹H and 8,174 ± 8,803 Hz along ¹³C. All spectra were collected at a sample temperature of 293 K.

3.3 NMR processing and multivariate analysis

All processing, treatment and statistical modeling was performed in GNU Octave 3.6 [22] using routines currently available in the MVAPACK toolbox for NMR chemometrics [23]. The 2D raw serial files were loaded [24], apodized with a squared-sine window, zero-filled once along ¹H and twice along ¹³C, and Fourier-transformed. Spectra from the liver cell extracts were manually phase-corrected and cropped (1.0 – 6.6 ppm along ¹H; 16 – 112 ppm along ¹³C), and spectra from the MEF extracts were similarly phase-corrected and cropped (1.25 – 6.2 ppm along ¹H; 8 – 102 ppm along ¹³C). Both uniform and GAI-binning were performed on each data tensor using minimum ¹H and ¹³C bin widths of 0.025 ppm and 2.5 ppm, respectively, and a GAI resolution parameter of 0.1. Binned regions identified to be less intense than three times the standard deviation of the spectral noise (k = 3) were removed after binning. The mean spectrum of the entire processed liver dataset, superimposed with bins identified by both uniform and GAI-binning, is shown in Figure 2.

Figure 2.

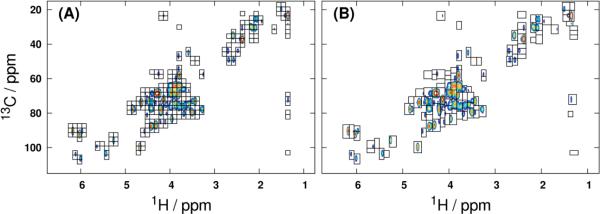
Processed ¹H-¹³C HSQC mean spectrum of the liver data tensor, with overlaid uniform (A) and GAI (B) bin boundaries. The dataset was binned with minimum bin widths along ¹H and ¹³C of 0.025 ppm and 2.5 ppm, respectively. Retained bins all have maximum intensities no less than three times the standard deviation of the noise floor.

The applicability of GAI-binning to bilinear factorizations was demonstrated by modeling the data tensors using both PCA and OPLS-DA. For PCA modeling of the data, the spectral regions identified by each binning method were doubly integrated. Scores and loadings were then calculated using the Nonlinear Iterative Partial Least Squares (NIPALS) algorithm [25]. Internal leave-one-out cross-validation (LOOCV) of each computed PCA model was performed to yield model fit (R²_X) and predictive ability (Q²) statistics [26, 27]. For OPLS-DA, spectral data points within the identified bins were vectorized row-wise into a data matrix as previously described [9]. During vectorization, all data points within each binned region are stacked into an observation vector, and data points not within bins are excluded. The use of vectorization prior to supervised modeling facilitates the creation of backscaled pseudospectral OPLS loadings, which hold greater ease of interpretation over binned loadings [28]. Modeling by an OSC-filtered NIPALS algorithm [29] and 100 rounds of seven-fold Monte Carlo internal cross-validation (MCCV) [30] were performed to compute data fit (R²_X), response fit (R²_Y) and predictive ability (Q²) statistics. The binned data matrices produced via double integration were also subjected to OPLS-DA modeling in the same manner as the vectorized data. All OPLS-DA models were further validated using CV-ANOVA [31] and 1,000 iterations of response permutation testing [32] to rigorously ensure model reliability. Backscaled predictive OPLS loadings were computed from the vectorized bins according to previously published works [9, 33]. During backscaling, OPLS loading vectors were scaled by the inverse of their original Pareto scaling coefficients and then unstacked into a two-dimensional pseudospectrum using bin information. Data points not included in the vectorized loadings were set to zero in the backscaled pseudospectrum. All data matrices were normalized using Probabilistic Quotients (PQ) [34] and then Pareto scaled [35] prior to modeling.

4. RESULTS AND DISCUSSION

Processing of the liver extract spectra yielded a real data tensor of 24 ¹H-¹³C HSQC spectra having 442x149 points each, and processing of the fibroblast spectra yielded a tensor of 17 spectra having 1071x172 real data points each. The observation counts (N), variable counts (K) and PCA/OPLS cross-validation statistics (R², Q²) for each dataset and variable reduction method are summarized in Table 1. Further validation results from the OPLS models, all of which indicate varying degrees of high model reliability, are also summarized in Table 2. Through examination of the variable counts within Table 1, it is readily apparent that GAI-binning is dramatically more effective than uniform binning at discriminating between signal and noise regions within spectral data. On average, GAI-binning segmented each data tensor into less than half the number of bins produced by uniform binning, and produced PCA models with markedly higher R²_X and Q² statistics. Moreover, even with the greatly reduced variable counts produced by GAI-binning relative to uniform binning, the OPLS Q² statistics between the two methods are statistically indistinguishable. In fact, the variable counts resulting from GAI-binning these third-order tensors are substantially lower than the few hundred variables typically produced by binning one-dimensional spectra. Resulting scores from PCA modeling of the GAI-binned liver data tensor are shown in Figure 3.

Table 1.

Data matrices and PCA/OPLS model statistics.

		Integration					Vectorization
			PCA		OPLS			OPLS
		K	R2x	Q2	R2y	Q2	K	R2y	Q2
Liver	Unif.	248	0.82	0.71	0.993	0.938 ± 0.002	11,160	0.993	0.929 ± 0.003
N = 24	GAI	113	0.89	0.75	0.991	0.928 ± 0.003	10,474	0.994	0.933 ± 0.003
MEF	Unif.	334	0.48	0.40	0.994	0.974 ± 0.004	18,348	0.994	0.963 ± 0.005
N = 17	GAI	93	0.71	0.56	0.994	0.973 ± 0.005	18,789	0.996	0.962 ± 0.006

Table 2.

OPLS-DA cross-validation p values.

		Integration		Vectorization
		Permutation	CV-ANOVA	Permutation	CV-ANOVA
Liver	Unif.	< 0.001	3.24 × 10−11	< 0.001	4.70 × 10−11
N = 24	GAI	< 0.001	3.34 × 10−10	< 0.001	9.74 × 10−11
MEF	Unif.	< 0.001	3.56 × 10−10	< 0.001	1.73 × 10−9
N = 17	GAI	< 0.001	1.37 × 10−9	< 0.001	2.34 × 10−9

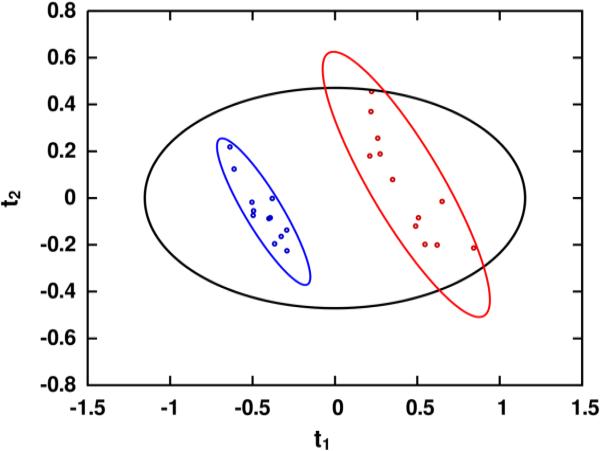
Figure 3.

Principal component analysis scores resulting from modeling the GAI-binned ¹H-¹³C HSQC data matrix, indicating a high degree of separation between experimental groups. Model fit (R²_X) and predictive ability (Q²) were 0.68 and 0.64 for the first principal component (Q₁) and 0.12 and 0.09 for the second (t₂). Class separations of this magnitude are readily achievable using data matrices generated by GAI-binning, due in large part to the low variable counts it generally produces.

Backscaled predictive OPLS-DA loadings of the vectorized ¹H-¹³C HSQC spectral data tensors (Figure 4) lend further support for the use of multidimensional binning in metabolic fingerprinting experiments. Even when vectorization is performed in place of integration to produce a data matrix, binning offers an effective means of variable selection: only 10,474 of 65,858 variables (16%) were retained when GAI-binning was used as a pre-filter prior to modeling the liver data. A similar reduction was observed in the fibroblast dataset, where GAI-binning retained 18,789 of 184,212 total variables for a 90% reduction in dimensionality. These substantially reduced variable counts offered by binning translate to more well-conditioned bilinear modeling problems. As the dimensionality of the input dataset is increased further, the reductions in variable count afforded by multidimensional binning are expected to become even more dramatic. While the variable counts produced by vectorization of uniformly binned data tensors are comparable to those from GAI-binning, it is critical to recognize that the uniformly binned regions contain more noise data points than their GAI-binned counterparts, and thus offer a less efficient dimensionality reduction (cf. Figure 2).

Figure 4.

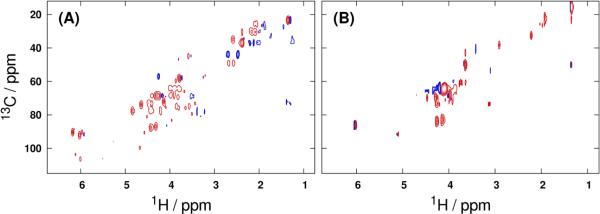
Backscaled full-resolution pseudospectral loadings from OPLS-DA modeling of the GAI-reduced (A) liver and (B) fibroblast ¹H-¹³C HSQC data tensors. Positive and negative loadings are represented by red and blue contours, respectively.

Spectral regions produced by GAI-binning (Figure 2) demonstrate several important properties of the combined binning and noise removal processes. Because t₁ noise and truncation artifacts yield phase-incoherent negative spectral excursions after Fourier transformation, ‘unrelaxed’ GAI-binning (R = 1) tends to preferentially subdivide near such regions, producing elongated bins along the F₁ dimension. Decreasing the resolution parameter from its maximum value shrinks these bins to contain only true signals. Thus, an objective rule for determining an optimal resolution parameter during binning is to decrease R until all bins shrink to contain a minimal amount of noise. Once an optimal resolution parameter has been identified, a suitable noise threshold (k) must be determined such that all noise bins are removed without loss of bins containing weak signals. However, once optimal R and k have been determined for a given set of experimental conditions, they may be applied during GAI-binning to any data collected at later times under the same conditions to achieve ideal results. Our selections of resolution parameter (R = 0.1) and noise threshold (k = 3) were made according to the above criteria through a manual visual examination of the binning results, but it is conceivable that objective metrics of the criteria could be constructed that facilitate automated determination of these parameters.

Finally, like AI-binning, the execution time of GAI-binning scales quadratically with the number of spectral data points, and scales approximately linearly with both the number of spectral dimensions and the number of observations. Typical runtimes for binning two-dimensional datasets range from seconds to a few minutes, depending mostly on the data point count. Thus, while zero-filling may be used to increase the digital resolution of data being input into GAI-binning, it should be applied sparingly to avoid unnecessarily long computation times during bin region determination.

5. CONCLUSIONS

Generalized Adaptive Intelligent binning is a logical extension of the previously established Adaptive Intelligent binning algorithm [14] to multidimensional datasets, and provides a model-free alternative to peak-fitting and peak-picking as a means of variable selection in multivariate analyses. Furthermore, GAI-binning is a more intelligent method to extract signal regions from multidimensional spectral data tensors than uniform binning, and may be used to generate very low-dimensionality data matrices via multiple integration or efficiently noise-filtered data matrices via vectorization. Our C++ implementations of 1D and 2D GAI-binning are freely available as part of the open-source MVAPACK chemometrics toolbox [23], which may be downloaded at http://bionmr.unl.edu/mvapack.php.

Highlights.

• Generalizations to AI-binning afford binning of multidimensional datasets

• Use of binning is an alternative to peak-picking multidimensional spectra

• Highly effective means of dimensionality reduction for PCA or PLS