Abstract
The healing of bone defects is a challenge for both tissue engineering and modern orthopaedics. This problem has been addressed through the study of scaffold constructs combined with mechanoregulatory theories, disregarding the influence of chemical factors and their respective delivery devices. Of the chemical factors involved in the bone healing process, bone morphogenetic protein-2 (BMP-2) has been identified as one of the most powerful osteoinductive proteins. The aim of this work is to develop and validate a mechano-chemical regulatory model to study the effect of BMP-2 on the healing of large bone defects in silico. We first collected a range of quantitative experimental data from the literature concerning the effects of BMP-2 on cellular activity, specifically proliferation, migration, differentiation, maturation and extracellular matrix production. These data were then used to define a model governed by mechano-chemical stimuli to simulate the healing of large bone defects under the following conditions: natural healing, an empty hydrogel implanted in the defect and a hydrogel soaked with BMP-2 implanted in the defect. For the latter condition, successful defect healing was predicted, in agreement with previous in vivo experiments. Further in vivo comparisons showed the potential of the model, which accurately predicted bone tissue formation during healing, bone tissue distribution across the defect and the quantity of bone inside the defect. The proposed mechano-chemical model also estimated the effect of BMP-2 on cells and the evolution of healing in large bone defects. This novel in silico tool provides valuable insight for bone tissue regeneration strategies.
Introduction
The repair of critical size bone fractures is an important challenge facing modern orthopedics researchers. The gold standard procedure for critical size defect repair consists of filling the defect with autografted bone harvested from the iliac crest [1]. However, in addition to the limited availability of graft tissue, this practice is associated with limitations such as poor vascularisation and poor bone remodeling, which can compromise full recovery [2]. To overcome these problems, the development of new methods to promote bone regeneration in critical size fractures has been an important focus in tissue engineering [3–9].
In 1965, Marshall Urist demonstrated that the organic component of bone induces bone formation and that this bone morphogenetic potential was due to one or more proteins [10]. Those bone morphogenetic proteins (BMPs) were purified and sequenced in the late 1980s [11,12], and they are now produced via recombinant DNA technology (rhBMP) [12,13].
Of the 20 proteins that compose the BMP family, BMP-2 appears to be the most relevant osteoinductive growth factor [14,15] for bone formation [16,17] and bone healing [18,19]. BMP-2 promotes cell chemotaxis, proliferation and differentiation towards the osteogenic pathway as well as extracellular matrix production, protein secretion and mineralization [20]. Futhermore, the beneficial effects of BMP-2 on fracture healing are well established [21], and medical devices releasing BMP-2 have already been designed and approved by the FDA (Food and Drug Administration) [22,23], specifically for spinal fusions and open tibia fractures.
Several computational mechanoregulatory models have been proposed to study natural bone fracture healing [24–27]. Claes et al. [28] computed stress and strain in sheep tarsal fractures and determined a set of rules for tissue differentiation. Lacroix and Prendergast [29], following the differentiation rule proposed by Prendergast et al. [30], presented a biomechanical model where tissue differentiation; within a fixed callus geometry; is stimulated by fluid flow and shear strain. In the work of Gómez-Benito et al. [31] cell populations per se are introduced, cellular differentiation is influenced by the local mechanical environment and callus geometry growth is also simulated. Despite the primary focus being mechanical stimuli alone, Bailón-Plaza and van der Meulen [32] considered chondrogenic and osteogenic growth factor gradients to drive tissue differentiation and bone healing. Additionally, the latter bioregulation model was complemented with a mechanical stimulus [33] and angiogenesis [34,35] within a mechanobioregulatory framework.
In the view of bone tissue regeneration, computational models have been applied to study bone growth inside scaffolds. Adachi et al. [36] first developed a computational framework to study the balance between scaffold degradation and new bone formation. Using a mechanoregulatory algorithm, Kelly and Prendergast [37] proposed ideal mechanical properties in a scaffold for cartilage regeneration in osteochondral defects. Similarly, Byrne et al. [38] addressed the necessary commitment between scaffold properties such as porosity, elasticity and scaffold degradation to improve bone regeneration by combining a mechanoregulation algorithm with a 3D lattice approach. Sanz-Herrera et al. [39] considered a mathematical phenomenological model to evaluate bone regeneration inside a scaffold and qualitatively compared it with previous in vivo experiments [40]. Recently, Checa and Prendergast [41] studied the effects of cell seeding and mechanical loading inside a biodegradable scaffold on scaffold vascularisation and tissue ingrowth.
More recently, in silico models have been developed in order to provide a better understanding of large bone union/impaired healing. So, Carlier et al. [42,43] developed a multi-scale approach to study the influence of vascularization during bone healing. Importantly, oxygen was shown to be a critical element for a successful healing to be attained in large bone defects. In addition, Moore et al. [44] also developed an in silico model to study the “one stage transport” surgical procedure which considers a periosteum layer surrounding the bone defect. In this model, BMP-2 production increased with higher levels of strain in the periosteum. The endogenous increase of BMP-2 levels increased cell activity and bone tissue production, and bone bridging in large bone defects was successfully predicted.
To the best of our knowledge, we did not find any previous computational studies assessing the use of growth factor delivery devices in large bone defects, due to the very fact that mechanical and chemical stimuli are traditionally treated separately. In order to tackle this issue, we hypothesize that the mechanical stimulus coordinated by the chemical stimulus can provide an integrated outline to deal with systems where a combination of both stimuli plays an important role. Thus, we propose in this work an in silico mechano-chemical model with the purpose of predicting the healing in large bone defects, given the effect of BMP-2 released in the defect. Given this, we present the following results: (1) based on the argument that BMP-2 is one of the most important growth factors involved in bone fracture healing [21,45–47], we collected quantitative data on the effects of BMP-2 on cell proliferation, migration, differentiation, maturation and extracellular matrix (ECM) production (2) the effects of BMP-2 on cells were then incorporated into a mechanoregulatory model, hence combining and integrating mechanical and biological stimuli [48] and (3) finally, we defined a mechano-chemical model to simulate healing of a critical size fracture with a hydrogel incorporated as a BMP-2 delivering device. The results obtained were then compared with the in vivo results of Boerkel et al. [49] on the healing of large femoral defects in mice.
Materials and Methods
To incorporate BMP-2 into mechanobiological healing bone models, we searched for experimental data describing the effect of BMP-2 on cellular behavior. Additionally, we described the equilibrium between BMP-2 production and consumption. Then, we developed a model to simulate an alginate hydrogel used to deliver BMP-2, as used in the in vivo study by Boerckel et al. [49]. We evaluated in silico the healing potential of BMP-2 in a rat femoral large bone defect.
Effect of BMP-2 on cells
Many aspects of cell behavior are influenced by BMP-2, including chemotaxis, proliferation, differentiation towards the osteogenic pathway, ECM production and mineralisation [20]. However, the effect of BMP-2 on cell activity is dose-dependent [49–51]. Therefore, in our approach we considered BMP-2 dose-dependent chemical stimulus, represented by g (in ng. cm −3). Next, we focused on the effect of BMP-2 for each of the enumerated aspects of cellular activity.
Cell proliferation is an increase in the cell population due to cell division. In general, BMP-2 regulates cell proliferation [47,52,53] in a dose-dependent manner. Knippenberg et al. [52] observed that the number of cells nearly doubled when cells were treated with BMP-2 at a concentration of 10 ng. cm −3 was added. However, Kim et al. [21] observed that cell proliferation was almost unchanged for BMP-2 concentrations between 50 and 200 ng. cm −3. Moreover, for high concentrations of BMP-2 ranging from 500 – 2000 ng. cm −3, cellular proliferation was significantly reduced in a dose-dependent manner. These observations are summarised in Fig 1, which illustrates the impact of BMP-2 on cell proliferation. In the proposed data adjustment, medium without BMP-2 does not exert an influence on cell proliferation, there is a strong effect on proliferation for low concentrations of BMP-2, a threshold of cellular proliferation is reached within the 50 – 200 ng. cm −3 concentration range and proliferation is reduced at higher concentrations of BMP-2. It should be noted that the fold values are relative to a control experiment lacking BMP-2, performed by the referenced authors.
Fig 1. Influence of BMP-2 concentration on MSC proliferation.
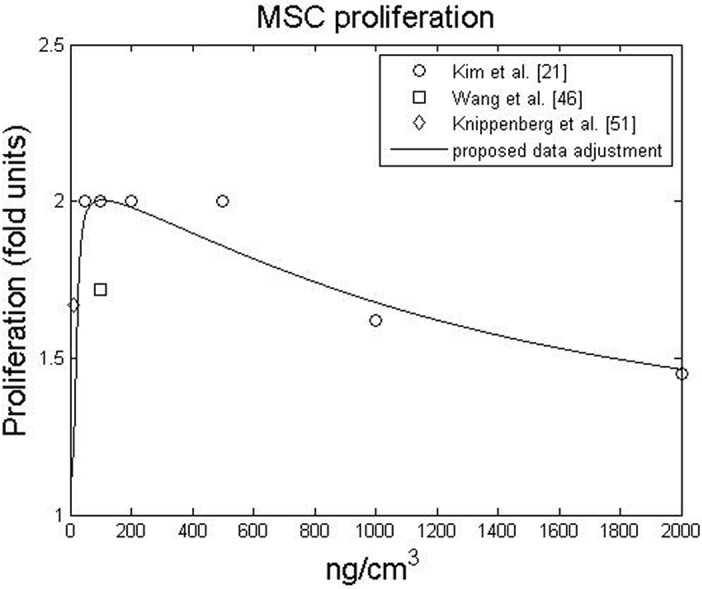
Proliferation is expressed as a fold increase relative to proliferation without BMP-2
Cell migration is also influenced by BMP-2, as BMPs exert a chemotactic effect on cells (i.e., cellular attraction to a chemical) [54,55]. Lind et al. [56] observed that cellular chemotaxis is a BMP-2-dependent bell-shaped function centered on a BMP-2 concentration of 1 ng. cm −3. There is grosso modo an increase in the chemotactic effect of BMP-2 from 0.01 ng. cm −3 to 1 ng. cm −3 followed by a decrease for concentrations from 1 ng. cm −3 to 100 ng. cm −3 [56]. Lind et al. [56] also found that the peak at 1 ng. cm −3 promoted a 2.2-fold increase in osteoblast chemotaxis, and similar results were observed for U2-OS cells (primitive transformed cells of mesenchymal origin). Fiedler et al. [54] observed that 1 ng. cm −3 of BMP-2 stimulated 2.2-fold and 3.5-fold increases in the migration of osteoblasts and mesenchymal progenitor cells (or MSCs) respectively. Fig 2 summarizes the dose-dependent, chemotactic effect of BMP-2 on MSCs and osteoblasts.
Fig 2. Influence of BMP-2 concentration on MSC (top) and bone cells (bottom) chemotaxis.
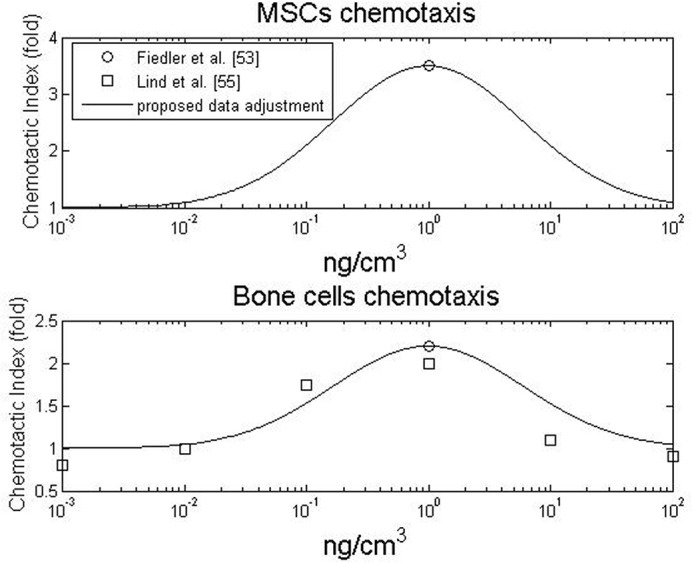
Chemotaxis is expressed as a fold increase relative to cell migration without BMP-2
During fracture healing, MSCs can differentiate into cartilage cells, fibroblasts and bone cells [57]. BMP-2 is essential for bone healing [18] and is present in the fracture gap throughout healing [18,58]. However, some studies have concluded that BMP-2 inhibits the cartilage phenotype [52], which is essential for soft callus formation [45] and subsequent endochondral ossification [59]. Moreover, when cells go through a certain differentiation path, this is usually measured by gene expression which does not allow an objective quantification of the fold increase of cell differentiation due to BMP-2. Consequently, in order to have a well-defined set of differentiation rules, we followed a mechanistic approach [60], which states that the mechanical deformation provides enough stimulus for cells to differentiate [61,62]. So far this approach could be the classical one taken by many authors in the topic of bone healing simulation [24–29]. Nonetheless, BMP-2 is essential to trigger healing [45,46] and for that reason we assume that at least a minimal physiological concentration (g min) is required for cellular activity to occur.
In recent years, the effect of BMP on cartilage hypertrophy has been studied [51,63]. Notably, Caron et al. [63] demonstrated that BMP-2 had almost no influence on the hypertrophic phenotype at concentrations below 0.3 ng. cm −3. However, chondrocyte maturation is dose-dependent for higher concentrations of BMP-2. For example, cartilage hypertrophy increased approximately 2-fold at a concentration of 3 ng. cm −3 and approximately 3.8-fold at a concentration of 30 ng. cm −3 [63]. The effect of BMP-2 on chondrocyte maturation is summarised in Fig 3. We were not able to find data on the effect of very high BMP-2 concentrations on chondrocyte hypertrophy. Thus we assumed an asymptotic behaviour at 3.8-fold for concentrations above 30 ng. cm −3.
Fig 3. Influence of BMP-2 on chondrocyte hypertrophy.
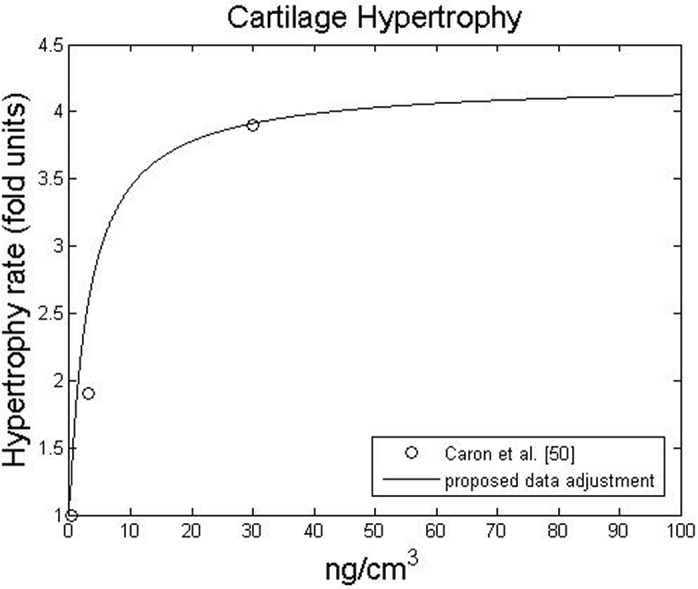
Chondrocyte hypertrophy is expressed as a fold increase relative to chondrocyte hypertrophy without BMP-2.
After the experiments performed by Urist [10], BMPs have been increasingly researched for their effects on bone cells and tissue. Recently, the osteoinductive power of BMPs has been stressed by many authors [45,47,52,64–67]. In many studies, the osteoinductive potential of BMP-2 has been explored not by measuring the number of bone cells per se, but rather by the amount of extracellular proteins produced [45,66] and their relative gene expression levels [47,52]. From a proteomic perspective, Ryoo et al. [66] and Tsuji et al. [45] noticed increases in osterix and osteocalcin production in the presence of BMP-2. From a gene expression perspective, Knippenberg et al. [52] observed that 10 ng. cm −3 of BMP-2 promoted a 2.3-fold increase in osteopontin expression. More recently, Wang et al. [47] observed dose-dependent proportional increases in the expression of osteocalcin (up to 3.1-fold) and osterix (up to 5.5-fold) within the 0 – 200 ng. cm −3 concentration range. Based on these data and assuming the existence of an asymptote at higher concentration [67], the effect of BMP-2 on bone tissue production is presented in Fig 4.
Fig 4. Influence of BMP-2 on bone tissue production.
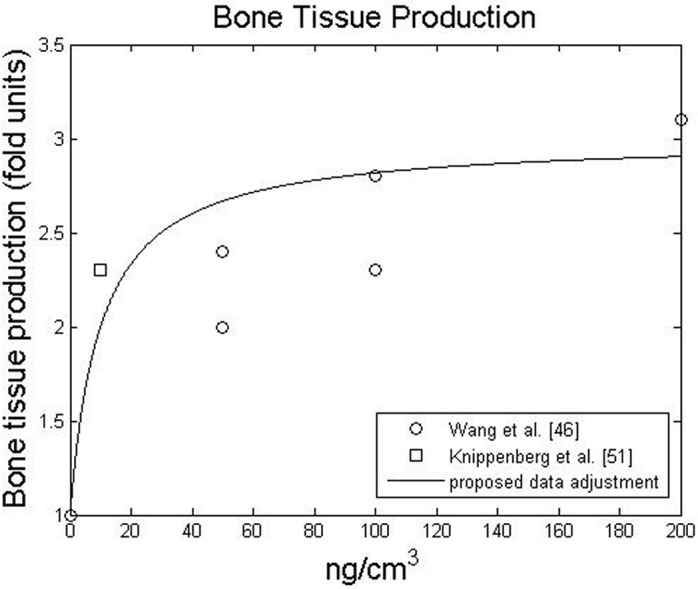
Bone tissue production is expressed as a fold increase relative to bone tissue production without BMP-2
Thus far, we have quantitatively described how cells are affected by BMP-2 supplemented medium. However, to understand the effect of BMP-2 at normal physiological concentration, we must first determine the physiological concentration range. A wide range of values was found in the literature. For example, Huang et al. [68] studied the amounts of BMP-2 produced by osteoprogenitors and osteoblasts in vitro and found concentrations of 0.01 – 0.3 ng. cm −3. Similar values have been reported in other studies, including those of Park et al. [69] and Wang et al. [70], who measured average concentrations of 0.087 ng. cm −3 and 0.072 ng. cm −3 respectively, in healthy human subjects. However, higher values have also been reported. For example, Wang et al. [71], found their control group to have an average concentration of 0.51 ng. cm −3. Based on this data, we can say that BMP-2 physiological concentration can be globally found within the 0.008 – 0.5 ng. cm −3 range. Consequently, at normal physiological conditions, the cellular processes of proliferation, chemotaxis, maturation and matrix production are very close to 1-fold.
2.2. Modelling the dynamics of BMP-2
Data on BMP-2 can be used to modulate cellular behavior. To define the equilibrium equation of BMP-2, we considered that BMP-2 concentration, g, can vary due to cellular consumption (subdivided between background consumption, and consumption due to cellular events [68]), molecular half-life degradation, cellular production and molecular diffusion:
| (1) |
Cell proliferation, cartilage cell hypertrophy, bone production and cell differentiation can all be considered liable cell events, capable of causing variations in BMP-2 concentration. Because proliferation increases the number of cells, we assumed that physiological levels of BMP-2 would be replenished quickly enough. However, we underestimated BMP-2 consumption due to cartilage hypertrophy as well as bone tissue production. Therefore, BMP-2 consumption due to differentiation alone stands as
| (2) |
where δ differentiation is an indicator function (δ = 1 if there is differentiation, δ = 0 otherwise), g is the concentration of BMP-2 and g min is the low boundary of physiological concentration. As described by Eq (2), whenever a differentiation event occurs, such as MSC differentiation towards chondroblastic or osteoblastic fates, all the BMP-2 in the medium is consumed, resulting in the minimum physiological BMP-2 level: g min = 0.008 ng. cm −3 [68]. BMP-2 was assumed to have no effect, on the fibroblastic differentiation pathway.
As stated by Lander et al. [72] and Umulis et al. [73], BMP-2 molecules in an aqueous medium bind reversibly with BMP-2 receptors (BMPR). When bound, the BMP-BMPR complex can undergo endocytosis. The kinetics of this process are analogous to Michaelis-Menton kinetics [73] considering BMP-2 as the substrate and BMPR as the catalyst, such that:
| (3) |
where is analogous to the Michaelis constant and V max is the maximum rate at which BMP-2 is consumed [73]. MSCs and bone cells are assumed to be the main contributors to BMP-2 consumption [20,45,47,68,74].
In vivo BMP-2 half-life was also considered to take part in molecule degradation and was taken into account as shown in Eq (1). We propose that the degradation behavior follows an exponential decay with a half-life t 1/2 = 0.42 days as determined by Bramono et al. [75]:
| (4) |
where the is the half-life rate parameter such as .
We define BMP-2 production term due to cell activity as
| (5) |
where c s and c b are the MSC and bone cell concentrations respectively, and α prod, γ and γ 0 are three parameters. These three parameters are adjusted to guarantee the following: (1) cells require the minimum BMP-2 concentration in their medium, thereupon they will secrete it more quickly if the levels are sub-physiological and (2) when the BMP-2 level is within physiological range (0.008 – 0.05 ng. cm −3), the production rate must not drive g outside of that range. Note that the proposed physiological range comprises the endogenous BMP-2 concentration observed during murine fracture healing range (18 – 22 pg/ml) [76].
Together, the background consumption and the production rates promote a rapid input of BMP-2 when its levels are low as well as a faster consumption when it is in excess, hence guaranteeing the maintenance of normal physiological levels.
Finally, we defined BMP-2 diffusion according to Fick’s Law
| (6) |
where D g is the diffusion coefficient of BMP-2.
2.3. Alginate hydrogel
Alginate hydrogels are biocompatible and stable colloidal networks [77] useful in bioengineering applications such as tissue engineering and drug delivery devices [50,78,79]. According to Boerckel et al. [49], the use of an alginate hydrogel serves two main purposes: 1) to control the BMP-2 release profile and 2) to provide support for cell migration. Moreover, in our model we also considered degradation kinetics.
In the literature, several authors have provided a detailed description of the release [80,81], degradation [82] and swelling [83] mechanisms of hydrogels in the light of thermodynamics theory. Nevertheless, the system approached here is complex and besides the release, degradation and swelling mechanisms, we also have to consider cells and cell-hydrogel interactions such as cell migration and enhanced hydrolysis due to cellular influence. Therefore, we decided to use a simpler approach as described below.
Concerning BMP-2 release, the release profile of BMP-2 from an alginate hydrogel presents a good fit with an exponential decay, as shown by Boerckel et al. [49]. We hypothesized that the loss of signal corresponded to the half-life degradation of BMP-2. Therefore we consider two types of BMP-2: the BMP-2 which is encapsulated in the gel denoted g gel, and the BMP-2 that is moving in the fluid denoted g. We considered that BMP-2 encapsulated can undergo half-life degradation and is also gradually released in the meantime. Both behaviors were modelled by an exponential decay, characterized by and λ rel respectively. Thus, the BMP-2 amount in the gel varies according to the following equation:
| (7) |
where λ rel (a) depends on the normalized amount of the alginate a as will be explained later in Eq 13. The amount of BMP-2 released from the hydrogel into the fluid will increase BMP-2 concentration in fluid. The released BMP-2 is now available for cell and in particular can undergo the half-life degradation characterized in Eq (4) with degradation constant . Thus the complete equilibrium equation with the released and the in vivo degradation terms stands as:
| (8) |
We assumed that a gel exclusively composed of alginate molecules does not permit cell migration. In fact, cells do not naturally adhere to the alginate polymer [84]. However, small RGD peptides can be mixed into the gel to mimic the adhesion sites of the extracellular matrix, thus allowing cell migration inside the gel [84,85]. Although it is possible, we considered the migration rate into the alginate to be low [86,87].
To our knowledge, no alginate-degrading enzyme exists in humans [88]. However, alginate degradation occurs in vivo through the loss of ionic cross-links and random hydrolysis of the polymer [85]. As suggested by Boerckel et al. [49], cells can have an indirect influence on alginate hydrogel degradation. As cell and tissue invasion occurs, the ion exchange rate increases, and water penetrates further into the hydrogel, thereby enhancing its degradation.
Based on the previous description, we modelled hydrogel degradation considering that (1) the hydrogel follows an aging degradation behaviour, (2) the cellular influence on degradation is predominant over other effects and (3) the degradation rate is proportional to the number of cells. The model summarized in Eq (9) considers these effects:
| (9) |
where a(t) is the normalized amount of alginate at time is the degradation rate of alginate at time t, c is the cell concentration, describes the bulk degradation coefficient and describes the degradation promoted by cellular invasion and activity. We assume that two main mechanisms regulate degradation of the alginate. First, bulk degradation which occurs through the hydrolysis of the polymer chains by the water in the gel pores. Second, cell-based degradation [49], the argument being that since alginate chains are degraded by hydrolysis, cellular invasion and activity destabilizes the ionic crosslinking, further exposing the hydrogel chains to hydrolysis. According to the proposed degradation model, the number of cells proportionately increases alginate degradation. However, if the cell population is constant, gel degradation only depends on time [89] and will proceed via the hydrolysis of random polymeric links [85] in an aging process [90].
We also included the regulatory effect of the hydrogel on cell migration and BMP-2 release. Concerning cellular migration, we simulated their motility through Eq (10)
| (10) |
where c is the cellular concentration, g is the BMP-2 in the fluid, D(a) is the cell diffusion coefficient and χ(a) is the chemotactic sensitivity coefficient. The values of D and χ were defined with a linear dependence on the amount of hydrogel a. Therefore
| (11) |
| (12) |
where D 0 and χ 0 corresponds to the diffusion and chemotactic coefficients when the gel matrix does not exist. We considered here that migration is heavily impaired by alginate, although a weak random migration is allowed. In fact, cells are not keen on alginate and when presented with the alginate gel alone the migration is very weak, as Boerckel et al. showed [49]. It can also be seen that dense gels can impede cells from migrating even in the presence of chemical queues. Nonetheless, this obstacle is gradually reduced as the hydrogel degradates.
Also concerning cell migration, MSCs were not allowed to migrate through mineralized matrix [31]. It may happen however, that during the defect infilling, both non-mineralized and mineralized tissue temporarily inhabit the same space for a limited time period. Therefore, we assumed that MSCs are not allowed to migrate through a certain volume if mineralized tissue is the main tissue in that volume.
Finally, we also assumed that the way BMP-2 is released would have to be influenced by the amount of alginate. The reasoning behind this assumption comes from the idea that as the alginate is degraded, its contact surface increases thus increasing the release rate of BMP-2. Accordingly, the degradation constant λ rel is defined with a linear dependency on the amount of alginate hydrogel:
| (13) |
where is a constant that quantifies the release rate of BMP-2.
2.4. Use of BMP-2 to heal critical size fractures
We aim to study, the healing effect of BMP-2 on critical fractures in silico. We have shown the influence of BMP-2 on cell behaviour in terms of fold increases relative to cells not treated with BMP-2. Assuming that previous mechanoregulatory models [31,57] implicitly consider BMP-2 only at the physiological level, we can update these models by fold increasing the mechanical effects on cells and tissues, given BMP-2 influence.
The main idea behind the coupling is stated by several authors who stress that BMP-2 is a modulating factor [47,52,63,68]. In fact, BMP-2 can play a major role in modulating the sequential events leading to bone formation [58]. Based on this motto, the fold increase in proliferation, migration, differentiation, maturation and matrix production were determined by the modulating functions presented in Figs 1–4, respectively.
The suggested BMP-2 modulation can be applied to any mechanoregulatory model, as long as it considers the behaviour to be modulated. In this work, we used the mechanistic model presented by Gómez-Benito et al. [31] and García-Aznar et al. [57], as it already considers all modulated effects (i.e., proliferation, migration, differentiation, maturation and matrix production.
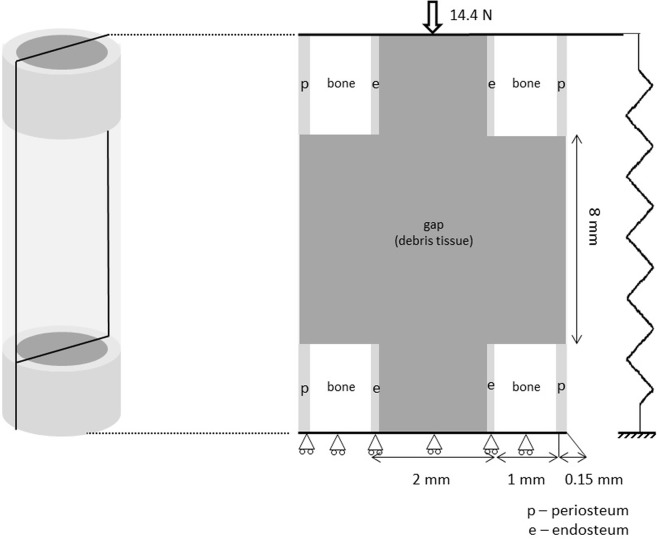
To evaluate the predictive ability of the model, we simulate the in vivo experiments of Boerckel et al. [49], who investigated the effect of BMP-2, released by an alginate hydrogel, in an 8 mm critical bone defect, in the diaphysis of a rat femur. The geometry of the rat femur diaphysis is considered as an idealized cylinder, to which only axial loads are applied. Given the cylindrical symmetry, our study was performed on one longitudinal section. From a mechanical perspective we assumed 2D-plane strain [91, 92]. From a mass diffusion perspective, the 2D model considered a unitary thickness, meaning that every point within the model domain is surrounded by a control volume. Thus we kept using volume units (ng/cm 3) while working with BMP-2 concentrations. The femur geometry is presented in Fig 5 and includes the cortical bone, endosteum, periosteum and gap, which was set at 8 mm [49].
Fig 5. Rat idealised geometry with the respective dimensions, different bone parts and load.
We applied an axial load of 14.4 N which corresponds to the maximum axial load during the rat gait [93]. We used a fixator with a stiffness of 277 N. mm −1 estimated from the polysulfone fixator used in vivo by Boerckel et al. [49]. In agreement with the original model by Gómez-Benito et al. [31], as bone healing occurs, cells proliferate, migrate, differentiate and produce biological tissues. The tissues considered were debris tissue, granulation tissue, cartilage, fibrous tissue, woven bone and cortical bone. All tissues were assumed to be isotropic poroelastic biphasic materials. Their properties are summarised in Table 1.
Table 1. Poroelastic mechanical properties considered for the different tissues [31,94–96] and for the alginate hydrogel.
| Tissue | E (MPa) | ν | k (mm 2) |
|---|---|---|---|
| Debris tissue | 1.85 | 0.048 | 7 × 10−12 |
| Granulation tissue | 7.79 | 0.048 | 1 × 10−14 |
| Cartilage tissue | 27.05 | 0.103 | 5 × 10−15 |
| Calcified cartilage | 57.05 | 0.108 | 5 × 10−15 |
| Fibrous tissue | 80.07 | 0.127 | 1 × 10−14 |
| Woven bone | 982.48 | 0.295 | 1 × 10−17 |
| Cortical bone | 20 × 103 | 0.3 | 1 × 10−17 |
| Alginate hydrogel | 0.05 [98,101] | 0.048 | 7 × 10−12 |
We assumed that alginate hydrogel is a poroelastic biphasic material. The Poisson’s ratio and the permeability were considered to be within the same order of magnitude of those of debris tissue [97], and the Young modulus was set at E Hg = 0.05 MPa [98–101].
Since the mechano-chemical model proposed is an extension of the mechanical model proposed by Gómez-Benito et al. [31], the mechanical stimulus is computed as described in the work of Gómez-Benito et al. [31]. Briefly, at each iteration a finite element mechanical analysis is used to compute the mechanical stimulus. Tissues are considered poroelastic, hence described by an elastic modulus, a Poisson’s coefficient and a permeability coefficient. Knowing the tissue distribution and their material properties, the material constants at each Gauss point are determined with an average weighted by the tissue fraction, as it was proposed by Gómez-Bénito et al. [31]. Once the material properties are defined we applied the external loads. From the mechanical analysis the principal strains at each point are extracted and used to compute the mechanical stimulus (second invariant of the deviatoric strain tensor). Given the computation of the mechanical stimulus, we now have the necessary information to run the mechanistic model.
We quantified the effects of BMP-2 on cell behavior in order to evaluate the use of BMP-2 in large bone defects. With this purpose, we defined a series of in silico experiments. For validation purposes and following the in vivo bone healing experiment by O’Neil et al. [102], we tested the proposed mechano-chemical model in a regular 2mm gap fracture. The aim of this study was to verify that BMP-2 at normal physiological concentrations, without any exogenous source, did not alter regular the regular simulation of bone healing. We next tested different conditions for large bone defects. The first condition corresponded to a control experiment, in which the gap was empty and contained no hydrogel or BMP-2 supply. In the second experiment, following the in vivo approach by Boerckel et al. [49], the gap was filled with alginate hydrogel alone, and no BMP-2 was provided. In the third and final experiment, following again the in vivo approach by Boerckel et al. [49], we implanted the alginate hydrogel soaked with 5 μg of BMP-2 into the bone defect. Besides the 5μg dose, and from a quantitative perspective only, other BMP-2 doses were also tested (0.1μg, 0.5μg, 1μg and 2.5μg), in order to further evaluate the quantitative predictive potential of the model.
Results
3.1. First experiment: validation for a 2mm gap
For the 2mm gap fracture, and following the in vivo bone healing experiment by O’Neil et al. [102], we studied the evolution of bone formation inside the callus and gap regions (Fig 6).
Fig 6. In silico results for a small gap (2mm).
The evolution of callus shape and bone tissue filling the callus and gap regions
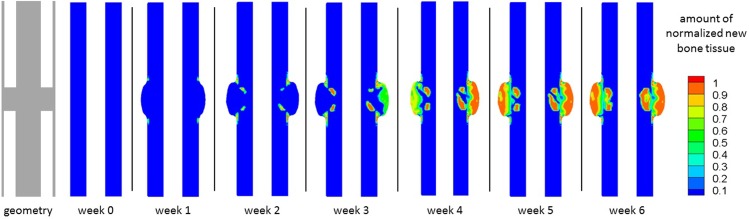
From a qualitative perspective, an exhaustive description of healthy bone healing as well as of all the features captured by the 2mm gap simulation is provided in the S1 File. Briefly, and concerning bone tissue formation, we observed that the callus progressively appeared during the first two weeks, intramembranous ossification occurred in the periosteum and new bone tissue slowly appeared far from the fracture site. From week 3 until week 5, the callus was progressively invaded by bone: endochondral ossification takes place and the hard callus was formed. By the end of week 5, the callus was fully filled with new bone tissue and began to act as a buttress, improving gap stability. By week 6, the increased stability brought by the hard callus allowed bone tissue to fill the gap, and the bone continuity was restored.
From a quantitative perspective, Fig 7 shows the predicted amount of normalized new bone formed during the 2mm fracture healing. There, the in silico results are plotted against the normalized amount of bone measured by O’Neil et al. [102] (also during a 2mm fracture healing). As we can observe, the amount of predicted bone closely follows the amount of measured bone in vivo.
Fig 7. Evolution of normalized new bone tissue in vivo and in silico.
fraction measure (blue) in vivo [102] and predicted in silico (red) for a rat fracture model of 2mm
Together, Figs 6 and 7 show that the model predictions mirror the description of healthy bone healing observed in vivo from both a qualitative and a quantitative perspective [102,103].
3.2. Second experiment: predictions of BMP-2 based healing of a large bone defect
For each of the remaining three experiments, we studied the evolution of bone formation inside the gap as well as the evolution of 5μg dose BMP-2 release over a period of 12 weeks [49]. These results are presented in Figs 8 and 9 respectively.
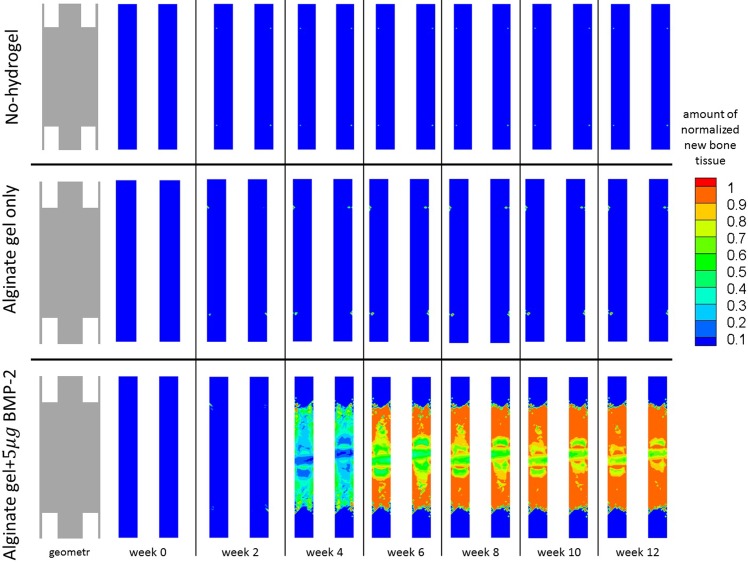
Fig 8. Evolution of new bone tissue.
Evolution of the normalized amount of new bone tissue inside the bone defect over 12 weeks, when: no hydrogel was placed inside the bone defect (top); an alginate hydrogel was placed inside the bone defect (middle), and an alginate hydrogel with 5μg of BMP-2 (bottom) was placed inside the bone defect.
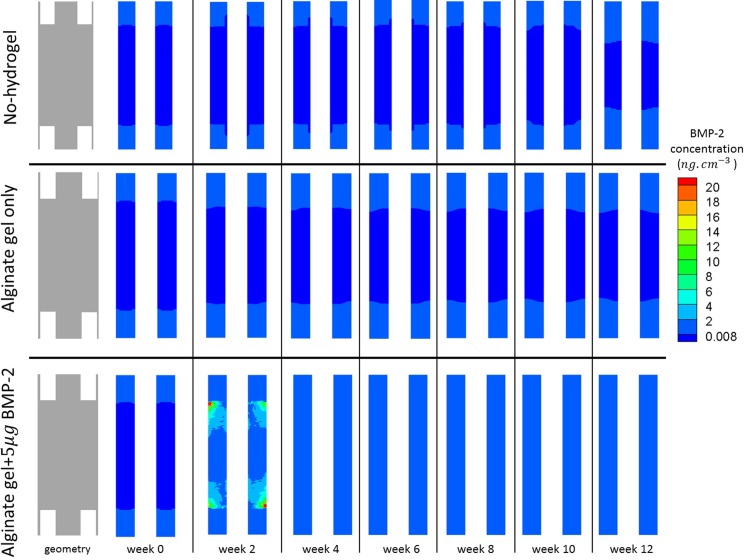
Fig 9. Evolution of BMP-2 concentration.
Evolution of BMP-2 concentration inside the bone defect over 12 weeks, when: no hydrogel was placed inside the bone defect (top); an alginate hydrogel was placed inside the bone defect (middle), and an alginate hydrogel with 5μg of BMP-2 (bottom) was placed inside the bone defect.
With respect to new bone formation (Fig 8), bone appeared and filled the gap only when both the hydrogel and BMP-2 were used. For the cases receiving hydrogel alone or no hydrogel, no new bone formation was detected.
When both hydrogel and BMP-2 were used (5μg dose), bone tissue formation inside the defect was low during the first month. It is just at the fourth week that the produced amount of new bone tissue crosses the 10% threshold. Thereafter, the amount of bone gradually increased inside the gap. By the end of week 12, new bone tissue occupied approximately 85% of the defect and the bone tissue distribution tended to be greater (around 90%) in the regions next to cortical bone.
The BMP-2 concentration was either low and close to the physiological levels or almost non-existent for both the no-hydrogel and alginate only cases (Fig 9). However, when hydrogel and BMP-2 (5μg dose) were used simultaneously, we observed an initial burst of BMP-2, which lasted for the first two weeks and then gradually decreases until week 6. From week 6 until the end of week 12, the BMP-2 concentration remained within the physiological range.
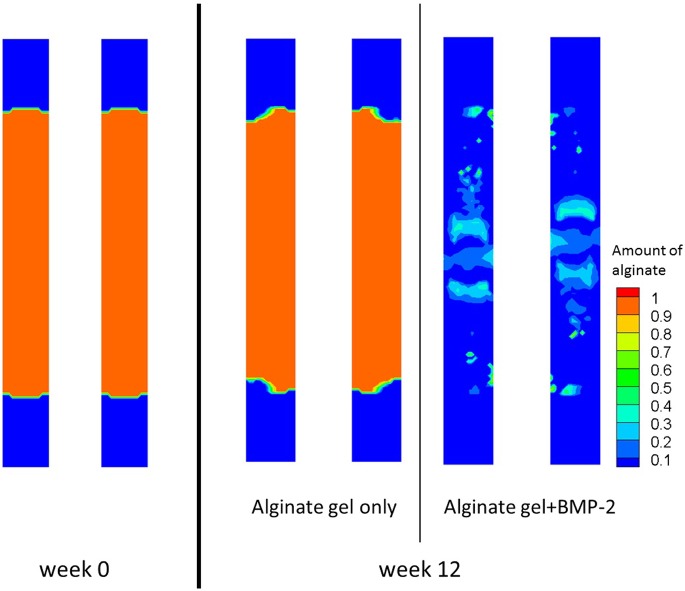
The evolution of alginate was also analyzed at week 0 and week 12 (Fig 9). At week 0, the gap was completely filled with the hydrogel. By week 12, the hydrogel remained nearly intact when alginate alone was used, but the amount of alginate was severely reduced when BMP-2 was present. In the latter case, approximately 10% of the hydrogel remained inside the gap. Although some small isles with a slightly greater amount of alginate persisted, the hydrogel was more degraded in the regions adjacent to the cortical bone than in the peripheral regions of the defect.
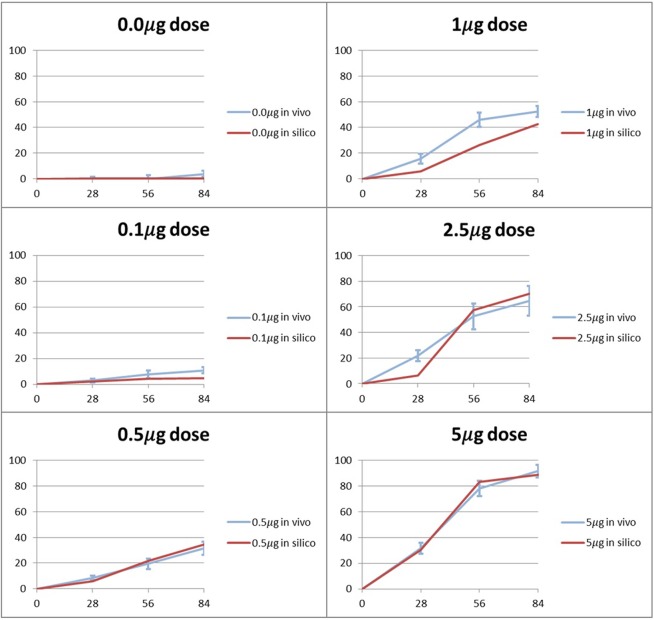
From a quantitative perspective, in Fig 10 we show the amount of bone predicted in silico, for the different BMP-2 doses (0.0μg, 0.1μg, 0.5μg, 1μg, 2.5μg, 5μg), against the bone amount measured in vivo by Boerckel et al. [49] for the same BMP-2 doses. One can observe that for all cases, the curves predicting bone formation in silico follow the bone amount measured in vivo.
Fig 10. Evolution of bone defect filling with new bone tissue in vivo and in silico.
Percentage of the defect volume filled with bone tissue, for different doses of BMP-2.
Globally, the in silico curves presented in Fig 10 follows the tendency obtained by the in vivo curves. Briefly, during the first 28 days, there is an initial increase in the bone amount. Between 28 and 56 days, the bone production rate increases. Finally, from day 56 to day 84, the bone production rate decelerates until the end of the simulation.
Also, we can observe in Fig 10 that the in silico simulations capture the progressive increase in bone volume with BMP-2 dose: the release of a greater BMP-2 dose is accompanied by the formation of a greater amount of bone in the defect. In fact, according to the model proposed in this work, bone tissue production (and mineralization) depends linearly: on the number of bone cells (as proposed by Gómez-Benito et al. [31]) and on the chemical stimulus provided by BMP-2 (Fig 4). On the one hand, a greater BMP-2 dose attracts more cells through chemotaxis. On the other hand, a greater BMP-2 dose also improves the bone tissue production rate. Together, these two effects explain why a greater BMP-2 dose promotes defect infill with bone tissue. To see the bone tissue distributions inside the defect, please consult the S2 File.
At the end of the simulations, we found that the more accurate prediction was made for the 0.1μg case whose predicted amount of bone deviates from the in vivo measurements by 0.4%. The worst prediction corresponds to the 1.0μg case which deviates from the in vivo experiments by 10%. Nevertheless, the latter margin can be considered acceptable from an engineering and biological point of view. In addition, the error found corresponds to an under prediction of bone volume, in circumstances (1.0μg dose) where defect non-union still is observed in vivo.
However, when high doses are used (2.5μg and 5μg) bone bridging occurs and the amount of bone predicted is more accurate (5.6% and 2.9% respectively). Actually, it seems that for intermediary doses a lower production of bone volume can occur, despite the fact that defect non-union keeps being predicted. Therefore, the model seems to provide a conservative prediction: it clearly shows that a larger dose is effectively required for defect bridging.
Discussion
After simulating the healthy bone healing in a 2mm fracture, we simulated the experiments for large bone defects. To verify the quality of the defect filling, Boerckel et al. [49] assessed some qualitative indicators such as defect bridging, bone volume, torsion to failure and made histological observations of cell and tissue invasion into the defect. In vivo, Boerckel et al. [49] did not observe defect bridging when a hydrogel alone was placed into the defect. Nevertheless, when gel containing 5μg of BMP-2 was implanted, the bone defect was effectively bridged with bone tissue. Our in silico results are very similar (Fig 8). Bone bridging occurred when hydrogel and BMP-2 were added and no bridging occurred when hydrogel alone was implanted. Notably, bone tends to be more densely distributed next to the cortical region. Because our model assumes that the periosteum is the main progenitor cell source, increased cell accumulation also increases bone tissue production in this region of the defect.
When neither hydrogel nor BMP-2 was added into the defect, no bridging was observed in silico. This result was somewhat expected: in the absence of a real support that allows for cell adhesion, cells cannot migrate. It should be noted however that the no-hydrogel case presented in Fig 8, was not tried by Boerckel et al. [49]. Instead it is used here as a control experiment of the model presented by Gómez-Benito et al. [31] in order to verify whether or not large bone defects are within the range of validity of the referred model. Without any cellular support or molecular cue, we would expect cellular invasion and ECM production into the gap to be almost non-existent. Indeed, we did not observe any cell invasion or ECM formation; in particular, bone tissue (Fig 8) did not appear over the twelve week period. Combining the observations of the 2mm gap experiment and the no-hydrogel case for an 8mm defect, we noticed that for both regular size gaps (2mm) and large bone defects (8mm) the proposed mechano-chemical model correctly predicts bone union and non-union, respectively. Therefore, the model proposed here is able to predict different healing patterns for different gap dimensions.
Comparing bone tissue formation between the 2mm fracture and the 8mm defect with BMP-2 soaked hydrogel, we notice that bone formation in the former case follows the formation of the external periosteal callus. The mechanistic model proposed by Gómez-Benito et al. [31], which is at the basis of our mechano-chemical model, considers that this domain variation is caused by two main phenomena: increased cell proliferation (in particular MSCs) and cartilage hypertrophy. In our numerical simulations, domain variation is not observed for the large defect. On the one hand the stability provided by the external fixator is high, thus enhancing a quick differentiation of MSCs into bone cells which do not have enough time to proliferate. On the other hand, whenever cartilage appears, it is quickly replaced by bone. Hence, there is never a significant amount of cartilage nor enough time for hypertrophy to change the model geometry.
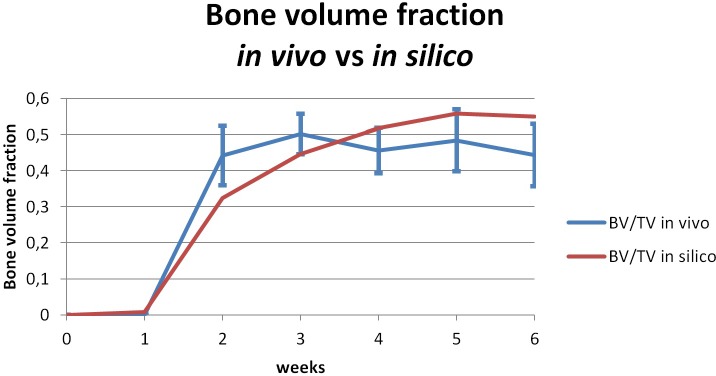
Bone volume and torsion to failure, are quantitative indicators of defect bridging. Bone volume can be calculated, as shown in Fig 9. Although bone volume is formed more rapidly in vivo than in silico, bone volume inside the defect in vivo and in silico is very similar after twelve weeks. In silico, the global evolution of bone tissue formation inside the gap is quantitatively estimated. The sometimes slower initial bone formation may be due to a simplification that ignores osteoprogenitors cells others than MSCs [31,57]. In fact, if sources such as bone marrow and muscle osteoprogenitors were considered [104], more bone cells would be present inside the defect, which would accelerate initial bone tissue production inside the gap.
Boerckel et al. [49] found that even when bridging occurs, there is cellular and tissue invasion and a significant, yet incomplete, degradation of the hydrogel. Similarly, we observed in silico cell invasion whenever the hydrogel was implanted. Through hydrogel degradation (Fig 11), we observed the indirect effect of invading cells. When BMP-2 was used, hydrogel degradation was increased, reflecting increased cellular invasion. As observed in vivo, the alginate never fully degraded and the hydrogel remaining in silico was analogous to the hydrogels islets observed in vivo.
Fig 11. Alginate hydrogel normalised distribution inside the bone defect.
Alginate hydrogel normalised distribution inside the bone defect after 12 weeks, for the case where alginate alone is implanted inside the bone defect and for the case where alginate with 5μg of BMP-2 is implanted inside the bone defect.
So far we proposed a mechano-chemical model that incorporates the effect of BMP-2 on cell events which regulate tissue regeneration. While Moore et al. [105] focused on the stimulus of endogenous BMP-2, which depended on the mechanical strain, in this work the BMP-2 stimulus provided by an exogenous source was considered as well as its modulatory interplay with the mechanical stimulus. To the best of our knowledge, this is the first in silico model that considers the bone induction properties of exogenous BMP-2 to correctly predict bone defect bridging. The developed model also predicts the amount of bone and its distribution in the defect at twelve weeks.
Nevertheless, we have to keep in mind that our model presents some limitations, which have been carefully analyzed. First, we observed that defect bridging occurred more slowly in the first few weeks (Fig 11), which could be attributed to other osteoprogenitors cell sources that were not considered, such as bone marrow and the surrounding soft tissues. Secondly, by not considering the surrounding soft tissues and the MSCs provided by them, certain phenomena observed in vivo such as ectopic bone formation cannot be recovered by the in silico simulations of this model.
Thirdly, the 2D geometry used in this work also presents some limitations. For instance, in their in vivo study, Boerckel et al. [49] measured the stiffness to failure. The current model was defined using 2D-plane strain to represent the symmetry plane. However, to measure this last mechanical value, the current 2D model would have to be updated to a 3D model to provide greater insight and further validation. Furthermore, we underestimate the healing of the medullary canal. This simplification is based on the assumption that two main MSCs sources contribute to bone formation in the cortical gap defect: the periosteum and the endosteum sources. Our assumption is that cells coming from the periosteum domain are the ones that are going to contribute the most to the cortical gap regeneration, while we do not consider the contribution of endosteal cells to the regeneration of the cortex. Therefore we consider that cells from the endosteum mainly affect bone formation in the endosteum region. Certainly, the underestimation of the endosteal region can slightly alter the mechanical environment; however, we have developed different simulations verifying that the mechanical contribution of the endosteal callus is not significant. Therefore, the rationale for not including the intramedullary space is not only mechanical [106] but more based on how cells distribute around the defect.
In our model, we did not consider bone remodeling phenomena. We took this simplification for two reasons: first, bone remodeling can take up to several years [107] and the time period considered reaches only 12 weeks, a time frame when remodeling does not play a major role yet. Second, as suggested by Boerckel et al. [49], the presence of the alginate impairs an already slow bone remodeling process. Therefore, this assumption is adequate given that we focus on the short-term response. Nevertheless, future updates of the presented model could incorporate this effect in order to predict both the bone volume inside the defect and its mechanical properties.
In contrast to previous qualitative healing models that incorporate growth factors, we have taken a quantitative approach instead of a qualitative one [25,31,32,34,57]. Although this new perspective is based on experimental data and thus requires fewer parameters, it always depends on the data available in the literature. For instance, the influence of high concentrations of BMP-2 was only available for cell proliferative behaviour (Fig 1), so we assumed an upper asymptote for chondrocyte hypertrophy at high concentrations. Following the same rationale, we only considered the effects of BMP-2 on cell behaviours that were described in the literature. A description of the effects of BMP-2 on fibroblasts, for example, was not found in the literature and, therefore, was not considered. In this context a sensitive analysis for the modulatory curves was done (see S3 File) and the results suggest that alternative curves did not cause a significant behavioral change. Nevertheless, whenever new data are available, it can easily be incorporated into the model to update the proposed modulation curves (Figs 1–4) or even to suggest new ones for new cellular behaviors.
Moreover, we must also stress that BMP-2 is just one in the myriad of growth factors involved in bone healing. We focused on BMP-2 specifically because it is considered by many authors to be one of the most important growth factors for bone healing [45,47] and bone tissue regeneration [14,15]. Given the availability of quantitative data, other growth factors can also be considered in the future to improve our approach.
In this work, our initial working hypothesis is that the mechanical stimulus interacting with the biochemical stimulus can be a useful approach to study this complex system where both stimuli play an important regulatory role. Thus, BMP-2 was introduced following what several authors in the literature consider to be its modulatory effect [52,63,68,70]. From a mathematical point of view, this assumption is translated as the product between mechanical and chemical stimuli dependent terms.
Conclusion
Previous in silico healing studies have shown that mechano-regulatory models are useful for qualitatively predicting the evolution of bone healing in small gap fractures [29,31,32,34,57]. Following the same mechanical perspective, recent studies on large bone defects have focused on the mechanical performance and stability due to rigid scaffold constructs [6,38,39,41]. In this work, we proposed a novel in silico mechano-chemical approach that puts a greater emphasis on a growth factor, specifically BMP-2, as a chemical stimulus. This was achieved by collecting quantitative experimental data concerning the effect of the growth factor on cells and tissues. This model brings up the opportunity of testing in silico the recent advances made on large bone defects healing, which show an enhanced defect bridging through the use of BMP-2 [108]. Importantly, we successfully predicted the healing and non-healing of a large bone defect, with BMP-2 delivery rather than a rigid scaffold. Moreover, our results showed a good qualitative and quantitative agreement with previous in vivo studies [49]. This novel in silico tool can provide further insight for bone tissue regeneration strategies to better determine the necessary doses of BMP-2 that guarantees bone healing, to optimize the release kinetics so that bridging is achieved with as less BMP-2 as possible thus enhancing bone healing [108].
Appendix 1
In this appendix we define the constants and parameters used in this paper.
g min = 0.008 ng. cm −3 is the low boundary of the in vivo concentration range of BMP-2
D g = 0.2 mm 2 day −1 is the diffusion coefficient of BMP-2 in the alginate hydrogel [108], D g = 8.64 mm 2 day −1 is the diffusion coefficient of BMP-2 in vivo [109] and α prod = 2 × 10−9 ng. ml −1 cell −1 day −1, γ = 15 (ng/mL)−1 and γ 0 = 0.01 are three parameters that define the BMP-2 production function
V max = (c s + c b) × 1.43 × 10−7 ng. cm −3.day −1.cell −1 is the maximum rate at which BMP-2 is consumed by cells [73]. MSC and bone cells are assumed to be the main contributors to BMP-2 consumption [20,45,47,68,74].
is a constant analogous to the Michaelis constant [73]
λ r = 0.217 day −1 is the decay constant in the BMP-2 release profile [49]
is the hydrogel degradation constant for bulk degradation and is the degradation constant due to cell influence
characterizes de the release rate of BMP-2 from the hydrogel
is the half-life time of BMP-2 encapsulated inside the hydrogel and is the half-life time of BMP-2 in vivo [75].
Supporting Information
(PDF)
(PDF)
(PDF)
Acknowledgments
This work was funded by Fundação para a Ciência e Tecnologia through the IDMEC, under LAETA, project UID/EMS/50022/2013 and through the PhD grant SFRH/BD/80458/2011. This research was supported by the Spanish Ministry of Economy and Competitiveness (Grant DPI2012-32888, project partially funded by the European Union through the European Regional Development Fund) and the European Research Council (ERC) through project ERC-2012-StG306751.
Data Availability
All the data are contained within the paper.
Funding Statement
This work was funded by the Fundação para a Ciência e Tecnologia through the IDMEC (Institute of Mechanical Engineering), under LAETA (Associated Laboratory for Energy, Transports and Aeronautics), project UID/EMS/50022/2013 and through the PhD grant SFRH/BD/80458/2011, the Spanish Ministry of Economy and Competitiveness (Grant DPI2012-32888, project partially funded by the European Union through the European Regional Development Fund), and the European Research Council (ERC) through project ERC-2012-StG306751. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Sasso RC, LeHuec JC, Shaffrey C, (2005), Iliac crest bone graft donor site pain after anterior lumbar interbody fusion: a prospective patient satisfaction outcome assessment. J Spinal Disord Tech, 18,(Suppl):S77–81. [DOI] [PubMed] [Google Scholar]
- 2. Arrington ED, Smith WJ, Chambers HG, Bucknell AL, Davino NA, (1996), Complications of iliac crest bone graft harvesting. Clinical Orthopaedics and Related Research, 9, 329–300. [DOI] [PubMed] [Google Scholar]
- 3. De Biase P, Capanna R (2005) Clinical applications of BMPs. Injury, 36, 43–46. [DOI] [PubMed] [Google Scholar]
- 4. Oest ME, Dupont KM, Kong HJ, Mooney DJ, Guldberg RE (2007) Quantitative assessment of scaffold and growth factor-mediated repair of critically sized bone defects. Journal of Orthopaedic Research, 25, 941–950. [DOI] [PubMed] [Google Scholar]
- 5. Rai B, Oest ME, Dupont KM, Ho KH, Teoh SH, Guldberg RE (2007) Combination of platelet-rich plasma with polycaprolactone-tricalcium phosphate scaffolds for segmental bone defect repair. J Biomed Mater Res A, 81, 888–899 [DOI] [PubMed] [Google Scholar]
- 6. Roohani-Esfahani SI, Dunstan CR, Davies B, Pearce S, Williams R, Zreiqat H (2012), Repairing a critical-sized bone defect with highly porous modified and unmodified baghdadite scaffolds, Acta Biomaterialia, 8, 4162–4172 10.1016/j.actbio.2012.07.036 [DOI] [PubMed] [Google Scholar]
- 7. Sebald H, Klenke FM, Siegrist M, Albers CE, Sebald W, Hofstetter W (2012), Inhibition of engogenous antagonists with an engineered BMP-2 variant increases BMP-2 efficacy in rat femoral defect healing, Acta Biomaterialia, 8, 3816–3820 10.1016/j.actbio.2012.06.036 [DOI] [PubMed] [Google Scholar]
- 8. Polak SJ, Levengood SKL, Wheeler MB, Maki AJ, Clark SG, Johnson AJW (2011), Analysis of the roles of microporosity and BMP-2 on multiple measures of bone regeneration and healing in calcium phosphate scaffolds, Acta Biomaterialia, 7, 1760–1771 10.1016/j.actbio.2010.12.030 [DOI] [PubMed] [Google Scholar]
- 9. Marsell R, Einhorn TA (2010), Emerging bone healing therapies, J Orthop Trauma, 24, S4–S8 10.1097/BOT.0b013e3181ca3fab [DOI] [PubMed] [Google Scholar]
- 10. Urist MR (1965), Bone: formation by autoinduction, Science, 150, (3698):893–9. [DOI] [PubMed] [Google Scholar]
- 11. Luyten FP, Cunningham NS, Ma S, Muthukumaran N, Hammonds RG, Nevins WB, et al. (1989) Purification and partial amino acid sequence of osteogenin, a protein initiating bone differentiation. J. Biol. Chem. 264, 13377–13380 [PubMed] [Google Scholar]
- 12. Wozney JM, Rosen V, Celeste AJ, Mitsock LM, Whitters MJ, Kriz RW, et al. (1988), Novel regulators of bone formation: molecular clones and activities. Science 242, 1528–1534. [DOI] [PubMed] [Google Scholar]
- 13. Wozney JM (1992) The bone morphogenetic protein family and osteogenesis. Mol. Reprod. Dev. 32, 160–167. [DOI] [PubMed] [Google Scholar]
- 14. Zara J, Lee M, Siu R, Li W, Wu B, Zhang X, et al. (2011), High Doses of Bone Morphogenetic Protein 2 Induce Structurally Abnormal Bone and Inflammation In Vivo, Tissue Engineering, 17, 1389–1399 10.1089/ten.TEA.2010.0555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Schwarz C, Wulsten D, Ellinghaus A, Lienau J, Willie M, Duda GN (2013), Mechanical load modulates the stimulatory effect of BMP-2 in a rat nonunion model, Tissue Eng Part A, 19, 1–2:247–54 10.1089/ten.TEA.2012.0265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Chen D, Harris MA, Rossini G, Dunstan CR, Dallas SL, Fenq JQ, et al. (1997). Bone morphogenetic protein 2 (BMP-2) enhances BMP-3, 4 and bone cell differentiation marker gene expression during the induction of mineralized bone matrix formation in cultures of fetal rat calvarial osteoblasts. Calcified Tissue International, 60, 3:283–290 [DOI] [PubMed] [Google Scholar]
- 17. Lu Y, Lee JS, Nemke B, Graf BK, Royalty K, Ill RI, et al. (2012), Coating with a modular bone morphogenetic peptide promotes healing of a bone-implant gap in an ovine model, PLOS One, 7, 11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kloen P, Paola M, Helfet D, Borens O, Richmond J, Goumans M. (2003) BMP signaling components are expressed in human fracture callus, Bone, 33, 362–371 [DOI] [PubMed] [Google Scholar]
- 19. Liu J, Mao K, Liu Z, Wang X, Cui F, Guo W, et al. (2013), Injectable biocomposites for bone healing in rabbit femoral condyle defects, PLOS One, 8, 10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Huang Z, Ren P, Ma T, Smith L, Goodman S (2010), Modulating osteogenesis of mesenchymal stem cells by modifying growth factor availability, Cytokine, 51, 305–310 10.1016/j.cyto.2010.06.002 [DOI] [PubMed] [Google Scholar]
- 21. Kim H, Oxendine I, Nobuhiro K (2013) High-concentration of BMP2 reduces cell proliferation and increases apoptosis via DKK1 and SOST in human primary periosteal cells, Bone, 54, 141–150 10.1016/j.bone.2013.01.031 [DOI] [PubMed] [Google Scholar]
- 22. McKay B, Sandhu HS (2002) Use of recombinant human bone morphogenetic protein-2 in spinal fusion applications. Spine 27, S66 [DOI] [PubMed] [Google Scholar]
- 23. Carlisle E, Fischgrund JS (2005), Bone morphogenetic proteins for spinal fusion. Spine 5, 240S [DOI] [PubMed] [Google Scholar]
- 24. Carter D, Beaupré G, Giori N, Helms J (1998), Mechanobiology of skeletal regeneration, Clinical Orthopaedics and Related Research, S355, S41–55. [DOI] [PubMed] [Google Scholar]
- 25. Isaksson H, van Donkelaar CC, Huiskes R, Yao J, Ito K (2008) Determinig the most important cellular characteristics for fracture healing using design of experiments methods, Journal of Theoretical Biology, 255, 1:26–39 10.1016/j.jtbi.2008.07.037 [DOI] [PubMed] [Google Scholar]
- 26. Isaksson H, van Donkelaar CC, Huiskes R, Ito K (2009), Sensitivity of tissue differentiation and bone healing predictions to tissue properties, Journal of Biomechanics, 42, 5:555–564 10.1016/j.jbiomech.2009.01.001 [DOI] [PubMed] [Google Scholar]
- 27. Vetter A, Liu Y, Manjubala I, Sander O, Epari DR, Fratzl P et al. (2011), The mechanical heterogeneity of the hard callus influences local tissue strains during boné healing: A finite elemento study based on sheep experiments, Journal of Biomechanics, 22, 3:517–523 [DOI] [PubMed] [Google Scholar]
- 28. Claes LE, Heigele CA (1999). Magnitudes of local stress and strain along bony surfaces predict the course and type fracture healing. Journal of Biomechanics, 32, 255–266. [DOI] [PubMed] [Google Scholar]
- 29. Lacroix D, Prendergast P (2002). A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading. Journal of Biomechanics, 35, 1163–1171. [DOI] [PubMed] [Google Scholar]
- 30. Prendergast P, Huiskes R, Soballe K (1996). Biophysical stimuli on cells during tissue differentiation at implant interfaces. Journal of Biomechanics, 30, 539–548. [DOI] [PubMed] [Google Scholar]
- 31. Gómez-Benito M, García-Aznar J, Kuiper J, Doblaré M (2005). Influence of fracture gap size on the pattern of long bone healing: a computational study. Journal of Theoretical Biology, 235, 105–119 [DOI] [PubMed] [Google Scholar]
- 32. Bailón-Plaza A, van der Meulen MCH (2001), A mathematical Framework to study the effects of growth factor influences on Fracture healing, Journal of Theoretical Biology, 212, 191–209 [DOI] [PubMed] [Google Scholar]
- 33. Bailón-Plaza A, van der Meulen MCH (2003), Beneficial effects of moderate, early loading and adverse effects of delayed or excessive loading on bone healing, Journal of Biomechanics, 36, 1069–1077 [DOI] [PubMed] [Google Scholar]
- 34. Geris L, Vander Sloten J, Van Oosterwyck H (2010) Connecting biology and mechanics in fracture healing: an integrated mathematical modeling framework for the study of nonunions, Biomechanics and Modeling in Mechanobiology, 9, 713–724 10.1007/s10237-010-0208-8 [DOI] [PubMed] [Google Scholar]
- 35. Geris L, Reed AAC, Sloten JV, Simpson AHRW, van Oosterwyck H (2010), Occurrence and treatment of bone atrophic non-unions investigated by an integrative approach, PLOS Computational Biology, 6, 9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Adachi T, Osako Y, Tanaka M, Hojo M, Hollister S (2006), Framework for optimal design of porous scaffold microstructure by computational simulation of bone regeneration, Biomaterials, 27, 3964–3972 [DOI] [PubMed] [Google Scholar]
- 37. Kelly DJ, Predergast PJ (2006), Prediction of the optimal mechanical properties for a scaffold used in osteochondral defect repair, Tissue Engineering, 12, 9:2509–19 [DOI] [PubMed] [Google Scholar]
- 38. Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ (2007), Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: Application of mechanobiological models in tissue engineering, Biomaterials, 28, 5544–5554 [DOI] [PubMed] [Google Scholar]
- 39. Sanz-Herrera JA, García-Aznar JM, Doblaré M (2008), A mathematical model for bone tissue regeneration inside a specific type scaffold, Biomechanics and Modeling in Mechanobiology, 7, 355–366 [DOI] [PubMed] [Google Scholar]
- 40. Pothuaud L, Fricain JC, Pallu S, Bareille R, Renard M, Durrieu MC, et al. (2005) Mathematical modelling of the distribution of newly formed bone in bone tissue engineering. Biomaterials, 26,33: 6788–97. [DOI] [PubMed] [Google Scholar]
- 41. Checa S, Prendergast PJ (2010), Effect of cell seeding and mechanical loading on vascularization and tissue formation inside a scaffold: A mechano-biological model using a lattice approach to simulate cell activity, Journal of Biomechanics, 43, 961–968 10.1016/j.jbiomech.2009.10.044 [DOI] [PubMed] [Google Scholar]
- 42. Carlier A, Geris L, van Gastel N, Carmeliet G, Van Oosterwyck H (2015) Oxygen as a critical determinant of bone fracture healing–A multiscale model, Journal of Theoretical Biology, 365, 247–264 10.1016/j.jtbi.2014.10.012 [DOI] [PubMed] [Google Scholar]
- 43.Carlier A, Geris L, Bently K, Carmeliet G, Carmeliet P, Van Oosterwyck H (2012) MOSAIC: A multiscale model of osteogenesis and sprouting angiogenesis with lateral inhibition of endothelial cells, PLOS Computational Biology [DOI] [PMC free article] [PubMed]
- 44.Moore SR, Saidel GM, Knothe U, Knothe Tate ML (2014) Mechanistic, mathematical model to predict the dynamics of tissue genesis in bone defects via mechanical feedback and mediation of biochemical factors, PLOS Computational Biology [DOI] [PMC free article] [PubMed]
- 45. Tsuji K, Bandyopadhyay A, Harfe B, Cox K, Kakar S, Gerstenfeld L, et al. (2006) BMP-2 activity, although dispensable for bone formation is required for the initiation of fracture healing, Nature genetics, 38, 1424–1429 [DOI] [PubMed] [Google Scholar]
- 46. Mi M, Jin H, Wang B, Yukata K, Sheu T, Han Ke Q, et al. (2013) Chondrocyte BMP-2 signaling plays an essential role in bone fracture healing, Gene, 10, 211–218 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Wang Q, Huang C, Xue M, Zhang W (2011) Expression of endogenous BMP-2 in periosteal progenitor cells is essential for bone healing, Bone, 48, 524–532 10.1016/j.bone.2010.10.178 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Marsell R, Einhorn TA (2011), The biology of fracture healing, Injury, 42–6, 551–555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Boerckel J, Kolambkar Y, Dupont K, Uhrig B, Phelps E, Stevens H, et al. (2011), Effects of protein dose and delivery system on BMP-mediated bone regeneration, Biomaterials, 32, 5241–5251 10.1016/j.biomaterials.2011.03.063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Seeherman H, Wozney J, Li R (2002), Bone morphogenetic protein delivery systems, Spine, 27, 165:S16–23 [DOI] [PubMed] [Google Scholar]
- 51. Caron M, Emans P, Cremers A, Surtel D, Coolsen M, van Rhijn L, et al. (2013), Hypertrophic differentiation during chondrogenic differentiation of progenitor cells is stimulated by BMP-2 but suppressed by BMP-7, Osteoarthritis and Cartilage, 21, 604–613 10.1016/j.joca.2013.01.009 [DOI] [PubMed] [Google Scholar]
- 52. Knippenberg M, Helder MN, Zandieh Doulabi B, Wuisman PI, Klein-Nulend J (2006) Osteogenesis versus chondrogenesis by BMP-2 and BMP-7 in adipose stem cells. Biochemical and biophysical research communications 342:902–8. 10.1016/j.bbrc.2006.02.052 [DOI] [PubMed] [Google Scholar]
- 53. Reddi AH, Cunninggham NS (1993), Initiation and promotion of bone differentiation by bone morphogenetic proteins, Journal of Bone and Mineral Research, 8, Suppl 2:S499–509 [DOI] [PubMed] [Google Scholar]
- 54. Fiedler J, Röderer G, Günther KP (2002), BMP-2, BMP-4, and PDGF-bb stimulate chemotactic migration of primary human mesenchymal progenitor cells, Journal of Cell Biochemistry, 87, 3:305–312 [DOI] [PubMed] [Google Scholar]
- 55. Sieber C, Kopf J, Hiepen C, Knaus P (2009) Recent advances in BMP receptor signaling. Cytokine & growth factor reviews 20:343–55. 10.1016/j.cytogfr.2009.10.007 [DOI] [PubMed] [Google Scholar]
- 56. Lind M, Eriksen EF, Bünger C (1996), BMP-2 but not BMP-4 and -6 stimulates chemotactic migration of human osteoblasts, human marow osteoblasts, and U2-OS cells, Bone, 18, 1:53–57 [DOI] [PubMed] [Google Scholar]
- 57. García-Aznar J, Kuiper J, Gómez-Benito M, Doblaré M, Richardson J (2007). Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth. Journal of Biomechanics, 40, 1467–1476. [DOI] [PubMed] [Google Scholar]
- 58. Onishi T, Ishidou Y, Nagamine T, Yone K, Imamura T, Kato M, et al. (1998), Distinct and Overlapping Patterns of Localization of Bone Morphogenetic Protein (BMP) Family Members and a BMP Type II Receptor During Fracture Healing in Rats, Bone, 22:605–612. [DOI] [PubMed] [Google Scholar]
- 59. McKinley T (2003). Principles of fracture healing The Medicine Publishing Company Ldt, 209212. [Google Scholar]
- 60. Pauwels F (1960). Eine neue theorie über den einflub mechanischer reize auf die differenzierung der stützgewebe. Z. Anat Entwicklunggsgesichichte, 121, 478–515. 14431062 [Google Scholar]
- 61. Rowlands AS, George PA, Cooper-White JJ (2008) Directing osteogenic and myogenic differentiation of MSCs: interplay of stiffness and adhesive ligand presentation, American Journal of Physiology–Cell Physiology, 295,1037–44 [DOI] [PubMed] [Google Scholar]
- 62. Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification (2006), Cell, 126:677–689 [DOI] [PubMed] [Google Scholar]
- 63. Miljkovic ND, Cooper GM, Marra KG (2008) Chondrogenesis, bone morphogenetic protein-4 and mesenchymal stem cells. Osteoarthritis and cartilage / OARS, Osteoarthritis Research Society 16:1121–30. 10.1016/j.joca.2008.03.003 [DOI] [PubMed] [Google Scholar]
- 64. Li RH, Wozney JM (2001), Delivering on the promise of bone morphogenetic proteins. Trends in biotechnology, 19, 255–265. [DOI] [PubMed] [Google Scholar]
- 65. Dragoo JL, Choi JY, Lieberman JR, Huang J, Zuk PA, Zhang J, et al. (2003) Bone induction by BMP-2 transduced stem cells derived from human fat. Journal of orthopaedic research: official publication of the Orthopaedic Research Society 21:622–9. 10.1016/S0736-0266(02)00238-3 [DOI] [PubMed] [Google Scholar]
- 66. Ryoo H-M, Lee M-H, Kim Y-J (2006) Critical molecular switches involved in BMP-2-induced osteogenic differentiation of mesenchymal cells. Gene 366:51–7. 10.1016/j.gene.2005.10.011 [DOI] [PubMed] [Google Scholar]
- 67. Zheng LW, Wong MCM, Rabie ABM, Cheung LK (2006) Evaluation of recombinant human bone morphogenetic protein-2 in mandibular distraction osteogenesis in rabbits: Effect of dosage and number of doses on formation of bone. The British journal of oral maxillofacial surgery 44:487–94. 10.1016/j.bjoms.2005.09.005 [DOI] [PubMed] [Google Scholar]
- 68. Huang Z, Nelson ER, Smith RL, Goodman SB (2007) The sequential expression profiles of growth factors from osteoprogenitors to osteoblasts in vitro. Tissue engineering 13:2311–20. 10.1089/ten.2006.0423 [DOI] [PubMed] [Google Scholar]
- 69. Park Y, Kim JW, Kim DS, Kim EB, Park SJ, Choi WS, et al. (2008), The bone morphogenesis protein-2 (BMP-2) is associated with progression to metastatic disease in gastric cancer, Cancer Res Treat., 40, 3:127–132 10.4143/crt.2008.40.3.127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Wang C, Yang KD, Ko J, Huang C, Huang H, Wang F (2009), The effects of shockwave on bone healing and systemic concentrations of nitric oxide (NO), TGF-β1, VEGF and BMP-2 in long bone non-unions, Nitric Oxide, 20, 298–303 10.1016/j.niox.2009.02.006 [DOI] [PubMed] [Google Scholar]
- 71. Wang YK, Sun WF, Liu XG, Deng J, Yan BE, Jiang WY, et al. (2011), Comparative study of serum level of BMP-2 and heterotopic ossification in traumatic brain injury and fracture patients, Zhongguo Gu Shang, 24, 399–403 [PubMed] [Google Scholar]
- 72. Lander AD, Nie Q, Wan FYM (2002) Do morphogen gradients arise by diffusion? Developmental Cell 2:785–796. [DOI] [PubMed] [Google Scholar]
- 73. Umulis D, O’Connor MB, Blair SS (2009) The extracellular regulation of bone morphogenetic protein signaling. Development (Cambridge, England) 136:3715–28. 10.1242/dev.031534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Wozney JM (2002), Overview of bone morphogenetic proteins, Spine, 27, 16S:S2–S8 [DOI] [PubMed] [Google Scholar]
- 75. Bramono DS, Murali S, Rai B, Ling L, Poh W T, Lim ZX, et al. (2012), Bone marrow-derived heparin sulfate potentiates the osteogenic activity of bone morphogenetic protein-2 (BMP-2), Bone, 50, 954–964 10.1016/j.bone.2011.12.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Glass GE, Chan JK, Freidin A, Feldmann M, Horwood NJ, Nanchahal J (2011) TNF-α promotes fracture repair by augmenting the recruitment and differentiation of muscle-derived stromal cells, PNAS,108:1585–1590 10.1073/pnas.1018501108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Draget KI, Smidsrød O, Skjåk-Bræk G (2005). Alginates from Algae. Biopolymers Online.
- 78. Sapir Y, Kryukov O, Cohen S (2011), Integration of multiple cell-matrix interactions into alginate scaffolds for promoting cardiac tissue regeneration, Biomaterials, 32, 1838–1847 10.1016/j.biomaterials.2010.11.008 [DOI] [PubMed] [Google Scholar]
- 79. Sun J, Tan H (2013), Alginate-based biomaterials for regenerative medicine applications, Materials, 6, 1285–1309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Peppas NA, Brannon-Peppas L (1996) Controlled release of fragrances from polymers I. Thermodynamic analysis, Journal of Controlled Release, 40:245–250 [Google Scholar]
- 81. Siepmann J, Peppas NA (2001) Modeling of drug release from delivery systems based on hydroxypropyl methylcellulose (HPMC), Advanced Drug Delivery Reviews, 48:139–157 [DOI] [PubMed] [Google Scholar]
- 82. Birnbaum DT, Brannon-Peppas L (2003) Molecular weight distribution changes during degradation and release of PLGA nanoparticles containing epirubicin HCI, Journal of Biomaterials Science, Polymer Edition, 14:87–102 [DOI] [PubMed] [Google Scholar]
- 83. Brannon-Peppas L, Peppas NA (1991) Equilibrium swelling behavior of dilute ionic hydrogels in electrolytic solutions, Journal of Controlled Release, 16:319–330 [Google Scholar]
- 84. Rowley JA, Madlambayan G, Mooney D (1999), Alginate hydrogels as synthetic extracellular matrix materials, Biomaterials, 20, 45–53 [DOI] [PubMed] [Google Scholar]
- 85. Andersen T, Strand B, Alsberg E, Christensen BE (2012), Alginates as biomaterials in tissue engineering, Carbohydrate Chemistry, 37, 227–258 [Google Scholar]
- 86.Vardar E (2010), Investigation of cell migration and proliferation in agarose based hydrogels for tissue engineering applications, (M.Sc. dissertation)
- 87. Topman G, Shoham N, Sharabani-Yosef O, Lin F (2013), A new technique for studying directional cell migration in a hydrogel-based three-dimensional matrix for tissue engineering model systems, Micron, 51, 9–12 10.1016/j.micron.2013.06.002 [DOI] [PubMed] [Google Scholar]
- 88. Holme HK, Lindmo K, Kristiansen A, Smidsrød O (2001), Thermal depolymerization of chitosan chloride, Carbohydrate Polymers, 46, 287–294 [Google Scholar]
- 89. Gombotz WR, Wee SF (1998), Protein release from alginate matrices, Advanced Drug Delivery Reviews, 31, 267–285 [DOI] [PubMed] [Google Scholar]
- 90. Plavsic MB, Pajic-Lijakovic I, Lazic N, Bugarski B, Putanov P (2013), Catalytic degradation processes and swelling of alginate bio-medical gels under influence of oxigen, Materials and Manufacturing Processes, 24:10–11, 1190–1196 [Google Scholar]
- 91. Giori NJ, Ryd L, Carter D (1995), Mechanical influences on tissue differentiation at bone-cement interfaces, The Journal of Arthroplasty, 10, 4:514–522 [DOI] [PubMed] [Google Scholar]
- 92. Gardner TN, Mishra S, Marks L (2004), The role of osteogenic index, octahedral shear stress and dilatational stress in the ossification of a fracture callus, Medical Engineering and Physics, 26, 493–501 [DOI] [PubMed] [Google Scholar]
- 93. Wehner T, Wolfram U, Henzler T, Niemeyer F, Claes L, Simon U (2010), Internal forces and moments in the femur of the rat during gait, Journal of Biomechanics, 43, 2473–2479 10.1016/j.jbiomech.2010.05.028 [DOI] [PubMed] [Google Scholar]
- 94.Jacobs CR (1994). Numerical simulation of bone adaptation to mechanical loading. Ph.D. Thesis, Stanford University.
- 95. Ament C, Hofer E (2000), A fuzzy logic model of fracture healing, Journal of Biomechanics, 33, 961–968. [DOI] [PubMed] [Google Scholar]
- 96.Lacroix D (2001) Simulation of tissue differentiation during fracture healing. Ph.D. Thesis.
- 97. Albro MB, Chahine NO, Caligaris M, Wei VI, Likhitpanuchkul M, Ng KW, et al. (2010), Osmotic loading of spherical gels: a biomimetic study of hindered transport in the cell protoplasm, Journal of Biomechanical Engineering, 129, 503–510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Lee KY, Mooney DJ (2001) Hydrogels for tissue engineering, Chemical Reviews, 101, 7:1869–1879 [DOI] [PubMed] [Google Scholar]
- 99. Ahearne M, Yang Y, Liu K (2008), Mechanical characterization of hydrogels for tissue engineering applications, Topics in Tissue Engineering, 4, Chap.12 [Google Scholar]
- 100. Forster REJ, Thürmer F, Wallrapp C, Lloyd AW, Macfarlane W, Phillips GJ, et al. (2010), Characterisation of physic-mechanical properties and degradation potential of calcium alginate beads for use in embolization, Journal of Materials Science, 21, 2243–2251 10.1007/s10856-010-4080-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Khetan S, Guvendiren M, Legant WR, Cohen DM, Chen CS, Burdick JA (2013), Degradation-mediated cellular traction directs stem cell fate in covalently crosslinked three-dimensional hydrogels, Nature Materials, 12, 458–465 10.1038/nmat3586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. O’Neil KR, Stutz CM, Mignemi NA, Burns MC, Murry MR Nyman JS, et al. (2012), Micro-computed tomography assessment of the progression of fracture healing in mice, Bone, 50, 1357–1367 10.1016/j.bone.2012.03.008 [DOI] [PubMed] [Google Scholar]
- 103. Nyman JS, Munoz S, Jadhav S, Mansour A, Yoshii T, Mundy GR, et al. (2009), Quantitative measures of femoral fracture repair in rats derived by micro-computed tomography, Journal of Biomechanics, 42, 891–897 10.1016/j.jbiomech.2009.01.016 [DOI] [PubMed] [Google Scholar]
- 104. Rumi MN, Deol GS, Singapuri KP, Pellegrini VD (2005), The origin of osteoprogenitor cells responsible for heterotopic ossification following hip surgery: an animal model in the rabbit, Journal of Orthopaedic Research, 23, 34–40 [DOI] [PubMed] [Google Scholar]
- 105. Moore SR, Saidel GM, Knothe U, Knothe Tate ML (2014) Mechanistic, mathematical model to predict the dynamics of tissue genesis in bone defects via mechanical feedback and mediation of biochemical factors, Plos Computational Biology, 10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106. Cheung G, Zalzal P, Bhandari M, Spelt JK, Papini M (2004), Finite elemente analysis of a femoral retrograde intramedullary nail subjected to gait loading. Medical Engineering and Physic, 25:93–108 [DOI] [PubMed] [Google Scholar]
- 107. Wraighte PJ, Scammell BE (2006), Principles of fracture healing, Surgery (Oxford), 24, 198–207 [Google Scholar]
- 108. Kolambkar YM, Dupont KM, Boerckel JD, Huebsch N, Mooney DJ, Hutmacher DW, et al. (2011), An alginate-based hybrid system for growth factor delivery in the functional repair of large bone defects, Biomaterials, 32(1):65–74 10.1016/j.biomaterials.2010.08.074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Badugu A, Kraemer C, Germann P, Menshykau D, Iber D (2012) Digit patterning during limb development as a result of the BMP-receptor interaction, Scientific Reports, 2, 991 10.1038/srep00991 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
Data Availability Statement
All the data are contained within the paper.