Experimental comparison of parametric versus nonparametric analyses of data from the cold pressor test

Abstract

Parametric statistical methods are common in human pain research. They require normally distributed data, but this assumption is rarely tested. The current study analyzes the appropriateness of parametric testing for outcomes from the cold pressor test (CPT), a common human experimental-pain test. We systematically reviewed published CPT studies to quantify how often researchers test for normality and how often they use parametric vs. non-parametric tests. We then measured the normality of CPT data from 7 independent small-to-medium cohorts and one study of >10,000 subjects. We then examined the ability of two common mathematical transformations to normalize our skewed data-sets. Lastly, we performed Monte Carlo simulations on a representative dataset to compare the statistical power of the parametric t-test vs. the nonparametric Wilcoxon Mann Whitney (WMW) test. We found that only 39% of published CPT studies (47/122) mentioned checking data distribution, yet 72% (88/122) used parametric statistics. Furthermore, among our 8 data sets, CPT outcomes were virtually always non-normally distributed and mathematical transformations were largely ineffective in normalizing them. The simulations demonstrated that the non-parametric WMW test had greater statistical power than the parametric t-test for all scenarios tested– for small effect sizes, the WMW had up to 300% more power.

Introduction

Pain research is challenging because of the subjective nature of sensation, but during the last two decades pain research in humans has advanced dramatically due in part to the development and validation of multiple outcome measures.^6,31 However, the statistical methods used to determine if differences in outcomes between two study groups are or are not significant have not been subject to rigorous evaluation. Even in well-designed and conducted studies, using the wrong statistical test to analyze outcomes can have major implications for the study’s power. Erroneous conclusions can derail the progress of a promising new pain treatment, or slow the pace of understanding pain mechanisms.

This study evaluates the prevalence and appropriateness of parametric vs. nonparametric statistical analyses in evaluating measured differences in the perception and severity of pain sensations between two groups of subjects. A fundamental principle of statistics is that parametric analyses such as the t-test and analysis of variance (ANOVA) are only accurate if the data being analyzed comes from a population in whom the outcome variable is normally distributed.²⁴ Hence, researchers are supposed to check that their data are normally distributed before applying parametric analyses.

Contrary to the impressions of statistical pioneers such as Gauss and Galton,¹⁴ the normality of real-world distributions cannot be taken for granted. The largest study of psychometric and education measures found that none of the 440 data sets studied were normally distributed and only 3% remotely resembled a normal curve (i.e., symmetric with light tails).¹⁴ Studies from medical fields have generated similar conclusions. Perhaps closest to pain research is Colliver et al. study of in 68 cohorts comprising 1,326 patients undergoing general anesthesia where neither blood pH nor H⁺ measurements were normally distributed.⁵ However, distribution of the outcome data is often not mentioned in published manuscripts.²² Insofar as we know, only two previous pain related studies have compared the use of parametric vs. nonparametric analysis.^33,27 Here we focus on the cold pressor test (CPT), a widely used human-pain experimental paradigm.^12,15,34 In the CPT, subjects are asked to immerse one hand in a cold water bath and to keep it submerged for as long as possible up to a safety limit (normally 1–5 minutes). Three outcomes are commonly measured: Subjects indicate the time when the cold becomes painful (“cold pain threshold”), and when it becomes so painful that they must withdraw their hands from the water (“cold pain tolerance”). Subjects also rate their maximal pain intensity during immersion on a numerical pain scale at the end of the procedure (“cold pain intensity”).¹⁵ Although developed for other purposes, the CPT is commonly used in experimental pain research because it is simple to administer, reliable, inexpensive, and induces strong pain sensations.

In the current paper, we examined the consequences of applying parametric and non-parametric analyses to these three measures in several ways. First we conducted a systematic critical review of published CPT studies to define how often data normality was examined, the use of transformations and whether parametric or non-parametric analyses had been used. Then we examined the normality of multiple sets of our own CPT data to assess how often real CPT data in normally distributed and we applied corrective mathematical transformations to evaluate the success of this procedure to normalize the data. Lastly, we performed a Monte Carlo simulation study¹³, based on the CPT datasets to compare the power of the parametric t-test against the non-parametric Wilcoxon Mann Whitney test (WMW).

Materials and Methods

Characterizing the statistical approaches used in published CPT studies

We searched the MEDLINE database on March 1^st 2014 using the terms: ‘cold pressor test’ AND ‘tolerance’ AND ‘pain’. This identified 193 articles, of which we were able to obtain the full text from 141. Among them, 8 were excluded because cold-pain outcomes were not the dependent variable, 9 because cold-pain tolerance was not assessed using time to hand withdrawal, and 2 were reviews. Ultimately, 122 articles were analyzed.

Supplemental Table 1 in the Appendix summarizes the parameters we collected from each study: (1) PMID number (2) country of origin, (3) year of publication, (4) statistical approach (parametric versus non-parametric), (5) mention of the normality of the distribution (any mention, regardless of outcome), (6) use of mathematical transformations. Additional data collected but not shown in Table S1 included journal name, first author, number of subjects, group allocation (balanced or not), study design (between/within subject analysis), P-value, effect size (calculated, when possible), and approach for handling non-normal distribution (if applicable and available). When assessing study design (between/within subject analysis), studies were categorized as a ‘between-subject” analysis if cold pain tolerance was compared between groups at least once. We defined “balanced groups” as samples that differed in size (n value) by no more than 30%. In case inexact significant P-values (i.e. P < 0.05, P < 0.01, P < 0.001) were reported (n=37), or when non-significant P-values were not reported (i.e. ‘none significant’ was reported but with no P-value; n=20) P-values were coded as missing data.. Forty four studies reported their mean values and standard deviations or standard errors and these used to calculate the effect sizes. In studies making multiple comparisons, the largest effect size was recorded.

Analysis of outcome data from different independent CPT studies

CPT data were analyzed from 648 healthy volunteers who served as subjects in 7 independent pain research studies performed in the Human Experimental Pain Research Laboratory at the University of Haifa, Israel. All studies were conducted in the same laboratory, using the same methods and apparatus, and all subjects provided written informed consent to a research protocol that had been approved by the university ethical committee. All subjects were student volunteers recruited through advertisements posted at local universities. Across all studies, subjects were eligible for enrollment if they were healthy and free from chronic pain, did not use medications other than oral contraceptives, and could understand the study’s purpose and instructions. Exclusion criteria were any type of medical or painful condition, pregnancy, use of medications, or history of drug abuse.

Haifa studies #1 (n=40, Pud 2010, unpublished data) and #6 (n=109¹⁸) had assessed the role of hand dominance in pain sensitivity; study #2 (n=48, Pud 2009, unpublished data) had studied the association between experimental pain outcomes and sleep-related measures; study #3 (n=62, unpublished data) had assessed the effects of virtual reality on experimental pain outcomes; study #4 (n=91¹⁷) had assessed the associations between experimental pain outcomes and personality dimensions; study #5 (n=105²⁸) had assessed the effects of apomorphine on pain sensitivity; and study #7 (n=193²⁹) had assessed the association between experimental pain and candidate genes. In cases where the study had assessed the effect of an intervention (studies #3 and #5), the baseline measures (before intervention) were analyzed.

The Heto CBN 8–30 Lab cold pressor apparatus (Allerod, Denmark) was used for all Haifa studies. This temperature-controlled water bath is continuously stirred by a pump. Subjects placed their right hands with fingers spread into the water bath, whose temperature was maintained at 1°C. A stopwatch measured the thresholds of cold pain and cold pain tolerance. A 180 s cut-off time was used for safety, and the pain tolerance for subjects who did not withdraw their hands for the entire 180 s was recorded as 180 s. immediately after hand withdrawal, subjects verbally rated their maximal pain intensity using a 0–100 numerical pain score (NPS).

To evaluate very large datasets, we also analyzed CPT data collected at Tromsø University, Norway. Data were available from 10,486 individuals, 51.5 % women, age 30–87 years. Participants had been recruited from the general population of the Tromsø municipality in northern Norway (for details see¹¹). All subjects had provided written informed consent to a protocol approved by the regional ethical committee. The response rate was 65.7%. Participants had been excluded from CPT if they reported previous health problems in connection with cold-exposure (e.g. cold-allergy, Reynaud’s phenomenon) or if they were unable understand instructions. No other exclusion criteria were applied.

The Tromsø apparatus consisted of a refrigerated water bath FP40HE (Julabo Lobortechnik GmbH, Germany) connected to an external 13L Plexiglas container. Water had been circulated at 13L/min to maintain water temperature at 3 °C as measured in the external container. Participants had placed their dominant hand and wrist in the water and maintained it there as long as possible, up to a maximum of 106 s. Numeric pain ratings (0–10) had been obtained at 4 seconds and every 9 seconds thereafter until hand withdrawal; the cold-pain tolerance time had been recorded by a stopwatch.

Although visual inspection of the data histograms clearly demonstrated non-normal distributions, statistical assessment of normality was additionally performed for descriptive reasons using the SPSS for Windows version 19 statistical package (SPSS, Inc., Chicago, IL). The Shapiro-Wilk test (SW) and Kolmogorov-Smirnov tests (KS) were used to assess the normality of raw and the transformed data. Data was judged to be normally distributed if p>0.05 on either the SW or KS tests.

Monte Carlo simulations for comparing statistical power of the Wilcoxon Mann Whitney test (WMW) and the t-test in assessing CPT outcomes

We performed Monte Carlo simulations using all three CPT outcomes (intensity, tolerance, and threshold) obtained from all cohorts. Simulation results based on the baseline measures of dataset number 5 are described in detail. To demonstrate that these results are not cohort specific, examples of simulation results from the Tromsø (n=10,486), smallest Haifa (cohort #1, n=40), and the largest (cohort #7, n=193) cohorts are described.

A program was written for R (64 bit version 3.02 (2013-09-25). The CPT dataset was sampled with replacement. The independent-samples t-test and the WMW test were conducted assuming homoscedasticity. The number of repetitions per experiment was 1,000,000. Nominal α was set at 0.05, 0.01, and 0.001. For each CPT outcome, 16 simulations with different n scenarios were conducted as follows: (n₁, n₂) = (20,20), (15,25), (25,15), (30,30), (15,45), (45,15), (45,45), (60,30), (30,60), (60,60), (45,90), (90,45), (120,120), (150,90), (90,150), and (240,240). n₁ and n₂ values were randomly sampled with replacement from the data set. To model a “difference in location” parameter, a specific effect size (i.e., fraction or multiple of the data set’s standard deviation) was added to n₂ for each iteration of an experiment. The added effect sizes to model a treatment in shift in location parameters were d = 0.2σ, 0.5σ, and 0.8 σ, which Cohen defined as small, medium and large, respectively⁴; and 1.2σ and 2.0σ, defined by Sawilowsky as very large and huge, respectively, where σ defined as the population standard deviation of data set #5²³. One- and two-tailed Type I error rates of the WMW and the t-test are presented below:

One Tailed Test

The t-test’s Type I errors for data sampled from the intensity and tolerance datasets were within sampling error of nominal α. However, the t-test’s Type I errors for data sampled from the threshold dataset for nominal α = 0.05 was .0470, for α = 0.01 was .0075, and for α = 0.001 was .0005. Although these results met Bradley’s (1978)² liberal definition of robustness at 0.5α ≤ Type I error ≤ 1.5α, they did not meet Bradley’s conservative definition of robustness at 0.9α ≤ Type I error ≤ 1.1α. The WMW test, being nonparametric, produced correct Type I errors within sampling errors.

Two Tailed Test

Type I errors for data sampled from the intensity and tolerance datasets for the non-directional layout also yielded results within the sampling error of nominal α. The t-tests results for the threshold data, however, were non-robust. With nominal α = 0.05, the expected Type I error rates are 0.025 at each tail, but the obtained rejection rates were conservative at 0.0208 and 0.0230, respectively. Similarly, the lower tail rejection rates for nominal α = 0.01 (0.005 expected) and .001 (0.0005 expected) were .0069 and .0002, respectively.

Results

Assessment of statistical approach used in published CPT studies

The 122 articles analyzed (see Table S1 in the appendix) were published between 1977 and 2013. The mean number of subjects per study was 71.9 ± 80 (range = 4 – 613, with plus articles with n > 10,000 excluded to avoid enlarging the mean). The mean reported P-value was 0.0516 ± 0.12 (range P=0.001 to P=0.61). 17.2% (21) of studies reported non-significant differences. We were able to calculate effect sizes for 44 studies and among them the mean effect size was 0.69 ± 0.54 (range 0.04 to 2.89). In 72% effect sizes were less than 0.8, meaning small or moderate.

Overall, 72.1% of the studies (88/122) used parametric analyses and 27.9% (34/122) used non-parametric analyses. 71.3% (87) used between-subjects comparisons and among them, 74.7% (65) used parametric analyses and 25.3% used non-parametric analyses. Group sizes were balanced in 77.9 % of studies and unbalanced in 22.1%. In 61.5% of the studies (75) no information about normality of the data distribution was provided. Among the 38.5% of studies that mentioned testing for normality, 82.1% found that cold-pain tolerance was non-normally distributed; among them 44.2% used logarithmic (34.1%) or other (10.1%) transformations to try and improve the normality of their datasets, and 37.9% used non-parametric analyses.

One cannot conclude that a given study used the appropriate parametric/non-parametric analysis without inspection of its raw data distribution. However, we can conclude that 37% (45/122) of the reviewed study’s conclusions might be at risk since in these studies: (1) data normality was not tested; (2) between subject design was used and (3) parametric analysis was applied.

Outcome data from different independent CPT studies

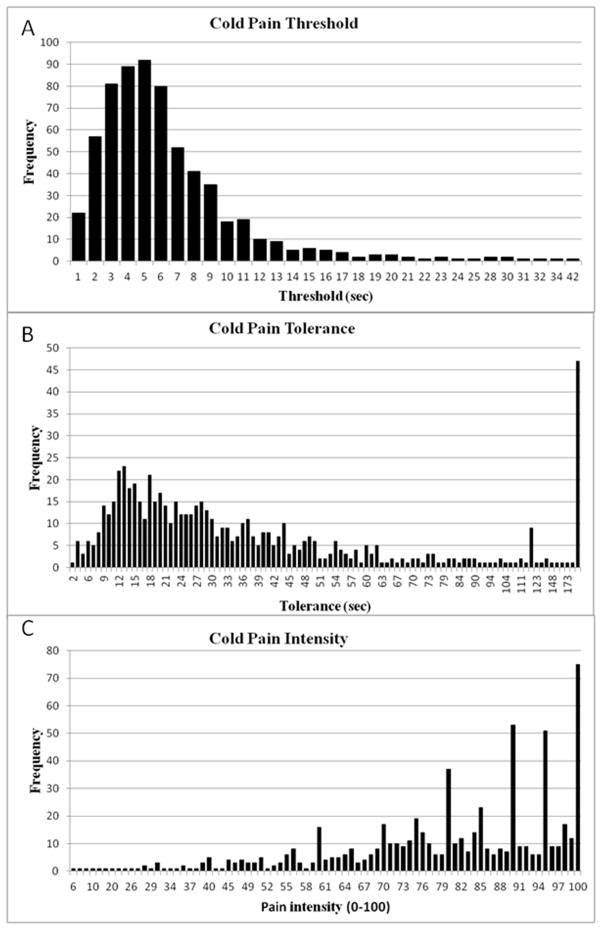
Table 1 summarizes the analyses of the 7 Haifa cohorts plus all the Haifa cohorts combined (n = 648). 95.8% (23/24) of the CPT outcomes were non-normal with only cold-pain threshold in the smallest cohort (#1) being normally distributed based on the Shapiro-Wilk test but not on the Kolmogorov-Smirnov test. Figure 1 depicts the distributions of the three CPT outcome measures in the combined Haifa cohort to visually demonstrate that all three CPT outcomes deviate significantly from the normal ‘bell-shaped’ curve.

Table 1.

Statistics of threshold, tolerance, and pain intensity in the 7 Haifa cohorts separately and combined

Cohort number		#1	#2	#3	#4	#5	#6	#7	All combined
n		40	48	62	91	105	109	193	648
% Female		55%	0%	50%	47%	39%	52%	55%	46.30%
Age mean±STD (range)		25.8±4 (20–39)	25.9±4.7 (18–45)	24.2±3.7 (18–35)	Currently Missing	26.1±3.6 (18–36)	24.6±2.5 (20–32)	24.6±3.7 (18–47)	25±3.7 (18–47)
Threshold	Mean	4.8	5.2	5	7	7.1	7.8	6.3	6.45
	Mode	5	2	3	8	4	5	5	5
	Median	4.5	4.5	4	6	6	6	5	5
	Range	1–11	1–13	1–19	1–24	1–32	1–42	1–31	1–42
	Skewness, Kurtosis	0.56, −.31	2.32, 7.58	2.07, 7.88	1.53, 3.14	2.06, 6.19	2.54, 8.28	3.03, 12.53	2.71, 10.9
	SW test (P-value)	P=0.065	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
	KS test (P-value)	P=0.034,	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
Tolerance	Mean	55.3	45.1	33.8	52.1	61.4	32.5	39	44.3
	Mode	180	25	12	120	180	13	18	180
	Median	28.5	26	20.5	37	42	18	29	28
	Range	4–180	8–180	6–180	6–180	6–180	2–180	4–180	2–180
	Skewness, Kurtosis	1.46, 0.57	2.1, 3.3	2.98, 8.36	1.38, 1.35	1.26, 0.26	2.83, 7.36	2.73, 7.53	2.02, 3.17
	SW test (P-value)	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
	KS test (P-value)	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
Pain intensity	Mean	79.2	90.8	83.4	72.5	88.8	78	74.5	79.5
	Mode	100	100	90	56	100	100	95	100
	Median	85	95	85	72	95	77	81	83
	Range	6–100	40–100	40–100	20–100	28–100	26–100	6–100	6–100
	Skewness, Kurtosis	−1.31, 1.07	−2.33, 7.37	−0.84, 0.46	−0.44, 0.191	−2.14, 5.04	−0.69, 0.45	−1.3, 1.39	−1.23, 1.58
	SW test (P-value)	P<0.001	P<0.001	P=0.001	P=0.001	P<0.001	P<0.001	P<0.001	P<0.001
	KS test (P-value)	P<0.001	P<0.001	P=0.001	P=0.001	P<0.001	P<0.001	P<0.001	P<0.001

SW- Shapiro-Wilk test; KS- Kolmogorov-Smirnov test (KS). Bold p-value represents normal distribution.

Figure 1.

Distribution of (A) cold-pain threshold, (B) cold-pain tolerance and (C) cold-pain intensity in the combined Haifa cohort (n=648).

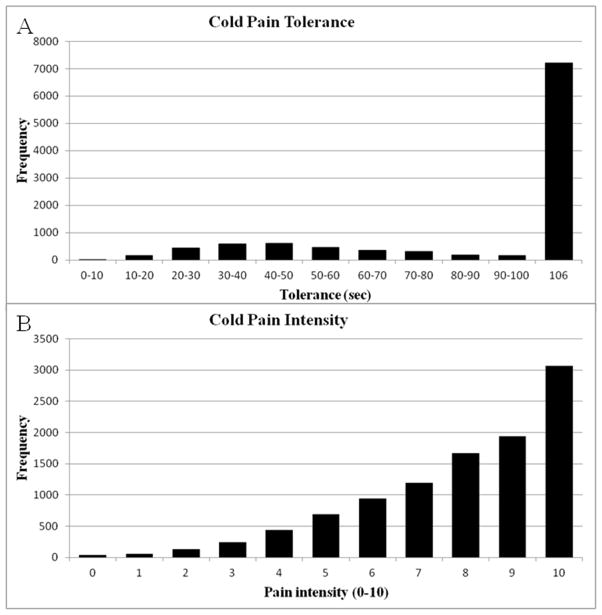
Analysis of the very large Tromsø study yielded the same conclusion. Table 2 shows that none of its CPT outcomes were normally distributed. Figure 2 depicts the distribution of cold pain tolerance and cold pain intensity. Among its 10,486 subjects, 7,157 (68.3%) endured the entire 106 s immersion. The resulting frequency distribution is therefore severely right censored, as expected with an upper time limit cutoff. However, it is highly unlikely that extending this limit would significantly normalize the dataset, since pain ratings do not increase noticeably after the first 60s, and for some participants they actually decrease (data not shown).

Table 2.

Statistics of cold pain tolerance and pain intensity in the large population-based study cohort from Tromsø.

The Tromsø cohort
n		10,486
% Female		0.515
Age range		30–87
Tolerance	Mean	88.17
	Mode	106
	Median	106
	Range	5.4–106
	Skewness, Kurtosis	−1.26, −0.39
	SW test (P-value)	P<0.001
	KS test (P-value)	P<0.001
Pain Intensity	Mean	7.84
	Mode	10
	Median	8
	Range	0–10
	Skewness, Kurtosis	−1.01, 0.49
	SW test (P-value)	P<0.001
	KS test (P-value)	P<0.001

Figure 2.

Distribution of (A) cold-pain tolerance and (B) cold-pain intensity in the Tromsø Study cohort.

Efficacy of mathematical transformations for improving normality of CPT data

Table 3 summarizes the results of our analysis of the usefulness of the two most common transformations used in attempt to normalize skewed datasets (logarithmic (Log) and square root (SqR) transformations)³⁰ such as the skewed CPT data from the Haifa datasets depicted in Figure 1. For cold pain threshold, Log transformation normalized 50% (4/8) of the datasets as assessed by the Shapiro-Wilk test but only 12.5% (1/8) of the datasets as assessed by the Kolmogorov-Smirnov test. The SqR transformation only normalized one (12.5%) dataset (#1) as measured by both Shapiro-Wilk and Kolmogorov-Smirnov tests. For cold-pain tolerance, Log transformation normalized 25% (2/8) of the Haifa datasets as analyzed by the Shapiro-Wilk test, and 62.5% (5/8) of datasets by the Kolmogorov-Smirnov test. The SqR transformation was unable to normalize any of the cold-pain tolerance datasets. For pain intensity, both the Log and the SqR transformations were able to normalize data from one data set (based only on the Kolmogorov-Smirnov test). Similarly, following Log and SQR transformations the Tromsø Study data remained non-normally distributed (Table 4). Overall, for both cold-threshold and the cold-tolerance data, the Tromsø data could be normalized 22% (7/32) of the time. Only 6% (2/32) of the attempts to normalize cold-pain intensity data were successful.

Table 3.

Results of the Shapiro-Wilk and Kolmogorov-Smirnov test performed on the transformed variables from the Haifa studies.

Cohort	#1 (n=40)	#2 (n=48)	#3 (n=62)	#4 (n=91)	#5 (n=105)	#6 (n=109)	#7 (n=193)	All combined (n=648)
LOG Threshold
Skewness, Kurtosis	−0.71, −0.01	−0.12, −0.01	−0.38, 0.818	−0.35, 0.20	−0.23, 0.11	0.15, 0.19	0.07, 1.44	−0.8, 0.486
SW test (P-value)	P=0.013	P=0.292	P=0.029	P=0.100	P=0.110	P=0.122	P<0.001	P<0.001
KS test (P-value)	P=0.028	P=0.200	P=0.004	P=0.038	P=0.020	P=0.010	P<0.001	P<0.001
SqR Threshold
Skewness, Kurtosis	−0.37, −0.58	1.07, 1.95	0.75, 1.92	0.6, 0.56	0.84, 1.24	1.32, 2.36	1.52, 4.33	1.2, 2.73
SW test (P-value)	P=0.286	P=0.005	P=0.009	P=0.018	P=0.001	P<0.001	P<0.001	P<0.001
KS test (P-value)	P=0.200	P=0.015	P=0.003	P=0.046	P=0.007	P<0.001	P<0.001	P<0.001
LOG Tolerance
Skewness, Kurtosis	0.181, −0.566	0.749, 0.182	0.96, 1.07	0.07, −0.82	0.97, −0.84	0.57, 0.79	0.42, 0.67	0.347, −0.1
SW test (P-value)	P=0.066	P=0.006	P=0.001	P=0.102	P=0.003	P=0.001	P<0.001	P<0.001
KS test (P-value)	P=0.130	P=0.072	P=0.079	P=0.200	P=0.055	P=0.003	P=0.020	P<0.001
SqR Tolerance
Skewness, Kurtosis	1.03, −0.12	1.568, 1.71	2.14, 4.72	0.75, −0.26	0.78, −0.49	1.96, 3.8	1.70, 3.42	1.33, 1.18
SW test (P-value)	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
KS test (P-value)	P<0.001	P<0.001	P<0.001	P=0.004	P<0.001	P<0.001	P<0.001	P<0.001
LOG Intensity
Skewness, Kurtosis	−2.79, 10.05	−3.33, 14.75	−1.44, 2.96	−1.68, 6.10	−3.13, 11.27	−1.73, 4.95	−3.05, 11.52	−3.29, 16.24
SW test (P-value)	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001	P<0.001
KS test (P-value)	P<0.001	P<0.001	P<0.001	P=0.065	P<0.001	P<0.001	P<0.001	P<0.001
SqR Intensity
Skewness, Kurtosis	−1.85, 3.78	−2.79, 10.62	−1.11, 1.45	−0.92, 1.96	−2.59, 7.74	−1.13, 2.07	−1.96, 4.41	−1.93, 5.3
SW test (P-value)	P<0.001	P<0.001	P<0.001	P=0.001	P<0.001	P<0.001	P<0.001	P<0.001
KS test (P-value)	P<0.001	P<0.001	P<0.001	P=0.200	P<0.001	P=0.005	P<0.001	P<0.001

SW = Shapiro-Wilk test; KS = Kolmogorov-Smirnov test (KS).

Bolding of p-values indicates results originating from a normal distribution.

Table 4.

Results of the Shapiro-Wilk and Kolmogorov-Smirnov test performed on the transformed variables from the Tromsø study.

The Tromsø cohort
LOG Tolerance
Skewness, Kurtosis	−1.81, 2.697
SW test (P-value)	P<0.001
KS test (P-value)	P<0.001
SqR Tolerance
Skewness, Kurtosis	−1.45, 0.75
SW test (P-value)	P<0.001
KS test (P-value)	P<0.001
LOG Intensity
Skewness, Kurtosis	−2.16, 6.42
SW test (P-value)	P<0.001
KS test (P-value)	P<0.001
SqR Intensity
Skewness, Kurtosis	−1.89, 5.66
SW test (P-value)	P<0.001
KS test (P-value)	P<0.001

SW = Shapiro-Wilk test; KS = Kolmogorov-Smirnov test (KS).

Monte Carlo simulations for comparing power of the Wilcoxon Mann Whitney (WMW) and the t-test

Examples of the results of Monte Carlo simulations from the #5 Haifa cohort are presented in Table 5. The left side of the table reports the power of the t-test, for 5 different effect sizes (0.2, 0.5, 0.8, 1.2, & 2.0) assuming a treatment modeled as a shift in location parameter, with nominal α set at three different levels (0.05, 0.01, and 0.001). The right side of the table reports the power of WMW test under the same study conditions. For the entire spectrum of effect sizes, the WMW was found to be much more powerful than the t-test. The results in this table simulate balanced layouts of n=60 (30 participants in each group). Similar results, demonstrating the superiority of the WMW test for all other study conditions (48 tables per cohort) are not shown but can be requested from S. Sawilowsky.

Table 5.

5A: Comparative power of Independent Samples t test and Wilcoxon Mann Whitney (WMW) test, n1 = n2 = 30; 1,000,000 repetitions, for pain thershold data
α	t					WMW
	Effect Size (Cohen’s d)
	0.2	0.5	.8	1.2	2	0.2	0.5	.8	1.2	2
0.05	0.1518	0.6069	0.9378	0.9992	1	0.4105	0.826	0.9993	1	1
0.01	0.0531	0.3723	0.8195	0.9936	1	0.1863	0.5984	0.9928	1	1
0.001	0.0105	0.1563	0.5853	0.9584	1	0.045	0.2806	0.9419	0.9997	1

5B: Comparative power of Independent Samples t test and Wilcoxon Mann Whitney (WMW) test, n1 = n2 = 30; 1,000,000 repetitions, for pain tolerance data
α	t					WMW
	Effect Size (Cohen’s d)
	0.2	0.5	.8	1.2	2	0.2	0.5	.8	1.2	2
0.05	0.1196	0.4798	0.8598	0.9954	1	0.3195	0.8275	0.976	0.9974	1
0.01	0.0351	0.2474	0.6675	0.9729	1	0.1305	0.6184	0.9118	0.9854	0.9997
0.001	0.0056	0.0766	0.3721	0.8701	1	0.0276	0.3165	0.7237	0.9223	0.9961

5C: Comparative power of Independent Samples t test and Wilcoxon Mann Whitney (WMW) test, n1 = n2 = 30; 1,000,000 repetitions, for pain intensity data
A	t-test					WMW
	Effect Size (Cohen’s d)
	0.2	0.5	.8	1.2	2	0.2	0.5	.8	1.2	2
0.05	0.1286	0.5044	0.8577	0.9918	1	0.3946	0.8273	0.989	0.9994	1
0.01	0.0375	0.2791	0.6816	0.9621	1	0.1833	0.6232	0.9521	0.9952	1
0.001	0.0051	0.0983	0.4154	0.8576	0.9997	0.0476	0.3247	0.8151	0.9645	0.9999

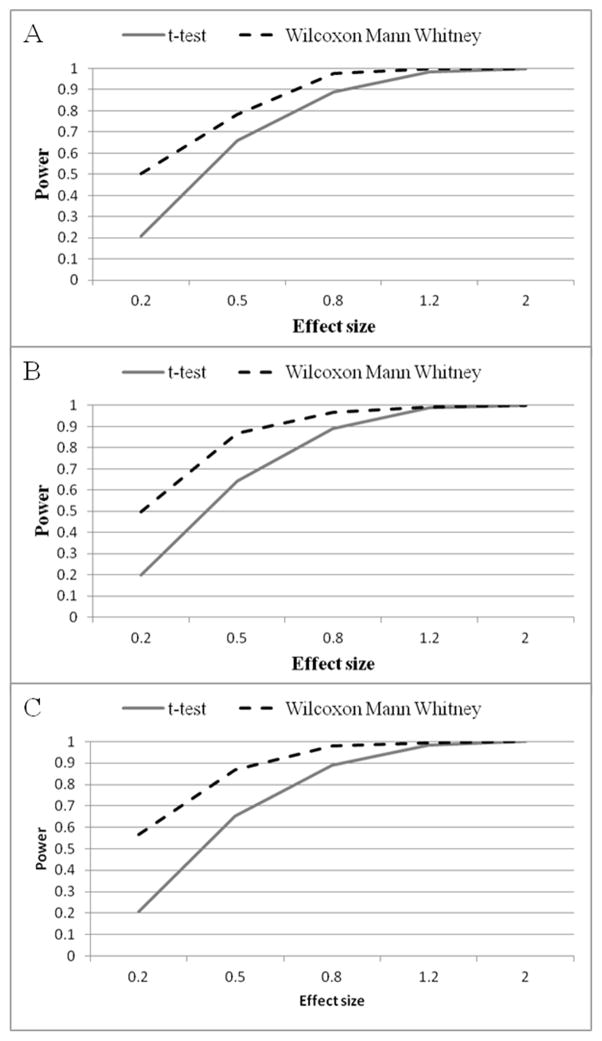
Figure 3 summarizes the results of simulation to compare the average power of the t-test and the WMW across all 16 sample sizes studied with α set at 0.05 and evaluating power over the full range of effect sizes. This revealed that for all three CPT measures and for small (0.2), medium (0.5) and large (0.8) effect sizes, the WMW was superior to the t-test. For example, for α = 0.05, using the pain threshold and an effect size of 0.2, the power of the WMW (0.50) averaged 2.5 times larger than the power of the t-test (0.21). For medium effect size, power of the WMW (0.78) was 18% higher than the power of the t-test (0.66), while for large effect size the power of the WMW (0.97) was 9% greater than for the t-test (0.89). The only situation in which the power of the t-test approached that of the WMW was for huge effect sizes (1.2 and 2).

Figure 3.

Average power of the Independent Samples t-test and the Wilcoxon Mann Whitney across all effect size scenarios (α level= 0.05). (A) For cold threshold scores (B) For cold tolerance scores; (C) For pain intensity scores.

Similarly, for pain tolerance outcomes, α=0.05, and simulation based on effect size of 0.2, the average power of the WMW (0.50) was 2.5 times larger than the t-test (0.20). For medium effects the WMW (0.87) had 36% more power than the t-test (0.64), and for large effects the WMW (0.97) had 9% greater than the t-test (0.89). The only situation in which the power of the t-test approached that of the WMW was for huge effect sizes (1.2 and 2).

For pain intensity outcomes and effect size of 0.2, average power of the WMW (0.57) was almost three times larger than for the t-test (0.21). For medium effects, the power of the WMW (0.87) was 34% higher than the t-test power (0.65), and for large effect size the WMW (0.98) was 10% more powerful than for the t-test (0.89). The WMW and t-test had similar power only for huge effect sizes (1.2 and 2), because above an effect size of 1.2 they both reach a maximum plateau at power of 1. For α = 0.01 and 0.001, the superior power of the WMW was even greater as sample sizes increased.

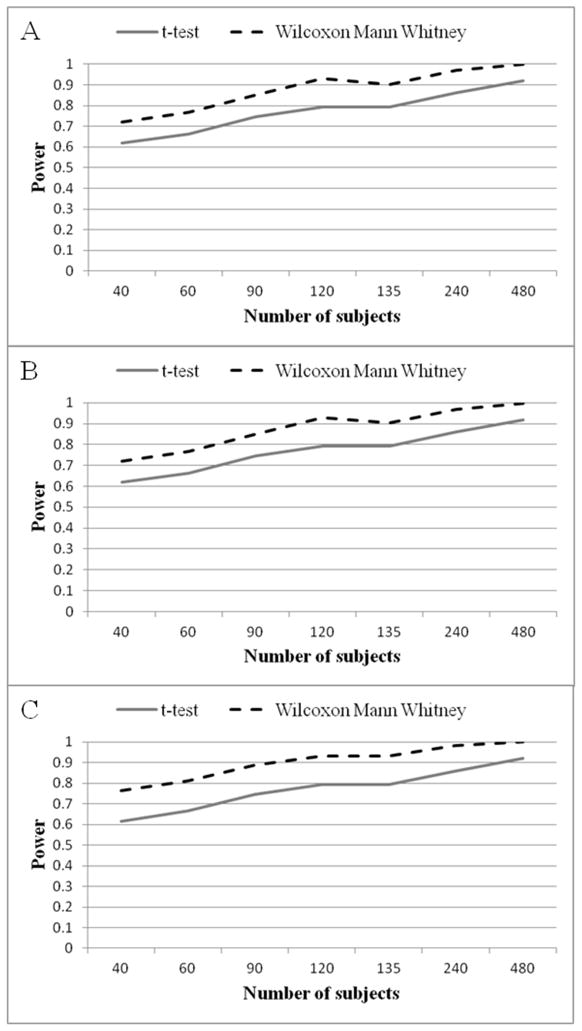
To assess the possible role of sample size on the power of WMW and the t-test, the average power across all effect sizes was calculated and plotted (Figures 4) with sample size on the horizontal axis (α level= 0.05). This demonstrates that the WMW is more powerful than the t-test for all simulated sample sizes.

Figure 4.

Average power of the Independent Samples t-test and the Wilcoxon Mann Whitney across all number of subjects scenarios (α level= 0.05). (A) Cold threshold scores (B) Cold tolerance scores; (C) Pain intensity scores.

We also examined the role of group allocation, by comparing simulation results of the balanced vs. unbalanced group allocations of the WMW and the t-test (Figure S1). For small effect sizes, unbalanced allocation result in a 0.1–0.2 power loss in both tests.

Additional simulation studies, based on all other cohorts revealed similar or even higher power advantage. For example, when simulation (n1=30, n2=30, alpha=0.05) used data from the Tromsø cohort (n=10,486), the WMW enjoyed an enormous power advantage of over five times the comparative statistical power than the t-test (t-test power=0.1914, WMW power=0.9961) for the tolerance dataset, and twice as powerful (t-test power=0.1944, WMW power=0.3892) for the pain intensity dataset.

When simulating (n₁=30, n₂=30, alpha=0.05) using data from Haifa smallest cohort (cohort #1, n=40), the WMW conveyed a huge power advantage for tolerance (t-test power=0.1913, WMW power=0.8338) and intensity data (t-test power=0.1915, WMW power=0.3532). However, there was only a slight benefit for data sampled from the threshold dataset (t-test power=0.1922, WMW power=0.1960), Similarly, when simulating (n1=30, n2=30, alpha=0.05) using the biggest Haifa cohort (#7, n=193), analysis of the tolerance (t-test power=0.2059, WMW power=0.6613) and intensity data (t-test power=0.1928, WMW power=0.3375) data demonstrated large power advantages, whereas negligible differences was found for threshold data (t-test power=0.2135, WMW power=0.2000).

Discussion

These results show that although the vast majority (72%) of published CPT studies used parametric statistics, only 39% even mentioned testing for normality, and among them, only 18% found cold-pain tolerance to be normally distributed. Pain researchers may not be fully aware of the implication of this and manuscript reviews may not sufficiently emphasize it. Secondly, our analysis of raw data from multiple independent small, medium, and very large CPT datasets reveals that CPT outcomes are only rarely normally distributed and most often mathematical transformations are ineffective in normalizing non-normal sets of CPT data. The results also suggest that when considering transformations of non-normal cold thresholds, Log transformation, followed by Shapiro-Wilk test for normality is preferable, whereas for cold tolerance data, Log transformation followed by Kolmogorov-Smirnov test is preferable. Other statistical tests may be better for other pain measures. For example, survival analysis may be preferable for tolerance data.²⁶

Thirdly, Monte Carlo simulations based on multiple CPT datasets established that the non-parametric WMW test is almost always more statistically powerful than the t-test, meaning that applying t-tests to non-normal CPT data sets might compromise study conclusions and lead to false negative conclusions. The power superiority of non-parametric methods for non-normal data sets is most relevant for between-group comparisons when the treatment is modeled as a shift in location (along the x axis) of the data curve. In contrast, within-group comparisons (i.e. cross-over, a.k.a. before vs. after design) are more powerful to begin with (given the reduction in error variance associated with individual differences), thus non-parametric approaches offer little power advantage under these conditions.³ Among the reviewed studies, the most relevant to our discussion are those with between-subject-design, but 75% of these used parametric analyses. Taken together, these results suggest that parametric analyses should not be the primary statistical method for analyzing CPT data as they currently are. As previously reported,, several common misconceptions may lead researchers to choose parametric approaches when non-parametric statistics are more appropriate.²² False statements are common, such as “Wilcoxon should only be used when the data is originally in the form of ranks”, or “in small samples studies”, or that “that is more powerful”.

The greater power of nonparametric tests for between-group studies means that using them can reduce the number of subjects needed for adequate power. For instance, our pain tolerance data show that when comparing treatment and control groups containing 30 subjects each, the power of the WMW test is 0.3195 for detecting a typical small (0.20) treatment effect, whereas analysis by t-test would require 120 subjects per group for comparable power (.3401). It is commonly stated that the WMW test should be used only for small samples, but Sawilowsky refuted this assumption.²² For instance, in analyzing cold-pain intensity, if α = 0.001, effect size = 0.2, and sample size = 240 per group, the one-tailed power for the WMW was .92 whereas power of the t-test was only 0.14. To achieve similar power for t-test analysis, group size would have to be 1,011. Thus, nonparametric statistics can save time, effort, risk to subjects, and cost.

Strengths of our study include the fact that we analyzed multiple independent datasets from different countries, covering the full range of sample sizes used for CPT pain research (n = 40 – 10,468). Importantly, although our 7 Haifa cohorts included only healthy young students, our findings can be generalized to the general population since the very large Tromsø study sampled unscreened healthy and unhealthy participant alike who are physically able to make it to the study site. 32% of the Tromsø cohort reported having chronic pain, a prevalence not elevated from that in the normal population in Norway¹ or the U.S.⁸

Our Monte Carlo simulations also spanned the full gamut of sub-sample sizes (40 – 480) as well as a wide range of group allocation scenarios. Group allocation is important because if poor results are found under balanced layout, this will be exacerbated for unbalanced layouts. Another strength is that we applied multiple methods (review of published studies, data re-analyses, and Monte Carlo simulation) all of which supported the conclusions that non-parametric statistics should be used to analyze CPT data.

A limitation is that we only analyzed CPT, one specific type of pain dataset. However, our results may have clinical implications because CPT is increasingly being used as a clinical tool due to the growing emphasis on mechanism-based pain diagnosis and the use of quantitative sensory testing. In addition, we propose that our conclusions likely apply to other types of human experimental pain research because many are designed with safety limits or artificial cut points that produce skewed distributions with one tail truncated. Measuring pain intensity using strong nociceptive stimuli also generates a skewed distribution with mostly high values and a truncated right tail and weak stimuli similarly produce truncated left tails. Only stimuli that elicit midrange responses avoid this. Findings from other scientific fields conclusively demonstrate the superiority of non-parametric approaches when the normality assumption is violated for treatments inducing shifts in location along the x axis of the dependent variable.^{16, 19, 20, 25}

These results are relevant for clinical trials of new pain treatments which often compare outcomes between two groups (treatment vs. control), that are likely to be non normally distributed. Most trials of pain therapies only include patients with pain intensities ≥4/10,³¹ increasing the probability of non-normal distribution. Moreover, changes in pain intensity are commonly used as outcomes. Based on the fact that only some patients respond,^7,8,32 skewed distributions can be expected. From our experience, patient reported outcome (PRO) data collected from studies of medical conditions is only rarely completely normal. Although they are often analyzed with parametric statistics, they can equally well be analyzed using non-parametric statistics which require fewer assumptions about the structure of the data and are equally efficient in most real data circumstance. “Since at the design stage of a clinical study we cannot be certain of the distribution of the outcome data, it seems prudent to assume non normality and design the analyses accordingly.

Another limitation is that we only compared the WMW and t-test, thus we cannot generalize to all parametric vs. non-parametric analyses. We know of only two prior pain-related studies, one comparing the power of WMW vs. analysis of covariance (ANCOVA) in a simulation based on headache and shoulder-pain trials.³³ Post-treatment scores were compared between groups using baseline score as covariant for ANCOVA. This demonstrated that ANCOVA is better for moderate but not for extremely non-normal distributions, but as Sawilowky noted, there are no good nonparametric equivalents to ANCOVA.²⁴ Torrence et al.²⁷ compared the power of ANOVA, t-tests, Kruskall–Wallis, Mann–Whitney U-tests, and evaluated bootstrapping and Log transformation for analyzing skewed results of SF-36 questionnaire (the Medical Outcomes Study 36 Item Short-Form), a very common secondary outcome measure in pain trials.² They concluded that the statistical tests were equivalent, but they only studied a very large cohort (n~3,000) with very high power, thus their conclusions cannot be applied to studies of hundreds or tens of subjects, or when small effect sizes are anticipated.

Another limitation deserves notice: Given the large number of subjects pooled in the current study, assessing relations between demographic characteristics and pain measures distribution is possible, but it is beyond the scope of the current paper.

Current approaches to evaluating normality of datasets include the classical Lilliefor’s test, (an adjustment to the Kolmogorov-Smirnov test), the Shapiro-Wilk’s test, the Anderson-Darling test, and the D’Agostino-Pearson test. An alternative is visual inspection of plotting, such as a Q-Q plot. However both approaches constitute multiple comparisons and thus increase the probability of Type I error and require corrections such as Bonferroni’s.²¹ Therefore, if the data are not known to be normally distributed, or suspected to be non-normally distributed, then the parametric test should be avoided.

Our results suggest that the current automatic application of parametric analyses to CPT studies should change, and require demonstrating the normality of outcome data. For the vast majority of CPT studies with non-normal data, the nonparametric Wilcoxon Mann Whitney test is much more powerful than the parametric t-test. Although statistical textbooks recommend nonparametric analyses for non-normally distributed data, and we have demonstrated that normal distributions are rare in CPT data as in biomedical research in general,^{10, 14, 22} parametric analysis is still routinely used CPT studies.

Supplementary Material

1

Table S1: Retrospective assessment of statistical approach used in published studies

2. Figure S1.

Comparison of power in balanced vs. unbalanced group allocation. Average power of the Independent Samples t-test and the Wilcoxon Mann Whitney across all effect size scenarios (α level= 0.05). (A) For cold threshold scores (A1 t-test, A2 Wilcoxon Mann Whitney); (B) For cold tolerance scores (B1 t-test, B2 Wilcoxon Mann Whitney); (C) For pain intensity scores (C1 t-test, C2 Wilcoxon Mann Whitney).

Perspective.

These results demonstrate that parametric analyses of CPT data are routine but incorrect, and that they likely increase chances of failing-to-detect significant between-group differences. They suggest that non-parametric analyses become standard for CPT studies, and that assumptions of normality be routinely tested for other types of pain outcomes as well.

Highlights.

• The appropriateness of using parametric analysis on cold pressor data was studied

• In most previously published studies data distribution was not mentioned

• However, vast majority of these studies used parametric analyses

• CPT measures collected at 8 independent studies were not normally distributed

• Monte Carlo simulations reveal that non-parametric approach is more appropriate