Nonaddtive Effects of Mixed Crowding on Protein Stability

Abstract

The crowded environments inside cells can have significant effects on the folding stability and other biophysical properties of proteins. In this study on how macromolecular crowding affects protein folding, we took a significant step toward realistically mimicking intracellular environments by using a mixture of two crowding agents, Ficoll and dextran. We found that the mixed crowding exerts a greater stabilizing effect than the sum of the two individual crowding agents. Therefore, the composition of crowders, not just the total concentration, has a significant influence on the effects of crowding on protein folding. Since the composition of intracellular macromolecules varies within the lifetime of a cell, our finding may provide an explanation for age being an important risk factor for protein aggregation-related diseases such as Alzheimer’s disease and Parkinson’s disease.

INTRODUCTION

The total protein and RNA concentrations inside cells reach 300–400 g/l.¹ Together macromolecules are estimated to occupy over 30% of cellular volume. Intracellular macromolecular crowding can now be visualized by cryoelectron tomography.² Such in vivo environments are obviously very different from the dilute solutions encountered in most biophysical studies of proteins and nucleic acids. The differences in solvent conditions can have significant effects on the thermodynamics and kinetics of protein folding, binding, aggregation, and other more complex biological events.³ Past in vitro studies of macromolecular crowding on protein folding stability have focused on single species of crowding agents.^4–7 Here we report a study using a mixture of two crowding agents and show that the mixed crowding exerts a greater stabilizing effect than the sum of the two individual crowding agents. The nonadditive effect of mixed crowding has profound implications for macromolecular crowding inside cells.

MATERIALS AND METHODS

Materials

The particular FKBP used in the present was a single mutant, with residue Arg42, which form a salt bridge with Asp37, substituted by Ala (Figure 1). The mutant has an unfolding free energy in the absence of crowding agents that is 0.7 kcal/mol lower than the counterpart of the wild-type protein.⁵ The lower unfolding free energy corresponds to a lower midpoint urea concentration (from 3.1 M to 2.7 M). Upon adding crowding agents, the midpoint urea concentration increases but still falls in a range convenient for experimental measurements. The introduction of the Arg42 to Ala mutation and the expression and purification of the protein were carried out just like in our previous study.⁵

Fig. 1.

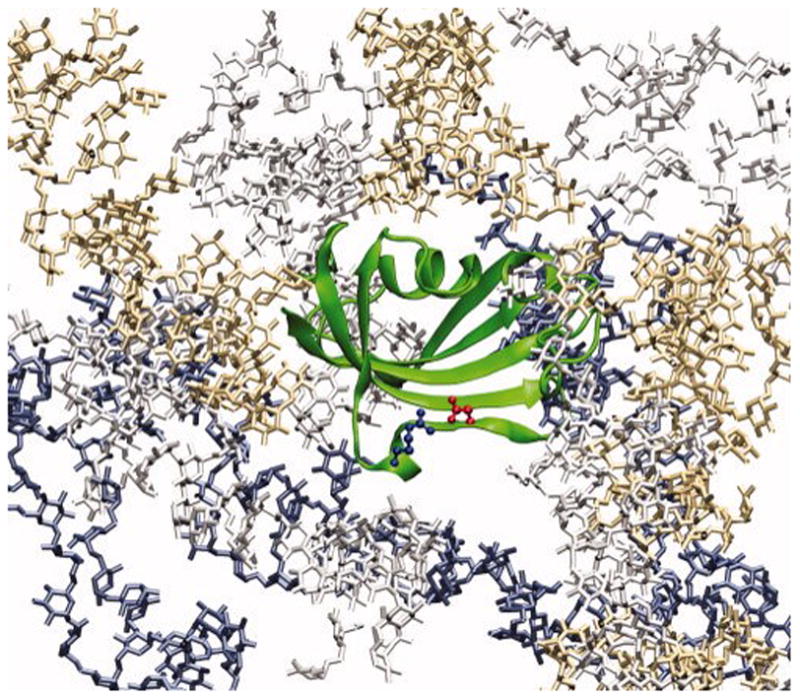
Illustration of a FKBP molecule (green ribbon) surrounded by dextran molecules. A salt bridge between Asp37 and Arg42 is shown as ball-and-stick. The FKBP studied here carries the Arg42 to Ala mutation.

Two different types of polysaccharides, dextran and Ficoll, were used as crowding agents. Both have been used separately in previous studies on the effects of macromolecular crowding on protein folding stability.^4,5,7 Dextran is a branched glucan, consisting of D-glucose monomers linked by glycosidic bonds (Figure 1). Depending on the chain length, the molecular weight of dextran can vary. In this study seven sizes of dextran, with molecular weight at 6, 10, 20, 40, 70, 100, and 150 kD, were used. Dextran with the different sizes was purchased from Sigma-Aldrich (St. Louis, MO) or TCI America (Portland, OR). Ficoll is a neutral, highly branched polysaccharide. It is thought to have roughly a spherical shape.⁸ The Ficoll used in the present study had a molecular weight of 70 kD and was purchased from Sigma-Aldrich (St. Louis, MO).

Measurement of unfolding free energy

Following our previous study,⁵ the unfolding free energy was measured by urea denaturation. Previously, different cuvettes containing the same FKBP concentration but increasing urea concentrations were used to generate the progress curve of urea denaturation. Here the progress curve was obtained by sequentially titrating urea into a single cuvette with a given starting concentration for FKBP. To measure the effect of macromolecular crowding, the crowding agents with indicated concentrations were added to both the FKBP solution in the cuvette and in the titrating urea solution. The buffer was 50 mM potassium phosphate at pH 6.5 with 100 mM KCl. All urea denaturation experiments were done at 21.5 °C.

The progress curve of urea denaturation was monitored by measuring tryptophan fluorescence at 356 nm on a Varian Cary Eclipse spectrofluorometer with an excitation wavelength of 294 nm. Our previous study⁵ and other studies cited therein have established that FKBP undergoes two-state folding. In our previous and present studies, a number of experiments were done to ensure that the tryptophan fluorescence intensities measured during urea denaturation reported the equilibrium between the native and denatured states of FKBP. These include:

1. Monitoring urea denaturation by both tryptophan fluorescence and circular dichroism (CD). Fluorescence and CD signals were found to report a single folding/unfolding transition.

2. Successive dilution of FKBP samples denatured by ~7 M urea. Fluorescence intensities on these fully denatured samples and on samples with lower urea concentrations were measured. Dilution then took place after a waiting time of over 24 hours. The diluted samples had urea and protein concentrations reduced to one half and then to one quarter. The fluorescence intensities of the diluted samples, after correcting for protein dilution, were found to be in agreement with those measured in the first day on samples with the same urea concentrations.

3. During urea denaturation, after each change in urea concentration, the fluorescence intensity was monitored as a function of time to ensure adequate time was allowed for equilibration. The fluorescence intensity was found to be constant from a few minutes to over 20 minutes. In the end, an equilibration time of 5 minutes was used.

4. A series of samples obtained by sequential titration of urea and a collection of individual samples prepared by adding different urea concentrations were found to yield identical progress curves. The two types of samples followed very different schedules of equilibration.

After correcting for protein dilution upon sequential titration of urea, the tryptophan fluorescence intensity (F) as a function of urea concentration ([U]) was fitted to the following equation^9,10

$$F=\frac{(F_{0\mathrm{N}}+s_{\mathrm{N}}[\mathrm{U}])+(F_{0\mathrm{D}}+s_{\mathrm{D}}[\mathrm{U}])e^{-(\mathrm{\Delta }G-m[\mathrm{U}])/k_{\mathrm{B}}T}}{1+e^{-(\mathrm{\Delta }G-m[\mathrm{U}])/k_{\mathrm{B}}T}}$$ (1)

where ΔG and m are the intercept and slope, respectively, of a linear extrapolation of the unfolding free energy to zero urea concentration, F_0N and s_N are the intercept and slope, respectively, of the native-state baseline, and F_0D and s_D are their counterparts of the denatured-state baseline.

For each concentration of the crowding agent (or, in the case of mixed crowding, each combination of concentrations of the crowding agents), urea denaturation measurements were done at least in duplicates, by different experimenters on different days. The fluorescence data sets in the different repeats were first fitted to equation (1) with both ΔG and m treated as global parameters while F_0N, s_N, F_0D, and s_D as specific to a particular data set. A typical fit of the raw data is shown in Figure 2. The fitted values of ΔG and m in dilute solution and under 17 sets of crowding conditions are listed in Table 1. The m values fluctuated around 1.7, without any apparent trend. The fitting errors of ΔG were ~0.1 kcal/mol.

Fig. 2.

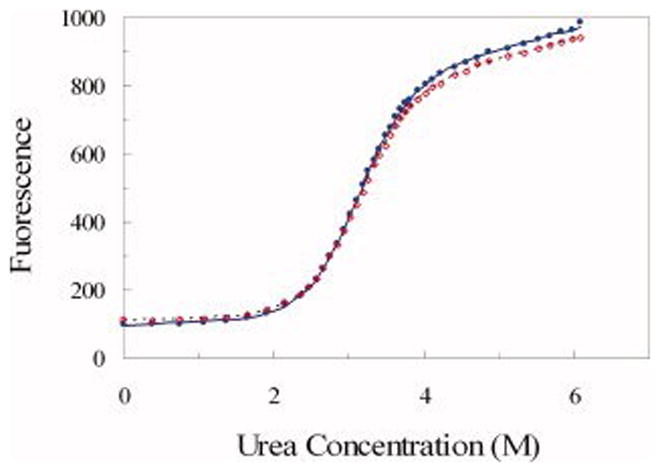
Fitting of FKBP tryptophan fluorescence under urea denaturation to equation (1). Two sets of data from repeat experiments in the presence of 100 g/l dextran 40 kD are shown as circles and diamonds, respectively. The fits, shown as solid and dotted curves, were done with floating m; the fitted values of m and ΔG are listed in Table 1.

Table 1.

Effects of crowding agents on the unfolding free energy

Crowding Agents	Concentrations (g/l)	m floating		m = 1.73
		ma	ΔG	ΔGb
None		1.61	4.39 ± 0.08	4.76
Dextran 6 kD	50	1.70	4.74 ± 0.11	4.83
Dextran 6 kD	100	1.75	5.10 ± 0.09	5.04
Dextran 6 kD	150	1.92	5.81 ± 0.14	5.22
Dextran 6 kD	200	1.71	5.60 ± 0.11	5.68
Dextran 10 kD	100	1.74	5.13 ± 0.12	5.09
Dextran 20 kD	100	1.69	4.98 ± 0.09	5.12
Dextran 40 kD	100	1.71	5.31 ± 0.07	5.35
Dextran 70 kD	100	1.66	4.96 ± 0.12	5.19
Dextran 100 kD	100	1.77	5.26 ± 0.29	5.14
Dextran 150 kD	100	1.78	5.15 ± 0.10	5.01
Ficoll 70	50	1.73	4.65 ± 0.08	4.65
Ficoll 70	100	1.67	4.69 ± 0.11	4.86
Ficoll 70	150	1.80	5.13 ± 0.09	4.93
Ficoll 70	200	1.67	4.95 ± 0.13	5.12
Dextran 6 kD/Ficoll 70	150/50	1.73	5.80 ± 0.10	5.79
Dextran 6 kD/Ficoll 70	100/100	1.79	5.64 ± 0.08	5.47
Dextran 6 kD/Ficoll 70	50/150	1.68	5.28 ± 0.09	5.46

^aFitting errors on m were 0.03 to 0.04 kcal/mol/M.

^bFitting errors on ΔG were below 0.02 kcal/mol.

It is well known that fitted values of ΔG and m are strongly correlated. Their ratio, ΔG/m, corresponding to the urea concentration, C_1/2, at the midpoint of the folding/unfolding transition, was determined with high accuracy in each fit. Fitting using C_1/2 and m, instead of ΔG and m, as floating parameters showed that the errors of C_1/2 were below 0.01 M. The random fluctuations of the fitted m values suggested to us that the crowding agents did not have a significant effect on the m value. To facilitate the comparison of ΔG in the presence and absence of crowding, we therefore chose to fix m at 1.7 kcal/mol/M and refit all the raw data. There was no noticeable deterioration in the quality of fitting in comparison to the initial fitting in which m was allowed to float. The refitted values of ΔG are also reported in Table 1, with errors below 0.02 kcal/mol. In the next section, the ΔΔG results calculated from this set of ΔG values are used to report the effects of crowding on the folding stability of FKBP. Nearly identical results for ΔΔG were obtained when the fixed value of m was changed between 1.6 and 1.8 kcal/mol/M.

Theoretical prediction of crowding effects on folding stability

The effect of crowding on the folding stability can be calculated as³

$$\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\Delta }{\mu }_{\mathrm{D}}-\mathrm{\Delta }{\mu }_{\mathrm{N}}$$ (2)

where Δμ_N and Δμ_D are the crowding-induced changes in chemical potential of a protein in the native and denatured states, respectively. We have developed a theory for predicting ΔΔG due to mixed crowding.¹¹ The protein molecule in the native state was modeled as a sphere (with radius R_N); the crowding agents were modeled as spheres with different radii R_i. Then Δμ_N was predicted according to the scaled particle theory as 

$$\mathrm{\Delta }{\mu }_{\mathrm{N}}/k_{\mathrm{B}}T=-ln(1-\varphi )+{(1-\varphi )}^{-1}\sum _i{\varphi }_i(3z_i+3{z_i}^2+{z_i}^3)+{(1-\varphi )}^{-2}\sum _i{\varphi }_i{z}_i\sum _i{\varphi }_i(9z_i/2+3{z_i}^2)+3{(1-\varphi )}^{-3}{\left(\sum _i{\varphi }_i{z}_i\right)}^3$$ (3)

where k_BT is thermal energy; z_i = R_N/R_i; 

$${\varphi }_i=2.52\times {10}^{-3}({R_i}^3/M_i)C_i$$ (4)

is the volume fraction of species i crowding agent, with its radius R_i in Å, its molecular weight M_i in Dalton, and its concentration C_i in g/l; and $\varphi ={\displaystyle \sum _i}{\varphi }_i$. The protein in the denatured state was modeled as a Gaussian chain (with radius of gyration denoted by R_g), with Δμ_D given by 

$$\mathrm{\Delta }{\mu }_{\mathrm{D}}/k_{\mathrm{B}}T=-ln(1-\varphi )+3\sum _i{\varphi }_i{y_i}^2(1+2/{\pi }^{1/2}{y}_i)-9\sum _{i,j}{\varphi }_i{\varphi }_j{y}_i{y}_{j}ln{y}_{i,j>}$$ (5)

where y_i = R_g/R_i. The last term was used only when y_{i, j>} = R_g/R_{i, j>}, where R_{i, j>} denotes the larger of R_i and R_j, is greater than 1.

RESULTS AND DISCUSSION

Effects of single crowding agents

We studied the effects of two crowding agents, Ficoll 70 and dextran with molecular weight ranging from 6 kD to 150 kD, on the folding stability of the FK506 binding protein (FKBP). Previous studies have established that FKBP undergoes two-state folding.⁵ The unfolding free energy (ΔG) was measured by monitoring the fluorescence of a single tryptophan in FKBP at different urea concentrations. The effect of Ficoll 70 on the folding stability of wild-type FKBP was reported previously⁵ and was re-measured on the Arg42 to Ala mutant in the present study (Table 1). The resulting changes in ΔG in the Ficoll 70 concentration range of 0 to 200 g/l, calculated using the ΔG values listed in the last column of Table 1, are comparable to those published previously.

To see whether the size of dextran, as indicated by its molecule weight, influences its effect on the folding stability, the unfolding free energy of FKBP in the presence of dextran with molecular weight ranging from 6 kD to 150 kD, each at a fixed concentration of 100 g/l, was separately measured. Results for ΔΔG, calculated from the measured ΔG values listed in the last column of Table 1, are displayed in Figure 3. Like Ficoll 70, dextran, regardless of size, was found to have a stabilizing effect. However, the level of stabilization clearly varied with the size of dextran. In particular, a maximum in stabilization was n apparent at an intermediate dextran molecular weight, 40 kD. In addition, the increase in FKBP stability by any species of dextran was higher than that by Ficoll 70 at the same concentration. Together, these results demonstrate that the stabilization of different crowding agents, even present at the same concentration, can be significantly different.

Fig. 3.

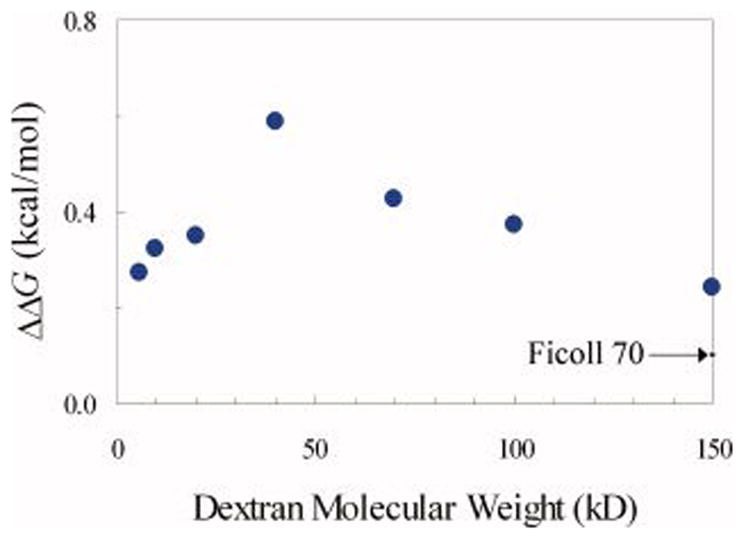
The change in the unfolding free energy of FKBP by dextran species with different molecular weights. The crowder concentration was fixed at 100 g/l. The effect of Ficoll 70 at the same concentration is indicated by an arrow on the right.

Effects of mixed crowding

The effects of mixing dextran 6 kD and Ficoll 70 at a total concentration of 200 g/l on the stability of FKBP were studied. The unfolding free energy was measured in the presence of the two crowding agents with mixing ratios of 1:0, 3:1, 1:1, 1:3, and 0:1. Results for ΔΔG, calculated from the measured ΔG values listed in the last column of Table 1, are shown in Figure 4. To see whether the effects of the two crowding agents were additive, for each mixing ratio we also determined ΔΔG values for both crowding agents alone at the constituent concentrations. For example, in the presence of the 1:3 mixture, consisting of 50 g/l of dextran 6 kD and 150 g/l of Ficoll 70, ΔΔG was found to be 0.7 kcal/mol. In the presence of 50 g/l of dextran 6 kD alone, ΔΔG was found to be 0.1 kcal/mol; the counterpart for 150 g/l of Ficoll 70 alone was 0.2 kcal/mol. Adding up the last two results would estimate a ΔΔG value of 0.3 kcal/mol for the mixture, which is significantly less than the measured value of 0.7 kcal/mol (recall that the experimental errors on ΔΔG were < 0.02 kcal/mol). The ΔΔG values obtained from the additive estimate for 3:1, 1:1, and 1:3 mixtures are also displayed in Figure 4 for comparison. The comparison shows that the stabilization effects exerted by mixtures of dextran 6 kD and Ficoll 70, at a total concentration of 200 g/l, are greater than the sum of the constituent crowding agents, by ~0.5 kcal/mol.

Fig. 4.

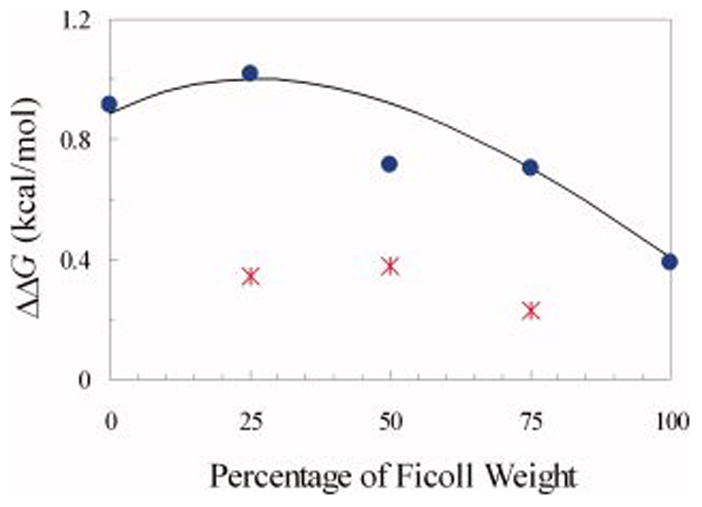
The change in the unfolding free energy of FKBP by mixed crowding. Two crowding agents, dextran 6 kD and Ficoll 70, were mixed at a total concentration of 200 g/l. Circles show the measured ΔΔG values; stars (*) show the estimates by adding up the effects of the constituent crowding agents alone. The curve shows the prediction of our theory,¹¹ with the radius of FKBP in the native state taken as 20 Å and the radius of gyration of FKBP in the denatured state as 45 Å. The sizes of dextran 6 kD and Ficoll 70 were modeled to contract at increasing concentrations of the crowding agents (C_dex and C_Fic, in units of g/l): R_dex (Å) = 16.5 – 0.03C_dex – 0.04C_Fil and R_Fil (Å) = 44 – 0.04C_dex – 0.04C_Fil. The concentration-induced contraction of these crowding agents was implicated in previous studies.^21–23

Test of theoretical prediction

The dependence of stabilization on the size, as controlled by the molecular weight, of a given type of crowding agent, shown in Figure 3, is the first of its kind, as is the effect of a mixture of two crowding agents shown in Figure 4. Our study of mixed crowding was motivated in part by a study of Du et al.,¹² who studied the effects of mixing dextran 70 kD or Ficoll 70 with DNA on the refolding yield of creatine kinase. Our focus here is on a fundamental thermodynamic quantity, the unfolding free energy of a two-state folding protein. The results presented here are valuable for test theories for macromolecular crowding.

Simple theories of crowding have achieved a degree of success, e.g., in explaining why macromolecular crowding is expected to increase folding stability.^11,13–15 However, given the crudeness of these theories (e.g., with the folded protein and the crowding agents modeled as spheres), whether they can pass the test of the present comprehensive study on the subtle effects of crowding is an open question. To explore this question, we tried to fit our own theory of mixed crowding¹¹ to the experimental data presented here. The basic conclusion is that, while it is possible to fit some of the data, it is not possible to fit all the data. As an illustration, we show in Figure 4 that the data on mixed crowding can be fitted by the theory with parameters listed in the figure legend. However, with the same parameters, the theory performs poorly in predicting the effect of dextran 6 kD alone as a function of its concentration (Figure 5).

Fig. 5.

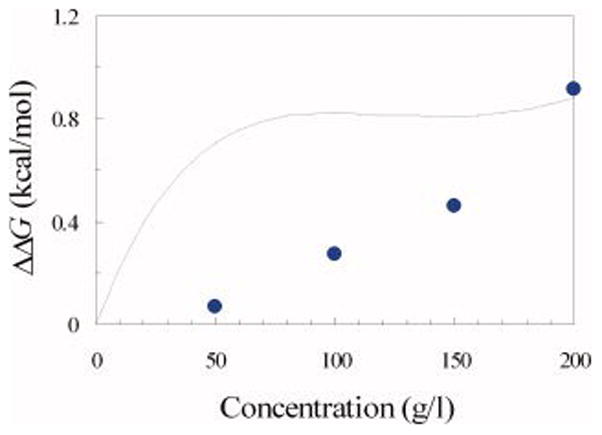
The change in the unfolding free energy of FKBP by dextran 6 kD. Circles show the measured ΔΔG values. The curve is the theoretical prediction, with the parameters listed in the legend of Figure 4.

Quantitative account of the kinds of effects of macromolecular crowding on protein folding stability reported here may well require atomistic modeling of both the protein undergoing the folding transition and the crowding agents. Calculation of folding free energies from molecular dynamics simulations of proteins in the presence of simple spherical crowders have been reported.^16,17 On the other hand, atomistic simulations of crowding conditions can now reach the concentration range of crowding agents in our experiments.¹⁸ Our study will likely motivate atomistic modeling of crowding effects on protein stability. It may also spur similar experimental studies on other proteins and with other crowding agents.

Physiological implications

This study demonstrates that the composition of macromolecular crowders, even at a fixed total concentration, can have a significant influence on the effect of crowding, and the variation with composition cannot be predicted additively from measurements on single species of crowders. This finding has profound implications. First, the cytoplasm is composed of a large number of different species of macromolecules, each by itself not necessarily at a high concentration. Our study suggests that not only the total concentration, but also the composition, of intracellular macromolecules should be taken into consideration in mimicking the intracellular environment by in vitro experiments. Such in vitro experiments complement (and avoid some of the complications associated with) in vivo measurements of folding stability ^19,20. Second, the composition of intracellular macromolecules can vary significantly during the lifetime of a cell. Our study implies that the effects of the intracellular environments exerted on the folding stability and other biophysical properties of proteins can vary significantly with time; such a variation may play a role in protein aggregation-related diseases such as Parkinson’s disease and Alzheimer’s disease, for which age is an important risk factor.