Internal pilots for a class of linear mixed models with Gaussian and compound symmetric data

SUMMARY

An internal pilot design uses interim sample size analysis, without interim data analysis, to adjust the final number of observations. The approach helps to choose a sample size sufficiently large (to achieve the statistical power desired), but not too large (which would waste money and time). We report on recent research in cerebral vascular tortuosity (curvature in three dimensions) which would benefit greatly from internal pilots due to uncertainty in the parameters of the covariance matrix used for study planning. Unfortunately, observations correlated across the four regions of the brain and small sample sizes preclude using existing methods. However, as in a wide range of medical imaging studies, tortuosity data have no missing or mistimed data, a factorial within-subject design, the same between-subject design for all responses, and a Gaussian distribution with compound symmetry. For such restricted models, we extend exact, small sample univariate methods for internal pilots to linear mixed models with any between-subject design (not just two groups). Planning a new tortuosity study illustrates how the new methods help to avoid sample sizes that are too small or too large while still controlling the type I error rate.

1. INTRODUCTION

1.1. Importance of medical imaging

In December 2000, the National Institute of Biomedical Imaging and Bioengineering (NIBIB) became the newest institute within the National Institutes of Health (NIH) in the United States. The authors of the NIBIB Establishment Act (Public Law 106–580) [1] were motivated partially by the desire to ensure that ‘…the fields of medical science that have contributed the most to the detection, diagnosis, and treatment of disease in recent years receive appropriate emphasis.’ Established and developing imaging techniques will allow for more accurate diagnosis of disease and will improve our understanding of the molecular mechanisms of diseases and their responses to therapy [2]. In our opinion, medical imaging stands next to genetics in future importance to health and biometric research. In fact, the fields of imaging and genetics will become more linked, as it is predicted that the use of genetic information will change the focus of imaging from diagnosis and recognition of disease to prediction and prevention [2].

1.2. Motivating example

Even the very earliest development of malignant tumours appears to dramatically affect the structure of blood vessels [3]. Figure 1 displays a vessel map of a normal person, with roughly 25–50 segments in each of four regions of the brain (anterior, posterior, left middle, and right middle). Quantifying the shape of the vessels in the brain is appealing for diagnostic and treatment purposes of diseases that change the morphology of blood vessels, such as brain cancer. Recent advances allow measuring cerebral vascular tortuosity (bending, twisting, or winding) automatically from magnetic resonance imaging (MRI). Consequently, the assessment of tortuosity may provide a noninvasive method of identifying even small malignant tumours [4]. Additionally, since successful treatment leads to normalization of tortuosity abnormalities, monitoring the tortuosity may be a way to assess the response to treatment of the malignant tumour [3]. Hence, scientists and regulators expect such biomarkers to greatly help in providing ‘faster, better, cheaper’ ways to evaluate and bring to market new treatments [5].

Figure 1.

Two views of cerebral vasculature in four regions. Vessel map created automatically from MRI.

Bullitt et al. [6] sought a reference model for comparison to patients with anomalies by examining six indices of cerebral vessel structure in 13 normal participants. The vessels of the brain have never been systematically quantified in three dimensions. Although no single tortuosity measure seems likely to capture all information, for the sake of brevity we discuss only one measure. Specifically, we examine the sum of all positive angles between successive trios of equally spaced vessel points, divided by the total path length (radians/cm), for all vessels in a region (SOAM1). Surgeons typically partition the brain into four different regions when focusing on cerebral vasculature. In order to provide more stable estimates of ‘normal’ vasculature for later comparison to ‘abnormal’, it would be ideal to group vessels from similar regions. Repeated measures ANOVA, applied to each measure separately, was used to compare the four brain regions. The authors tentatively concluded that left-middle and right-middle regions could be combined, leaving three distinct regions (anterior, posterior, middle).

Empirical features of the data from the previous study (tests of normality, skewness, kurtosis, measures of homogeneity, etc.) suggest a compound symmetric and Gaussian distribution. Although restrictive, compound symmetry arises naturally with a sampling scheme that creates exchangeability. Since each index combines information from 25 to 50 vessels in a region, logical properties of the measurement process imply such exchangeability. In addition to imaging applications, laboratory settings, such as the analysis of blood aliquots, may naturally give rise to data with the same exchangeability. Cluster samples of students within classrooms, patients within clinics, etc. typically display exchangeability, but may have variable cluster size.

Unintended protocol deviations in the tortuosity study caused the spatial resolution of an MRI to vary. Consequently, the investigators decided to recruit a new group of subjects. With no other alternative, the investigators used the estimated covariance matrix from the first study to choose the size of the second sample. However, the sample size chosen could be either too large or too small. Thus, an internal pilot design has great appeal [7].

1.3. Methods for analysing the data of interest: a small sample of Gaussian repeated measures

Many applications in medical imaging, genetics, and a variety of other laboratory settings, involve only a small number of independent observations, with repeated measures. Such data, including the tortuosity data, could be analysed with mixed model techniques. Vonesh and Chinchilli [8] provided a thorough introduction to mixed models with Gaussian errors. In the applications of interest, the focus centres on making accurate inferences about between-subject and within-subject expected values (‘fixed effects’).

As simulations by a variety of authors, including Catellier and Muller [9] and Schaalje et al. [10] have demonstrated, the Kenward–Roger [11] method provides the best approach for tests of mean parameters in linear mixed models with Gaussian errors. However, simulations also make it clear that (even with the best available method) the potential for inaccurate inference remains in small samples. Furthermore, iterative methods in mixed model software sometimes fail to converge in simulated samples. We leave the description of estimation and inference for the variance components (‘random effects’) to future research.

When missing data are not present, and the data have compound symmetric covariance, the ‘univariate’ approach to repeated measures (UNIREP) [12] provides exact tests in small samples, as well as estimates guaranteed to exist that require no iterative calculations. Also, the test is uniformly most powerful (among unbiased and similarly invariant tests), and has exact power methods (even in small samples).

Disallowing missing or mistimed data obviously restricts the use of the UNIREP approach. However, it still has great value due to the widespread importance of applications in imaging. Medical images from CT, MRI, ultrasound and other modalities automatically create multivariate and repeated measures data with no missing or mistimed data. For example, the tortuosity data have the required features and, hence, the UNIREP approach is preferred. In addition to imaging, a great variety of research paradigms based on the laboratory create multivariate and repeated measures data with no missing or mistimed data. Examples occur in bench research, animal and human work in toxicology, as well as many types of phases I and II pharmaceutical research. Thus, although we focus primarily on imaging, the UNIREP approach has a wide variety of applications in addition to imaging.

1.4. Univariate internal pilot designs

Jennison and Turnbull [13] reviewed internal pilot designs in clinical trials. Proschan [14] provided a more recent review of internal pilot designs when the outcome is continuous or dichotomous. In the case of continuous outcomes, most research involves only the independent groups t-test setting. Obviously not all designs, or even all clinical trials, involve only two groups. Therefore, Coffey and Muller [15–17] described methods and many exact (small sample) results for any univariate linear model with fixed predictors and Gaussian errors. Many t-test results are special cases.

Such designs include interim sample size adjustment, without interim data analysis. For univariate linear models with Gaussian errors, internal pilot designs begin with a planned sample size of n₀, based on fixed means and planning variance ${\sigma }_0^2$. The first n₁ observations give ${\hat{\sigma }}_1^2$. Recomputing sample size based on ${\hat{\sigma }}_1^2$ leads to adjusting the sample size up or down, as a function of ${\hat{\sigma }}_1^2$. The final sample size is denoted by n₊, with the minimum and maximum final sample sizes using this procedure denoted by n_+,min and n_+,max, respectively. Expected sample size and hence power increases if ${\sigma }_0^2$ was too small compared to ${\hat{\sigma }}_1^2$, while expected sample size typically decreases below n₀ (when allowed) if ${\sigma }_0^2$ was too large.

Due to the fact that the final sample size becomes a random variable under an internal pilot design, great care must be taken when choosing a test statistic to use at the conclusion of the study. An unadjusted test ignores the randomness of the final sample size and uses the fixed sample test statistic and critical value. However, the risk of test size inflation may offset the benefits in the minds of many researchers [18]. Hence, the focus in the two group univariate setting has shifted to retaining the benefits of an internal pilot design while controlling test size. Coffey and Muller [17] evaluated several methods which control test size, even in small samples. Only a bounding method, which modifies the critical value used for the final hypothesis test to ensure that the maximum test size is not greater than the target level, proved robust across the entire range of conditions considered. Since any method for data analysis which preserves the test size at the target level will be preferred over the unadjusted test, if the price in power and expected sample size is not too high, the bounding method should become the default. The free software GLUMIP [19] (http://www.soph.uab.edu/coffey/) implements the bounding method.

1.5. Internal pilot designs for repeated measures

Currently, no general methods allow controlling test size with internal pilot designs in studies with correlated observations. Several authors have recently considered sample size re-estimation with correlated observations in groups of varying size. Lake et al. [20] considered an unadjusted test for internal pilots with cluster sampling. Zucker and Denne [21] considered a two-group internal pilot design with particular patterns of repeated measures and described large sample modifications of mixed model tests. Tolerance of missing and mistimed data played a key role. Simulations supported the approach for the limited range of conditions considered. Coffey and Muller [22] used simulations to evaluate whether the mild conservatism of the Geisser-Greenhouse test would compensate for the liberal test size often induced by an internal pilot design. Unfortunately, the approach failed to control test size in some conditions, especially with small to moderate sample sizes.

Given the interest in small samples inherent with the tortuosity example, we are not comfortable with any of the techniques. Furthermore, the theory needed to apply the bounding or any other method to the design of interest has not been available. Hence, new methods are needed which control test size, while still providing the advantages of internal pilot designs for the repeated measures setting of the tortuosity data. Essentially, we require the intersection of techniques for analysing repeated measures data, internal pilot designs, and small samples. At first glance, it would seem that this requires new theory specific to this setting. However, we can take advantage of the special properties of the tortuosity example (no missing or mistimed observations, factorial within-subject design, common between-subject design for all responses, compound symmetric covariance matrix) to implement an internal pilot design which achieves the same exact, small sample performance as previously known univariate methods.

Combining two well-known pieces, UNIREP theory and exact internal pilot theory for univariate models, provides the solution. However, demonstrating the validity of the approach requires a (new) explicit proof of the concept. Furthermore, implementing the approach in practice requires a constructive derivation of the explicit forms needed for internal pilot calculations. We include both below.

2. INTERNAL PILOTS FOR A RESTRICTED CLASS OF LINEAR MIXED MODELS

2.1. Notation

Throughout, A = {a_jk} indicates a matrix, with transpose A′ = {a_kj}, while a is an n × 1 vector (always a column). In particular, the notation 1_n indicates a vector of n 1’s. If A = [a₁ a₂ … a_n] then $[\text{vec}(\mathbf{A})]\prime =[{\mathbf{a}}_1^{\prime }{\mathbf{a}}_2^{\prime }\dots {\mathbf{a}}_n^{\prime }]$ and the Kronecker product is A ⊗ B = {a_jkB}. With Dg(x) a diagonal matrix with (j, j) element x_j, the spectral decomposition of A = A′ is A = V Dg(λ)V′, with VV′ = V′V = I_n = Dg(1_n). The rank of a matrix is the maximum number of linearly independent rows or columns. Square and full rank A has a unique and full-rank inverse, A⁻¹. Schott [23] has details.

Writing y ~ 𝒩_p(μ, Σ) indicates y is a vector Gaussian with mean E(y) = μ. The p × p covariance, 𝒱(y) = Σ, has eigenvalue λ_k≥0, the variance of principal component k (1≤k≤p). The designs of interest involve a factorial within-subject design. For factor k with p_k levels, compound symmetry implies covariance ${\mathbf{\Sigma }}_{\mathrm{c}\mathrm{s}}(p_k,{\rho }_k,{\sigma }_k)={\sigma }_k^2\{{\rho }_k{\mathbf{1}}_{p_k}{\mathbf{1}}_{p_k}^{\prime }+(1-{\rho }_k){\mathbf{I}}_{p_k}\}$, with ${\sigma }_k^2$ the common variance and ρ_k the common correlation. The matrix Σ_cs(p_k, ρ_k, σ_k) has two distinct eigenvalues, ${\lambda }_{1,k}={\sigma }_k^2[1+(p_k-1){\rho }_k]$ and ${\lambda }_{2,k}={\sigma }_k^2(1-{\rho }_k)$. Having $0<{\sigma }_k^2$ and −1/(p − 1)<ρ_k<1 guarantee 0<λ_1,k and 0<λ_2,k. More generally, Kronecker (product) compound symmetry has, with p = [p₁ … p_m]′, ρ = [ρ₁ … ρ_m]′, and σ = [σ₁ … σ_m]′,

$${\mathbf{\Sigma }}_{\mathrm{c}\mathrm{s}}(\mathbf{p},\mathbf{\rho },\mathbf{\sigma })=\underset{k=1}{\overset{m}{\otimes }}{\mathbf{\Sigma }}_{\mathrm{c}\mathrm{s}}(p_k,{\rho }_k,{\sigma }_k)$$ (1)

a p_* × p_* matrix, with $p_{*}={\prod }_{k=1}^m{p}_k$. If p = [2 2]′, ρ = [ρ₁ ρ₂]′ and σ = [σ₁ σ₂]′ then

$${\mathbf{\Sigma }}_{\mathrm{c}\mathrm{s}}(\mathbf{p},\mathbf{\rho },\mathbf{\sigma })={\sigma }_1^2{\sigma }_2^2\left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\rho }_2\hfill & \hfill {\rho }_1\hfill & \hfill {\rho }_1{\rho }_2\hfill \\ \hfill {\rho }_2\hfill & \hfill 1\hfill & \hfill {\rho }_1{\rho }_2\hfill & \hfill {\rho }_1\hfill \\ \hfill {\rho }_1\hfill & \hfill {\rho }_1{\rho }_2\hfill & \hfill 1\hfill & \hfill {\rho }_2\hfill \\ \hfill {\rho }_1{\rho }_2\hfill & \hfill {\rho }_1\hfill & \hfill {\rho }_2\hfill & \hfill 1\hfill \end{array}\right]$$ (2)

The covariance pattern includes compound symmetry as an important special case. However, except in special cases, Σ_cs(p, ρ, σ) does not itself exhibit compound symmetry.

A linear mixed model for p_i-correlated observations on independent sampling unit i ∈ {1, …, N} (referred to as subject, for convenience) may be written as

$${\mathbf{y}}_i={\mathbf{X}}_i\mathbf{\beta }+{\mathbf{Z}}_i{\mathbf{d}}_i+{\mathbf{e}}_i$$ (3)

Here, the q × 1 vector β contains unknown parameters, while the p_i × q matrix X_i contains known constants. The matrix X_i combines between- and within-subject design (‘fixed effects’) information to specify the expected value vector for subject i, namely E(y_i) = X_iβ. The p_i × m matrix Z_i contains known constants which partially determines the covariance structure for subject i through the m × 1 random vector, d_i, of unobserved, subject-specific ‘random effects’. Many assumptions are summarized by the statement

$$\left[\begin{array}{c}\hfill {\mathbf{d}}_i\hfill \\ \hfill {\mathbf{e}}_i\hfill \end{array}\right]~{𝒩}_{m+p_i}\left\{\right[\begin{array}{c}\hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill \end{array}],[\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{di}(\mathbf{\tau })\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill {\mathbf{\Sigma }}_{ei}(\mathbf{\tau })\hfill \end{array}\left]\right\}$$ (4)

Properties of Z_i, d_i and e_i fully determine $𝒱({\mathbf{y}}_i)={\mathbf{Z}}_i{\mathbf{\Sigma }}_{di}(\mathbf{\tau }){\mathbf{Z}}_i^{\prime }+{\mathbf{\Sigma }}_{ei}(\mathbf{\tau })$, but have no effect on E(y_i). Fully identifying the covariance model requires additional constraints. If Kronecker compound symmetry holds, then τ′ = [ρ′ σ′]. With one within-subject factor (m = 1), a ‘random effect’ coding has Z_i ≡ 1_p, Σ_di (τ) ≡ σ²ρ and Σ_ei (τ) ≡ σ²(1 − ρ)I_p. Exactly the same 𝒱(y_i) results if Z_i ≡ 0 and $𝒱({\mathbf{e}}_i)\equiv {\sigma }^2[{\mathbf{1}}_p{\mathbf{1}}_p^{\prime }\rho +{\mathbf{I}}_p(1-\rho )]$, which has y_i = X_iβ + e_i.

2.2. A restricted class of linear mixed models

In the remainder of the paper we consider a restricted class of linear mixed models with Gaussian errors which meet the following restrictions: (1) no missing or mistimed observations (all subjects have the same number of observations at the same within-subject levels), (2) factorial within-subject design, (3) common between-subject design for all responses, (4) homogeneity between subjects, which requires 𝒱(y_i) to have the same parameters (and dimensions) for all subjects, and (5) 𝒱(y_i) = Σ_cs(p, ρ, σ). Although the data must have complete balance within-subject, imbalance of any sort may occur in the between-subject design.

The tortuosity data provide a particularly simple example of satisfying the restrictions due to having only one factor within-subject (m = 1) and p_* = p₁ = 4 brain regions. Also, y_i = {y_ij} is always in the same order: anterior, left, posterior, right. Compound symmetry requires equal variance in the four regions and constant correlation among region pairs. Obviously, this is a special case of the more general Kronecker compound symmetry, with Σ_i = Σ_cs(4, ρ, σ).

2.3. Better data analysis for models in the restricted class

The following theorem has very important theoretical and practical implications. A mixed model that meets the restrictions described above allows dramatically better data analysis than is available with the general mixed models. More precisely, incorrectly casting a model from the restricted class in the linear mixed model framework yields suboptimal inference, particularly in small samples. However, as of this writing, we do not know of any mixed model software that automatically takes advantage of the restrictions, except in a special case with particular control statements. Fortunately, UNIREP methods in widely available commercial and free software will conveniently provide the optimal results.

Theorem 1

For a fixed sample size, any linear mixed model meeting the restrictions described above may be analysed with the corresponding UNIREP model. The approach provides exact and optimal estimates without iterative calculations. The ‘uncorrected’ test provides exact and optimal inference, even in small samples, for any testable parameter in the model (the appendix contains a proof).

As noted earlier, achieving the improvements in practice typically requires avoiding mixed model software and using programs for UNIREP analysis with the uncorrected test. Such an analysis is available in many commercial software packages via a repeated measures option in multivariate linear model modules (such as the REPEATED statement in SAS/GLM^®). Free SAS/IML^® software (at http://www.bios.unc.edu/~muller) also provides exact UNIREP data analysis.

The tortuosity example allows illustrating the conversion from a mixed model in the restricted class to a UNIREP model. For clarity, we have focused on a rather simple example to illustrate the benefit of the results. It is important to recognize that the results apply to a broad range of models with any combination of within- and between-subject factors, provided the Kronecker compound symmetry assumption holds. With one factor within-subject (m = 1) in the tortuosity example, a mixed model for subject i has p_* = p₁ = 4. Choosing Z_i ≡ 0 and 𝒱(e_i) = Σ_cs(4, ρ, σ) implies y_i = X_iβ+e_i. Stacking data for N subjects gives n = N · p length vectors ${\mathbf{y}}_{\mathrm{s}}=[{\mathbf{y}}_1^{\prime }{\mathbf{y}}_2^{\prime }\dots {\mathbf{y}}_N^{\prime }]$ and e_s, while ${\mathbf{X}}_{\mathrm{s}}=[{\mathbf{X}}_1^{\prime }{\mathbf{X}}_2^{\prime }\dots {\mathbf{X}}_N^{\prime }]$ is n × q. Hence, y_s = X_sβ+e_s and y_s ~ 𝒩_n(X_sβ, I_N ⊗ Σ_i). The stacked model describes the ‘univariate’ approach to repeated measures in matrix notation (without requiring balance between subjects).

2.4. Power and internal pilot analysis for the restricted class

Unfortunately, as Verbeke and Molenberghs [24] noted, very little is known about non-null distributions in mixed models. Hence, Theorem 1 also improves power analysis for the restricted class of linear mixed models since exact power can now be computed by using the corresponding UNIREP model. A growing number of commercial packages provide exact power for UNIREP analysis. Additionally, free SAS/IML^® software (at http://www.bios.unc.edu/~muller) provides exact power for the UNIREP formulation.

At first glance, Theorem 1 provides no help for internal pilot designs because the (internal pilot) theory for UNIREP models is no better developed than that for mixed models. However, the following theorem and corollary allow transforming the model in such a way as to allow using univariate power analysis, univariate internal pilot theory and univariate software for the restricted class of models.

Theorem 2

(a) The ‘univariate’ approach to repeated measures implicitly defines a set of 2^m distinct univariate linear models with i.i.d. errors. (b) Jointly, the univariate models provide optimal non-iterative estimates of estimable parameters and optimal exact inference for all main effects and interactions of between- and within-subject factors (the appendix contains a proof).

Aggregating observations with common variances define a set of independent, univariate models. Separately, each model satisfies the assumptions of a univariate linear model with i.i.d. Gaussian errors. Consequently, the optimal statistical properties of the univariate model apply. The benefits include completely avoiding convergence difficulties, easy access to well-documented model fitting diagnostics, and automatic inheritance of many optimal estimation and inference properties.

The following corollary to Theorem 2 allows applying a wide array of internal pilot methods previously developed. Equally important, the corollary allows using existing software for all internal pilot planning and analysis for mixed models in the restricted class.

Corollary

Analysing any linear mixed model in the restricted class in terms of the implicitly defined univariate models allows directly applying all known exact and approximate internal pilot theory for univariate models.

As noted earlier, most authors have published internal pilot results for only the two group (t-test) setting. More generally, all methods described by Coffey and Muller [15–17] apply to any univariate general linear model with fixed effects and independent Gaussian errors, and any standard general linear vector hypothesis, not just two group t-tests. The primary test of interest for the tortuosity example involves a comparison of the four brain regions, a three degrees of freedom ANOVA hypothesis (in the transformed univariate model). Hence, study planning requires the more general methods of Coffey and Muller.

In practice, the programming complexity underlying the collection of univariate models in Theorem 2 dictates that the equivalent UNIREP formulation in Theorem 1 should be used for data analysis of the restricted class. In contrast, even though power calculations are available for the multivariate model [12], scientists and statisticians are generally more comfortable with power calculations for the univariate model. In addition, more statistical packages at the present time provide algorithms for univariate power calculations. Consequently, the univariate models in Theorem 2 have great appeal for power and sample size calculations for the restricted class.

3. PLANNING A TORTUOSITY STUDY

3.1. Converting to a set of univariate models

The first tortuosity study, with no between-subject factors (grand mean only) and one within-subject factor (region), illustrates the principles of Theorem 2. Choosing cell mean coding [25] for brain region results in the within-subject design matrix X_W,i = I₄ and the between-subjects design matrix X_B,i = 1 (the appendix contains definitions). Hence, X_i = I₄ ⊗ 1 = I₄ and β = [μ_A μ_L μ_P μ_R]′ contains means for anterior, left middle, posterior, and right-middle brain regions, respectively. As mentioned earlier, we found compound symmetry and a Gaussian distribution to be reasonable assumptions in the example. Having m = 1 within-subject factor leads to two distinct univariate models, with variances corresponding to the distinct eigenvalues of Σ_cs(4, ρ, σ). Here, λ₁ = σ²(1+3p) provides the error variance for a test of the grand mean with 1 numerator degree of freedom and N − 1 denominator degrees of freedom. In turn, λ₂ = σ²(1 − ρ) provides the error variance for tests of differences among regions with 3 numerator degrees of freedom and 3(N − 1) denominator degrees of freedom.

Extending the design to include gender and age (with three groups) as between-subject factors illustrates the principle that adding between-subject predictors does not increase the number of distinct error variances for the transformed data. Table I summarizes the effects and associated variances. Tests that involve only between-subject factors (i.e. the grand mean, gender effect, age effect, and gender by age interaction) can be conducted using a univariate linear model with variance λ₁ = σ²(1+3p) and N −6 denominator degrees of freedom. Similarly, tests that involve the within-subject factor can be conducted using a univariate linear model with variance λ₂ = σ²(1 − ρ) and 3(N − 6) denominator degrees of freedom.

Table I.

ANOVA table for the univariate models associated with the tortuosity example.

Source	d.f.	Variance
Grand mean	1
Gender	1
Age	2
Gender × age	2
Error between	N − 6	λ1 = σ2(1 + 3ρ)
Region	3
Region × gender	3
Region × age	6
Region × gender × age	6
Error within	3(N − 6)	λ2 = σ2(1 − ρ)
Total	4N

Note: One within-subject factor (region) and two between-subject factors (gender, age).

Exact inference is not available for any hypothesis that involves observations with two or more distinct variances. For example, adding gender as a between-subject factor raises the possibility of comparing mean response for females in one region to mean response for males in another region, which involves both λ₁ and λ₂. In practice, scientific interests rarely lead to such hypotheses, and we ignore such comparisons in the remainder of the paper.

3.2. Initial planning

We based sample size planning on power for one particular index of tortuosity, SOAM1. However, as noted in the introduction, vessel abnormality most likely involves more than one dimension of variation. Altogether, six response measures are of interest. Muller and Stewart [26, Chapter 6] discussed the special concerns for repeated measures of multivariate responses. Given the limited choices, and the desire for an internal pilot, data and power analysis will use $\alpha =\frac{0.05}{6}$ to control type I error rate. Despite the concern about conservatism of a Bonferroni correction, the small number of tests and typically modest role of α in determining power combine to make the approach practical and effective.

The new tortuosity study will be powered to test the null hypothesis that mean vascular tortuosity is constant across the four regions. In particular, H₀: Cβ = 0, with β = [μ_A μ_L μ_P μ_R]′ and C = [1₃ − I₃]. The investigators seek a sample size such that the study will have at least 90 per cent power to detect a single mean difference of δ = 0.20. Equivalently, β = [μ․+δ μ․ μ․ μ․]′ with μ· the grand mean. The nature of the test ensures that any additional differences would only increase power.

In considering power analysis with repeated measures, it is important to carefully maintain distinctions among the (1) number of independent sampling units, (2) total number of observations, and (3) degrees of freedom for any particular test. The restricted class of models considered herein assumes that the number of independent sampling units can be varied, while the number of repeated measures within each sampling unit is always fixed. Hence, the total number of observations varies as a multiple of the number of independent sampling units. Furthermore, although degrees of freedom vary directly with the number of independent sampling units, the actual value depends on the particular hypothesis of interest. Consequently, we couch all discussions in terms of the number of independent sampling units (N).

We need covariance parameter values to compute the required sample size. For the initial tortuosity study, a ‘univariate’ approach to repeated measures ANOVA gave λ̂₁ = 0.1852 and ${\hat{\lambda }}_2=(\frac{0.0686}{3})$, which correspond to ρ̂ = 0.64 and σ̂² = 0.0635. The estimates may be used for initial planning of the new study based on a UNIREP ANOVA power analysis using the free POWERLIB program (at http://www.bios.unc.edu~muller), although the validity of the estimates may be questioned due to the protocol deviations described earlier. The analysis suggests a sample size of n₀ = 18 MRI’s, i.e. independent sampling units (with 72 total observations; four repeated measures).

We recommend casting the problem in a UNIREP ANOVA framework and using the (free) POWERLIB program, or other free or commercial software, for fixed sample power calculations. Without access to such software, exactly the same power values could be computed from the appropriate univariate model implied by the conversion formulas in Theorem 2. For the tortuosity data example, testing the hypothesis H₀: Cβ = 0, where β and C are defined as above, is equivalent to testing H₀: C_*β_* = 0, with C_* = I₃ and V′_⊥pkβ, with V_⊥pk the three ‘trend’ eigenvectors of Σ_cs(4, ρ, σ). The power analysis can then be based on a univariate linear model with i.i.d. errors; specifically, e_i ~ 𝒩(0, λ₂).

3.3. Planning an internal pilot

The required sample size computed in the previous section was based on the estimated covariance matrix from the initial tortuosity study. However, since the spatial resolution of a recorded MRI varied, the estimated covariance matrix values could be either too large or too small. Hence, an internal pilot design has great appeal. Given that the tortuosity data satisfy the restrictions described above, we may use exact internal pilot results after appropriate transformation of the mixed model to a set of univariate linear models. No additional programming is required for implementing an internal pilot design for the restricted setting of the tortuosity example. We merely need to carefully think about the problem and apply the appropriate transformation to reduce the hypothesis test of interest to an equivalent test in a univariate setting. After doing so, any valid approach for implementing internal pilot designs in the univariate setting, e.g. the bounding method contained in the GLUMIP program, can be used. For the tortuosity example, an internal pilot design may be implemented with an originally planned sample size of n₀ = 18 subjects based on an initial planning variance value, ${\lambda }_{2,0}={\hat{\lambda }}_2=(\frac{0.0686}{3})$, not σ̂².

An important decision when planning any study that proposes to implement an internal pilot design is the choice of n₁ = πn₀, the size of the internal pilot sample for re-estimating the variance. Clearly, there is a need to determine the final sample size as early as possible. The decision may be affected by other key features, such as whether there is a finite maximum limit on the final sample size and whether the originally planned sample size will be allowed to decrease if the original variance value was too large. Hence, the choice is not always obvious. We believe that the choice of n₁ should depend on the scientific setting and be influenced by the particular costs and logistical issues for any particular study design. The free software which implements the methods we recommend allows the user to consider the tradeoffs among a wide range of choices.

We illustrate the process of choosing the size of the internal pilot sample for the tortuosity example, allowing a reduction of the final sample size. We did not impose a finite maximum sample size, although some realistic maximum will usually need to be specified in practice. We considered n₁ ∈ {9, 12, 15, 18}, which corresponds to a range of π values between 0.5 and 1.

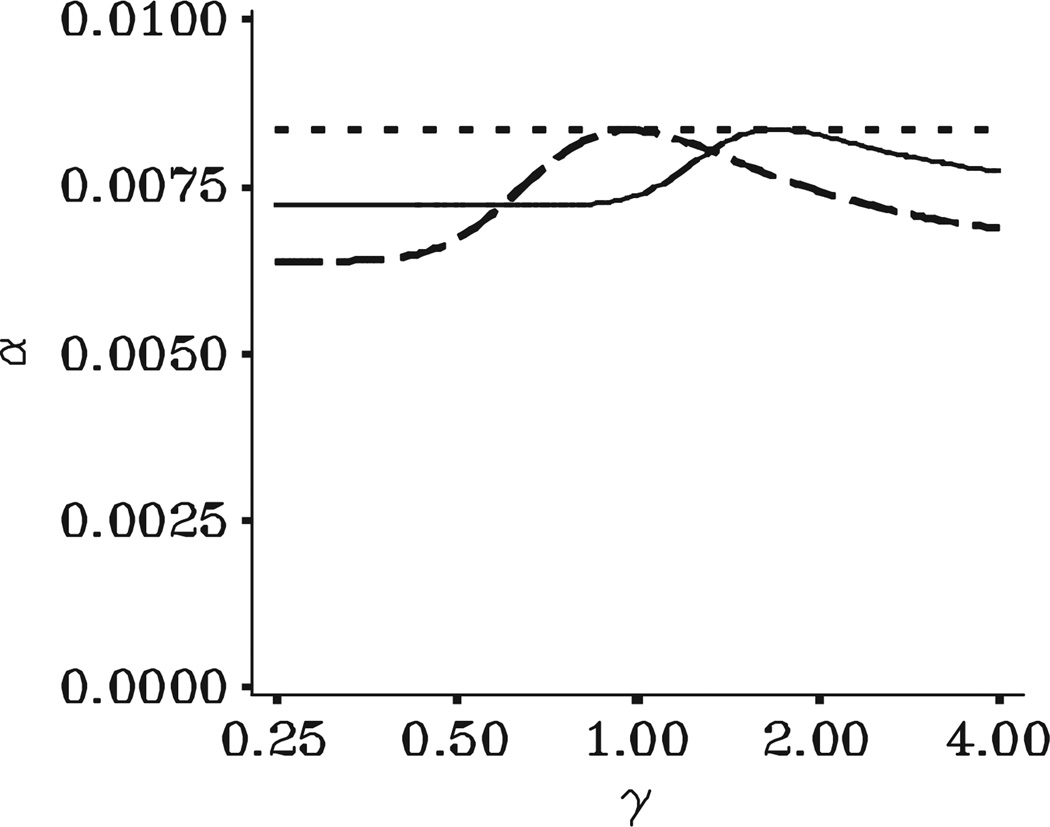
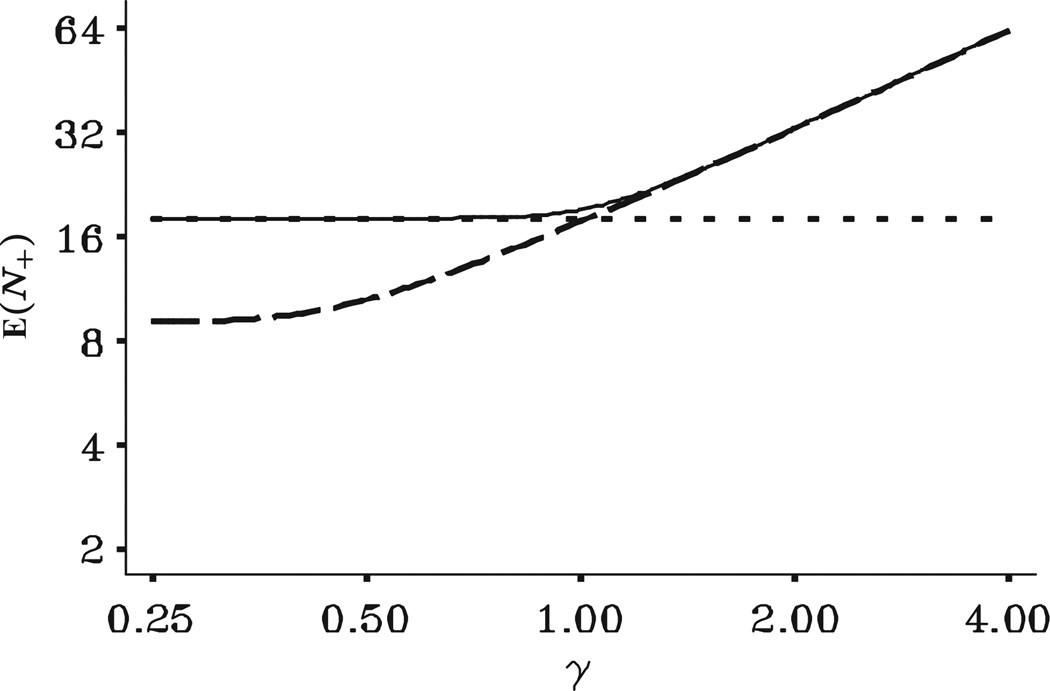
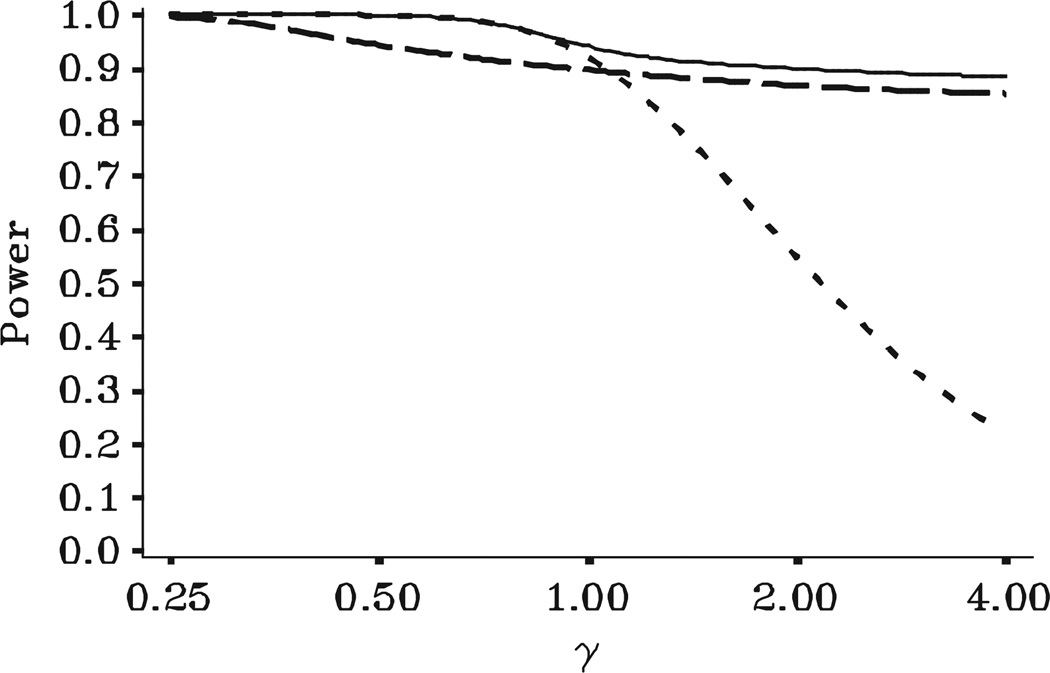
Figures 2–4 illustrate the test size, power, and expected sample size, respectively, of the bounding method. For clarity, the figures include curves only for the two extreme values of n₁ since the curves for intermediate values of n₁ lie between the two curves shown. A line for the fixed sample design with n₀ = 18 subjects provides a useful reference curve. All curves are shown as functions of γ = λ₂/λ_2,0, the ratio of the true variance to the initial variance value used for study planning. Hence, γ>1 implies that the initial variance value understated the true variance and the study as originally planned is under powered. Similarly, γ<1 implies that the initial variance value overstated the true variance. The figures demonstrate the tremendous richness of information available to researchers when planning internal pilot designs. Our consulting experience has convinced us that such plots allow scientists to visualize the tradeoffs among various study designs and engages them in a collaborative manner that is rewarding to them and the statistician.

Figure 2.

Type I error rate for bounding test with n_+,min = n₁ and n_+,max = ∞ as a function of γ = γ₂/γ_2,0 for tortuosity differences among p = 4 brain regions with ${\alpha }_{\mathrm{t}}=\frac{0.05}{6}$, P_t = 0.90, C_* = I₃, β_* = V′_T β, and ${\sigma }_0^2={\lambda }_{2,0}=(\frac{0.0686}{3})$. Fixed design with n₀ = 18: · · ·; IP bounding with n₁ = 9; – – –; IP bounding with n₁ = 18: ----.

Figure 4.

Expected number of MRI scans for bounding test with n_+,min = n₁ and n_+,max = ∞ as a function of γ = λ₂/λ_2,0 for tortuosity differences among p = 4 brain regions with ${\alpha }_{\mathrm{t}}=\frac{0.05}{6}$, P_t = 0.90, C_* = I₃, β_* = V′_T β, and ${\sigma }_0^2={\lambda }_{2,0}=(\frac{0.0686}{3})$. Fixed design with n₀ = 18: · · ·; IP bounding with n₁ = 9; – – –; IP bounding with n₁ = 18: ----.

Figure 2 illustrates that, for any choice of n₁, the bounding method controls test size across the entire range of γ. Figure 3 illustrates the primary benefit of an internal pilot design. Unlike a fixed sample size design, whenever γ>1, the bounding method maintains power near the target level of 90 per cent for any choice of n₁. Hence, regardless of the choice of n₁, the power can be greatly increased above that of a fixed sample design while still controlling type I error. Figure 4 demonstrates that, if γ>1, maintaining power comes at the cost of an increase in expected sample size. However, ignoring variability in n₊ due to small n₁, the average increase in sample size is fairly consistent for any n₁. In contrast, γ<1 (original variance value too large) causes big differences in expected sample size as a function of n₁. If it were known that γ<1, the sample size should be re-estimated as early as possible in order to allow reducing the sample size. For the tortuosity example, the only ‘costs’ involve the time and money from including too many subjects. Based on the desire to use as many observations as possible for the variance re-estimation and the need to make a final decision regarding the sample size before data were collected on all of the n₀ = 18 subjects per group, we chose a value of n₁ = 15 subjects per group.

Figure 3.

Power for bounding test with n_+,min = n₁ and n_+,max = ∞ as a function of γ = λ₂/λ_2,0 for tortuosity differences among p = 4 brain regions with ${\alpha }_{\mathrm{t}}=\frac{0.05}{6}$, P_t = 0.90, C_* = I₃, β_* = V′_T β, and ${\sigma }_0^2={\lambda }_{2,0}=(\frac{0.0686}{3})$. Fixed design with n₀ = 18: · · ·; IP bounding with n₁ = 9; – – –; IP bounding with n₁ = 18: ----.

4. DISCUSSION

4.1. Advantages of the approach

The model restrictions allow defining analysis methods for a useful class of internal pilot designs with correlated observations. The methods guarantee test size control while retaining the advantages of internal pilot designs, even with small sample sizes. The approach inherits all optimal properties of methods for univariate linear models, including a range of exact results. As a consequence, the approach has the substantial advantage of requiring no new software for internal pilot study planning. For fixed sample sizes, although the restricted class of interest may be cast naturally as mixed models, current mixed model software should be avoided. Simply recognizing equivalent model representations allows exact inference using widely available, standard software. The two main methodological components of the exposition are not necessarily new by themselves: (1) transformation of the restricted class of linear mixed models to a UNIREP model which then allows for, (2) application of exact internal pilot theory for univariate linear models to the restricted class of mixed models. However, to our knowledge the possibility of combining the components has never been explicitly proposed. Furthermore, finding explicit forms to justify the approach and give computable and convenient forms for the link between the two areas of research was not necessarily trivial.

4.2. Limitations and future research

The approach applies only to estimation and inference for within-subject and between-subject ‘fixed effects’ in the restricted class of models. As noted earlier, we leave the specification of estimation and inference for variance components to future research.

Community-based cluster samples that use classrooms or clinics as the independent sampling unit (cluster) naturally induce exchangeability, but have variable cluster size. Hence, generalizing the methods by allowing missing or mistimed data or an unequal number of observations within each independent sampling unit would provide a valid way to take advantage of internal pilot designs in community-based trials.

Future research to extend internal pilot designs to more complex repeated measures would be useful. Ideally, new results will remove all restrictions on the class of mixed models available for internal pilot designs. However, general fixed sample tests are not available which guarantee accuracy of inference in small samples.

Any choice of covariance model must be defended. Kronecker compound symmetry only arises naturally in a sampling scheme with some form of exchangeability. Violating the assumption can badly inflate test size. Most observations collected over time (that we have encountered) violate the principle of exchangeability. Consequently, the current methods are not suitable for measures repeated over time (including longitudinal data). Allowing other covariance models would extend the utility of the methods to a wide range of laboratory-based research that avoid missing data. Given the needs of our colleagues in medical imaging, we are currently pursuing such new methods.

APPENDIX A

The methods presented here depend on creating and converting between coding schemes. The essence matrix [27] simplifies the discussion. An N observation by q predictors design matrix, X, has G × q essence matrix Es(X), which contains one and only one copy of each unique row of X. Each X_g = row_g[Es(X)] describes one of G groups of subjects. With N_g observations in group g,

$$\mathbf{X}=\left[\begin{array}{c}\hfill {\mathbf{X}}_1\otimes {\mathbf{1}}_{N_1}\hfill \\ \hfill {\mathbf{X}}_2\otimes {\mathbf{1}}_{N_2}\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{X}}_G\otimes {\mathbf{1}}_{N_G}\hfill \end{array}\right]$$ (A1)

Cell-mean coding has Es(X) = I_G for a one-way design. Reference cell, effect and polynomial coding also give G × G, full rank Es(X) and X. Classical ANOVA coding has less than full-rank Es(X) = [1_G I_G]. See Muller and Fetterman [25] for more details.

The following three lemmas are needed in proving Theorem 1.

Lemma 1

(1) Any less than full-rank model has a linearly equivalent full-rank model. (2) Parameters estimable (or testable) in one model are also estimable (or testable) in a linearly equivalent model. (3) Parameters of linearly equivalent models are linear transformations of each other. (4) Any coding scheme which creates a linearly equivalent model may be used without loss of any information.

Proof

Helms [27] gave a proof.

Lemma 2

The essence matrix of a factorial design may be chosen as the Kronecker product of one-way essence matrices for the individual factors. Parallel results hold for contrasts.

Proof

Examining parameters implied by the process allows verifying the result for a two-way design. Induction on the number of factors completes the proof.

Lemma 3

Cell mean, reference cell, effect, polynomial and classical ANOVA coding all create linearly equivalent models. A matrix exists to convert any one to another, with Es(X₁) = Es(X₂)T_2→1 and X₁ = X₂T_2→1. If X₁ and X₂ are full rank then T_2→1 is square and full rank.

Proof

Muller and Fetterman [25] gave a proof.

Parameters necessarily exactly track the design variables. The associated contrast matrices, C and θ₀ for H₀: Cβ = θ₀, must also track the same pattern. One-way design parameters split naturally into the grand mean and the set of group differences. Reference-cell coding uses ${\mathbf{C}}_0(G)=[1{\mathbf{1}}_{G-1}^{\prime }/G]$ for the grand mean, and C_D(G) = [0 I_G−1] for group differences.

For a two-way design, if Es(X_{A × B}) = Es(X_A) ⊗ Es(X_B) then β = β_A ⊗ β_B, with β_{A, j} · β_B,k appropriately interpreted as β_{A, j;B,k}. Similarly, if A has G_A levels, B has G_B levels, then C_{A × B} = C_D(G_A) ⊗ C_D(G_B) allows testing the A × B interaction. Testing A uses C_A = C_D(G_A) ⊗ C₀(G_B), and B uses C_B = C₀(G_A) ⊗ C_D(G_B).

Proof of Theorem 1

(1) Given $p_i\equiv p_{*}{\prod }_{k=1}^m{p}_k$ and y_i ~ 𝒩_p* [X_iβ, Σ_cs(p, ρ, σ)], the mixed model may be written as y_i = X_iβ + e_i by choosing Z_i = 0. (2) Disallowing repeated covariates and missing or mistimed data implies both (a) factorial structure within-subject and (b) the same between-subject design matrix for each observation on subject i, X_B,g(i). (3) With N subjects, the between-subject design matrix is ${\mathbf{X}}_B=[{\mathbf{X}}_{B,g(1)}^{\prime }\dots {\mathbf{X}}_{B,g(N)}^{\prime }]\prime$ an N × q_B matrix with Es(X_B) G × q_B, which implies G groups. (4) By Lemma 1, the full-rank coding may be used for within-subject factor k, giving design matrix X_W,k, p_k × p_k for k ∈ {1, 2, …, m}. (5) By Lemma 2, without loss of generality ${\mathbf{X}}_i=({\otimes }_{k=1}^m{\mathbf{X}}_{W,k})\otimes {\mathit{X}}_{B,g(i)}$ for $p_{*}\times p_{*}({\otimes }_{k=1}^m{\mathbf{X}}_{W,k})$. (6) Hence for the special class of models, β is (q_B · p_*) × 1, and can be written as β = vec(B), with q_B × p_* B = [β₁ … β_p*]. Throughout, Y = [y₁ … y_N]′ and E = [e₁ … e_N]′ are N × p. (7) Cell mean coding may be used within-subject without loss of generality (Lemma 3). Doing so gives

$${\mathbf{y}}_i=\left[\right(\underset{k=1}{\overset{m}{\otimes }}{\mathbf{I}}_{p_k})\otimes {\mathbf{X}}_{B,g(i)}]\mathbf{\beta }+{\mathbf{e}}_i=({\mathbf{I}}_{p_{*}}\otimes {\mathbf{X}}_{B,g(i)})\text{vec}(\mathbf{B})+{\mathbf{e}}_i=\text{vec}([{\mathbf{X}}_{B,g(i)}{\mathbf{\beta }}_1\dots {\mathbf{X}}_{B,g(i)}{\mathbf{\beta }}_{p_{*}}])+{\mathbf{e}}_i=({\mathbf{X}}_{B,g(i)}\mathbf{B})\prime +{\mathbf{e}}_i\iff {\mathbf{y}}_1^{\prime }=({\mathbf{X}}_{B,g(i)}\mathbf{B})+{\mathbf{e}}_i^{\prime }{\text{row}}_i(\mathbf{Y})={\text{row}}_i({\mathbf{X}}_B\mathbf{B})+{\text{row}}_i(\mathbf{E})$$ (A2)

(8) The last equation is equivalent to one row of the multivariate model formulation of UNIREP analysis, as in Muller and Barton [12], namely Y = X_BB + E with i.i.d. [row_i (E)]′ ~ 𝒩_p* [0,Σ_cs (p, ρ, σ)].

Proof of Theorem 2

All notations are the same as in the proof of Theorem 1. (1) Eigenvectors of Σ_cs(p_k, ρ_k, σ_k) are V_pk = [v_0,k V_⊥pk], known constants depending only on p_k, and not on {i, ρ_k, σ_k}. Eigenvalues are ${\mathbf{\lambda }}_{p_k}^{\prime }=[{\lambda }_{1,k}{\lambda }_{2,k}{\mathbf{1}}_{p_k-1}^{\prime }]$, with ${\lambda }_{1,k}={\sigma }_k^2\{1+(p_k-1){\rho }_k\}$ and ${\lambda }_{2,k}={\sigma }_k^2(1-{\rho }_k)$. The first eigenvector is ${\mathbf{v}}_{0,k}={\mathbf{1}}_{p_k}{p}_k^{-1/2}$. The remaining eigenvectors, V_⊥pk, may be taken to be the orthonormal polynomial trends for p_k points. (2) Therefore,

$${\mathbf{\Sigma }}_{\mathrm{c}\mathrm{s}}(\mathbf{p},\mathbf{\rho },\mathbf{\sigma })=\underset{k=1}{\overset{m}{\otimes }}[{\mathbf{V}}_{p_k}\mathrm{D}\mathrm{g}({\mathbf{\lambda }}_{p_k})\mathbf{V}{\prime }_{p_k}]=\left(\underset{k=1}{\overset{m}{\otimes }}{\mathbf{V}}_{p_k}\right)[\underset{k=1}{\overset{m}{\otimes }}\mathrm{D}\mathrm{g}({\mathbf{\lambda }}_{p_k})]\left(\underset{k=1}{\overset{m}{\otimes }}\mathbf{V}{\prime }_{p_k}\right)$$ (A3)

(3) Premultiplying by $\mathbf{T}={\otimes }_{k=1}^m{\mathbf{V}}_{p_k}^{\prime }$ a matrix of known constants gives

$$\mathbf{T}{\mathbf{y}}_i=\mathbf{T}{\mathbf{X}}_i\mathbf{\beta }+\mathbf{T}{\mathbf{e}}_i$$ (A4)

$${\mathbf{y}}_{i*}={\mathbf{X}}_{i*}\mathbf{\beta }+{\mathbf{e}}_{i*}$$

and ${\mathbf{e}}_{i*}~{𝒩}_n[\mathbf{0},{\otimes }_{k=1}^m\mathrm{D}\mathrm{g}\{\mathbf{\lambda }(p_k,{\rho }_k,{\sigma }_k)\}]$. (4) Considering all observations gives

$$({\mathbf{I}}_N\otimes \mathbf{T}){\mathbf{y}}_{\mathrm{s}}=({\mathbf{I}}_N\otimes \mathbf{T}){\mathbf{X}}_{\mathrm{s}}\mathbf{\beta }+({\mathbf{I}}_N\otimes \mathbf{T}){\mathbf{e}}_{\mathrm{s}}$$ (A5)

$${\mathbf{y}}_{\mathrm{s}*}={\mathbf{X}}_{\mathrm{s}*}\mathbf{\beta }+{\mathbf{e}}_{\mathrm{s}*}$$

and ${\mathbf{e}}_{\mathrm{s}*}~{𝒩}_n(\mathbf{0},{\mathbf{I}}_N\otimes [{\otimes }_{k=1}^m\mathrm{D}\mathrm{g}\{\mathbf{\lambda }(p_k,{\rho }_k,{\sigma }_k)\}])$. Hence, all n = N · p (Gaussian) elements of ei* are statistically independent, although usually not homogeneous. (5) With only two distinct eigenvalues per factor, exactly 2^m distinct variances exist in 𝒱(e_s*). (6) Here, (I_N ⊗ T) is n × n and full rank which ensures y_s = X_sβ + e_s is linearly equivalent to y_s* = X_s*β + e_s*. (7) Permuting all observations into sets with the same variance within each set defines 2^m distinct models with i.i.d. errors. Jointly the models allow estimating β, which is the complete set of parameters in the original model.