Extending the Range for Force Calibration in Magnetic Tweezers

Abstract

Magnetic tweezers are a wide-spread tool used to study the mechanics and the function of a large variety of biomolecules and biomolecular machines. This tool uses a magnetic particle and a strong magnetic field gradient to apply defined forces to the molecule of interest. Forces are typically quantified by analyzing the lateral fluctuations of the biomolecule-tethered particle in the direction perpendicular to the applied force. Since the magnetic field pins the anisotropy axis of the particle, the lateral fluctuations follow the geometry of a pendulum with a short pendulum length along and a long pendulum length perpendicular to the field lines. Typically, the short pendulum geometry is used for force calibration by power-spectral-density (PSD) analysis, because the movement of the bead in this direction can be approximated by a simple translational motion. Here, we provide a detailed analysis of the fluctuations according to the long pendulum geometry and show that for this direction, both the translational and the rotational motions of the particle have to be considered. We provide analytical formulas for the PSD of this coupled system that agree well with PSDs obtained in experiments and simulations and that finally allow a faithful quantification of the magnetic force for the long pendulum geometry. We furthermore demonstrate that this methodology allows the calibration of much larger forces than the short pendulum geometry in a tether-length-dependent manner. In addition, the accuracy of determination of the absolute force is improved. Our force calibration based on the long pendulum geometry will facilitate high-resolution magnetic-tweezers experiments that rely on short molecules and large forces, as well as highly parallelized measurements that use low frame rates.

Introduction

In magnetic tweezers experiments, a strong magnetic field gradient is used to exert force and twist onto single biomolecules that are attached to magnetic particles (1,2). In addition, to ascertain dynamical or force-induced conformational changes, the length of the biomolecular tether under tension is determined. For this, camera-based particle tracking is typically applied (3–7). Magnetic tweezers have been widely used to study the mechanical properties of biological (8,9) and synthetic (10) polymers, to investigate the response of DNA upon supercoiling (1,11–15), and to resolve the real-time dynamics of DNA-interacting proteins, such as DNA-binding proteins (16–18), enzymes that regulate DNA supercoiling (19–21), and molecular motors (22–27).

A quantitative understanding of any experiment performed with magnetic tweezers requires precise knowledge of the applied forces, e.g., to extract the mechanical parameters of polymers in force-extension measurements (8,9) and to study the force (23,28) or torque (18,21) dependence of biomolecular processes. The forces acting on the molecule of interest are most often derived from the thermal fluctuations of the tethered particle in a direction perpendicular to the applied force, referred to here as lateral direction (29,30). However, the finite camera acquisition frequency influences the noise measurements due to averaging over high-frequency components (low-pass filtering) and aliasing (31). Therefore, fluctuations are typically analyzed in the frequency domain using power spectral density (PSD) analysis (3,32). This makes it possible to correct for the acquisition artifacts as well as for low-frequency drift in the bead-position trajectories.

The magnetic bead at the end of the molecular tether can be thought of as an inverted pendulum oscillating around its point of equilibrium in the lateral direction. However, the motion in the two lateral directions differs, because the magnetization of the superparamagnetic particles typically used in such experiments is anisotropic. This effectively pins the anisotropy axis of the beads to the direction of the magnetic field (30). For the most common magnetic-field configuration (with the field in the lateral direction), this causes two different pendulum lengths: 1) a short pendulum for displacements along the magnetic field, for which the pendulum length equals approximately the tether length due to the pinned particle orientation; and 2) a long pendulum in the direction perpendicular to the magnetic field, for which the pendulum length can be modeled by the sum of the tether length and the bead radius, since the bead is free to rotate around the field direction (Figs. 1 and 2). Until now, the short-pendulum configuration generally has been used for force calibration, since in the first approximation only the translational motion of the bead in this direction has to be considered.

Figure 1.

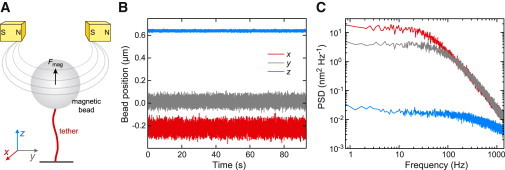
(A) Scheme of the experimental setup. (B) Time trajectories for the x, y, and z positions of a magnetic bead with a nominal radius of ∼520 nm attached to a 1.9-kbp-long DNA molecule held at a force of 4.9 ± 0.1 pN. The position signals were recorded at 2800 Hz. (C) Power spectral densities (PSDs) for the time trajectories shown in (B). The spectra shown were obtained by averaging 40 individual PSDs.

Figure 2.

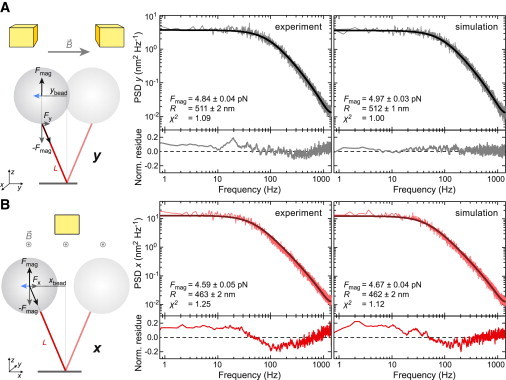
Fits of PSD spectra for lateral bead fluctuations considering only a single oscillator. (A) Bead fluctuations along the magnetic field lines (y direction). In this direction, the bead orientation remains fixed (see sketch at left), such that the effective pendulum length of the bead-DNA system equals the DNA length. Shown are the PSDs (light gray) of an experimentally determined and a simulated position trajectory, as well as fits (dark gray) to the data that are based on a single Lorentzian according to Eqs. 5 and 6. (B) Bead fluctuations perpendicular to the magnetic field lines (x direction). When approximated by a simple pendulum (see sketch at left), its effective length equals to the sum of the DNA length and the bead radius due to the bead rotation accompanying the DNA displacement. Shown are the PSDs (light red) of an experimentally determined and a simulated position trajectory, as well as the fit (dark red) to the data based on a single Lorentzian according to Eqs. 5 and 7. The fit residues normalized by the PSD at the given frequency are shown below the PSD spectra. Values provided in the graphs were obtained from the fits. Experiments were carried out using 1.9-kbp-long DNA molecules and beads with a nominal radius of ∼520 nm. The simulation was carried out for a force of 4.92 pN and a bead radius of 515 nm.

In recent studies, tethers with reduced length (shorter than the bead diameter) have been used more frequently (6,24,26,33,34), particularly in high-resolution magnetic-tweezers measurements, due to their increased stiffness along the molecule axis. Such tethers represent a severe challenge for direct force calibration. First, the force accuracy suffers from the increased error in determining the molecule length. Second, the bead fluctuations are shifted to higher frequencies at which acquisition artifacts become limiting when using camera frame rates on the order of 100 Hz (35). An increased pendulum length promises to overcome both of these limitations. Therefore, in previous studies, the force as a function of magnet position in short-tether experiments was inferred indirectly from calibration measurements on long tethers using the same bead type (33,36). In this case, an increased force error due to bead-to-bead variations of the magnetic moment has either to be acceptable or additionally to be corrected. Alternatively, however, an increased pendulum length can be achieved by calibrating the forces using the long-pendulum geometry, where the pendulum length comprises the bead radius in addition to the tether length (33). This promises a direct, and thus more precise, calibration even on short tethers. For this reason, we investigate here in detail the use of the long-pendulum geometry for force calibration in magnetic tweezers and compare it for the same tether length to results obtained for the short-pendulum geometry. Using bead tracking at kHz rates (6), as well as Brownian dynamics simulations, we show that for the long pendulum, the lateral and also the rotational displacement of the bead has to be considered to allow a correct analysis of the PSDs. We derive an analytic model for this type of bead motion that returns accurate values for the force and the bead radius when fitting experimental and simulated data. Due to the effective pendulum elongation, the bead fluctuations are shifted to lower frequencies. Compared to the short-pendulum geometry, this significantly increases the maximum force that can be calibrated at a given frame rate. In addition, the absolute force accuracy is improved and the method is much less sensitive to underestimations of the DNA length (e.g., in the case of off-center attached tethers). We therefore recommend the use of our force-calibration scheme based on the long-pendulum geometry on a routine basis. We note that our procedure does not require any technical modifications of the established magnetic tweezers technology. To facilitate its application, we provide a software tool that implements this method.

Materials and Methods

DNA substrate preparation

The DNA substrates for the magnetic tweezers experiments were prepared as previously described (15,22). For the 1.9 kbp construct (15), a custom-made plasmid was digested using the restriction enzymes XhoI and PvuI, providing a linear 1865 bp fragment with corresponding sticky ends on either side. Biotin- or digoxigenin-modified attachment handles were made by digesting a 1.2 kbp biotin- and a digoxigenin dUTP-labeled PCR fragment from plasmid pBluescript II SK+ (Stratagene, La Jolla, CA) with XhoI or PvuI, respectively, approximately in the middle of the fragments. The labeled fragments were subsequently ligated to the 1865 bp fragment and purified from an agarose gel, avoiding exposure to ethidium bromide or ultraviolet light (37). For the 6.6 kbp construct (22), plasmid pNLrep (37) was digested with BsrGI and BamHI, ligated to correspondingly digested biotin and digoxigenin handles, and then purified.

Sample preparation

Fluidic cells for the magnetic tweezers experiments were built from two coverslips and a cut parafilm spacer that formed the final chamber. The bottom coverslip was spin-coated on the inside with polystyrene before cell assembly. 3 μm carboxylated polystyrene beads (Invitrogen, Carlsbad, CA) in 1 M NaCl were added and incubated for at least 1 h to ensure adherence to the polystyrene film. The fluidic cell was incubated with 50 μg/mL antidigoxigenin in phosphate-buffered saline for 1 h. Afterward, it was incubated for 1 h with 10 mg/mL bovine serum albumin to prevent nonspecific binding to the bottom of the cell. DNA constructs were bound to streptavidin-coated superparamagnetic microspheres with nominal radii of 0.52 or 1.4 μm (MyOne or M-280 beads, respectively; Invitrogen) and flushed into the fluidic cell. The measurements were performed at room temperature in phosphate-buffered saline at pH 7.5.

Magnetic tweezers

Our high-resolution magnetic tweezers setup has been described previously (6). It consists of a home-built inverted microscope equipped with a 100× (NA 1.25) objective (Olympus, Center Valley, PA). The bead sample was mounted onto a piezo-actuated nanopositioning stage (P-517.3CD, Physik Instrumente, Karlsruhe, Germany). The sample was illuminated using either a fiber-coupled mercury arc lamp (LSB610, LOT-Oriel, Darmstadt, Germany) equipped with a 550/100 nm band-pass filter (AHF Analysentechnik, Tübingen, Germany) for 2.8 kHz data acquisition or an LED emitting around 625 nm (CR5111AWY, Roithner Lasertechnik, Vienna, Austria) for 300 Hz data acquisition. Imaging was carried out with a high-speed CMOS camera (EoSens CL MC1362, Mikrotron, Unterschleissheim, Germany). Two permanent NeFeB magnets (W-05-N50-G, Supermagnete, Gottmadingen, Germany) mounted onto a motorized stage above the sample were used to generate the magnetic field gradient for the magnetic tweezers experiments. Images were streamed to a computer (Precision T7500 Work Station, Dell, Round Rock, TX) equipped with an image acquisition card (NI PCIe 1429, National Instruments, Austin, TX) and a fast GPU (GeForce GTX 480, Nvidia, Santa Clara, CA) and analyzed in real time (6).

PSD calculation and fitting

PSDs were calculated from long position trajectories that were split into n = 40 parts of equal length. PSDs of these subtrajectories were averaged to provide the PSD plots shown. Applied forces and bead radii were obtained by fitting the PSDs using Eqs. 5 and S13, which directly provided values for the force and the bead radius. Direct-weighted fitting of PSD data was carried out as described by Flyvbjerg and co-workers (38,39) using the theoretical expectation value for the standard deviation as weight (38). This overestimates the amplitude of the theoretically expected PSD by (n + 1)/n (39). To account for this, the fitting is in practice accomplished by standard least-mean-square fitting of the reciprocal experimental PSD $S_a^{\text{exp}}{\left(f\right)}^{-1}$ with the inverse bias-corrected theoretical PSD, $S_a^{\text{theor}}{\left(f\right)}^{-1}n/\left(n+1\right)$ (38), where $S_a^{\text{theor}}$ corresponds to the expressions given in Eqs. 5 and S13. The weight is then provided by $S_a^{\text{exp}}{\left(f\right)}^{-1}/\sqrt{n}$. This PSD fitting method results in parameters with considerably smaller stochastic errors compared to unweighted fitting. It is bias-free and numerically robust (39). A software in Labview (National Instruments) that implements PSD analysis for magnetic tweezers using the formulas that are derived in this manuscript is available for download at the author’s homepage (http://www.uni-muenster.de/Biologie.AllgmZoo/Gruppen/Seidel/Download).

Brownian dynamics simulations

Brownian dynamics simulations were carried out using software written in Labview based on the explanations and equations provided in Results. For the simulation time increment, Δt_sim, values between 1 μs and 10 μs were chosen, such that δa_diff for a given coordinate a (see Results) was small compared to the mean-square displacement $\langle a^2\rangle$ over long times. The total simulation time for a given condition varied between 10 and 300 s. Averaging over the positions of subsequent time points provided the down-sampling of the simulated position trajectory to a similar rate that was used in the experiments. Simulated position trajectories were subjected to the PSD calculation and force calibration procedure described above.

F_DNA, the force that the tethered DNA exerts on the bead, was calculated from the DNA length, L, at a given time point using the Marko-Siggia formula for an extensible wormlike-chain (WLC) model, which includes the entropic and elastic elasticity of DNA (40,41):

$$F_{\text{DNA}}=\frac{k_{\text{B}}T}{p}\left[\frac{1}{4{\left(1-L/L_0+F_{\text{DNA}}/S\right)}^2}-\frac{1}{4}+\left(\frac{L}{L_0}-\frac{F_{\text{DNA}}}{S}\right)\right],$$ (1)

where L₀ is the DNA contour length, p the persistence length, S the DNA stretch rigidity, k_B the Boltzmann constant, and T the temperature. For Eq. 1, an analytical solution was obtained for F_DNA using Cardano’s method. The full solution is given in the Supporting Material. We note that the solution for F_DNA can be inserted into an improved version of the Marko-Siggia formula (42) to obtain a more precise analytical function for the force-extension relation of an extensible WLC molecule. The resulting equation (see Supporting Material and Fig. S1) provides a precise and convenient way to fit force-extension data of double-stranded DNA between 0.1 and 40 pN.

Results

Force calibration in magnetic tweezers through PSD analysis

To calibrate magnetic tweezers, typically a simple pendulum model in the limit of small displacements is used (29,30). The magnetic bead, at which the force F_mag is acting, is assumed to be attached to a rigid rod of length l (Fig. 1). When displacing the pendulum laterally by a distance a, the backdriving force is given by F_a = −F_mag/l × a. This expression is equivalent to the behavior of a Hookean spring with the spring constant k_a = F_mag/l. Using the equipartition theorem, one can write, for the thermally induced mean-square displacement of the pendulum along a,

$$E_{\text{therm}}=\frac{1}{2}{k}_a\langle a^2\rangle =\frac{1}{2}{k}_{\mathrm{B}}T,$$ (2)

where k_B is the Boltzmann constant and T the temperature. This directly provides the acting magnetic force using the lateral bead fluctuations:

$$F_{\text{mag}}=\frac{k_{\mathrm{B}}T}{\langle a^2\rangle }l.$$ (3)

In practice, $\langle a^2\rangle$ is typically not calculated from the variance of a long time trajectory of the pendulum position, a. Rather k_a, and thus F_mag, are obtained in the frequency domain to avoid artifacts from the camera acquisition and instrument drift.

The dynamics of a Hookean spring coupled to an element with viscous drag coefficient γ_a is described by a Lorentzian function for the (single-sided) PSD (31):

$$S_a\left(f\right)=\frac{4k_{B}T{\gamma }_a}{k_a^2}\frac{1}{1+{\left(f/f_c\right)}^2},$$ (4)

where f is the frequency and the characteristic cutoff frequency is f_c = k_a/(2πγ_a). For magnetic tweezers, the bead position is determined from camera images taken at sampling frequency f_s. Each image provides a mean position of the bead over the exposure time τ_e of the camera such that the amplitude of high-frequency movements averages out. Furthermore, all frequencies larger than half the sampling frequency of the camera are seen as lower-frequency components—an effect called aliasing. Both low-pass filtering and aliasing provide the following corrections to the PSD from Eq. 4 (30,32,35):

$$S_a^{\text{corr}}\left(f\right)=\sum _{n=-\infty }^{\infty }\frac{4k_{B}T{\gamma }_a}{k_a^2}\frac{1}{1+{\left(\left|f+n{f}_{\text{s}}\right|/f_{\text{c}}\right)}^2}\frac{{\text{sin}}^2\left(\pi {\tau }_{\text{e}}\left|f+n{f}_{\text{s}}\right|\right)}{{\left(\pi {\tau }_{\text{e}}\left|f+n{f}_{\text{s}}\right|\right)}^2},$$ (5)

with 0 < f < f_s/2. The term for n = 0 provides the native PSD (Eq. 4) corrected for low-pass filtering by the camera, whereas the higher-order summands provide the high-frequency contributions to the low-frequency spectrum due to the aliasing correction. When f_s = 1/τ_e, aliasing is sufficiently corrected by the term for n = −1 only (35), as applied throughout this article. We note that for f_s = 1/τ_e, an analytic solution for the whole sum in Eq. 5 is also available (32).

The formula for the corrected PSD is then used to fit the PSD calculated from the measured time trajectory along a. This way, k_a and F_mag are obtained (see below).

Simple harmonic model describes fluctuations for the short, but not the long, pendulum

In typical magnetic-tweezers experiments on single biomolecular or synthetic tethers, a magnetic field gradient, and thus a magnetic force, is applied in the vertical direction, whereas the actual magnetic field is oriented in the horizontal direction (here referred to as the y direction; see Fig. 1 A). Since the magnetization of the beads is anisotropic (30), the beads align with their anisotropy axis parallel to the field lines. Thus, the bead orientation is pinned for bead movements along y, such that the effective pendulum length equals the length, L, of the DNA molecule at the given force. In this situation we get

$$k_y=\frac{F_{\text{mag}}}{L}\text{and}{\mathit{\gamma }}_{\text{y}}=6\mathit{\pi \eta R}\times {\mathit{C}}_{\mathrm{\parallel }}\left(\mathit{L}\right),$$ (6)

where η is the viscosity of the solution, R the bead radius, and $C_{\parallel }$ (L) a correction of the Stokes drag coefficient for translational movements parallel to the nearby surface at distance L (see Supporting Material).

Alternatively, one can consider the lateral fluctuations perpendicular to the field (x direction in here, see Fig. 1 B). The bead is free to rotate around its anisotropy axis. Therefore, along x the effective pendulum stretches from the bead center to the molecule attachment at the surface and its length is L + R. When assuming a perfectly stretched pendulum with the bead center and both DNA attachment points located all on one line we now get:

$$k_x=\frac{F_{\text{mag}}}{L+R}\text{and}{\mathit{\gamma }}_{\text{x}}=6\mathit{\pi \eta R}\times {\mathit{C}}_{\mathrm{\parallel }}\left(\mathit{L}\right)+\frac{8\pi \eta R}{{\left(1+L/R\right)}^2}{C}_{\varphi }\left(L\right),$$ (7)

where the second term in the sum for γ_x is due to the additional rotational motion of the bead accompanying every lateral displacement. C_φ(L) is the correction term of the rotational drag coefficient for rotational motions near the surface at distance L (see Supporting Material).

To test whether consistent results are obtained when calibrating the magnetic force using fluctuations either along x or along y, we attached magnetic beads with a nominal radius of 0.52 μm to 1.9-kbp-long DNA molecules. We recorded a long time trajectory of the magnetic bead position in all three dimensions with respect to a reference particle at a fixed magnet position. High-speed real-time tracking was carried out at 2800 Hz (6). The PSDs were calculated for the position trajectories along x and y. Subsequently, they were subjected to a weighted fit with Eq. 5 that was corrected for amplitude bias (see Materials and Methods). The relations for the spring constants and the drag coefficients (Eqs. 6 and 7) were directly inserted into Eq. 5, such that the fit directly provided values for the force and the bead radius. For L, we used the average DNA extension along z (i.e., the height of the bead at the given force above the surface) from the same measurement. When the fit model describes the experimental data, the reduced χ² is expected to approach a value of 1 for the weights applied.

For the fluctuations along y, the experimental PSD was well fitted by the model (χ² = 1.09), providing a force of 4.84 ± 0.04 pN and a bead radius of 511 ± 2 nm (Fig. 2 A). Along x, the fit residue displayed significant systematic deviations over the entire frequency range, with χ² = 1.25 being ≫1 (Fig. 2 B). The obtained force of 4.59 ± 0.05 pN was significantly lower than that for y, and the bead radius of 463 ± 2 nm was ∼10% lower than expected. This suggests that the fluctuations perpendicular to the magnetic field lines are not well described by the simple harmonic model.

Brownian dynamics simulations reproduce the difference for both pendulum directions

To investigate the origin of the more complex PSD form for fluctuations along x, we set up Brownian dynamics simulations for the magnetic bead. We considered the translational motion of the bead in all three dimensions and, as an extension of previous work (35), also its rotational motion around the center axis along y. For each type of displacement, we calculated at each simulation step the acting force, F_a, (torque for rotation) and a random displacement due to the particle diffusion, δa_diff. The displacement (translational or angular) per simulation step in a given direction was calculated by

$$\Delta a=\frac{F_a}{{\gamma }_a}\Delta t_{\text{sim}}+\delta a_{\text{diff}},$$ (8)

where Δt_sim is the time increment between simulation steps. δa_diff was drawn randomly from Gaussian distributed values with variance 2k_BT/γ_a × Δt_sim. For the four bead coordinates x_bead, y_bead, z_bead, and φ_bead (the angular position of the DNA attachment point in the xz plane; see Fig. 3 A), the coordinates of the DNA attachment point at the bead were obtained from x_DNA = x_bead + R∙sin(φ_bead), y_DNA = y_bead and z_DNA = z_bead − R × cos(φ_bead). The stretching force of the DNA F_DNA is calculated from the DNA length $L=\sqrt{x_{\text{DNA}}^2+y_{\text{DNA}}^2+z_{\text{DNA}}^2}$ using the extensible WLC model (see Materials and Methods). With this, the forces for translational displacements of the bead are given by:

$$\begin{array}{c}{F}_x=-F_{\text{DNA}}\times x_{\text{DNA}}/L\\ F_y=-F_{\text{DNA}}\times y_{\text{DNA}}/L\\ F_z=-F_{\text{DNA}}\times z_{\text{DNA}}/L+F_{\text{mag}}\end{array}.$$ (9)

For the rotational displacement, the torque on the bead is calculated from the cross product of the bead’s radial vector to the DNA attachment point, $\overrightarrow{R}$ and ${\overrightarrow{F}}_{\text{DNA}}$ (Fig. 3 A), providing

$${\Gamma }_{\varphi }=-F_{\text{DNA}}\times R/L\left(x_{\text{DNA}}\text{cos}{\varphi }_{\text{bead}}+z_{\text{DNA}}\text{sin}{\varphi }_{\text{bead}}\right).$$ (10)

The drag coefficients are provided by

$$\begin{array}{c}{\gamma }_{x,y}=6\pi \mathit{\eta R}\times {\mathit{C}}_{\mathrm{\wedge }}\left(\mathit{L}\right)\text{for}\text{lateral}\text{translational}\text{displacements}\text{along}\mathit{x}\text{or}\mathit{y},\\ {\mathit{\gamma }}_z=6\mathit{\pi \eta R}\times {\mathit{C}}_{\mathrm{\perp }}\left(\mathit{L}\right)\text{for}\text{axial}\text{displacements}\text{and}\\ {\gamma }_{\phi }=8\pi \mathit{\eta }{\mathit{R}}^3\times C_{\phi }\left(L\right)\text{for}\text{angular}\text{displacements},\end{array}$$ (11)

where $C_{\mathrm{\perp }}$ (L) is the surface correction factor for axial displacements.

Figure 3.

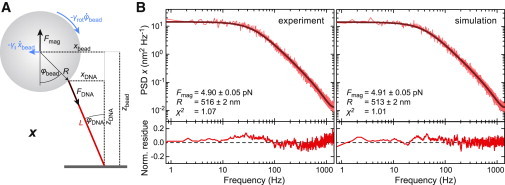
Fitting the PSD spectra for the lateral bead fluctuations perpendicular to the magnetic field lines considering two coupled oscillators. (A) More realistic scheme of the bead-DNA system where the angular displacement of bead and DNA are allowed to differ from each other. (B) PSDs (light red) of the experimentally determined and the simulated position trajectory from Fig. 2 and fits (dark red) to the data that are based on a double Lorentzian according to Eq. S13. The fit residues normalized by the PSD at the given frequency are shown below the PSD spectra. Values provided in the graphs were obtained from the fits. The simulation was carried out using a force of 4.92 pN and a bead radius of 515 nm.

Using the above equations, we carried out simulations of the bead position using R = 515 nm, L₀ = 700 nm, F_mag = 4.92 pN, and Δt_sim = 1 μs. Averaging over 357 subsequent positions provided time trajectories with a time increment close to the experimental sampling rate of 2800 Hz.

The PSD for the trajectories along y was well fit by the simple harmonic model (Eq. 5) providing χ² = 1.0. The obtained values for the magnetic force (4.97 ± 0.03 pN) and the bead radius (512 ± 1 nm) were close to the input parameters for the simulations (Fig. 3 A). In contrast to this, but in agreement with the experiments, the fit of the PSD for the x coordinate provided significant systematic deviations (χ² = 1.16). Also, significantly lower values for force (4.67 ± 0.04 pN) and radius (462 ± 2 nm) were obtained compared to the input parameters. This suggests that our simulation model reproduces the main components for describing the bead motion in both lateral directions. Considering the equations for the simulations (see above), the only mathematical difference arises from the addition of the rotational fluctuations of the bead that will manifest themselves in the x, but not the y, coordinate. Therefore, we hypothesize that the rotational fluctuations cause the more complex form of the PSD along x.

An analytical solution for the PSD with both lateral and angular bead displacements

We sought to derive a formula for the PSD along x by considering rotational bead displacements in addition to the lateral translation (see Fig. 3 A). In the limit of small displacements for x_DNA and φ, we can in first order approximate z_DNA ≈ L and F_DNA ≈ F_mag considering DNA to be a stiff rod with fixed length. With this, Eq. 10 becomes

$${\Gamma }_{\varphi }\approx -F_{\text{mag}}\times R\left(\frac{x_{\text{DNA}}}{L}+{\varphi }_{\text{bead}}\right)=-F_{\text{mag}}\times R\left(\frac{x_{\text{DNA}}}{L}-\frac{x_{\text{bead}}-x_{\text{DNA}}}{R}\right),$$ (12)

where we approximated φ_bead with –(x_bead − x_DNA)/R.

With the acting random force for bead translation, F_trans(t), and the random torque for bead rotation, –F_rot(t) × R, one can now describe the system by a set of Langevin equations:

$$\begin{array}{c}-{\gamma }_{\varphi }{\dot{\varphi }}_{\text{bead}}+{\Gamma }_{\varphi }=-F_{\text{rot}}\left(t\right)\times R\\ -{\gamma }_x{\dot{x}}_{\text{bead}}+F_x=F_{\text{trans}}\left(t\right)\end{array}.$$ (13)

Inserting Eqs. 9, 11, and 12, and substituting φ with –(x_bead − x_DNA)/R and x_DNA with x_bead − x_rot, Eq. 13 becomes

$$\begin{array}{c}-\frac{{\gamma }_{\varphi }}{R^2}{\dot{x}}_{\text{rot}}-F_{\text{mag}}\left(\frac{1}{L}+\frac{1}{R}\right)x_{\text{rot}}+\frac{F_{\text{mag}}}{L}{x}_{\text{bead}}=F_{\text{rot}}\left(t\right)\\ -{\gamma }_x{\dot{x}}_{\text{bead}}+\frac{F_{\text{mag}}}{L}{x}_{rot}-\frac{F_{\text{mag}}}{L}{x}_{\text{bead}}=F_{\text{trans}}\left(t\right)\end{array}.$$ (14)

For such a form of coupled linear Langevin equations, an analytic expression for the PSD of x_bead was derived previously (30), and we obtain:

$$S_x^{\text{coupl}}\left(f\right)=\frac{4k_{\text{B}}T}{{\left(2\pi \right)}^2\left(1+C^2{\gamma }_x{\gamma }_{\varphi }/R^2\right)}\left(\frac{{\gamma }_{\varphi }{C}^2}{R^2}\frac{1}{f_{+}^2+f^2}+\frac{1}{{\gamma }_x}\frac{1}{f_{-}^2+f^2}\right),$$ (15)

with $C=2\pi f_{+}L/F_{\text{mag}}-\left(L+R\right)R/{\gamma }_{\varphi }$ and f_± being the characteristic frequencies of the system:

$$2\pi f_{\pm }=\frac{F_{\text{mag}}}{L}\left[\frac{\left(L+R\right)R}{2{\gamma }_{\varphi }}+\frac{1}{2{\gamma }_x}\pm \frac{1}{2}\sqrt{{\left(\frac{\left(L+R\right)R}{{\gamma }_{\varphi }}+\frac{1}{{\gamma }_x}\right)}^2-\frac{4LR}{{\gamma }_x{\gamma }_{\varphi }}}\right].$$ (16)

The PSD for the coupled translational and rotational fluctuations is a sum of two Lorentzians. The characteristic frequencies correspond to the normal modes of the system. The lower characteristic frequency, f₋, is therefore very similar, but not identical, to the cutoff frequency that is calculated from the spring constant and the drag coefficient given by Eq. 7 for the naive pendulum of length R + L. Equation 15 is considerably more complex than the simple Lorentzian PSD given by Eq. 4. However, it is worth mentioning that it does not contain additional parameters.

Fluctuations of the long pendulum are described by coupled translational and rotational bead motions

We used Eq. 15 to fit the PSDs for bead motions perpendicular to the magnetic field. To this end, we applied the corrections for low-pass filtering by the camera and aliasing as described above (see Eq. 5), providing an analytical solution of the corrected PSD for coupled translational and rotational fluctuations (see Eq. S13 for the full formula). When fitting the PSDs from experiment and simulation, the newly derived equation provided substantially improved fits, with χ² = 1.07 and 1.01, respectively. The fit residue displayed significantly reduced deviations as compared to the single Lorentzian fit model (Fig. 3). We obtained force values of 4.90 ± 0.05 pN and 4.91 ± 0.05 pN and bead radii of 516 ± 2 nm and 513 ± 2 nm for experiment and simulation, respectively. These values were now very similar to the forces obtained for the y direction, and in the case of the simulations, they were, within error, equal to the input values. This indicates that indeed the double Lorentzian function describes the PSDs for bead movements perpendicular to the magnetic field much better than the simple model does while still using the same number of fitting parameters.

To test whether the different values obtained for the two different fitting models were only specific to the particular experimental conditions, we recorded a set of long position trajectories at 2800 Hz for the same bead and DNA configuration at different applied forces ranging from ∼0.25 pN to ∼12 pN. For the x direction, the forces obtained with the double Lorentzian model agreed within error with the forces determined for the y direction (Fig. 4 A). However, the forces obtained along x with the simple Lorentzian model exhibited deviations of up to 25%. These deviations were most pronounced at low forces and less severe for larger forces. A similar behavior was observed for the bead radii (Fig. 4 B). The double Lorentzian model applied to the fluctuations along x provided radii of ∼515 nm over the whole force range. In a similarway, constant radius values were obtained for the fluctuations along y. For the simple Lorentzian model applied to fluctuations along x, we obtained deviations at low force of up to 20% that decreased to 7% at the highest forces. When evaluating time traces from simulations that mimicked the experimental conditions, we observed a behavior similar to that for the experiments. Analyzing the fluctuations along x with the double Lorentzian model and the fluctuations along y with the single Lorentzian model faithfully returned the input values for the forces and radii. When applying the single Lorentzian model to the fluctuations in x, significantly lower values were obtained for forces and radii. This further corroborates that fluctuations perpendicular to the magnetic field are best described by the double Lorentzian model that considers the bead rotations.

Figure 4.

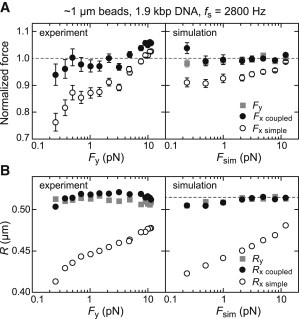
(A) Normalized forces and (B) radii obtained from PSD analysis of experimental (left) and simulated (right) time traces taken at 2800 Hz for different external forces. The experiments used 1.9-kbp-long DNA molecules and magnetic beads with a nominal radius of 525 nm. For the simulations, a DNA contour length of 700 nm and a bead radius of 515 nm (dashed line in B) were applied. Shown are the fit results when analyzing the PSDs, for the y coordinate using a simple Lorentzian (F_y, R_y) and the PSDs for the x coordinate using a simple (F_{x simple}, R_x simple), as well as a double Lorentzian (F_{x coupled}, R_{x coupled}; see legend). Forces from experiments were normalized by F_y and forces from simulations by the applied force, F_sim.

Force calibration using the long pendulum axis at lower acquisition rates

The experimental position trajectories considered so far were acquired using real-time high-speed tracking (6) at a rate of 2800 Hz. However, magnetic tweezers are more typically operated at rates between 60 and 300 Hz (15,29). These rates may already be smaller than the higher characteristic frequency, f₊, of the second Lorentzian of Eq. 15. When fitting the PSD data for the x direction, the contribution of the second Lorentzian may thus be hidden by the dominance of the first Lorentzian in the low-frequency range, such that values similar to those for a single Lorentzian fit would be obtained.

To test whether a double Lorentzian fit would be necessary to obtain correct force and radius values at the acquisition frequencies typically used, we first carried out Brownian dynamics simulations using R = 515 nm and L₀ = 700 nm, as before, but down-sampled the position data to a frequency of 300 Hz. Similar to the simulations at 2800 Hz, a simple Lorentzian fit to the PSD data along x provided a significant underestimation of the bead radius and the force up to 2 pN (compare Figs. S2 and 4). For >7 pN, these parameters were slightly overestimated. Overall, the deviations for the 300 Hz data were less strong compared to the 2800 Hz data, in agreement with our expectations (see above). As anticipated, the double Lorentzian fit returned correct values for force and radius throughout the applied force range (Fig. S2). Analyzing the fluctuations along y also provided correct values for these parameters up to ∼5 pN. Beyond that, incorrect values were returned (Fig. S2), since the cutoff frequency already approached half the sampling frequency due to the shorter pendulum.

To further substantiate the requirement for a double Lorentzian fit for analyzing the fluctuations along x, we carried out additional measurements at a sampling rate of 300 Hz using large magnetic beads with a nominal diameter of 2.8 μm and 6.6-kbp-long DNA molecules. In addition, we performed corresponding Brownian dynamics simulations using R = 1.3 μm and L₀ = 2.3 μm, with the position data being down-sampled to 300 Hz. As for the 2800 Hz data we obtained forces and bead radii by fitting the corresponding PSDs. When applying a single Lorentzian fit to the experimental PSD data along y or a double Lorentzian fit to the PSD data along x, we obtained constant values of ∼1.3 μm for the bead radius throughout the force range (0.8–80 pN) (Fig. 5, A and B). A single Lorentzian fit to the experimental PSD data along x provided up to 20% lower bead radii at lower forces but reached ∼1.3 μm at higher forces (Fig. 5 B). A very similar behavior was observed for the simulated data, suggesting that for the applied conditions, the double Lorentzian model is required to describe correctly the PSDs along x. At small forces, the forces obtained from single Lorentzian fits to the experimental PSD data for both the x and y coordinates were lower than those obtained from the double Lorentzian fit to the PSD along x (Fig. 5 A). At high forces, the single Lorentzian fit to the PSD along x provided values similar to those obtained by the double Lorentzian fit, whereas forces obtained for the y coordinate were again significantly lower. For the simulated data, the forces obtained for the y and x coordinates when we applied a single and a double Lorentzian fit, respectively, reproduced the input force within error. A single Lorentzian fit to the PSDs along x underestimated the input force by up to 8% for forces of 1 and 2 pN, similar to the experimental observation.

Figure 5.

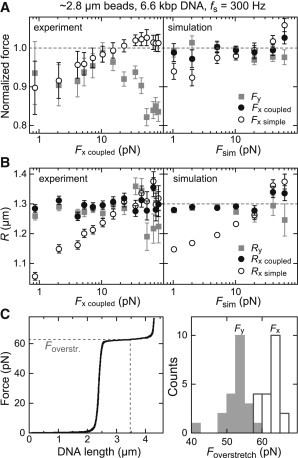
(A) Normalized forces and (B) radii obtained from PSD analysis of experimental (left) and simulated (right) time traces taken at 300 Hz for different external forces. The experiments used 6.6-kbp-long DNA molecules and magnetic beads with a nominal radius of ∼1.4 μm. For the simulations, a DNA contour length of 2.3 μm and a bead radius of 1.3 μm (dashed line in B) were applied. Shown are the fit results when analyzing the PSD for the y coordinate using a simple Lorentzian (F_y, R_y) and the PSD for the x coordinate using a simple (F_{x simple}, R_{x simple}), as well as a double Lorentzian (F_{x coupled}, R_{x coupled}, see legend). Forces from experiments were normalized by F_{x coupled} and forces from simulations by the applied force, F_sim. (C, left) DNA overstretching experiment (force derived from F_{x coupled}). (C, right) Histogram of the overstretching forces from 22 molecules determined using F_{x coupled} (open bars) and F_y (gray bars).

Improved force accuracy for calibrations based on the long pendulum

The results for the 2.8 μm magnetic beads confirm that a double Lorentzian model should be applied when characterizing the PSD for fluctuations perpendicular to the magnetic field. However, it is surprising to note that for these beads the forces obtained from the y coordinate are significantly lower than those obtained for the x coordinate. This behavior was consistently observed for many of the molecules investigated (Fig. S3). To resolve which coordinate provides the correct force, we carried out DNA overstretching experiments. When stretching torsionally unconstrained DNA, the molecule undergoes the so-called overstretching transition at a well characterized force of ∼65 pN (29,43–46). This is seen as an ∼1.7-fold elongation of the molecule at relatively constant force during which B-form DNA either denatures or converts into so-called S-DNA with basepairing maintained. Using the 6.6 kbp DNA substrate we carried out overstretching experiments (Fig. 5 C), for which we calibrated the forces either for the x or the y coordinate. We determined the overstretching force, F_over, as the force reached when half the DNA is overstretched. For the x coordinate, the correct overstretching force of 63 ± 3 pN (mean ± SD) was obtained, whereas the y coordinate returned a value of 52 ± 4 pN (Fig. 5 C). This suggests that the characterization of the fluctuations along x (with the appropriate model) provides a higher accuracy for force calibration in magnetic tweezers experiments than the fluctuations along y (see discussion below).

A possible reason for the underestimation of the forces when using the y coordinate may be that the DNA length has been underestimated, since for this direction the calculated force is directly proportional to the tether length. Since the DNA length at a given force is estimated from the height of the bead above the surface, underestimations can result from an off-center attachment (Fig. 6 A, inset) of the DNA (30) or from asphericities of the magnetic beads. To test the influence of an underestimated DNA length, we carried out Brownian dynamics simulations for increasing off-center attachments (between 0 and 450 nm), applying R = 515 nm, L₀ = 700 nm, and F = 4.92 pN and down-sampling the position data to 300 Hz (see Supporting Material for modifications of the simulation procedure). Indeed, the forces obtained for the y coordinate strongly decreased with increasing off-center attachment (Fig. 6 A; the forces were >40% lower for the largest off-center attachment of 450 nm). The strong force underestimation was found to be directly proportional to the underestimation of the DNA length (Fig. 6 A, solid line). In contrast, the forces obtained for the x coordinate were only mildly affected even for the largest off-center attachment, where a reduction of <5% was obtained. The obtained bead radii decreased slightly with increasing off-center attachment by up to 10% in a similar manner for both coordinates (Fig. 6 B). Similar results were also obtained when sampling the position data at 2800 Hz.

Figure 6.

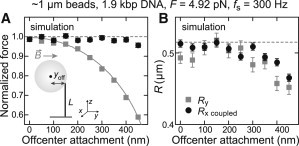
Force calibration for an off-center attachment of the DNA to the magnetic bead. (A) Normalized forces and (B) radii obtained from PSD analysis of simulated time traces taken at 300 Hz for different magnitudes of off-center attachment. For the simulations, a DNA contour length of 700 nm and a bead radius of 515 nm (dashed line in B) were applied. Shown are the fit results when analyzing the PSD for the y coordinate using a simple Lorentzian (F_y, R_y) and the PSD for the x coordinate using a double Lorentzian (F_{x coupled}, R_{x coupled}; see legend). Forces were normalized by the applied force, F_sim. (Inset, A) Sketch of the investigated bead-DNA geometry. The orientation of the magnetic bead is pinned by the magnetic field lines along y. Due to the random attachment position of the DNA on the bead, this leads to an off-center attachment, y_off, of variable degree in this direction. The DNA length is typically estimated from the mean bead height above the surface. It is thus underestimated in the case of an off-center attachment. The solid line in (A) shows the estimated DNA length normalized by the actual DNA length at the given force, which describes well the forces obtained for calibrations based on the short pendulum.

Discussion

Here, we demonstrated that one can use the long-pendulum direction, i.e., the bead fluctuations perpendicular to the applied field (x coordinate), to precisely calibrate the applied force in magnetic tweezers experiments. To do so, the PSD of the bead position had to be fitted with a model that accounted for the additional rotational fluctuations of the bead in this direction that are coupled to the translational motion. We derived an analytical formula for the model that consists of two Lorentzians. Overall, it is remarkable that our fitting model, which considers only a lateral, but not an axial, bead displacement, faithfully returned the applied force and the bead radius over a force range spanning two orders of magnitude (Figs. 4, 5, and S2, A and B). This also strongly suggests that the rotational fluctuations of the bead are the dominating factor for the more complex shape of the PSD along x. Other factors, e.g., a partial pinning of the bead rotation (due to displacement of the anisotropy axis from the magnetic field direction in off-center attached molecules (30)) and the drag coefficient of the DNA itself seem to play less significant roles. However, future refinements of the PSD analysis should consider such deviations from the idealized bead pendulum.

The application of the double Lorentzian fitting function was required not only at kilohertz acquisition rates but also at the lower data acquisition rates more typically used in magnetic tweezers experiments. Deviations of the bead radius returned by the fits from the actual value indicated very sensitively when a simple Lorentzian could not describe the PSD data along x (Figs. 4 B, 5 B, and S2 B) or when acquisition artifacts due to an insufficient sampling rate were too strong (see the high force points for the y coordinate in Fig. S2 A). A stringent determination of the bead radius alongside the force calibration, as performed here, therefore provides an important consistency check.

Our fitting model for the PSD along x relies on the same number of fit parameters as the PSD fitting model along y. It can thus likewise be applied. However, for two reasons we think that the force calibration relying on the long pendulum is to be recommended over that relying on the short pendulum.

• 1.The long-pendulum configuration (x) provides a lower cutoff/characteristic frequency than the short-pendulum configuration (y). As previously determined empirically, the force calibration error rises to ∼10% when the cutoff frequency approaches 40% of the acquisition frequency (35). Thus, the longer pendulum allows calibration of higher maximum forces for a given acquisition rate (see Fig. S2 A) or the usage of lower acquisition rates to calibrate a given force. To obtain a simple guideline for the maximum force that can be calibrated, we provide for different molecule lengths plots of the force-dependent cutoff frequency for the short pendulum using the relation f_c = k_y/(2πγ_y), whose parameters are given by Eq. 6. We furthermore provide the characteristic frequencies f₋ and f₊ for the long pendulum according to Eq. 16 (Fig. 7). The maximum force that can be calibrated is then approximately the point at which f_c, and correspondingly f_−, reach 40% of the applied acquisition frequency (Fig. 7, dashed lines). Particularly for short tether lengths, much higher forces can be calibrated for the long compared to the short pendulum, reaching, for 1 μm beads, an almost threefold difference at L₀ = 0.5 μm and still a 1.4-fold difference at L₀ = 2 μm. The point at which f₊ reaches the 40% limit of the applied acquisition frequency is approximately the force above which a single Lorentzian fit provides results similar to those provided by the double Lorentzian fit to the PSD data of the long pendulum. This rough guideline is in agreement with the data presented here (compare Fig. 7 with Figs. 4, 5 and S2, A and B).
• 2.For the 2.8 μm magnetic beads, the absolute accuracy of the calibrations is significantly better for the long pendulum compared to the short pendulum (Fig. 5). For 1 μm beads, such large differences are not obtained. We attribute the deviations, particularly at low force, to underestimations of the DNA length in the short-pendulum configuration. The DNA is often attached to the magnetic bead in an off-center configuration (30). To obtain the absolute DNA length, the lowest possible bead position (at low force or elevated supercoiling) is determined, with the bead remaining pinned along the field. For molecules with more significant off-center attachment, this returns lower tether lengths and underestimates the real pendulum length and thus the force. Additional length underestimation may result from the significant asphericity of the magnetic beads (47). As shown by the simulations, force determination based on the x direction is much less sensitive to an underestimation of the DNA length (Fig. 6), since the length of the long pendulum (i.e., the distance between the bead center and the surface attachment point of the tether) is still correctly obtained, even in the case of an off-center attachment. In addition, the force underestimation for the short-pendulum configuration may result from rotational fluctuations of the magnetic bead around the x direction due to an imperfect pinning of the particle in the field. Such fluctuations can be observed along the z direction (30) but will appear equally along the y direction on top of the lateral displacement of the bead. Since the pinning stiffness saturates at forces >5 pN, the contribution of these fluctuations will be most pronounced at higher forces.

Figure 7.

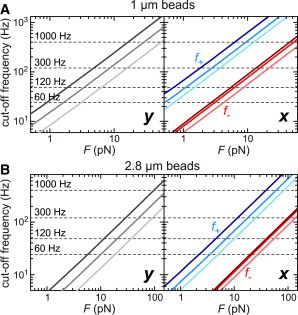
Simple guideline for the maximum force that can be calibrated at a given acquisition frequency for 1 and 2.8 μm beads and different DNA lengths. (A) Cutoff frequencies calculated for 1.03 μm beads for DNA contour lengths of 0.5, 1.0, and 2.0 μm (dark, intermediate, and light levels, respectively, of a given color). Fluctuations along the field lines (left, y-direction) are governed by a single cutoff frequency that was calculated using the relation f_c = k_y/(2π γ_y), where the parameters are given by Eq. 6. Fluctuations perpendicular to the field lines (right, x-direction) are better described using two cutoff frequencies calculated according to Eq. 16. (B) Cutoff frequencies calculated for 2.8 μm beads for DNA contour lengths of 1, 2, and 4 μm calculated as described in (A). Horizontal dashed lines represent the maximum possible cutoff frequency for the indicated acquisition frequency at which the force calibration error does not exceed 10%. As previously determined empirically, the force calibration error reaches ∼10% when the cutoff frequency approaches 40% of the acquisition frequency. The force calibration limit can be determined from the crossing point of solid and dashed lines for the given molecule length and acquisition frequency. For fluctuations along x, crossing points with the plots for f₋ should be taken to estimate the force calibration limits, whereas crossing points with the plots for f₊ provide the approximate upper limit up to which the double Lorentzian PSD fit significantly outperforms the single Lorentzian PSD fit. To see this figure in color, go online.

Conclusions

In summary, we demonstrate here that forces in magnetic tweezers experiments can be faithfully obtained based on the lateral fluctuations of the bead perpendicular to the magnetic field. This significantly expands the upper end of the force range that can be calibrated at a given tether length and acquisition rate, for which we provide a simple guideline (see Fig. 6). Our method is therefore particularly recommended for applications involving high forces, limiting molecule lengths, or low frame rates, such as high-resolution tracking of molecular motors (6,24,26), mechanical sequencing of DNA (34), or highly parallelized measurements on many molecules (48–50). In general, our calibration scheme does not exhibit any disadvantages compared to calibrations based on the short-pendulum geometry. Since it is less sensitive to underestimations of the DNA length, and since, also, the absolute force accuracy is improved when using large magnetic particles, we recommend that our method is used on a routine basis and provides analytical formulas (Eqs. 15 and S13) as well as a software implementation for convenient PSD fitting.

Author Contributions

R.S. designed the research; P.D., H.B., and A.H. performed the research; D.J.K. contributed analytic tools; R.S. and P.D. analyzed the data; and R.S. wrote the article.

Supporting Citations

References (51–54) appear in the Supporting Material.