Cell Shape Dynamics Reveal Balance of Elasticity and Contractility in Peripheral Arcs

Abstract

The mechanical interaction between adherent cells and their substrate relies on the formation of adhesion sites and on the stabilization of contractile acto-myosin bundles, or stress fibers. The shape of the cell and the orientation of these fibers can be controlled by adhesive patterning. On nonadhesive gaps, fibroblasts develop thick peripheral stress fibers, with a concave curvature. The radius of curvature of these arcs results from the balance of the line tension in the arc and of the surface tension in the cell bulk. However, the nature of these forces, and in particular the contribution of myosin-dependent contractility, is not clear. To get insight into the force balance, we inhibit myosin activity and simultaneously monitor the dynamics of peripheral arc radii and traction forces. We use these measurements to estimate line and surface tension. We found that myosin inhibition led to a decrease in the traction forces and an increase in arc radius, indicating that both line tension and surface tension dropped, but the line tension decreased to a lesser extent than surface tension. These results suggest that myosin-independent force contributes to tension in the peripheral arcs. We propose a simple physical model in which the peripheral arc line tension is due to the combination of myosin II contractility and a passive elastic component, while surface tension is largely due to active contractility. Numerical solutions of this model reproduce well the experimental data and allow estimation of the contributions of elasticity and contractility to the arc line tension.

Introduction

The shape and mechanical properties of adherent cells emerge as the result of the interaction of the cytoskeleton with the extracellular environment. In particular, the organization of the actin-myosin II system is known to be strongly influenced by the configuration of the adhesive substrate (1–4). For instance, the formation of actin-myosin filament bundles, known as stress fibers, depends on the geometry and stiffness of the substrate (5). The orientation and tension characteristics within these fibers are important for many cellular processes such as polarization, migration, and proliferation. To understand how external cues control mechanical properties of stress fibers and influence downstream cell processes (5–7), it is useful to study standardized cell geometries. Regular adhesive micropatterns have been extensively used in this perspective, to create specific cell shapes with reproducible layouts of stress fibers. On patterns displaying nonadhesive gaps wider than 4 μm, concave stress fibers are observed bridging the gaps at the cell periphery (5,8–10). These peripheral arcs are stably anchored to focal adhesions, and the tension in the arcs is thus expected to be transduced into traction forces onto the substrate.

Given the tight coupling between cell shape and mechanical tension (11–14), several studies have dealt specifically with how the curvature of peripheral arcs arises from their mechanical properties, using either analysis of cell shape (5,15,16), or analysis of both shape and traction forces (17,18). The simplest way to explain the inward curvature of an arc is to use a contour model in which the line tension λ in the arc is balanced by the surface tension σ coming from the cell bulk and by adhesive forces at the corners where the arcs are anchored to focal adhesions (17). At equilibrium, the radius R of an arc along its free length is determined by the ratio of the tensions R = λ/σ. However, the natures of the surface tension and the line tension in the arc are not fully understood. It has been argued that the surface tension comes both from the actin-myosin contractility in the cytoskeletal cortex and the cell membrane. However, the magnitude of membrane tension is estimated to be one order of magnitude lower than cortical tension, so the surface tension is expected to be defined by cortical tension (19,20). The nature of the line tension has been subject to debate: it is generally assumed that it is dependent on myosin-driven contractility, but it is unclear whether elasticity contributes to tension (15,17,21–23). It remains to be established how myosin activity affects the mechanical behavior and shape of peripheral arcs.

To elucidate the contribution of myosin-dependent contractility, we study how the coupling between cell shape and cell tension is modified by altered myosin activity. Previous works reported that myosin inhibition often leads to a loss of a coherent cell shape, with the appearance of large invaginations in the cytoplasm and uncontrolled protrusive behavior (24,25). To avoid this and to obtain a reproducible cell shape while modifying myosin activity, we use adhesive patterning and low concentrations of drugs. We simultaneously measure cell shape, traction forces, and tension in the arcs at various contractility levels in these defined geometries and compare the experimental results with simulations based on different hypotheses about the nature of line tension. Our results help to establish the roles of myosin-dependent contractility and passive elasticity in arc tension and shape.

Materials and Methods

Cell culture

Rat embryonic fibroblasts (REF-52) were cultured in Dulbecco’s modified Eagle’s medium supplemented with 1% penicillin-streptomycin, 1% L-glutamine, and 10% FCS (fetal calf serum) (all from Gibco, Grand Island, NY). Two days before experiments, cells were transfected with LifeAct EGFP (Ibidi, Martinsried, Germany) in antibiotic-free medium using Fugene HD (Promega, Madison, WI). After 24 h, cells were detached with 0.02% EDTA in PBS (phosphate-buffered saline) and 0.25% trypsin (Gibco), and seeded on the patterned substrates. They were left to spread for at least 12 h before experiments. Just before the experiments, cells were washed with imaging medium (Leibovitz-15, obtained from Gibco, supplemented with 10% FCS), which was used during all live experiments.

Polyacrylamide gels and patterning

PAA (polyacrylamide) solution was prepared following well-established protocols (26) to obtain gels with a stiffness of 8 or 16 kPa. The Young moduli of the gels were then controlled using an AFM in force spectroscopy mode and results were fitted using the Hertz model. Gels were polymerized in two layers, the top one containing red fluorescent beads (Fluospheres F8810; Molecular Probes, Eugene, OR), as described in Tseng et al. (3) and Tse and Engler (26). Briefly, a glass coverslip was treated with APTMS ((3-aminopropyl) trimethoxysilane and glutaraldehyde (both from Sigma-Aldrich, St. Louis, MO) to allow strong gel attachment. The first layer of ∼40 μm was first polymerized with APS (ammonium peroxydisulfate; Sigma-Aldrich) between the support bottom coverslip and a Surfacil-treated (Thermo Fisher Scientific, Rockford, IL) top glass coverslip of 22 mm in diameter. A 10 μm-thick second PAA layer was then polymerized between the first PAA layer and a patterned glass coverslip on which adhesive protein was locally adsorbed. The second PAA solution was supplemented with sulfo-SANPAH (Thermo Fisher Scientific) to allow cross-linking of the adhesive protein.

The patterned coverslips were fabricated using standard ultra-violet photolithography techniques, as described in Guillou et al. (27). Briefly, clean glass coverslips were coated with Shipley S1805 positive photoresist (CTS, Antony, France), and insulated through a chrome mask by ultra-violet light. After development of the insulated photoresist using a CD26 developer (CTS), human plasma fibronectin (Millipore, Zug, Switzerland) was adsorbed on the patterned surface (concentration 10 μg/mL) for 90 min at 37°C. Fibrinogen conjugated with Alexa Fluor 647 (Molecular Probes) was added to the solution to visualize the pattern. The remaining photoresist was quickly stripped in ethanol. For fixed-cell experiments on glass substrates, the glass coverslips were treated with ODTS (octadecyltrichlorosilane; Sigma-Aldrich) before the photolithography process to allow stronger protein attachment.

Drugs

Y27632 at 10 μM and blebbistatin at 50 μM (Calbiochem, Darmstadt, Germany) were diluted in the imaging medium before addition.

Imaging

Imaging was performed on an inverted Axiovert 200M system with a 63× Plan-Apochromat, oil immersion objective (N.A. 1.4; Carl Zeiss, Oberkochen, Germany). We used a motorized platform (MS-2000, Applied Scientific Instrumentation, with NanoDrive controller; Mad City Labs, Madison, WI) to scan the sample. Acquisition was performed using a CoolSnap HQ2 camera (PhotoMetrics, Tucson, AZ) and the Multi-Dimensional Acquisition module of the software METAMORPH (Molecular Devices, Sunnyvale, CA). For live experiments, a sticky-slide channel setup (Ibidi) was used to allow easy changes of medium using small volumes. The different drugs were prepared just before the experiments and added to the imaging medium to reach the desired final concentration. After 30 min drugs were washed out with Leibovitz-15 (Gibco).

Immunostaining

Before fixation, cells were washed with serum-free medium. Cells were first fixed with 4% paraformaldehyde in cytoskeleton buffer at 4°C for 15 min, then permeabilized with 0.2% Triton X-100 in the same buffer for 10 min at 4°C. Cytoskeleton buffer contained 60 mM PIPES, 25 mM HEPES, 2 mM MgCl₂, and 1 mM Na-orthovanadate in distilled water, pH 6.9. Just before use, 1 mM PMSF and 0.5% Triton X-100 were added to the buffer. Immunostaining was then performed using standard protocols. The primary antibodies mouse anti-MYH9 (Abnova, Taipei, Taiwan), rabbit anti-myosin IIb (Cell Signaling, Beverly, MA), mouse anti-α-actinin, and rabbit anti-myosin light chain (both from Abcam, Cambridge, UK) were incubated for 1 h, then rinsed with PBS. Secondary antibodies anti-mouse TRITC, anti-mouse FITC (both from Sigma-Aldrich), anti-rabbit Alexa Fluor 568, and Alexa Phalloidin (both from Molecular Probes) were incubated for 1 h as well, then rinsed with PBS.

Traction force microscopy

The positions of fluorescent beads embedded in the gel were recorded before and during the drug treatment and after the cells were detached from the gel using PBS/EDTA and trypsin. Bead displacements were computed using particle image velocimetry. Traction stresses were obtained by Fourier-transform traction cytometry. Algorithms working with the software IMAGEJ (National Institutes of Health, Bethesda, MD) were taken from Tseng et al. (3) (and freely downloaded from https://sites.google.com/site/qingzongtseng/tfm). The total traction force magnitude was then calculated by integrating all traction stresses under the cell effective adhesive area.

Cantilever-based experiments

Fiber tension was measured with custom-made SU-8 ultrasoft cantilevers according to the protocol described in Piacentini et al. (28). Briefly, cells were seeded on cross-shaped three-dimensional PDMS patterns with fibronectin coating on the top. Cycles of four radial compressions of increasing depth were applied to the peripheral arcs with an ultrasoft cantilever, at a speed of 5 μm/s. Two types of cantilevers were used: 5 × 5 × 700 μm and 5 × 10 × 700 μm. Their corresponding spring constants were 2.28 nN/μm and 4.56 nN/μm. Cycles of compression were performed several times before adding the drug and every 4–5 min during drug incubation. It was assumed that bundle tension remained constant during one compression cycle, which is justified by the short duration of the compression cycle (2.5 min) with respect to the time of drug treatment (30 min) and the fact that bundle length did not change significantly (<2% (28)) due to the compression. Additionally, we verified that compression did not induce significant changes in cell morphology, i.e., that the attachment sites of the peripheral bundles to the adhesive pattern did not shift. R, d, and initial bundle-cantilever distance were thus measured once before each cycle. At each compression, the deflection of the cantilever and the indentation of the bundle were measured, and from this, the force on the cantilever and the bundle deflection angle were computed. For small indentations, the force increases linearly with the deflection (28). For each cycle of compressions, bundle tension was then measured from the slope of the force-deflection angle curves (detailed method in Piacentini et al. (28)).

Image processing

Radius of curvature of actin arcs was measured using a custom script written for the software MATLAB (The MathWorks, Natick, MA) on images thresholded manually using the software IMAGEJ (National Institutes of Health). Briefly, the contour of the arc was detected, and then a circle was fitted to three points along the smoothed profile (Fig. S1 in the Supporting Material). The final radius is an average of at least three radii measured while moving the three points along the profile. The distance between the three points was adjusted to have SD <10%.

Numerical solution and scoring

All numerical solutions of equations were obtained using custom scripts written with the software MATLAB. The steps of the fit procedure are detailed below.

• 1.From the force F and radius R measurements, the evolution of λ and σ are computed using Eqs. 2 and 3, before and during the drug treatment.
• 2.The values at t₀ (before adding the drug) of the traction force magnitude F₀, the initial arc radius R₀, and the spanning distance d are used to set the initial parameters of the model.
• 3.The surface tension experimental values are fitted with a simple exponential decay using integrated fitting options (nonlinear least-squares method).
• 4.The characteristic time τ of the surface tension decay is used as the simulation timescale.
• 5.The simulated surface tension σ/σ₀ is then imposed to follow this exponential decrease in time. Equation 6 is solved for R, at each timepoint, for different values of the initial ratio R_a = λ_a/σ₀. R_a was incremented by 0.1 μm, corresponding to increments in the initial active tension term λ_a of σ₀ × 0.1 μm. Because the radius R₀ and force F₀ fix the values of λ₀ at the first timepoint, changing λ_a will modulate the bundle stiffness EA so that Eq. 6 is satisfied at t₀. The higher the value of λ_a, the lower will be the bundle stiffness. R and F change monotonically with λ_a, providing a unique value of λ_a that will yield the correct evolution of R/R₀ and F/F₀. To find the best parameter value, numerical solutions were scored as follows: the root-mean-square error was computed for every experimental point, and a total score was given by aggregating all relative errors (Eq. 1). We then chose the parameters giving the minimal error between the predicted R_num and F_num and the experimental values R_exp and F_exp:

$$\text{Score}=\frac{{\langle {\left(R_{\text{exp}}-R_{\text{num}}\right)}^2\rangle }^{1/2}}{R_0}+\frac{{\langle {\left(F_{\text{exp}}-F_{\text{num}}\right)}^2\rangle }^{1/2}}{F_0}.$$ (1)

Results

Molecular composition of peripheral arcs

Previous studies of cells spreading on micropatterned substrates have shown that fibroblasts create thick arc-shaped actin bundles at the cell edge to bridge nonadhesive gaps (5,8–10). We use here cross-shaped adhesive patterns with branches of length 30–40 μm to study these peripheral arcs in fibroblasts in a systematic way (Fig. 1 A). The inward curvature of the arcs has been explained by the equilibrium between surface tension and line tension (Fig. 1 B). Line tension could result from myosin activity, passive elasticity, or a combination of the two (15,17,21). We first investigated whether the molecular composition of the arcs is consistent with the generation of active and/or elastic tension. We found that α-actinin as well as myosin IIa and myosin IIb were prominent components of the arcs (Fig. 1, A and B). In this respect, peripheral arcs were thus similar to transverse arcs, which also contain myosin II and hence are able to contract, but different from dorsal stress fibers that only contain α-actinin (29–31). Notably, the arrangement of the cross-linkers in the peripheral arcs was not periodic as in sarcomeric muscle fibers, as shown by the profiles in Fig. 1 B. The profiles nonetheless displayed multiple zones rich in myosin and α-actinin, consistent with a series of contractile (nonidentical) units. The presence of both active and passive cross-linkers suggests that the peripheral arcs can develop active and/or elastic tension (32).

Figure 1.

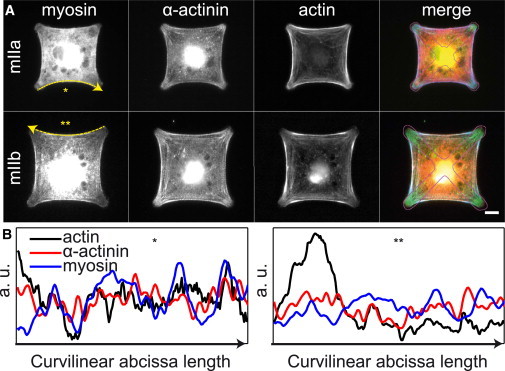
Architecture of peripheral arcs. (A) Fluorescence images of REF-52 cells on cross-shaped patterns, showing isoforms IIa (top row) or IIb (bottom row) of nonmuscle myosin II, α-actinin, and F-actin. The last column is a merge of all three proteins (myosin in red, α-actinin in green, actin in blue, and the contour of the adhesive pattern is shown in magenta). Scale bar, 10 μm. (B) Intensity profiles along one arc of actin (black), α-actinin (red), and myosin (blue), showing multiple zones rich in myosin II and α-actinin. Profiles were normalized by the mean intensity over the bundle length. Note that no periodic bands were observed. The corresponding bundles and the scanning direction are indicated (^∗, ^∗∗, or yellow arrows) in (A). Bundle lengths are 40 μm (^∗) and 50 μm (^∗∗).

Shape response to contractility inhibition

We first looked at how cell shape changed in response to contractility-inhibiting drugs, for cells spread on patterned soft polyacrylamide gels as well as rigid glass substrates. We used either one of the two drugs: Y27632, a ROCK inhibitor that reduced myosin light-chain (MLC) phosphorylation levels, or blebbistatin, which inhibited the motor activity of myosin II. Upon treatment with either 10 μM Y27632 or 50 μM blebbistatin we observed two distinct behaviors. In a minority of cells, there was a loss of cell coherence resulting in a shrinkage of the cell body and a massive extension of protrusions creating many concavities and irregularities in the cell shape (24,25,30). However, in the vast majority of cells, cytoplasmic coherence was maintained, with increased radii of curvature of the arcs, resulting in an overall increase of the cell area (Table 1 and Movie S1). This response was predominant on both soft and rigid substrates. Cells having reached the end of the pattern branches, the only possible gain in area came from the nonadhesive zones. However, cell area increase was not always isotropic. The four peripheral arcs present on each cross-shaped pattern did not systematically have the same response. In some cases, the radius of one arc decreased, while the others increased. Therefore, cell area is a better indicator of the overall cell response than the behavior of individual arcs. The numbers of cells that increased their area for the different substrates and drugs are summarized in Table 1. Overall, area increase was observed in >86% of cells.

Table 1.

Quantification of cell response to myosin inhibition

Description	Number of Cells with Area Increase	Quantitative Response (%)
		t0 + 10 min		t0 + 30 min
		(A−A0)/A0	(F−F0)/F0	(A−A0)/A0	(F−F0)/F0
10 μM Y27632	57 out of 63	+17	−35	+32	−50
50 μM blebbistatin	16 out of 22	+3	−52	+5	−83

Column 2 gives the total number of cells for which an area increase was observed in response to myosin inhibition, irrespective of the substrate (glass or PAA gel). Columns 3–6 give the percentages of change in area and force magnitude after 10 and 30 min of drug incubation for cells on PAA gels, as plotted in Fig. 2.

Dynamics of line and surface tension from traction force microscopy data

Simultaneously to monitoring cell shape, we performed traction force microscopy (TFM) on the patterned polyacrylamide gels to follow the evolution of cell force during contractility inhibition. Full-spread cells were imaged for 20 min in control conditions, before adding a contractility-inhibiting drug. Inhibiting myosin activity resulted in a drop of traction force magnitude, as was expected and previously reported (3,33,34). Fig. 2 A illustrates this response, showing the shape and traction stresses for one representative cell before myosin inhibition (on the left) and after 30 min of Y27632 treatment (on the right). For this cell, the mean radius increased linearly to twice its initial value, corresponding to a 20% increase in area, while the total force magnitude dropped below 20% of its initial value during the 30 min of myosin inhibition, as shown in Fig. 2 B. The evolution of area and traction force magnitude averaged over all cells showed similar trends (Fig. 2 C and Table 1), setting aside the small initial dip in cell area, coming from a fast initial contraction of some cells likely due to a transient liquid flow when the drug was added. After washing out the drug with normal medium, traction forces were observed to grow again, confirming that the observed lower contractility state is due to myosin inhibition. Comparing the two myosin inhibitors, we observed that blebbistatin and Y27632 had similar effects on cells, both leading to decreased traction forces and increased radii, although the changes were different in magnitude (see Discussion for possible reasons).

Figure 2.

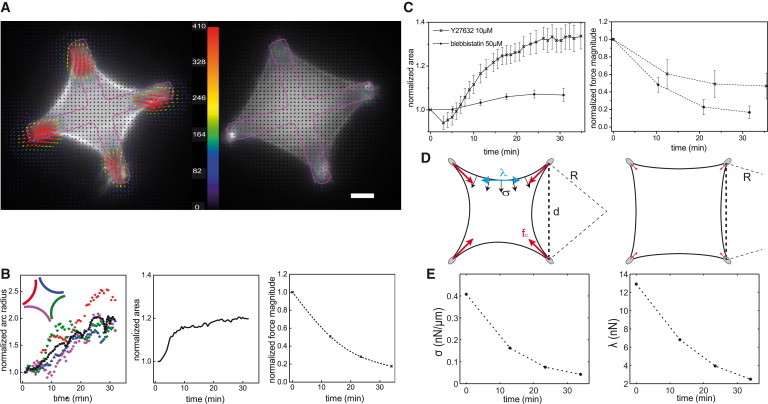
Shape and tension response to myosin inhibition of a REF-52 cell on a cross-shaped pattern. (A) F-actin and traction stress vectors before myosin inhibition (left) and after 30-min incubation with Y27632 at 10 μM (right) showing the cell area increase. F-actin was labeled using LifeAct EGFP. (Colored arrows, color-scale in Pa) Traction stress vectors. Maximum stress is 1020 Pa (before inhibition) and 180 Pa (after inhibition). Color bar is linear up to 410 Pa; (red arrows) all higher stresses. (Magenta overlay) Adhesive pattern contour. Scale bar, 10 μm. (B) Plots of radius (left), area (center), and total force magnitude (right) over time of Y27632 incubation for the cell shown in (A); all are normalized to their initial values. (Left panel) Evolutions of each bundle radius (scatter, with the color-coding indicated in the inset) and of the mean radius (black dots) are given. (C) Mean normalized area (left) and mean normalized force (right) for cells on PAA gels. (x) Y27632-treated cells (n = 18); (o) blebbistatin-treated cells (n = 8). Bars are the standard error of the mean. After 30 min of incubation, the drug was washed out with normal imaging medium. (D) Sketch of a cell on a cross-shape pattern under control conditions (left) and contractility-inhibited conditions (right). The line tension λ (cyan), surface tension σ (black), and force at adhesions f_c (red) are depicted, as well as the spanning distance d and arc radius R. (E) Surface tension (left) and line tension (right) calculated for the cell shown in (A)–(C) from Eqs. 2 and 3.

We next investigated how the Laplace equilibrium, expressed as

$$R=\lambda /\sigma$$ (2)

was shifted by myosin inhibition (Fig. 2 D). We assume the line tension λ to be homogeneous within one arc, and the surface tension σ, normal to the cell edge, to be also homogeneous within the cell. In contractility-inhibiting conditions, both surface tension and line tension are likely to decrease. However, the increase in the radius of curvature could happen only if the surface and line tension do not change in the same manner, e.g., if the surface tension drops while the line tension stays constant, or the surface tension drops faster than the line tension. We set out to find in which proportions surface tension and line tension respond to myosin inhibition.

The experimental measurements of the traction forces and of the curvature radii are in principle sufficient to infer the evolution of line and surface tensions: by considering a cell attached to the substrate at its four corners, the forces at adhesions can be expressed as a function of geometrical parameters and of the line tension (17). We assume that the cell has a fourfold symmetry (i.e., four arcs having the same curvature and same line tension, and a uniform spanning distance between the adhesions, see Fig. S1) and the traction forces are exerted at the tips of the adhesive branches with equal magnitude f_c at the four quadrants of the cell. Together with Eq. 2, this simplification allows us to calculate unique values of λ and σ for each cell from the knowledge of the spanning distance d, the mean radius of the arcs R, and the traction force magnitude F = 4f_c exerted by the cell (illustrated in Fig. 2 D):

$$\sigma =\frac{F}{2\sqrt{2}\left(d+2R\sqrt{1-d^2/4R^2}\right)}.$$ (3)

Our measurements showed that both line and surface tension decreased during contractility inhibition, but the drop of surface tension was more pronounced than that of line tension (Fig. 2 E): with fivefold decrease in the traction force and a 1.5-fold increase in the arc radius, Eqs. 2 and 3 give an approximately sevenfold decrease of surface tension and 4.5-fold decrease of the line tension. The decay of both λ and σ is consistent with the hypothesis that they each depend on myosin activity, but in different ways.

Direct experimental measurements of line tension using an ultrasoft cantilever

To confirm the estimations of λ and σ from TFM experiments, we measured line tension using an alternative protocol presented in Piacentini et al. (28). We applied small radial deformations to the peripheral arcs with ultrasoft cantilevers, of spring constants of 2.3 and 4.6 nN/μm. The increase of fiber indentation with the cantilever displacement depends on the tension within the fiber, yielding λ (see Materials and Methods and Piacentini et al. (28) for details). This was done on a different substrate than TFM experiments (rigid PDMS three-dimensional patterns, Young modulus E ≈ 2 MPa), one that was incompatible with traction force measurements. ROCK inhibitor Y27632 was applied in the same conditions as previously, resulting in a drop of fiber tension. Note that in this case a minor retraction of the arcs was observed, possibly due to repetitive mechanical perturbation. We observed a close-to-linear decrease of λ in time (Fig. S2), confirming that line tension depends on myosin activity. Typically λ decayed by 2.5% per min (R² = 0.77). We can use the values of λ and of the radii of curvature R to infer σ from Eq. 2, yielding values of initial surface tension between 0.1 and 2.3 nN/μm, in the same range as that extrapolated from TFM experiments. These independent measurements validate our initial estimations of the decay of λ.

Contractile elastic bundle model

The experimental results presented above show that both the surface tension and the line tension decay as myosin activity decreases, but to different extents. It was reported that ROCK controls MLC phosphorylation locally in the center of the cell (35), but given that blebbistatin and ROCK inhibitor Y27632 produce qualitatively similar effects, different responses of λ and σ are not likely to stem from a localized action of ROCK. We checked how the distribution of phosphorylated myosin in cells was affected by the inhibitors. Fig. 3 shows staining for actin and phosphorylated myosin light chain (pMLC). In all cells, myosin remained colocalized with actin bundles. In blebbistatin-treated cells, there are still high levels of pMLC. That was expected, because blebbistatin does not affect light chain phosphorylation, but instead freezes myosin in a weakly bound state. In Y27632-treated cells, the level of pMLC had greatly decreased both in the arcs and in the bulk of the cell. Therefore, the action of Y27632 was not spatially limited to the center of the cell.

Figure 3.

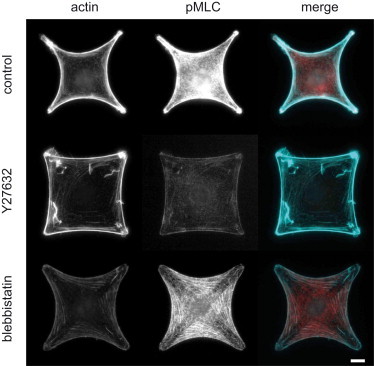
Myosin involvement in line and surface tension. Immunostaining of cells in control conditions and under Y27632 and blebbistatin treatment. Cells were stained for actin (left), and pMLC (center). (Right column) Merge of actin (cyan) and pMLC (red). Scale bar, 10 μm.

We assume that both Y27632 and blebbistatin act by limiting the number of active motors, in function of the drug concentration, thus reducing the myosin-dependent contractility both in the peripheral arcs and in the bulk of the cell. A lesser effect of myosin inhibition on the line tension could then be explained by the existence of a myosin-independent component in the line tension. In previous theoretical works, line tension in stress fibers has been considered to be solely active, i.e., myosin-dependent but strain-independent (36,37), solely elastic, i.e., dependent linearly on strain (15), or a combination of both (22,32). As argued above, an entirely active behavior does not account for increasing arc radius: if both line tension and surface tension were directly proportional to the number of motors, the equilibrium radii would not change (using Eq. 2), contrary to what has been experimentally observed. On the other hand, an entirely elastic force proportional to bundle strain

$${\lambda }_{el}=\frac{EA}{L_0}\left(L-L_0\right)$$

could explain the decay of line tension, because an increase in curvature radius would diminish bundle length L (i.e., bundle would straighten) and hence the strain. The decrease of line tension would be strongly dependent on how much the bundle length changes.

We propose here to use a general model, associating an active contractility with elasticity in the line tension. We neglect a possible elastic contribution to the surface tension, as has been done in existing cable network models (15,21,38). Because the drug response developed over a relatively long timescale (tens of minutes), we assume that the observed states represent mechanical equilibrium with motors working at their stall force; thus the surface tension is directly proportional to the number of active motors, as is the active part of line tension λ_a. The total line tension is then the sum of the two contributions:

$$\lambda ={\lambda }_a+{\lambda }_{el}.$$ (4)

Two additive components here correspond to a system in which the active and elastic elements are connected in parallel. The myosin-independent elastic term will dominate once the motors are inhibited, leading to increased radii; as the arcs straighten, the elastic tension will diminish as well. On the other hand, a motor connected in series to an elastic bundle is equivalent to the purely active case, because the total force in this arrangement is equal to the active force developed by motors. Thus, a series arrangement cannot explain our observed change of radius. Note that this consideration is not contradictory to the possibility that several contractile units connected in series exist in a fiber; in this case, each unit could have elastic and active elements in parallel. We thus assume such a parallel arrangement, with the line tension being the sum of active and elastic contributions. To determine the elastic contribution, it is necessary to know the rest-length of the bundle. Note that to explain bundle straightening due to elastic tension, the rest length should be smaller than the shortest length measured in the experiments. We notice indeed that even after myosin inhibition there is some remaining tension in the bundle, indicating a positive elastic tension; moreover, because actin filaments buckle under compression, no negative elastic tension can develop. In the limiting case of a straight bundle, L = d; the rest-length in the model is taken as equal to the spanning distance L₀ = d (15,22) (though, in principle, a value smaller than d is possible). The bundle stiffness EA (product of Young Modulus E of the bundle by the cross-section A) is assumed to remain constant during myosin inhibition (see Discussion):

$${\lambda }_{el}=\frac{EA}{d}\left(L-d\right).$$ (5)

Expressing L and λ in terms of d and R and combining Eqs. 1, 3, and 4 yields an implicit equation for R:

$$R=\frac{{\lambda }_a}{\sigma }+\frac{EA}{\sigma d}\left(2R\arcsin \left(d/2R\right)-d\right).$$ (6)

Fitting the model to experimental data

We chose to impose an exponential decrease of σ, as was observed in the TFM experiments during myosin inhibition. We then solved Eqs. 3 and 6 for different timepoints and compared the evolution of traction force magnitude, radius of curvature, and line and surface tensions with the experimental data. Our numerical results reproduced qualitatively the exponential decay of traction forces and the increase in cell area. We next validated this model on a single cell basis. The 10 cells (seven treated with Y27632 and three with blebbistatin) that were the most symmetric in shape, and with similar responses of each arc to myosin inhibition, were used. For each cell, we searched for the best value of λ_a to fit the evolution of F, R, λ, and σ (see Materials and Methods for details of the numerical procedure). Briefly, the initial values of F₀, R₀, λ₀, and σ₀ were set from the last data point before addition of the drug, and an exponential decay of σ/σ₀ was imposed with characteristic time τ. Equation 6 was then solved at each timepoint for incremented values of λ_a. The value of λ_a yielding the lowest score (Eq. 1) determined the active contribution to the line tension, and from the initial values and Eq. 4, we deduced the elastic contribution as well. An example is given in Fig. 4 A for a representative cell (F₀ = 102 nN, d = 38.7 μm, R₀ = 31.6 μm, σ₀ = 0.41 nN/μm, and λ₀ = 1.9 nN, τ = 14 min). The numerical results (solid lines) compare well with the experimental results (circles): the magnitudes and slopes of both R and F (left plot), as well as for the line and surface tensions (right plot), are the same as for the experimental data. The root-mean square errors are <1% for F, λ, and σ, and <8% for R. The results of simulations for 10 different cells, normalized to their initial values, were averaged and are shown in Fig. 4 B. The color bands indicate the standard deviations (SDs) around the mean values. The good agreement of the numerical results with our experimental observations (Fig. 2 C) demonstrates that the superposition of elastic and contractile terms is an accurate description of the tension in peripheral arcs. Dispersion in these results reflects the different ratios of elastic and active contributions from cell to cell, but also partly comes from the variability of initial values: despite standardized adhesion localization imposed by micropatterning, we observed variability in initial values of F₀ (SD was 80% of mean value) and of R₀ (SD was 30% of mean value).

Figure 4.

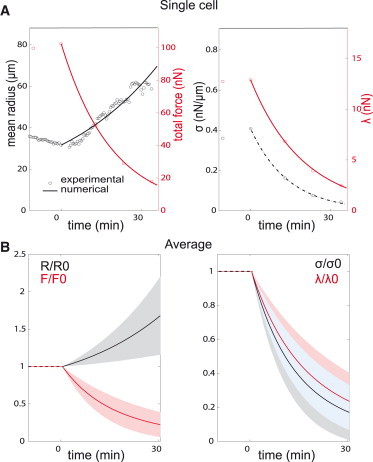
Fitting experimental results with the contractile elastic bundle model. (A) Experimental (O) and numerical results (solid lines) showing evolutions of forces, arc radius and line and surface tension for a representative Y27632-treated cell. (Left) Mean arc radius (black) and total traction force (red); (right) surface tension (black) and line tension (red). Drug was added at time t = 0. Surface tension was fitted with an exponential decay (indicated by the dotted line, tau = 14.1 min). Best value found for the active tension was λ_a = 0.28 nN. (B) Average of the numerical results for 10 cells (7 Y27632 + 3 blebbistatin-treated), normalized to their initial values. (Bands) SDs around the mean values found over all cells; (solid lines) average values. (Left) Arc radius (black) and traction force (red); (right) surface tension (black) and line tension (red). The blue band in the middle corresponds to the overlap of the black band (mean σ ± SD) and the red band (mean λ ± SD). (Dashed red and black lines) Reminders that values are constant at t < 0.

The values found for the initial active, elastic, and total tensions of the 10 cells on PAA gels and one cell on a PDMS substrate are plotted in Fig. 5 and summarized in Table 2. Initial line tension was found to be between 12 and 130 nN. Interestingly, most of the cells displayed one dominant contribution to the line tension, being either mostly active or mostly (or entirely) elastic, suggesting there are two modes for tension buildup in acto-myosin bundles (see Discussion); but, on average, the active contribution was of 64% of total line tension. Those cells that had a higher elastic contribution correspond to those that lost less traction force during contractility inhibition, explaining why, on average, forces dropped only 50% in Y27632-treated cells (Fig. 2 C). However, the elastic tension never did exceed 20 nN, regardless of the initial line tension magnitude. Cells therefore gained more tension by increasing the myosin activity (see inset of Fig. 5 A). Note that the relative weight of each contribution is dependent on how the rest-length is set, such that a L₀ smaller than d would lead to a higher active contribution; but the best fits were always obtained for L₀ = d.

Figure 5.

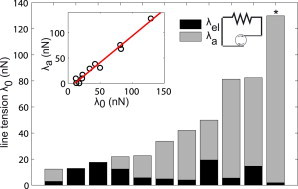
Balance of elastic and active contributions to the line tension. Values found by the model for the elastic contribution λ_el (dark bars, represented by the spring) and the contractile contribution λ_a (gray bars, represented by the active element) to the total line tension λ₀ for 11 different cells. In 10 cells, λ₀ was measured with the TFM technique; in one cell (^∗), λ₀ was measured with cantilever-based technique. (Inset) The active contribution as a function of total line tension, with a linear fit (red dotted line). To see this figure in color, go online.

Table 2.

Mean values ± SE for initial line tension, active contribution, bundle stiffness, and cell bulk surface tension

Description	λ0 (nN)	λa (nN)	EA (nN)	σ0 (nN/μm)
PAA gels	37.1 ± 8.2	27.3 ± 8.3	386 ± 143	0.73 ± 0.16
PDMS	100.54 ± 16.44	127	26.3	1.10 ± 0.41

Row 2 gives the values extracted from TFM data on PAA gels using the numerical model. Row 3 gives λ-values measured with ultrasoft cantilevers: λ₀ and σ₀ are averages over five cells, and λ_a and EA is computed for one cell only, so no SE given (and this explains why λ_a > λ₀). The value σ₀ was computed from λ₀ and R₀ using Eq. 2.

Discussion

In this work, we combined experimental measurements of the dynamics of traction forces and shape of individual living cells with an analytical model to estimate the mechanical properties of peripheral acto-myosin fibers. We found that the fiber radius increased upon inhibition of myosin contractility (Figs. 2, 3, and 4). These experimental results are consistent with a previous study (39) on living cells, but others, measuring populations of fixed cells, found curvature radii 2–5 times smaller for Y27632 treatment with respect to control cells (5,15). Following the life of individual cells during drug treatment, we have also occasionally observed collapse of the cytoplasm between the branches of adhesive pattern leading to a decrease of apparent arc radii. This type of response became dominant when the cells were spread on adhesive pattern for only a short time (as in Théry et al. (5)) or treated with drugs in the absence of serum (as in Bischofs et al. (15)). But in all these cases of cell collapse, the peripheral arcs were disassembled. In contrast, our study focuses on the situation where myosin activity was reduced, but the cytoskeletal organization remained largely intact (Fig. S3), so that it was possible to measure a line tension in the arcs.

We present two independent measurements of the line tension under myosin inhibition. The cantilever-based experiments gave a direct estimate, while on PAA gels λ was interpolated from R and F. These two set of values are compared in Table 2 and Fig. S2. The magnitudes of the drop in tension during the 30 min of drug incubation are similar, down to 20–40% of the initial tension on the PDMS substrates, and to 10–20% on the PAA gels. These correspond to initial fiber tensions distributed between 60 and 150 nN on the PDMS substrates, and 12 and 85 nN on PAA gels; they then fall to 20–60 nN, and 1–10 nN, respectively. The same trend is observed for the surface tension, which is two times higher on PDMS than on PAA gels (1.1 nN/μm compared to 0.67 nN/μm). Both values corroborate existing estimates (17,28). The higher amplitude of λ and σ on the PDMS substrates may be explained by the substrate rigidity which is 200 times greater than the PAA rigidity (∼2 MPa compared to 10 kPa), as cells develop more force on more rigid substrates (40,41). The values of line tension determined here are higher than what is, for instance, reported in Albert and Schwarz (22), where the total line tension was found at ∼5.5 nN. However, this value was obtained from MCF10A cells, which are less contractile than REF cells. We also found that substrate-dependent differences in the rate of λ decrease. On PDMS, tension loss was nearly linear, whereas it appeared exponential on PAA gels. This apparent difference may be due to a difference in timescale (τ ≈ 10 min or τ > 30 min). Note that because the line tension was measured every 4–5 min on the PDMS substrates and every 10 min on the PAA gels, the timescale estimations are only orders of magnitude. Repeated indentations could explain these small differences. In the cantilever-based experiments, the fiber was mechanically perturbed several times, which could cause higher values of λ over time.

In both TFM and cantilever-based experiments, we explain the increase in arc radius under myosin inhibition by the fact that surface tension in the cell bulk drops faster than the line tension in the peripheral arc. Indeed, a model of a contractile elastic bundle, in which the line tension is the sum of elastic and active contributions, accurately reproduces the experimental behavior of peripheral arcs. This is the simplest model to account for our experimental observations, where we kept linear dependencies of line and surface tension on motor activity. We cannot exclude the possibility that there are some forms of dependence, more complex in nature, which may also result in similar trends, although there are no theoretical or experimental indications of what these could be. However, the hypothesis of elasticity is biologically justified by the presence of cross-linking proteins, and the bundle stiffness is expected to depend on the nature and the structure of these cross-linkers. Note that myosin could be necessary in the formation of an elastic structure, even though the elastic forces mentioned here are myosin-independent. Nonetheless, our results indicate that elastic behavior allows cell expansion independently of active processes. It was already known that cells spread on homogeneous substrates expand when myosin is inhibited, due to higher membrane protrusion activity (25,42); but by using patterned substrates, we here demonstrate that cell expansion could also be due to elastic forces. Passive elastic forces could thus contribute to shape dynamics in cells.

Other models have attempted to distinguish between active and passive contributions to cytoskeletal tension, but have not addressed the dynamic aspect (22), or have concentrated on much shorter timescales, during which viscous effects were dominant (39,43). Here, for the first time to our knowledge, we separately estimate the active tension and elasticity in fibers (see Table 2), and demonstrate that combined elastic and active contributions account for the shape changes upon modulation of myosin contractility. This has been done considering that bundle stiffness EA stays constant during myosin inhibition. The values found for 11 different cells are dispersed over several orders of magnitude, with a first group between 30 and 200 nN, and a second group above 350 nN (Table 2).

A previous analysis of static cell populations proposed that line tension variations could be due either to bundle stiffness (elasticity control mode), or to active contractility (tension control mode) (15). However, it was not possible to distinguish between these two modes. We here bring experimental evidence for the existence of both these modes and show that they are in most cases complementary, as illustrated in Fig. 5. The corresponding values of EA both for tension control and for elasticity control are consistent with other numerical estimations, in which values between 40 and 2000 nN were found (22). An existing experimental estimation also gives a stiffness of 46 nN for isolated stress fibers of vascular smooth muscle cells (44). This range of values shows that different organizations of the acto-myosin cytoskeleton and cross-linking proteins can generate bundles of various strengths, either within a population of cells or across different cell types. It is interesting to note that although line tension is higher on the more rigid PDMS, bundle stiffness was actually lower than on the PAA gels, showing that substrate stiffness may have opposite effects on myosin activity and on bundle elasticity.

The assumption of a constant bundle stiffness may need to be reconsidered, given that the elastic properties are likely dependent on the density and on the activity of myosin motors and on other cross-linkers such as α-actinin (32). It has been shown that blebbistatin reduces the rigidity of actin meshworks (45), presumably due to its effect on myosin. It is possible that Y27632 also reduces EA. Changes in bundle stiffness can be estimated by computing the strengths of the arcs, given by the relative actin intensity of the arcs with respect to the cell interior (15). Our measurements suggest that arcs are weaker and thinner after myosin inhibition, indicating that there could be some remodeling of the cytoskeleton (data not shown). To estimate the possible effect of a decrease of stiffness, we assumed that EA dropped half as fast as σ. However, this did not lead to major differences in the numerical solutions or to better agreement with our experimental data, suggesting that such variation of bundle stiffness does not significantly impact cellular response.

However, a drop in bundle stiffness faster than the loss in surface tension would lead to lower radii, thus shrinking cells. Yet another behavior is found when the type of evolution of the stiffness differs from that of the surface tension: the radius may then change nonmonotonically, e.g., first decreasing as the changes in stiffness dominate, then increasing when the drop in surface tension becomes more important. Different types of dynamical behavior may be discovered when the living cell dynamics are studied more extensively. The interplay between the motor inhibition kinetics and the changes in bundle stiffness could account partially for the minor differences in the response to blebbistatin or Y27632. Indeed, Y27632 and blebbistatin use different mechanisms to inhibit myosin. This could lead to different effects of each drug on EA: because blebbistatin acts directly on the motors, its effect on contractility should be faster, and may be reinforced by a stronger drop in bundle stiffness. Additionally, inhibition of LIM-kinase by Y27632 could lead to a marginal overactivation of cofilin. Cofilin-mediated disassembly of actin filaments would contribute to an increased drop of surface tension (46). The differential effect of blebbistatin on bundle stiffness and of Y27632 on surface tension may provide an explanation for our experimental results (Fig. 2), in which traction forces decayed faster and radii increased less in blebbistatin-treated cells than in Y27632-treated cells. Further work should be focused on clarifying the relationship between bundle stiffness and contractility.

Conclusions

Acto-myosin bundles are prominent cytoskeletal features involved in many cellular and supracellular processes, whose mechanism it is important to understand. We studied the equilibrium of shape and tension in peripheral arcs of adherent fibroblasts on micropatterned substrates. Inhibiting myosin with low concentrations of either Y27632 or blebbistatin resulted in a concomitant increase of peripheral arcs’ radii of curvature and drop of traction forces down to 20 or 50% depending on the myosin inhibitor, of their initial level. These changes in shape are coupled to changes in line and surface tensions, as captured by the tension equilibrium law. We showed by different techniques that both λ and σ decrease, although not at the same rate. This is explained by the superposition of myosin-independent elasticity and myosin-dependent contractility in the line tension. Our numerical results demonstrate that the model of contractile elastic bundle appropriately describes the mechanical response of arcs during myosin inhibition. We found that the active contribution scales with the total line tension in the arcs. This model could be further refined to include the change of bundle stiffness and to explore how the force-shape coupling is controlled during contractility modulation, cell spreading, or cytoskeleton remodeling.

Author Contributions

C.L. carried out experiments and performed numerical simulations; C.L., C.G., and B.V. analyzed the data; C.L., A.B.V., C.G., and B.V. developed the theoretical model and wrote the article; and J.-J.M. supervised research.

Supporting Material

Movie S1. Dynamic Cellular Response to Y27632 Treatment

REF 52 cell transfected with LifeAct EGFP on a cross-shaped pattern, imaged for 15 minutes before and 15 minutes after Y27632 addition. Scale bar, 10 μm.