Abstract
This study evaluated the positron emission tomography (PET) imaging performance of the Ingenuity TF 128 PET/computed tomography (CT) scanner which has a PET component that was designed to support a wider radioactivity range than is possible with those of Gemini TF PET/CT and Ingenuity TF PET/MR. Spatial resolution, sensitivity, count rate characteristics and image quality were evaluated according to the NEMA NU 2–2007 standard and ACR phantom accreditation procedures; these were supplemented by additional measurements intended to characterize the system under conditions that would be encountered during quantitative cardiac imaging with 82Rb. Image quality was evaluated using a hot spheres phantom, and various contrast recovery and noise measurements were made from replicated images. Timing and energy resolution, dead time, and the linearity of the image activity concentration, were all measured over a wide range of count rates. Spatial resolution (4.8– 5.1 mm FWHM), sensitivity (7.3 cps kBq−1), peak noise-equivalent count rate (124 kcps), and peak trues rate (365 kcps)were similar to those of the Gemini TF PET/CT. Contrast recovery was higher with a 2 mm, body-detail reconstruction than with a 4 mm, body reconstruction, although the precision was reduced. The noise equivalent count rate peak was broad (within 10% of peak from 241–609 MBq). The activity measured in phantom images was within 10% of the true activity for count rates up to those observed in 82Rb cardiac PET studies.
Keywords: positron emission tomography, performance, high count rate
1. Introduction
Hybrid combinations of positron emission tomography (PET) and x-ray computed tomography (CT) are commonly used in clinical radiology and are generally multipurpose instruments for oncology, neurology and cardiology. Technological advances in both the data collection and image generation components of the PET system affect different clinical applications in different ways. Accordingly, a variety of physical performance metrics are typically measured in order to characterize an instrument.
One recent area of attention in clinical PET/CT has been high count rate, quantitative imaging, driven in part by an interest in myocardial blood flow estimation from a dynamic sequence of 82Rb-PET images. In PET/CT, quantification of flow can be combined with qualitative PET perfusion or CT-based coronary applications, potentially providing complementary value to qualitative perfusion PET/CT (Ziadi et al 2011) or coronary arterial calcium evaluation (Curillova et al 2009). Among the technical challenges inherent in 82Rb-PET is achieving high scanner sensitivity that is stable across a wide range of count rates from when a bolus goes through the field-of-view (FOV) to when the activity has dispersed and decayed over several half-lives (Klein et al 2010). In cardiac applications, compensation for insufficient performance has included modification of the sampling scheme (Raylman et al 1993) or infusion profile (deKemp et al 2006) in order to avoid the adverse effects of inaccurate images (Meyer and Weibrecht 2006). The Philips Ingenuity TF 128 PET/CT is a new hybrid scanner combining a time-of-flight (TOF) PET capable of operating over a wide range of activity, with a 128-channel Ingenuity CT. Although it shares a name with the Philips Ingenuity TF PET/MR (Zaidi et al 2011), the PET components of the two systems are different.
In this study, we measured the spatial resolution, sensitivity and count rate characteristics of the scanner according to the NEMA NU 2–2007 standard (NEMA 2007) which has been commonly used in the literature and is an updated version of the methods described previously (Daube-witherspoon et al 2002). A newer version of that standard has since been published, with only minor modifications to the methods. We also assessed the image quality using common ACR accreditation measurements. We augmented these standard methods with two new ones in order to measure image variance and dynamic range. The standard tests provided a basis for comparison with other past and present scanners, while the new methods evaluated the performance characteristics which are especially important to the quantitative accuracy of the images and performance over a wide dynamic range of activity.
2. Methods
2.1. Tomograph
The Ingenuity TF 128 (Philips Healthcare, Cleveland, OH, USA) is a PET/CT scanner combining a modular, LYSO-based PET component with a 128-channel CT component. The CT is based on the Ingenuity CT (Philips Healthcare), a helical CT scanner with 4 cm axial coverage. The PET component has a ring diameter of 90 cm using 28 detector modules constructed as 23 (radial) by 44 (axial) matrices of 4 × 4 × 22 mm3 LYSO crystal elements coupled to photomultiplier tubes and spanning 18 cm axially, in a similar construction to the Philips Gemini TF (Surti et al 2007). The system uses a 4.5 ns hardware coincidence window for its standard FOV, acquires data exclusively in three-dimensional (3D) mode, and records events from all combinations of detector rings in a list-mode format which includes each coincident pair’s detector element indices, energies and TOF difference. Compared to prior systems, the acquisition subsystem has been revised, including the electronics responsible for processing trigger signals and energy sums obtained from the photomultiplier tubes, digitizing the signals, determining coincidences and event positions, applying acceptance windows and transferring the data via high-speed Ethernet to the reconstruction server. The scanner’s built-in reconstruction protocols were used, in which data are typically reconstructed into static, gated or dynamic images. Three different reconstruction FOV are supported: 256 mm diameter for brain studies (1282 × 90, 2 mm isotropic voxels), 576 mm for typical whole-body studies (2882 × 90 voxels, 2 mm or 1442 × 45, 4 mm voxels), and 676 mm for large patient, whole-body studies (1692 × 45, 4 mm voxels). Images are reconstructed using a TOF, list-mode, blob-based, ordered subsets maximum likelihood expectation maximization algorithm (TOF-OSEM) (Popescu et al 2004, Wang et al 2006). Corrections performed in the reconstruction model account for detector efficiency using a component-based method (Wang et al 2007), scatter using a combination of single scatter and Monte Carlo simulation, and randoms using smoothed delay-line coincidence data (Casey and Hoffman 1986). The reconstruction software compensates for changes in TOF resolution as a function of measured detector count rate by setting the TOF kernel width based on the average singles rate in each frame (e.g. each bed position within a whole body study or each time-frame within a dynamic study), the TOF resolution is determined based on the average singles rate within that frame. A Richardson–Lucy, maximum-likelihood resolution recovery process, i.e. image-space, point-spread function recovery (PSF), can be optionally included in the reconstruction protocol, in which the number of recovery iterations and width of the Gaussian regularization kernel can be selected (Lucy 1974, Richardson 1972, Snyder and Miller 1985). Based on the manufacturer’s recommendations, one iteration and a kernel width of 6 mm full width at half of this maximum (FWHM) was used in order to achieve a compromise between resolution recovery (controlled by the number of Richardson–Lucy iterations) and noise control (controlled by the kernel width).
2.2. Scanner resolution, sensitivity and count rate
Spatial resolution was measured by suspending a 1 mm outer diameter, glass capillary tube containing 5 MBq 18F-fluorodeoxyglucose (FDG) in the FOV. The axial extent of the activity in the tube was 1 mm, with the length of the tube parallel to the scanner’s axis. The source was placed at transverse (x, y) positions (0, −10), (100, 0) and (0, –100) mm at z = 0 and 45 mm from the center of the axial FOV, for a total of six positions. These and subsequent coordinates are specified according to the DICOM coordinate system (NEMA 2011), considering all phantoms as being positioned head-first, supine. List-mode data were acquired at each position and then reconstructed using 3D Fourier reprojection with an unapodized filter (Matej et al 2001). Profiles through the tube were constructed from image data following the instructions in NEMA 2–2007 (NEMA 2007), each profile’s maximum was determined using a quadratic fit, and their widths specified as FWHM and full width at tenth maximum (FWTM). The entire spatial resolution experiment was repeated thrice, and the mean and standard deviation (SD) of the widths among the three acquisitions were calculated.
To measure the energy resolution and TOF resolution dependence on count rate, outside the scope of NEMA and ACR, data were collected using the same capillary tube positioned within 2 mm of the scanner’s isocenter. The raw energy and TOF difference for each detected coincidence were read from the data. Energy values were accumulated into histograms. The scanner’s time-offset calibration, a lookup table of time-shifts for each combination of crystal pairs (Griesmer et al 2006), was applied to the raw TOF differences. The resulting data were binned to form sinograms including TOF coordinates. To generate summary statistics regarding the TOF performance, each sinogram row (i.e. distance coordinate) was shifted as necessary to account for any deviation in source position from the exact center. The sinograms were then collapsed over the within-plane angle noting the circularly symmetric source geometry, and only coincidences from the central, direct planes (e.g. those lines of response approximately perpendicular to the scanner axis) were included, thus generating a histogram of TOF errors. Data were corrected for randoms using the delayed window method. The FWHM of each TOF- or energy-histogram was determined using the same method as for the spatial resolution profiles, described above. For this data analysis and many of the other non-standard methods used in this study, software routines are available from the corresponding author.
NEMA sensitivity was measured using a plastic line source, 700 mm long, with a 1 mm inner diameter and containing 10 MBq18F-FDG. Five measurements were taken using a series of five concentric, aluminum sleeves (NEMA PET Sensitivity Phantom, Data Spectrum, Hillsborough, NC, USA). The source was positioned at the center of the FOV and also 100 mm above center, for a total of ten acquisitions. Data were binned into histograms of lines of response, i.e. non-uniformly spaced sinograms, which were then corrected for estimated randoms. The randoms fraction was calculated as the ratio between the number of delays and the number of prompts in the list-mode data. Sensitivities, defined as count rates per unit activity, were plotted as the logarithm of sleeve thickness and extrapolated to an attenuationfree sensitivity value. Slice position was calculated as the average of the axial positions of the two detector elements for each event.
To determine NEMA trues, scatter, randoms, and noise-equivalent count rate (NECR) curves, a 700 mm long, 3.2 mm diameter plastic tube in a polyethylene scatter phantom (NEMA PET Scatter Phantom, Data Spectrum) was used. The tube was filled with 856 MBq, at scan start, of 18F-FDG. The phantom was positioned on the scanner’s patient table and centered in the FOV, which resulted in the line of radioactivity being 45 mm below the transverse center. Data were acquired in intervals with pauses interspersed, so as to obtain files of sizes that were convenient to manage. Data from each interval were binned into a sinogram, and the count rates and scatter fraction calculated, as described in the NEMA procedure (NEMA 2007). The NECR was calculated using a measured, delay-line estimate of randoms and with k = 1 in the denominator, as is appropriate for a system with intrinsic radioactivity and reconstruction in which the randoms estimate is smoothed.
2.3. Image quality and accuracy
Image resolution, noise and quantitative accuracy were characterized using an anthropomorphic phantom containing six thin-walled, glass spheres (PET Emission Phantom IEC, PTW, Freiburg, Germany). A 4:1 sphere:background contrast was targeted by filling the phantom background to one-quarter of its volume, mixing in 65 MBq (at scan start) of 18F-FDG, drawing from that mixture to fill the six spheres, and then filling the remainder of the background volume with water to a total volume of 10.1 L and then mixing. This phantom has the same dimensions as is used in the NEMA standard, although in this experiment all six spheres contained radioactive solution and no lung cylinder or adjacent phantom was used. Actual values for the activity concentrations of the solutions, before and after the background dilution, were obtained from aliquots assayed using a well counter (LKB Wallac 1282) crosscalibrated to the dose calibrator and scanner. The phantom was positioned in the center of the scanner FOV as previous results indicated that the precise axial location of the spheres relative to the detector ring plane does not impact the measured contrast (Muzic and Kolthammer 2006). A low-dose CT scan was acquired for attenuation correction, and then a two-bed-position PET scan was conducted with a scan duration of 900 s per bed position so that the region of the phantom to be analyzed was within the (approximately 50%) overlap region of the scan, thus representative of whole-body imaging.
To assess the effect of the acquisition duration on image quality, we generated replicate list data with different, simulated acquisition durations. We obtained replicates by dealing successive, 10 ms intervals from the original list data into separate output lists. For example, for ten 1 s replicates, events in 1000 10 ms intervals, spaced uniformly throughout the original list file, were sampled cyclically into ten output list files. In this way, each replicate has similar decay and randoms characteristics so that differences in data can be attributed solely to statistical fluctuations. Each file was then reconstructed using two TOF-OSEM reconstruction protocols: our standard ‘body’ protocol with the whole-body settings, i.e. 4 mm isotropic image voxels, three iterations and 33 subsets, and a relaxation parameter of 1.0; and a second ‘body-detail’ protocol using 2 mm isotropic image voxels, three iterations and 33 subsets, and a relaxation parameter of 0.5. The relaxation parameter controls the magnitude of change that each iteration makes to the image (Wang et al 2006). The reconstructed images were not post-filtered. With the 2 mm reconstruction, we also processed the data with PSF compensation set to one iteration and a 6 mm regularization kernel. These parameters were selected to achieve some resolution recovery without creating excessive noise.
In each image we measured the activity concentration in each sphere using four methods of defining the region of interest (ROI):
Cmax Maximum concentration, analogous to SUVmax.
C2D Mean concentration in 2D ROI with diameter equal to the true sphere size; NEMA method.
C3D Analogous to C2D but using a spherical volume of interest.
C50 Mean concentration within an isocontour at 50% of max (Boellaard et al 2010).
We then calculated the recovery coefficients (RC) using each of Cmax, C50 and C3D. The percent contrast (QH) for each hot sphere was calculated using C2D, i.e. according to (NEMA 2007):
| (1) |
| (2) |
where Ctrue is the sphere activity concentration calculated from the aliquot, Cbg is the image-derived activity concentration in the phantom background, and Ctrue,bg is the background activity concentration calculated from the aliquot.
All values for RC were scaled according to the ratio of the measured (mean) phantom background activity concentration to the true background activity concentration, thus using the background to calibrate the scanner’s activity concentration scale factor. Region positions were determined from the highest-count (900 s) images and were then applied to all durations. Noise in the phantom background, i.e. background variability (BV), was represented by calculating the mean among the replicates, of the SDs of the C3D of 60 background regions. The sizes and positions of those background regions were defined according to NEMA NU 2–2007 (NEMA 2007). RCmax from the 300 s images were used to assess reconstructed spatial resolution by fitting the integral of a 3D Gaussian distribution to the RCs (Kessler et al 1984). In fitting, we estimated both the width of the Gaussian integral and its amplitude, having observed that RCs calculated from the data were greater than one for large spheres.
2.4. Dynamic range
One potential application of a high count-rate capacity scanner is dynamic imaging of short-lived radiotracers such as 15O-water and 82Rb. At early times, as the bolus passes through the FOV, the count rate is very high, whereas at late times the activity decays to near the background count rate. To characterize the quantitative accuracy of the scanner over a challenging yet clinically realistic dynamic range, we performed a phantom acquisition in which 82Rb from a 82Sr/82Rb generator infusion system (Bracco Diagnostics Inc, Princeton, NJ, USA) was delivered to a phantom during the PET acquisition. The infusion system was calibrated such that a 925 MBq requested dose yielded a 925 MBq delivery. A 20 cm diameter, water-filled cylinder was placed vertically, i.e. its axis normal to the scanner axis, on the scanner’s patient table, so that 82Rb could be infused through the fill port. A 68Ge cylinder with a 60 mm diameter and 150 mm length (UPET05, Eckert and Ziegler, Valencia, CA, USA) was positioned adjacent to the water-filled cylinder to serve as a reference source with activity that should be essentially constant over the duration of the acquisition. Separate, sequential studies were acquired over a range of requested 82Rb doses: 370, 740, 1110 and 1480 MBq. For each of these four acquisitions, the scanner acquisition was started at the time the start button on the infusion was pressed and list-mode events were acquired for 10 min, with a minimum of a 10 min gap between injections.
The data were divided into a dynamic sequence with uniform, 15 s duration frames, and the frames were independently reconstructed. Regions corresponding to the 82Rb and 68Ge portions of the image were determined by fitting each voxel to a decaying exponential; the radionuclides were conveniently and readily differentiated by comparing fit parameters to their known half-lives, and background voxels were identified by their low amplitude and were then excluded. A decaying exponential was fit to the 82Rb data after 2 min, i.e. after the completion of tracer infusion and mixing, and the 68Ge was expected to maintain a constant activity throughout the sequence.
In a separate experiment to examine the stability of timing and energy resolution at high count rates, a 3 mL syringe (8.7 mm inner diameter) containing 1.97 GBq, at scan start, of 11C was centered in the FOV and imaged. The syringe was fastened to a foam block on the scanner’s patient table. PET data were collected in 15 s acquisitions spaced over 210 min, followed by a final, 180 min duration acquisition. For each acquisition and also at several time points extracted from the final list, the time difference and energy values of the coincidence events were accumulated into histograms and those histograms’ FWHMs were calculated.
2.5. CQIE tests
We also evaluated the scanner according to the acquisition guidelines used in the ACR phantom and qualification through the National Cancer Institute’s Centers of Quantitative Imaging Excellence (CQIE) program (MacFarlane 2006, Scheuermann et al 2009). For ACR, the recommended phantom with PET faceplate (Jaszczak Deluxe Flangeless ECT phantom, Data Spectrum) containing fillable cylinders of 8, 12, 16 and 25 mm diameter and air-, water- and polytetrafluoroethylene-filled, 25 mm cylinders was used. The phantom background was filled with 26.3 MBq (at scan start) 18F-FDG. A PET scan was performed with a duration of 120 s per bed position, as is our clinical standard for patients weighing between 150 and 200 lb. Images were evaluated qualitatively for contrast, uniformity and spatial resolution. Standardized uptake values (SUVs) were evaluated for both the phantom background and the fillable cylinders (ACR 2011). For CQIE, we followed the instructions from the ACRIN PET core lab (ACRIN 2013). Briefly, a 20 cm diameter, 30 cm long uniform cylinder was filled with 75.5 MBq, at scan start, 18F-FDG solution and then mixed. First, a two-bed-position scan was performed with 90 s duration per bed position and was then reconstructed into a single image volume. Next, a single-bed-position scan was performed with a 25 min duration, and the data were reconstructed in a dynamic sequence with frames 16 × 5 s+7 × 10 s+5 × 30 s + 5 × 60 s + 5 × 180 s. The 4 mm, body reconstruction protocol described above was used for all scans. Cylindrical ROIs were drawn on each cylinder of the ACR phantom image, and the mean activity concentration was recorded. A circular ROI was drawn on each transverse slice of the CQIE phantom image except for the first three and last three slices which were ignored per the manufacturer’s recommendations, and the mean activity concentration was recorded. The volume-averaged activity concentration was calculated for the two-bed-position image and also for each frame of the dynamic sequence.
3. Results
3.1. Detector resolution, sensitivity and count rate
The calculated spatial resolution and sensitivity values are shown in table 1. Each point source position was within a 3 mm radius from the desired position, as measured by its 3D centroid in the image. The centered and 10 cm off-center sensitivities were 7.39 counts s−1 kBq−1 (cps kBq−1) and 7.28 cps kBq−1. The randoms fraction in the sensitivity data was 9.9%. The slice sensitivity profiles are triangular, as shown in figure S1 (supplementary data are available from stacks.iop.org/PMB/59/3843/mmedia), as is expected in a scanner with a 3D geometry and no axial-angle restriction. The timing and energy resolutions measured using the capillary source were 502 ps FWHM and 56.8 keV FWHM, respectively.
Table 1.
Scanner performance characteristics.
| Spatial resolution | mm FWHMa | mm FWTMa | |
|---|---|---|---|
| 10 mm | Transverse | 4.84 ± 0.13 | 9.79 ± 0.16 |
| Axial | 4.73 ± 0.07 | 9.67 ± 0.18 | |
| 100 mm | Radial | 5.25 ± 0.16 | 10.55 ± 0.53 |
| Tangential | 5.01 ± 0.07 | 10.08 ± 0.15 | |
| Axial | 5.23 ± 0.37 | 10.48 ± 0.60 | |
| Sensitivity | |||
| Centered | 7.39 cps kBq−1 | ||
| 100 mm | 7.28 cps kBq−1 | ||
| Energy resolution | 56.8 keV (11.1%) | ||
| TOF difference resolution | 502 ps | ||
FWHM: Full-width at half-maximum; FWTM: Full-width at tenth-maximum.
Mean ± SD of three experiments.
3.2. Count rate
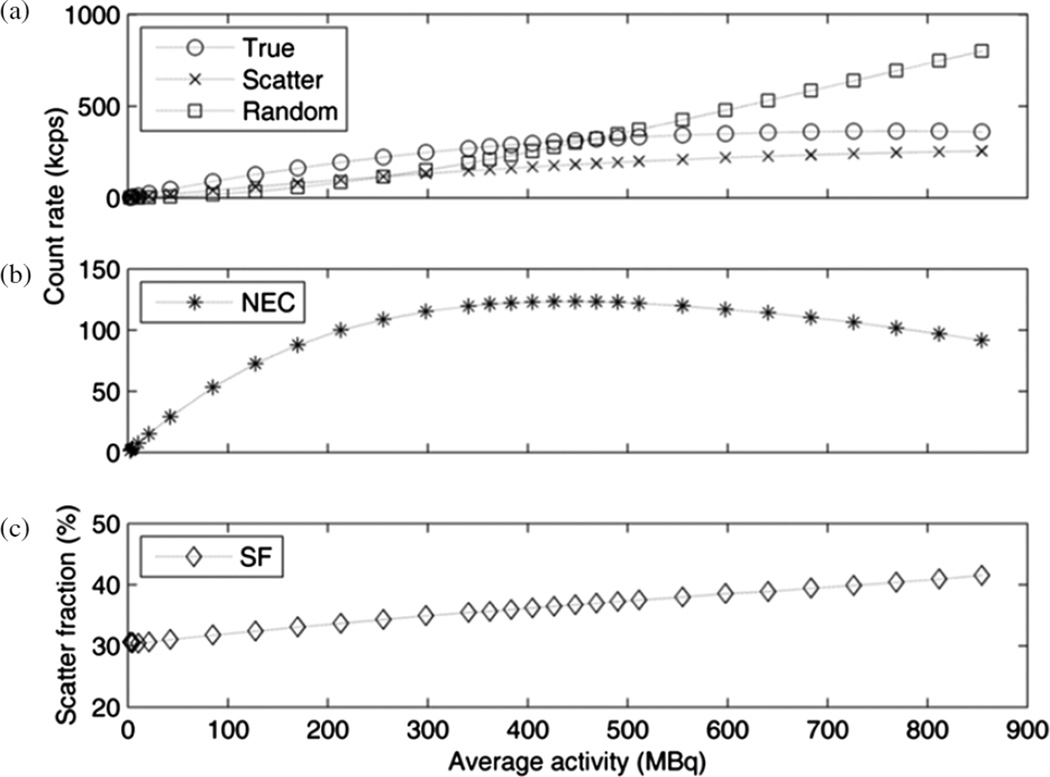
Count rates, measured using the NEMA scatter phantom, are shown in figure 1. The maximum NECR was 124 100 cps (124.1 kcps) when there was 447 MBq (20.3 kBq mL−1) in the phantom. The maximum true event rate was 364.5 kcps, measured with 769 MBq (35.0 kBq mL−1) in the phantom. The scatter fraction was 36.7% at peak NECR and ranged from 30.4% at low count rates up to a maximum of 41.5% at a singles rate of 77 Mcps.
Figure 1.
(a) True, scatter and random curves calculated according to NEMA NU 2– 2007; (b) noise-equivalent count rate; (c) scatter fraction.
3.3. Image quality
The aliquots obtained during phantom filling contained 5.9 kBq mL−1 (background) and 21.2 kBq mL−1 (spheres) corrected to the start of acquisition, so that the actual contrast ratio was 3.59. Analysis of images with two bed positions using 600 s of data duration per bed position, i.e. a low-noise situation, allowed focus on various contrast-recovery metrics which assess the partial volume effects as well as the accuracy of activity concentration in images. The contrast RC (equation (1)), calculated using each of Cmax, C50 and C3D, as well as the percent contrast QH (equation (2)), are shown in table 2.
Table 2.
Contrast recovery for spheres in the anthropomorphic phantom, 600 s data duration per bed position, calculated using different methods. The true activity concentration was 21.2 kBq mL−1 and the true contrast was 3.59.
| Diameter (mm) |
Body | Body-detail | Body-detail + PSF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QH | RCmax | RC3D | RC50 | QH | RCmax | RC3D | RC50 | QH | RCmax | RC3D | RC50 | |
| 37 | 0.68 | 1.03 | 0.72 | 0.87 | 0.72 | 1.10 | 0.79 | 0.89 | 0.81 | 1.21 | 0.86 | 1.00 |
| 28 | 0.68 | 1.03 | 0.70 | 0.87 | 0.72 | 1.10 | 0.76 | 0.90 | 0.84 | 1.27 | 0.85 | 1.05 |
| 22 | 0.63 | 1.01 | 0.65 | 0.84 | 0.66 | 1.03 | 0.72 | 0.86 | 0.80 | 1.27 | 0.83 | 1.05 |
| 17 | 0.58 | 0.98 | 0.57 | 0.78 | 0.58 | 0.98 | 0.66 | 0.82 | 0.74 | 1.34 | 0.76 | 1.06 |
| 13 | 0.46 | 0.74 | 0.51 | 0.64 | 0.58 | 1.02 | 0.65 | 0.81 | 0.73 | 1.23 | 0.74 | 0.96 |
| 10 | 0.17 | 0.40 | 0.37 | 0.38 | 0.38 | 0.75 | 0.50 | 0.62 | 0.39 | 0.74 | 0.52 | 0.63 |
QH: Percent contrast calculated from the mean in a 2D region, as in NEMA NU 2–2007.
RCmax: Ratio of measured Cmax to the true activity concentration.
RC3D: Ratio of measured C3D to the true activity concentration.
RC50: Ratio of measured C50 to the true activity concentration.
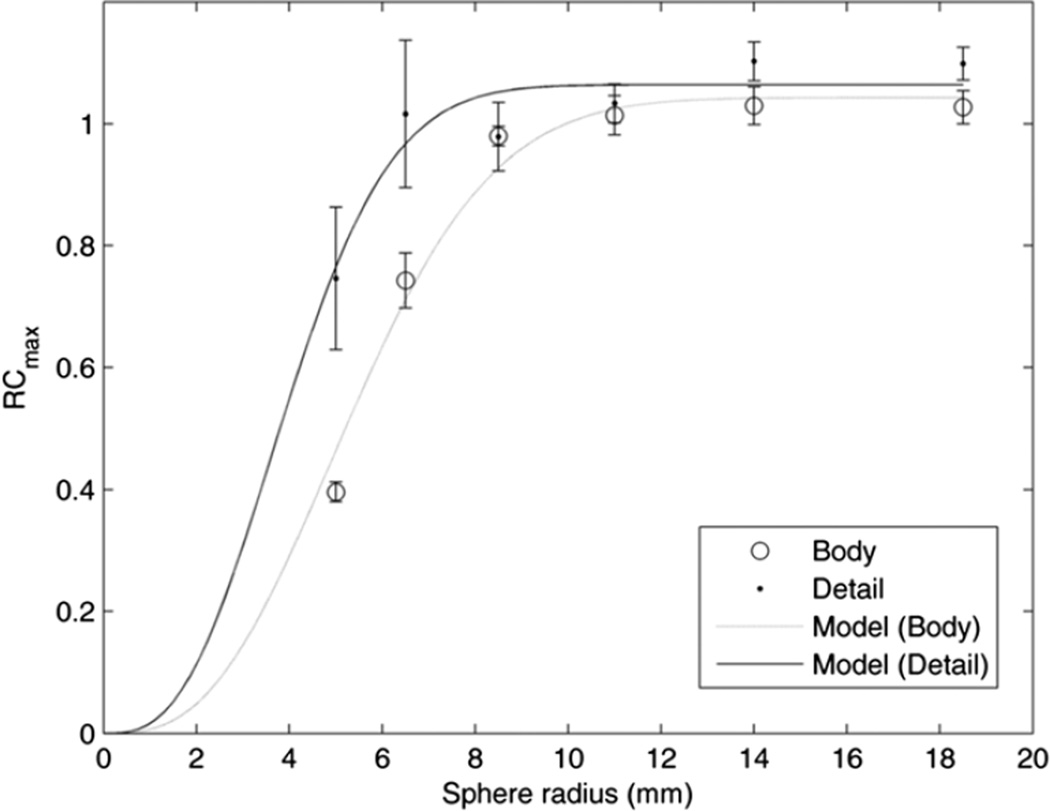
We then generated replicate lists and images in order to measure the variation of the contrast RCs as well as the sphere and background activity concentrations. Using three replicates with 300 s duration, we calculated the mean and maximum activity concentrations in the spheres in each replicate image using a 3D region the size of the sphere. The results are shown in figure 2, along with the theoretical RCmax calculated by integrating a 3D Gaussian (Kessler et al 1984). The 4 mm reconstruction best matches the 3D Gaussian model with a resolution of 8.1 mm FWHM and a maximum RCmax = 1.04. The 2 mm reconstruction best matches a resolution of 6.0 mm FWHM with a maximum RCmax = 1.06.
Figure 2.
RCmax for spheres and background regions, for the 4 mm, whole-body (circles) and the 2mmbody-detail (dots) reconstructions, both with 300 s duration. Error bars are ±SD of three replicates. The best-fit resolution curves are shown, whose resolutions are 6.0 mm FWHM (body-detail) and 8.1 mm FWHM (body).
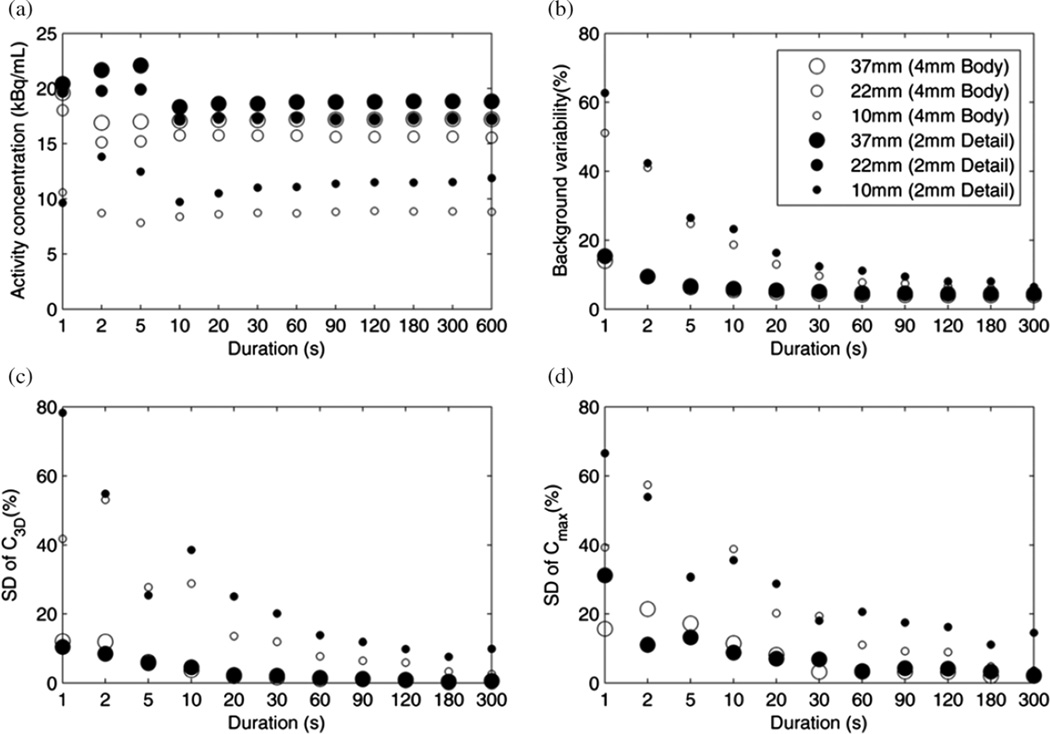
We then analyzed the data from the different data durations obtained by dividing the original list data into replicates, as described in section 2; the results are shown in figure 3. The mean sphere activities (C3D) remained within 10% of those with the full duration, down to 2 s duration with the body reconstruction and down to 20 s duration with the body-detail reconstruction. BV increased with smaller region size and lower scan duration, but did not depend on the reconstructed voxel size. Precision, as characterized by calculating the SD among the replicates of Cmax and C3D, improved with increasing duration, larger reconstructed voxel size and increasing sphere size.
Figure 3.
Spheres phantom measurements for different simulated scan durations. (a) Activity concentration C3D for 10 mm, 22 mm and 37 mm spheres (small, medium and large markers), with 4 mm (open circles) and 2 mm (filled circles) reconstructions. (b) NEMA background variability decreased with increasing scan duration. (c) Precision, i.e. relative SD among replicates of C3D and (d) Cmax.
3.4. Dynamic range
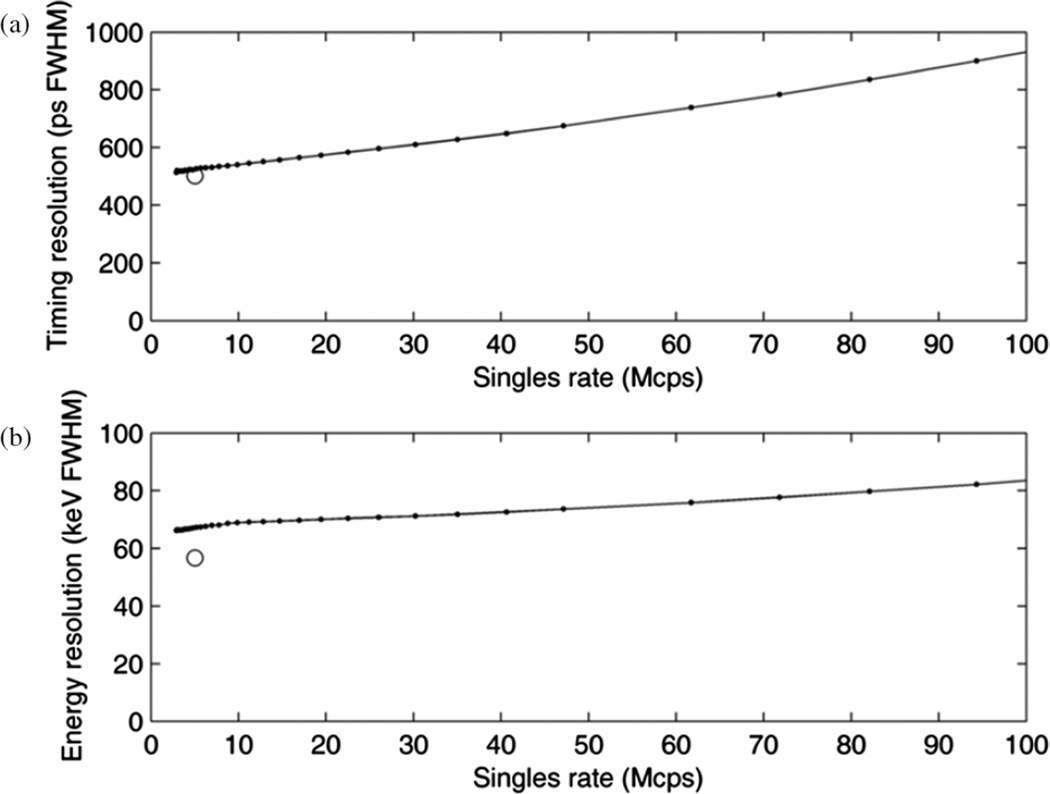
Timing and energy resolution measured using the 11C source vary with count rate, as shown in figure 4. The initial singles rate (with 1.97 GBq) reported by the scanner was 230 × 106 cps (230 Mcps). A time difference resolution of 514 ps FWHM was measured with the 11C source at a low singles rate of 3.9 Mcps. This was slightly larger than the 502 ps FWHM measured with the 18F capillary source. This difference is consistent with the larger physical size of the 11C source. As noted previously in table 1, an energy resolution of 11.1% was measured with the capillary source, whereas the energy resolution at low count rate measured with the 11C syringe source was 13.0%. As expected, the energy resolution increased with count rate, as shown in figure 4(b).
Figure 4.
TOF difference resolution (a) and energy resolution (b) over a range of singles rates. Two experiments are shown, i.e. the 8.7 mm diameter, 11C syringe (connected dots) and the 1 mm diameter, 18F capillary (open circle).
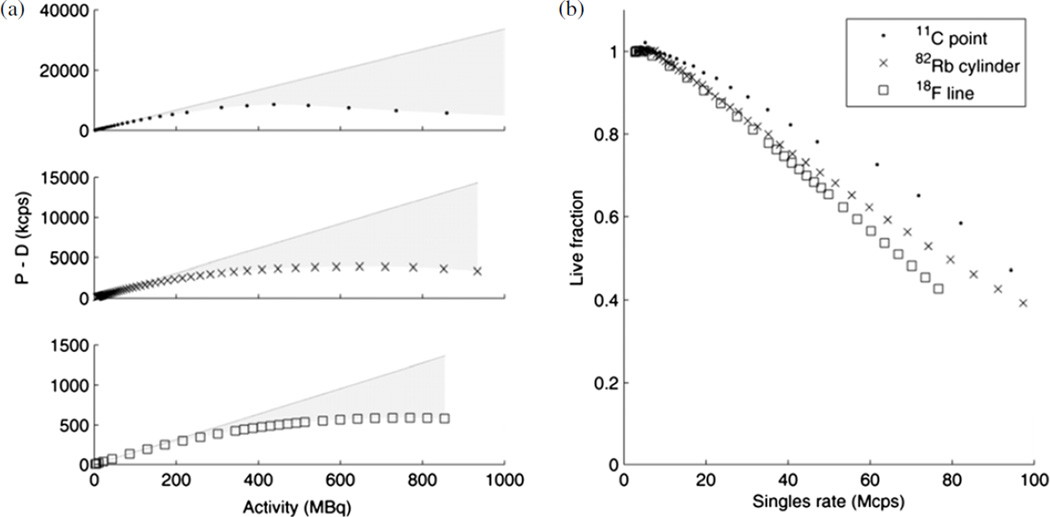
The 82Rb infusions with requested activities of 370, 740, 1110 and 1480 MBq resulted in activities at the end of infusion of 363 MBq (18 s infusion duration), 677 MBq (24 s), 921 MBq (36 s) and 1066 MBq (72 s), respectively, as reported by the infusion generator and confirmed by the detected singles rates. Live-time fractions (the fraction of the time the system is available for counting, i.e. one minus dead-time fraction) were calculated from each of the three decay series experiments, i.e. the 82Rb/68Ge fillable and solid phantoms, the 11C syringe and the 18F NEMA scatter phantom data. The linear extrapolations fit to low-activity data points are shown in figure 5(a) in which the shaded area above each of the measured curves represents the possible events lost to dead time. The singles or coincidence sensitivity differed for each phantom experiment, as expected from their different geometries and as indicated by the different slopes in figure 5(a). The three phantoms’ live fraction, i.e. the fraction of possible events detected, differed but decreased smoothly according to the singles rate, as shown in figure 5(b).
Figure 5.
(a) Randoms-corrected (prompts–delays) coincidence rates for 18F, 82Rb and 11C phantoms. A line is extrapolated from the low-activity data points of each phantom, and the shaded area between the line and the measured data is an approximation of the lost counts. (b) Live fraction is the fraction of events that are detected, i.e. the ratio of the data to the extrapolated line.
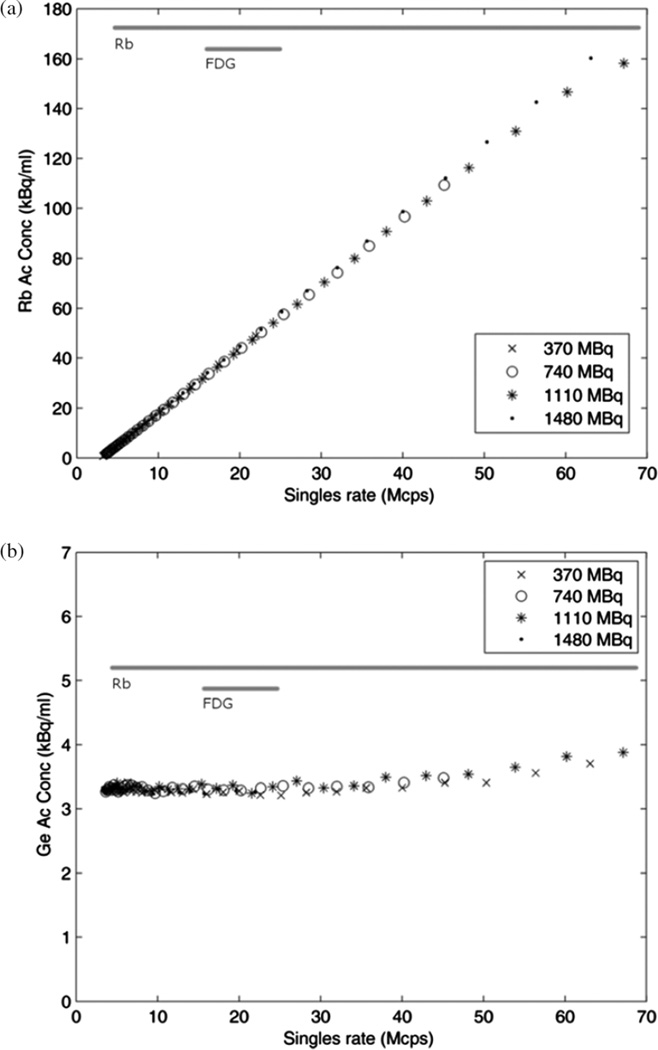
Considering each of the four infusions, the activity concentration in the 82Rb region of the image was consistent among the acquisitions and linear from low activity up to a singles rate of approximately 65 Mcps, as shown in figure 6(a). Figure 6(b) shows the activity concentration measured in the 68Ge region which is constant up to a singles rate of 40 Mcps and then increases slightly to a maximum at 65Mcps (13% higher than at low count rates), presumably reflecting an over-correction for count losses.
Figure 6.
(a) Image-measured activity concentration of 82Rb region in four phantom experiments with different starting activities, and (b) of the 68Ge region. Horizontal bars indicate typical ranges of singles rate in clinical scans, narrow for 18F-FDG and wide for dynamic, 82Rb data.
3.5. CQIE tests
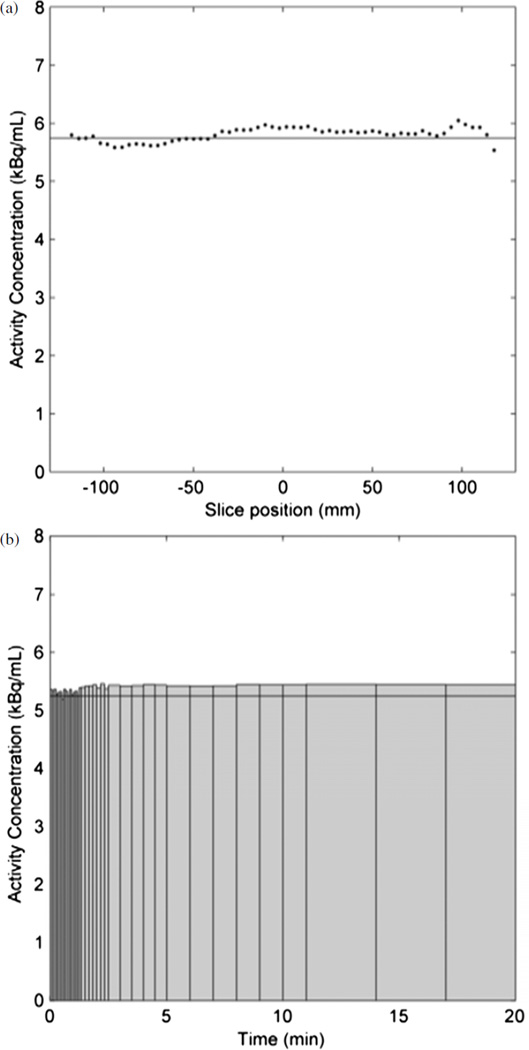
In the qualitative evaluation of the ACR phantom, all four, fillable cylinders were readily seen. Four of the six resolution objects were also seen. Image uniformity was good and no artifacts were seen. Representative, single, 4 mm thick, transverse slices of the spheres and rods sections are shown in figure S2 (supplementary data are available from stacks.iop.org/PMB/59/3843/mmedia). In the uniform phantom, the accuracy of the activity concentration and the variation among frames were calculated; the mean activity concentration in the two-bed-position image, ignoring the three slices at each end of the volume, was 0.6% lower than that measured from the phantom aliquot, i.e. a volume-averaged SUV of 0.99. The slice mean activity concentrations in the static scan, figure 7(a), ranged from 0.99 to 1.04, and the frame mean activity concentration in the dynamic image, figure 7(b), ranged from 0.96 to 1.05, of that measured from the phantom aliquot.
Figure 7.
(a) Mean activity concentration per slice in the uniform phantom in the two bed position scan; (b) mean activity concentration in each frame of the dynamic scan, decay-corrected to the first frame; bar widths represent frame duration. Horizontal lines indicate the true activity concentrations.
4. Discussion
As many of the physical characteristics of the detector are similar to those of the Gemini TF, the NEMA sensitivity, spatial resolution and count rates were compared to the measurements from Surti (Surti et al 2007), given in parentheses following our results. The average spatial resolution agreed at the center, 4.8 ± 0.1 (4.8) mm FWHM, and at 10 cm, 5.1 ± 0.1 (5.1) mm FWHM. The sensitivity was 7.3 (6.6) cps kBq−1, thus indicating that the reduced, 4.5 ns hardware coincidence window did not decrease the trues sensitivity. We noted that our new measurement was similar to other Gemini TF published values of 7.4 and 7.0 (Kolthammer and Surti 2009,Muzic and Kolthammer 2006). The peak NECR was 124 kcps at 20.3 BqmL−1 (125 kcps at 17.4 kBq mL−1). The Peak Trues rate, 365 kcps at 35.0 kBq mL−1 (274 kcps at 17.4 kBq mL−1), exemplifies the higher count throughput of Ingenuity TF compared to Gemini TF. As shown in figure 1, the count rate peak is also broader, i.e. the range of activity for which the NECR is above 90% of its peak value spans 368 MBq, from 241 to 609 MBq (163 MBq, from 275 to 438 MBq), of particular importance for scans spanning a wide range of activity. The scatter fraction had a minimum value of 30.4% and increased with activity (figure 1(c)), in tandem with the decrease in precision of the energy measurement and which resulted in a gradual increase in energy resolution (figure 4(b)).
There are several results of our analysis of the spheres phantom which may be useful for our understanding of clinical hotspot imaging. The three reconstruction protocols used represent the likely range of processing methods used in our clinical practice: from general-purpose, whole-body reconstruction with 4 mm voxels to body-detail reconstructions with 2 mm voxels and PSF compensation. The differences in contrast recovery, e.g. QH ranging from 0.17 to 0.39 for a 10 mm sphere (table 2), are important to note when interpreting clinical SUV measurements of small lesions. PSF compensation offered additional contrast recovery, although the PSF RCmax values greater than one suggest a positive bias in the sphere activity concentrations (table 2). This finding may reflect the sensitivity of the RCmax metric to spurious pixel values and suggest the use of other than ‘max’ metrics. Indeed, Boellaard (2011) also saw RCs exceed one when they were derived from SUV max values. The effective image spatial resolution, as assessed by fitting an integrated Gaussian model to RCmax, was found to be 8.1 mm FWHM and 6.0 mm FWHM from the body and body-detail reconstructions, respectively (figure 2); this spatial resolution metric is more directly relatable to clinical imaging than the detector resolution values measured using a point source in air. These results also indicate that the body-detail reconstruction protocol available on the scanner does indeed provide higher spatial resolution than the default body protocol. Generating and analyzing replicate images of a standard image quality phantom was useful, in that we were able to explicitly measure the SD of the activity concentration measured in a 3D region, and which ranged from 78% of the mean among replicates in a small sphere with the body-detail reconstruction and 1 s data duration to <1% in a large sphere for durations longer than 90 s. Importantly, this SD represents the variability in pixel values that would be expected if the phantom study could be exactly repeated and thus indicates the effect of the reconstruction protocol and feature size on the precision of activity concentration measurements such as SUV3D and SUVmax.Although the SD represents the uncertainty of a single SUV measurement, the values shown in figure 3(a) are means among the replicate images, so their uncertainty is smaller than the SDs in figure 3(c).
We investigated the operational range of the scanner with the objective of performing 82Rb-PET based myocardial blood flow measurements, in particular using 925 MBq infusions so that the same data can be used to generate conventional static and gated perfusion images (Dilsizian et al 2009), and which leads to an average peak singles rate of approximately 65 Mcps. Energy resolution increases from 57 keV FWHM at 3 Mcps singles to 76 keV at 65 Mcps singles (figure 4(b)), thus corresponding to an increase in SF from 30.4% to 38.0% (figure 1(c)), and which remains well within the range typically obtained in modern PET imaging. Time difference resolution increases over this range (figure 4(a)). As the effective sensitivity gain due to TOF depends on timing resolution (Karp et al 2008), the effective sensitivity gain thus decreases relative to that at low count rates. Because the correct (i.e. degraded) TOF resolution is used in reconstruction, no other effects of the timing degradation are expected. In the low-activity region in which the effective sensitivity gain of TOF would likely be most needed to compensate for low counts, the timing resolution is close to 500 ps. Although we measured time difference resolution and energy resolution using small sources, we expect that the detector’s performance is similar when using extended sources, as both characteristics are determined by how an individual detector handles an individual annihilation photon. The live fraction decreased smoothly (figure 5) with increasing singles rate for the three decay-series experiments. We attribute differences among the three experiments to the difference in source geometry, which would differ in their scatter and attenuation characteristics and impact the relative rates of singles and coincidences. We explicitly measured the quantitative linearity of the pixel values by positioning a 68Ge phantom adjacent to a 82Rb phantom, showing a wide linear range and in which both phantom regions show a linear response from a low rate up to 65 Mcps singles.
5. Conclusions
The system we evaluated showed similar sensitivity, spatial resolution and peak NECR to its predecessor, Gemini TF (Surti et al 2007). Improved dynamic range was demonstrated by a broader peak in the NECR curve as well as linear reconstructed image activity concentration in a combined 82Rb and 68Ge phantom experiment. By reconstructing replicate images of a spheres phantom, we were able to explicitly study the precision of activity concentration measurements with different acquisition durations and to also evaluate the effect of reconstruction on image spatial resolution. Overall, the system performance is suitable for application in high-countrate PET applications.
Acknowledgments
We would like to thank Patrick Wojtylak CNMT, Andres Kohan MD and Matt Smith for their help with data acquisition and Benjamin Lorman for his help with data processing and reconstruction. Angela Da Silva, PhD and Piotr Maniawski, MS provided technical review, and Bonnie Hami, MA provided editorial assistance in the preparation of the manuscript. This work was supported in part by an Ohio Third FrontierMedical Imaging Program grant (TECH 11-046) from the State of Ohio Department of Development.
Footnotes
Online supplementary data available from stacks.iop.org/PMB/59/3843/mmedia
References
- ACR. PET phantom instructions for evaluation of PET image quality. Reston, VA: American College of Radiology; 2011. [Google Scholar]
- ACRIN. ACRIN PET/CT Qualification Instructions. Philadelphia, PA: American College of Radiology Imaging Network; 2013. [Google Scholar]
- Boellaard R. Need for standardization of 18F-FDG PET/CT for treatment response assessments. J. Nucl. Med. 2011;52(Suppl. 2):93S–100S. doi: 10.2967/jnumed.110.085662. [DOI] [PubMed] [Google Scholar]
- Boellaard R, et al. FDG PET and PET/CT: EANM procedure guidelines for tumour PET imaging: version 1.0. Eur. J. Nucl. Med. Mol. Imaging. 2010;37:181–200. doi: 10.1007/s00259-009-1297-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casey ME, Hoffman EJ. A technique to reduce noise in accidental coincidence measurements and coincidence efficiency calibration. J. Comput. Assist. Tomogr. 1986;10:845–850. [PubMed] [Google Scholar]
- Curillova Z, Yaman BF, Dorbala S, Kwong RY, Sitek A, El Fakhri G, Anagnostopoulos C, Di Carli MF. Quantitative relationship between coronary calcium content and coronary flow reserve as assessed by integrated PET/CT imaging. Eur. J. Nucl. Med. Mol. Imaging. 2009;36:1603–1610. doi: 10.1007/s00259-009-1121-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daube-witherspoon ME, et al. PET performance measurements using the NEMA NU 2–2001 standard. J. Nucl. Med. 2002;43:1398–1409. (PMID: 12368380) [PubMed] [Google Scholar]
- deKemp R, Klein R, Lortie M, Beanlands R. Constant-activity-rate infusions for myocardial blood flow quantification with 82Rb and 3D PET. Proc. Conf. Record of the IEEE Nuclear Science Symposium and Medical Imaging Conf. 2006:3519–3521. [Google Scholar]
- Dilsizian V, Bacharach SL, Beanlands RS, Bergmann SR, Delbeke D, Gropler RJ, Knuuti J, Schelbert HR, Travin MI. PET myocardial perfusion and metabolism clinical imaging. J. Nucl. Cardiol. 2009;16:651. [Google Scholar]
- Griesmer JJ, Laurence T, Cooke S, Karp JS, Perkins AE, Kolthammer JA. Time-of-flight quality control for a new Philips Gemini PET/CT scanner. J. Nucl. Med. 2006;47:391P. [Google Scholar]
- Karp JS, Surti S, Daube-Witherspoon ME, Muehllehner G. Benefit of time-of-flight in PET: experimental and clinical results. J. Nucl. Med. 2008;49:462–470. doi: 10.2967/jnumed.107.044834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessler RM, Ellis JR, Eden M. Analysis of emission tomographic scan data: limitations imposed by resolution and background. J. Comput. Assist. Tomogr. 1984;8:514–522. doi: 10.1097/00004728-198406000-00028. [DOI] [PubMed] [Google Scholar]
- Klein R, Beanlands RSB, deKemp Ra. Quantification of myocardial blood flow and flow reserve: technical aspects. J. Nucl. Cardiol. 2010;17:555–570. doi: 10.1007/s12350-010-9256-9. [DOI] [PubMed] [Google Scholar]
- Kolthammer J, Surti S. Performance characteristics of a large-bore PET/CT scanner. J. Nucl. Med. 2009;50(Suppl. 2):1545. [Google Scholar]
- Lucy LB. An iterative technique for the rectification of observed distributions. Astron. J. 1974;79:745–754. [Google Scholar]
- MacFarlane CR. ACR accreditation of nuclear medicine and PET imaging departments. J. Nucl. Med. Technol. 2006;34:18–24. (PMID: 16517965) [PubMed] [Google Scholar]
- Matej S, Lewitt RM. 3D-FRP: direct fourier reconstruction with fourier reprojection for fully 3D PET IEEE Trans. Nucl. Sci. 2001;48:1378–1385. [Google Scholar]
- Meyer C, Weibrecht M. Variation of kinetic model parameters due to input peak distortions and noise in simulated Rb PET perfusion studies. Proc. Conf. Record of the IEEE Nuclear Science Symposium and Medical Imaging Conf. 2006:2703–2707. [Google Scholar]
- Muzic RF, Kolthammer JA. PET performance of the GEMINI TF: a time- of-flight PET/CT scanner. Proc. Conf. Record of the IEEE Nuclear Science Symposium and Medical Imaging Conf. 2006:1940–1944. [Google Scholar]
- NEMA. NEMA Standards PublicationNU2–2007: performance measurements of positron emission tomography. Rosslyn, VA: National Electrical Manufacturers Association; 2007. [Google Scholar]
- NEMA. Digital imaging and communications in medicine (DICOM) Rosslyn, VA: National Electrical Manufacturers Association; 2011. [Google Scholar]
- Popescu LM, Matej S, Lewitt RM, et al. Iterative image reconstruction using geometrically ordered subsetswith list-mode data. Proc.Conf. Record of the IEEE Nuclear Science Symposium and Medical Imaging Conf. 2004:3536–3540. [Google Scholar]
- Raylman R, Caraher JM, Hutchins GD. Sampling requirements for dynamic cardiac PET studies using image-derived input functions. J. Nucl. Med. 1993;34:440–447. PMID: 8441036. [PubMed] [Google Scholar]
- Richardson WH. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 1972;62:55–59. [Google Scholar]
- Scheuermann JS, Saffer JR, Karp JS, Levering AM, Siegel BA. Qualification of PET scanners for use in multicenter cancer clinical trials: the American college of radiology imaging network experience. J. Nucl. Med. 2009;50:1187–1193. doi: 10.2967/jnumed.108.057455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder DL, Miller MI. The use of sieves to stabilize images produced with the EM algorithm for emission tomography. IEEE Trans. Nucl. Sci. 1985;32:3864–3872. [Google Scholar]
- Surti S, Kuhn A, Werner ME, Perkins AE, Kolthammer JA, Karp JS. Performance of Philips Gemini TF PET/CT scanner with special consideration for its time-of-flight imaging capabilities. J. Nucl. Med. 2007;48:471–480. (PMID: 17332626) [PubMed] [Google Scholar]
- Wang W, Hu Z, Gagnon D. A new component approach to efficiency normalization for 3D PET. IEEE Trans. Nucl. Sci. 2007;54:92–99. [Google Scholar]
- Wang W, et al. Systematic and distributed time-of-flight list mode PET reconstruction. Proc. Conf. Record of the IEEE Nuclear Science Symposium and Medical Imaging Conf. 2006:1715–1722. [Google Scholar]
- Zaidi H, Ojha N, Morich M, Griesmer J, Hu Z, Maniawski P, Ratib O, Izquierdo-Garcia D, Fayad ZA, Shao L. Design and performance evaluation of a whole-body Ingenuity TF PET-MRI system. Phys. Med. Biol. 2011;56:3091–3106. doi: 10.1088/0031-9155/56/10/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziadi MC, Dekemp RA, Williams KA, Guo A, Chow BJ, Renaud JM, Ruddy TD, Sarveswaran N, Tee RE, Beanlands RS. Impaired myocardial flow reserve on rubidium-82 positron emission tomography imaging predicts adverse outcomes in patients assessed for myocardial ischemia. J. Am. Coll. Cardiol. 2011;58:740–748. doi: 10.1016/j.jacc.2011.01.065. [DOI] [PubMed] [Google Scholar]